Abstract
Neutron stars are remarkable natural laboratories that allow us to investigate the fundamental constituents of matter and their interactions under extreme conditions that cannot be reproduced in terrestrial laboratories. This chapter gives a brief pedagogical introduction to the physics of matter at very high densities (i.e. up to several times the density of atomic nuclei) that hopefully could be useful to researchers in pulsars’ astrophysics and related areas.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
9.1 Introduction
With central densities exceeding by several times the density of atomic nuclei (ρ 0 ≃ 2.6 × 1014 g∕cm3) neutron stars (NSs) are the densest macroscopic objects in the universe. They represent the limit beyond which gravity overwhelms all the other forces of nature and leads to the formation of a black hole. Neutron stars thus represent incomparable natural laboratories that allow us to investigate the constituents of matter and their interactions under extreme conditions that cannot be reproduced in any terrestrial laboratory, and to explore the phase diagram of quantum chromodynamics (QCD) in a region which is presently inaccessible to numerical calculations of QCD on a space-time lattice.
The global properties of NSs (mass, radius, maximum mass, maximum spin frequency, etc.) primarily depend on the equation of state (EoS) of strong interacting matter, i.e. on the thermodynamic relation between the matter pressure (P), the energy density (ε) and the temperature (T). The EoS of dense matter is also a basic ingredient for modeling various astrophysical phenomena related to NSs, as core-collapse supernovae and binary neutron star (BNS) mergers .
Determining the correct EoS model which describes NSs is a fundamental problem of nuclear physics, particle physics and astrophysics, and major efforts have been made during the last few decades to solve it by measuring different NS properties using the data collected by various generations of X-ray and γ-ray satellites and by ground-based radio telescopes.
The recent detection of gravitational waves from the binary neutron star mergers, GW170817 [1, 2] and GW190425 [3] is giving a big boost to the research on dense matter physics. Gravitational wave signals, from BNS inspiral and especially from the BNS post-merger phase, offer in fact a unique opportunity to test different dense matter EoS models. Gravitational wave astronomy thus opened a new window to explore matter under extreme conditions.
The accurate measurements of the masses,Footnote 1 M = 1.97 ± 0.04 M ⊙ [4] and M = 2.01 ± 0.04 M ⊙ [5], of the NSs in PSR J1614-2230 and PSR J0348+0432 respectively, and the recent mass measurement \(M = 2.14^{+0.10}_{-0.09} \, M_\odot \) [6] for the neutron star in the millisecond pulsar J0740+6620, have ruled out all the EoS models which cannot support such high values of stellar masses.
In principle, in a microscopic approach, the EoS of dense matter should be derived starting from the matter constituents and their mutual interactions using quantum theory of many-body systems (see e.g. [7]). This is a very ambitious goal, and its level of difficulty depends on what degrees of freedom (constituents particles) we chose to describe dense matter and on how we model their mutual interactions (particularly the strong interaction).
Due to the large values of the stellar central density, various particle species and phases of dense matter are expected in NS interiors. In particular various “exotic” constituents, as for example hyperons, or a phase with deconfined quarks, are expected in neutron star interiors. Thus different types of “neutron stars” (nucleon stars , hyperon stars , hybrid stars , strange stars ) are hypothesized to exist.
In this chapter, we do not discuss the techniques to constrain “neutron star” EoS models, which can be found in several existing reviews (e.g., [8,9,10]).
9.2 Neutron Star Physics in a Nutshell: Basic Concepts
As we already mentioned in Sect. 9.1, different particle species and different phases of dense matter are expected in neutron star interiors. This can be understood by the following basic arguments.
-
1.
Gravity holds matter together at increasingly high density as one moves from the neutron star surface to its center. Thus gravity acts as a piston to compress matter at extreme densities.
-
2.
Stellar constituents are different species of identical fermionsFootnote 2 (n, p, …., e −, μ −), consequently they must have an antisymmetric wave function for particle exchange. Thus, in the non-interacting quasi-particle approximation, the particles for each fermionic species must obey the Pauli principle . As a consequence their chemical potentials (μ n, μ p, …., μ e, μ μ) are rapidly increasing function of the density.
-
3.
Finally the weak interaction change the isospin and strangeness content of dense matter to minimize the energy per baryon of the system.
Thus following Harrison et al. [11] (see also [12]) by catalyzed matter , we mean matter at baryon number density n, in which the baryons and leptons abundances (Y i = n i∕n) are such as to absolutely minimize the total energy per baryon (ε∕n). Such matter is in equilibrium with respect to the strong and weak (“chemical equilibrium”) interactions.Footnote 3 For a multicomponent system in chemical equilibrium, the abundances of its constituents are fixed uniquely by two thermodynamic variables, e.g. by the baryon number density n and the total entropy per baryon s. The EoS can then be expressed as:
where ρ = ε∕c 2 is the total mass density, inclusive of rest–mass density ρ 0 = ε 0∕c 2. The total energy density is denoted as ε = ε 0 + ε ′ and the internal energy density ε ′ includes the total kinetic energy density of all the particles plus the potential energy density due to the interactions among the particles of the system (this potential energy density does not include the gravitational potential energy density). Finally P is the total pressure.
In addition, one must know how the entropy per baryon depends on the baryon number density. Then one gets a one-parameter EoS
to be used to solve the stellar structure equations in general relativity.
A neutron star cools, within a few hours after birth, to temperatures in the range of 107–109 K [15]. These temperatures are very small when compared to nuclear matter energy scale (Fermi energies). Typical values for the Fermi energy in the core of a neutron star are of the order of tens to hundreds MeV (as the density increases going towards the center).Footnote 4 Then we assume s(n) = 0 (or equivalently T(n) = 0) within the whole star. We refer to such a state of matter as cold catalyzed matter .
The first theoretical calculation of the structure of a neutron star was performed in 1939 by J. Robert Oppenheimer and George M. Volkoff [16]. At that time, the theoretical and experimental investigation of the nuclear force was just at the beginning. The Yukawa’s theory on the nuclear interaction based on meson exchange dates from 1935. But the important feature of a strong short distance repulsion between two nucleons was recognized only at the beginning of 1950s. Moreover, the first systematic experimental data on the phase shifts measured in nucleon-nucleon (NN) scattering experiments, and the first phenomenological NN potentials where available only in the late 1950s (for an historical outline on the early stages of the concept of nuclear forces see ref. [17]).
In view of this poor knowledge of the nuclear interaction, Oppheneimer and Volkoff disregarded it completely and assumed in their calculation [16] the EoS of an ideal relativistic Fermi gas of neutrons. This extreme approximation reveals the main features of neutron stars’ properties. The most important of these features is the existence of a maximum possible mass for neutron stars, which according to the Oppenheimer–Volkoff calculations is M max = 0.71M ⊙.
In the following, before we undertake our main task, regarding the influence of the strong interaction on the equation of state of dense matter and on neutron stars’ structure, we imagine to “switch off” the strong interaction and focus on the role played by the weak interaction and the Pauli principle on dense matter physics.
9.2.1 The Role of Weak Interaction and Pauli Principle
An isolated neutron is unstable with respect to the decay process
having a mean life τ = (880.2 ± 1.0) s ∼ 14 min 40 s. The neutron decay is caused by the weak interaction and releases an energy Q = (m n − m p − m e)c 2 ≃ 0.78 MeV which is shared by the three particles in the final state.
Consider now a system of stable Footnote 5 non-interacting neutrons with a given baryon number density n n.
What happens to the system if we “turn on” the weak interaction?
Do all neutrons decay to protons, electrons and electron-type anti-neutrinos?
The answer is yes, but below a threshold baryon density n ∗ that we will evaluate in the next pages. For densities above n ∗ the neutron decay process (9.4) is Pauli-blocked and the system will reach an equilibrium configuration with appropriate concentrations Y i of the different particles.
9.2.1.1 Inverse β-decay
To answer the above questions consider a system of protons and electrons with number densities n p = n e (i.e. an electric charge neutral system), and neglect both the electromagnetic interactions between the particle and the strong interaction between protons. We refer to this system as an ideal {p, e −}-gas. We want to calculate the value n ∗ of the baryon density above which the inverse β-decay process
is energetically possible. We consider protons and neutrons as two ideal non-relativistic gases and electrons as an ideal ultra-relativistic gas (i.e. we neglect the electron rest mass).Footnote 6 Under these conditions the chemical potential μ p for protons (inclusive of its rest energy) can be written as:
where \(k_{F_p}\) (the Fermi momentum of protons in units of the reduced Plank’s constant ħ) is related to the proton number density n p by the equation
The electron chemical potential is given by \(\mu _e = \hbar c k_{F_e}\), where the electron Fermi momentum \(k_{F_e}\) is related to the electron number density n e by an equation similar to eq. (9.7). The threshold density n ∗ for the inverse β-decay (9.5) is set by the condition
which is valid for the neutrino–free matter (\(\mu _{\nu _e} = \mu _{{\bar \nu }_e} = 0\)).Footnote 7
The charge neutrality condition implies \(k_{F_p} = k_{F_e}\,\), thus the threshold density condition can be written as
As we have already supposed (and we can verify a posteriori) at these densities protons are non relativistic, thus \( \frac {\hbar }{m_p c} k_{F_p} << 1\), consequently from the previous equation the threshold value for the proton Fermi momentum is
The corresponding threshold baryon density is thus \(n_p^* \simeq 0.944 \times 10^{31} \mathrm {cm^{-3}} = 9.44 \times 10^{-9}~\mathrm {fm^{-3}}\) and the threshold mass density is \(\rho ^* \simeq m_p n_p^* \simeq 1.58 \times 10^7\,\mathrm {g/cm^3}\).
A more accurate determination of the inverse β-decay threshold density can be obtained considering fully relativistic electrons, i.e. considering the effect of the electron rest mass on their chemical potential (\(\mu _e = [(\hbar c k_{F_e})^2 + (m_e c^2)^2 ]^{1/2}\)). In this case one has:

where  is the electron reduced Compton’s wave length. Thus one has \(\rho ^* \simeq m_p n_p^* \simeq 1.22 \times 10^7\,\mathrm {g/cm^3}\).
is the electron reduced Compton’s wave length. Thus one has \(\rho ^* \simeq m_p n_p^* \simeq 1.22 \times 10^7\,\mathrm {g/cm^3}\).
9.2.1.2 β-stable Nuclear Matter
Consider now a system of ideal non-relativistic neutrons and protons (with number densities n n and n p respectively) and ideal ultra-relativistic electrons (with density n e): ideal {n, p, e −}-gas. The equilibrium conditions for the weak processes (9.4) and (9.5) and the charge neutrality condition can be written as
where, as before, we consider neutrino–free matter. At nucleon densities n = n n + n p which are much larger than the threshold density n ∗ for the inverse β decay processes, we can neglect the neutron-proton mass difference. In this case from Eqs. (9.12) and (9.13) one can easily obtain the proton fraction Y p = n p∕n in β-equilibrium as the solution of the following equation:

where  is the nucleon reduced Compton’s wave length, with m
N = 938.92 MeV∕c2 being the average nucleon mass. For example at nuclear matter saturation density n
0 = 0.16 fm−3 one has Y
p ∼ 0.005, whereas at n = 5n
0 = 0.8 fm−3 one has Y
p ∼ 0.021. Thus up to several times the nuclear saturation density n
0, the ideal {n, p, e
−}-matter is almost pure neutron matter, as assumed by Oppenheimer and Volkoff in their paper [16].
is the nucleon reduced Compton’s wave length, with m
N = 938.92 MeV∕c2 being the average nucleon mass. For example at nuclear matter saturation density n
0 = 0.16 fm−3 one has Y
p ∼ 0.005, whereas at n = 5n
0 = 0.8 fm−3 one has Y
p ∼ 0.021. Thus up to several times the nuclear saturation density n
0, the ideal {n, p, e
−}-matter is almost pure neutron matter, as assumed by Oppenheimer and Volkoff in their paper [16].
As we will discuss in some detail in the following pages, the nuclear interaction substantially modifies the composition of matter, producing a much larger proton fraction in β-stable nuclear matter.
9.2.1.3 The Muon Threshold
An isolated muon (m μ = 105.658 MeV∕c2) is unstable with respect to the weak decay process
having a mean life τ = 2.197 × 10−6 s.
In dense {n, p, e −}-matter, when the electron chemical potential μ e is sufficiently high, it is energetically convenient to turn electrons into muons via the weak process
To calculate the threshold density for muons’ appearance in dense matter, we consider a charge neutral ideal {n, p, e −}-gas in a regime where neutrons and protons are non-relativistic and electrons ultra-relativistic. We further consider neutrino–free matter i.e. \(\mu _{\nu _e} = \mu _{{\bar \nu }_e} = \mu _{\nu _\mu } = \mu _{{\bar \nu }_\mu } = 0\).
The threshold density for muons’ appearance is set by the condition:
Thus, at threshold, the electron Fermi momentum \(k_{F_e}\) must be equal to the inverse muon reduced Compton’s wave length  . The charge neutrality condition n
p = n
e (at threshold n
μ = 0) implies \(k_{F_p} = k_{F_e}\), and the chemical equilibrium between neutrons, protons and electrons gives μ
n − μ
p = μ
e.
. The charge neutrality condition n
p = n
e (at threshold n
μ = 0) implies \(k_{F_p} = k_{F_e}\), and the chemical equilibrium between neutrons, protons and electrons gives μ
n − μ
p = μ
e.
For ideal non-relativistic neutron and proton gases, and neglecting the neutron-proton mass difference one thus gets:
which can be rewritten in terms of the total nucleon density n = n n + n p as

With simple algebra from this equation one gets for the threshold nucleon density for muons’ appearance

where we have used  . Thus the threshold mass density for muons’ appearance in (ideal) dense nuclear matter is
. Thus the threshold mass density for muons’ appearance in (ideal) dense nuclear matter is
which is about 2.7 times the value of the central density ρ 0 ≃ 2.6 × 1014 g∕cm3 at the center of heavy atomic nuclei.
9.3 Nuclear Matter and Nucleon Stars
We now undertake the main task of this chapter and investigate the role of the strong interaction on the EoS of dense matter and on the properties of neutron stars. In the present work, we will not discuss the properties and the EoS of the neutron star crust (see e.g. [13]), but we will focus on the study of the EoS describing the thermodynamic properties of the neutron star core.
In the simplest and conservative picture the core of a NS is modeled as an electrically neutral uniform fluid of neutrons, protons, electrons and muons in equilibrium with respect to the weak interaction (β-stable nuclear matter). These neutron stars are often called nucleon stars . Even in this simplified picture, the microscopic determination of the EoS from the underlying nuclear interactions remains a formidable theoretical problem. In fact, one has to determine the EoS to extreme conditions of high density and high neutron-proton asymmetry, i.e. in a regime where the EoS is poorly constrained by nuclear data and experiments.
A prerequisite of any EoS of dense matter to be used in NS structure calculations, in core-collapse supernovae and in BNS mergers numerical simulations, relates to its capability to reproduce some basic empirical properties of nuclear matter at and around the nuclear saturation density n 0 = 0.16 fm−3 (cf. Sect. 9.3.1.1).
The nuclear symmetry energy (cf. Sect. 9.3.1) is one of the most relevant quantities to control the composition, and the pressure of β-stable nuclear matter [18, 19], and therefore many NS attributes such as the radius, moment of inertia, and crustal properties [20, 21].
Another important issue is related to the role of three-nucleon interactions (TNIs) on the EoS at high density. In fact, it is well known that TNIs are essential to reproduce the experimental binding energy of few-nucleon (A = 3, 4) systems [22, 23] and the empirical saturation point (n 0 = 0.16 fm−3, (E∕A)0 = −16 MeV) of symmetric nuclear matter.
As shown by various microscopic calculationsFootnote 8 [24,25,26,27,28] of the EoS of β-stable nuclear matter, based on realistic nucleon-nucleon (NN) interactions supplemented with TNI , it is possible to obtain NS sequences with maximum mass M max > 2 M ⊙ and thus in agreement with presently measured masses. However, the value of M max strongly depends on the strength of the TNI at high density [27], thus indicating that few-body nuclear systems properties and/or nuclear matter saturation properties can not be used to constrain the TNI at high density. In addition, the central density for the maximum mass configuration for these nucleon stars is in the range n c(M max) = (6–8) n 0.
In the present work, we do not make any attempt to discuss the various quantum many-body methods used to derive the EoS of nuclear matter, or more generally of baryonic matter (when other baryons are considered in addition to nucleons). We also do not attempt to make a review of recent studies on the neutron star matter EoS.
With the purpose of illustrating basic NS properties and discussing various possibilities for their inner structure, we will make use of some representative EoS models. Some of these are very popular EoS models, widely used in many astrophysical applications, and others are models on which the present author has worked on during his research activity.
9.3.1 Isospin-Asymmetric Nuclear Matter
The energy per nucleon \(\widetilde E \equiv E/A\,\) of isospin-asymmetric nuclear matter, with neutron number density n n and proton number density n p, contains the information to give a complete thermodynamic description of the system at zero temperature. \({\widetilde E}(n_n, n_p)\) can be expressed as a function of the total nucleon number density n = n n + n p and of the isospin-asymmetry parameter (shortly the asymmetry parameter),
where Y p = n p∕n is the proton fraction. The case β = 0 corresponds to symmetric nuclear matter (SNM) i.e. matter with n n = n p, whereas the case with β = 1 corresponds to pure neutron matter (PNM) .
Due to the charge symmetry of the nuclear interactions, \(\widetilde E\) must be the same exchanging all neutrons to protons and vice versa, thus \(\widetilde E\) must depend on even-power of the asymmetry parameter:Footnote 9
where the first term \({\widetilde E}(n, 0)\equiv {\widetilde E}_{SNM}(n)\,\) is the energy per nucleon of SNM, and the function in front of the β 2 term, is the nuclear symmetry energy
Microscopic calculations of asymmetric nuclear EoS [18] show that terms S k(n) with k > 2 in Eq. (9.23) can be neglected, then one can safely use the so-called “parabolic approximation” in the asymmetry parameter β for the energy per particle of asymmetric nuclear matter up to β = 1 ,
In the parabolic approximation the symmetry energy can be written as the difference between the energy per particle of PNM and SNM
This greatly reduces the numerical effort in all the quantum many-body approaches to derive the EoS of isospin-asymmetric and β-stable nuclear matter.
9.3.1.1 The Empirical Saturation Point of SNM
Due to the saturation properties of nuclear interactions, \({\widetilde E}_{SNM}(n)\) has a minimum at a density n 0 which is set by the condition \([\partial \widetilde E_{SNM}/\partial n]_{n_0} = 0\). The corresponding value of the energy per nucleon \(\widetilde E_0 \equiv {\widetilde E}_{SNM}(n_0)\) is called the saturation energy. These two quantities (n 0, \(\widetilde E_0\)) locate the so called saturation point of SNM , which represents its ground state.
The empirical value for n 0 is obtained from the measured values of the central density of heavy nuclei (e.g. from electron-nucleus scattering experiments) taking into account corrections due to the finite size of atomic nuclei and to the Coulomb interaction which is not considered in nuclear matter. The value of the saturation energy \(\widetilde E_0\) corresponds to the volume coefficient (with a minus sign) of the semi-empirical Bethe–Weizsäker mass formula , which is obtained from the fit of measured nuclear masses. From the above quoted experimental information one thus get the empirical saturation point of SNM :
9.3.1.2 The Incompressibility of SNM
Around the saturation density the energy per particle of SNM can be expanded as
The coefficient
is called the incompressibility of SNM . Its value can be extracted from experimental data on giant resonance in atomic nuclei. The empirical value for this quantity is in the range [32, 33]:
9.3.1.3 Properties of the Nuclear Symmetry Energy Around the Saturation Point
The symmetry energy can be expanded in series around the saturation density
where \(E_{sym}^0 \equiv E_{sym}(n_0)\) is the value of the symmetry energy at the saturation density, and the parameter
is called the symmetry energy slope parameter. The values of these two quantities can be extracted using various nuclear physics experimental data (see e.g. [34]). For example \(E_{sym}^0\) corresponds to the symmetry coefficient of the semi-empirical Bethe–Weizsäker mass formula , obtained from the fit of measured nuclear masses. The values for these two quantities lies in the ranges [34] :
9.3.1.4 Saturation Properties of Nuclear Matter for EoS Models
In Fig. 9.1 we plot the energy per nucleon of SNM as a function of the nucleon number density for the following four representative microscopic EoS models: WFF [24], APR [26], BL [28] and KVLBG [35] (case β = ∞ and r 3 = 1.4 fm in their Table I). All these EoS models have been obtained within quantum many-body approaches starting from two-body and three-body nuclear interactions. The properties of these EoS models, at the calculated saturation point, are reported in Table 9.1.
Energy per nucleon of SNM as a function of the nucleon density n for the four considered EoS models. The yellow box represents the empirical saturation “point” Eq. (9.27). The curve for the APR EoS has been obtained by the authors of Ref. [26] adding an ad hoc density dependent correction term to their microscopic results to reproduce the empirical saturation point of SNM (see Tab VI last column and pag. 1815 in Ref. [26])
Notice that the WFF EoS does not reproduce the empirical saturation point of SNM , whereas in the case of the APR EoS an ad hoc density dependent correction term has been added by the authors of Ref. [26] to their microscopic results (see Tab VI last column and pag. 1815 in Ref. [26]) to reproduce the empirical saturation point of SNM .
9.3.2 β-stable Nuclear Matter: Role of the Nuclear Interactions
In this subsection we want to emphasize the role played by the nuclear interactions on the composition of β-stable nuclear matter. We consider the case of neutrino–free matter.
At any given value of the nucleon number density n, the composition of β-stable nuclear matter is obtained solving the following equations:
It can be shown that the difference between the neutron and proton chemical potentials (neglecting their mass difference) can be written as:
where the partial derivatives are taken for constant nucleon number density n.
To begin with, we neglect for the moment the presence of muons. In this case the β-stability conditions (9.34) and (9.35) reduce to Eqs. (9.12) and (9.13). At the densities found in the neutron star core (ρ > 1014 g∕cm3) electrons can be considered as an ideal ultra-relativistic gas, so
Using the chemical equilibrium condition μ e = μ n − μ p and Eq. (9.36), from the charge neutrality condition n e = n p = Y p n one gets:
which defines in an implicit way the proton fraction Y p = Y p(n) at β-equilibrium and can be solved numerically for each given and fixed value of the nucleon number density n.
From Eq. (9.38) we see that the composition of β-stable nuclear matter is ruled not only by the weak interaction but also by the strong interaction which enters in the energy per nucleon \({\widetilde E}(n,Y_p)\).
In the parabolic approximation (9.25) for \({\widetilde E}(n,Y_p)\) one has
thus the proton fraction Y p(n) is the solution of the equation
Consequently the composition of β-stable nuclear matter is a result of the density dependence of the nuclear symmetry energy.
In the density region for which Y p << 1∕2, an approximate solution of the equilibrium condition (9.40) is
which exhibits the high sensitivity of Y p to the value of the symmetry energy and to its density dependence.
In Fig. 9.2 we plot the symmetry energy for the four considered microscopic nuclear matter EoS models. In the same figure, to quantify the influence of the nuclear interactions on this quantity, we plot the symmetry energy for an ideal {n, p}-system (black dotted curve)). It is apparent that E sym(n) is heavily influenced by the nuclear interactions, and its behavior at large density (n > 2n 0) is still quite uncertain. The two bands in Fig. 9.2 represent the constraints on the symmetry energy obtained in Ref. [36] using the excitation energies to isobaric analog states (IAS) in nuclei (yellow band labeled IAS) and with the additional constraints from neutron skin thickness Δr np of heavy nuclei [36, 37] (orange band labeled IAS+Δr np). Notice that some of the considered EoS models (particularly the WFF EoS) do not fulfill the above mentioned empirical constraints.
Nuclear symmetry energy as a function of the nucleon number density for the four considered EoS models. The black dotted curve represents E sym(n) for an ideal {n, p}-gas. The yellow band, labeled IAS, represents the constraints on the symmetry energy obtained in [36] using the excitation energies of isobaric analog states (IAS) in nuclei. The additional constraints from neutron skin thickness Δr np of heavy nuclei [36, 37] give the more limited region covered by the orange band labeled IAS+Δr np
To illustrate the role of the nuclear interactions on the composition of β-stable nuclear matter, we plot in Fig. 9.3 the particle fractions Y i = n i∕n for the various matter constituents in the case of the BL EoS model. As one can see, neutrons are still the most abundant species, but now the proton fraction Y p is much higher with respect to the case where nuclear interactions are ignored (ideal gas). For example, one has Y p(n 0) = 5.7 × 10−2 and Y p(5n 0) = 26.6 × 10−2, to be compared with the values reported in Sect. 9.2.1.2 for the ideal gas. These results are also in line with the previous discussion on the role of the symmetry energy (cf. Eq. (9.40)) and with the results reported in Fig. 9.2.
Due to charge neutrality, a large proton fraction also implies a large electron fraction Y e. Thus the nuclear interactions have the effect to lower the threshold density for muons’ appearance in dense matter. In the case of the BL EoS, the muon threshold density is n ∗ = 0.12 fm−3 = 0.75 n 0, to be compared with the one for the ideal {n, p, e}-gas: n ∗ = 0.43 fm−3 = 2.7 n 0.
9.3.3 Nucleon Stars Properties
Once one has determined the particle fractions Y i(n) in β-stable matter, the nucleonic contribution ε N(n) to the total energy density is given by
The nucleonic contribution P N(n) to the total pressure can thus be computed using the thermodynamic relation
Finally the leptonic contributions ε L and P L, to the total energy density and total pressure respectively, are computed using the expressions for relativistic ideal Fermi gases of electrons and muons.
The structural properties of non-rotating neutron stars can be obtained integrating numerically the equation for hydrostatic equilibrium in general relativity [16, 38]
and
where G is the gravitational constant and m(r) is the gravitational mass enclosed within a sphere of radial coordinate r (surface area 4πr 2).
Starting with a central energy density ε c ≡ ε(r = 0), we integrate out Eqs. (9.44) and (9.45) until the energy density equals the one corresponding to the density of iron ε surf∕c 2 = 7.86 g/cm3. This condition determines the stellar surface and specifies the neutron star radius R (through the surface area 4πR 2) and the stellar gravitational mass
The total baryon number of a star with central baryon density n c = n(r = 0) is given by
and the baryonic mass (or “rest mass”) of the neutron star is
where m u is a baryonic mass unit that we take equal to m u = m(12 C)∕12 = 1.6605 × 10−24 g. Other choices for m u are some times used in the literature as m u = m n or m u = m(56 Fe)∕56. These choices for m u only make a small change in the calculated stellar binding energy since \(\Delta \mathcal {B}/(M_{B}c^2) \sim 0.01\).
The total binding energy of the star is thus
which represents the total energy liberated during the neutron star birth.
The stellar structure equations (9.44), (9.45) and (9.47) have been integrated using the microscopic EoS (in tabular form) for β-stable nuclear matter described in the previous sections to model the neutron star core, whereas to model the stellar crust (i.e. for nucleonic density ≤0.08 fm−3) we have used the SLy4 [39] EoS.
In Fig. 9.4 we plot the gravitational mass as a function of the radius in the case of nucleon stars for the considered EoS models. Notice that all the considered EoS models are compatible with present measured neutron star masses and particularly with the mass M = 2.01 ± 0.04 M ⊙ [5] of the neutron stars in PSR J0348+ 0432. The cyan and magenta regions give the mass and radius values for the high mass and low mass components respectively, extracted [2] from the gravitational wave signal for the event GW178017 in the case of low-spin priors for the two inspiraling NSs. The properties of the maximum mass configuration for the considered EOS models are reported in Table 9.2.
Gravitational mass as a function of the stellar radius in the case of nucleon stars for the considered EoS models. The strip with boundaries marked with orange lines stands for the measured mass M = 2.01 ± 0.04 M ⊙ of the neutron stars in PSR J0348+0432. The cyan and magenta regions give the mass and radius values for the high mass and low mass components respectively, extracted [2] from the gravitational wave signal for the event GW178017 in the case of low-spin priors for the two inspiraling neutron stars
9.4 Hyperons in Neutron Stars: The Hyperon Puzzle
Just as nucleons, hyperons are baryons.Footnote 10 However they possess an additional quantum number \({\cal {S}}\), called strangeness , which is zero for nucleons. The strangeness quantum number is related to their quark structure. In fact, hyperons contain at least one strange (s) quark, whereas nucleons are formed by up (u) and down (d) quarks. The properties of the baryons belonging to the so called baryon octet J P = (1∕2)+, i.e. having spin J = 1∕2 and positive parity P, are listed in Table 9.3.
Other hyperons ( Σ∗−, Σ∗0, Σ∗+, Ξ∗−, Ξ∗0 and Ω−) belong to the baryon decuplet J P = (3∕2)+. Among these we mention the Ω− hyperon, which is a sss quark state with strangeness \({\cal {S}} = -3\) and mass \(m_{\Omega ^-} = 1672~\mathrm {MeV/c^2}\). Due to their large masses, hyperons of the baryon decuplet are not expected in neutron stars. In the following we thus consider only members of the baryon octet J P = (1∕2)+.
Hyperons are unstable with respect to various weak decay processes. For example an isolated Λ particle mainly decays via the following mesonic decay modes
where in parenthesis we give the branching ratio for each of the two processes. Other rare weak decay modes, as for example \(\, \Lambda \rightarrow p + e^- + {\bar \nu }_e\,,\;\) are also possible.
9.4.1 β-stable Hyperonic Matter
At the high densities found in the core of nucleon stars (see Table 9.2) hyperons are expected among the stellar constituents. Hyperons’ formation in dense matter can be understood by the basic and general physical arguments discussed in Sect. 9.2. As soon as the chemical potentials of nucleons and electrons become sufficiently large, it is energetically convenient to convert nucleons into hyperons via weak interaction processes. For example the Λ hyperons can be formed through the weak process p + e −→ Λ + ν e when the Λ chemical potential fulfills the condition μ Λ = μ p + μ e = μ n. The Σ− hyperons can be formed e.g. through the weak process n + e −→ Σ− + ν e when the Σ− chemical potential fulfills the condition \(\, \mu _{\Sigma ^-} = \mu _n + \mu _e \,\) (we consider neutrino–free matter). Other hyperons can be formed with similar weak interaction processes. Thus at sufficiently large density, nuclear matter turns into hyperonic matter (also referred to as hypernuclear matter).
At any given value of the total baryon density
the composition of hyperonic matter (i.e. the values of the particle fractions Y i = n i∕n for the various particle species) is set the following equations between the chemical potentials of the different constituents
with the additional condition given by electric charge neutrality
Once again we consider neutrino-free matter. The solution of Eqs. (9.52)–(9.57) give the composition Y i(n) (i = n, p, Λ, Σ−, … , e −, μ −) for β-stable hyperonic matter.
To begin with, to estimate the threshold baryon density n ∗[ Λ] for Λ hyperons in dense matter, we neglect the strong interaction. We thus consider an ideal {n, p, e−}-gas in β-equilibrium. The Λ-threshold condition is given by μ n = μ p + μ e = m Λ c 2. Assuming non-relativistic nucleons, one easily gets n ∗[ Λ] = 0.86 fm−3 = 5.4 n 0.
To illustrate the role of the strong interaction on the threshold density values of different hyperons, we show in Fig. 9.5 (upper panel) the chemical potentials μ i for the different stellar constituents. These results have been obtained [40, 41] within the many-body Brueckner-Hartree-Fock (BHF) approach and using the following interactions: the Argonne v18 (Av18) nucleon-nucleon (NN) interaction [42]; the TNI used in [25] to reproduce the empirical nuclear matter saturation point; the Nijmegen ESC08b potential [43] to describe the hyperon-nucleon (YN) interaction . No hyperon-hyperon (YY) interaction and no three-body interactions of the type nucleon-nucleon-hyperon (NNY), NYY and YYY have been considered [40, 41]. The onset of Λ hyperons occurs at n ∗[ Λ] = 0.35 fm−3 = 2.19 n 0. Thus the strong interaction moves the Λ-threshold density to a lower value with respect to the one relative to the ideal {n, p, e−}-gas case. The Σ− hyperon occurs at \(n^{*[\Sigma ^-]} = 0.64~{\mathrm {fm}}^{-3} = 4\,n_0\). Notice that, due to the strong interaction, the hyperons chemical potential , below the corresponding threshold density, is not equal to its corresponding rest mass energy m Y c 2. The calculated threshold densities for Λ and Σ− hyperons are thus well below the predicted central densities \(n_c^{max}\) (see Table 9.2) for the maximum mass configuration of nucleon stars .
The composition of β-stable hyperonic matter is reported in Fig. 9.5 (lower panel). Notice that at n = 5 n 0 hyperons represent about 43% of the total number of baryons.
9.4.2 Hyperon Stars
The effect of hyperons on the EoS is shown in Fig. 9.6 (upper panels), where we compare the EoS for β-stable pure nucleonic matter (curves Av18+TNI) with that of β-stable hyperonic matter (curves Av18+TNI+ESC08b). As we can see the presence of hyperons produces a significant reduction of the pressure of the system. As a consequence, solving the relativistic stellar structure equations, we find a considerable decrease of the stellar maximum mass from M max = 2.28 M⊙ to M max = 1.38 M⊙ when hyperons are included among the stellar constituents. The prediction of a value for M max < 2 M ⊙ is a common feature of various hyperon stars structure calculations and particularly of those based on microscopic hyperonic matter EoSs [27, 44,45,46,47].
Upper panels: EoS of β-stable matter illustrating the energy density as a function of the total baryon density (upper left panel) and the pressure versus the energy density (upper right panel). The upper (lower) curves refer to the case of nuclear (hyperonic) matter. Lower panels: gravitational mass as a function of the stellar radius (lower left panel) and of the central baryon density (lower right panel) in the case of nucleon stars (upper curves) and hyperon stars (lower curves). The dashed horizontal line represents the measured mass [5] of the neutron star in the pulsar PSR J0348+0432
Thus, on the one hand the presence of hyperons in neutron stars seems unavoidable, on the other hand their presence results in a stellar maximum mass not compatible with measured NS masses. This baffling problem is known as the “hyperon puzzle” in neutron stars.
Clearly, one should try to trace back the origin of the hyperon puzzle to the underlying NY and YY two-body interactions or to the possible repulsive NNY, NYY and YYY three-body interactions. Unfortunately, these two- and three-body strangeness \({\cal {S}} \neq 0\) baryonic interactions are rather uncertain and poorly known. Basically this is due to the scarce amount of experimental data and to the considerable difficulties in their theoretical analysis. This situation is in sharp contrast to the case of the NN interaction , which is satisfactorily well known, mostly due to the large number of scattering data and to the huge amount of measured properties of stable and unstable nuclei. The study of hypernuclei (i.e. nuclei containing one or more hyperons) [48,49,50,51,52] and more in general of hypernuclear physics [53,54,55] is partially filling this gap and hopefully will give in the near future the possibility to have accurate and reliable description of the S ≠ 0 baryonic interactions.
Presently, this is a very active research field both from an experimental [52, 56] and a theoretical [56, 57] point of view. Within this contest, the use of microscopic EoS of hyperonic matter in the study of NS structure is of fundamental importance for the understanding of strong interactions involving hyperons, and particularly to learn how these interactions behave in a dense many-body system.
9.4.3 Hyperonic Three-Body Interactions as Possible Solutions of the Hyperon Puzzle
As already mentioned TNIs play an important role in nuclei and in nuclear matter. Thus, within a unified description of the interactions between baryons, it is rather evident to suppose the existence of hyperonic three-body interactions. The NNΛ interaction was in fact first hypothesized [58, 59] at the end of the 1950s, i.e. during the early days of hypernuclear physics, as an important ingredient to calculate the binding energy of hypernuclei. Since then the NNΛ interaction received considerable attention in many other studies on hypernuclei [60,61,62,63,64,65,66,67,68]. It is thus quite natural to expect that hyperonic three-body interactions can influence the EoS of dense matter and can represent a likely candidate to solve the hyperon puzzle [69,70,71,72,73].
To emphasize the effect of hyperonic three-body interactions on the EoS of hyperonic matter and on M max, we consider the simplified situation where we include only the Λ hyperons and ignore the possible appearance of other hyperon species. We thus consider a {n, p, Λ, e −, μ −}-system in β-equilibrium and under the influence of NN, NNN and NΛ interactions, to which we add a NNΛ three-body interaction (see Ref. [72] for more details).
The composition of β-stable hyperonic matter is presented in the upper left panel of Fig. 9.7. The continuous lines (labeled as NSC97a) display the particle fractions Y i when only NN, NNN, and NΛ interactions are included, whereas the dashed lines (labeled as NSC97a+NN Λ1) display the particle fractions when the NNΛ three-body interaction is added. The effect of the NNΛ interaction is twofold. First it shifts the Λ-threshold density to a larger value with respect to the case in which the NNΛ interaction is not included. Second it strongly reduces the Λ concentration and consequently increases back the neutron and proton concentrations. The effect of the NNΛ interaction on the EoS can be examined looking at the results reported in the upper right panel of Fig. 9.7, where we plot the total pressure P as function of the total energy density ε for β-stable matter. The continuous line represent the EoS for nucleonic matter under the influence of NN and NNN interactions. The inclusion of the Λ hyperons and of a NΛ interaction produces a sizable softening of the EoS (dashed line) i.e. strongly reduces the pressure. When the NNΛ interaction is added the pressure abundantly increases (dot-dashed line) and the EoS is stiffened, almost back to the nucleonic case.
Upper left panel: particle fractions Y i in β-stable hyperonic matter as a function of the baryon density. The continuous lines (labeled as NSC97a) display the particle fractions Y i when only NN, NNN, and NΛ interactions are included, whereas the dashed lines (labeled as NSC97a+NN Λ1) display the particle fractions when the NNΛ three-body interaction is added. Upper right panel: EoS for β-stable hyperonic matter including (dot-dashed line) or not including (dashed line) the NNΛ interaction. The EoS for pure nucleonic matter (continuous line) is also shown for comparison. Lower panel: mass-radius sequences for the various EoS models with (dot-dashed lines) and without (dashed lines) the NNΛ interaction. Results for nucleon stars (continuous line) are shown for comparison. The two colored bands represent the measured masses of the neutron stars in PSR J0348+0432 and PSR J0740+6620. The results reported in this figure are adapted from Ref. [72] where the reader can find more details on the strong interaction models used to derive the EoS. Credit: Logoteta et al., Eur. Phys. J. A 55, 207 (2019). License: CC BY 4.0
Next in the lower panel of Fig. 9.7, we plot the mass-radius equilibrium sequences for various EoS models with (dot-dashed lines) and without (dashed lines) the NNΛ interaction. Notice that two different models (NSC97a and NSC97e) for the NΛ interaction have been used (see Ref. [72] for more details). The mass-radius curve for nucleon stars (continuous line) is shown for comparison. The two colored bands represent the measured masses of the neutron stars in the pulsar PSR J0348+0432 [5] and PSR J0740+6620 [6]. These results thus give a strong indications that hyperonic three-body interactions could represent a likely solution of the hyperon puzzle in neutron stars [72].
9.5 Quark Matter in Neutron Stars
Neutron star structure calculations (see e.g. Table 9.2) based on a large variety of modern EoS of nuclear or hyperonic matter, predict a maximum stellar central density (the one for the maximum mass star configuration) in the range of 4–8 times the saturation density n 0 of nuclear matter. Thus the core of a neutron star is one of the best candidates in the universe where a transition from a phase where quarks are confined within baryons and mesons (hadronic matter) to a quark deconfined phase (quark matter) could occur. This possibility was realized by several researchers [74,75,76,77,78,79] soon after the introduction of quarks as the fundamentals building blocks of hadrons.
Neutron stars which possess a quark matter core either as a mixed phase of deconfined quarks and hadrons or as a pure quark matter phase are called hybrid stars [14]. In the following the more conventional neutron stars in which no fraction of quark matter is present, will be referred to as hadronic stars (HSs) . This family thus includes nucleon stars (Sect. 9.3) and hyperon stars (Sect. 9.4), or compact stars containing a Bose–Einstein condensate of negative pions (π −) or negative kaons (K −) (not discussed in this chapter).
According to the quark model, baryons are bound states of three quarks (q 1 q 2 q 3), and mesons are quark–anti-quark \((q_1 \bar {q}_2\)) bound states. Each quark has spin 1/2 (thus quarks are fermions) and baryon number 1/3. There are six different flavors of quarks: up (u), down (d), strange (s), charm (c), top (t) and bottom (b). Each quark possesses an electric charge, which is a fraction of the electron charge magnitude e = 1.602 × 1019 C. The values of the mass and electric charge for quarks of each flavor are listed in Table 9.4.
Quarks posses an internal degree of freedom, the color degree of freedom. The color charge is responsible for the strong interaction. There are three different colors a quark can carry. The colors are labeled red, green, and blue with associated anticolors. Quarks interact each other via the exchange of massless particles called gluons. Gluons themselves have color charge and so they mutually interact via the strong interaction. All the observed meson and baryon states are colorless, namely either color-anticolor combinations in the case of mesons, or equal mixture of red, green, and blue in the case of baryons.
The number density n q for a given quark flavor is related to the corresponding Fermi momentum \(k_{F_q}\) by the equation
Notice that the previous relation differs by a factor of three from the similar equation for an electron gas or for a proton gas (Eq. (9.7)). The extra factor of three is due to the color degree of freedom. Quark states, for any given flavor, are in fact degenerate with respect to spin (ν spin = 2) and with respect to color (ν color = 3). Since to each quark is assigned a baryon number 1∕3, the baryon number density for a system containing quarks of different flavors with partial number densities n q is given by
Weak interaction processes can change the quark flavor (see e.g. Eqs. (9.63)–(9.67)).
If quark matter is present in neutron stars, it can be shown that the chemical potential μ s for the strange quark is larger than its rest energy. Thus the s quark must be included in the description of the stellar quark matter core, in addition to the u and d quarks [14].
We give now a simple argument to show why charm, bottom and top quarks are not expected in a neutron star core. The reason is that c, b, and t quarks are much more massive than u, d, and s quarks (see Table 9.4). We thus assume m u = m d = m s = 0 and consider an ideal {u, d, s, e −}-gas,Footnote 11 with m e = 0, in equilibrium with respect to the weak interaction and with total electric charge equal to zero (see Eqs. (9.62)–(9.69) below). Under these hypothesis it can be shown that n u = n d = n s and n e = 0. As a consequence the baryon density n = (n u + n d + n s)∕3 is n = n s.
The creation of the charm quark, e.g. through the weak process
requires the chemical potential of the s quark should be at least equal to the charm quark rest energy, consequently we get
which implies n ≥ 27 fm−3, i.e. a baryon number density at least equal to about 170 times the normal saturation density n 0 of nuclear matter, in other words a density much higher than the maximum expected central density in neutron stars.
Thus the quark matter phase expected in neutron stars is a mixture of u, d, and s quarks, together with an appropriate number of electrons to guarantee electric charge neutrality. This phase of dense matter is called strange quark matter (SQM) . For consistency with the strangeness quantum number \({\cal {S}}\) assigned to hyperons and nucleons (see Table 9.3), quarks u and d have no strangeness (\({\cal {S}} = 0\)), whereas the s quark has strangeness \({\cal {S}} = -1\).
9.5.1 β-stable Strange Quark Matter
The composition of β-stable SQM is determined by the requirement of electric charge neutrality
and equilibrium with respect to the weak processes:
which, in neutrino–free matter, can be written in terms of the corresponding chemical potentials as
Considering now two different EoS models, one for the hadronic phase and the other for the quark phase, and assuming a first-order transition between the two phases, one can construct the EoS for hybrid star matter as described in detail in the book by N. K. Glendenning [14].
As an example of the composition of hybrid star matter, we plot in Fig. 9.8 (see figure caption for informations on the EoS models) the particle fractions Y i for the different stellar constituents as a function of the baryon density n. The hadronic phase extends up to n ≃ 0.26 fm−3. Above this density value one has the mixed hadron-quark phase which extend up to n ≃ 1.16 fm−3. Finally for larger densities one has a pure SQM phase.
Particle fractions Y i for the different stellar constituents as a function of the baryon density n. The quark fraction is defined as Y i = n i∕(3n), since quarks have baryon number 1∕3, where n i is the number density of quarks of flavor i (u, d, s). For nucleons, hyperons, electrons and muons Y i = n i∕n. The hadronic phase is described by the GM3 EoS model and the quark phase by the bag model EoS with bag constant B = 136.6 MeV∕fm3 and m s = 150 MeV, m u = m d = 0. See [14] for details on the EoS models and on the phase-transition modeling
It has been show (see e.g. Ref. [80,81,82,83,84]) that several of the current models of hybrid stars are compatible with present measured NS masses.
9.5.2 Strange Stars
Even more intriguing than the existence of a quark matter core in a neutron star, is the possible existence of a new family of compact stars consisting completely of β-stable SQM . Such compact stars have been referred to in the literature, as strange quark stars or shortly strange stars (SSs) . The investigation of such a possibility is extremely relevant not only for astrophysics, but for high energy physics too.
The possible existence of SS is a direct consequence of the so called strange matter hypothesis [85,86,87].
According to this hypothesis, SQM could be the true ground state of matter. In other words, the energy per baryon of SQM (at the baryon density where the pressure is equal to zero) is supposed to be less than the lowest energy per baryon found in atomic nuclei, which is about 930.4 MeV for the most bound nuclei (56Fe, 58Fe, and 62Ni).
If the strange matter hypothesis is true, then a nucleus with A nucleons, could in principle lower its energy by converting to a strangelet (i.e. a drop of SQM ). However, this process requires a very high-order simultaneous weak interactions to convert about a number A of u and d quarks of the nucleus into s quarks. The probability for such a process is thus proportional to \(G_{F}^{2A}\), where G F is the Fermi constant. As a consequence, for a large enough baryon number (A > A min ∼ 5), this probability is extremely low, and the mean-life time for an atomic nucleus to decay to a strangelet is much higher than the age of the universe. In addition, finite size effects (surface and shell effects) place a lower limit (A min ∼ 10–103, depending on the assumed model parameters) on the baryon number of a stable strangelet even if bulk SQM is stable [88,89,90].
On the other hand, a step by step production of s quarks, at different times, would produce hyperons in the nucleus, i.e. a system (hypernucleus) with a higher energy per baryon with respect to the original nucleus. Thus, according to the strange matter hypothesis , the ordinary state of matter, in which quarks are confined within hadrons, is a metastable state having a mean-life time much higher than the age of the universe.
The success of traditional nuclear physics, in explaining an astonishing amount of experimental data, provides a clear indication that quarks in a nucleus are confined within protons and neutrons. Thus, the energy per baryon for a droplet of u, d quark matter (non-strange quark matter) must be higher than the energy per baryon of a nucleus with the same baryon number. These stability conditions in turn may be used to constrain the parameters entering in models for the EoS of SQM [88].
In summary, our present understanding of the properties of ultra-dense hadronic matter, does not allow us to exclude or to accept a priory the validity of the strange matter hypothesis . Thus strange stars may exist in the universe.
We consider only bare strange stars , i.e. we neglect the possible presence of a crust of normal (confined) matter above the deconfined quark matter core [91]. For stars with M ∼ 1 M ⊙ the thickness of this crust is on the order of 10–100 m, therefore the presence of a crust will not affect the predicted value of the radius of strange star candidates [92,93,94,95].
Strange stars are the natural site for various possible color superconducting phases of quark matter [96, 97], and matter in their interiors might be characterized by the formation of different crystalline structures [98, 99]. These crystalline structures might be relevant to model pulsar glitches in strange stars .
Computations of fully general relativistic equilibrium sequences of rapidly spinning compact stars [100] are very important to study millisecond pulsars and other fast spinning compact objects. Recent work [101] has shown that rapidly spinning SSs can have gravitational masses and spin frequencies at least up to ∼3 M ⊙ and ∼1250 Hz, and thus fully consistent with present measured values for these quantities.
9.6 Two Coexisting Families of Compact Stars
According to the current accepted paradigm there exist in the universe only one family of neutron stars. Thus making accurate measurements of the mass and radius of several neutron stars, one could in principle determine the dense matter EoS solving the so called relativistic inverse stellar problem [102, 103]
In the following we discuss the possibility of having two coexisting families of compact stars: hadronic stars and quark stars (QSs) (i.e. hybrid stars or strange stars ). This possibility and the stellar conversion mechanism to jump from the HS family to the QS family has been proposed several years ago in these papers [104,105,106,107] and since then has been investigated by many authors [108,109,110,111,112,113,114,115,116,117,118,119,120,121].
The basic assumption for the two-families scenario of compact stars is that in the low temperature T and high baryon chemical potential region of the QCD phase diagram (which is the one relevant for neutron star physics) the quark deconfinement transition is a first-order phase transition. This assumption is supported by several QCD inspired models [122, 123].
As it is well known, first-order phase transitions, in different physical systems, are triggered by the nucleation of a critical size drop of the new (stable) phase in a metastable mother phase. This is a very common phenomenon in nature (e.g. fog or dew formation in supersaturated vapor, ice formation in supercooled water) and plays an important role in many scientific disciplines (e.g. in atmospheric science, meteorology, cosmology, biology) as well as in many technical applications (e.g. in metallurgy).
One of the most exciting astrophysical consequences of the nucleation process of quark matter in the core of massive hadronic stars is that above a threshold value of their mass, HSs are metastable [104,105,106,107] to the “decay” (conversion) to QSs. This stellar conversion process liberates a huge amount of energy (a few 1053 erg) and it could be the energy source of Gamma Ray Bursts (GRBs) [124]. In addition, within this scenario, one has two coexisting families of compact stars, and the members of these two families could have similar values for their gravitational masses but different values for their radii [106].
The metastability of HSs originates from the finite size effects (which represent the driving “force” of first-order phase transitions) in the formation process of the first QM drop in the hadronic environment.
In cold (T = 0) bulk matter the quark deconfinement transition takes place at the static transition point defined by the Gibbs’ criterion for phase equilibrium
where μ H = (ε H + P H)∕n H and μ Q = (ε Q + P Q)∕n Q are the Gibbs energies per baryon (average chemical potentials ) for the hadron and quark phase respectively, ε H (ε Q), P H (P Q) and n H (n Q) denote respectively the total (i.e., including leptonic contributions) energy density, the total pressure and baryon number density for the hadronic (quark) phase.
Consider now the more realistic situation in which one takes into account the energy cost due to finite size effects (e.g. surface effects) in creating a drop of deconfined QM in the hadronic environment. As a consequence of these effects, the formation of a critical-size drop of QM is not immediate and it is necessary to have an overpressure ΔP = P − P 0 with respect to the static transition point . Thus, above P 0 (see Fig. 9.9 left panel), hadronic matter is in a metastable state, and the formation of a real drop of QM occurs via a quantum nucleation mechanism.
Left panel: Gibbs energy per baryon versus pressure for the hadronic-phase (HP) and the quark phase in which the flavor content is equal to that of the β-stable hadronic system at the same pressure (Q*P). Above P 0 the HP is metastable. Right panel: Mass-radius relation for hadronic stars (HS) and strange stars (SS) . The configuration marked with an asterisk represents the HS for which the central pressure is P c = P 0 and thus the nucleation time is τ = ∞. The conversion process of the HS, with a gravitational mass equal to the critical mass M cr, into the final SS is denoted by the full circles connected by an arrow. The lower horizontal green line represents the mass M = 1.4398 ± 0.0002 M ⊙ [126] of the pulsar PSR B1913+16, whereas the higher horizontal green lines represent the mass M = 2.01 ± 0.04 M ⊙ of PSR J0348+0432 [5]. Adaped from Ref. [120] where details on the employed EoS models can be found. Credit: Bhattacharyya et al., ApJ, 848, 65 (2017) Ⓒ AAS. Reproduced with permission
Small localized fluctuations in the state variables of the metastable hadronic phase will give rise to virtual drops of the stable quark phase. These fluctuations are characterized by a time scale \(\nu _0^{-1} \sim 10^{-23}\) s. This time scale is set by the strong interactions (responsible for the deconfinement phase transition), and it is many orders of magnitude shorter than the typical time scale for the weak interactions. Quark flavor must therefore be conserved during the deconfinement transition [106, 108, 125]. We refer to this form of deconfined matter, in which the flavor content is equal to that of the β-stable hadronic system at the same pressure, as the Q*-phase [106]. Soon after a critical size drop of Q*-matter is formed, the weak interactions will have enough time to act, changing the quark flavor fraction of the deconfined droplet to lower its energy, and a droplet of β-stable quark matter is formed (hereafter the Q-phase). This first seed of β-stable quark matter will trigger the conversion [124] of the HS to a QS (i.e. to a strange star or to an hybrid star depending on whether or not the strange matter hypothesis [85,86,87] is satisfied).
Thus, an HS having a central pressure larger than P 0 is metastable with respect to the conversion to a QS. These metastable HSs have a mean-life time which is related to the nucleation time τ to form the first critical-size drop of deconfined matter in their interior.Footnote 12 When τ is short compared to typical pulsar ages, the metastable HS will be likely converted to a stable QS. Following Ref. [104,105,106] we define as the critical mass configuration for the HS family the stellar configuration having a gravitational mass for which the nucleation time τ = τ(P c), at the center of the star, is equal to one year:Footnote 13 M cr ≡ M HS(τ = 1 yr).
Since it is very unlikely to observe an HS with M HS > M cr, the critical mass M cr plays the role of an effective maximum mass for the hadronic branch of compact stars [106]. Differently from the Oppenheimer–Volkov maximum mass \(M^{HS}_{max}\), which is determined by the overall stiffness of the EoS for hadronic matter, the value of M cr will depend in addition on the bulk properties of the EoS for quark matter and on the properties at the interface between the confined and deconfined phases of matter (e.g., the surface tension σ).
These findings are exemplified in the right panel of Fig. 9.9, where we show the mass-radius (MR) curve for hadronic stars (HS) and that for strange stars (SS) .Footnote 14 The configuration marked with an asterisk on the HS curve represents the HS for which the central pressure is equal to P 0 and thus the nucleation time is τ = ∞. Above this point all the HS configurations are metastable. The black filled circle on the HS sequence represents the critical mass configuration M cr, whereas the red filled circle on the SS curve represents the strange star which is formed from the conversion of the HS with M HS = M cr. As we can see, for the EoS parametrizations used in the calculations reported in Fig. 9.9 (see [120] for details on the employed EoS models), PSR B1913+16 is likely an HS, whereas PSR J0348+0432 is a SS.
We assume [124] that during the stellar conversion process the total number of baryons in the star, or in other words the stellar baryonic mass M B, is conserved. Thus the total energy liberated in the stellar conversion is given [124] by the difference between the gravitational masses of the critical mass HS (M cr) and that of the final QS (M fin) configuration with the same baryonic mass: E conv = (M cr − M fin)c 2.
In the case of the EoS models used to get the results reported in Fig. 9.9 one has E conv = 2.67 × 1053 erg. Using different EoS models for both the HM and the QM phases one has [104,105,106, 124] E conv = 0.5 – 4.0 × 1053 erg.
This huge amount of released energy will cause a powerful neutrino burst, likely accompanied by intense gravitational waves emission, and conceivably it could cause a second delayed (with respect to the supernova forming the HS) explosion. Under favorable physical conditions this second explosion could be the energy source of a powerful GRB [104, 105, 124]. This scenario is thus able to explain a “delayed” connection between supernova explosions and GRBs.
The stellar conversion process, described so far, will start to populate the new branch of quark stars (strange stars for the case reported in Fig. 9.9) i.e. the part of the stellar sequence above the filled red circle in Fig. 9.9. Long term accretion on the QS can next produce stars with masses up to the maximum mass \(M^{QS}_{max}\) for the quark star configurations. Thus within this scenario one has two coexisting families of compact stars: HSs and QSs [106]. The quark star branch is occasionally referred to as the “third family” of compact stars, considering white dwarfs as the first family and HSs as the second family. Notice also that there is a range of values of stellar gravitational mass (see Fig. 9.9) where HSs and QSs with the same gravitational mass, but with different radius, can exist.
As discussed in [120], the possibility of having of two coexisting families of compact stars has very interesting implications for millisecond pulsars. In fact, performing fully general relativistic numerical computations of the structure of fast-spinning compact stars, the authors of Ref. [120] found that the HS to QS conversion process causes a simultaneous spin-up and decrease in gravitational mass of the star. This is a new type of millisecond pulsar evolution through a new mechanism, which gives rise to relatively lower mass compact stars with higher spin rates. This could have considerable implications for the observed mass and spin distributions of millisecond pulsars [127]. Such a stellar conversion can also rescue some massive, spin-supported millisecond pulsars from collapsing into black holes [120].
Notice that for the EoS models used in [120] the stellar conversion process generates a SS with a radius (R SS) smaller than the one (R HS) of the critical mass HS (see the right panel of Fig. 9.9) and with a gravitational mass M fin < M cr (i.e. E conv > 0).
Within the two-families scenario, in the case of soft EoSs for the hadronic phase and stiff quark matter EoSs satisfying the strange matter hypothesis , it is possible to have a stellar conversion process which generates a SS with R SS > R HS (and M fin < M cr) [121]. At first glance this process could seem not possible since the gravitational binding energy \(\mathcal {B}_G^{SS}\) of the final SS configuration is smaller than the gravitational binding energy \(\mathcal {B}_G^{HS}\) of the critical mass HS. However for a relativistic star the total binding energy \(\mathcal {B}\) can be written as the sum of two contributions [124] \(\mathcal {B} = \mathcal {B}_G + \mathcal {B}_I\), the gravitational binding energy \(\mathcal {B}_G\) and the internal binding energy \(\mathcal {B}_I\). The latter quantity includes the contribution of the internal energy (kinetic and strong interaction energies) of stellar matter. Thus the stellar conversion energy can be written [124] as \(E^{conv} = (\mathcal {B}_I^{SS} - \mathcal {B}_I^{HS}) + (\mathcal {B}_G^{SS} - \mathcal {B}_G^{HS}) \equiv E^{conv}_I + E^{conv}_G\). As a consequence in the case of strange stars the gain in the internal binding energy could overcompensate (see Fig. 1 and Table I in [124]) the decrease of the gravitational binding energy thus producing an exothermic (i.e. E conv > 0) process.
The conversion between stars having R SS > R HS could have peculiar consequences for the evolution of millisecond pulsars (which have not yet been explored) and for binary compact star mergers. As an example of the latter case we mention the possibility that the secondary component of mass (2.50–2.67) M ⊙ (a value in the mass-gap between NSs and black holes) of the binary merger GW190814 [128] was a strange quark star [129].
Finally, as pointed out and discussed in [106], the possibility of having metastable HSs, together with the expected existence of two distinct families of compact stars, demands an extension of the concept of maximum mass of a “neutron star” with respect to the classical one introduced in 1939 by Oppenheimer and Volkoff.
Notes
- 1.
Stellar masses will be given in unit of the mass of the Sun, M ⊙ = 1.988 × 1033g.
- 2.
The star may also contain species of identical bosons as in the case of negative pions (π −) or negative kaons (K −) condensation.
- 3.
- 4.
k B T = 1 MeV corresponds to T ≃ 1.134 × 1010 K.
- 5.
i.e. imagine for a moment to “switch off” the weak interaction.
- 6.
This is possible if the electron Fermi momentum satisfies
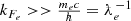 , thus for densities
, thus for densities 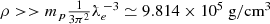 .
. - 7.
Neutrino are trapped in neutron star interior for a few tens of second after their birth [15].
- 8.
Including those considered in the present chapter.
- 9.
Notice that the presence of tiny charge-symmetry breaking (CSB) and charge-independence breaking (CIB) terms in the nuclear interaction (for a review, see e.g. [29]) could invalidate Eq. (9.23). For example a CSB component in the NN interaction produces a linear (and more generally odd-power) β-term in Eq. (9.23) [30]. However, it has been numerically demonstrated by various authors (e.g. [30] and [31]) that the effects on \({\widetilde E}(n, \beta )\) and on the nuclear symmetry energy of CSB and CIB terms in the nucleon-nucleon interaction are essentially negligible.
- 10.
Hadrons, i.e. particles subject to the strong interaction, can be classified in two groups: baryons if they have spin J = 1∕2, 3∕2, 5∕2, …, or mesons if they have spin J = 0, 1, 2, … . According to the hadrons’ quark model, baryons are colorless bound states of three quarks (q 1 q 2 q 3), and mesons are colorless quark–anti-quark \((q_1 \bar {q}_2\)) bound states.
- 11.
The strong interaction between quarks can be neglected due to the asymptotic freedom of QCD which, for the purpose of the present estimate, is a reasonable approximation at the high densities found in neutron stars cores.
- 12.
The actual mean-life time of the HS will depend on the mass accretion or on the spin-down rate which modifies the nucleation time τ via an explicit time dependence of the stellar central pressure.
- 13.
Since the nucleation time is extremely sensitive to the value of the stellar central pressure P c and thus to its corresponding gravitational mass M HS(P c) (see Fig. 4 and 5 in Ref. [106]), the critical mass value is not influenced by the particular choice τ = 1 yr.
- 14.
The SQM EoS used to calculate the QS configurations reported in Fig. 9.9 satisfies the strange matter hypothesis.
References
Abbott, B.P., et al.: LIGO scientific collaboration and Virgo collaboration. Phys. Rev. Lett. 119, 161101 (2017)
Abbott, B.P., et al.: LIGO scientific collaboration and Virgo collaboration. Phys. Rev. Lett. 121, 161101 (2018)
Abbott, B.P., et al.: LIGO scientific collaboration and Virgo collaboration. arXiv:2001.01761
Demorest, P.B., Pennucci, T., Ransom, S., Roberts, M., Hessels, J: Nature 467, 1081 (2010)
Antoniadis, J., et al.: Science 340, 1233232 (2013)
Cromartie, H.T., Fonseca, E., M Ransom, S., et al.: Nat. Astron. 4, 72 (2020)
Fetter, A.L., Walecka, J.D.: Quantum Theory of Many-Particle Systems. McGraw-Hill Book Company, New York (1971)
Bhattacharyya, S.: Adv. Space Res. 45, 949 (2010)
Watts, A.L.: AIP Conference Proceedings 2127, 020008 (2019). https://doi.org/10.1063/1.5117798
Miller, M.C.: Astrophysical constraints on dense matter in neutron stars. In: Belloni, T.M., Méndez, M., Zhang, C. (eds.) Timing Neutron Stars: Pulsations, Oscillations and Explosions. Astrophysics and Space Science Library, vol. 461. Springer, Berlin, Heidelberg (2021). https://doi.org/10.1007/978-3-662-62110-3_1
Harrison, B.K., Wakano, M., Wheeler, J.A.: La Structure et l’Evolution de l’Univers. Stoops, Brussels (1958)
Harrison, B.K., Thorne, K.S., Wakano, M., Wheeler, J.A.: Gravitation Theory and Gravitational Collapse. University of Chicago Press, Chicago (1965)
Chamel, N., Haensel, P.: Living Rev. Relativ. 11, 10 (2008)
Glendenning, N.K.: Compact Stars: Nuclear Physics, Particle Physics, and General Relativity. Springer, New York (2000)
Prakash, M., Bombaci, I., Prakash, M., Ellis, J.P., Lattimer, J.M., Knorren, R.: Phys. Rep. 280, 1 (1997)
J. R. Oppenheimer, G. M. Volkoff, Phys. Rev 55, 374 (1939)
Brown, L.M., Rechenberg, H.: The Origin of the Concept of Nuclear Forces. Institute of Physics Publishing, Bristol and Philadelphia (1996)
Bombaci, I., Lombardo, U.: Phys. Rev. C 44, 1892 (1991)
Zuo, W., Bombaci, I., Lombardo, U.: Eur. Phys. J. A 50, 12 (2014)
Lattimer, J.M.: Gen. Rel. Grav. 46, 1713 (2014)
Lattimer, J.M., Prakash, M.: Phys. Rep. 621, 127 (2016)
Kalantar-Nayestanaki, N., Epelbaum, E., Messchendorp, J.G., Nogga, A.: Rep. Prog. Phys. 75, 016301 (2012)
Hammer, H.W., Nogga, A., Schenk, A.: Rev. Mod. Phys. 85, 197 (2013)
Wiringa, R.B., Fiks, V., Fabrocini, A.: Phys. Rev. C, 38, 1010 (1988)
Baldo, M., Bombaci, I., Burgio, G.F.: A&A 328, 274 (1997)
Akmal, A., Pandharipande, V.R., Ravenhall, D.G.: Phys. Rev. C 58, 1804 (1998)
Li, Z.H., Schulze, H.-J.: Phys. Rev. C 78, 028801 (2008)
Bombaci, I., Logoteta, D.: A&A 609, A128 (2018)
Miller, G.A., Opper, A.K., Stephenson, E.J.: Ann. Rev. Nucl. Part. Sci. 56, 253 (2006)
Haensel, P.: J. Phys. G 3, 373 (1997)
Müther, H., Polls, A., Machleidt, R.: Phys. Lett. B 445, 259 (1999)
Blaizot, J.P., Gogny, D., Grammaticos, B.: Nucl. Phys. A 265, 315 (1976)
Shlomo, S., Kolomietz, V.K. Colò, G.: Eur. Phys. J. A 30, 23 (2006)
Li, B.A., Han, X.: Phys. Lett. B 727, 276 (2013)
Kievsky, A., Viviani, M., Logoteta, D., Bombaci, I., Girlanda, L.: Phys. Rev. Lett. 121, 072701 (2018)
Danielewicz, P., Lee, J.: Nucl. Phys. A 922, 1 (2014)
Roca-Maza, X., et al.: Phys. Rev. C 87, 034301 (2013)
Tolman, R.C.: Proc. Nat. Acad. Sci. (USA) 20, 169 (1934)
Gulminelli, F., Raduta, Ad.D.: Phys. Rev. C 92, 055803 (2015)
Bombaci, I., Logoteta, D.: EPJ Web of Conferences 117, 07005 (2016)
Bombaci, I.: JPS Conf. Proc. 17, 101002 (2017)
Wiringa, R.B., Stoks, V.G.J., Schiavilla, R.: Phys. Rev. C 51, 38 (1995)
Rijken, Th.A., Nagels, M.M., Yamamoto, Y.: Nucl. Phys. A 835, 160, (2010)
Baldo, M., Burgio, G.F., Schulze, H.-J.: Phys. Rev. C 61, 055801 (2000)
Vidaña, I., Polls, A., Ramos, A., Engvik, L., Hjorth-Jensen, M.: Phys. Rev. C 62, 035801 (2000)
Schulze, H.-J., Rijken, Th.A.: Phys. Rev. C 84, 035801 (2011)
Djapo, H., Schaefer, B.-J., Wambach, J.: Phys. Rev. C 81, 035803 (2010)
Hashimoto, O., Tamura, H.: Progr. Part. Nucl. Phys. 57, 564 (2006)
Millener, D.J.: Lect. Notes Phys. 724, 31 (2007)
Rappold, C., et al., HypHI Collaboration: Nucl. Phys. A 913, 170 (2013)
Feliciello, A., Nagae, T.: Rep. Progr. Phys. 78, 096301 (2015)
Tamura, H., et al.: Proceedings, 11th International Conference on Hypernuclear and Strange Particle Physics (HYP 2012): Barcelona, Spain, October 1–5, 2012. Nuclear Phys., vol. A914, p. 99 (2013)
Botta, E., Bressani, T., Garbarino, G.: Eur. Phys. J. A 48, 41 (2012)
Curceanu, C., et al.: Acta Phys. Pol. B 46, 203 (2015)
Gal, A., Hungerford, E.V., Millener, D.J.: Rev. Mod. Phys. 88, 035004 (2016)
Tolos, L., Fabbietti, L.: Progr. Part. Nucl. Phy. 112, 103770 (2020)
Petschauer, S., Haidenbauer, J., Kaiser, N., Meißner, U.-G., Weise, W.: Front. Phys. 8, 12 (2020)
Spitzer, R.: Phys. Rev. 110, 1190 (1958)
Bach, G.G.: Nuovo Cimento XI, 73 (1959)
Dalitz, R.H.: 9th Int. Ann. Conf. on High-Energy Physics. Academy of Sciences, USSR, vol. I, p. 587 (1960)
Bodmer, A., Sampanthar, S.: Nucl. Phys. 31, 251 (1962)
Conte, F., Iwao, S.: Nucl. Phys. 58, 291 (1964)
Bodmer, A.R., Murphy, J.W.: Nucl. Phys. 64, 593 (1965)
Gal, A.: Phys. Rev. 152, 975 (1966); Gal, A.: Phys. Rev. Lett. 18, 568 (1967)
Bhaduri, R.K., Losieau, B.A., Nogami, Y.: Ann. Phys. 44, 57 (1967)
Gal, A., Soper, J.M., Dalitz, R.H.: Ann. Phys. 63, 53 (1971)
Bodmer, A.R., Usmani, Q.N., Carlson, J.: Phys. Rev. C 29, 684 (1984)
Yamamoto, Y.: Phys. Rev. C 36, 2166 (1987)
Vidaña, I., Logoteta, D., Providencia, C., Polls, A., Bombaci, I.: Europhys. Lett. 94, 11002 (2011)
Yamamoto, Y., Furumoto, T., Yasutake, N., Rijken, Th.: Phys. Rev. C 90, 045805 (2014)
Lonardoni, D., Lovato, A., Gandolfi, S., Pederiva, F.: Phys. Rev. Lett. 114, 092301 (2015)
Logoteta, D., Vidaña, I., Bombaci, I.: Eur. Phys. J. A 55, 207 (2019)
Gerstung, D., Kaiser, N., Weise, W.: Eur. Phys. J. A 56, 175 (2020)
Ivanenko, D., Kurdgelaidze, D.F.: Lett. Nuovo Cimento 2, 13 (1969)
Itho, N.: Prog. Teor. Phys. 44, 291 (1970)
Iachello, F., Langer, W.D., Lande, A.: Nucl. Phys. A 219, 612 (1974)
Collins, J.C., Perry, M.J.: Phys. Rev. Lett. 34, 1353 (1975)
Baym, G., Chin, S.A.: Phys. Lett. B 62, 241 (1976)
Keister, B.D., Kisslinger, L.S.: Phys. Lett. B 64, 117 (1976)
Lenzi, C.H., Lugones, G.: Astrophys. J. 759, 57 (2012)
Bonanno, L., Sedrakian, A.: A&A 539, A16 (2012)
Orsaria, M., Rodrigues, H., Weber, F., Contrera, G.A.: Phys. Rev. C 89, 015806 (2014)
Bombaci, I., Logoteta, D.: MNRAS 433, L79 (2013)
Whittenbury, D.L., Matevosyan, H.H., Thomas, A.W.: Phys. Rev. C 93, 035807 (2016)
Bodmer, A.R.: Phys. Rev. D 4, 1601 (1971)
Terazawa, H.: INS Rep. 336 (Univ. Tokyo, INS) (1979); J. Phys. Soc. Jpn. 58, 3555 (1989); 58, 4388 (1989); 59, 1199 (1990)
Witten, E.: Phys. Rev. D 30, 272 (1984)
Farhi, E., Jaffe, R.L.: Phys. Rev. D 30, 2379 (1984)
Madsen, J.: Phys. Rev. D 50, 3328 (1994)
Mustafa, M.G., Ansari, A.: Phys. Rev. D 53, 5136 (1996)
Alcock, C., Farhi, E., Olinto, A.: Astrophys. J. 310, 261 (1986)
Dey, M., Bombaci, I., Dey, J., Ray, S., Samanta, B.C.: Phys. Lett. B 438, 123 (1998); Phys. Lett. B 447, 352 (1999); Phys. Lett. B 467, 303 (1999)
Li, X.-D., Bombaci, I., Dey, M., Dey, J., van den Heuvel, E.P.J.: Phys. Rev. Lett. 83, 3776 (1999)
Li, X.-D., Ray, S., Dey, J., Dey, M., Bombaci, I.: Astrophys. J. 527, L51 (1999)
Xu, R.X., Qiao, G.J., Zhang, B.: Astrophys. J. 522, L109 (1999)
Casalbuoni, R., Nardulli, G.: Rev. Mod. Phys. 76, 263 (2004)
Alford, M.G., Schmitt, A., Rajagopal, K., Schafer, T.: Rev. Mod. Phys. 80, 455 (2008).
Anglani, R., Casalbuoni, R., Ciminale, M., Ippolito, N., Gatto, R., Mannarelli, M., Ruggeri, M.: Rev. Mod. Phys. 86, 509 (2014)
Buballa, M., Carignano, S.: Progr. Part. Nucl. Phys. 81, 39 (2015)
Bhattacharyya, S., Bombaci, I., Bandyopadhyay, D., Thampan, A.V., Logoteta, D.: New Astron. 54, 61 (2017)
Bhattacharyya, S., Bombaci, I., Logoteta, D., Thampan, A.V.: MNRAS 457, 3101 (2016)
Lindblom, L.: Astrophys. J. 398, 569 (1992)
Riley, T.E., et al.: MNRAS 478, 1093 (2018)
Berezhiani, Z., Bombaci, I., Drago, A., Frontera, F., Lavagno, A.: Nucl. Phys. B Proc. Suppl. 113, 268 (2002)
Berezhiani, Z., Bombaci, I., Drago, A., Frontera, F., Lavagno, A.: Astrophys. J. 586, 1250 (2003)
Bombaci, I., Parenti, I., Vidaña, I.: Astrophys. J. 614, 314 (2004)
Drago, A., Lavagno, A., Pagliara, G.: Eur. Phys. J. A 19, 197 (2004)
Lugones, G., Bombaci, I.: Phys. Rev. D 72, 065021 (2005)
Drago, A., Lavagno, A., Parenti, I.: Astrophys. J. 659, 1519 (2007)
Bombaci, I., Lugones, G., Vidaña, I.: A&A 462, 1017 (2007)
Bombaci, I., Panda, P.K., Providencia, C., Vidaña, I. : Phys. Rev. D 77, 083002 (2008)
Bombaci, I., Logoteta, D., Panda, P.K., Providencia, C., Vidaña, I.: Phys. Lett. B 680, 448 (2009)
Bombaci, I., Logoteta, D., Providencia, C., Vidaña, I.: A&A 528, A71 (2011)
Drago, A., Lavagno, A., Pagliara, G.: Phys. Rev. D 89, 043014 (2014)
Bombaci, I., Logoteta, D., Vidaña, I., Providencia, C.: Eur. Phys. J. A 52, 58 (2016)
Drago, A., Lavagno, A., Pagliara, G., Pigato, D.: Eur. Phys. J. A 52, 40 (2016)
Drago, A., Pagliara, G.: Eur. Phys. J. A 52, 41 (2016)
Drago, A., Lavagno, A., Metzger, B., Pagliara, G.: Phys. Rev. D 93, 103001 (2016)
Pili, A.G., Bucciantini, N., Drago, A., Pagliara, G., Del Zanna, L.: MNRAS 462, L26 (2016)
Bhattacharyya, S., Bombaci, I., Logoteta, D., Thampan, A.V.: Astrophys. J. 848, 65 (2017)
Drago, A., Pagliara, G.: Phys. Rev. D 102, 063003 (2020)
Hsu, S.D.H., Schwetz, M.: Phys. Lett. B 432, 203 (1998)
Fodor, Z., Katz, S.D.: JHEP 04, 050 (2004)
Bombaci, I., Datta, B.: Astrophys. J. 530, L69 (2000)
Olesen, M.L.: Madsen, J.: Phys. Rev. D 49, 2698 (1994)
Hulse, R.A., Taylor, J.H.: Astrophys J. 195, L51 (1975); Weisberg, J.M., Nice, D.J., Taylor, J. H.: Astrophys J. 722, 1030 (2010)
Patruno, A., Haskell, B., Andersson, N.: Astrophys. J. 850, 106 (2017)
Abbott, R., et al.: Astrophys. J. Lett. 896, L44 (2020)
Bombaci, I., Drago, A., Logoteta, D., Pagliara, G., Vidaña, I.: Phys. Rev. Lett. 126, 162702 (2021)
Acknowledgements
I thank the editors of the present book, Sudip Bhattacharyya, Alessandro Papitto, and Dipankar Bhattacharya, for inviting me to write this chapter. I dedicate this work to my beloved son, Paride.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Bombaci, I. (2022). The Equation of State of Neutron Star Matter. In: Bhattacharyya, S., Papitto, A., Bhattacharya, D. (eds) Millisecond Pulsars. Astrophysics and Space Science Library, vol 465. Springer, Cham. https://doi.org/10.1007/978-3-030-85198-9_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-85198-9_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-85197-2
Online ISBN: 978-3-030-85198-9
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)














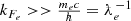 , thus for densities
, thus for densities 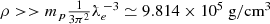 .
.