Abstract
Point-free topology is the study of the category of locales and localic maps and its dual category of frames and frame homomorphisms. These notes cover the topics presented by the first author in his course on Frames and Locales at the Summer School in Algebra and Topology. We give an overview of the basic ideas and motivation for point-free topology, explaining the similarities and dissimilarities with the classical setting and stressing some of the new features.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
Math. Subj. Classification
Introduction
Topology can be cultivated as the natural geometry of places (“spots”) and their interrelations. One does not have to think of them as sets of points: they can be thought as entities in their own right (similarly as lines in classical geometry are not sets of incident points). Such (point-free) approach to general geometry appeared in topology already in the late thirties and forties, started to be systematically cultivated in the last decades of previous century, and flourishes since. It has turned out that by forgetting about points one does not lose really important information (unless, of course, when needing a topology as technical means for solving a problem in a concrete—typically otherwise structured—set, which is another matter). On the contrary, one gains important new insights into the general structure of space and obtains results that are in some respects better than the classical counterparts, or such that have no classical counterparts at all. Also, the point-free approach opens door to applications in theoretical computer science.
In this text we would like to introduce the reader to point-free thinking, to illustrate the reasoning (for this, we present some proofs hoping to persuade the reader that the techniques are in fact fairly friendly) and present some results to illustrate the merits of the approach. In Prologue we expound point-free topology as a natural synthetic general geometry and briefly outline the history. Then we discuss the necessary order-theoretic background, the relation to classical spaces, and some categorical aspects. Next we introduce the reader to some concrete facts about point-free spaces (locales), and finally we present a few facts showing their advantages and merits.
1 Prologue
1.1 General Topology
General (set-theoretic) topology is a generalized geometry. Note, however, that it fundamentally differs from the classical geometry: it lacks a synthetic variant preceding the current analytic one. Let us explain.
In the classical (synthetic Euclidean) geometry we work with entities like points, lines, or planes, entities of their own right. One studies their interrelations, in particular the incidence, which should not be confused with the set-theoretic \(\in \). A point can be incident (or non-incident) with a line. A line p, however, is not identified with the set of all the points incident with p, and similarly in stereometry, the relation between lines and planes is not a set-theoretic inclusion.
Only much later, in the analytic version, one starts with a beforehand given set of elements (say, pairs of numbers); points, lines, etc., are defined as specific types of subsets (the fact that points are represented as one-element subsets is more or less accidental and not important for what we want to emphasize).
General topology, like many modern structures, comes right away in the analytic form: one starts with a set, and the structure is given by assigning specific roles to some of the subsets.
1.2 A Synthetic Generalized Geometry
The following is not an account of what historically happened. Let us just pretend designing a synthetic generalized geometry from scratch. We will do it modelling the intuition of the behavior of “pieces of space” (we will call them spots) as we think about them in the “space around us”.
1.2.1 Order
First, the system L of such spots is naturally ordered:
a spot can be an extension of another one
(we do not have in mind a set-theoretic inclusion—a spot is not a set of elements—just think of a spot being larger than another one).
1.2.2 Glueing Spots Together
Next, given a system A of spots we can think of conglutinating (merging, pasting) them together and obtaining a new one. It will be the smallest spot larger than all the \(a\in A\) and hence, formally, this amounts to assuming that the ordered L is a complete lattice, and that the systems A combine to their suprema (joins) \(\mathop {\textstyle \bigvee }A\).
1.2.3 Meeting Conglutinated Spots
It is natural to assume that
a spot b meets the result of pasting the \(a\in A\) together, the conglutination \(\mathop {\textstyle \bigvee }A\), only if it meets some of the constituents \(a\in A\).
Formally,

It is easy to see that this means precisely that our complete lattice admits pseudocomplements. Thus, our (we hope admittedly natural) assumptions lead us to the conclusion that
a general synthetic geometry can be viewed as a complete pseudocomplemented lattice.
1.2.4 One More Assumption
Finally, let us agree that at least some naturally defined sublattices of L are synthetic geometries as well. Confining ourselves to the up-sets  we obtain the condition (meet) strengthened to
we obtain the condition (meet) strengthened to

and this is easily seen to be equivalent to the frame distribution law

Complete lattices satisfying (frm) are called frames; taking into account that this is equivalent with the Heyting structure (see 2.6 below) and that it is a more expedient condition than the mere existence of pseudocomplements, we can view frames as representatives of fairly general synthetic geometries. And there will be a strong corroboration of this view in the next subsections.
1.3 A More Realistic Account of the Events
The development of topology did not follow the reckoning outlined in the subsection 1.2. General topology has been created as an analytic theory, preceding a synthetic one; but the synthetic successor turns out to be precisely what we have obtained above. Moreover it leads to a suitable definition of mappings between generalized geometries, which we have in 1.2 not even started to contemplate.
Modern topology originated in the pioneering Hausdorff’s article [23] published in 1914. The intuition behind the introduced general concept of a space is based on the natural distinction between a set surrounding a point as opposed to a set just including it: think of a ship in a lake surrounded by water from all the sides as opposed to a landed one touching a pier. The structure of a space, carried by a set, is constituted by determining the neighborhoods \(U\ni x\) as special subsets of X containing x, satisfying very natural assumptions.
Soon (already in the twenties) an equivalent alternative approach based on the notion of an open set (in the original concept setting: a set that is a neighborhood of all its points; and on the other hand, if we start with the notion of an open set we can define a neighborhood of x as a \(U\ni x\) such that there is an open V with \(x\in V\subseteq U\)). Comparing it with the neighborhood intuition it might look somewhat less transparent to start with (trading an obvious intuition for technical advantages which are indisputable), but nowadays we know better: in fact it is the intuition of a synthetic version of topology as outlined above: an open set, a set without boundary, is a good model of a spot, and the system of open sets constitutes a complete sublattice \(\Omega (X)\) of the powerset of X closed under arbitrary unions and finite meets, and hence satisfying the frame distribution law. Thus we have here an example (in fact a typical one) of a frame, a general geometry presented in subsection 1.2.
1.3.1 A Few Historical Notes
Although one did not necessarily have in mind developing synthetic topology, the ideas of harnessing lattice theory in topology (via the lattices of open resp. closed sets) appeared already in the late thirties and in the forties. The Stone duality [53] replacing (very special) topological spaces and continuous maps by Boolean algebras and homomorphisms is deservedly a most cited example. But one should not forget the outstanding Wallman’s article [55] where the lattice technique allowed for an ingenious compactification (and not only that: the author is consequent in the lattice technique even to the point of using a specific point-free separation axiom).
In the fifties the attempts to develop a variant of topology without points became more and more frequent. It is not our intention to present here a detailed history. The reader can find a short account in the introduction to our monograph [44], but we can particularly recommend the excellent Johnstone’s “The point of pointless topology” [29] and “Elements of the history of locale theory” [33]. Here let us just state that the basic concepts started to settle in late fifties [14, 16, 42] and continued in works of Banaschewski, who had been regarding to topology from a lattice-theoretic point of view since 1953 [3], Dowker, Isbell, Johnstone, Joyal and Tierney, that the first stage of the theory culminated in the monograph [28], and that the theory flourishes.
1.4 Frame Homomorphisms
We have spoken of spaces, either classical or point-free, as objects. The most important concept of classical topology, however, is continuity. What is the counterpart of continuous maps in the point-free context? The characteristic property of continuous maps is that they preserve openness by preimage. Thus, with a continuous map \(f:X\rightarrow Y\) there is associated a mapping \(\Omega (f):\Omega (Y)\rightarrow \Omega (X)\) sending each U to \(\Omega (f)(U)=f^{-1}[U]\). Since preimage preserves unions and intersections and since all unions of open sets are open and finite intersections of open sets are open as well, we see that \(\Omega (f)\) preserves arbitrary joins and finite meets. This has been adopted for the definition of a frame homomorphism: it is a mapping \(h:L\rightarrow M\) between frames preserving all joins and finite meets.Footnote 1
1.4.1 Note
The general geometry (leading, ultimately, to frames) was based on the idea of spots that can merge and the relation of intersecting. Thus, while the former really has to do with joins, the latter involves only the question whether \(x\wedge y=0\) or \(x\wedge y\ne 0\). Thus we can naturally ask whether the appropriate maps between geometries should not be those that
-
(1)
preserve all joins, and
-
(2)
satisfy the implication \(x\wedge y=0\ \Rightarrow \ h(x)\wedge h(y)=0\).
It turns out that in a large (and important) class of frames such maps are frame homomorphisms anyway (see [13]). But in full generality these conditions are weaker.
2 Background
2.1 Posets
When dealing with posets we will use the standard notation. If necessary we use different symbols for different orders, but if there is no danger of confusion we write simply \(\le \) (like in saying that “\(f:(X,\le )\rightarrow (Y,\le )\) is monotone if \(x\le y\) implies that \(f(x)\le f(y)\)” even if there is in fact on Y a relation different from that on X—similarly like we do not hesitate to use the same arrow symbol “\(\rightarrow \)” when indicating morphisms in two distinct categories).
We write

and abbreviate  ,
,  . An element a is an upper (resp. lower) bound of \(A\subseteq (X,\le )\) if
. An element a is an upper (resp. lower) bound of \(A\subseteq (X,\le )\) if  (resp.
(resp.  ) and the least upper (resp. largest lower) bound, if it exists is called the supremum or join (resp. infimum or meet) of A and denoted by \(\mathop {\textstyle \bigvee }A\) resp. \(\mathop {\textstyle \bigwedge }A\). We also use symbols \(a\vee b\) for \(\mathop {\textstyle \bigvee }\{a,b \} \), \(a_1\vee \cdots \vee a_n\), \(\mathop {\textstyle \bigvee }_{i\in I}a_i\), and, similarly, with \(\mathop {\textstyle \bigwedge }\) or \(\wedge \), in the obvious sense.
) and the least upper (resp. largest lower) bound, if it exists is called the supremum or join (resp. infimum or meet) of A and denoted by \(\mathop {\textstyle \bigvee }A\) resp. \(\mathop {\textstyle \bigwedge }A\). We also use symbols \(a\vee b\) for \(\mathop {\textstyle \bigvee }\{a,b \} \), \(a_1\vee \cdots \vee a_n\), \(\mathop {\textstyle \bigvee }_{i\in I}a_i\), and, similarly, with \(\mathop {\textstyle \bigwedge }\) or \(\wedge \), in the obvious sense.
The least resp. largest element of \((X,\le )\), that is, \(\mathop {\textstyle \bigvee }\emptyset \) resp. \(\mathop {\textstyle \bigwedge }\emptyset \), if it exists will be denoted by 0 resp. 1.
The poset obtained by reversing the order, that is \((X,\le ')\) with \(x\le ' y\ \equiv \ y\le x\) is called the dual of \((X,\le )\) and denoted as \((X,\le )^{{\text {op}}}\). We may also write \(\le ^{{\text {op}}}\) for thus defined \(\le '\).
2.1.1 Lattices
A poset in which all the subsets have infima and suprema are called complete lattices. If all finite sets have suprema and infima we speak of bounded lattices, in case of non-void finite sets simply of lattices.
2.2 Adjunctions
We say that monotone maps
are (Galois) adjoint, f to the left and g to the right, and write \(f \dashv g\), if

It is standard and (very easy) to see that this is equivalent with assuming that

Note that from these inequalities it readily follows that

2.2.1 Facts
(a) Generally, left adjoints preserve all existing suprema and right adjoints preserve all existing infima.
(b) On the other hand, if X, Y are complete lattices then each \(f :X \rightarrow Y\) preserving all suprema is a left adjoint (i.e. it has an adjoint on the right), and each \(g :Y \rightarrow X\) preserving all infima is a right adjoint.
Proof
(a) Let f be a left adjoint and \(s=\mathop {\textstyle \bigvee }A\) in X. Then obviously f(s) is an upper bound of f[A]. Now let b be a general upper bound of f[A], that is, let \(f(a)\le b\) for all \(a\in A\). Then for all \(a\in A\), \(a\le g(b)\), hence g(b) is an upper bound of A, hence \(s\le g(b)\), and finally \(f(s)\le b\).
(b) Let f preserve all joins. Set \(g(y)=\mathop {\textstyle \bigvee }\{z \ | \ f(z)\le y\} \). If \(f(x)\le y\) then trivially \(x\le g(y)\). On the other hand if \(x\le g(y)=\mathop {\textstyle \bigvee }\{z \ | \ f(z)\le y\} \) then \(f(x)\le f(\mathop {\textstyle \bigvee }\{z \ | \ f(z)\le y\} )=\mathop {\textstyle \bigvee }\{f(z) \ | \ f(z)\le y\} \le y\). \(\square \)
2.3 For Category Minded Readers: Posets as Special Categories
A category is said to be thin if for any two objects A, B there is at most one morphism \(A\rightarrow B\). A poset \((X,\le )\) (more generally, a preordered set) is a thin category in which a morphism \(x\rightarrow y\) is the statement that \(x\le y\), if it holds true: reflexivity of \(\le \) provides the identity morphisms and transitivity provides the composition of morphisms.
Note that, on the other hand
every thin category is a preordered partially ordered class,
(which differs from a partially ordered set by possibly being carried by a proper class, and by \(a\le b\) and \(b\le a\) for isomorphic distinct objects a, b).
Monotone maps \(f:(X,\le )\rightarrow (Y,\le )\) are in this perspective precisely the functors between such categories.
Now the adjunction from 2.2 is a special case of the adjunction of functors \(L:\mathscr {A}\rightarrow \mathscr {B}\) and \(R:\mathscr {B}\rightarrow \mathscr {A}\) in categories. Recall (adj1) and compare
further compare (adj2) with the adjunction units
and (adj3) with

(in the general case the latter has to be assumed, in the thin case it comes for free and becomes the former).
Further realize that the (partial order) upper or lower bounds are precisely the categorical upper or lower bounds in the thin case, and infima resp. suprema coincide with products and coproducts:

Thus, the first fact in 2.2.1 is a special case of preservation of colimits and limits by left and right adjoint functors. Since equalizers (resp. coequalizers) exist trivially in thin categories, the existence of limits (resp. colimits) means existence of products (resp. coproducts), that is, infima (resp. suprema). Hence, complete lattices are the complete (and cocomplete) such categories.
The correspondence of the second fact in 2.2.1 with the theorems on the existence of adjoint functors is not quite so straightforward. One has to keep in mind that in general categories we do not have a proper counterpart to the concept of a complete lattice: in complete and cocomplete categories we consider small (set) diagrams in large (class carried) categories (and large diagrams would not make sense) while in complete lattices we admit (and need) “diagrams of the same size”. But there are theorems that present adjoint functors under reasonable circumstances.
To finish this short excursion to categorial reasoning: we have seen posets and Galois adjunction as a special case of adjunction in categories. It is, however, sometimes also profitable to look at the situation the other way, namely as primarily a phenomenon in posets extended to categories where instead of one arrow between nodes one has labelled ones, with structured labelling.
2.4 Some Special Posets
A meet resp. join semilattice has \(a\wedge b\) resp. \(a\vee b\) for any a, b (and consequently all non-empty finite meets resp. joins); if it is obvious from the context whether the meets or joins are meant, one speaks simply of a semilattice.
We have already introduced lattices, bounded lattices and complete lattices in 2.1.1. Further, a lattice is distributive if we have
(the equivalence may be slightly surprising; it is important to realize that it amounts to the fact that the dual of a distributive lattice is also distributive).
2.5 Pseudocomplements, Supplements and Complements
We might consider a more general situation, but for our purposes everything in the remaining part of this section will happen in bounded lattices L. A pseudocomplement (resp. supplement) of an element \(a\in L\) is an element b such that
None of them has to exist, but if it does it is obviously uniquely determined. If it exists we usually denote it by \(a^*\) resp. \(a^\#\).
A complement of a is an element b such that \(a\wedge b=0\) and \(a\vee b=1\). It does not have to exist and in general it is not even uniquely determined. But in a distributive lattice there is at most one and if it exists it is simultaneously a pseudocomplement and a supplement. One then speaks of a complemented element and the complement is usually denoted \(a^*\) (if there is no danger of confusion, otherwise another symbol, e.g. \(a^{\mathsf{c}}\), is used).
2.6 Heyting Algebras
A bounded lattice L is called a Heyting algebra if there is a binary operation \(x\!\rightarrow \!y\) (the Heyting operation) such that for all a, b, c in L,

Recall 2.2 and realize that (Hey) says precisely that for every b
-
the mapping \(b\!\rightarrow \!(-)=(x\mapsto b\!\rightarrow \!x):L\rightarrow L\) is a right Galois adjoint of \((-)\wedge b=(x\mapsto x\wedge b):L\rightarrow L\)
and hence
-
(H1)
the operation \(\rightarrow \!\), if it exists, is uniquely determined; thus, being Heyting is in fact a condition on the meet in L,
-
(H2)
in a Heyting algebra one has \((\mathop {\textstyle \bigvee }A)\wedge b=\mathop {\textstyle \bigvee }_{a\in A}(a\wedge b)\) for any \(A\subseteq L\) such that \(\mathop {\textstyle \bigvee }A\) exists, and \(b\!\rightarrow \!\mathop {\textstyle \bigwedge }A=\mathop {\textstyle \bigwedge }_{a\in A}(b\!\rightarrow \!a)\) for any \(A\subseteq L\) such that \(\mathop {\textstyle \bigwedge }A\) exists,
-
(H3)
and if L is complete then the distributivity rule
$$\begin{aligned} (\mathop {\textstyle \bigvee }A)\wedge b=\mathop {\textstyle \bigvee }_{a\in A}(a\wedge b) \end{aligned}$$is a necessary and sufficient condition for the existence of a Heyting operation on L.
2.6.1 Notes
(a) Unlike the plain distributivity \((a\vee b)\wedge c= (a\wedge c)\vee (b\wedge c)\) the distributivity from (H3) is not carried over to the dual. See 3.2.2 below.
(b) It follows immediately from (Hey) that \(a\le b\rightarrow c\) iff \(b\le a\rightarrow c\). This is a contravariant Galois adjunction that yields moreover the rule
-
(H4)
\(\displaystyle (\mathop {\textstyle \bigvee }A)\rightarrow b=\mathop {\textstyle \bigwedge }_{a\in A}(a\rightarrow b).\)
(c) Dually one defines a coHeyting algebra as a bounded lattice with a binary operation (coHeyting operation) \(c\smallsetminus b\) (called the difference) such that
The importance of this concept will be apparent in 5.4 below.
2.6.2 A Few Heyting Rules
In the sequel we will often need to compute with the Heyting operation. Here are some formulas that are immediate consequences of (Hey).
-
(1)
\(a\le b\!\rightarrow \!a\) (since \(a\wedge b\le a\)).
-
(2)
\(1\!\rightarrow \!a=a\) (since \(x\le a\) iff \(x\wedge 1\le a\), that is, \(x\le 1\!\rightarrow \!a\)).
-
(3)
\(a\!\rightarrow \!b=1\) iff \(a\le b\) (since \(1\le a\!\rightarrow \!b\) iff \(1\wedge a\le b\)).
-
(4)
\(a\wedge (a\!\rightarrow \!b)\le b\) (since \(a\!\rightarrow \!b\le a\!\rightarrow \!b\), the well known “modus ponens” rule).
-
(5)
\(a\wedge (a\!\rightarrow \!b)=a\wedge b\) (\(\le \) by (4) and \(\ge \) by (1)).
And here are three further useful ones, perhaps slightly less trivial, but still very simple.
-
(6)
\(a\!\rightarrow \!(b\!\rightarrow \!c)=(a\wedge b)\!\rightarrow \!c=b\!\rightarrow \!(a\!\rightarrow \!c)\)
(we have \(x\le a\!\rightarrow \!(b\!\rightarrow \!c)\) iff \(x\wedge a\le b\!\rightarrow \!c\) iff \(x\wedge a\wedge b\!\rightarrow \!c\) iff \(x\le (a\wedge b)\!\rightarrow \!c\)).
-
(7)
\(a\!\rightarrow \!b= a\!\rightarrow \!c\) iff \(a\wedge b=a\wedge c\)
(\(\Rightarrow \): By (5) and (4), \(a\wedge b=a\wedge (a\!\rightarrow \!b)=a\wedge (a\!\rightarrow \!c)=a\wedge c\). \(\Leftarrow \): By (3) and (H2), \(a\!\rightarrow \!b=(a\!\rightarrow \!a)\wedge (a\!\rightarrow \!b)= a\!\rightarrow \!(a\wedge b)=a\!\rightarrow \!(a\wedge c)=a\!\rightarrow \!c\)).
-
(8)
\(x=(x\vee a)\wedge (a\!\rightarrow \!x)\)
(by (4) and (1), \((x\vee a)\wedge (a\!\rightarrow \!x)=(a\wedge (a\!\rightarrow \!x))\vee (x\wedge (a\!\rightarrow \!x))\le x\); on the other hand, by (1), \(x\le (x\vee a)\wedge (a\!\rightarrow \!x)\)).
2.6.3 Pseudocomplement Rules
In a Heyting algebra one obviously has a pseudocomplement, namely \(a^*=a\!\rightarrow \!0\), with the following obvious properties:
-
(1)
\(a\le b\ \Rightarrow \ b^*\le a^*\).
-
(2)
\(a\le a^{**}\) and \(a^{***}=a^*\).
-
(3)
\((\mathop {\textstyle \bigvee }A)^*=\mathop {\textstyle \bigwedge }_{a\in A} a^*\) for any \(A\subseteq L\) such that \(\mathop {\textstyle \bigvee }A\) exists (De Morgan law). Caution: the dual law for \(\mathop {\textstyle \bigwedge }A\) does not hold in general.
(Note that in \(\Omega (X)\), \(U^*\) is the interior of \(X\smallsetminus U\).)
Dually, in a coHeyting algebra one has the supplement \(a^\#=1\smallsetminus a\).
On the other hand we easily prove
2.6.4 Observation
Let b have a complement \(b^{\mathsf{c}}\) in a distributive lattice L. Then
Thus, in a Heyting algebra we have for any complemented element b, \(b\!\rightarrow \!c=b^*\vee c\) and in a coHeyting algebra we have for any complemented element b, \(c\smallsetminus b=c\wedge b^\#\).
Note
All the assumptions are essential, though. In particular the formulas \(b\!\rightarrow \!c=b^*\vee c\) resp. \(c\smallsetminus b=c\wedge b^\#\) hold for complemented elements only; the Heyting resp. coHeyting operation cannot be thus reduced to pseudocomplementing resp. supplementing in no other case.
2.7 Boolean Algebras
A Boolean algebra is a distributive lattice in which every element is complemented. From 2.6.4 we immediately obtain
Corollary
A Boolean algebra is both a Heyting and a coHeyting algebra.
3 Frames and Spaces
3.1 The Category of Frames
A frame (resp. coframe) is a complete lattice L satisfying the distributivity law

for all \(A\subseteq L\) and \(b\in L\). A frame homomorphism \(h:L\rightarrow M\) between two frames is a mapping preserving all joins and all finite meets. The resulting category will be denoted by
Similarly we have coframe homomorphisms between coframes preserving all meets and finite joins.
3.2 Spaces and Frames. The Functor \(\Omega \)
A typical frame is the lattice \( \Omega (X) \) of all open subsets of a topological space. Furthermore, if \(f:X\rightarrow Y\) is a continuous mapping we have a frame homomorphism \(\Omega (f):\Omega (Y)\rightarrow \Omega (X)\) defined by \(\Omega (f)(U)=f^{-1}[U]\). Thus we obtain a contravariant functor
a basic link between classical spaces and what will turn out to be the generalized ones (see already in 3.5.2 below, then in 3.9, and again and again).
3.2.1 A Warning
Let us agree that our spaces will be, from now on, always \(T_0\): the frames \(\Omega (X)\) will be central in our approach to spaces and it will make no sense to discuss classical points that cannot be distinguished by open sets. In particular we will, without further particular mentioning, use the following
Observation
Let \(f,g:X\rightarrow Y\) be distinct continuous maps, and let Y be \(T_0\). Then \(\Omega (f)\ne \Omega (g)\).
(Indeed, if \(f(x)\ne g(x)\) consider a U such that, say, \(g(x)\notin U\ni f(x)\). Then \(x\in \Omega (f)(U)\smallsetminus \Omega (g)(U)\).)
3.2.2 Notes
(a) Unlike plain (finite) distributivity, the frame distributivity typically does not carry over to the dual, that is, a frame is seldom simultaneously a coframe. Take e.g. any \(T_1\)-space X with a non-isolated point x and an open set \(W\ni x\). Set \(V=W\smallsetminus \{x \} \) and \(\mathcal U=\{U\in \Omega (X) \ | \ x\in U\} .\) Then \(\mathop {\textstyle \bigwedge }\mathcal U=\mathrm{int}\,\mathop {\textstyle \bigcap }\mathcal U=\emptyset \) and hence \((\mathop {\textstyle \bigwedge }\mathcal U)\cup V=V\) while \(\mathop {\textstyle \bigwedge }\{U\cup V \ | \ U\in \mathcal U\} =W\ne V\).
(b) As the example shows, coframes will seldom come as models of (generalized) spaces. They will play, however, a fundamental role in the study of the structure of generalized subspaces.
3.3 The Heyting Structure
Recall 2.6 (and 2.2). The distributivity rule (frm) makes a frame a Heyting algebra and computing with the Heyting operation will be extensively used; similarly we will use computing with the difference in coframes. But we have to keep in mind that the category \(\mathsf{Frm}\) is not that of (complete) Heyting algebras: frame homomorphisms generally do not respect the Heyting operation.
3.4 Prime Elements and Sobriety
Recall that an element \(p<1\) in a distributive lattice is prime if
(compare with primeness of numbers); equivalently, \(a\wedge b\le p\) only if \(a\le p\) or \(b\le p\) (readily deduced replacing \(a\wedge b\le p\) by \((a\vee p)\wedge (b\vee p)=(a\wedge b)\vee p=p\)).
Typical prime elements in \(\Omega (X)\) are the open sets \(X\smallsetminus \overline{\{x \} }\). A \(T_0\)-space is sober [44] if there are no other primes in \(\Omega (X)\).
3.4.1 Notes
(a) Sobriety is a very common property of topological spaces. For instance every Hausdorff space is sober:
Suppose a prime \(P\in \Omega (X)\) lacks two distinct points x and y. Separate them by disjoint \(U\ni x\) and \(V\ni y\) and consider the intersection \(P=(P\cup U)\cap P\cup V)\) where P contains none of \(P\cup U\), \(P\cup V\).
Or, Scott spaces are mostly sober. On the other hand, sobriety is incomparable with the axiom \(T_1\).
(b) Because of the relation with the Hausdorff axiom, sobriety is sometimes viewed as one of the so-called separation axioms. But as it was rightly pointed out by Marcel Erné, it is, rather, a completion condition akin to the completion in metric or more generally uniform spaces. As we will see in the following proposition, it amounts to the assumption that filters that have the natural property of a neighborhood system have “a point in the center” that is, are really neighborhood systems.
Recall that a filter F in a distributive lattice is prime if \(a\vee b\in F\) implies that \(a\in F\) or \(b\in F\), and completely prime if \(\mathop {\textstyle \bigvee }_{i\in I} a_i\in F\) implies that some \(a_i\in F\) for any system \(\{a_i \ | \ i\in I\} \). A typical completely prime filter in \(\Omega (X)\) is the system \(\mathcal U(x)=\{U \ | \ x\in U\} \) of all neighborhoods of a point x.
3.4.2 Proposition
A (\(T_0\)-)space is sober iff each completely prime filter in \(\Omega (X)\) is \(\mathcal U(x)\) for some \(x\in X\).
Proof
\(\Rightarrow \): Let X be sober and let \(\mathcal F\subseteq \Omega (X)\) be a completely prime filter. Set \(V_0= \mathop {\textstyle \bigcup }\{V\in \Omega (X) \ | \ V\notin \mathcal F\} \). By completeness, \(V_0\notin \mathcal F\), hence it is the largest such open set, and

Now if \(U_1\cap U_2\subseteq V_0\) then both of the \(U_i\) cannot be in \(\mathcal F\) (since it is a filter); thus, for some i, \(U_i\subseteq V_0\) and \(V_0\) is prime, and by sobriety \(V_0=X\smallsetminus \overline{\{x_0 \} }\) for some \(x_0\). Thus by (\(*\)), \(U\in \mathcal F\) iff \(U\nsubseteq X\smallsetminus \overline{\{x_0 \} }\) which holds precisely when \(x_0\in U\), that is, \(U\in \mathcal U(x_0)\).
\(\Leftarrow \): Let \(V_0\) be prime. Set \(\mathcal F=\{U\in \Omega (X) \ | \ U\nsubseteq V_0\} \). Obviously \(\mathcal F\) is a complete prime filter, hence \(\mathcal U(x_0)\) for some \(x_0\), so that \(U\nsubseteq V_0\) iff \(x_0\in U\), that is, \(U\subseteq V_0\) iff \(U\subseteq X\smallsetminus \overline{\{x_0 \} }\) and we conclude that \(V_0=X\smallsetminus \overline{\{x_0 \} }\). \(\square \)
3.5 Theorem
Let Y be sober and let \(h:\Omega (Y)\rightarrow \Omega (X)\) be a frame homomorphism. Then there is precisely one continuous map \(f:X\rightarrow Y\) such that \(h=\Omega (f)\).
Proof
Obviously a preimage \(h^{-1}[\mathcal F]\) of a completely prime filter is a completely prime filter. Take an \(x\in X\) and consider \(h^{-1}[\mathcal U(x)]\). By sobriety and 3.4.2 it is \(\mathcal U(y)\) for some \(y\in Y\). Choose such y and denote it by f(x). Thus, \(h^{-1}[\mathcal U(x)]=\mathcal U(f(x))\), that is,
hence thus defined f is continuous and \(h=\Omega (f)\). Uniqueness of f follows immediately from \(T_0\) property: if \(f(x)\ne g(x)\) choose a U such that, say,  showing that \(\Omega (f)(U) \ne \Omega (g)(U)\). \(\square \)
showing that \(\Omega (f)(U) \ne \Omega (g)(U)\). \(\square \)
Thus the restriction \(\Omega :\mathsf{Sob}\rightarrow \mathsf{Frm}\) of \(\Omega \) is a full embedding.
3.5.1 Corollary
A sober space X can be homeomorphically reconstructed from the frame \(\Omega (X)\) as the set
endowed with the topology consisting of the \(\widetilde{U}=\{h \ | \ h(U)=1\} \) with \(U\in \Omega (X)\).
(Indeed, consider the one-point space \(P=\{* \} \). Then \(\Omega (P)=\{\emptyset ,P \} \cong \{0,1 \} \) and we can consider the elements \(x\in X\) represented by the continuous maps \(f_x\) with \(f_x(*)=x\). Those are then by 3.5 in a one-to-one correspondence with the \(h_x=\Omega (f_x)\), and \(h_x(U)=1\) iff \(x = f_x(*)\in U\).)
3.5.2 Locales—So Far Formally
Consider, so far just formally, the dual of the category of frames. It is called the category of locales and it will be studied later in a more transparent and useful concrete form. For the purposes of this section, however, it will be simply
with frame homomorphisms understood in opposite direction for morphisms. Then we have a covariant functor
and Theorem 3.5 can be interpreted as that this functor embeds sober spaces, a substantial part of the category of spaces, into \(\mathsf{Loc}\) as a full subcategory. This justifies viewing frame theory, the “point-free topology”, as an extension of (at least a substantial part) of the classical one. This point of view will be corroborated and confirmed in the sequel; in this section we only wish to demonstrate the basic linkage between the two.
3.6 Points and Spectra
The role of the sobriety in 3.5 and 3.5.1 was in the one-to-one correspondences, not in detecting (classical) points in the lattice \(\Omega (X)\): any point x in any space X is represented by the map \((*\mapsto x):P\rightarrow X\). This leads to the definition of a point in a frame L as a map of locales \(\Omega (P)\rightarrow L\), that is, a frame homomorphism \(L\rightarrow \Omega (P)=\mathbf{2}=\{0,1 \} \) (cf. Clementino [15]).
The following representations of points will come handy.
3.6.1 Proposition
(1) Points h in L are in a one-to-one correspondence with the completely prime filters F in L given by \(h\mapsto F_h=\{x \ | \ h(x)=1\} \) and \(F\mapsto h_F\) with \(h_F(x)=1\) iff \(x\in F\).
(2) Points h in L are in a one-to-one correspondence with the prime elements p of L given by \(h\mapsto p_h= \mathop {\textstyle \bigvee }\{x \ | \ h(x)=0\} \) and \(p\mapsto h_p\) with \(h_p(x)=1\) iff \(x\nleq p\).
Proof
It is a matter of straightforward checking. \(\square \)
3.6.2 Spectra
In the following construction we will represent points as completely prime filters (briefly, cp-filters). This has technical advantages but it is also fairly intuitive: think of points represented by their systems of neighborhoods. The morphisms in \(\mathsf{Loc}\) will be (so far) represented as frame homomorphisms, one has only to be careful with the interchanged domain and codomain.
The spectrum of a frame L is the topological space
where \(\Sigma _a=\{F \ | \ a\in F\} \). Note that

so that \(\{\Sigma _a \ | \ a\in L\} \) is really a topology. For each frame homomorphism \(h:M\rightarrow L\) (\(L\rightarrow M\) in \(\mathsf{Loc}\)) set \(\Sigma (h)(F) =h^{-1}[F]\). We have

hence, each \(\Sigma (h)\) is continuous and we have obtained a functor
Observation
Each \(\Sigma (L)\) is a sober space.
(If \(F\nsubseteq G\), with \(a\in F\), \(a\notin G\) then \(G\notin \Sigma _a\ni F\). Thus \(\Sigma (L)\) is \(T_0\). Let \(\Sigma _a\) be a prime in \(\Omega \Sigma (L)\). Set \(p=\mathop {\textstyle \bigvee }\{b\in L\mid \Sigma _b\subseteq \Sigma _a\}\). In particular, \(\Sigma _p=\Sigma _a\). If \(x\wedge y\le p\) then \(\Sigma _x\cap \Sigma _y\subseteq \Sigma _p=\Sigma _a\) and hence, say, \(\Sigma _x\subseteq \Sigma _p\) so that \(x\le p\). Thus, p is a prime in L. Now note that \(F\in \overline{\{G\}}\) iff \(F\subseteq G\). Consider the \(F=F_{h_p}\) from 3.6.1. We have \(G\notin \overline{\{F\}}\) iff \(G\nsubseteq F\) iff \(h_p(c)=0\) for some \(c\in G\) iff \(c\le p\) for some \(c\in G\) iff \(G\in \Sigma _p=\Sigma _a\). Hence, \(\Sigma _a=\Sigma (L)\smallsetminus \overline{\{F\}}\).)
Theorem
\(\Sigma \) is a right adjoint to \(\Omega \).
Proof
Consider the mappings
given by \(\sigma _L(a)=\Sigma _a\) and \(\rho _X(x)=\mathcal U(x)=\{U \ | \ x\in U\} \). We have already seen in (\(\Sigma 1\)) that \(\sigma _L\) is a homomorphism, and since

\(\rho _X\) is continuous.
Next, they constitute natural transformations \(\sigma :\Omega \Sigma \rightarrow \mathrm{Id}\) (viewed as in \(\mathsf{Loc}\)) and \(\rho :\mathrm{Id}\rightarrow \Sigma \Omega \): indeed,
(recall (\(\Sigma 2\))), and \(\Sigma \Omega (f)(\rho _X(x))=\Omega (f)^{-1}[\mathcal U(x)]=\{U \ | \ f^{-1}[U]\in \mathcal U(x)\} =\{U \ | \ x\in f^{-1}[U]\} = \{U \ | \ f(x)\in U\} =\rho _Y(f(x))\).
Finally, we have to check that the compositions

and

result in identities. We have
and
\(\square \)
3.7 Spatial Frames
A frame L is said to be spatial if it is isomorphic to \(\Omega (X)\) for some space X. The adjointness counit \(\sigma \) of the spectrum offers an expedient criterion of spatiality. We have that
a frame L is spatial iff \(\sigma _L\) is one-to-one
(which is the same as saying that it is an isomorphism). Indeed, by the definition of the space \(\Sigma (L)\), \(\sigma _L\) is always onto, hence if the condition holds we have, trivially, \(L\cong \Omega \Sigma (L)\). On the other hand in the identity in (\(\Sigma 4\)) above, \(\sigma _{\Omega (X)}\) is a coretract and hence an isomorphism. Now if there is an isomorphism \(\phi :L\rightarrow \Omega (X)\) we obtain from the transformation commutativity an isomorphism
Note that in view of 3.6.1 this condition can be reformulated as saying that for any two \(a,b\in L\) with \(a\nleq b\) there is a prime p such that \(b\le p\) and \(a\nleq p\), and hence

3.8 Sober Reflection
The unit \(\rho \) constitutes a reflection of \(\mathsf{Top}\) to \(\mathsf{Sob}\). We have that
a space X is sober iff \(\rho _X\) is a homeomorphism.
Indeed, \(\rho _X\) is invertible by 3.5 and by (\(\Sigma 3\)), \(\rho _X[U]=\rho _X[\rho _X^{-1}(\Sigma _U)]=\Sigma _U\), so that an invertible \(\rho _X\) is an open map. The converse follows from Observation 3.6.2.
3.9 Classical and Generalized (Point-Free) Spaces
Now we are ready for a rough outline of the relation of the point-free and classical spaces.

On the one hand the point-free theory extends the classical one (or, at least a substantial part of it; precisely, the subcategory of sober spaces). On the other hand, the scope of the generalized is much larger; we will present two simple examples shortly. The reader may of course ask whether such an extension is useful. It turns out that it is, as will be hopefully apparent from the following sections.
3.9.1 Two Easy Examples
First, consider a complete Boolean algebra B without atoms (e.g., the lattice of all regular open setsFootnote 2 of any Euclidean space). There are no primes at all: indeed, let p be one. Since it is not an atom, there is an x with \(p<x<1\). We have \(x^*\wedge x=0\le p\), hence \(x^*=0\) and \(x=1\), a contradiction.
Next, take such a B again and consider \(L=\{(x,y)\in B\times B \ | \ x\le y\} \). Since all the (0, x) are in L we obtain by the same reasoning as above that a prime in L has to be of the form (q, 1) and hence there are no primes to separate distinct (0, a) and (0, b).
The latter example seems to be very similar to the former, but it is in fact much more interesting. While Boolean frames are something like a generalization of discrete spaces (albeit constituting a much more colorful class), the frames L of this example are geometrically rather peculiar (do not forget that a subframe is, due to the contravariance, geometrically more like a quotient space, not like a subspace): interpreted as spaces they are behaving like Hausdorff ones, while on the other hand they are not even subfit (see 7.6.2 below) which is a property weaker than \(T_1\)!
4 Categorical Remarks
4.1 Semilattices and a Free Functor
Under a semilattice we here understand a meet semilattice with 0 and 1, and semilattice homomorphisms preserve \(\wedge , 0\) and 1.
4.1.1 Biproduct
Note that in the category of semilattices (similarly like in abelian groups), the cartesian product with the injections and projections as in the following diagram

constitutes a biproduct (note that \(p_1\iota _1\wedge p_2\iota _2=\text {id}\) and check the coproduct and product properties).
4.1.2 A Free Construction
For a semilattice L consider the down-set lattice

ordered by inclusion. Further, define \(\lambda =\lambda _L:L\rightarrow \mathfrak D(L)\) by setting  . Obviously,
. Obviously,
\(\mathfrak D(L)\) is a frame and \(\lambda \) is a semilattice homomorphism
(since we take only the non-empty down-sets, the zero of \(\mathfrak D(L)\) is \(\{0 \} \); all the other joins are the unions).
Proposition
Let M be a frame and let \(h:L\rightarrow M\) be a semilattice homomorphism. Then there is precisely one frame homomorphism \(\widetilde{h}:\mathfrak D(L)\rightarrow M\) such that the diagram

commutes. This \(\widetilde{h}\) is given by the formula \(\widetilde{h}(U)=\mathop {\textstyle \bigvee }\{h(a) \ | \ a\in U\} \).
Proof
Since for a down-set U,  we have for a (possible) frame homomorphism \(\widetilde{h}\) commuting as desired \(\widetilde{h}(U)=\mathop {\textstyle \bigvee }\{\widetilde{h}\lambda (a) \ | \ a\in U\} =\mathop {\textstyle \bigvee }\{ h(a) \ | \ a\in U\} \); hence the formula and the unicity. Obviously, this formula gives a mapping \(\widetilde{h}:\mathfrak D(L)\rightarrow M\) that preserves all joins, and \(\widetilde{h}(L)=1\). Finally, we have
we have for a (possible) frame homomorphism \(\widetilde{h}\) commuting as desired \(\widetilde{h}(U)=\mathop {\textstyle \bigvee }\{\widetilde{h}\lambda (a) \ | \ a\in U\} =\mathop {\textstyle \bigvee }\{ h(a) \ | \ a\in U\} \); hence the formula and the unicity. Obviously, this formula gives a mapping \(\widetilde{h}:\mathfrak D(L)\rightarrow M\) that preserves all joins, and \(\widetilde{h}(L)=1\). Finally, we have
so \(\widetilde{h}\) is indeed a frame homomorphism. \(\square \)
4.2 Free Objects in \(\mathsf{Frm}\)
For a set X define
ordered by \(\le \;=\;\supseteq \) so that we have the meet \(A\wedge B=A\cup B\). Denote by \(\beta _X\) the mapping
Then we have for each meet-semilattice S with 1 and each mapping \(f:X\rightarrow S\) precisely one meet-semilattice homomorphism \(\overline{f}:F(X)\rightarrow S\) such that the diagram

commutes and \(\overline{f}(\emptyset )=1\), namely the homomorphism defined by \(\overline{f}(A)=\bigwedge _{x\in A} f(x)\).
The free frame over a set can be now obtained combining F and \(\mathfrak D\), that is, as \(\mathfrak {D}F(X)\). This provides a functor \(\mathfrak {D}F:\mathsf {Set}\rightarrow \mathsf{Frm}\) right adjoint to the forgetful functor \(\mathsf{Frm}\rightarrow \mathsf {Set}\).
4.3 Algebraic Aspects of \(\mathsf{Frm}\)
The category \(\mathsf{Frm}\) is clearly equationally presentable i.e. its objects are described by a (proper class of) operations, namely
-
0-ary: \(0,1:L^0\rightarrow L\),
-
binary: \(L^2\rightarrow L\), \((a,b)\mapsto a\wedge b\),
-
\(\boldsymbol{\kappa }\)-ary (any cardinal \(\boldsymbol{\kappa }\)): \(L^\kappa \rightarrow L\), \((a_i)_\kappa \mapsto \bigvee _\kappa a_i\),
and equations
-
\((L,\wedge ,1)\) is an idempotent commutative monoid,
-
with a zero element satisfying the absorption law \(a\wedge 0=0=0\wedge a\),
-
\(\bigvee _0 a_i=0\), \(a_j\wedge \bigvee _\kappa a_i=a_j\), \(a\wedge \bigvee _\kappa a_i=\bigvee _\kappa (a\wedge a_i)\).
Then, by general results of category theory (see Manes [40], Chapter 1, or Johnstone [28]), it follows that
4.3.1 Proposition
\(\mathsf{Frm}\) has all (small) limits (i.e., it is a complete category) and they are constructed exactly as in the category \(\mathsf {Set}\) of sets (i.e., the forgetful functor \(\mathsf{Frm}\rightarrow \mathsf {Set}\) preserves them).
Combining this with the fact that it has free objects over \(\mathsf {Set}\), \(\mathsf{Frm}\) is a monadic category over \(\mathsf {Set}\) [40]. This means that, in particular,
4.3.2 Proposition
-
(1)
\(\mathsf{Frm}\) has all (small) colimits (i.e., it is a cocomplete category).
-
(2)
The monomorphisms in \(\mathsf{Frm}\) are exactly the injective homomorphisms.
-
(3)
Epimorphisms in \(\mathsf{Frm}\) need not be surjective but the regular epimorphisms are precisely the surjective homomorphisms.
-
(4)
Every morphism in \(\mathsf{Frm}\) can be factored (uniquely up to isomorphism) as a regular epimorphism followed by a monomorphism.
-
(5)
Quotients are described by congruences.
4.3.3 A Consequence: Presentations by Generators and Relations
The fact that one has free frames and quotient frames implies, in particular, that, like in traditional categories of algebras, we may present frames by generators and relations: take the quotient of the free frame on the given set of generators modulo the congruence generated by the pairs (u, v) for the given relations \(u=v\).
For example, the point-free space of reals is introduced as the frame of reals \({\mathfrak {L}(\mathbb {R})}\) [6, 34] generated by all ordered pairs (p, q) (\(p,q\in \mathbb {Q}\)), subject to the relations
-
(R1)
\((p,q)\wedge (r,s)=(p\vee r,q\wedge s)\),
-
(R2)
\((p,q)\vee (r,s)=(p,s)\) whenever \(p\le r<q\le s\),
-
(R3)
\((p,q)=\mathop {\textstyle \bigvee }\{(r,s)\mid p<r<s<q\}\),
-
(R4)
\(\mathop {\textstyle \bigvee }_{p,q\in \mathbb {Q}}(p,q)=1\).
This provides a development of the “theory of function rings C(X)” in frames and locales [6] and the treatment of more general point-free real functions (see e.g. [22]).
As another example, the product of two locales L and M (see 4.5 below) is the frame generated by all pairs \(a\otimes b\), \(a\in L\), \(b\in M\), subject to the relations
-
(P1)
\(1\otimes 1=1\),
-
(P2)
\(a\otimes 0=0\otimes b=0\),
-
(P3)
\((a\otimes b)\wedge (a'\otimes b')=(a\wedge a')\otimes (b\wedge b')\),
-
(P4)
\(\mathop {\textstyle \bigvee }_{i\in I}(a_i\otimes b)=(\mathop {\textstyle \bigvee }_{i\in I} a_i)\otimes b, \; \mathop {\textstyle \bigvee }_{i\in I}(a\otimes b_i)=a\otimes (\mathop {\textstyle \bigvee }_{i\in I} b_i)\).
For further examples, see e.g. [21, 36].
4.4 Taking Quotients
In general, extending a binary relation to a congruence (and subsequent factorizing) in an algebra can be a hard task. In frames, however, it is surprisingly easy.
4.4.1 Saturation
Let \(R\subseteq L\times L\) be an arbitrary relation on a frame L. An element \(s\in L\) is said to be R-saturated (briefly, saturated) if
The set of all R-saturated elements of L is a frame: since \(b\!\rightarrow \!(-)\) is a right adjoint, it is closed under meets, and by 2.6.2(6) we have for any x and aRb, \(a\!\rightarrow \!(x\!\rightarrow \!s)=x\!\rightarrow \!(a\!\rightarrow \!s)=x\!\rightarrow \!(b\!\rightarrow \!s)=b\!\rightarrow \!(x\!\rightarrow \!s)\), hence it is also closed under the Heyting operation and therefore it is a complete Heyting algebra, hence a frameFootnote 3 (with the same meets and the same Heyting operation as in L but not necessarily the same joins). It will be denoted by L/R.
We will show that L/R is the quotient of L by the congruence generated by R, and more.
4.4.2 The Associated Nucleus
For any \(a\in L\) set
We have
Proposition
(1) For every \(a\in L\) and \(s\in L/R\), \(a\!\rightarrow \!s=\nu (a)\!\rightarrow \!s\).
(2) \(\nu \) is a nucleus, that is, it is monotone, \(a\le \nu (a)\), \(\nu \nu (a)=\nu (a)\) and \(\nu (a\wedge b)=\nu (a)\wedge \nu (b)\).
Proof
(1) For any x we have trivially \(x\le a\!\rightarrow \!s\) iff \(a\le x\!\rightarrow \!s\) and since this last is in L/R, this is the same as \(\nu (a)\le x\!\rightarrow \!s\), and this is equivalent with \(x\le \nu (a)\!\rightarrow \!s\).
(2) The first three formulas are trivial, and also trivially \(\nu (a\wedge b)\le \nu (a)\wedge \nu (b)\). Now since \(a\wedge b\le \nu (a\wedge b)\), we have, by (1), \(a\le b\!\rightarrow \!\nu (a\wedge b)=\nu (b)\!\rightarrow \!\nu (a\wedge b)\), hence \(\nu (a)\le \nu (b)\!\rightarrow \!\nu (a\wedge b)\) and finally \(\nu (a)\wedge \nu (b)\le \nu (a\wedge b)\). \(\square \)
4.4.3 Proposition
\(\nu \) understood as a mapping \(L\rightarrow L/R\) is an onto frame homomorphism, we have for aRb, \(\nu (a)=\nu (b)\), and if a frame homomorphism \(h:L\rightarrow M\) is such that \(h(a)=h(b)\) for all aRb then there is an \(\overline{h}:L/R\rightarrow M\) such that \(\overline{h}\cdot \nu =h\).
Furthermore, \(\overline{h}(s)=h(s)\) for all \(s\in L/R\).
Proof
\(\nu \) preserves finite meets by 4.4.2(2). The joins \(\mathop {\textstyle \bigsqcup }\) in L/R are given by \(\mathop {\textstyle \bigsqcup }s_i=\nu (\mathop {\textstyle \bigvee }s_i)\) (if \(t\in L/R\) and \(t\ge s_i\) for all i then \(t\ge \mathop {\textstyle \bigvee }s_i\) and \(t=\nu (t)\ge \nu (\mathop {\textstyle \bigvee }s_i)\)) and hence \(\nu (\mathop {\textstyle \bigvee }a_i)\le \nu (\mathop {\textstyle \bigvee }\nu (a_i))=\mathop {\textstyle \bigsqcup }\nu (a_i)\le \nu (\mathop {\textstyle \bigvee }a_i)\). Hence \(\nu \) is a frame homomorphism.
Next, if aRb then \(1=a\!\rightarrow \!\nu (a)=b\!\rightarrow \!\nu (a)\) and hence \(b\le \nu (a)\), and \(\nu (b)\le \nu (a)\); equality by symmetry.
Finally, let \(h:L\rightarrow M\) be such that \(h(a)=h(b)\) for aRb. Set \(\sigma (a)=\mathop {\textstyle \bigvee }\{x \ | \ h(x)\le h(a)\} \). Then obviously

Hence we have \(x\le \sigma (a)\) iff \(h(x)\le h(a)\) (‘\(\Rightarrow \)’ by (\(*\)) and ‘\(\Leftarrow \)’ by the definition of \(\sigma \)) so that for any uRv we have for any x, \(x\le u\rightarrow \sigma (a)\) iff \(x\wedge u\le \sigma (a)\) iff \(h(x\wedge v)=h(x\wedge u)\le h(a)\) iff \(x\wedge v\le \sigma (a)\) iff \(x\le v \!\rightarrow \!\sigma (a)\). Thus, \(\sigma (a)\) is saturated, hence \(a\le \nu (a)\le \sigma (a)\) and we have
so that \(h(a)=h\nu (a)\) and the statement follows. \(\square \)
4.4.4 Proposition
Let there be a join-basis \(C\subseteq L\) such that for all \(c\in C\) and aRb we have \((a\wedge c)R (b\wedge c)\). Then s is R-saturated iff for all aRb, \(a\le s\) iff \(b\le s\).
Proof
If the statement holds we have for every \(c\in C\) and aRb, \(c\wedge a\le s\) iff \(c\wedge b\le s\), that is, \(c\le a\!\rightarrow \!s\) iff \(c\le b\!\rightarrow \!s\), and \(a\!\rightarrow \!s=b\!\rightarrow \!s\). On the other hand, if s is saturated then in particular \(a\!\rightarrow \!s=1\) iff \(b\!\rightarrow \!s=1\). \(\square \)
4.5 Product in \(\mathsf{Loc}\) (Coproduct in \(\mathsf{Frm}\)) Concretely
We will present a construction of the coproduct in the category of frames [28, 45]. It will be done for just two factors; the idea of the general case is precisely the same, only one has to use a more complicated notation which makes the presentation less transparent. The reader may do the general construction as a simple exercise taking instead of the \(\iota _i:L_i\rightarrow L_1\times L_2\) below in the role of the coproduct in the category of semilattices the general coproduct in that category, namely
where \(\iota _i(a)=(x_j)_{j\in J}\) with \(x_i=a\) and \(x_j=1\) otherwise.
On the frame \(\mathfrak D(L_1\times L_2)\) define a relation R by setting

Note that
-
the void index set is not excluded, hence we have

for all \(a\in L_1\) and \(b\in L_2\);
-
it is easy to check that the R-saturated \(U\in \mathfrak D(L_1\times L_2)\) are precisely those that
$$\text{ for } \text{ any } (a_i,b)\in U, i\in I, \text{ also } (\mathop {\textstyle \bigvee }_{i\in I}a_i,b)\in U,$$$$\text{ and, } \text{ for } \text{ any } (a,b_i)\in U, i\in I, \text{ also } (a,\mathop {\textstyle \bigvee }_{i\in I}b_{i})\in U\;\;\;\;\;\;\;$$(the relation satisfies the conditions of 4.4.4, hence we can use the simplified saturation formula).
Theorem
The maps
are frame homomorphisms and constitute a coproduct in \(\mathsf{Frm}\).
Proof
Let \(h_i:L_i\rightarrow M\) be frame homomorphisms. Consider first the semilattice homomorphism \(h':L_1\times L_2\rightarrow M\) obtained for the \(h_i\) understood as semilattice homomorphisms (recall 4.1) and, using 4.1.2, lift it to a frame homomorphism \(g=\widetilde{h}':\mathfrak D(L_1\times L_2)\rightarrow M\). Consider the following diagram.

The \(\lambda \iota _i\) are semilattice homomorphisms that generally do not need to preserve the joins in \(L_i\). The nucleus homomorphism \(\nu _R\), however, obviously provides the necessary equalities, and since it preserves meets, we obtain frame homomorphisms \(\nu _R\lambda \iota _i\). Using the formula for \(\widetilde{h}'\) from 4.1.2 (and taking into account that obviously \(h'(a,b)=h_1(a)\wedge h_2(b)\)) we easily check that it respects the relation R and hence we have, by 4.4.3, a frame homomorphism h such that \(h\nu _R=g\) and hence \(h\nu _R\lambda \iota _i=h_i\). Finally, the

obviously generate \(\mathfrak D(L_1\times L_2)\) by joins, and \(\nu _R\) is onto, so that h is uniquely determined by \(h\overline{\iota }_1\) and \(h\overline{\iota }_2\). \(\square \)
5 \(\mathsf{Loc}\) as a Concrete Category. Localic Maps and Sublocales
5.1 Localic maps
Since frame homomorphisms \(h:M\rightarrow L\) preserve all joins they have uniquely defined right adjoints \(f=h_*:L\rightarrow M\). We will use them for a concrete representation of the category \(\mathsf{Loc}\) of locales [43, 44]. Thus, from now on we will speak of the meet preserving maps \(f:L\rightarrow M\) between frames with left adjoints \(f^*\) that are frame homomorphisms as of localic maps. The category \(\mathsf{Loc}\) will be that with frames as objects (in this context we often—although not always—speak of them as of locales) and localic maps as morphisms.
5.2 Proposition
A meet preserving map \(f:L\rightarrow M\) is a localic map iff
-
(a)
\(f(x)=1\) only if \(x=1\), and
-
(b)
for all \(y\in M\) and \(x\in L\), \(f(f^*(y)\!\rightarrow \!x)=y\!\rightarrow \!f(x)\) (this identity is often referred to as the Frobenius identity).
Proof
Set \(h=f^*\). The point is in determining when h preserves finite meets. First, we have to have \(h(1)=1\); this makes in the adjunction the condition \(1=h(1)\le x\) iff \(1\le f(x)\), hence (a).
We have
If \(h(x)\wedge h(y)=h(x\wedge y)\) the first inequalities coincide and we have for all x, \(x\le f(h(y)\!\rightarrow \!z)\) iff \(x\le y\!\rightarrow \!f(z)\), hence \(f(h(y)\!\rightarrow \!z)= y\!\rightarrow \!f(z)\). On the other hand, if \(f(h(y)\!\rightarrow \!z)= y\!\rightarrow \!f(z)\) we have for all z, \(h(x)\wedge h(y)\le z\) iff \(h(x\wedge y)\le z\), hence \(h(x)\wedge h(y)=h(x\wedge y)\). \(\square \)
5.2.1 Examples
(1) For each continuous map \(f:X\rightarrow Y\), the localic map right adjoint to \(\Omega (f)\) is given by
(2) Recall 3.6. A point of a locale L is a localic map \(p:\mathbf{2}\rightarrow L\). Then \(p(1)=1\) and \(p(0)=a\ne 1\) is a prime in L: \(x\wedge y\le a=p(0)\) iff \(p^*(x)\wedge p^*(y)\le 0\) hence \(p^*(x)=0\) or \(p^*(y)=0\), that is, \(x\le p(0)=a\) or \(y\le p(0)=a\).
5.3 Aside: Spectrum in Thus Represented Category of Locales
Recall 3.6.2. Let us represent points as primes. We have
Observation
Let \(f:L\rightarrow M\) be a localic map. Then for every prime p in L, f(p) is prime in M.
(Indeed, since \(p\ne 1\), \(f(p)\ne 1\), and \(a\wedge b\le f(p)\) iff \(f^*(a)\wedge f^*(b)\le p\) iff \(f^*(a)\le p\) or \(f^*(b)\le p\) iff \(a\le f(p)\) or \(b\le f(p)\).)
Set
where \(\Sigma _a=\{p \ | \ a\nleq p\} \) and take (using Observation) for \(\Sigma (f):\Sigma (L)\rightarrow \Sigma (M)\) simply the restriction of f. By the adjunction we have
and we easily see that \(\Sigma _0=\emptyset \), \(\Sigma _1=\Sigma (L)\), \(\Sigma _{a\wedge b}=\Sigma _a\cap \Sigma _b\) and \(\Sigma _{\mathop {\textstyle \bigvee }a_i}=\mathop {\textstyle \bigcup }\Sigma _{a_i} \). Thus, the \(\Sigma (L)\) are topological spaces and the \(\Sigma (f)\) are continuous maps, and we have a functor \(\mathsf{Loc}\rightarrow \mathsf{Top}\) (this time without any formal reversals). If we now define \(\sigma _L(a)=\Sigma _a\) and \(\rho _X:X\rightarrow \Sigma \Omega (X)\) by setting \(\rho _X(x)=X\smallsetminus \overline{\{x \} }\) we can easily check all the equalities corresponding to those of 3.6.2.
5.4 Sublocales and the Coframe \(\mathsf{S}(L)\)
Natural candidates for subobjects in a category are extremal monomorphisms. In \(\mathsf{Frm}\), extremal epimorphisms are precisely the onto frame homomorphisms and hence the extremal monomorphisms in our representation of \(\mathsf{Loc}\) will be the adjoints to these, namely precisely the one-to-one localic maps (recall the identities (adj3) in any adjunction; they show that onto maps correspond to one-to-one maps and vice versa).
Thus, a natural subobject of a locale L is a subposet \(S\subseteq L\) that is a frame in the induced order, such that the embedding map \(j_S:S\subseteq L\) is a localic one. First of all, it is closed under meets and the left adjoint of \(j_S\) is obviously given by the formula
(understood as a map \(L\rightarrow S\) it has to be a frame homomorphism; usually, however one considers it as a map \(L\rightarrow L\) and one speaks of the nucleusFootnote 4 of S). By 5.2 we have that for every \(s\in S\) and every \(x\in L\), \(x\!\rightarrow \!s\in S\), because in this case \(x\!\rightarrow \!s=x\!\rightarrow \!j_S(s)=j_S(\nu _S(x)\!\rightarrow \!s)\in S\). This leads to the following definition.
A sublocale of a locale (frame) L is a subset \(S\subseteq L\) such that
-
(S1)
for every \(M\subseteq S\), \(\mathop {\textstyle \bigwedge }M\in S\), and
-
(S2)
for every \(x\in L\) and every \(s\in S\), \(x\!\rightarrow \!s\in S\).
(We have already seen that if \(j_S:S\subseteq L\) is a localic map then (S1) and (S2) hold. On the other hand, if S satisfies (S1) and (S2) then it is closed under meets and the Heyting operation, and hence it is a locale (with the same meets and the same Heyting operation as in LFootnote 5). By (S1), \(j_S\) has a left adjoint \(\nu _S\) as above. By (S2), \(x\!\rightarrow \!s=j_S(x\!\rightarrow \!s)\), and for any u, \(u\le x\!\rightarrow \!s\) iff \(x\le u\!\rightarrow \!s\) iff \(\nu _S(x)\le u\!\rightarrow \!s\) iff \(u\le \nu _S(x)\!\rightarrow \!s\) so that

and hence \(j_S(\nu _S(x)\!\rightarrow \!s)=x\!\rightarrow \!s=x\!\rightarrow \!j_S(s)\) and \(j_S\) is a localic map by 5.2—the condition with 1 is trivial since \(j_S\) is one-to-one.)
5.4.1 The Complete Lattice \(\boldsymbol{\mathsf{S}(L)}\)
Obviously any intersection of sublocales is a sublocale so that we have a complete lattice
of sublocales of L. We immediately see that the join in \(\mathsf{S}(L)\) is given by the formula
(every sublocale containing all \(S_i\) has to contain this set, and on the other hand this set is a sublocale by property 2.6(H2) of the Heyting operator).
By (S1) every sublocale contains the top 1. Thus, the smallest sublocale, corresponding to the classical empty subspace, is \( \mathsf{O}=\{1 \} . \)
5.4.2 Proposition
\(\mathsf{S}(L)\) is a coframe.
Proof
We need to show that \((\mathop {\textstyle \bigcap }_{i\in I}S_i)\vee T= \mathop {\textstyle \bigcap }_{i\in I}(S_i\vee T)\). The inclusion \(\subseteq \) is obvious. Hence, consider an \(x\in \mathop {\textstyle \bigcap }_{i\in I}(S_i\vee T)\). Then for every i there are \(s_i\in S_i\) and \(t_i\in T\) such that \(x=s_i\wedge t_i\). Set \(t=\mathop {\textstyle \bigwedge }t_i\). We have
so that \(x=s_i\wedge t\) for all i. Then, by rule 2.6.2(7), all the \(t\rightarrow s_i\) coincide; denote by s the common value. Since \(s=t\rightarrow s_i\in S_i\), \(s\in \mathop {\textstyle \bigcap }_{i\in I} S_i\) and we conclude by 2.6.2(5) that \(x=t\wedge s_i=t\wedge (t\rightarrow s_i)=t\wedge s\in (\mathop {\textstyle \bigcap }_{i\in I}S_i)\vee T\). \(\square \)
5.5 Open and Closed Sublocales
Each element \(a\in L\) is associated with a closed sublocale \(\mathfrak c(a)\) and an open sublocale \(\mathfrak o(a)\),Footnote 6

(the equivalence of the two expressions for \(\mathfrak o(a)\) follows immediately from 2.6.2(6)).
5.5.1 Proposition
\(\mathfrak o(a)\) and \(\mathfrak c(a)\) are complements of each other.
Proof
If \(x\in \mathfrak o(a)\cap \mathfrak c(a)\) we have \(a\le x=a\rightarrow x\), hence \(a=a\wedge a\le x\) and \(x=a\rightarrow x=1\) by 2.6.2(3). On the other hand, each \(x\in L\) is by 2.6.2(8) equal to \((a\rightarrow x)\wedge (a\vee x)\in \mathfrak o(a)\vee \mathfrak c(a)\). \(\square \)
5.5.2 Proposition
We have the following formulas
Proof
We will prove the formulas for \(\mathfrak c\), those for \(\mathfrak o\) will then follow by De Morgan formulas. They are simple observations:
 ,
,  , \(x\ge \mathop {\textstyle \bigvee }a_i\) iff \(x\ge a_i\) for all i, and finally, \(x\ge a\wedge b\) iff \(x=(x\vee a)\wedge (x\vee b)\), that is, iff
, \(x\ge \mathop {\textstyle \bigvee }a_i\) iff \(x\ge a_i\) for all i, and finally, \(x\ge a\wedge b\) iff \(x=(x\vee a)\wedge (x\vee b)\), that is, iff  . \(\square \)
. \(\square \)
5.5.3 Proposition
A general sublocale S can be represented by open and closed sublocales as follows:
Proof
I. If \(s\in S\) then for arbitrary x, \(x\rightarrow s\in S\). Hence by 2.6.2(8) and (nucleus)
On the other hand, if a is in \(\mathop {\textstyle \bigcap }\{\mathfrak c(\nu _S(x))\vee \mathfrak o(x) \ | \ x\in L\} \) then, in particular, it is in \(\mathfrak c(\nu _S(a))\vee \mathfrak o(a)\) and therefore \(a=x\wedge (a\rightarrow y)\) with \(x\ge \nu _S(a)\). Since \(a\le a\rightarrow y\) we have \(a\le y\), hence \(a\rightarrow y=1\), so that \(a=x\ge \nu _S(a)\) and \(a=\nu _S(a)\), that is, \(a\in S\).
II. Since \(\nu _S(\nu _S(x))=\nu _S(x)\) it suffices, in view of I, to show that if \(\nu _S(x)=\nu _S(y)\) then \(S\subseteq \mathfrak c(y)\vee \mathfrak o(x)\). Let \(s\in S\). We have \(s=(s\vee y)\wedge (y\rightarrow s)=(s\vee y)\wedge (\nu _S(y)\rightarrow s)=(s\vee y)\wedge (\nu _S(x)\rightarrow s)=(s\vee y)\wedge (x\rightarrow s)\in \mathfrak c(y)\vee \mathfrak o(x)\). \(\square \)
5.6 Closure, Density and Isbell’s Theorem. Interior
Like in spaces we have the closure of a sublocale, the smallest closed sublocale containing S (cf. [15]). It is determined by a particularly simple formula, namely

(a closed set containing S has to contain \(\mathop {\textstyle \bigwedge }S\) and has to be an up-set). Consequently we have also an extremely simple criterion of density:
5.6.1 Observation
A sublocale \(S\subseteq L\) is dense in L iff it contains the bottom 0.
5.6.2 Booleanization
For a frame L set
Obviously it is a sublocale: we have \(a^*=a\!\rightarrow \!0\) and \(\mathop {\textstyle \bigwedge }_i(a_i\!\rightarrow \!0)=(\mathop {\textstyle \bigvee }_i a_i)\!\rightarrow \!0\) by 2.6(H4), making for (S1); (S2) follows from 2.6.2(6).
\(\mathfrak B(L)\) is a Boolean algebra, the largest Boolean algebra in among the sublocales. It is called the Booleanization of L, and it is a very old construction known from algebraic logic (Glivenko [20]).
5.6.3 Theorem
(Isbell’s Density Theorem) A sublocale \(S\subseteq L\) is dense iff it contains \(\mathfrak B(L)\). Thus, each locale L contains a smallest dense sublocale, namely \(\mathfrak B(L)\).
Proof
A dense sublocale contains 0 and hence, by (S2), all the \(x\!\rightarrow \!0\), that is, all the sublocale \(\mathfrak B(L)\) which is itself dense, since \(0=1\!\rightarrow \!0\). \(\square \)
5.6.4 Notes
(a) This fact has no counterpart in classical topology. So e.g. in the frame of reals the sublocales of rationals and irrationals have still a very rich intersection (which, then, cannot be represented as a classical subspace). In the next pages we will pay some attention to the relation of sublocales and subspaces of classical spaces.
(b) The Booleanization \(\mathfrak B(\Omega (X))\) is an example of advantages of the point-free approach. It is in fact a very natural space, namely the space of regular open sets, that typically has no classical representation.
5.6.5 Interior
Similarly one defines the interior of a sublocale S as the largest open sublocale contained in S. We have \(\mathfrak o(a)\subseteq S\) iff \(\mathfrak c(a)\supseteq S^\#\) iff \(a\le \mathop {\textstyle \bigwedge }S^\# \) iff \(\mathfrak o(a)\subseteq \mathfrak o(\mathop {\textstyle \bigwedge }S^\#)\) so that
Note that this can be read in terms of the coHeyting difference as
in analogy with the classical relation between interior and closure (the dual formula does not hold, though; see e.g. [19] for more information).
5.7 Subspaces and Sublocales I. The Axiom \(T_D\)
This is a preparatory subsection. We will proceed in the next section after we will know more about images and preimages; now we will discuss just the correctness of point-free representation of subspaces.
5.7.1 Sublocales Induced by Subspaces
Consider a space X, a subspace \(Y\subseteq X\) and the embedding mapping \(j_Y:Y\subseteq X\). Then we have the onto frame homomorphism
with the adjoint localic map \(\kappa _Y:\Omega (Y)\rightarrow \Omega (X)\), an extremal monomorphism in \(\mathsf{Loc}\), given by
(since \(U\cap Y\subseteq V\) iff \(U\subseteq (X\smallsetminus Y)\cup V\) and U is open). This suggests the natural representation of Y as the sublocale
Such sublocales \(S_Y\) of (locales representing) spaces are usually referred to as the induced sublocales, more precisely, sublocales induced by subspaces.
5.7.2 The Axiom \(T_D\)
We have already seen that even in the most natural spaces like the Euclidean space of reals (we will learn later that in fact the contrary is rather rare) there are sublocales that are not (induced by) subspaces. This is in fact a very useful feature of point-free topology. There is, however, another hitch that has to be taken into account: the space has to have a certain very weak property to have the subspaces represented correctly.
The following property was introduced in Aull and Thron [1], and in the same year, in Thron [54], it was already used to prove one of the first results about the reconstruction of X from \(\Omega (X)\). Since then it turned out to be a very important property in comparing classical and point-free theory (see e.g. [49]). A \(T_D\)-spaceFootnote 7 is a space X in which

5.7.3 Proposition
The representation of subspaces in \(\Omega (X)\) as above is correct in the sense that distinct subspaces induce distinct sublocales iff the space X satisfies \(T_D\).
Proof
\(\Rightarrow \): Let X be a space in which \(T_D\) does not hold and let x be such that none of the \(U\smallsetminus \{x \} \) with open \(U\ni x\) is open. Then for \(Y=X\smallsetminus \{x \} \) we have \(\kappa _Y(U\cap Y)=U\) for any \(U\in \Omega (X)\); indeed, if \(x\in U\) then
otherwise \(\kappa _Y(U\cap Y)=\kappa _Y(U)=\mathrm{int}\,(\{x\}\cup U)=U\). Hence \(S_Y=\Omega (X)=S_X\).
\(\Leftarrow \): Note that the nucleus of the \(S_Y\) is given by
Let \(T_D\) hold and let Y, Z be distinct subspaces (with, say, \(Y\ni x\notin Z\)). Choose an open \(U\ni x\) with \(V=U\smallsetminus \{x \} \) open. Then \( \nu _Y(U)\ne \nu _Y(V)\) while \(\nu _Z(U)= \nu _Z(V)\). Hence \(\nu _Y\ne \nu _Z\) and thus the corresponding sublocales \(S_Y\) and \(S_Z\) are distinct. \(\square \)
5.8 Aside: Spatialization as a Sublocale
Recall 3.7. The full subcategory of all spatial locales in \(\mathsf{Loc}\) will be denoted by \(\mathsf{Loc}_{\mathsf {sp}}\). Let \(\mathsf {Pr}(L)\) denote the set of all primes p in a locale L and set
Obviously \(\mathsf {Sp}(L)=L\) for a spatial L.
5.8.1 Lemma
\(\mathsf {Sp}(L)\) is a sublocale of L.
Proof
Obviously \(\mathsf {Sp}(L)\) is closed under meets. Now if \(A\subseteq \mathsf {Sp}(L)\) then \(x\rightarrow \mathop {\textstyle \bigwedge }A=\mathop {\textstyle \bigwedge }_{p\in A}(x\rightarrow p)\in \mathsf {Sp}(L)\) since \(x\rightarrow p\in \mathsf {Pr}(L)\cup \{1\}\) for every \(x\in L\) and \(p\in \mathsf {Pr}(L)\): if \(a\wedge b\le x\rightarrow p\) then \(a\wedge b\wedge x\le p\); if \(x\le p\) we have \(x\rightarrow p=1\), else \(a\wedge b\le p\) and then, say, \(a\le p\le x\rightarrow p\). \(\square \)
Note further that \(\mathsf {Sp}(L)\in \mathsf{Loc}_{\mathsf {sp}}\) since \(\mathsf {Pr}(\mathsf {Sp}(L))=\mathsf {Pr}(L)\).
5.8.2 Lemma
If \(f:L\rightarrow M\) is a localic map then we have a localic map \(\mathsf {Sp}(f):\mathsf {Sp}(L)\rightarrow \mathsf {Sp}(M)\) defined by \(\mathsf {Sp}(f)(a)=f(a)\).
Proof
Since f preserves meets, we have by Observation 5.3, \(f[\mathsf {Sp}(L)]\subseteq \mathsf {Sp}(M)\), and hence we have a map \(\mathsf {Sp}(L)\rightarrow \mathsf {Sp}(M)\) defined as in the statement; obviously it preserves meets. Since we have for the embeddings \(j_L:\mathsf {Sp}(L)\subseteq L\), \(f\cdot j_L=j_M\cdot \mathsf {Sp}(f)\), that is, \(j_L^*\cdot f^*=\mathsf {Sp}(f)^*\cdot j_M^*\), we have, for any \(a\in \mathsf {Sp}(L)\) and \(b\in \mathsf {Sp}(M)\), by (nucleus),
and \(\mathsf {Sp}(f)\) is a localic map. \(\square \)
Thus we have a functor
(clearly a reflection of \(\mathsf{Loc}\) on \(\mathsf{Loc}_{\mathsf {sp}}\)). Recall the representation of the adjointness counit \(\sigma _L=(a\mapsto \Sigma _a):L\rightarrow \Omega \Sigma (L)\) of the spectrum from 5.3. Restricting it to \(\mathsf {Sp}(L)\), we get a description of the spatialization of a locale L (3.9) as a sublocale of L:
5.8.3 Proposition
\(\sigma _L:\mathsf {Sp}(L)\rightarrow \Omega \Sigma (L)\) is a frame isomorphism.
Proof
We have already mentioned in 5.3 that \(\Sigma _1=\mathsf {Pr}(L)\) and \(\Sigma _{a\wedge b}=\Sigma _a\cap \Sigma _b\). It is also easy to check that
so that we have a frame homomorphism. \(\sigma _L\) is clearly one-to-one in \(\mathsf {Sp}(L)\); it is onto since
\(\square \)
6 Images and Preimages. Localic Maps as Continuous Ones. Open Maps
6.1 Proposition
Let \(f:L\rightarrow M\) be a localic map. For every sublocale \(S\subseteq L\) the image f[S] is a sublocale of M.
Proof
Trivially, f[S] is closed under meets. Now take an \(s\in S\) and an arbitrary \(x\in M\). We have \(x\!\rightarrow \!f(s)= f(f^*(x)\!\rightarrow \!s)\in f[S]\) since \(f^*(x)\!\rightarrow \!s\in S\). \(\square \)
6.1.1 An (Epi, Extremal Mono) Factorization
In consequence we have in \(\mathsf{Loc}\) the factorizations

Indeed, g obviously preserves meets, hence it has a left adjoint, and we have \(f^*=g^*j^*\) with \(f^*\) and \(j^*\) frame homomorphisms, \(j^*\) onto, and hence \(g^*\) is a frame homomorphism.
6.2 Localic Preimage
By the formula for join in \(\mathsf{S}(L)\) we have for each subset \(A\subseteq L\) closed under meets the sublocale
the largest sublocale contained in A.
The preimage \(f^{-1}[S]\) of a sublocale is obviously closed under meets, but the condition (S2) typically fails. We set
and call this sublocale the localic preimage of S.
Conventions We will sometimes work with both \(f^{-1}[S]\) and \(f_{-1}[S]\). To avoid confusion we will speak of the former as of the set preimage. Further, \(f^{-1}[M]\) is closed under meets for any meet-preserving f and any M that is closed under meets and hence we have a sublocale \(f_{-1}[M]=f^{-1}[M]{_{\mathsf{sl}}}\) for any such M. We will refer to such a situation stating that \(f_{-1}[M]\) makes sense.
6.2.1 Proposition
Localic preimages of closed resp. open sublocales are closed resp. open. More precisely, we have \(f_{-1}[\mathfrak c(a)]=f^{-1}[\mathfrak c(a)]=\mathfrak c(f^*(a))\) and \(f_{-1}[\mathfrak o(a)]=\mathfrak o(f^*(a))\).
Proof
I.  iff \(f(x)\ge a\) iff \(x\ge f^*(a)\).
iff \(f(x)\ge a\) iff \(x\ge f^*(a)\).
II. For a general element \(f^*(a)\!\rightarrow \!x\) of \(\mathfrak o(f^*(a))\) we have \(f(f^*(a)\!\rightarrow \!x)= a\!\rightarrow \!f(x)\in \mathfrak o(a)\), hence \(\mathfrak o(f^*(a))\subseteq f^{-1}[\mathfrak o(a)]\) .
Now let S be a sublocale contained in \(f^{-1}[\mathfrak o(a)]\); we will show that \(S\subseteq \mathfrak o(f^*(a))\). Set \(b=f^*(a)\) and take an \(s\in S\). We have \((b\!\rightarrow \!s)\!\rightarrow \!s\in S\) and hence \(f((b\!\rightarrow \!s)\!\rightarrow \!s)\in \mathfrak o(a)\) so that, using 2.6.2(6), we compute
and since for a localic map f, \(f(x)=1\) only if x =1 we see that \((b\!\rightarrow \!s)\!\rightarrow \!s=1\). But then \(b\!\rightarrow \!s\le s\), and since always \(s\le b\!\rightarrow \!s\) we conclude that \(s\in \mathfrak o(b)\). \(\square \)
6.3 Proposition
For any localic map \(f:L\rightarrow M\) we have the adjunction

Hence, the image map \(f[-]\) preserves all joins and the preimage map \(f_{-1}[-]\) preserves all meets.
Proof
We have \(f[S]\subseteq T\) iff \(S\subseteq f^{-1}[T]\) iff \(S\subseteq f_{-1}[T]\), the first being the standard set-theoretical image-preimage adjunction, the second because S is a sublocale. \(\square \)
Note
It can be further proved that \(f_{-1}[-]\) is a coframe homomorphism that preserves complements while \(f[-]\) is a colocalic map [44].
6.4 Points, Sublocales and Subspaces
Each sublocale contains, trivially, the top element, and the sublocale \(\mathsf{O}=\{1 \} \) plays the role of the void subspace. We have an easy
Proposition
The sublocales containing just one non-trivial element are the \(P=\{p,1 \} \) with p prime.
Proof
If p is prime and if \(x\!\rightarrow \!p\ne 1\) then \(x \nleq p\) and since \(x\wedge (x\!\rightarrow \!p)\le p\) then \(x\!\rightarrow \!p\le p\) and hence \(x\!\rightarrow \!p=p\) by 2.6.2(1).
If \(x\!\rightarrow \!p\in \{p,1 \} \) and if \(x\wedge y\le p\) then either \(x\!\rightarrow \!p=1\) and \(x\le p\) or \(x\!\rightarrow \!p=p\) and \(y\le x\!\rightarrow \!p=p\). \(\square \)
6.4.1 One-Point Sublocales
The sublocales \(P=\{p,1 \} \) with p prime are called one-point sublocales, or simply point sublocales. Note that this is in agreement with the representation of points as primes. From formula (spatial) and the formula for join in \(\mathsf{S}(L)\) we immediately obtain
Observation
A frame L is spatial iff \(L=\mathop {\textstyle \bigvee }\{P \ | \ P\ \text {point sublocale of}\ L\} \).
In particular in a space X we have the one-point sublocales
of \(\Omega (X)\) and we obtain
6.4.2 Observation
\(\Omega (X)=\mathop {\textstyle \bigvee }\{P^X_x \ | \ x\in X\} \).
(Note that here we have simply used the fact that an open \(U\subseteq X\) is the intersection \(\mathop {\textstyle \bigcap }\{X\smallsetminus \overline{\{x \} } \ | \ x\notin U\} \). Thus, if X is not sober we actually have not needed all the prime like in the previous statement.)
6.4.3 Induced Sublocales of \(\Omega (X)\) in Terms of Point Sublocales
Let X be a topological space and \(Y\subseteq X\) a subspace. Recall from 5.7.1 the sublocale \(S_Y\subseteq \Omega (X)\) induced by Y. We have
Theorem
In \(\mathsf{S}(\Omega (X))\), \(S_Y=\mathop {\textstyle \bigvee }\{P^X_y \ | \ y\in Y\} \).
Proof
We have \(S_Y= \kappa _Y[\Omega (Y)]\) where \(\kappa _Y\) is the localic map adjoint to the embedding homomorphism \(\Omega (j)=(U\mapsto U\cap Y):\Omega (X)\rightarrow \Omega (Y)\). From 5.7.1 we know that \( \kappa _Y(V)=\mathrm{int}\,((X\smallsetminus Y)\cup V) \) (the largest open \(U\subseteq X\) such that \(U\cap Y=V\)). By 6.4.2, \(\Omega (Y)=\mathop {\textstyle \bigvee }\{P^Y_y \ | \ y\in Y\} \) and hence by 6.3, \( S_Y=\mathop {\textstyle \bigvee }\{\kappa _Y(P^Y_y) \ | \ y\in Y\} \) and it suffices to prove that \(\kappa _Y(P^Y_y)= P^X_y\), that is, that for \(y\in Y\),
which, since the closure in Y is the intersection of the closure in X with Y, amounts to \(\mathrm{int}\,((X\smallsetminus Y)\cup (Y\smallsetminus \overline{\{y \} }))=X\smallsetminus \overline{\{y \} }\). The inclusion \(\supseteq \) is trivial. Now let U be open and \(U\subseteq (X\smallsetminus Y)\cup (Y\smallsetminus \overline{\{y \} })\). We have to prove that \(U\subseteq X\smallsetminus \overline{\{y \} }\). Suppose the contrary. Then there is a \(z\in U\cup \overline{\{y \} }\), hence \(y\in U\) which is a contradiction: y is neither in \(X\smallsetminus Y\) nor in \(Y\smallsetminus \overline{\{y \} }\). \(\square \)
6.4.4 Note
All sublocales of spaces are induced only exceptionally. For a \(T_D\)-space (recall 5.7.2) the following statements are equivalent.
-
(1)
All sublocales of \(\Omega (X)\) are induced by subspaces,
-
(2)
\(\mathsf{S}(\Omega (X))\) is Boolean,
-
(3)
X is scattered, that is, every infinite subset of X contains an isolated point.
6.5 Geometry of Localic Maps
Localic maps were introduced in a rather formal way: in the first step the category \(\mathsf{Frm}\) was just turned upside down to formally obtain covariance; in the second step one gained concreteness by another formal measure, namely by taking Galois adjoints. It may come as a pleasant surprise that thus formally obtained maps are characterized among non-structured maps like classical continuous maps, namely by preserving closedness and openness (the latter in some strict sense) by preimages.Footnote 8 In classical spaces it suffices to assume one, obtaining the other for free, here we will have to assume both explicitly: the complements of closed sublocales have to be formed in \(\mathsf{S}(L)\) and not set-theoretically as in classical topology, and \(\mathsf{S}(L)\) is not quite so simple as the Boolean algebra of all subsets.
6.5.1 Lemma
Let L, M be frames and let \(f:L\rightarrow M\) be a mapping such that for every closed sublocale \(B\subseteq M\) the (set-theoretical) preimage \(f^{-1}[B]\) is closed. Then f preserves meets (and hence has a left adjoint).
Proof
In particular, preimages of up-sets are up-sets and hence f is continuous in the Alexandroff (quasidiscrete) topology of the posets L, M, and consequently monotone.
Next, for every \(b\in M\) we have an \(a\in L\) such that  . The a is obviously uniquely determined; let us denote it by h(b). The equality
. The a is obviously uniquely determined; let us denote it by h(b). The equality  can be rewritten as
can be rewritten as

Realizing that h is monotone (if \(b\le b'\) we have  and hence
and hence  and \(h(b)\le h(b')\)) we conclude that (\(*\)) makes f a right Galois adjoint, hence a mapping preserving all meets. \(\square \)
and \(h(b)\le h(b')\)) we conclude that (\(*\)) makes f a right Galois adjoint, hence a mapping preserving all meets. \(\square \)
6.5.2 Theorem
Let L, M be frames. Then a mapping \(f:L\rightarrow M\) is localic iff
-
for every closed A, \(f^{-1}[A]\) is closed, \(f^{-1}[\mathsf{O}] =\mathsf{O}\), and
-
for every open U, \(f_{-1}[U]=f^{-1}[U^{\mathsf{c}}]^{\mathsf{c}}\) (and hence it is open).
(Note that because of the first condition and 6.5.1 the use of the symbol \(f_{-1}[U]\) makes sense—recall the convention in 6.2.)
Proof
Every localic map satisfies the conditions by 6.2.1. Thus, let \(f:L\rightarrow M\) be a plain map satisfying the conditions. Since \(f^{-1}[\mathsf{O}] =\mathsf{O}\) we have \(f(a)=1\) only if \(a=1\) and by 6.5.1 we know there is a right adjoint h, hence it remains to prove that \(f(h(a)\!\rightarrow \!x)=a\!\rightarrow \!f(x)\).
Consider a  so that \(B^{\mathsf{c}}=\mathfrak o(a)\). Thus,
so that \(B^{\mathsf{c}}=\mathfrak o(a)\). Thus,  and by the second assumption we have \(\mathfrak o(h(a))\subseteq f^{-1}[\mathfrak o(a)]\). Consequently
and by the second assumption we have \(\mathfrak o(h(a))\subseteq f^{-1}[\mathfrak o(a)]\). Consequently

for some y and we have to prove that \(a\!\rightarrow \!y= a\!\rightarrow \!f(x)\), that is, by 2.6.2(7), that \( a\wedge y= a\wedge f(x) \).
\(\ge \): Trivially, \(f(x)\le f(h(a)\!\rightarrow \!x)=a\!\rightarrow \!y\), and hence \(a\wedge f(x)\le y\).
\(\le \): Using the adjunction inequality \(\text {id}\ge h f\) and \((*)\) we have
hence \(\mathop {\textstyle \bigvee }\{h(u) \ | \ u\wedge a\le y\} \le h(a)\!\rightarrow \!x \) and so (recall rule (5) of 2.6.2)
Consequently, \(h(a\wedge y)\le h(a)\wedge h(y)\le x\) and finally \(a\wedge y\le f(x)\). \(\square \)
6.6 Joyal-Tierney Theorem
This is a very interesting useful characterisation of open localic maps, that is, of localic maps \(f:L\rightarrow M\) such that the image \(f[\mathfrak o(a)]\) of every open sublocale is open.
6.6.1 A Technical Replacement
It will be technically of advantage to replace embeddings of open sublocales \(\mathfrak o(a)\) by isomorphic representations by means of the frames  as indicated in the following diagram where \(j_a\) is the embedding \(\mathfrak o(a)\subseteq L\) and the dotted isomorphism consists of
as indicated in the following diagram where \(j_a\) is the embedding \(\mathfrak o(a)\subseteq L\) and the dotted isomorphism consists of  and
and  .
.

6.6.2 Theorem
(Joyal and Tierney [35]) A localic map \(f:L\rightarrow M\) is open iff the adjoint frame homomorphism \(h=f^*\) is a complete Heyting homomorphism, that is, if it preserves (also) all meets and the Heyting operation.
Proof
For each \(a\in L\) we have a uniquely defined \(\phi (a)\) such that \(f[\mathfrak o(a)]=\mathfrak o(\phi (a))\) resulting in the decomposition
(where \(j_a:\mathfrak o(a)\subseteq L\) and \(j_{\phi (a)}:\mathfrak o(\phi (a))\subseteq M \) are the embeddings). Obviously this map \(\phi :L\rightarrow M\) is monotone. In terms of the adjoining frame homomorphism we thus have \(j_a^*\cdot h= g^*\cdot j_{\phi (a)}^*\). Replacing the \(j^*\)’s isomorphically as in (open) we obtain a commutative diagram

Thus the openness of f is characterized by the existence of a monotone \(\phi :L\rightarrow M\) such that
or, equivalently,

For \(x=1\), in particular, \(\phi (a)\le y\) iff \(a\le h(y)\) so that \(\phi \) is a left adjoint of h and hence h preserves all meets. Further, we have by (\(*\)), for arbitrary a, \(a\le h(x)\!\rightarrow \!h(y)\) iff \(a\wedge h(x)\le h(y)\) iff \(x\wedge \phi (a)\le y\) iff \(\phi (a)\le x\!\rightarrow \!y\) iff \(a\le h(x\!\rightarrow \!y)\) and hence \(h(x)\!\rightarrow \!h(y)= h(x\!\rightarrow \!y)\).
On the other hand, if h preserves the Heyting operation, we have \(x\wedge \phi (a)\le y\) iff \(\phi (a)\le x\!\rightarrow \!y\) iff \(a\le h(x\!\rightarrow \!y)= h(x)\!\rightarrow \!h(y)\) iff \(h(x)\wedge a\le h(y)\), hence \((*)\). \(\square \)
For a thorough investigation of extensions of theorems 6.5.2 and 6.6.2 to the algebraic (not necessarily complete) setting of implicative semilattices or algebras see Erné, Picado and Pultr [18].
7 Examples
In this final section we will, first, show a few examples of point-free reasoning; in particular we present the Banaschewski-Mulvey compactification [8, 9], illustrating on the one hand that the point-free techniques can be simpler than the classical ones, and on the other hand that one can obtain better facts than in the classical setting.
At the end we will mention, without proofs, a few more examples of facts that are more satisfactory than the classical ones.
7.1 Regularity
Consider the relation between open sets of a space defined by \(V\prec U\) iff \(\overline{V}\subseteq U\). Thus, obviously, \(x\in V\prec U\) is the same as saying that there are disjoint open sets \(V\ni x\), \(W\supseteq X\smallsetminus U\), and hence the property of regularity of a space X can be expressed by stating that each open set \(U\subseteq X\) is the union \(\mathop {\textstyle \bigcup }\{V \ | \ V\prec U\} \).
This can be extended to the point-free context. Define, in a locale L, the relation \(\mathfrak o(b)\prec \mathfrak o(a)\) between open sublocales iff \(\overline{\mathfrak o(b)}\subseteq \mathfrak o(a)\), and declare L as regular if
Recall 5.6. Since \(\overline{\mathfrak o(b)}=\mathfrak c(b^*)\), then \(\mathfrak o(b)\prec \mathfrak o(a)\) iff \(\mathfrak c(b^*)\cap \mathfrak c(a)=0\), that is, \(b^*\vee a=1\). Hence L is regular iff
where \(b\prec a\) (b is rather below a) in L iff \(b^*\vee a=1\) (or, equivalently, if there is a u such that \(b\wedge u=0\) and \(u\vee a=1\)).
Regularity in frames is a very expedient property, easier to work with than e.g. variants of the Hausdorff property (see below in 7.6.2) and hence it has often appeared in point-free reasoning (from its early stages) whenever one needed spaces with a “non-trivial separation”. In the following we will present a few examples; technically we will typically work in frames, with localic interpretation added.
Compare the facts in 7.3.1, 7.2.3 and 7.2.4 below with the standard facts from classical topology concerning Hausdorff resp. compact Hausdorff spaces. Also in the point-free context they hold more generally, but the necessary technique is much more involved. The simplicity of the proofs presented here indicates why the regularity is so popular in point-free topology.
7.1.1 Lemma
If \(a_1,a_2\prec b\) then \(a_1\vee a_2\prec b\), if \(a\prec b_1,b_2\) then \(a\prec b_1\wedge b_2\), and if \(a\prec b\) then \(b^*\prec a^*\).
Proof
If \(a_i^*\vee b=0\) then \((a_1\vee a_2)^*\vee b=(a_1^*\wedge a_2^*)\vee b=1\). If \(a^*\vee b_i=1\) then \(a^*\vee (b_1\wedge b_2)=1\). If \(a^*\vee b=1\) then \(a^*\vee b^{**}=1\). \(\square \)
7.1.2 Lemma
If \(h:L\rightarrow M\) is a frame homomorphism and \(x\prec y\) then \(h(x)\prec h(y)\) . Consequently each sublocale of a regular frame is regular.
Proof
Apply h on the equalities \(x\wedge u=0\), \(u\vee y=1\). For the second statement consider the onto homomorphism h adjoint to the embedding \(S\subseteq L\). For \(b=h(a)\in S\) we have \(b=h(\mathop {\textstyle \bigvee }\{x \ | \ x\prec a\} )=\mathop {\textstyle \bigvee }\{h(x) \ | \ x\prec a\} \). \(\square \)
7.2 Dense Maps
A localic map \(f:L\rightarrow M\) is dense if \(\overline{f[L]}=M\), which is the same as saying that \(f(0)=0\). For the adjoint frame homomorphism we then have \(h(x)=0\) iff \(x\le f(0)=0\) which leads to defining a frame homomorphism to be dense if \(h(x)=0\) implies that \(x=0\), and (so far for technical reasons only) as codense if \(h(x)=1\) implies that \(x=1\).
7.2.1 Lemma
Let a homomorphism \(h:M\rightarrow L\) be codense and let M be regular. Then h is one-to-one.
Proof
Let \(h(a)=h(b)\) and let \(a\nleq b\). Then there is an \(x\prec a\), \(x\nleq b\). Since \(x^*\vee a=1\) we have \(h(x^*\vee b)=h(x^*\vee a)=1\), hence \(x^*\vee b=1\). Consequently, \(x=x\wedge (x^*\vee b)=x\wedge b\) and \(x\le b\), a contradiction. \(\square \)
7.2.2 Compactness
The concept of compactness is naturally extended to the point-free context: a cover of a frame L is a subset \(A\subseteq L\) such that \(\mathop {\textstyle \bigvee }A=1\), and a frame L is compact if every cover of L has a finite subcover.
7.2.3 Proposition
Let M be regular, L compact, and let a homomorphism \(h:M\rightarrow L\) be dense. Then it is one-to-one. Thus, a dense localic map \(f:L\rightarrow M\) with L compact and M regular is onto.
Proof
Let \(h(a)=1\). By regularity, \(a=\mathop {\textstyle \bigvee }\{b \ | \ b\prec a\} \), hence \(1= h(a)=\mathop {\textstyle \bigvee }\{h(b) \ | \ b\prec a\} \) and by compactness there are \(b_i\), \(i=1,\dots ,n\), such that \(1=\mathop {\textstyle \bigvee }_{i=1}^nh(b_i)\). Set \(c=\mathop {\textstyle \bigvee }_{i=1}^nb_i\). Then \(h(c)=1\) and by 7.1.1 \(c\prec a\), and we have \(c^*\vee a=1\). Now \(h(c^*)=h(c)\wedge h(c^*)=0\) and by density \(c^*=0\) and we obtain that \(a=1\). Hence h is also codense, and it is one-to-one by 7.2.1. \(\square \)
7.2.4 Corollary
Each compact sublocale of a regular frame is closed.
(Decompose the embedding mapping \(S\subseteq L\) into the embedding mappings \(S\subseteq \overline{S}\subseteq L\) and use 7.1.2).
7.3 Theorem
(Banaschewski Coequalizer Theorem) Let \(h_1,h_2:M\rightarrow L\) be frame homomorphisms and let M be regular. Set \(c=\mathop {\textstyle \bigvee }\{h_1(x)\wedge h_2(y) \ | \ x\wedge y=0\} .\) Then

is the coequalizer of \(h_1\) and \(h_2\).
In a localic formulation: the equalizer of any two localic maps \(f_1,f_2:L\rightarrow M\) with regular M is a closed sublocale of L, namely \(\mathfrak c(\mathop {\textstyle \bigvee }\{f^*_1(x)\wedge f^*_2(y) \ | \ x\wedge y=0\} )\).
Proof
First, let us prove that \(\gamma h_1=\gamma h_2\). By symmetry, it suffices to show that \(h_1(a)\le h_2(a)\vee c\). Let \(x\prec a\). Then \(h_1(x)\wedge h_2(x^*)\le c\) and hence \(h_1(x)= h_1(x)\wedge (h_2(x^*)\vee h_2(a))\le c\vee h_2(a)\). Since by regularity \(a=\mathop {\textstyle \bigvee }\{x \ | \ x\prec a\} \) we obtain \(h_1(a)=\mathop {\textstyle \bigvee }\{h_1(x) \ | \ x\prec a\} \le h_2(a)\vee c\).
Now let \(gh_1=gh_2\) for some homomorphism \(g:L\rightarrow K\). Then
so that we can define  by setting \(\widetilde{g}(x)=g(x)\) to obtain \(\widetilde{g}\cdot \gamma =g\). \(\square \)
by setting \(\widetilde{g}(x)=g(x)\) to obtain \(\widetilde{g}\cdot \gamma =g\). \(\square \)
7.3.1 Corollary
Let M be regular and let the localic maps \(f_1,f_2:L\rightarrow M\) coincide on a dense sublocale of L. Then \(f_1=f_2\).
7.4 Complete Regularity
While in the case of regularity we have just presented some parallels with the classical result, here we will be able to present an example of a considerable improvement, namely an extension of the Stone-Čech compactification that is not only technically very simple, but also choice-free (!).
In a frame L let us say that an element x is completely below y and write \(x\prec \!\!\prec y\) if there are \(x_d\) for diadically rationals d between 0 and 1 such that

A frame is completely regular if
7.4.1 Notes
(a) Again, similarly like with regularity, a space X is completely regular in the classical sense iff \(\Omega (X)\) is completely regular as just defined. A continuous real function \(f:X\rightarrow \mathbb {R}\) such that \(f(x)=0\) for all x in an open U and f constantly 1 on \(X\smallsetminus U\) can be obtained by inserting \(x\in V\prec \!\!\prec U\) and setting \(f(y)=\inf \{d \ | \ y\in V_d\} \) (similarly like in the construction of the function separating two closed sets in Urysohn’s Lemma).
(b) Instead of the set D of diadically rational numbers we can take any countable order-dense subset \(D'\) of the unit interval. The point is just in creating an interpolative sub-relation of \(\prec \) and for this D is particularly transparent.
(c) One immediately sees that \(\prec \!\!\prec \) is the largest interpolative sub-relation of \(\prec \) (meaning: an R such that for aRb there is always a c with aRcRb—this is not necessarily true for \(\prec \) itself). The construction of the largest interpolative subrelation given by the formula \((*)\) is not quite choice-free (it needs the Axiom of Countably Dependent Choice). This can be avoided by defining \(\prec \!\!\prec \) simply as the largest interpolative sub-relation of \(\prec \) (the union of all such subrelations). All we need (in particular the properties in 7.4.2 below) can be proved for thus defined \(\prec \!\!\prec \) to obtain a fully choice-free theory (see Banaschewski and Pultr [12]); it is of course, more involved.
7.4.2 Some Properties
From 7.1.1 and quite similarly like in 7.1.2 we obtain
Facts
(a) \(\prec \!\!\prec \) is interpolative and if \(a_1,a_2\prec \!\!\prec b\) then \(a_1\vee a_2\prec \!\!\prec b\), if \(a\prec \!\!\prec b_1,b_2\) then \(a\prec \!\!\prec b_1\wedge b_2\), and if \(a\prec \!\!\prec b\) then \(b^*\prec \!\!\prec a^*\).
(b) Each sublocale of a completely regular frame is completely regular.
7.5 A Point-Free Stone-Čech Compactification
(Banaschewski and Mulvey [8, 9]) For a frame L set
ordered by inclusion.
7.5.1 Lemma
\(\mathfrak J(L)\) is a compact frame.
Proof
Since intersections of ideals are ideals, it is a complete lattice. It is easy to check that the join in \(\mathfrak J(L)\) is given by the formula
Trivially, \((\mathop {\textstyle \bigvee }J_i)\cap K\supseteq \mathop {\textstyle \bigvee }(J_i\cap K)\) and if \(x_1\vee \cdots \vee x_n\in (\mathop {\textstyle \bigvee }J_i)\cap K\) with \(x_j\in J_{i_j}\) then \(x_j\in K\) (an ideal is a down-set), hence \(x_j\in J_{i_j}\cap K\), and \(x_1\vee \cdots \vee x_n\in \mathop {\textstyle \bigvee }(J_i\cap K)\).
Finally, if \(\mathop {\textstyle \bigvee }J_i=L\) we have in particular \(1\in \mathop {\textstyle \bigvee }J_i\), hence \(1=x_1\vee \cdots \vee x_n\) with \(x_j\in J_{i_j}\); but then \(1\in \mathop {\textstyle \bigvee }_{j=1}^nJ_{i_j}\) and hence \(L=\mathop {\textstyle \bigvee }_{j=1}^nJ_{i_j}\). Thus \(\mathfrak J(L)\) is compact. \(\square \)
7.5.2 Regular Ideals
An ideal J is regular if for every \(x\in J\) there is a \(y\in J\) such that \(x\prec \!\!\prec y\). In a completely regular frame L we have the regular ideals (recall the interpolation)
and we have, for every ideal J,
7.5.3 Lemma
Let L be completely regular. Then the set
is a compact completely regular frame.
Proof
Obviously any intersection of regular ideals is a regular ideal, and from 7.4.2 we easily infer that a join of regular ideals is regular as well. Thus, \(\mathfrak R(L)\) is a subframe of \(\mathfrak J(L)\), and as (obviously) a subframe of a compact frame is compact, it is compact.
It remains to be proved that it is completely regular. We have, for each \(J\in \mathfrak R(L)\),
and since obviously \(x\le x'\prec \!\!\prec y'\le y\) implies \(x\prec \!\!\prec y\), it remains to be proved that
Interpolate \(b\prec \!\!\prec x\prec y\prec \!\!\prec a\). Then we have \(y\in \sigma (a)\) and (recall 7.4.2) \(x^*\in \sigma (b^*)\) and hence \(1=x^*\vee y\in \sigma (b^*)\vee \sigma (a)\) and \(\sigma (b^*)\vee \sigma (a)=L\); on the other hand, trivially \(\sigma (b^*)\cap \sigma (b)=\{0 \} \) since \(x\in \sigma (b^*)\cap \sigma (b)\) makes \(x\le b\wedge b^*\). \(\square \)
7.5.4 \(\mathfrak R(L)\) as a Compactification of L
Define \(v=v_L:\mathfrak R(L) \rightarrow L\) by setting \(v(J)=\mathop {\textstyle \bigvee }J\) and consider \(\sigma _L= (a\mapsto \sigma (a)): L\rightarrow \mathfrak R(L)\). We have \(v(\sigma (a))=a\) and \(L\subseteq \sigma (v(L))\), hence v is a left Galois adjoint of \(\sigma \), and hence it preserves all joins. Further, since J, K are down-sets,
and hence v is a frame homomorphism (and \(\sigma \) is a localic map). Since \(\mathop {\textstyle \bigvee }J=0\) only if \(J=\{0 \} \) and v is obviously onto, we have (recall 7.2) that
each \(\sigma _L\) is a dense embedding of L into \(\mathfrak R(L)\).
The construction \(\mathfrak R\) can be extended to a functor by setting  and it is easy to check that v is a natural transformation. Thus, to show we have here
and it is easy to check that v is a natural transformation. Thus, to show we have here
a compactification akin to the Stone-Čech compactification of spaces
it suffices to show that for L compact the homomorphism \(v_L\) is an isomorphism, and since we already know that generally \(v(\sigma (a))=a\) and \(L\subseteq \sigma (v(L))\), it suffices to prove that for a compact L, \(\sigma (v(J))\subseteq J\). Thus, let \(x\in \sigma (v(J))\). In particular \(x\prec \mathop {\textstyle \bigvee }J\), hence \(x^*\vee \mathop {\textstyle \bigvee }J=1\) and hence, by compactness, there are \(y_1,\dots , y_n\) in J such that \(x^*\vee y_1\vee \cdots \vee y_n=1\). J is an ideal, hence \(y=y_1\vee \cdots \vee y_n\in J\), and \(x^*\vee y=1\), hence \(x\le y\) and we conclude that \(x\in J\).
7.5.5 Comments
Note that the construction is much simpler than the construction of the compactification in classical spaces. Further note that we have not used the Axiom of Choice and not even the rule of Excluded Middle. Hence the construction is fully constructive. Furthermore, it is easy to see that if a reflection is constructive then also the fact that the limits, in particular the products, are in the smaller category, is constructive. Thus, in contrast with the situation in classical spaces where the compactness of products of (in this case Hausdorff) compact spaces is compact is equivalent with a choice principle,Footnote 9 products of compact completely regular frames in \(\mathsf{Loc}\) are compact.
Now the reader may start to doubt whether this compactification is at all closely related to the Stone-Čech one. We have been so far careful in stating that it is akin to that. But this was just a cagey formulation in a situation when we could not comment about it properly. In fact, by the Hofmann-Lawson duality [4, 24] in particular the products of completely regular spaces exactly correspond to the products of the corresponding frames, hence the Banaschewski-Mulvey compactification does extend the Stone-Čech one. How is this possible? (Not very) roughly speaking, Tychonoff theorem does not need the choice for proving the compactness: products of compact spaces are always compact, without the Axiom of Choice, however, they can be non-spatial.
7.6 A Glimpse of Other Separation Axioms
(see [47] for more information) Normality can be immediately copied from classical topology: a frame is normal if

To present just a simple fact:
7.6.1 Proposition
In a normal frame the relation \(\prec \) interpolates.
Proof
Let \(a\prec b\). Then there is an x with \(a\wedge x=0\) and \(x\vee b=1\). By normality, there are u, v with \(x\vee u=1=v\vee b\) and \(u\wedge v=0\) which makes \(a\prec u\prec b\). \(\square \)
7.6.2 Lower Separation, in Particular Subfitness
About mimicking the Hausdorff axiom let us just mention that it is a complex area, with more candidates [47]. An interesting fact is that the candidates that are conservative, that is, applied to classical spaces agree with the classical Hausdorff property, do not behave as good as the so-called strong Hausdorff property, which is not conservative but parallels very well properties of Hausdorff spaces.
Instead of \(T_1\) we have a very expedient, weaker, subfitness. A frame is subfit if

Obviously, \(T_1\)-spaces are subfit (if \(x\in U\smallsetminus V\) set \(W=X\smallsetminus \{x \} \) to obtain \(U\cup W=X\ne V\cup W\)). This property goes back to Wallman, 1938 (in a pioneering article [55] of point-free thinking, published long before point-free topology started to develop; it was later rediscovered [25], and only recently really appreciated [17, 30, 38]). To show a simple application, let us prove the following
7.6.3 Proposition
A normal subfit frame is regular and hence, by 7.6.1 , completely regular.
Proof
Suppose a normal subfit L is not regular. Then there is an \(a\ne b=\mathop {\textstyle \bigvee }\{x \ | \ x\prec a\} \). Since \(a\nleq b\) there is a c with \(a\vee c\ne b\vee c\). By normality there are u, v with \(u\wedge v=0\), \(u\vee a=1\) and \(v\vee c=1\). But then \(v\prec a\), hence \(v\le b\) and we obtain a contradiction \(b\vee c\ge v\vee c=1\). \(\square \)
(In classical topology one usually speaks on normal \(T_1\)-spaces being (completely) regular, but of course subfitness suffices in the classical context as well.)
Subfitness has a lot of useful consequences. Here let us just mention a slightly surprising formula for pseudocomplement (where, in fact we will use even slightly less).
7.6.4 Proposition
In a subfit frame we have \( a^*=\mathop {\textstyle \bigwedge }\{x \ | \ x\vee a=1\} . \)
Proof
Set \(b=\mathop {\textstyle \bigwedge }\{x \ | \ x\vee a=1\} \). If \(x\vee a=1\) then \(a^*=a^*\wedge (x\vee a)=a^*\wedge x\), hence \( a^*\le x\) and we see that \( a^*\le b\). Thus, if \(b\ne a^*\) we have \(a\wedge b\ne 0\) and hence there is a \(c\ne 1\) such that \(c\vee (a\wedge b)=1\). Then \(c\vee a=1\) and \(c\vee b=1\), by the former \( b\le c\), and by the latter \(c=c\vee b=1\), a contradiction. \(\square \)
Note
Thus, in a subfit frame we can compute the pseudocomplement by a formula for supplement. It is not generally a supplement, though: for that we would need the coframe distributivity. But of course we have the consequence that
a subfit frame that is also a coframe is a Boolean algebra.
7.7 A Few More Examples
We will finish with a few examples of point-free facts that are more satisfactory than the classical counterparts. We will present them in an easily understandable form and provide references, but will not go into details.
7.7.1 Choice-Free Product Compactness
In 7.5.5 we have shown, using a choice-free reflection, that compactness of the product of completely regular locales is choice-free. In fact
this holds for any frames whatsoever
but the proof is more involved [5, 27, 37].
7.7.2 Uniform Completion
The structure of frames can be naturally enriched, like that of classical spaces. Thus we have, e.g., a theory of uniform frames [44, 48], with the concept of completeness and completion quite parallel to the classical counterparts. But (after 7.7.1 not quite surprisingly)
7.7.3 Paracompact Locales
The reader may remember the concept of paracompactness that comes in many equivalent forms (the usual one requiring a locally finite refinement for every cover, another stating that the system of all covers constitutes a uniformity), has many useful applications, but behaves very badly (even a product of a paracompact space with a metric one may not be paracompact). Contrasting with this,
the subcategory of paracompact locales is reflective in \(\mathsf{Loc}\)
There is also an elegant characterisation (not holding classically) stating that
a frame is paracompact iff it admits a complete uniformity
(Isbell [25], see also [10, 44, 50]).
7.7.4 Lindelöf Locales
Also one has that
the subcategory of Lindelöf locales is reflective in \(\mathsf{Loc}\) [39]
(the very important subcategory of Lindelöf spaces is not reflective in \(\mathsf{Top}\)).
7.7.5 Localic Groups
Extending the concept of a topological group one has the localic groups (standardly considering theory of groups over the category \(\mathsf{Loc}\) instead of over \(\mathsf{Top}\)) with properties similar to the classical ones (natural uniformities, etc.). But there is a fact that is fundamentally different (and somehow more satisfactory considering the classical zero group obtained as \(\mathbb R/\mathbb Q\), dividing a group by an infinitely smaller one), the Closed Subgroup Theorem
7.7.6 Measures
In classical measure theory, one has to restrict measure in the Euclidean space \(\mathbb {R}^n\) to special measurable subsets in order to avoid Vitali and Banach-Tarski paradoxes. Instead, by enlarging the powerset \(\mathscr {P}(\mathbb {R}^n)\) of subsets of \(\mathbb {R}^n\) to the lattice of sublocales \(\mathsf{S}(\Omega (\mathbb {R}^n))\) (recall 5.7.3 and 6.4.4), the point-free approach produces an isometry-invariant measure on all sublocales of \(\Omega (\mathbb {R}^n)\), consistent with Lebesgue measure (Simpson [52]). In particular,
every subset in \(\mathbb {R}^n\) is assigned a measure
via the inclusion of \(\mathscr {P}(\mathbb {R}^n)\) in \(\mathsf{S}(\Omega (\mathbb {R}^n))\). The contradictions are avoided because disjoint subsets need not be disjoint as sublocales: although the intersection of two such sublocales has no points, they nevertheless overlap in \(\mathsf{S}(\Omega (\mathbb {R}^n))\).
Notes
- 1.
- 2.
That is, the opens \(U=\mathrm{int}\,\overline{U}\), “open sets without lesions”, the open sets one thinks about first.
- 3.
This proof shows indeed more: L/R is a sublocale of L, see 5.4 below.
- 4.
Nuclei in L are in a one-one correspondence with onto frame homomorphisms with domain L hence constitute an alternative representation for sublocales in L [44].
- 5.
The joins \(\mathop {\textstyle \bigsqcup }\) in S are given by \(\mathop {\textstyle \bigsqcup }s_i=\nu _S(\mathop {\textstyle \bigvee }s_i)\) (if \(t\in S\) and \(t\ge s_i\) for all i then \(t\ge \mathop {\textstyle \bigvee }s_i\) and \(t=\nu _S(t)\ge \nu _S(\mathop {\textstyle \bigvee }s_i)\)).
- 6.
The reader might have expected
 for the definition of \(\mathfrak {o}(a)\). This subset of L is not a sublocale, but the intuition is not wide from the target:
for the definition of \(\mathfrak {o}(a)\). This subset of L is not a sublocale, but the intuition is not wide from the target:  is isomorphic to \(\mathfrak o(a)\) which is the image of the localic map adjoint to the map
is isomorphic to \(\mathfrak o(a)\) which is the image of the localic map adjoint to the map  .
. - 7.
The importance of this condition is comparable with that of sobriety. Note that in a way these two conditions are dual to each other: while sobriety requires that we cannot add a point to X without changing \(\Omega (X)\), \(T_D\) says that we cannot subtract a point.
- 8.
More precisely: a map is localic iff each closed sublocale has a closed preimage whose complement is contained in the preimage of the complement of the original sublocale, and the least subocales are preserved.
- 9.
References
Aull, C.E., Thron, W.J.: Separation axioms between \(T_0\) and \(T_1\). Indag. Math. 24, 26–37 (1963)
Baboolal, D., Picado, J., Pillay, P., Pultr, A.: Hewitt’s irresolvability and induced sublocales in spatial frames. Quaest. Math. 43, 1601–1612 (2020)
Banaschewski, B.: Untersuchen uber Filterräume. Doctoral dissertation, Universität Hamburg (1953)
Banaschewski, B.: The duality of distributive continuous lattices. Can. J. Math. 32, 385–394 (1980)
Banaschewski, B.: Another look at the localic Tychonoff theorem. Comment. Math. Univ. Carolinae 29, 647–656 (1988)
Banaschewski, B.: The Real Numbers in Pointfree Topology. Textos de Matemática, vol. 12, University of Coimbra (1997)
Banaschewski, B., Hong, H.S., Pultr, A.: On the completion of nearness frames. Quaest. Math. 21, 19–37 (1998)
Banaschewski, B., Mulvey, C.J.: Stone-Čech compactification of locales I. Houston J. Math. 6, 301–312 (1980)
Banaschewski, B., Mulvey, C.J.: Stone-Čech compactification of locales II. J. Pure Appl. Algebra 33, 107–122 (1984)
Banaschewski, B., Pultr, A.: Paracompactness revisited. Appl. Categ. Struct. 1, 181–190 (1993)
Banaschewski, B., Pultr, A.: Cauchy points of uniform and nearness frames. Quaest. Math. 19, 101–127 (1996)
Banaschewski, B., Pultr, A.: A constructive view of complete regularity. Kyungpook Math. J. 43, 257–262 (2003)
Banaschewski, B., Pultr, A.: On weak lattice and frame homomorphisms. Algebra Univers. 51, 137–151 (2004)
Bénabou, J.: Treillis locaux et paratopologies. Séminaire Ehresmann, 1re année, exposé 2, Paris (1958)
Clementino, M.M.: Separação e Compacidade em Categorias. Doctoral dissertation, University of Coimbra (1992)
Ehresmann, C.: Gattungen von lokalen strukturen. Jber. Deutsch. Math. Verein 60, 59–77 (1957)
Erné, M.: Distributors and Wallman locales. Houston J. Math. 34, 69–98 (2008)
Erné, M., Picado, J., Pultr, A.: Adjoint maps between implicative semilattices and continuity of localic maps. Algebra Universalis (to appear)
Ferreira, M.J., Picado, J., Pinto, S.: Remainders in pointfree topology. Topology Appl. 245, 21–45 (2018)
Glivenko, V.: Sur quelque points de la logique de M. Brouwer. Bull. Acad. R. Belg. Cl. Sci. 15, 183–188 (1929)
Gutiérrez García, J., Mozo Carollo, I., Picado, J.: Presenting the frame of the unit circle. J. Pure Appl. Algebra 220, 976–1001 (2016)
Gutiérrez García, J., Picado, J., Pultr, A.: Notes on point-free real functions and sublocales. In: Clementino, M.M., Janelidze, G., Picado, J., Sousa, L., Tholen, W. (eds.) Categorical Methods in Algebra and Topology, vol. 46, pp. 167–200. Textos de Matemática, DMUC (2014)
Hausdorff, F.: Grundzüge der mengenlehre. Veit & Co., Leipzig (1914)
Hofmann, K.H., Lawson, J.D.: The spectral theory of distributive continuous lattices. Trans. Am. Math. Soc. 246, 285–310 (1978)
Isbell, J.R.: Atomless parts of spaces. Math. Scand. 31, 5–32 (1972)
Isbell, J.R., Kříž, I., Pultr, A., Rosický, J.: Remarks on localic groups. In: Borceux, F. (ed.) Categorical Algebra and Its Applications (Proceedings of the International Conference on Louvain-La-Neuve 1987). Lecture Notes in Mathematics, vol. 1348, pp. 154–172. Springer, Berlin (1988)
Johnstone, P.T.: Tychonoff’s theorem without the axiom of choice. Fund. Math. 113, 21–35 (1981)
Johnstone, P.T.: Stone Spaces. Cambridge Studies in Advanced Mathematics, vol. 3. Cambridge University Press, Cambridge (1982)
Johnstone, P.T.: The point of pointless topology. Bull. Am. Math. Soc. (N.S.) 8, 41–53 (1983)
Johnstone, P.T.: Wallman compactification of locales. Houston J. Math. 10, 201–206 (1984)
Johnstone, P.T.: A simple proof that localic groups are closed. Cahiers Topologie Géom. Différentielle Catég. 29, 157–161 (1988)
Johnstone, P.T.: A constructive “closed subgroup theorem’’ for localic groups and groupoids. Cahiers Topologie Géom. Différentielle Catég. 30, 3–23 (1989)
Johnstone, P.T.: Elements of the history of locale theory. In: Lowen, R., Aull, C.E. (eds.) Handbook of the History of General Topology, vol. 3, pp. 835–851. Kluwer Academic Publishers, Dordrecht (2001)
Joyal, A.: Nouveaux fondaments de l’analyse. Lectures Montréal 1973 and 1974 (unpublished)
Joyal, A., Tierney, M.: An Extension of the Galois Theory of Grothendieck, vol. 309. AMS: Memoirs of the American Mathematical Society, Providence (1984)
Klinke, O.: A presentation of the assembly of a frame by generators and relations exhibits its bitopological structure. Algebra Univers. 71, 55–64 (2014)
Kříž, I.: A constructive proof of the Tychonoff’s theorem for locales. Comment. Math. Univ. Carolinae 26, 619–630 (1985)
Macnab, D.S.: Modal operators on Heyting algebras. Algebra Univers. 12, 5–29 (1981)
Madden, J.J., Vermeer, J.: Lindelöf locales and realcompactness. In: Mathematical Proceedings of the Cambridge Philosophical Society, vol. 99, pp. 473–480 (1986)
Manes, E.G.: Algebraic Theories. Graduate Texts in Mathematics, vol. 26. Springer, Heidelberg (1976)
Niefield, S.B., Rosenthal, K.I.: Spatial sublocales and essential primes. Topology Appl. 26, 263–269 (1987)
Papert, D., Papert, S.: Sur les treillis des ouverts et paratopologies. Séminaire Ehresmann (1re année, exposé 1), Paris (1958)
Picado, J., Pultr, A.: Locales Treated Mostly in a Covariant Way. Textos de Matemática, vol. 41. University of Coimbra (2008)
Picado, J., Pultr, A.: Frames and Locales: Topology Without Points. Frontiers in Mathematics, vol. 28. Springer, Basel (2012)
Picado, J., Pultr, A.: Notes on the product of locales. Math. Slovaca 65, 247–264 (2015)
Picado, J., Pultr, A.: Axiom \(T_D\) and the Simmons sublocale theorem. Comment. Math. Univ. Carolinae 60, 541–551 (2019)
Picado, J., Pultr, A.: Separation in Point-Free Topology. Birkhäuser/Springer, Cham (2021)
Pultr, A.: Pointless uniformities I. Complete regularity. Comment. Math. Univ. Carolinae 25, 91–104 (1984)
Pultr, A., Tozzi, A.: Separation axioms and frame representation of some topological facts. Appl. Categ. Struct. 2, 107–118 (1994)
Pultr, A., Úlehla, J.: Notes on characterization of paracompact frames. Comment. Math. Univ. Carolinae 30, 377–384 (1989)
Simmons, H.: Spaces with Boolean assemblies. Colloq. Math. 43, 23–29 (1980)
Simpson, A.: Measure, randomness and sublocales. Ann. Pure Appl. Log. 163, 1642–1659 (2012)
Stone, M.H.: The theory of representations for Boolean algebras. Trans. Am. Mat. Soc. 40, 37–111 (1936)
Thron, W.J.: Lattice-equivalence of topological spaces. Duke Math. J. 29, 671–679 (1962)
Wallman, H.: Lattices and topological spaces. Ann. Math. 39, 112–126 (1938)
Acknowledgements
The authors gratefully acknowledge financial support from the Centre for Mathematics of the University of Coimbra (UIDB/00324/2020, funded by the Portuguese Government through FCT/MCTES) and from the Department of Applied Mathematics (KAM) of Charles University (Prague). The first author also acknowledges the UCL project Attractivité internationale et collaborations de recherche dans le cadre du Coimbra group 2017–2020 and an ERASMUS+ Staff Mobility Grant from the University of Coimbra that supported his visit to the Université catholique de Louvain.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Picado, J., Pultr, A. (2021). Notes on Point-Free Topology. In: Clementino, M.M., Facchini, A., Gran, M. (eds) New Perspectives in Algebra, Topology and Categories. Coimbra Mathematical Texts, vol 1. Springer, Cham. https://doi.org/10.1007/978-3-030-84319-9_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-84319-9_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-84318-2
Online ISBN: 978-3-030-84319-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



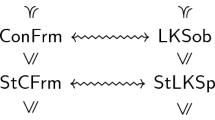

 for the definition of
for the definition of  is isomorphic to
is isomorphic to  .
.