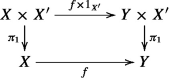An Introduction to Regular Categories

Abstract

This paper provides a short introduction to the notion of regular category and its use in categorical algebra. We first prove some of its basic properties, and consider some fundamental algebraic examples. We then analyse the algebraic properties of the categories satisfying the additional Mal’tsev axiom, and then the weaker Goursat axiom. These latter contexts can be seen as the categorical counterparts of the properties of 2-permutability and of 3-permutability of congruences in universal algebra. Mal’tsev and Goursat categories have been intensively studied in the last years: we present here some of their basic properties, which are useful to read more advanced texts in categorical algebra.

Introduction

In categorical algebra some structural properties of varieties of universal algebras are investigated by replacing the arguments involving elements of an algebraic structure and its operations with other ones using relations and commutative diagrams. A typical example is provided by the study of Mal’tsev categories [11], which can be seen as the categorical counterpart of Mal’tsev varieties (in the sense of [37]), also called 2-permutable varieties in the literature. Instead of requiring the existence, in the algebraic theory of the variety, of a ternary term p(x, y, z) verifying the identities $p(x,y,y)=x$ and $p(x,x,y)= y$, one asks that any internal reflexive relation in the category is an equivalence relation. This categorical property, with its many equivalent formulations, has turned out to be strong enough to establish, in the regular context, many of the well known properties of Mal’tsev varieties (see [8] for a recent survey on the subject, and the references therein).

This survey article can be seen as a first introduction to the basic categorical notions which are useful to express the exactness properties of various kinds of algebraic varieties in the sense of universal algebra. The main goal of this text is to introduce the reader to the notion of regular category, which is fundamental in category theory, since abelian categories, elementary toposes and varieties of universal algebras are all regular categories. Special attention will be paid to the so-called calculus of relations, which provides a powerful method to prove results in regular categories, possibly satisfying some additional exactness conditions. A good knowledge of the fundamentals of regular categories is useful to understand many of the recent developments in categorical algebra. The Mal’tsev axiom gives the opportunity to illustrate this method: in a regular category this axiom is equivalent to the permutability of the composition of equivalence relations, in the sense that any pair R and S of equivalence relations on a given object are such that $R \circ S = S \circ R$. Some recent results concerning the more general Goursat categories [10, 21] will then be explained in the last section. These aspects are useful to illustrate many of the links between exactness properties in categorical algebra, the so-called Mal’tsev conditions in universal algebra, and the validity of suitable homological lemmas [18, 19, 32].

1 Regular Categories

The notion of regular category plays an important role in the categorical understanding of algebraic structures. Regular categories capture some fundamental exactness properties shared by the categories $\mathsf {Set}$ of sets, $\mathsf {Grp}$ of groups, $\mathsf {Ab}$ of abelian groups, R-$\mathsf {Mod}$ of modules on a commutative ring R and, more generally, by any variety $\mathscr {V}$ of universal algebras. Topological models of “good” algebraic theories, such as the categories $\mathsf {Grp(Top)}$ of topological groups and $\mathsf {Grp(Comp)}$ of compact Hausdorff groups are also regular. Other examples will be considered later on in Sects. 1.3 and 3.1. The basic idea is that any arrow in a regular category can be factorized through an (essentially unique) image, and that these factorizations are stable under pullbacks.

Regular categories also have a prominent role in categorical logic (see [30], for instance, and the references therein). However, in this introductory course we shall only focus on the algebraic examples, with the goal of illustrating the importance of regular categories in categorical algebra.

In order to understand the notion of regular category it is useful to compare a few types of epimorphisms: this will be the subject of the following section (see [7] for further details).

1.1 Strong and Regular Epimorphisms

Definition 1.1

An arrow $f :A \rightarrow B$ in a category $\mathscr {C}$ is a strong epimorphism if, given any commutative square

in $\mathscr {C}$, where $m :C \rightarrow D$ is a monomorphism, there exists a unique arrow $t :B \rightarrow C$ such that $m \circ t = h$ and $t \circ f= g$.

Remark 1.2

If the category $\mathscr {C}$ has binary products, then every strong epimorphism is an epimorphism. Indeed, if $f :A \rightarrow B$ is a strong epimorphism, and $u,v :B \rightarrow C$ are two arrows such that $u \circ f =v \circ f$, one can then consider the diagonal $(1_C, 1_C)= \Delta :C \rightarrow C \times C$ and the commutative square

Since $\Delta$ is a monomorphism, there is a unique $t :B \rightarrow C$ such that $\Delta \circ t = (u,v)$ and $t \circ f = u \circ f =v \circ f$. It follows that

$$u= p_1 \circ (u,v) = p_1 \circ \Delta \circ t = t = p_2 \circ \Delta \circ t = p_2 \circ (u,v)= v,$$

where $p_1 :C \times C \rightarrow C$ and $p_2 :C \times C \rightarrow C$ are the product projections.

Lemma 1.3

An arrow $f :A \rightarrow B$ is an isomorphism if and only if $f:A \rightarrow B$ is a monomorphism and a strong epimorphism.

Proof If f is both a strong epimorphism and a monomorphism, one considers the commutative square

The unique (dotted) arrow $t :B \rightarrow A$ such that $f \circ t = 1_B$ and $t \circ f= 1_A$ is the inverse of f. The converse implication is obvious.    $\square$

Exercise 1.4

Prove that strong epimorphisms are closed under composition, and that, if the composite $g \circ f$ of two composable arrows is a strong epimorphism, then g is a strong epimorphism. Show that if $g \circ f$ is a strong epimorphism, with g a monomorphism, then g is an isomorphism.

Definition 1.5

An arrow $f :A \rightarrow B$ is a regular epimorphism if it is the coequalizer of two arrows in $\mathscr {C}$.

Exercise 1.6

Prove that any regular epimorphism is an epimorphism.

Definition 1.7

A split epimorphism is an arrow $f :A \rightarrow B$ such that there is an arrow $i :B \rightarrow A$ with $f \circ i = 1_B$.

Observe that the axiom of choice in the category $\mathsf {Set}$ says precisely that any epimorphism is a split epimorphism. This is not the case in the categories $\mathsf {Grp}$ of groups or $\mathsf {Ab}$ of abelian groups, for instance. We are now going to prove the following chain of implications:

Proposition 1.8

Let $\mathscr {C}$ be a category with binary products. One then has the implications

split epimorphism $\Rightarrow$ regular epimorphism $\Rightarrow$ strong epimorphism $\Rightarrow$ epimorphism

Proof If $f :A \rightarrow B$ is split by an arrow $i :B \rightarrow A$, then f is the coequalizer of $1_A$ and $i \circ f$. Indeed, one sees that $f \circ (i \circ f )= f = f \circ 1_A.$ Moreover, if $g :A \rightarrow X$ is such that $g \circ ( i \circ f) = g \circ 1_A$, then $\phi = g \circ i$ is the only arrow with the property that $\phi \circ f = g$.

Assume then that $f :A \rightarrow B$ is a regular epimorphism. It is then the coequalizer of two arrows, say $u :T \rightarrow A$ and $v :T \rightarrow A$: consider the commutative diagram

with m a monomorphism. The equalities

$$m \circ g \circ u = h \circ f \circ u = h \circ f \circ v = m \circ g \circ v$$

imply that $g \circ u = g \circ v$. The universal property of the coequalizer f implies that there is a unique $t :B \rightarrow C$ such that $t \circ f = g$. This arrow t is also such that $m \circ t = h$, so that f is a strong epimorphism.

The fact that any strong epimorphism is an epimorphism when $\mathscr {C}$ has binary products has been shown in Remark 1.2.    $\square$

1.2 Quotients in Algebraic Categories

Let us then consider some examples of quotients in the categories of sets, of groups and of topological groups, which will be useful to explain the general construction in regular categories.

Let $f :A \rightarrow B$ be a map in $\mathsf {Set}$, and

$$\mathrm {Eq}(f)= \{(x,y) \in A \times A \mid f(x)=f(y) \}$$

its kernel pair, i.e. the equivalence relation on A identifying the elements of A having the same image by f. This equivalence relation can be obtained by building the pullback of f along f:

Exercise 1.9

Show that any regular epimorphism f in a category with kernel pairs is the coequalizer of its kernel pair $(\mathrm {Eq}(f), p_1, p_2)$.

In the category $\mathsf {Set}$ of sets one sees that the canonical quotient $\pi :A \rightarrow A/\mathrm {Eq}(f)$ defined by $\pi (a) = \overline{a}$ is the coequalizer of $p_1$ and $p_2$. This yields a unique arrow $i :A/\mathrm {Eq}(f) \rightarrow B$ such that $i \circ \pi = f$:

The map i is defined by $i(\overline{a})=f(a)$ for any $\overline{a} \in A/\mathrm {Eq}(f)$. This gives a factorization $i \circ \pi$ of the arrow f, where $\pi$ is a regular epimorphism (= a surjective map) and i is a monomorphism (= an injective map) in the category $\mathsf {Set}$.

The same construction is possible in the category $\mathsf {Grp}$ of groups. Indeed, given a group homomorphism $f :G \rightarrow G'$, one can consider the kernel pair $\mathrm {Eq}(f)$ which is again obtained by the pullback (4.1.i) above, but this time computed in the category $\mathsf {Grp}$. The equivalence relation $\mathrm {Eq}(f)$ is a group, as a subgroup of the product $G \times G$ of the group G with itself. The canonical quotient $\pi :G \rightarrow G / \mathrm {Eq}(f)$ is a group homomorphism, and this allows one to build the following commutative diagram in $\mathsf {Grp}$

where $\pi$ is a regular epimorphism and i is a monomorphism, exactly as in $\mathsf {Set}$.

In the category $\mathsf {Grp(Top)}$ of topological groups, where the arrows are continuous homomorphisms, it is again possible to obtain the same kind of factorization regular epimorphism-monomorphism for any arrow. We write $(G, \cdot , \tau _G)$ for a topological group, where $\tau _G$ is the topology making both the multiplication $\cdot$ and the inversion of the group continuous. Given a continuous homomorphism $f :(G, \cdot , \tau _G) \rightarrow (G', \cdot , \tau _{G'})$ in $\mathsf {Grp(Top)}$, the kernel pair $(\mathrm {Eq}(f), \cdot , \tau _i)$ is a topological group for the topology $\tau _i$ induced by the product topology $\tau _{G \times G}$ of the topological group $(G \times G, \cdot , \tau _{G \times G})$. At the algebraic level the quotients in $\mathsf {Grp(Top)}$ are actually computed as in $\mathsf {Grp}$, and then equipped with the quotient topology $\tau _q$. In this way one gets the following commutative diagram

where $\pi$ is the canonical quotient. It turns out that $\pi$ is the coequalizer of the projections $p_1$ and $p_2$ in $\mathsf {Grp(Top)}$, and the induced arrow

$$i :(G/\mathrm {Eq}(f), \cdot , \tau _q) \rightarrow (G',\cdot , \tau _{G'})$$

is a monomorphism (since it is injective). Note that this factorization is not the one where the direct image f(G) of the continuous homomorphism is equipped with the subspace topology induced by the topology of $(G',\cdot , \tau _{G'})$.

There are many other categories where the same construction as in $\mathsf {Set}, \mathsf {Grp}$ and $\mathsf {Grp(Top)}$ is possible, for instance in the category $\mathsf {Rng}$ of rings, $\mathsf {Mon}$ of monoids, $\mathsf {Ab}$ of abelian groups and, more generally, in any variety $\mathscr {V}$ of universal algebras.

All these are examples of regular categories in the following sense:

Definition 1.10

[2] A finitely complete category $\mathscr {C}$ is regular if

• coequalizers of kernel pairs exist in $\mathscr {C}$;

• regular epimorphisms are pullback stable in $\mathscr {C}$.

1.3 Examples of Regular Categories

• The category $\mathsf {Set}$ is regular. We have observed that the coequalizers of kernel pairs exist in $\mathsf {Set}$, and it remains to check the pullback stability of regular epimorphisms. Consider a pullback

  

  in $\mathsf {Set}$ where p is a surjective map (i.e. a regular epimorphism), and let us show that $\pi _2$ is also surjective. Let a be an element in A; there exists then an $e \in E$ such that $p(e)=f(a)$. This shows that there is an $(e,a) \in E \times _B A$ such that $\pi _2 (e, a) = a$, and $\pi _2$ is surjective. The same argument still works in the category $\mathsf {Grp}$ of groups, by taking into account the fact that regular epimorphisms therein are precisely the surjective homomorphisms, and that pullbacks are computed in $\mathsf {Grp}$ as in $\mathsf {Set}$. For essentially the same reason the categories $\mathsf {Rng}$ of rings, $\mathsf {Mon}$ of monoids, and R-$\mathsf {Mod}$ of modules on a ring R are also regular categories. More generally, any variety $\mathscr {V}$ of universal algebras is a regular category, any quasivariety—such as the category $\mathsf {{Ab}_{t.f.}}$ of torsion-free abelian groups—and also any category monadic over the category of sets, as for instance the category $\mathsf {CHaus}$ of compact Hausdorff spaces, and the category $\mathsf {Frm}$ of frames.

• The category $\mathsf {Grp(Top)}$ of topological groups is regular [10]. The main point here is that the canonical quotient $\pi :(H, \cdot , \tau _H) \rightarrow (H/\mathrm {Eq}(f), \cdot , \tau _q)$ of a topological group $(H, \cdot , \tau _H)$ by the equivalence relation $(\mathrm {Eq}(f), \cdot , \tau _i)$ which is the kernel pair of an arrow $f :(H, \cdot , \tau _H) \rightarrow (G, \cdot , \tau _G)$ in $\mathsf {Grp(Top)}$ is an open surjective homomorphism. To check this latter fact, let us write $K = \ker (\pi )$ for the kernel of $\pi$, and let us then show that

  $$\pi ^{-1} (\pi (V)) = V \cdot K$$

  for any open $V \in \tau _H$. On the one hand if $z= v\cdot k$, where $v \in V$ and $k \in K$, one has

  $$\pi (z) = \pi (v\cdot k) = \pi (v)\cdot \pi (k) = \pi (v) \in \pi (V),$$

  so that $z \in \pi ^{-1} (\pi (V))$. Conversely, if $z \in \pi ^{-1} (\pi (V))$, then $\pi (z) = \pi (v_1)$, for a $v_1 \in V$, so that $v_1^{-1} \cdot z \in K$, and $z = v_1 \cdot k$, for a $k \in K$.

  This implies that

  $$\pi ^{-1}( \pi (V) )= (\bigcup _{k \in K} V\cdot k ) \in \tau _H.$$

  Indeed, the function $m_k :G \rightarrow G$ defined by $m_k (x)= x\cdot k$ for any $x \in G$ (with fixed $k \in K$) is a homeomorphism, hence $V \cdot k = m_k (V) \in \tau _H$, since $V\in \tau _H.$ We have then shown that $\pi (V)$ is open for any $V \in \tau _H$, and the map $\pi$ is open. It follows that in $\mathsf {Grp(Top)}$ the regular epimorphisms are the open surjective homomorphisms. To conclude that $\mathsf {Grp(Top)}$ is a regular category it suffices to recall that the open surjective homomorphisms are pullback stable (a well known fact which can be easily checked). More generally, the models of any Mal’tsev theory in the category of topological spaces, i.e. any category of topological Mal’tsev algebras, is a regular category [31]. Notice that also the category $\mathsf {Grp(Haus)}$ of Hausdorff groups, or $\mathsf {Grp(Comp)}$ of compact Hausdorff groups are regular [4] (see also [13] for the categorical properties of topological semi-abelian algebras).

• As mentioned in the Introduction any abelian category [9] is a regular category, as is any elementary topos [30].

• The category $\mathsf {Top}$ of topological spaces, unlike $\mathsf {Grp(Top)}$, is not regular. The main reason is that in $\mathsf {Top}$ regular epimorphisms are quotient maps, and these are not pullback stable (see [3] for a counter-example, for instance).

1.4 Canonical Factorization

We are now going to show that any arrow in a regular category has a canonical factorization as a regular epimorphism followed by a monomorphism, exactly as in the examples of the categories $\mathsf {Set}, \mathsf {Grp}$ and $\mathsf {Grp(Top)}$ recalled here above.

Theorem 1.11

Let $\mathscr {C}$ be a regular category. Then

• 1. any arrow $f :A \rightarrow B$ in $\mathscr {C}$ has a factorization $f= m \circ q$, with q a regular epimorphism and m a monomorphism;

• 2. this factorization is unique (up to isomorphism).

Proof

• 1. Let $f :A \rightarrow B$ be an arrow in $\mathscr {C}$. Consider the diagram here below where $(\mathrm {Eq}(f), f_{1},f_{2})$ is the kernel pair of f, q is the coequalizer of $(f_{1},f_{2})$, and m the unique arrow such that $m\circ q=f$.

  

  We need to show that m is a monomorphism or, equivalently, that the projections $p_1 :\mathrm {Eq}(m) \rightarrow I$ and $p_2 :\mathrm {Eq}(m)\rightarrow I$ of the kernel pair of m are equal. For this, consider the diagram

  

  where all the squares are pullbacks. We know that the whole square is then a pullback, so that one can assume that $f_1= \phi _1 \circ a$ and $f_2= \pi _2 \circ b$. The arrow $\phi _2 \circ a = \pi _1 \circ b$ is then an epimorphism, as a composite of epimorphisms (we have used the pullback stability of regular epimorphisms). The fact that $\phi _1 \circ a = f_1$ and $\pi _2 \circ b = f_2$ implies that

  $$p_1 \circ ( \phi _2 \circ a)= q \circ \phi _1 \circ a = q \circ f_1 = q \circ f_2 = q \circ \pi _2 \circ b = p_2 \circ \pi _1 \circ b = p_2 \circ (\phi _2 \circ a).$$

  Since $\phi _2 \circ a$ is an epimorphism, it follows that $p_1 = p_2$, as desired.

• 2. To prove the uniqueness of the factorization one can use the fact that any regular epimorphism is a strong epimorphism.

   $\square$

Remark 1.12

The uniqueness of the factorization of any arrow f in Theorem 1.11 allows one to call the subobject $m :I \rightarrow B$ in diagram (4.1.ii) the (regular) image of f.

Proposition 1.13

In a regular category $\mathscr {C}$ the following properties are satisfied:

• 1. regular epimorphisms coincide with strong epimorphisms;

• 2. if $g\circ f$ is a regular epimorphism, then g is a regular epimorphism;

• 3. if g and f are regular epimorphisms, then $g\circ f$ is a regular epimorphism;

• 4. if $f :X \rightarrow Y$ and $g :X' \rightarrow Y'$ are regular epimorphisms, then the induced arrow $f\times g :X \times X' \rightarrow Y \times Y'$ is also a regular epimorphism.

Proof

• 1. One needs to check that any strong epimorphism $f :{A \rightarrow B}$ is a regular epimorphism. Consider the factorization $f=m \circ q$ of a strong epimorphism, with m a monomorphism and q a regular epimorphism (Theorem 1.11). The commutativity of the diagram

  

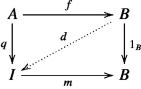
  yields a unique arrow $d:B \rightarrow I$ such that $d \circ f=q$ and $m \circ d=1_{B}$. This arrow d is the inverse of m, and f is then a regular epimorphism.

• 2. Follows from 1. and the properties of strong epimorphisms (Exercises 1.4).

• 3. Same argument as for 2.

• 4. If $f:X\rightarrow Y$ is a regular epimorphism, consider the commutative diagram

  

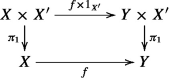
  which is easily seen to be a pullback. The arrow $f\times 1_{X'}$ is then a regular epimorphism and, similarly, one checks that $1_Y\times g$ is a regular epimorphism. Since $f \times g = (1_Y\times g)\circ (f\times 1_{X'})$, this arrow is a regular epimorphism by 3.

   $\square$

We are now going to give an equivalent formulation of the notion of regular category:

Theorem 1.14

Let $\mathscr {C}$ be a finitely complete category. Then $\mathscr {C}$ is a regular category if and only if

• 1. any arrow in $\mathscr {C}$ factorizes as a regular epimorphism followed by a monomorphism;

• 2. these factorizations are pullback stable: if $m\circ q$ is the factorization of an arrow $p :E \rightarrow B$, $f :A \rightarrow B$ any arrow, and the squares

  

  are pullbacks, then $m' \circ q'$ is the factorization of the pullback projection $\pi _2 :E \times _B A \rightarrow A$.

Proof When $\mathscr {C}$ is regular, 1. and 2. follow from Theorem 1.11.

For the converse, it is clear that 2. implies that regular epimorphisms are pullback stable. It remains to show that any kernel pair

of an arrow $f :X\rightarrow Y$ has a coequalizer. For this consider the regular epimorphism-monomorphism factorization $m\circ q$ of f (which exists by 1.), and observe that (4.1.iii) is also the kernel pair of the regular epimorphism q, since m is a monomorphism. The arrow q is then the coequalizer of its kernel pair (4.1.iii) (see Exercise 1.9).    $\square$

1.5 The Barr-Kock Theorem

The following result will be useful to prove the so-called Barr-Kock Theorem:

Lemma 1.15

Consider a commutative diagram

in a regular category $\mathscr {C}$, where the left-hand square and the external rectangle are pullbacks. If $k'$ is a regular epimorphism, then the right-hand square is a pullback.

Proof Consider the commutative diagram

where $(B' \times _{C'}{C}, \pi _1',\pi _2')$ is the pullback of $l'$ and c, and $(A' \times _{C'}{C}, \pi _1, \pi _2)$ is the pullback of $k'$ and $\pi _1'$, with $\alpha$ and $\beta$ the naturally induced arrows. The fact that the external rectangle is a pullback implies that the arrow $\alpha$ is an isomorphism. The arrow $\pi _2$ is a regular epimorphism (because $k'$ is one), so that $\pi _2 \circ \alpha = \beta \circ k$ is a regular epimorphism, and then $\beta$ is a regular epimorphism (see Proposition 1.13). The arrow $\beta$ is a monomorphism: this follows from the fact that the square

is a pullback, so that both the induced commutative squares

are pullbacks, where the (unique) dotted arrow making them commute is then a (regular) epimorphism. The arrows $p_1 :\mathrm {Eq}(\alpha ) \rightarrow A$ and $p_2 :\mathrm {Eq}(\alpha ) \rightarrow A$ are equal (since $\alpha$ is a monomorphism), so that the projections $p_1 :\mathrm {Eq}(\beta ) \rightarrow B$ and $p_2 :\mathrm {Eq}(\beta ) \rightarrow B$ are also equal, and then $\beta$ is a monomorphism.    $\square$

We are now ready to prove the following interesting result, often referred to as the Barr-Kock Theorem [1], although it was first observed by A. Grothendieck [24] in a different context (see also [7]):

Theorem 1.16

Let $\mathscr {C}$ be a regular category, and

a commutative diagram with f a regular epimorphism. If either of the left-hand commutative squares are pullbacks, then the right-hand square is a pullback.

Proof Consider the following commutative diagram

The assumptions guarantee that the left-hand face and the bottom face of the cube are pullbacks. By commutativity it follows that the rectangle

is also a pullback, as well as its left-hand square. Since f is a regular epimorphism, by Lemma 1.15 it follows that the right-hand square is a pullback.    $\square$

2 Relations in Regular Categories

Definition 2.1

An internal relation from X to Y in a category $\mathscr {C}$ is a graph

such that the pair $(r_{1},r_{2})$ is jointly monomorphic. When the product $X \times Y$ exists, this is equivalent to the fact that the factorization $(r_{1},r_{2}):R\rightarrow X\times Y$ is a monomorphism.

As usual, we identify two (internal) relations $R \rightarrow X\times Y$ and $S \rightarrow X\times Y$ when they determine the same subobject of $X \times Y$, i.e. the same equivalence class of monomorphisms with codomain $X \times Y$. If $X=Y$, one says that R is a relation on X.

• A relation R on X is reflexive when there is an arrow $\delta :X\rightarrow R$ such that $r_{1}\circ \delta =1_{X}=r_{2}\circ \delta$.

• R is symmetric if there is an arrow $\sigma :R\rightarrow R$ such that $r_{1}\circ \sigma =r_{2}$ and $r_{2}\circ \sigma =r_{1}$.

• Consider the pullback

  

  The relation R is transitive if there is an arrow $\tau : R\times _{X} R\rightarrow R$ such that $r_{1}\circ \tau =r_{1}\circ p_{1}$ and $r_{2}\circ \tau =r_{2}\circ p_{2}$.

A relation R on X is an equivalence relation if R is reflexive, symmetric and transitive. Of course, this abstract notion of equivalence relation gives in particular the usual one when $\mathscr {C}$ is the category of sets.

When $\mathscr {C}= \mathsf {Grp}$, an equivalence relation $R\subset X \times X$ in $\mathsf {Grp}$ is an equivalence relation on the underlying set of X which is also a subgroup of the group $X \times X$. In universal algebra, an internal equivalence relation in a variety is called a congruence.

Lemma 2.2

In a category with pullbacks the kernel pair of an arrow $f:X\rightarrow Y$ is an equivalence relation on X in $\mathscr {C}$.

Proof The arrows $p_1 :\mathrm {Eq}(f) \rightarrow X$ and $p_2 :\mathrm {Eq}(f) \rightarrow X$ are jointly monomorphic, since they are projections of a pullback. The universal property of the kernel pair $(\mathrm {Eq}(f), p_1,p_2)$ implies that there is a unique $\delta :X \rightarrow \mathrm {Eq}(f)$ such that $p_1 \circ \delta = 1_X= p_2 \circ \delta$

and $\mathrm {Eq}(f)$ is then reflexive. Similarly, the commutativity of the external part of the diagram

implies that there is a unique arrow $\sigma :\mathrm {Eq}(f) \rightarrow \mathrm {Eq}(f)$ such that $p_1 \circ \sigma = p_2$ and $p_2 \circ \sigma = p_1$, hence $\mathrm {Eq}(f)$ is symmetric. For the transitivity of $\mathrm {Eq}(f)$ one considers the following commutative diagram

where the back face is a pullback. The universal property of the kernel pair $( \mathrm {Eq}(f), p_1, p_2)$ shows that there is a unique $\tau$ such that $p_1 \circ \tau =p_1 \circ \pi _1$ and $p_2 \circ \tau = p_2 \circ \pi _2$.    $\square$

An important aspect of regular categories is that in these categories one can define a composition of relations, which has some nice properties.

In the category $\mathsf {Set}$, if $R \rightarrow X \times Y$ is a relation from X to Y and $S \rightarrow Y \times Z$ a relation from Y to Z, one usually defines the relation $S \circ R \rightarrow X \times Z$ by setting

$$S \circ R = \{ (x,z) \in X \times Z \, \mathrm{such \, that} \, \exists \, y \in Y \, \mathrm{with} \, xRy, ySz \}.$$

This construction is also possible in any regular category $\mathscr {C}$, thanks to the existence of regular images (Theorem 1.11). One first builds the pullback

and one then factorizes the arrow $(r_1 \circ \pi _1, s_2 \circ \pi _2) :R \times _Y S \rightarrow X \times Z$ as a regular epimorphism $q :R \times _Y S \rightarrow I$ followed by a monomorphism $i :I \rightarrow X \times Z$:

In $\mathsf {Set}$, the set I consists of the element $(x,z) \in X \times Z$ such that there is a $(u,y,v) \in R \times _Y S$ with $u=x$ and $v=z$: this is precisely $S \circ R$.

This composition is actually associative:

Theorem 2.3

Let $\mathscr {C}$ be a regular category. If $R \rightarrow A \times B$, $S \rightarrow B \times C$ and $T \rightarrow C \times D$ are relations in $\mathscr {C}$, one has the equality

$$T \circ (S\circ R)= (T \circ S) \circ R.$$

Proof Consider the diagram obtained by building the following pullbacks:

The proof consists in showing that the relations $T \circ (S\circ R)$ and $(T \circ S)\circ R$ are both given by the regular image $i :I \rightarrow A \times D$ in the factorization

as a regular epimorphism followed by a monomorphism of the arrow

$$(r_1 \circ p_1 \circ x_1, t_2 \circ q_2 \circ x_2 ) :X \rightarrow A \times D.$$

We leave it to the reader the verification of this fact, which uses the pullback stability of regular epimorphisms in a crucial way.    $\square$

This result allows one to define a new category starting from any regular category $\mathscr {C}$, the category $\mathsf {Rel} (\mathscr {C})$ of relations in $\mathscr {C}$. The objects are the same as the ones in $\mathscr {C}$, an arrow from X to Y is simply a relation from X to Y, and composition is the relational one defined above. For any relation R from X to Y the discrete relation (also called the equality relation) on X

is such that $R \circ \Delta _X=R$, and for any relation S from Z to X one has $\Delta _X \circ S=S$. It follows that the arrow $\Delta _X$ in $\mathsf {Rel}(\mathscr {C})$ is the identity on the object X for the composition in $\mathsf {Rel} (\mathscr {C})$.

There is a faithful functor $\Gamma :\mathscr {C}\rightarrow \mathsf {Rel} (\mathscr {C})$, where $\Gamma (f)$ is the graph of $f :X \rightarrow Y$, seen as a relation:

From now on we shall write $1_X$ for the discrete relation on X, which can also be seen as the relation $\Gamma (1_X)$.

Remark 2.4

$\mathsf {Rel} (\mathscr {C})$ is not only a category, but a (locally ordered) 2-category. Indeed, there is a natural partial ordering on its arrows, since the relations from X to Y are the subobjects of a fixed object $X \times Y$ of $\mathscr {C}$. This order is also compatible with the composition: if $R\le S$, then $R \circ T \le S \circ T$ whenever these composites are defined. This is the main argument to show that $\mathsf {Rel} (\mathscr {C})$ is a 2-category, which is actually locally-ordered: between any two arrows (or 1-cells) there is at most one 2-cell, and the only invertible 2-cells are the identities (see [30] for more details).

3 Calculus of Relations and Mal’tsev Categories

In this section we shall always assume that the category $\mathscr {C}$ is regular.

Given a relation $R= (R, r_1, r_2)$

from X to Y, we write $R^\circ = (R, r_2, r_1)$ for the opposite relation from Y to X:

Of course ${(R^\circ )}^\circ = R$. It is easy to see that a relation R is symmetric if and only if $R=R^\circ$. Additionally, a relation R is transitive when $R \circ R \le R.$ Moreover, in a regular category, any relation $(R,r_1,r_2)$ can be seen as the composite $R= r_2 \circ r_1^\circ$. By definition of the composition of relations, the relation $(X \times _Y Z, p_1, p_2)$ in a pullback

can be written as $g^\circ \circ f$. We leave the verification of the following properties to the reader:

Lemma 3.1

In a regular category $\mathscr {C}$:

• 1. any kernel pair $(\mathrm {Eq}(f), f_1, f_2)$ of an arrow $f :X \rightarrow Y$ can be written as $f^\circ \circ f$;

• 2. $f :X \rightarrow Y$ is a regular epimorphism if and only if $f \circ f^\circ = 1_Y$;

• 3. $f :X \rightarrow Y$ is a monomorphism if and only if $f^\circ \circ f = 1_X$.

The relations that are “maps”, i.e. of the form

for some arrow f in $\mathscr {C}$, have the following additional property:

Lemma 3.2

Any relation of the form (4.3.i) is difunctional:

$$f \circ f^\circ \circ f = f.$$

Proof The relation $f \circ f^\circ \circ f = f$ is obtained as the regular image of the external graph in the following diagram,

which is simply the regular image of the graph

Since $p_1 :\mathrm {Eq}(f) \rightarrow X$ is a split epimorphism, thus in particular a regular epimorphism (by Proposition 1.8), we see that the relation $f \circ f^\circ \circ f$ is given by the relation $(1_X, f)$ in the commutative diagram

as desired.    $\square$

In the category of sets the notion of difunctional relation was first introduced by J. Riguet [36]. A relation R is difunctional if the fact that $(x,y) \in R, (z,y) \in R$ and $(z,u) \in R$ implies that $(x,u)\in R$. This property can be expressed in any regular category as follows:

Definition 3.3

A relation $(R, r_1, r_2)$ from X to Y in a regular category is difunctional if

$$R \circ R^\circ \circ R = R.$$

The following notion was introduced by A. Carboni, J. Lambek and M.C. Pedicchio in [11], and it has been investigated in several articles in the last 30 years.

Definition 3.4

A finitely complete category $\mathscr {C}$ is called a Mal’tsev category if any internal reflexive relation in $\mathscr {C}$ is an equivalence relation.

The following characterization of regular Mal’tsev categories can be found in [11] (see also [34]). It is an example of a proof using the so-called calculus of relations.

Theorem 3.5

Let $\mathscr {C}$ be a regular category. Then the following conditions are equivalent:

• 1. for any pair of equivalence relations R and S on any object X in $\mathscr {C}$, $S \circ R$ is an equivalence relation;

• 2. for any pair of equivalence relations R and S on any object X in $\mathscr {C}$, $S \circ R = R \circ S$;

• 3. for any pair of kernel pairs $\mathrm {Eq}(f)$ and $\mathrm {Eq}(g)$ on any object X in $\mathscr {C}$, $\mathrm {Eq}(g) \circ \mathrm {Eq}(f) = \mathrm {Eq}(f) \circ \mathrm {Eq}(g)$;

• 4. any relation U from X to Y in $\mathscr {C}$ is difunctional;

• 5. any reflexive relation R on an object X in $\mathscr {C}$ is an equivalence relation;

• 6. any reflexive relation R on an object X in $\mathscr {C}$ is symmetric;

• 7. any reflexive relation R on an object X in $\mathscr {C}$ is transitive.

Proof

• $1. \Rightarrow 2.$ By assumption the relation $S \circ R$ is an equivalence relation, thus it is symmetric:

  $$(S \circ R)^\circ =S \circ R.$$

  Since both S and R are symmetric it follows that

  $$R \circ S = R^\circ \circ S^\circ = (S \circ R)^\circ = S \circ R.$$

• $2. \Rightarrow 3.$ Obvious, since any kernel pair is an equivalence relation (Lemma 2.2).

• $3. \Rightarrow 4.$ Any relation $(U, u_1, u_2)$ can be written as $U = u_2 \circ u_1^\circ$. The assumption implies that the kernel pairs $\mathrm {Eq}(u_1)$ and $\mathrm {Eq}(u_2)$ of the projections commute in the sense of the composition of relations (on the object U):

  $$(u_2^\circ \circ u_2) \circ (u_1^\circ \circ u_1)= (u_1^\circ \circ u_1) \circ (u_2^\circ \circ u_2).$$

  By keeping in mind that the relations $u_1$ and $u_2$ are difunctional (by Lemma 3.2) it follows that

  $$\begin{aligned} U= & {} u_2 \circ u_1^\circ \\= & {} (u_2 \circ u_2^\circ \circ u_2) \circ (u_1^\circ \circ u_1 \circ u_1^\circ ) \\= & {} u_2 \circ (u_2^\circ \circ u_2) \circ (u_1^\circ \circ u_1) \circ u_1^\circ \\= & {} u_2 \circ (u_1^\circ \circ u_1) \circ (u_2^\circ \circ u_2) \circ u_1^\circ \\= & {} (u_2 \circ u_1^\circ ) \circ (u_1 \circ u_2^\circ ) \circ (u_2 \circ u_1^\circ ) \\= & {} U \circ U^\circ \circ U. \end{aligned}$$

• $4. \Rightarrow 5.$ Let $(U,u_1, u_2)$ be a reflexive relation on an object X, so that $1_X \le U$. By difunctionality we have:

  $$U^\circ = 1_X \circ U^\circ \circ 1_X \le U \circ U^\circ \circ U = U,$$

  showing that U is symmetric. On the other hand:

  $$ U \circ U = U \circ 1_X \circ U \le U \circ U^\circ \circ U = U,$$

  and U is transitive.

• $5. \Rightarrow 6.$ Clear.

• $6. \Rightarrow 1.$ First observe that $S \circ R$ is reflexive, since both S and R are reflexive:

  $$ 1_X = 1_X \circ 1_X \le S \circ R.$$

  By assumption the relation $S \circ R$ is then symmetric, so that

  $$R \circ S = R^\circ \circ S^\circ = (S \circ R)^\circ = S \circ R.$$

  The relation $S \circ R$ is transitive:

  $$S \circ R = (S \circ S) \circ (R \circ R)= S \circ (S \circ R) \circ R= S \circ (R \circ S) \circ R = S \circ R \circ S \circ R.$$

  Observe that $5. \Rightarrow 7.$ is obvious, and let us prove that $7. \Rightarrow 4.$ Let $U= u_2 \circ u_1^\circ$ be any relation from X to Y. The relation

  $$u_2^\circ \circ u_2\circ u_1^\circ \circ u_1$$

  is reflexive, thus it is transitive by assumption. This gives the equality

  $$(u_2^\circ \circ u_2\circ u_1^\circ \circ u_1) \circ (u_2^\circ \circ u_2\circ u_1^\circ \circ u_1) = u_2^\circ \circ u_2\circ u_1^\circ \circ u_1, $$

  yielding

  $$u_2 \circ u_2^\circ \circ u_2\circ u_1^\circ \circ u_1 \circ u_2^\circ \circ u_2\circ u_1^\circ \circ u_1 \circ u_1^\circ = u_2 \circ u_2^\circ \circ u_2\circ u_1^\circ \circ u_1 \circ u_1^\circ .$$

  By difunctionality of $u_2$ and $u_1^\circ$ we conclude that

  $$ u_2 \circ u_1^\circ \circ u_1 \circ u_2^\circ \circ u_2\circ u_1^\circ = u_2 \circ u_1^\circ ,$$

  and

  $$U \circ U^\circ \circ U =U.$$

     $\square$

3.1 Examples of Mal’tsev Categories

The categories $\mathsf {Grp}$, $\mathsf {Ab}$, R-$\mathsf {Mod}$, $\mathsf {Rng}$ and $\mathsf {Grp(Top)}$ are all Mal’tsev categories. By Theorem 3.5 to see this it suffices to show that any (internal) reflexive relation R on any object X in these categories is symmetric. Let us check this property for the category $\mathsf {Grp}$ of groups: given an element (x, y) of a reflexive relation R which is also a subgroup of $X \times X$, we know that its inverse $(x^{-1}, y^{-1})$ is also in R and, by reflexivity, both (x, x) and (y, y) belong to R. It follows that

$$(x,x) \cdot (x^{-1}, y^{-1}) \cdot (y,y) = (x \cdot x^{-1} \cdot y, x \cdot y^{-1}\cdot y)= (y,x) \in R$$

and $\mathsf {Grp}$ is a Mal’tsev category. An inspection of the proof for $\mathsf {Grp}$ shows that the argument is still valid if the theory of an algebraic variety has a term p(x, y, z) such that $p(x,y,y)=x$ and $p(x,x,y)= y$. Varieties of algebras having such a ternary term p are called Mal’tsev varieties [37], or 2-permutable varieties, and the term p a Mal’tsev operation. This terminology is motivated by the famous Mal’tsev theorem asserting that a variety $\mathscr {V}$ of algebras has the property that each pair R and S of congruences on an algebra A in $\mathscr {V}$ permute, i.e. $R \circ S = S \circ R$ if and only if its theory has a ternary Mal’tsev operation [33].

Of course, any variety of algebras whose theory contains the operations and identities of the theory of groups is a Mal’tsev variety.

For a different example, consider the variety $\mathsf {QGrp}$ of quasigroups [37]: its algebraic theory has a multiplication $\cdot$, a left division $\backslash$ and a right division / such that $x\backslash (x \cdot y) = y$, $(x \cdot y) /y =x$, $x\cdot (x \backslash y)=y$ and $(x/y)\cdot y = x$.

A Mal’tsev operation for the theory of quasigroups is given by the term

$$p(x,y,z) = (x/(y\backslash y))\cdot (y\backslash z),$$

since

$$p(x,y,y) = (x/(y\backslash y))\cdot (y\backslash y) = x,$$

and

$$p(x,x,y) = (x/(x\backslash x))\cdot (x\backslash y) = (x \cdot (x \backslash x)/(x\backslash x))\cdot (x\backslash y) = x \cdot (x\backslash y) = y.$$

The category $\mathsf {Heyt}$ of Heyting algebras is a Mal’tsev variety [29], with a Mal’tsev operation defined by the term

$$p(x,y,z) = ((x\rightarrow y ) \rightarrow z) \wedge ((z \rightarrow y) \rightarrow x). $$

For the axioms and basic properties of Heyting algebras we refer the reader to [29], or to the Chapter Notes on point-free topology [35] in this volume. One observes that

$$\begin{aligned} p(x,x,y)= & {} ((x\rightarrow x ) \rightarrow y) \wedge ((y \rightarrow x) \rightarrow x) \\= & {} (1 \rightarrow y) \wedge ((y \rightarrow x) \rightarrow x) \\= & {} y \wedge ((y \rightarrow x) \rightarrow x) \\= & {} y \end{aligned}$$

and

$$\begin{aligned} p(x,y,y)= & {} ((x\rightarrow y ) \rightarrow y) \wedge ((y \rightarrow y) \rightarrow x) \\= & {} ((x\rightarrow y ) \rightarrow y) \wedge (1 \rightarrow x) \\= & {} ((x\rightarrow y ) \rightarrow y) \wedge x \\= & {} x. \end{aligned}$$

Other examples of regular Mal’tsev categories are: any regular additive category, therefore in particular any abelian category [9], and the dual of any elementary topos [10]. The category of ${\mathsf C}^*$-algebras and the category $\mathsf {Hopf}_{K, coc}$ of cocommutative Hopf algebras over a field K are also regular Mal’tsev categories [22, 23].

On the other hand, the categories $\mathsf {Set}$ of sets and $\mathsf {Mon}$ of monoids are regular categories which are not Mal’tsev ones. Indeed, the usual order relation $\le$ on $\mathbb N$ is an internal reflexive relation (both in $\mathsf {Set}$ and in $\mathsf {Mon}$) which is not symmetric.

3.2 Regular Pushouts

An important property of regular Mal’tsev categories is expressed in terms of diagrams of the form

where $d \circ g = f \circ c$, $c \circ t = s \circ d$, $g \circ t = 1_D$, $f \circ s = 1_B$, c and d are regular epimorphisms. As observed in [15] such a square is always a pushout. The following result is due to D. Bourn (see also [10]): here we give an alternative proof using the calculus of relations as in [19]:

Proposition 3.6

[6] A regular category $\mathscr {C}$ is a Mal’tsev category if and only if any pushout of the form (4.3.ii) has the property that the canonical morphism $(g,c) :C \rightarrow D \times _B A$ to the pullback of d and f is a regular epimorphism.

Proof The relation $(D \times _B A, p_1, p_2)$ which is the pullback of d and f can be expressed as the composite $f^\circ \circ d$. The regular image of $(g,c) :C \rightarrow D \times _B A$ is $c \circ g^\circ$, so that (g, c) is a regular epimorphism if and only if $f^\circ \circ d = c \circ g^\circ$. Now, the regular image $g(\mathrm {Eq}(c))$ of $\mathrm {Eq}(c)$ along g is defined as the regular image of the arrow $g \times g \circ (p_1, p_2) :\mathsf {Eq}(c) \rightarrow B \times B$, i.e. the subobject of $B \times B$ determined by the right-hand vertical arrow in the following commutative diagram

The commutativity conditions on the square (4.3.ii) imply that this relation is $\mathrm {Eq}(d)$:

$$g(\mathrm {Eq}(c)) = \mathrm {Eq}(d).$$

In a regular category this condition can be expressed by the equality

$$g \circ c^\circ \circ c \circ g^\circ = d^o \circ d.$$

Since $c \circ c^\circ = 1_A$ by Lemma 3.1 it follows that

$$\begin{aligned} f^\circ \circ d= & {} c \circ c^\circ \circ f^\circ \circ d \\= & {} c \circ g^\circ \circ d^\circ \circ d \\= & {} c \circ g^\circ \circ (g \circ c^\circ \circ c \circ g^\circ ) \\= & {} c \circ c^\circ \circ c \circ g^\circ \circ g \circ g^\circ \\= & {} c \circ g^\circ , \end{aligned}$$

where the fourth equality follows from the Mal’tsev assumption:

$$g^\circ \circ g \circ c^\circ \circ c= \mathrm {Eq}(g) \circ \mathrm {Eq}(c) = \mathrm {Eq}(c) \circ \mathrm {Eq}(g) = c^\circ \circ c \circ g^\circ \circ g.$$

For the converse, by Theorem 3.5 it suffices to show that any pair of equivalence relations $\mathrm {Eq}(f)$ and $\mathrm {Eq}(g)$ which are kernel pairs of two arrows f and g permute. Note that there is no restriction in assuming that f and g are regular epimorphisms, thanks to Theorem 1.11. Consider the kernel pair $(\mathrm {Eq}(f), f_1,f_2)$ of $f :X \rightarrow Y$ and the kernel pair $(\mathrm {Eq}(g), g_1,g_2)$ of $g :X \rightarrow Z$. We then consider the regular image of $\mathrm {Eq}(f)$ along g inducing the following commutative diagram

and observe that the assumption implies that $f_2 \circ \gamma ^\circ = g^\circ \circ r_2$ and $\gamma \circ f_1^\circ = r_1^\circ \circ g$. We then have the following identities:

$$\begin{aligned} \mathrm {Eq}(f) \circ \mathrm {Eq}(g)= & {} f_2 \circ f_1^\circ \circ g^\circ \circ g \\= & {} f_2 \circ \gamma ^\circ \circ r_1^\circ \circ g \\= & {} g^\circ \circ r_2 \circ r_1^\circ \circ g \\= & {} g^\circ \circ r_2 \circ \gamma \circ f_1^\circ \\= & {} g^\circ \circ g \circ f_2 \circ f_1^\circ . \\= & {} \mathrm {Eq}(g) \circ \mathrm {Eq}(f). \end{aligned}$$

   $\square$

4 Goursat Categories

In universal algebra a weaker property than the Mal’tsev axiom is the so-called 3-permutability of congruences. Given any two congruences R and S on an algebra A in a variety $\mathscr {V}$, the following equality holds:

$$R \circ S \circ R = S \circ R \circ S.$$

Definition 4.1

[10, 11] A regular category $\mathscr {C}$ is a Goursat category if

$$R \circ S \circ R = S \circ R \circ S$$

for any pair of equivalence relations R and S on any object X in $\mathscr {C}$.

Any regular Mal’tsev category $\mathscr {C}$ is a Goursat category: indeed, given any two equivalence relations R and S on an object X in $\mathscr {C}$, one has:

$$R \circ (S \circ R) = R \circ (R \circ S) = R \circ S = R \circ (S \circ S) = (S \circ R) \circ S.$$

An example of a Goursat category which is not a Mal’tsev one will be given at the end of this section, where we shall prove that implication algebras form a Goursat variety.

Among regular categories, Goursat categories are characterized by the property that equivalence relations are stable under regular images along regular epimorphisms [10]. Here below we give a direct proof which uses the calculus of relations:

Proposition 4.2

For a regular category $\mathscr {C}$ the following conditions are equivalent:

• 1. $\mathscr {C}$ is a Goursat category;

• 2. for any regular epimorphism $f :X \rightarrow Y$ and any equivalence relation R on X the regular image f(R) of R along f is an equivalence relation.

Proof

• $1. \Rightarrow 2$. When $(R, r_1, r_2)$ is an equivalence relation it is always true that the regular image $f(R) = f \circ R \circ f^\circ$ along a regular epimorphism $f :X \rightarrow Y$ is both reflexive and symmetric. Let us then prove that f(R) is also transitive: one has the equalities

  $$\begin{aligned} f(R) \circ f(R)= & {} f \circ R \circ f^\circ \circ f \circ R \circ f^\circ \\= & {} f \circ (f^\circ \circ f ) \circ R \circ ( f^\circ \circ f ) \circ f^\circ \\= & {} f \circ R \circ f^\circ \\= & {} f(R) \end{aligned}$$

  where the second equality follows from the Goursat assumption, and the third one from Lemma 3.2.

• $2. \Rightarrow 1$. Conversely, consider two equivalence relations $(R, r_1, r_2)$ and $(S, s_1, s_2)$ on a same object X in $\mathscr {C}$, and observe that the arrow $r_2 :R \rightarrow X$ is a split epimorphism, thus in particular a regular epimorphism. Then:

  $$\begin{aligned} R \circ S \circ R= & {} (r_2 \circ r_1^\circ )\circ (s_2 \circ s_1^\circ ) \circ (r_2 \circ r_1^\circ ) \\= & {} (r_2 \circ r_1^\circ )\circ (s_2 \circ s_1^\circ ) \circ (r_2 \circ r_1^\circ )^\circ \\= & {} r_2 \circ ( r_1^\circ \circ s_2 \circ s_1^\circ \circ r_1 ) \circ r_2^\circ \\= & {} r_2 (r_1^\circ \circ s_2 \circ s_1^\circ \circ r_1) \\= & {} r_2 (r_1^{-1} (S)). \end{aligned}$$

  Recall that the inverse image $r_1^{-1} (S)$ of the equivalence relation S along $r_1$ is obtained by taking the pullback

  

  and $r_1^{-1} (S)$ is always an equivalence relation. By taking into account this observation and the assumption 2., one deduces that the relation $r_2 (r_1^{-1} (S)) = R \circ S \circ R$ is transitive. It follows that

  $$\begin{aligned} S \circ R \circ S\le & {} R\circ S \circ R\circ S\circ R \\\le & {} (R \circ S \circ R) \circ (R \circ S \circ R) \\\le & {} R \circ S \circ R \end{aligned}$$

  and, symmetrically, $R \circ S \circ R \le S \circ R \circ S$, hence $S \circ R \circ S = R \circ S \circ R$.

   $\square$

Exercise 4.3

Show that the regular image of an equivalence relation in $\mathsf {Set}$ is not necessarily transitive.

4.1 Goursat Pushouts

In a Goursat category there is a class of pushouts that has a similar role to the one of regular pushouts in a regular Mal’tsev category:

Definition 4.4

Consider a commutative diagram (4.3.ii), and the induced arrow $\hat{c}$ making the following diagram commute:

Then the square (4.3.ii) is called a Goursat pushout [18] when the arrow $\hat{c}$ is a regular epimorphism.

The following result was proved in [18]. Here we give a different proof of one of the two implications, based on the calculus of relations:

Proposition 4.5

[18] For a regular category $\mathscr {C}$ the following conditions are equivalent:

• 1. $\mathscr {C}$ is a Goursat category;

• 2. any square (4.3.ii) is a Goursat pushout.

Proof

• $1. \Rightarrow 2$. If $\mathscr {C}$ is a Goursat category then

  $$\begin{aligned} c(\mathsf {Eq}(g))= & {} c \circ g^\circ \circ g \circ c^\circ \\= & {} c \circ (c^\circ \circ c) \circ (g^\circ \circ g) \circ (c^\circ \circ c) \circ c^\circ \\= & {} c \circ (g^\circ \circ g) \circ (c^\circ \circ c) \circ (g^\circ \circ g) \circ c^\circ \\= & {} c \circ g^\circ \circ d^\circ \circ d \circ g \circ c^\circ \\= & {} c \circ c^\circ \circ f^\circ \circ f \circ c \circ c^\circ \\= & {} f^\circ \circ f \\= & {} \mathsf {Eq}( f) \end{aligned}$$

  where the third equality follows from the Goursat assumption, the fourth one from $g(\mathsf {Eq}(c) )= \mathsf {Eq}(d)$, and the sixth one from the fact that c is a regular epimorphism (Lemma 3.1).

• $2. \Rightarrow 1$. Conversely, given a commutative diagram

  

  where $(R, r_1,r_2)$ is an equivalence relation, f is a regular epimorphism and $(T,t_1,t_2)$ is the regular image of R along f. We are to show that the relation $f(R)=T$ is an equivalence relation (by Proposition 4.2). Since the regular image of a reflexive and symmetric relation is always reflexive and symmetric, it suffices to show that T is transitive. This follows from the computation:

  $$\begin{aligned} T \circ T= & {} T \circ T^\circ \\= & {} t_2 \circ t_1^\circ \circ t_1 \circ t_2^\circ \\= & {} t_2 \circ (\overline{f} \circ r_1^\circ \circ r_1 \circ {\overline{f}}^\circ ) \circ t_2^\circ \\= & {} f \circ r_2 \circ r_1^\circ \circ r_1 \circ r_2^\circ \circ f^\circ \\= & {} f \circ R \circ R^\circ \circ f^\circ \\= & {} f \circ R \circ f^\circ \\= & {} T. \end{aligned}$$

  Remark that the assumption that any square of the form (4.3.ii) is a Goursat pushout has been used in the third equality, where it has been applied to the diagram

  

     $\square$

To conclude this short introduction to Goursat categories we give a characterization of those varieties of universal algebras which are 3-permutable by using the notion of Goursat pushout. This proof, originally discovered in [26], has a categorical version which has first been given in [18].

When $\mathscr {V}$ is a variety of universal algebras, we shall denote by $X = F(1)$ the free algebra on the one-element set.

Theorem 4.6

For a variety $\mathscr {V}$ of universal algebras the following conditions are equivalent:

• 1. $\mathscr {V}$ is 3-permutable: for any pair R, S of congruences on any algebra A in $\mathscr {V}$ one has the equality

  $$R \circ S \circ R = S \circ R \circ S;$$

• 2. the theory of $\mathscr {V}$ contains two quaternary operations p and q satisfying the identities

  $$p(x,y,y,z) =x, \quad q(x,y,y,z) = z, \quad p(x,x,y,y) = q(x,x,y,y). $$

Proof

• $1. \Rightarrow 2.$ Consider the commutative diagram

  

  where $\nabla _k$ is the codiagonal from the k-indexed copower of X to X (for $k \in \{2,3 \}$). The vertical arrows $\nabla _2 + \nabla _2$ and $\nabla _3$ are split epimorphisms, whereas the horizontal arrows are regular epimorphisms, so that the diagram is a Goursat pushout by Proposition 4.5. It follows that the unique morphism

  $$\overline{1 + \nabla _2 + 1} :\mathsf {Eq}(\nabla _2 + \nabla _2) \rightarrow \mathsf {Eq}(\nabla _3)$$

  in $\mathscr {V}$ making the diagram

  

  commute is a regular epimorphism (here $p_1$ and $p_2$ are the kernel pair projections), thus it is surjective. Observe that the terms $p_1 (x,y,z) =x$ and $p_3(x,y,z) = z$ are identified by $\nabla _3$, so that $(p_1, p_3) \in \mathsf {Eq}(\nabla _3)$. The surjectivity of $\overline{1 + \nabla _2 + 1}$ then implies that there are terms $(p,q) \in \mathsf {Eq}(\nabla _2 + \nabla _2)$ such that $\overline{1 + \nabla _2 + 1} (p,q) = (p_1, p_3)$. This latter property means exactly that

  $$p(x,y,y,z) =x, \quad q(x,y,y,z) = z,$$

  while the fact that $(p,q) \in \mathsf {Eq}(\nabla _2 + \nabla _2)$ gives the identity

  $$p(x,x,y,y) = q(x,x,y,y). $$

• $2. \Rightarrow 1.$ For the converse implication, take R and S two congruences on an algebra A in $\mathscr {V}$, and let us show that $R \circ S \circ R \le S \circ R \circ S$. For $(a,b) \in R \circ S \circ R$, let x and y be such that $(a,x) \in R$, $(x,y) \in S$ and $(y,b)\in R$. Then the fact that (a, a), (x, a), (y, b), (b, b) are in R implies that both (p(a, x, y, b), p(a, a, b, b)) and (q(a, x, y, b), q(a, a, b, b)) are in R. Since $p(a,a,b,b) = q(a,a,b,b)$ we deduce that $(p(a,x,y,b), q(a,x,y,b)) \in R$. On the other hand, the elements (a, a), (x, x), (x, y), (b, b) are all in S so that $(p(a, x, x, b),p(a, x, y, b))\in S$, $(q(a, x, x, b),q(a, x, y, b)) \in S$, hence (a, p(a, x, y, b)) and (b, q(a, x, y, b)) are both in S. We then observe that

  $$\begin{aligned} (a, p(a, x, y, b))&\in S&\\ (p(a, x, y, b), q(a, x, y, b))&\in R&\\ (q(a, x, y, b), b)&\in S&\end{aligned}$$

  we conclude that (a, b) belongs to $S \circ R \circ S$. It then follows that $R \circ S \circ R = S \circ R \circ S$, as desired.    $\square$

Remark 4.7

Note that one can give a proof of the Mal’tsev theorem characterizing 2-permutable varieties by using some categorical arguments similar to the ones in Theorem 4.6. This was first observed in [12] and, more recently, in [8].

Remark 4.8

A wide generalization of Theorem 4.6 was obtained by P.-A. Jacqmin and D. Rodelo in [27], where a categorical approach to n-permutability was developed. Thanks to their approach the authors have been able to characterize the property of n-permutability in terms of some specific stability properties of regular epimorphisms, which extend the one considered in [20] to study Goursat categories.

4.2 Implication Algebras

A typical example of 3-permutable variety, thus of a Goursat category, is provided by the variety $\mathsf {ImplAlg}$ of implication algebras [1]. The algebraic theory of the variety $\mathsf {ImplAlg}$ has a binary operation such that

• (A) $(xy)x=x$,

• (B) $(xy)y= (yx)x$,

• (C) $x(yz) = y(xz)$.

As explained in [25], to see that $\mathsf {ImplAlg}$ is 3-permutable, one first checks that the term xx is a constant: indeed, the identities

$$\begin{aligned} xx= & {} [(xy)x]x \qquad \qquad \quad \text {(by (A)) } \\= & {} [x(xy)](xy) \qquad \qquad \text {(by (B))} \\= & {} x [[x(xy)]y] \qquad \qquad \text {(by (C))} \\= & {} x[[((xy)x)(xy)]y] \qquad \text {(by (A))} \\= & {} x[(xy)y] \qquad \qquad \quad \text {(by (A))} \\= & {} (xy)(xy) \qquad \qquad \quad \text {(by (C))} \end{aligned}$$

imply that

$$xx = [x(yy)][x(yy)] = [y(xy)][y(xy] =yy,$$

and one denotes such an equationally defined constant by 1. This notation is justified by the fact that

$$1y = (yy)y =y.$$

One then verifies that the terms $p(x,y,z,u)= (zy)x$ and $q(x,y,z,u)=(yz)u$ are such that

$$\begin{aligned}&p(x,y,y,z) = (yy)x = 1x=x,\\&q(x,y,y,z)= (yy)z=1z=z, \end{aligned}$$

and

$$p(x,x,z,z) = (zx)x = (xz)z = q(x,x,z,z).$$

4.3 Diagram Lemmas and Goursat Categories

We conclude these notes by mentioning a connection between the validity of some suitable diagram lemmas and the permutability conditions on a regular category considered above. The classical $3\times 3$-Lemma in abelian categories [14] has been extended to several non-additive contexts by various authors (see [5, 28], for instance). An original extension to a non-pointed context was first established by D. Bourn in the context of regular Mal’tsev categories [6]. The main point in order to formulate the $3 \times 3$-Lemma in a category which does not have a 0-object is to replace the classical notion of short exact sequence with the notion of exact fork: a diagram of the form

is an exact fork if and only if $(R, r_1,r_2)$ is the kernel pair of f, and f is the coequalizer of $r_1$ and $r_2$. With this notion at hand the appropriate way of expressing the $3 \times 3$-Lemma is then the following, which is called the denormalized $3 \times 3$-Lemma: given any commutative diagram

in $\mathscr {C}$ such that

• $y_i \circ a_j = b_j \circ z_i$, $y\circ b_i = c_i \circ z$, $b\circ y_i = k_i \circ a$, $x \circ b = c \circ y$ (for $i,j \in \{1,2\}$),

• the three columns and the middle row are exact forks,

then the upper row is an exact fork if and only if the lower row is an exact fork.

S. Lack observed in [32] that this denormalized $3\times 3$-Lemma holds not only in regular Mal’tsev categories (as observed by D. Bourn [6]) but also in Goursat categories. Later on it turned out that the validity of the denormalized $3\times 3$-Lemma actually characterizes Goursat categories among regular ones:

Theorem 4.9

[18, 32] For a regular category $\mathscr {C}$ the following conditions are equivalent:

• 1. $\mathscr {C}$ is a Goursat category;

• 2. if the lower row in a diagram (4.4.ii) is an exact fork then the upper row is an exact fork;

• 3. if the upper row in a diagram (4.4.ii) is an exact fork then the lower row is an exact fork;

• 4. the denormalized $3\times 3$-Lemma holds in $\mathscr {C}$: the lower row is an exact fork if and only if the upper row is an exact fork.

We would like to point out that both the calculus of relations and the notion of Goursat pushout play a central role in the proof of this result. Note that a unification of both the classical $3\times 3$-Lemma and of the denormalized one in the context of star-regular categories is also possible [17]. Further results linking the Goursat property to natural conditions appearing in universal algebra—in relationship to congruence modularity—have been investigated in [21] (see also the references therein). Finally, let us mention that also Mal’tsev categories can be characterized via a suitable diagrammatic condition that is stronger than the denormalized $3\times 3$-Lemma, called the Cuboid Lemma [19].