Ring Epimorphisms, Gabriel Topologies and Contramodules

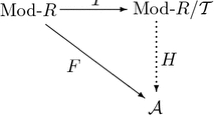
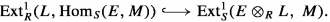Abstract

During the 1960s considerable work was done in order to understand the meaning of “epimorphism”. The notion plays an important role in categories of rings where the abstract category-theoretic meaning is now of common use.

The notion of ring epimorphism has relations with torsion theory and localisation theory. In particular, perfect right Gabriel topologies (in Stenström’s terminology) correspond bijectively to left flat ring epimorphisms.

In these notes we will consider two classes of modules defined in terms of a ring epimorphism: the comodules and the contramodules as introduced by Leonid Positselski. Adding mild conditions on the ring epimorphism we will extend classical results proved by Matlis for commutative rings by showing an equivalence between suitable subcategories of the two classes of comodules and contramodules.

Introduction During the 1960s considerable effort was done in order to understand the meaning of epimorphisms in various concrete categories. The notion plays an important role in categories of rings. Localisations of commutative rings with respect to multiplicative subsets are important examples of ring epimorphisms which are moreover, flat ring epimorphisms. A generalisation to noncommutative rings is accomplished by localisations with respect to Gabriel topologies, and flat ring epimorphisms correspond bijectively to a particular class of Gabriel topologies.

In Sect. 2 we will present a characterisation of ring epimorphisms by means of five equivalent conditions. Afterward in Sect. 3 we will introduce Gabriel topologies and their bijective correspondence with hereditary torsion pairs. Furthermore we will define rings and modules of quotients with respect to a Gabriel topology and outline some of their properties.

The purpose of our investigation is to generalise classical equivalences between subcategories of modules over rings to the case of subcategories of modules arising from a ring epimorphism between associative rings.

An important example of such equivalences is provided by the famous Brenner and Butler’s Theorem: A finitely generated tilting module T over an artin algebra $\Lambda$ gives rise to a torsion pair $(\mathcal {T},\mathcal {F})$, where $\mathcal {T}$ is the class of modules generated by T. If D denotes the standard duality and $\Gamma$ is the endomorphism ring of T, then D(T) is a cotilting $\Gamma$-module with an associated torsion pair $(\mathcal {X},\mathcal {Y})$ where $\mathcal {Y}$ is the class of modules cogenerated by D(T). The Brenner and Butler’s Theorem states that the functor $\mathrm {Hom}_{\Lambda }(T,-)$ induces an equivalence between the categories $\mathcal {T}$ and $\mathcal {Y}$ with inverse the functor $-\otimes _{\Gamma }T$, and the functor ${\text {Ext}}^1_{\Lambda }(T,-)$ induces an equivalence between $\mathcal {F}$ and $\mathcal {X}$ with inverse the functor ${\text {Tor}}^{\Gamma }_1(-, T)$.

For infinitely generated modules a first example of equivalences was provided by Harrison [6] in the category of abelian groups. One equivalence is provided by the tensor product functor $\mathbb {Q}/\mathbb {Z}\otimes _{\mathbb {Z}}-$, with the functor $\mathrm {Hom}_\mathbb {Z}(\mathbb {Q}/\mathbb {Z},{-})$ as inverse. In Matlis’ memoir [8, Sect. 3], the setting was generalised to the case of a commutative domain R and its quotient field Q establishing two kinds of equivalences between certain full additive subcategories of the category of R-modules. The first equivalence is provided by the functor of tensor product with the R-module Q/R with inverse the functor $\mathrm {Hom}_R(Q/R,{-})$. The second equivalence is given by the pair of functors ${\text {Tor}}_1^R(Q/R,{-})$ and ${\text {Ext}}^1_R(Q/R,{-})$, which are mutually inverse if restricted to suitable subcategories. Moreover, in the book [9] Matlis extended the first one of his two category equivalences to the setting of an arbitrary commutative ring R and its total ring of quotients Q.

Two further generalisations of the Matlis category equivalences appeared in the two recent papers [4, 12]. In the paper [12], Matlis category equivalences were constructed for a localisation $R[S^{-1}]$ of a commutative ring R with respect to a multiplicative subset $S\subset R$. Injectivity of the map $R\longrightarrow R[S^{-1}]$ was not assumed, but it was assumed that the projective dimension of the R-module $R[S^{-1}]$ was at most one. In the paper [4], Matlis category equivalence was constructed for certain injective epimorphisms of noncommutative rings $R\longrightarrow Q$, where Q is the localisation of R with respect to a one-sided Ore subset of regular elements.

In the paper [3] the first Matlis additive category equivalence is constructed for any ring epimorphism $f:R\longrightarrow U$ such that ${\text {Tor}}_1^R(U,U)=0$, and the second Matlis category equivalence is constructed under the assumption ${\text {Tor}}_1^R(U,U)=0={\text {Tor}}_2^R(U,U)$. Let us emphasize that neither injectivity of f, nor any condition on the projective or flat dimension of the R-module U is required for these results. Commutativity of the rings R and U is not assumed, either.

In these notes we present only some of the results proved in [3]. More precisely, in Sect. 5 we give details for the construction of the first Matlis additive category equivalence (Theorem 5.6).

Our key tools are the notions of comodules and contramodules. In Sect. 4 we introduce and discuss the subcategories of comodules and contramodules associated to a ring epimorphism. In Subsect.4.1 we justify the terminology starting with classical definitions of coalgebras and comodules over coalgebras and show a natural way to introduce the notion of contramodules over coalgebras.

1 Preliminaries

We will assume familiarity with basic notions on category theory like functors, natural transformations, equivalences of categories (see e.g. [15, Ch.1] or [7, Ch.1]).

We will mostly consider categories of modules over associative rings R with unit and we denote by $R\text {-}\mathrm {Mod}$, or $\mathrm {Mod}\text {-}R$ the categories of left, respectively right R-modules.

For every right, or left R-modules M and N, $\mathrm {Hom}_R(M, N)$ denotes the abelian group of all R-linear maps from M to N.

For every right R-module M and a left R-module N, $M\otimes _RN$ denotes the tensor product between M and N.

We will assume that the properties of the functor $\mathrm {Hom}_R(-,-)$ and of the tensor product functor $-\otimes _R-$ are well known.

A left (right) R-module P is projective if $\mathrm {Hom}_R(P,-)$ is an exact functor and a module M has projective dimension (${\text {p.dim}}$) at most one if it is an epimorphic image of a projective module with kernel a projective module.

A left (right) R-module E is injective if $\mathrm {Hom}_R(-,E)$ is an exact functor.

A right (left) R-module F is said to be flat if the functor $F\otimes _R-$ ($-\otimes _RF$) is exact and a module M has flat dimension (${\text {f.dim}}$) at most one if it is an epimorphic image of a flat module with kernel a flat module.

Moreover we will use the adjunction between the tensor product functor and the $\mathrm {Hom}$ functor. More specifically, if R and S are rings, $_SE_R$ is an S-R-bimodule, the pair of functors $(E\otimes _R-, \mathrm {Hom}_S(E, -))$ is an adjoint pair, that is:

$$\begin{aligned} E\otimes _R-:R\text {-}\mathrm {Mod}\longrightarrow S\text {-}\mathrm {Mod}; \qquad \mathrm {Hom}_S(E, -):S\text {-}\mathrm {Mod}\longrightarrow R\text {-}\mathrm {Mod}, \end{aligned}$$

and for every left R-module M and left S-module N there is an isomorphism of abelian groups, called the adjunction isomorphism

natural in M and N.

We recall the definition of the unit and the counit of this adjoint pair.

The unit is the natural transformation

$$\eta :\text {id}_{R\text {-}\mathrm {Mod}}\rightarrow \mathrm {Hom}_S(E, -)\circ E\otimes _R-\ ,$$

where for every $M\in R\text {-}\mathrm {Mod}$ the morphism $\eta _M$ is given by:

The counit is the natural transformation

$$\xi :E\otimes _R-\circ \mathrm {Hom}_S(E, -)\rightarrow \text {id}_{S\text {-}\mathrm {Mod}}$$

where for every $N\in S\text {-}\mathrm {Mod}$ the morphism $\xi _N$ is given by

The morphism $\eta _M$ and $\xi _N$ will be used in Sect. 5.

For more details on all these notions see e.g. [15, Ch.1] or [1, Ch.1 and 5] or [14, Ch. 2 and 3].

We will make use of some tools in homological algebra, namely the derived functors. In particular, we will deal with the left derived functors ${\text {Tor}}^R_i$ of the tensor product functor, and the right derived functors ${\text {Ext}}^i_R$ of the $\mathrm {Hom}_R$ functor.

For their construction and their properties see e.g. [16, Ch. 2 and 3].

In particular, for a right (left) R-module M, we have ${\text {p.dim}}M\le 1$ if and only if ${\text {Ext}}^2(M, -)=0$ and ${\text {f.dim}}M\le 1$ if and only if ${\text {Tor}}^R_2(M,-)=0$ (${\text {Tor}}^R_2(-, M)=0$).

2 Ring Epimorphisms

Definition 2.1

Let $\mathscr {C}$ be a category and $f:A\longrightarrow B$ be a morphism between two objects of $\mathscr {C}$.

f is an epimorphism if for every object $C\in \mathscr {C}$ and morphisms $g, h:B\longrightarrow C$, $g\circ f=h\circ f$ implies $g=h$.

A category $\mathscr {C}$ is concrete if there is a faithful functor F from $\mathscr {C}$ to the category of sets. The functor F makes it possible to think of the objects of the category as sets, possibly with additional structure, and of its morphisms as structure-preserving maps. Examples of concrete categories include trivially the category of sets, the category of topological spaces, the category of groups, the category of rings and the category of modules over a ring R. Every morphism in a concrete category whose underlying map is surjective is an epimorphism. In many concrete categories of interest the converse is also true.

Example 2.2

For instance if $f:X\longrightarrow Y$ is an epimorphism in the category of sets, consider $g:Y\longrightarrow \{0, 1\}$ the characteristic function of f(X) ( i.e. $g(f(x))=1$, for every $x\in X$ and $g(y)=0$ for every $y\in Y\setminus f(X)$) and let $h:Y\longrightarrow \{0, 1\}$ be the constant function such that $h(y)=1$ for every $y\in Y$. Then $g\circ f=h\circ f$, hence $g=h$ and $f(X)=Y.$

There are examples of concrete categories for which epimorphisms are not necessarily surjective maps as we are going to show.

Denote by $\mathsf {Rng}$ the category of associative unital rings. A ring homomorphism $f:R\longrightarrow U$ between two rings R, U is a ring epimorphism if it is an epimorphism in the category $\mathsf {Rng}$. That is, for every ring V and every ring homomorphisms $v,w:U \longrightarrow V$, $v\circ f = w\circ f$ implies $v = w$.

Example 2.3

(1) If I is a two sided ideal of a ring R, then the natural quotient morphism $q:R\longrightarrow R/I$ is a surjective map, hence a ring epimorphism.

(2) If R is a commutative ring, S a multiplicative subset of R, consider the ring of fractions $R_S=R[S^{-1}]$.

Recall that $R_S=\{\left[ \frac{r}{s}\right] \mid r\in R, s\in S\}$ where $\left[ \frac{r}{s}\right]$ is the equivalence class of the fraction $\frac{r}{s}$ under the equivalence relation defined by $\frac{r}{s}\sim \frac{r'}{s'}$ if and only if there is $t\in S$ such that $t(rs'-sr')=0$. The ring of fractions $R_S$ becomes a ring with the obvious ring operations (see [2, Ch 3]).

The natural localisation map $\psi :R\longrightarrow R_S,\, \psi (r)=\left[ \frac{r}{1}\right]$, is a ring epimorphism. Indeed, if U is a ring and $g,h:R_S\longrightarrow U$ are two ring homomorphisms such that $g\circ \psi =h\circ \psi$, then for every element $r\in R$ and every $s\in S$, we have $g(\left[ \frac{r}{s}\right] )=g(\left[ \frac{r}{1}\right] )g(\left[ \frac{s}{1} \right] ^{-1})$, where $g(\left[ \frac{s}{1} \right] ^{-1})$ is the inverse in U of $g(\left[ \frac{s}{1} \right] )=h(\left[ \frac{s}{1} \right] )$, hence $g(\left[ \frac{s}{1} \right] ^{-1})=h(\left[ \frac{s}{1} \right] ^{-1})$. Thus $g(\left[ \frac{r}{s}\right] )=h(\left[ \frac{r}{1}\right] )h(\left[ \frac{s}{1} \right] ^{-1})=h(\left[ \frac{r}{s}\right] )$. That is $g=h$.

(3) The above example shows that there are many ring epimorphisms which are not surjective. In fact, if S is a multiplicative subset of a commutative ring R such that the elements of S are not all invertible in R, then the localisation map $R\longrightarrow R_S$ is a non-surjective ring epimorphism. This applies in particular to the inclusion $\mathbb {Z}\hookrightarrow \mathbb {Q}.$

What do epimorphisms of rings look like? There is a list of equivalent conditions for a ring homomorphism to be an epimorphism which allow to have a better understanding of the notion.

We first note the following. Let $f:R\longrightarrow U$ be a ring homomorphism and let M be a left U-module. Then M is also a left R-module via the scalar multiplication $rx=f(r)x$ for every $x\in M$ and every $r\in R$. Similarly, a right U-module inherits the structure of right R-module via f.

In this way we can define a functor

$$\begin{aligned} f_{*}:U\text {-}\mathrm {Mod}\longrightarrow R\text {-}\mathrm {Mod}; \quad _UM\mapsto f_{*}(_UM) \end{aligned}$$

where $f_{*}(_UM)$ is M viewed as a left R-module via f. The functor $f_{*}$ is called the restriction functor. Similarly, for right U-modules and right R-modules.

In particular, the ring U is a left and right R-module and even an R-R-bimodule.

Consider the tensor product $U\otimes _RU$ which becomes an R-R bimodule and the morphisms

$$\begin{aligned} i_1:U\longrightarrow U\otimes _RU, \quad u\mapsto u\otimes 1, \end{aligned}$$

$$\begin{aligned} i_2:U\longrightarrow U\otimes _RU, \quad u\mapsto 1\otimes u, \end{aligned}$$

$$\begin{aligned} p:U\otimes _RU\longrightarrow U, \quad u\otimes v\mapsto uv, \end{aligned}$$

for every $u, v\in U$.

Proposition 2.4

Let $f:R\longrightarrow U$ be a ring homomorphism. The following conditions are equivalent:

• 1. f is a ring epimorphism.

• 2. For every U-U-bimodule M,

  $$\{x\in M\mid xr=rx, \forall r\in R\}=\{x\in M\mid xu=ux, \forall u\in U\}.$$

• 3. $i_1=i_2.$

• 4. The restriction functor $f_{*}$ is fully faithful.

• 5. $p:U\otimes _RU\longrightarrow U$ is an isomorphism as U-U-bimodules.

Proof

(1) $\Rightarrow$ (2) Let M be an U-U-bimodule. Consider the trivial extension of U by M, i.e. the ring

$$\begin{aligned} U\propto M=\left\{ \begin{pmatrix}u&{}x\\ 0&{}u\end{pmatrix}\mid u\in U, x\in M\right\} , \end{aligned}$$

with matrix operations. Fix $x\in M$ such that $xr=rx$, for every $r\in R$ and define two ring homomorphisms $g, h:U\longrightarrow U\propto M$ by

$$g(u)=\begin{pmatrix}u&{}0\\ 0&{}u\end{pmatrix},\quad h(u)=\begin{pmatrix}u&{}xu-ux \\ 0&{}u\end{pmatrix},\, \text {for every } u\in U.$$

Then $gf(r)=h(f(r))$ for every $r\in R$.

By (1) $g=h$, that is $xu=ux$ for every $u\in U$.

Conversely, fixing $x\in M$, if $xu=ux$ for every $u\in U$, then $xr=rx$ for every $r\in R$ by the way in which the R-module structure of M is defined via f.

(2) $\Rightarrow$ (3) Let $1\otimes _R1=x\in U\otimes _RU$. Then, for every $r\in R$, $xr=1\otimes _Rr=r\otimes _R1=rx$. Applying (2) to the U-U-bimodule $U\otimes _RU$ we conclude that $xu=ux$ for every $u\in U$, hence $(1\otimes _R1)u=1\otimes _Ru=u(1\otimes _R1)=u\otimes _R1$.

(3) $\Rightarrow$ (4) $f_{*}$ fully faithful means that for every left U-modules M and N there is an isomorphism of abelian groups

$$\begin{aligned} \mathrm {Hom}_U(M, N)\overset{\phi }{\longrightarrow }\mathrm {Hom}_R(f_{*}(M), f_{*}(M)). \end{aligned}$$

The morphism $\phi$ is easily seen to be injective and $\phi$ is surjective if every R-linear morphism between left U-modules is also U-linear. Let M, N be left U-modules and let $\alpha :M\longrightarrow N$ be an R-linear morphism. Fix $x\in M$, $u,v\in U$ and define $\beta :U\otimes _RU\longrightarrow N$ by $\beta (u\otimes _Rv)=u\alpha (vx)$. It is easy to check that $\beta$ is well defined since $\alpha$ is R-linear. By condition (3), $\beta (1\otimes _Ru)=\beta (u\otimes _R1)$ which yields $\alpha (ux)=u\alpha (x)$, hence $\alpha$ is U-linear.

(4) $\Rightarrow$ (1) Let V be a ring and $g,h:U\longrightarrow V$ be ring homomorphisms such that $g\circ f=h\circ f$. Then V can be viewed as a left U-module via h, that is for every $v\in V$ and $u\in U$ one has $uv=h(u)v$; but V can also be viewed as a left R-module via $g\circ f$, that is $rv=g(f(r))v$, for every $v\in V$ and every $r\in R$. Then g is R-linear; indeed $g(ru)=g(f(r)u)=g(f(r))g(u)=rg(u).$ By condition (4) g is also U-linear, hence $g(u)=ug(1) =uh(1)$ and by the left U-module structure on V via h we have $uh(1)=h(u)h(1)=h(u)$. We conclude that $g=h$.

(4) $\Rightarrow$ (5) The morphism $i_2$ is R-linear. Indeed, $i_2(ru)=1\otimes _Rru=r\otimes _Ru=r(1\otimes _Ru)$. By assumption $f_{*}$ is fully faithful, thus $i_2$ is also U-linear, that is $i_2(uv)=1\otimes _Ruv =ui_2(v)=u(1\otimes _Rv)=u\otimes _Rv.$ We conclude that $i_2$ is the inverse of p.

(5) $\Rightarrow$ (3) By definition $p(u\otimes _R1)=u=p(1\otimes _Ru)$. Thus $u\otimes _R1=1\otimes _Ru$.    $\square$

Remark 2.5

Clearly, the equivalent conditions in Proposition 2.4 can be stated and proved for right R-modules and right U-modules.

Definition 2.6

A ring epimorphism $f:R\longrightarrow U$ between associative rings R, U is said to be a homological ring epimorphism if ${\text {Tor}}^R_i(U,U)=0$ for every $i\ge 1$ and it is called a left (right) flat ring epimorphism if U is flat as a left (right) R-module.

Example 2.7

Let R be a commutative ring and $R_S=R[S^{-1}]$ be the localisation of R at a multiplicative subset S of R. Then the localisation map $\psi :R\longrightarrow R_S$ is a flat ring epimorphism (see [2, Proposition 3.3]).

In particular, if $\mathfrak p$ is a prime ideal of R and $R_{\mathfrak p}=R[(R\setminus \mathfrak p)^{-1}]$ the localisation map $R\longrightarrow R_{\mathfrak p}$ is a flat ring epimorphism.

Thus flat ring epimorphisms can be viewed as generalisations of localisations of commutative rings at multiplicative sets. As mentioned in the Introduction, Gabriel topologies allow to generalise to the non-commutative setting the notion of localisation and flat ring epimorphisms correspond to localisations with respect to a particular type of Gabriel topologies as we will explain next.

3 Gabriel Topologies, Torsion Pairs and the Ring of Quotients

A topological ring is a ring with a topology for which the ring operations are continuous functions. A topological ring is right linearly topological if it has a basis of neighbourhoods of zero consisting of right ideals.

A set $\mathcal {F}$ of right ideals of a ring R is the collection of open right ideals of the linearly topological ring R if and only if it satisfies the following conditions:

• (T1) If $I \in \mathcal {F}$ and $I \subseteq J$, then $J \in \mathcal {F}$.

• (T2) If $I, J \in \mathcal {F}$, then $I \cap J \in \mathcal {F}$.

• (T3) If $I \in \mathcal {F}$ and $r \in R$ then $I:r= \{s\in R\mid rs \in I\}$ belongs to $\mathcal {F}$.

The first two conditions just say that $\mathcal {F}$ is a filter of right ideals of R and if R is commutative $I:r$ contains I, thus condition (T3) follows by (T1).

Definition 3.1

A (right) Gabriel topology on R, denoted by $\mathcal {G}$, is a filter of open right ideals of a linearly topological ring R (thus satisfying (T1), (T2), (T3) ) such that the following additional condition holds.

• (T4) If I is a right ideal of R and there exists $J \in \mathcal {G}$ such that $I:r \in \mathcal {G}$ for every $r \in J$, then $I \in \mathcal {G}$.

Example 3.2

(1) If R is a commutative ring and S is a multiplicative subset of R, then $\mathcal {G}=\{J\le R\mid S\cap J\ne \emptyset \}$ is a Gabriel topology.

Indeed, (T1) is obvious and (T2) follows since for $s, t\in S$, $st\in S$. As for (T4), if $J\in \mathcal {G}$ and I is an ideal of R such that $I:r\in \mathcal {G}$ for every $r\in J$, let $s\in J\cap S$. Then there exist an element $t\in S$ such that $t\in I:s$, so $st\in I$ and thus $I\in \mathcal {G}$.

(2) If R is a commutative ring and I is a finitely generated ideal of R, then $\mathcal {G}=\{J\le R\mid J\supseteq I^n,\, \exists n\in \mathbb {N}\}$ is a Gabriel topology.

Indeed, (T1), (T2) and (T3) are obvious. Let $J\in \mathcal {G}$ and let $L\le R$ be such that $L:r\in \mathcal {G}$ for every $r\in J$. There is $n_0\in \mathbb {N}$ such that $J\ge I^{n_0}$. Let $(a_1, a_2,, \dots , a_k)$ be a set of generators of $I^{n_0}$. For every $i=1,2, \dots , k$ there is $n_i\in \mathbb {N}$ such that $L:a_i\ge I^{n_i}$. Then there is $m\in \mathbb {N}$ such that $L\ge I^m$ (take e.g. $m=n_0n$ where n is the supremum of the $n_i$’s).

Definition 3.3

A right R-module over a topological ring R is called discrete if the scalar multiplication $M\times R\rightarrow M$ is continuous with respect to the discrete topology on M and the topology on R, that is M is a topological R-module in the discrete topology. If R is a right linearly topological ring and $\mathcal {F}$ is the filter of open right ideals, a discrete right R-module M is called $\mathcal {F}$-discrete. This amounts to have that for every $x\in M$ the annihilator ideal of x, $\mathrm {Ann}_R x=\{r\in R\mid xr=0\}$, belongs to $\mathcal {F}$.

Recall that a class $\mathscr {C}$ of R-modules is closed under extensions if for every short exact sequence $0\rightarrow A\rightarrow B\rightarrow C\rightarrow 0$ with $A, C\in \mathscr {C}$, also B is in $\mathscr {C}$.

Proposition 3.4

Let $\mathcal {F}$ be a set of right ideals of R satisfying (T1), (T2) and (T3). Then $\mathcal {F}$ satisfies (T4) if and only if the class of $\mathcal {F}$-discrete modules is closed under extensions.

Proof

Assume that $\mathcal {F}$ satisfies (T4).

Let $0\rightarrow A\rightarrow B\rightarrow C\rightarrow 0$ be a short exact sequence of R-modules with A and C $\mathcal {F}$-discrete modules. W.l.o.g. we may assume that $A\le B$ and $C=B/A$. Let $x\in B$ and let $I=\mathrm {Ann}_R x$. If $x\in A$, then $I\in \mathcal {F}$. If $x\notin A$ consider the element $x+A\in C$. The annihilator $\mathrm {Ann}_R(x+A)=J$ is in $\mathcal {F}$ and $xJ\subseteq A$. Thus, for every $r\in J$, $xr\in A$ and the annihilator $\mathrm {Ann}_Rxr=J_r$ of the element xr is in $\mathcal {F}$. We have $I:r\supseteq J_r$, so $I\in \mathcal {F}$ by (T4), hence B is $\mathcal {F}$-discrete.

Conversely, assume that the class of $\mathcal {F}$-discrete modules is closed under extensions and let $I\le R$, $J\in \mathcal {F}$ be such that $I:r\in \mathcal {F}$ for every $r\in J$. We must show that $I\in \mathcal {F}$. Consider the short exact sequence

$$\begin{aligned} 0\rightarrow J/(I\cap J)\cong (I+J)/I\rightarrow R/I\rightarrow R/(I+J)\rightarrow 0. \end{aligned}$$

We show that $J/(I\cap J)$ and $R/(I+J)$ are $\mathcal {F}$-discrete modules.

$I+J\in \mathcal {F}$, since $(I+J)\ge J$ and $J\in \mathcal {F}$. The annihilator of an element $a+(I+J)\in R/(I+J)$ is $(I+J):a$ which is in $\mathcal {F}$ by (T3), hence $R/(I+J)$ is $\mathcal {F}$-discrete. If $r\in J$, then $\mathrm {Ann}_R(r+(I\cap J))=I:r$ which is assumed to be in $\mathcal {F}$. By assumption R/I is $\mathcal {F}$-discrete, hence $I=\mathrm {Ann}_R(1+I)$ is in $\mathcal {F}$.    $\square$

For a right Gabriel topology $\mathcal {G}$, denote by $\mathcal {T}_\mathcal {G}$ the class of $\mathcal {G}$-discrete modules.

Lemma 3.5

Let $\mathcal {G}$ be a right Gabriel topology. The class $\mathcal {T}_\mathcal {G}$ of $\mathcal {G}$-discrete modules is closed under submodules, direct sums, epimorphic images, and extensions.

Proof

The closure under submodules follows immediately by the definition. If $f{:} M\longrightarrow N$ is an R-linear map, then $\mathrm {Ann}_Rx\le \mathrm {Ann}_Rf(x)$ for every $x\in M$, thus the closure under epimorphic images follows by (T1). The annihilator of an element in a direct sum $\oplus _i M_i$ of modules $M_i$ contains the finite intersection of the annihilators of its finitely many non-zero components, hence the closure under direct sums follows by (T1) and (T2). The closure under extensions follows by Proposition 3.4.    $\square$

The above lemma actually says that $\mathcal {T}_\mathcal {G}$ is a hereditary torsion class as we are going to explain next. For a reference and more details on the notion of torsion pairs in module categories see [15, Ch. VI].

Definition 3.6

A torsion pair $(\mathcal {T}, \mathcal {F})$ in $\mathrm {Mod}\text {-}R$ is a pair of classes of modules which are mutually orthogonal with respect to the $\mathrm {Hom}$-functor and maximal with respect to this property. That is,

$$\begin{aligned} \mathcal {T}= \{T\in \mathrm {Mod}\text {-}R\mid \mathrm {Hom}_R(T, F)=0 \text{ for } \text{ every } F \in \mathcal {F}\}, \end{aligned}$$

$$\begin{aligned} \mathcal {F}= \{F\in \mathrm {Mod}\text {-}R\mid \mathrm {Hom}_R(T, F)=0 \text { for every } T \in \mathcal {T}\}. \end{aligned}$$

The class $\mathcal {T}$ is called a torsion class and $\mathcal {F}$ a torsion-free class.

A torsion pair $(\mathcal {T}, \mathcal {F})$ is called hereditary if $\mathcal {T}$ is also closed under submodules (which is equivalent to $\mathcal {F}$ being closed under injective envelopes).

We show that a torsion class is characterised by its closure properties.

Proposition 3.7

A class $\mathcal {T}$ of right R-modules is a torsion class if and only if it is closed under direct sums, epimorphic images and extensions.

Proof

The necessary condition follows by the properties of the $\mathrm {Hom}$-functor and the definition of a torsion class. For the sufficiency, assume that a class $\mathcal {T}$ has the stated closure properties. Let

$$\begin{aligned} \mathcal {F}=\mathcal {T}^{\perp _0}=\{F\in \mathrm {Mod}\text {-}R\mid \mathrm {Hom}_R(T, F)=0, \forall T\in \mathcal {T}\}\, \text {and} \end{aligned}$$

$$\begin{aligned} \mathcal {T}'=^{\perp _0}\mathcal {F}=\{X\in \mathrm {Mod}\text {-}R\mid \mathrm {Hom}_R(X, F)=0, \forall F\in \mathcal {F}\} \end{aligned}$$

we show that $\mathcal {T}'=\mathcal {T}$.

For every $X\in \mathrm {Mod}\text {-}R$ let $\mathcal {H}(X)=\{Z\le X\mid Z\in \mathcal {T}\}$ be the class of the submodules of X belonging to $\mathcal {T}$. Consider the submodule t(X) of X defined as $t(X)=\sum \limits _{Z\in \mathcal {H}(X)} Z$. Then $t(X)\in \mathcal {T}$ since it is the image in X of the natural map from the direct sum $\bigoplus \limits _{Z\in \mathcal {H}(X)}Z$ to X. Clearly t(X) is the maximal submodule of X contained in $\mathcal {T}$.

We show now that for every $X\in \mathcal {T}'$, the module X/t(X) belongs to $\mathcal {F}$. Indeed, if $T\in \mathcal {T}$ and $f:T\rightarrow X/t(X)$ is a nonzero morphism, let $0\ne Y/t(X)$ be the nonzero image of f. Then $Y/t(X)\in \mathcal {T}$, since it is an epimorphic image of $T\in \mathcal {T}$ and from the short exact sequence

$$\begin{aligned} 0\rightarrow t(X)\rightarrow Y\rightarrow Y/t(X)\rightarrow 0 \end{aligned}$$

and the closure under extensions of $\mathcal {T}$ we conclude that $Y\in \mathcal {T}$, that is $Y=t(X)$ contradicting the maximality of t(X). Thus $f=0$ and $X/t(X)\in \mathcal {F}$. The definition of $\mathcal {T}'$ yields that $X=t(X)$, that is $X\in \mathcal {T}$.    $\square$

Remark 3.8

Let $(\mathcal {T}, \mathcal {F})$ be a torsion pair. For every R-module M there is a short exact sequence

$$\begin{aligned} 0\rightarrow T\rightarrow M\rightarrow M/T\rightarrow 0, \end{aligned}$$

with $T\in \mathcal {T}$ and $M/T\in \mathcal {F}$. T is the torsion submodule of M, that is

$$\begin{aligned} T= t(M)=\sum \{Z\le M\mid Z\in \mathcal {T}\}. \end{aligned}$$

Example 3.9

(1) Let R be a commutative ring and S a multiplicative subset of R. Let $\mathcal {T}$ be the class of the R-modules X such that for every $x\in X$ there is an element $s\in S$ satisfying $xs=0$. Note that $\mathcal {T}$ coincides with the class of R-modules X such that $X\otimes _RR_S=0$. Let $\mathcal {F}$ be the class of R-modules Y such that for every $0\ne y\in Y$, $ys\ne 0$ for every $s\in S$. Then $(\mathcal {T}, \mathcal {F})$ is a hereditary torsion pair.

(2) If S is the set of regular elements r of R, that is the nonzero divisors (i.e. for every $a\in R$, $ra=0$ or $ar=0$ implies $a=0$) the localisation $R_{S}$ is denoted by Q and called the total quotient ring of R. In case R is a commutative domain, then Q is the quotient field of R. An R-module is simply called a torsion module if it belongs to the torsion class $\mathcal {T}$ in the hereditary torsion pair described in example (1) above.

Theorem 3.10

Let R be a ring. There is a bijective correspondence:

• 1. If $\mathcal {G}$ is a right Gabriel topology $\Phi ( \mathcal {G})= (\mathcal {T}_\mathcal {G}, \mathcal {F}_\mathcal {G})$ where $\mathcal {T}_\mathcal {G}$ is the class of the $\mathcal {G}$-discrete modules and

  $$\begin{aligned} \mathcal {F}_\mathcal {G}=\{Y_R\in \mathrm {Mod}\text {-}R\mid \mathrm {Hom}_R(R/J, Y)=0, \forall J\in \mathcal {G}\}. \end{aligned}$$

• 2. If $(\mathcal {T}, \mathcal {F})$ is a hereditary torsion pair, $\Psi ((\mathcal {T},\mathcal {F}))=\{J_R\le R\mid R/J\in \mathcal {T}\}$.

Proof

(1) For every Gabriel topology $\mathcal {G}$, the class of $\mathcal {G}$-discrete modules is a hereditary torsion class by Lemma 3.5 and Proposition 3.7. A module $T\in \mathcal {T}_\mathcal {G}$ is an epimorphic image of a direct sum of copies of modules R/J, for some $J\in \mathcal {G}$. Hence the description of the torsion-free class follows.

(2) Let $(\mathcal {T}, \mathcal {F})$ be a hereditary torsion pair and $\mathcal {G}=\{J_R\le R\mid R/J\in \mathcal {T}\}$. The closure of $\mathcal {T}$ under epimorphic images implies that $\mathcal {G}$ satisfies condition (T1). If I, J are in $\mathcal {G}$, then $R/I\oplus R/J\in \mathcal {T}$ and $\mathrm {Ann}_R(1+I, 1+J)=I\cap J$; hence (T2) is satisfied by $\mathcal {G}$. As for (T3), let $J\in \mathcal {G}$ and $r\in R$. Then $J:r=\{s\in R\mid rs\in J\}=\mathrm {Ann}_R(r+J)$. Since $\mathcal {T}$ is hereditary, the cyclic module $(r+J)R$ belongs to $\mathcal {T}$, thus $J:r\in \mathcal {G}$. At this point (T4) follows by Proposition 3.4 since $\mathcal {T}$ is closed under extensions.

If $\mathcal {G}$ is a Gabriel topology, it is clear by construction that $\Psi \circ \Phi (\mathcal {G})=\mathcal {G}$, since $J\in \mathcal {G}$ if and only if $R/J\in \mathcal {T}_\mathcal {G}$.

If $(\mathcal {T}, \mathcal {F})$ is a hereditary torsion pair and $\mathcal {G}= \Psi ((\mathcal {T}, \mathcal {F}))$, then a module $N\in \mathcal {T}_\mathcal {G}$ is an epimorphic image of a direct sum of cyclic modules of the form R/J for some $J\in \mathcal {G}$, hence $N\in \mathcal {T}$. Conversely, if $M\in \mathcal {T}$, then every cyclic submodule $xR\cong R/J$ of M is in $\mathcal {T}$, since $\mathcal {T}$ is hereditary, thus $J\in \mathcal {G}$ and consequently $M\in \mathcal {T}_\mathcal {G}$. We conclude that $\Phi \circ \Psi ((\mathcal {T}, \mathcal {F}))=(\mathcal {T}, \mathcal {F}).$    $\square$

Remark 3.11

Note that the hereditary torsion pair defined in Examples 3.9 (1) corresponds under the bijection of Theorem 3.10 to the Gabriel topology defined in Examples 3.2 (1).

If $\mathcal {G}$ is a Gabriel topology with corresponding torsion pair $(\mathcal {T}_\mathcal {G}, \mathcal {F}_\mathcal {G})$, a $\mathcal {G}$-discrete module is also called $\mathcal {G}$-torsion and a module in $\mathcal {F}_\mathcal {G}$ is called $\mathcal {G}$-torsion-free.

A Gabriel topology allows to generalise localisations of commutative rings to the case of non-commutative rings and as already mentioned, we will see that flat ring epimorphisms are localizations of particular types of Gabriel topologies.

In this section we state some notions and results on rings and modules of quotients with respect to a Gabriel topology. For their proofs we refer to [15, Chapter IX].

On a Gabriel topology $\mathcal {G}$ consider the partial order given by inclusion and for an arbitrary R-module N consider the direct system

$$\begin{aligned} \{\mathrm {Hom}_R(J, N); f_{IJ}\}_{J\in \mathcal {G},\,I\le J} \end{aligned}$$

where for every $I\le J$ the morphism

$$f_{IJ}:\mathrm {Hom}_R(J, N)\longrightarrow \mathrm {Hom}_R(I, N)$$

is the restriction map.

Given a module M, the module of quotients with respect to a Gabriel topology $\mathcal {G}$ is defined by:

$$ M_\mathcal {G}:= \varinjlim _{\begin{array}{c} J \in \mathcal {G} \end{array}} \mathrm {Hom}_R(J, M/t_\mathcal {G}(M)) $$

where $t_\mathcal {G}(M)$ is the torsion submodule of M in the torsion pair $(\mathcal {T}_\mathcal {G}, \mathcal {F}_\mathcal {G})$ corresponding to $\mathcal {G}$ under Theorem 3.10.

Furthermore, there is a natural homomorphism

$$\begin{aligned} \psi _M:M\cong \mathrm {Hom}_R(R, M) \longrightarrow M_\mathcal {G}\end{aligned}$$

For each R-module M, both the kernel and cokernel of the map $\psi _M$ are $\mathcal {G}$-torsion R-modules.

If $M=R$, then

$$R_\mathcal {G}:= \varinjlim _{\begin{array}{c} J \in \mathcal {G} \end{array}} \mathrm {Hom}_R(J, R/t_\mathcal {G}(R))$$

is a ring and is called the ring of quotients of R with respect to the Gabriel topology $\mathcal {G}$ and the morphism $\psi _R:R \longrightarrow R_\mathcal {G}$ is a ring homomorphism. Moreover, for each R-module M the module $M_\mathcal {G}$ is both an R-module and an $R_\mathcal {G}$-module.

A right R-module is $\mathcal {G}$-closed if the natural homomorphisms

$$\begin{aligned} M \cong \mathrm {Hom}_R(R, M) \longrightarrow \mathrm {Hom}_R (J, M) \end{aligned}$$

are all isomorphisms for each $J \in \mathcal {G}$.

This amounts to saying that $\mathrm {Hom}_R(R/J,M) =0$ for every $J \in \mathcal {G}$ (i.e. M is $\mathcal {G}$-torsion-free) and ${\text {Ext}}^1_R(R/J,M) =0$ for every $J \in \mathcal {G}$ (i.e. M is $\mathcal {G}$-injective). Moreover, if M is $\mathcal {G}$-closed then M is isomorphic to its module of quotients $M_\mathcal {G}$ via $\psi _M$. Conversely, every R-module of the form $M_\mathcal {G}$ is $\mathcal {G}$-closed. The $\mathcal {G}$-closed modules form a full subcategory of both $\mathrm {Mod}\text {-}R$ and $\mathrm {Mod}\text {-}R_\mathcal {G}$. In fact, every R-linear morphism of $\mathcal {G}$-closed modules is also $R_\mathcal {G}$-linear.

Remark 3.12

In general the natural ring homomorphism $\psi _R:R\longrightarrow R_\mathcal {G}$ is not a ring epimorphism, but in some important cases $\psi _R$ is even a flat ring epimorphism.

The following two results characterise when a ring homomorphism is a flat ring epimorphism and describe the associated Gabriel topology.

Theorem 3.13

[15, Theorem XI.2.1] Suppose $f :R \longrightarrow U$ is a ring homomorphism. Then the following are equivalent.

• (i) f is an epimorphism of rings which makes U into a flat left R-module.

• (ii) The family $\mathcal {G}$ of right ideals J such that $JU = U$ is a Gabriel topology, and the natural ring homomorphism $\psi :R \longrightarrow R_\mathcal {G}$ is equivalent to $f:R \longrightarrow U$. That is, there is a ring isomorphism $\sigma :U \longrightarrow R_\mathcal {G}$ such that $\sigma \circ f:R \longrightarrow R_\mathcal {G}$ is the natural homomorphism $\psi _R:R \longrightarrow R_\mathcal {G}$.

Proposition 3.14

[15, Proposition XI.3.4] Let $\mathcal {G}$ be a right Gabriel topology. Then the following conditions are equivalent.

• 1. $\psi _R:R \longrightarrow R_\mathcal {G}$ is a flat ring epimorphism and $\mathcal {G}= \{ J \le R \mid JR_\mathcal {G}= R_\mathcal {G}\}$.

• 2. $R_\mathcal {G}$ is $\mathcal {G}$-divisible, i.e. $JR_\mathcal {G}=R_\mathcal {G}$ for every $J\in \mathcal {G}$.

• 3. For every right R-module M, ${\text {Ker}}(M \rightarrow M \otimes _R R_\mathcal {G})$ is the $\mathcal {G}$-torsion submodule of M.

Definition 3.15

A right Gabriel topology satisfying the equivalent conditions of Proposition 3.14 is called a perfect Gabriel topology.

In particular, the right Gabriel topology $\mathcal {G}$ associated to a flat ring epimorphism $R \overset{u}{\longrightarrow }U$ is finitely generated and the $\mathcal {G}$-torsion submodule $t_\mathcal {G}(M)$ of a right R-module M is the kernel of the natural homomorphism $M\rightarrow M \otimes _R U$. Additionally, $K=U/u(R)$ is $\mathcal {G}$-torsion, hence $\mathrm {Hom}_R(K, U)=0$.

4 Comodules and Contramodules

We first introduce the definitions of “comodules and contramodules” via ring epimorphisms and in the next subsection we will explain how the terminology is borrowed from the coalgebras setting.

From now on $f:R\longrightarrow U$ will always denote a ring epimorphism of associative rings.

Recall from Sect. 2 that the functor of restriction of scalars

$$\begin{aligned} f_{*}:U\text {-}\mathrm {Mod}\rightarrow R\text {-}\mathrm {Mod}\end{aligned}$$

is fully faithful. Similar assertions hold for the categories of right modules.

We will say that a certain R-module “is a U-module” if it belongs to the image of the functor $f_{*}$.

We will use the notation U/R for the cokernel of the map $f:R\longrightarrow U$, so U/R is an R-R-bimodule.

Definition 4.1

• 1. A left R-module M is called a left U-comodule if

  $$ U\otimes _RM=0={\text {Tor}}^R_1(U,M). $$

  Similarly, a right R-module N is said to be a right U-comodule if

  $$\begin{aligned} N\otimes _RU=0={\text {Tor}}^R_1(N,U). \end{aligned}$$

• 2. A left (right) R-module C is called a left (right) U-contramodule if

  $$ \mathrm {Hom}_R(U,C)=0={\text {Ext}}^1_R(U,C). $$

Proposition 4.2

[5, dual of Proposition 1.1] Let $\mathscr {C}\subset R\text {-}\mathrm {Mod}$ be the class of all left U-comodules. Then:

• 1. $\mathscr {C}$ is closed under direct sums, cokernels of morphisms, and extensions in $R\text {-}\mathrm {Mod}$.

• 2. If ${\text {f.dim}}_RU\le 1$ as a right R-module, then $\mathscr {C}$ is closed also under kernels of morphisms.

Proof

(1) The closure under direct sums and extensions of left U-comodules follows by the properties of the tensor product functor and Tor functor.

Let $g:N\rightarrow L$ be a morphism between left U-comodules and consider the associated short exact sequences

$$\begin{aligned} (a)\quad 0\rightarrow {\text {Ker}}g\rightarrow N\rightarrow {\text {Im}}g\rightarrow 0;\quad (b)\quad 0\rightarrow {\text {Im}}g\rightarrow L\rightarrow {\text {Coker}}g\rightarrow 0 \end{aligned}$$

Applying the right exact functor $U\otimes _R-$ to sequence (b) we obtain

$$\begin{aligned} 0=U\otimes _RL\rightarrow U\otimes _R{\text {Coker}}g\rightarrow 0, \end{aligned}$$

so $U\otimes _R{\text {Coker}}g=0$. From sequence (a) we get

$$\begin{aligned} 0=U\otimes _RN\rightarrow U\otimes _R{\text {Im}}g\rightarrow 0, \end{aligned}$$

hence $U\otimes _R{\text {Im}}g=0$. The long exact sequence associated to (b) yields

$$\begin{aligned} 0={\text {Tor}}^R_1(U, L)\rightarrow {\text {Tor}}^R_1(U, {\text {Coker}}g)\rightarrow U\otimes _R{\text {Im}}g=0. \end{aligned}$$

Thus also ${\text {Tor}}^R_1(U, {\text {Coker}}g)=0$ and ${\text {Coker}}g$ is a left U-comodule.

(2) The assumption ${\text {f.dim}}_RU\le 1$ is equivalent to ${\text {Tor}}^R_2(U, -)=0$. Let $g:N\rightarrow L$ be a morphism between left U-comodules and consider the exact sequences as in part (1). From sequence (b) we get

$$\begin{aligned} 0={\text {Tor}}^R_2(U, {\text {Coker}}g)\rightarrow {\text {Tor}}^R_1(U, {\text {Im}}g)\rightarrow {\text {Tor}}^R_1(U, L)=0. \end{aligned}$$

So ${\text {Tor}}^R_1(U, {\text {Im}}g)=0$ and sequence (a) gives

$$\begin{aligned} 0={\text {Tor}}^R_1(U, {\text {Im}}g)\rightarrow U\otimes _R {\text {Ker}}g\rightarrow U\otimes _RN=0 \end{aligned}$$

and

$$\begin{aligned} {\text {Tor}}^R_2(U, {\text {Im}}g)=0\rightarrow {\text {Tor}}^R_1(U, {\text {Ker}}g)\rightarrow {\text {Tor}}^R_1(U, N)=0. \end{aligned}$$

We conclude that ${\text {Ker}}g$ is a left U-comodule.    $\square$

The dual situation is expressed by the following.

Proposition 4.3

[5, Proposition 1.1] Let $\mathscr {C}\subset R\text {-}\mathrm {Mod}$ be the class of all left U-contramodules. Then:

• 1. $\mathscr {C}$ is closed under products, kernels of morphisms, and extensions in $R\text {-}\mathrm {Mod}$.

• 2. If ${\text {p.dim}}_RU\le 1$ as a left R-module, then $\mathscr {C}$ is closed also under cokernels of morphisms.

Proof

(1) The closure under direct products and extensions follows by the closure properties of the functors $\mathrm {Hom}_R$ and ${\text {Ext}}_R^1$.

Let $g:C\rightarrow D$ be a morphism between left U-contramodules. The proof that ${\text {Ker}}g\in \mathscr {C}$ is analogous to the proof of Proposition 4.2 (1) applying the functors $\mathrm {Hom}_R$ and ${\text {Ext}}^1_R$ to the short exact sequences

$$\begin{aligned} 0\rightarrow {\text {Ker}}g\rightarrow C\rightarrow {\text {Im}}g\rightarrow 0;\quad \quad 0\rightarrow {\text {Im}}g\rightarrow D\rightarrow {\text {Coker}}g\rightarrow 0 \end{aligned}$$

(2) ${\text {p.dim}}_RU\le 1$ is equivalent to ${\text {Ext}}^2_R(U, -)=0$. Thus the proof follows similarly to the proof of Proposition 4.2 (2).    $\square$

4.1 Coalgebras, Comodules, Contramodules

We follow the presentation developed in [13, Section 1.1].

Let k be a field. Recall that a k-algebra A is a k-vector space with k-linear maps

$$\begin{aligned} A\otimes _kA\overset{m}{\longrightarrow }A, \qquad k\overset{e}{\longrightarrow }A, \end{aligned}$$

m is the multiplication map and e the unit satisfying associativity, i.e.:

and unitality, i.e.::

A left A-module is a k-vector space with a k-linear map (scalar multiplication)

$$\begin{aligned} A\otimes _kM\overset{\lambda }{\longrightarrow }M \end{aligned}$$

satisfying associativity, i.e.:

and unitality, i.e.:

$$\begin{aligned} \lambda \circ (e\otimes 1_M)=1_M, \quad k\otimes _kM\cong M\overset{e\otimes 1_M}{\longrightarrow }A\otimes _kM\overset{\lambda }{\rightarrow }M \end{aligned}$$

Dualising the above diagrams we get the notions of coalgebras and comodules.

Definition 4.4

A coalgebra $\mathscr {C}$ is a k-vector space with k linear maps

$$\begin{aligned} \mathscr {C}\overset{\mu }{\longrightarrow }\mathscr {C}\otimes _k\mathscr {C}, \qquad \mathscr {C}\overset{\varepsilon }{\longrightarrow }k, \end{aligned}$$

$\mu$ the comultiplication and $\varepsilon$ the counit satisfying coassociativity, i.e.:

and counitality, i.e.:

Definition 4.5

A left $\mathscr {C}$-comodule over a coalgebra $\mathscr {C}$ is a k-vector space N with a k-linear map (coaction map)

$$\begin{aligned} N\overset{\nu }{\longrightarrow }\mathscr {C}\otimes _kN \end{aligned}$$

satisfying coassociativity:

and counitality:

$$\begin{aligned} (\varepsilon \otimes 1_N) \circ \nu =1_N:\quad N\overset{\nu }{\longrightarrow }\mathscr {C}\otimes _kN\overset{\varepsilon \otimes 1_N}{\longrightarrow }N\cong k\otimes _kN. \end{aligned}$$

A right $\mathscr {C}$-comodule is defined as a k-vector space with a k-linear map

$$\begin{aligned} N\overset{\nu }{\longrightarrow }N\otimes _k\mathscr {C}\end{aligned}$$

satisfying the corresponding coassociativity and counitality conditions.

Note that having a left A-module M with a scalar multiplication $\lambda$ is the same as having a k-linear map

$$\begin{aligned} M\overset{p}{\longrightarrow }\mathrm {Hom}_k(A, M)\qquad x\mapsto \dot{x}:a\longrightarrow ax=\lambda (a\otimes _Rx) \end{aligned}$$

which satisfies the associativity:

$\mathrm {Hom}_k(m, M )\circ p= \mathrm {Hom}(A, p)\circ p$ (via the adjunction isomorphism):

and unitality:

$\mathrm {Hom}(e, M)\circ p=1_M$:

$$\begin{aligned} M\overset{p}{\longrightarrow }\mathrm {Hom}_k(A, M)\overset{\mathrm {Hom}(e, M)}{\longrightarrow }M=\mathrm {Hom}_k(k, M). \end{aligned}$$

The notion of a left $\mathscr {C}$-contramodule over a coalgebra $\mathscr {C}$ is obtained by dualizing the above description of a left A-module over a k-algebra A.

Definition 4.6

A left $\mathscr {C}$-contramodule over a coalgebra $\mathscr {C}$ is a k-vector space B with a k-linear map (contraaction map)

$$\begin{aligned} \mathrm {Hom}_k(\mathscr {C}, B)\overset{\pi _B}{\longrightarrow }B \end{aligned}$$

satisfying the contraassociativity which means:

$\pi _B\circ \mathrm {Hom}_k(\mu , B)=\pi _B\circ \mathrm {Hom}_k(\mathscr {C}, \pi _B)$ (via the adjunction isomorphism):

and contraunitality meaning:

$\pi _B\circ \mathrm {Hom}_k(\varepsilon , B)=1_B$:

$$\begin{aligned} \mathrm {Hom}_k(k, B)\cong B\overset{\mathrm {Hom}_k(\varepsilon , B)}{\longrightarrow }\mathrm {Hom}_k(\mathscr {C}, B)\overset{\pi _B}{\longrightarrow }B. \end{aligned}$$

An easy way to construct a left $\mathscr {C}$-contramodule is via a right $\mathscr {C}$-comodule.

Let M be a right $\mathscr {C}$-comodule with $M\overset{\nu _M}{\longrightarrow }M\otimes _k\mathscr {C}$ the right coaction map.

Let V be a k-vector space and let $B=\mathrm {Hom}_k(M, V)$. Then B is a left $\mathscr {C}$-contramodule with left contraaction map $\pi _B$ defined by the diagram:

Remark 4.7

([13, Sections 1.3–1.4]) The k-duality functor identifies the opposite of the category of vector spaces with the category of linearly compact vector spaces. Thus, up to inverting the arrows, every coalgebra $\mathscr {C}$ can be thought as a linearly compact topological algebra $\mathscr {C}^*$, called the dual topological algebra. Then the category of left $\mathscr {C}$-comodules is the full subcategory of discrete left $\mathscr {C}^*$-modules.

We illustrate now a particular example of a coalgebra $\mathscr {C}$, its associated dual topological algebra and describe the categories of $\mathscr {C}$-comodules and $\mathscr {C}$-contramodules.

Example of a coalgebra 4.8

[13, Section 1.3] Let k be a field. Let $\mathscr {C}$ be a k-vector space with countable basis denoted by the symbols $1^{*}, x^{*}, (x^2)^*\dots (x^n)^*\dots$ with comultiplication and counit given by

$$\begin{aligned} \mathscr {C}\overset{\mu }{\longrightarrow }\mathscr {C}\otimes _k\mathscr {C}; \quad (x^n)^*\longmapsto \sum \limits _{i+j=n}(x^i)^*\otimes (x^j)^*\end{aligned}$$

$$\begin{aligned} \mathscr {C}\overset{\varepsilon }{\longrightarrow }k; \quad 1^*\longmapsto 1, \quad (x^n)^*\longmapsto 0,\, \forall n\ge 1. \end{aligned}$$

The dual topological algebra $\mathscr {C}^*$ is isomorphic to the ring of formal power series k[[x]].

By Remark 4.7 a $\mathscr {C}$-comodule is a torsion k[[x]]-module.

Indeed a $\mathscr {C}$-comodule M is a k-vector space with a locally nilpotent operator i.e. a k-linear map $x:M\rightarrow M$ such that for every $z\in M$ there exists $m\in \mathbb {N}$ satisfying $x^m(z)=0$ so that M becomes a $\mathscr {C}$-comodule via

$$\begin{aligned} \nu _M:M\longrightarrow \mathscr {C}\otimes M; \qquad z\longmapsto \sum \limits _{n\ge 0}(x^n)^*\otimes x^n(z) \end{aligned}$$

A $\mathscr {C}$-contramodule B is the datum of a k-vector space with a k-linear map $\mathrm {Hom}_k(\mathscr {C}, B)\overset{\pi _B}{\longrightarrow }B$ satisfying the contraassociativity and the contraunitality which in our case means that for every sequence $b_0, b_1, \dots , b_n\dots$ of elements of B, there is an element $b\in B$ written formally as $\sum \limits _{n\ge 0}x^nb_n$ satisfying the axiom of linearity:

$$\begin{aligned} \sum _{n\ge 0} x^n(\alpha b_n+\beta c_n)=\alpha \sum _{n\ge 0} x^nb_n+\beta \sum _{n\ge 0}x^nc_n; \quad \forall \alpha , \beta \in k,\quad b_n, c_n\in B, \end{aligned}$$

the axiom of unitality:

$$\begin{aligned} \sum _{n\ge 0}x^nb_n=b_0,\quad \text {if }\,\,b_1=b_2=\dots =0 \end{aligned}$$

and the axiom of contraassociativity:

$$\sum \limits _{i\ge 0}x^i\sum \limits _{j\ge 0}x^jb_{ij}= \sum \limits _{n\ge 0}x^n\sum \limits _{i+j=n}b_{ij}, \quad \forall b_{ij}\in B, i, j\in \mathbb {N}.$$

Thus, a $\mathscr {C}$-contramodule B is determined by a single linear operator $x:B\rightarrow B$ such that $x(b)= 1\cdot 0+x\cdot b+x^2\cdot 0+x^3\cdot 0\dots$ (see [13, Section 1.6] or [11, Section 3]).

Now we justify the definitions of U-comodules and U-contramodules given above by exhibiting an example of a ring epimorphism $f:R\rightarrow U$ such that the U-comodules and U-contramodules correspond exactly to the $\mathscr {C}$-comodules and $\mathscr {C}$-contramodules for the coalgebra described in Example 4.8.

Example 4.9

[13, Section 1.3] Let $R=k[x]$ be the ring of polynomials in one variable over a field k, let $U=k[x,x^{-1}]$ be the ring of Laurent polynomials, and let $f:R\longrightarrow U$ be the natural inclusion. So U is obtained from R by inverting the single element x.

Let $\mathscr {C}$ be the coalgebra constructed in Example 4.8.

Since U is a flat R-module, and the $\mathscr {C}$-comodules are the torsion k[[x]]-modules, one sees that the full subcategory of U-comodules in $R\text {-}\mathrm {Mod}$ is equivalent to the category of $\mathscr {C}$-comodules.

An application of [11, Theorem 3.3] and the description of $\mathscr {C}$-contramodules illustrated in Example 4.8 yields that the full subcategory of U-contramodules in $R\text {-}\mathrm {Mod}$ is equivalent to the category of $\mathscr {C}$-contramodules.

5 First Matlis Category Equivalence

In this section we present some results obtained by using the notion of ring epimorphism as well as the notions of comodules and contramodules.

We show that these notions are useful tools allowing to achieve relevant results like for instance, a generalisation of classical equivalences between subcategories of the module category over commutative rings.

Indeed, by Theorem 5.6 we extend the first Matlis equivalence to a much more general setting and under much weaker assumptions ([3]).

We borrow the terminology going back to Harrison [6] and Matlis [10].

Definition 5.1

Let $f:R\longrightarrow U$ be a ring epimorphism.

• 1. A left R-module A is U-torsion-free if it is an R-submodule of a left U-module, or equivalently, if the morphism $A\overset{1_A\otimes f}{\longrightarrow }A\otimes _RU$ is injective.

• 2. A left R-module B is U-divisible if it is a quotient module of a left U-module, or equivalently, if the map $\mathrm {Hom}_R(U,B)\overset{\mathrm {Hom}(f, B)}{\longrightarrow }B$ is surjective.

Remark 5.2

It is easy to check that the class of all U-torsion-free left R-modules is closed under subobjects, direct sums, and products in $R\text {-}\mathrm {Mod}$. Any left R-module A has a unique maximal U-torsion-free quotient module, which is the image of the morphism $A\overset{1_A\otimes f}{\longrightarrow }A\otimes _RU$.

The class of all U-divisible left R-modules is closed under quotients, direct sums, and products. Any left R-module B has a unique maximal U-divisible submodule, which is the image of the morphism $\mathrm {Hom}_R(U,B)\overset{\mathrm {Hom}(f, B)}{\longrightarrow }B$.

Definition 5.3

• 1. A left R-module A is said to be U-torsion if its maximal U-torsion-free quotient is zero, or equivalently, if $A\otimes _RU=0$.

• 2. A left R-module B is said to be U-reduced if its maximal U-divisible submodule is zero, or equivalently, if $\mathrm {Hom}_R(U,B)=0$.

We first state a useful homological result which has interest in its own and which will be used later on.

Lemma 5.4

• 1. For any associative rings R and S, left R-module L, S-R-bimodule E, and left S-module M such that ${\text {Tor}}^R_1(E,L)=0$, there is a natural injective map of abelian groups

  

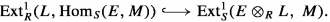
• 2. Dually, for any associative rings R and S, right R-module B, R-S-bimodule E, and left S-module C such that ${\text {Tor}}^R_1(B,E)=0$, there is a natural surjective map of abelian groups

  $$ {\text {Tor}}^S_1(B\otimes _RE,\>C)\twoheadrightarrow {\text {Tor}}^R_1(B,\>E\otimes _SC). $$

Proof

(1) Let $(a)\quad 0\longrightarrow H\longrightarrow P\longrightarrow L\longrightarrow 0$ be a short exact sequence in $R\text {-}\mathrm {Mod}$ with P a projective left R-module. Apply the functor $E\otimes _R-$ to sequence (a) obtaining

$$\begin{aligned} (b)\quad 0={\text {Tor}}^R_1(E, L)\longrightarrow E\otimes _RH\longrightarrow E\otimes _RP\longrightarrow E\otimes _RL\longrightarrow 0. \end{aligned}$$

Apply the functor $\mathrm {Hom}_R(-, \mathrm {Hom}_S(E, M))$ to sequence (a) and the functor $\mathrm {Hom}_S(-, M)$ to sequence (b) obtaining a diagram

where the left and central vertical arrows are the natural isomorphisms for the adjoint pair $(E\otimes _R-, \mathrm {Hom}_E(E, -))$ and the morphism $\alpha$ exists since ${\text {Ext}}^1_R(L, \mathrm {Hom}_S(E, M))$ is a cokernel.

By diagram chasing the commutativity of the diagram yields that $\alpha$ is injective. The details are left to the reader.

For the dual statement (2) start with a projective presentation

$$\begin{aligned} (c)\quad 0\longrightarrow H\longrightarrow P\longrightarrow B\longrightarrow 0 \end{aligned}$$

of B in $\mathrm {Mod}\text {-}R$ with P a projective right R-module. Apply the functor $-\otimes _RE$ to sequence (c) obtaining

$$\begin{aligned} (d)\quad {\text {Tor}}^R_1(B, E)=0\longrightarrow H\otimes _RE\longrightarrow P\otimes _RE\longrightarrow B\otimes _RE\longrightarrow 0. \end{aligned}$$

Apply the functor $-\otimes _SC$ to sequence (d) and the functor $-\otimes _R(E\otimes _SC)$ to sequence (c) obtaining a diagram

where the morphism $\beta$ exists since ${\text {Tor}}^R_1(B, E\otimes _SC)$ is a kernel.

By diagram chasing the commutativity of the diagram yields that $\beta$ is surjective.    $\square$

Remark 5.5

In [9] Matlis considers the flat injective ring epimorphism $R\rightarrow Q$ where Q is the total quotient ring of a commutative ring R, that is the localisation of R at the multiplicative set of all the regular elements of R (see Examples 3.9). In [9] a module C satisfying $\mathrm {Hom}_R(Q, C)=0={\text {Ext}}^1_R(Q, C)$ is called cotorsion and a module D such that $\mathrm {Hom}_R(Q, D)\rightarrow D$ is surjective is called h-divisible.

Then in [9, Corollary 2.4] the first Matlis equivalence states that the functors $Q/R\otimes _R-$ and $\mathrm {Hom}_E(Q/R, -)$ induce the equivalence:

where the notion of torsion is the classical one. That is an R-module M is torsion if for every element $x\in M$ there is a regular element $r\in R$ such that $rx=0$.

The following theorem relaxes as much as possible the assumptions in [9, Corollary 2.4] to provide what appears to be the best possible generalisation for the first of the two classical Matlis category equivalences (going back to Harrison’s [6, Proposition 2.1]).

Theorem 5.6

Let $f:R\longrightarrow U$ be a ring epimorphism, $U/R={\text {Coker}}f$. Assume ${\text {Tor}}^R_1(U,U)=0$.

Then the functors $(U/R)\otimes _R-$ and $\mathrm {Hom}_R(U/R,-)$ induce mutually inverse equivalences

Before proving the theorem we state a lemma showing that the functors $(U/R)\otimes _R-$ and $\mathrm {Hom}_R(U/R,-)$ take values in the pertinent classes.

Lemma 5.7

If ${\text {Tor}}^R_1(U,U)=0$, then

• 1. For any left R-module M, the left R-module $\mathrm {Hom}_R(U/R,M)$ is a U-torsion-free U-contramodule;

• 2. For any left R-module C, the left R-module $(U/R)\otimes _RC$ is a U-divisible U-comodule.

Proof

(1) From the surjection $U\longrightarrow U/R\rightarrow 0$ one sees that the left R-module $\mathrm {Hom}_R(U/R,M)$ is U-torsion-free as an R-submodule of the left U-module $\mathrm {Hom}_R(U,M)$.

Furthermore, since $U\otimes _RU=U$, we have $(U/R)\otimes _RU=0$, and therefore $\mathrm {Hom}_R(U,\mathrm {Hom}_R(U/R,M))\cong \mathrm {Hom}_R((U/R)\otimes _R U, M)=0$.

To show that ${\text {Ext}}^1_R(U,\mathrm {Hom}_R(U/R,M))=0$, observe that our assumptions $U\otimes _RU=U$ and ${\text {Tor}}^R_1(U,U)=0$ imply ${\text {Tor}}^R_1(U/R,U)=0$, because the map $(R/{\text {Ker}}(f))\otimes _RU\longrightarrow U\otimes _RU$ is an isomorphism.

We apply Lemma 5.4 (1) letting $L=_RU$ and E the R-R-bimodule U/R to get that

hence $\mathrm {Hom}_R(U/R,M)$ is a left U-contramodule.

The proof of part (2) is dual-analogous. The left R-module $(U/R)\otimes _RC$ is U-divisible as a quotient R-module of the left U-module $U\otimes _RC$. Since $U\otimes _R(U/R)=0$, we have $U\otimes _R(U/R)\otimes _RC=0$.

Apply Lemma 5.4 (2) letting $B=U_R$ and E the R-R-bimodule U/R to get

$$0={\text {Tor}}_1^R(U\otimes _R(U/R),\>C)\longrightarrow {\text {Tor}}^R_1(U,\>(U/R)\otimes _RC)\rightarrow 0.$$

Hence $(U/R)\otimes _RC$ is a left U-comodule.    $\square$

Proof of Theorem 5.6 By Lemma 5.7, the functor $M\longmapsto \mathrm {Hom}_R(U/R,M)$ takes U-divisible left U-comodules to U-torsion-free left U-contramodules and the functor $(U/R)\otimes _R-$ takes U-torsion-free left U-contramodules to U-divisible left U-comodules (in fact, they take arbitrary left R-modules to left R-modules from these two classes). It remains to show that the restrictions of these functors to these two full subcategories in $R\text {-}\mathrm {Mod}$ are mutually inverse equivalences between them.

First we consider the case of a U-divisible left U-comodule M and show that the counit morphism

$$\xi _M:(U/R)\otimes _R\mathrm {Hom}_R(U/R,M) \longrightarrow M$$

is an isomorphism.

Since M is U-divisible, we have a natural short exact sequence of left R-modules

$$(1)\quad 0\longrightarrow \mathrm {Hom}_R(U/R,M)\longrightarrow \mathrm {Hom}_R(U,M)\longrightarrow M\longrightarrow 0.$$

Since the left R-module $\mathrm {Hom}_R(U/R,M)$ is U-torsion-free, applying the functor $-\otimes _R \mathrm {Hom}_R(U/R,M)$ to the sequence $R\rightarrow U\rightarrow U/R\rightarrow 0$ we also have a natural short exact sequence of left R-modules

$$(2)\quad 0\rightarrow \mathrm {Hom}_R(U/R,M)\rightarrow U\otimes _R\mathrm {Hom}_R(U/R,M)\rightarrow (U/R)\otimes _R\mathrm {Hom}_R(U/R,M)\rightarrow 0.$$

Since M is a U-comodule, applying the functor $U\otimes _R{-}$ to the short exact sequence (1) produces an isomorphism

$$\begin{aligned} U\otimes _R\mathrm {Hom}_R(U/R,M)\cong U\otimes _R\mathrm {Hom}_R(U,M)\cong \mathrm {Hom}_R(U,M). \end{aligned}$$

Now the commutative diagram

shows that we have a morphism from the short exact sequence (2) to the short exact sequence (1) that is the identity on the leftmost terms, an isomorphism on the middle terms, and the counit morphism $\xi _M$ on the rightmost terms. Therefore, the counit morphism $\xi _M$ is an isomorphism.

Next we consider a U-torsion-free left U-contramodule C and show that the unit morphism

$$\eta _C:C\longrightarrow \mathrm {Hom}_R(U/R,\> (U/R)\otimes _RC)$$

is an isomorphism.

Since C is U-torsion-free, we have a natural short exact sequence of left R-modules

$$(3)\quad 0\longrightarrow C\longrightarrow U\otimes _RC\longrightarrow (U/R)\otimes _RC\longrightarrow 0. $$

Since the left R-module $(U/R)\otimes _RC$ is U-divisible, applying the functor $\mathrm {Hom}_R(-, (U/R)\otimes _RC)$ to the sequence $R\rightarrow U\rightarrow U/R\rightarrow 0$ we also have a natural short exact sequence of left R-modules

$$(4)\quad 0\rightarrow \mathrm {Hom}_R(U/R,\>(U/R)\otimes _RC)\rightarrow \mathrm {Hom}_R(U,\>(U/R)\otimes _RC) \rightarrow (U/R)\otimes _RC\rightarrow 0. $$

Since C is a U-contramodule, applying the functor $\mathrm {Hom}_R(U,{-})$ to the short exact sequence (3) produces an isomorphism

$$U\otimes _RC=\mathrm {Hom}_R(U,\>U\otimes _RC)\cong \mathrm {Hom}_R(U,\>(U/R)\otimes _RC).$$

Now the commutative diagram

shows that we have a morphism from the short exact sequence (3) to the short exact sequence (4) that is the identity on the rightmost terms, an isomorphism on the middle terms, and the unit morphism $\eta _C$ on the leftmost terms. Therefore, the unit morphism $\eta _C$ is an isomorphism.    $\square$

Further developments As noticed in the Introduction, the second Matlis category equivalence can be constructed in case $f:R\rightarrow U$ is a ring epimorphism such that ${\text {Tor}}^R_1(U,U)=0={\text {Tor}}^R_2(U,U)$ (see [3, Theorem 2.3]).

Further results in the setting of derived categories are obtained in [3] in case f is a homological ring epimorphism. Indeed, assuming that U has projective dimension at most 1 as a left R-module and flat dimension at most one as a right R-module, it is shown that there is what may be called the triangulated Matlis equivalence in [12], that is an equivalence between the (bounded or unbounded) derived category of complexes of R-modules with U-comodule cohomology modules and the similar derived category of complexes of R-modules with U-contramodule cohomology modules.

Finally, under certain additional assumptions (which hold for instance when f is injective) the exact embedding functors of the full subcategories of U-comodules and U-contramodules into the category $R\text {-}\mathrm {Mod}$ induce fully faithful functors between the corresponding derived categories and also an equivalence between the derived categories of the categories of U-comodules and U-contramodules.