Abstract
We present a Hamilton cycle in the k-sided pancake network and four combinatorial algorithms to traverse the cycle. The network’s vertices are coloured permutations \(\pi = p_1p_2\cdots p_n\), where each \(p_i\) has an associated colour in \(\{0,1,\ldots , k\,-\,1\}\). There is a directed edge \((\pi _1,\pi _2)\) if \(\pi _2\) can be obtained from \(\pi _1\) by a “flip” of length j, which reverses the first j elements and increments their colour modulo k. Our particular cycle is created using a greedy min-flip strategy, and the average flip length of the edges we use is bounded by a constant. By reinterpreting the order recursively, we can generate successive coloured permutations in O(1)-amortized time, or each successive flip by a loop-free algorithm. We also show how to compute the successor of any coloured permutation in O(n)-time. Our greedy min-flip construction generalizes known Hamilton cycles for the pancake network (where \(k=1\)) and the burnt pancake network (where \(k=2\)). Interestingly, a greedy max-flip strategy works on the pancake and burnt pancake networks, but it does not work on the k-sided network when \(k>2\).
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Many readers will be familiar with the story of Harry Dweighter, the harried waiter who sorts stacks of pancakes for his customers. He does this by repeatedly grabbing some number of pancakes from the top of the stack, and flipping them over. For example, if the chef in the kitchen creates the stack
 , then Harry can sort it by flipping over all four pancakes
, then Harry can sort it by flipping over all four pancakes
 , and then the top two
, and then the top two
 .
.
This story came from the imagination of Jacob E. Goodman [9], who was inspired by sorting folded towels [24]. His original interest was an upper bound on the number of flips required to sort a stack of n pancakes. Despite its whimsical origins, the problem attached interest from many mathematicians and computer scientists, including a young Bill Gates [12]. Eventually, it also found serious applications, including genomics [11].
A variation of the original story involves burnt pancakes. In this case, each pancake has two distinct sides: burnt and unburnt. When Harry flips the pancakes, the pancakes involved in the flip also turn over, and Harry wants to sort the pancakes so that the unburnt sides are facing up. For example, Harry could sort the stack
 by flipping all four
by flipping all four
 , then the top two
, then the top two
 , and the top one
, and the top one
 . Similar lines of research developed around this problem (e.g. [6, 11]). The physical model breaks down beyond two sides, however, many of the same applications do generalize to “k-sided pancakes”.
. Similar lines of research developed around this problem (e.g. [6, 11]). The physical model breaks down beyond two sides, however, many of the same applications do generalize to “k-sided pancakes”.
1.1 Pancake Networks
Interconnection networks connect single processors, or groups of processors, together. In this context, the underlying graph is known as the network, and classic graph measurements (e.g. diameter, girth, connectivity) translate to different performance metrics. Two networks related to pancake flipping are in Fig. 1.
The pancake network \(\mathbb {G}(n)\) was introduced in the 1980s [1] and various measurements were established (e.g. [14]). Its vertex set is the set of permutations of \(\{1,2,\ldots ,n\}\) in one-line notation, which is denoted \(\mathbb {P}(n)\). For example, \(\mathbb {P}(2) = \{12,21\}\). There is an edge between permutations that differ by a prefix-reversal of length \(\ell \), which reverses the first \(\ell \) symbols. For example, (3421, 4321) is the \(\ell =2\) edge between
 and
and
 . Goodman’s original problem is finding the maximum shortest path length to the identity permutation. Since \(\mathbb {G}(n)\) is vertex-transitive, this value is simply its diameter.
. Goodman’s original problem is finding the maximum shortest path length to the identity permutation. Since \(\mathbb {G}(n)\) is vertex-transitive, this value is simply its diameter.
The burnt pancake network \(\mathbb {\overline{G}}(n)\) was introduced in the 1990s [6]. Its vertex set is the set of signed permutations of \(\{1,2,\ldots ,n\}\), which is denoted \(\mathbb {\overline{P}}(n)\). For example, \(\mathbb {\overline{P}}(2) = \{12,1\bar{2},\bar{1}2,\bar{1}\bar{2},21,2\bar{1},\bar{2}1,\bar{2}\bar{1}\}\) where overlines denote negative symbols. There is an edge between signed permutations that differ by a sign-complementing prefix-reversal of length \(\ell \), which reverses the order and sign of the first \(\ell \) symbols. For example, \((\bar{2}\bar{1}34,1234)\) is the \(\ell =2\) edge between
 and
and
 .
.
The k-sided pancake network \(\mathbb {G}_{k}(n)\) is a directed graph that was first studied in the 2000s [15]. Its vertex set is the set of k-coloured permutations of \(\{1,2,\ldots ,n\}\) in one-line notation, which is denoted \(\mathbb {P}_{k}(n)\). For example, \(\mathbb {P}_{3}(2)\) is illustrated below, where colours the 0, 1, 2 are denoted using superscripts, or in
 .
.

There is a directed edge from \(\pi _1 \in \mathbb {P}_{k}(n)\) to \(\pi _2 \in \mathbb {P}_{k}(n)\) if \(\pi _1\) can be transformed into \(\pi _2\) by a colour-incrementing prefix-reversal of length \(\ell \), which reverses the order and increments the colour modulo k of the first \(\ell \) symbols. For example,  is a directed \(\ell =2\) edge.
is a directed \(\ell =2\) edge.
Notice that \(\mathbb {G}(n)\) and \(\mathbb {G}_{1}(n)\) are isomorphic, while \(\mathbb {\overline{G}}(n)\) and \(\mathbb {G}_{2}(n)\) are isomorphic, so long as we view each undirected edge as two opposing directed edges. It also bears mentioning that \(\mathbb {G}_{k}(n)\) is a (connected) directed Cayley graph, and its underlying group is the wreath product of the cyclic group of order k and the symmetric group of order n.
When the context is clear, or the distinction is not necessary, we use the term flip for prefix-reversal (when \(k=1\)), sign-complementing prefix-reversal (when \(k=2\)), and colour-incrementing prefix-reversal (when \(k>2\)).
1.2 (Greedy) Hamilton Cycles
In this paper, we are not interested in shortest paths in pancake networks, but rather Hamilton cycles. There are myriad ways that researchers attempt to build Hamilton cycles in highly-symmetric graphs, and the greedy approach is perhaps the simplest (see Williams [26]). This approach initializes a path at a specific vertex, then repeatedly extends the path by a single edge. More specifically, it uses the highest priority edge (according to some criteria) that leads to a vertex that is not on the path. The path stops growing when the current vertex is only adjacent to vertices on the path. A Hamilton cycle has been found if every vertex is on the path, and there is an edge from the final vertex to the first vertex. Despite its simplicity, the approach is known to work on many well-known graphs [26].
We show that the greedy approach works for the coloured pancake network \(\mathbb {G}_{k}(n)\) when we prioritize the edges by shortest flip length. More specifically, we start a path at \(1^0 2^0 \cdots n^0 \in \mathbb {P}_{k}(n)\), then repeatedly extend it to a new vertex along the edge that corresponds to the shortest colour-incrementing prefix-reversal. We refer to this as the greedy min-flip construction, denoted \(\mathsf {GreedyMin}_{k}(n)\), and it is illustrated in Fig. 1. When \(k=1\), the cycle that we create is identical to the one given by Zaks [27], and when \(k=2\), our cycle in the burnt pancake network was previously produced by Suzuki, N. Sawada, and Kaneko [16]; however, both of these papers describe their cycles recursively. The greedy construction of the cycles in the pancake and burnt pancake networks was previously given by J. Sawada and Williams [10, 20].
1.3 Combinatorial Generation
Ostensibly, the primary contribution of this paper is the Hamiltonicity of k-sided pancake networks. However, the authors’ primary motivation was not in finding a Hamilton cycle, but rather in investigating its contributions to combinatorial generation. Combinatorial generation is the research area devoted to the efficient and clever generation of combinatorial objects. By efficient we mean that successive objects can be generated in amortized O(1)-time or worst-case O(1)-time, regardless of their size. The former is known as constant amortized time (CAT), while the latter is known as loop-free. By clever we mean that non-lexicographic orders are often desirable. When describing these alternate orders, the authors make liberal use of the term Gray code—in reference to the eponymous binary reflected Gray code patented by Frank Gray [13])—and we refer to our Hamilton cycle as a colour-incrementing prefix-reversal Gray code for coloured permutations. Informally, it is a flip Gray code.
There are dozens of publications on the efficient generation of permutation Gray codes. In fact, comprehensive discussions on this topic date back to Sedgewick’s survey in 1977 [22], with more modern coverage in Volume 4 of Knuth’s The Art of Computer Programming [17]. However, to our knowledge, there are no published Gray codes for coloured permutations. This is surprising as the combinatorial [4, 5, 8, 18, 19] and algebraic [2, 3, 23] properties of coloured permutations have been of considerable interest. Work on the latter is due to the group theoretic interpretation of \(\mathbb {P}_{k}(n)\) as the wreath product of the cyclic and symmetric group, \(\mathbb {Z}_k\wr S_n\). We find our new Gray code of interest for two additional reasons.
-
1.
Other greedy approaches for generating \(\mathbb {P}(n)\) do not seem to generalize to \(\mathbb {P}_{k}(n)\).
-
2.
Flips are natural and efficient operations in certain contexts.
To expand on the first point, consider the Steinhaus-Johnson-Trotter (SJT) order of permutations, which dates back to the1600s [17]. In this order, successive permutations differ by an adjacent-transition (or swap) meaning that adjacent values in the permutations change place. In other words, the order for \(\mathbb {P}(n)\) traces a Hamilton path in the permutohedron of order n. For example, SJT order for \(n=4\) appears below

The symbols that are swapped to create the next permutation are underlined, and the larger value is in bold. The latter demarcation shows the order’s underlying greedy priorities: Swap the largest value. For example, consider the fourth permutation in the list, 4123. The largest value 4 cannot be swapped to the left (since it is in the leftmost position) or the right (since 1423 is already in the order), so the next option is to consider 3, and it can only be swapped to the left, which gives the fifth permutation 4132. If this description is perhaps too brief, then we refer the reader to [26].
Now consider greedy generalizations of SJT to signed permutations. The most natural generalization would involve the use of sign-complementing adjacent-transpositions which swap and complement the sign of two adjacent values. Unfortunately, any approach using these operations is doomed to fail. This is because the operation does not change the parity of positive and negative values. The authors experimented with other types of signed swaps—complementing the leftmost or rightmost value in the swap, or the larger or small value in the swap—without success.
More surprising is the fact that our greedy min-flip strategy works for coloured permutations, but the analogous max-flip strategy does not. For example, the max-flip strategy creates the following path in \(\mathbb {G}_{3}(2)\) before getting stuck.

The issue is that the neighbors of last coloured permutation in the path are already on the path. More specifically, a flip of length one transforms \(1^1 2^2\) into \(1^2 2^2\), and a flip of length two transforms \(1^1 2^2\) into \(2^0 1^2\), both of which appear earlier. The failure of the max-flip strategy on coloured permutations is surprising due to the fact that it works for both permutations and signed-permutations [10, 20].
To expand on the second point, note that the time required to flip a prefix is proportional to its length. In particular, if a permutation over \(\{1,2,\ldots ,n\}\) is stored in an array or linked list of length n, then it takes O(m)-time to flip a prefix of length mFootnote 1. Our min-flip strategy ensures that the shortest possible flips are used. In fact, the average flip length used in our Gray codes is bounded by \(e = 2.71828\cdots \) when \(k=1\), and the average is even smaller for \(k>1\).
We also note that flips can be the most efficient operation in certain situations. For example, consider a brute force approach to the undirected travelling salesman problem, wherein every Hamilton path of the n cities is represented by a permutation in \(\mathbb {P}(n)\). If we iterate over the permutations using a prefix-reversal Gray code, then successive Hamilton paths differ in a single edge. For example, the edges in 12345678 and 43215678 are identical, except that the former includes (4, 5) while the latter includes (1, 5). Thus, the cost of each Hamilton cycle can be updated from permutation to permutation using one addition and subtraction. More generally, flip Gray codes are the most efficient choice when the cost (or value) of each permutation depends on its unordered pairs of adjacent symbols. Similarly, our generalization will be the most efficient choice when the cost (or value) of each coloured permutation depends on its unordered pairs of adjacent symbols and the minimum distance between their colours.
1.4 New Results
We present a flip Gray code for \(\mathbb {P}_{k}(n)\) that corresponds to a Hamilton cycle in the k-sided pancake network. We present the following four different combinatorial algorithms for traversing the Hamilton cycle, each having unique and interesting properties:
-
1.
A greedy algorithm that is easy to describe, but requires an exponential amount of memory.
-
2.
A recursive algorithm, that reveals the structure of the listing and can be implemented in O(1)-amortized time.
-
3.
A simple successor rule approach that allows the cycle to start from any vertex (coloured permutation) and takes on average O(1)-time amortized over the entire listing.
-
4.
A loop-free algorithm to generate the flip-sequence iteratively.
Before we present these algorithms in Sect. 3, we first present some notation in Sect. 2. We conclude with a summary and related work in Sect. 4.
2 Notation
Let \(\pi = p_1p_2 \cdots p_n\) be a coloured permutation where each \(p_i = v_i^{c_i}\) has value \(v_i \in \{1,2,\ldots , n\}\) and colour \(c_i \in \{0,1,\ldots , k-1\}\). Recall that \(\mathbb {P}_{k}(n)\) denotes the set of k-coloured permutations of \(\{1,2,\ldots ,n\}\). Observe that \( \mathbb {P}_{1}(n)\) corresponds to regular permutations and \(\mathbb {P}_{2}(n)\) corresponds to signed permutations. For the remainder of this paper, it is assumed that all permutations are coloured.
As mentioned earlier, a flip of a permutation \(\pi \), denoted \(\mathsf {flip}_{i}(\pi )\), applies a prefix-reversal of length i on \(\pi \) that also increments the colour of the flipped elements by 1 (modulo k). As an example for \(k=3\):
A pre-perm is any prefix of a permutation in \(\mathbb {P}_{k}(n)\), i.e. \(\mathbf {p}=p_1p_2\cdots p_j\) is a pre-perm if there exist \(p_{j+1},\ldots p_{n}\) such that \(p_1p_2\cdots p_n\) is a permutation. Note that if \(j=n\), then the pre-perm is a permutation. Let \(\mathbf {p} = p_1p_2\cdots p_j\) be an arbitrary pre-perm for given a k. For a given element \(p_i=v_i^{c_i}\), let \(p_i^{+s}=v_i^{(c_{i}+s)\ ({\text {mod}}\ k)}\). For \(0 \le i < k\), let \(\mathbf {p^{+i}}\) denote \(p_1^{+i}p_2^{+i}\cdots p_j^{+i}\), i.e. \(\mathbf {p}\) with the colour of each element incremented by i modulo k. Note, \(\mathbf {p^{+0}} = \mathbf {p}\). Furthermore, let \(\rho (\mathbf {p}) = \mathbf {p^{+(k-1)}} \cdot \mathbf {p^{+(k-2)}} \cdots \mathbf {p^{+0}} = r_1r_2\cdots r_{m}\) be a circular string of length \(m=kj\) where \(\cdot \) denotes the concatenation of symbols. Let \(\mathbf {\rho (p)_{i}}\) denote the length \(j\,-\,1\) subword ending with \(r_{i-1}\).

For any pre-perm \(\mathbf {p}=p_1p_2\cdots p_j\), let \(\overleftarrow{\mathbf {p}}\) denote the reverse of \(\mathbf {p}\). i.e. \(\overleftarrow{\mathbf {p}}=p_jp_{j-1}\cdots p_2p_1\). Note that \(\overleftarrow{\mathbf {p}}\) is not equivalent to applying a flip of length j to \(\mathbf {p}\) when \(k>1\) as the colours of each symbol do not change in \(\overleftarrow{\mathbf {p}}\). For the remainder of this paper we will use \(\mathbf {p}\) to denote a pre-perm, and when it is clear we will use \(\pi \) to denote a permutation.
3 Constructions of a Cyclic Flip Gray Code for \(\mathbb {P}_{k}(n)\)
In this section we present four different combinatorial algorithms for generating the same cyclic flip Gray code for \(\mathbb {P}_{k}(n)\). We begin by studying the listing of permutations generated by a greedy min-flip algorithm. We define the flip-sequence of a listing of permutations as the sequence of the flip lengths used to generate the listing beginning with the first permutation. By studying the underlying recursive structure of the greedy listing, we provide a recursive description and its corresponding flip-sequence and prove it is equivalent to the flip-sequence generated by the greedy algorithm. This proves that the greedy algorithm generates all permutations in \(\mathbb {P}_{k}(n)\). We then present a successor-rule that determines the successor of a given permutation in the greedy min-flip listing in expected O(1)-time. We conclude by showing how the flip-sequence can be generated via a loop-free algorithm.
3.1 Greedy Algorithm
Recall that \(\mathsf {GreedyMin}_{k}(n)\) denotes the greedy algorithm on \(\mathbb {P}_{k}(n)\) that starts at permutation \(1^{0}2^{0}\cdots n^{0}\) and prioritizes the neighbors of each permutation in the k-sided pancake network by increasing flip length.

Unlike the max-flip approach, we will prove that \(\mathsf {GreedyMin}_{k}(n)\) exhaustively generates all permutations in \(\mathbb {P}_{k}(n)\) for all \(n,k \ge 1\). We also show that the last permutation in the listing differs by a flip of length n from the first permutation, so the listing is a cyclic flip Gray code. To prove this result, we study the underlying recursive structure of the resulting listings and examine the flip-sequences.
3.2 Recursive Construction
By applying the two observations made following the listing of \(\mathsf {GreedyMin}_{3}(3)\) in Example 2, we arrive at the following recursive definition for a listing of pre-perms, given a pre-perm \(\mathbf {p}\) of a permutation in \(\mathbb {P}_{k}(n)\):
where \(\mathbf {Rec}_{k}(p_x) = p_x^{+0}, p_x^{+1}, p_x^{+2},\ldots , p_x^{+(k-1)}\) and \(\rho (p) = r_1\cdots r_m\). Here, the operation \(\mathcal {L} \cdot r\) denotes the listing \(\mathcal {L}\) with r appended to every element in the listing. We prove that \(\mathbf {Rec}_{k}(1^02^0\cdots n^0)\) generates the same (exhaustive) listing of permutations as \(\mathsf {GreedyMin}_{k}(n)\).
Lemma 1
Let \(\mathbf {p}=p_1p_2p_3\cdots p_j\) be a pre-perm of a permutation in \(\mathbb {P}_{k}(n)\) for some \(n\ge j\). Then the first and last pre-perms in the listing \(\mathbf {Rec}_{k}(\mathbf {p})\) are \(\mathbf {p}\) and \(\overleftarrow{\mathbf {p^{+(k-1)}}}\), respectively.
Proof
The proof proceeds by induction on j. When \(j=1\), we have \(\mathbf {p}=\overleftarrow{\mathbf {p}}=p_1\), so \(\mathbf {Rec}_{k}(\mathbf {p}) = \mathbf {p}, \mathbf {p^{+1}}\), \(\mathbf {p^{+2}}, \ldots ,\) \(\mathbf {p^{+(k-1)}}\). Since \(\mathbf {p^{+(k-1)}}= \overleftarrow{\mathbf {p^{+(k-1)}}}\) the claim holds. Now for \(1 \le j < n\) and any pre-perm \(\mathbf {p}=p_1p_2\cdots p_j\) of a permutation in \(\mathbb {P}_{k}(n)\), suppose that the first and last pre-perms in \(\mathbf {Rec}_{k}(\mathbf {p})\) are \(\mathbf {p}\) and \(\overleftarrow{\mathbf {p^{+(k-1)}}}\) respectively. Let \(\mathbf {p}=p_1p_2\cdots p_j p_{j+1}\) be a pre-perm of a permutation in \(\mathbb {P}_{k}(n)\). By definition, the first pre-perm of \(\mathbf {Rec}_{k}(\mathbf {p})\) is the first pre-perm of \(\mathbf {Rec}_{k}(\mathbf {\rho (p)_{m}}) \cdot r_{m}\) where \(m=(j+1)k\). By definition of \(\mathbf {\rho (p)}\) and \(\mathbf {\rho (p)_{m}}\), it is clear that \(r_m=p_{j+1}\) and \(\mathbf {\rho (p)_{m}}=p_1p_2\cdots p_{j-1}p_j\). Applying the inductive hypothesis, the first pre-perm of \(\mathbf {Rec}_{k}(p_1p_2\cdots p_{j-1}p_j)\) is \(p_1p_2\cdots p_{j-1}p_j\). Therefore, the first pre-perm of \(\mathbf {Rec}_{k}(\mathbf {p})\) is \(p_1p_2\cdots p_{j-1}p_{j}\cdot p_{j+1}=\mathbf {p}\). Similarly, the last pre-perm of \(\mathbf {Rec}_{k}(\mathbf {p})\) is the last pre-perm of \(\mathbf {Rec}_{k}(\mathbf {\rho (p)_1}) \cdot r_1\). Now, \(r_1=p_1^{+(k-1)}\) and \(\mathbf {\rho (p)_1}= p_{2}p_3\cdots p_jp_{j+1}\) and, by the inductive hypothesis, the last pre-perm in \(\mathbf {Rec}_{k}(\mathbf {\rho (p)_1})\) is \(p_{j+1}^{+(k-1)}p_{j}^{+(k-1)}\cdots p_{2}^{+(k-1)}\). Therefore, the last pre-perm of \(\mathbf {Rec}_{k}(\mathbf {p})\) is \(\overleftarrow{\mathbf {p^{+(k-1)}}}\). \(\square \)
Define the sequence \(\sigma _{k,n}\) recursively as
where given a sequence \(\tau \), \(\tau ^j\) denotes j copies of \(\tau \) concatenated together. We will show that \(\sigma _{k,n}\) is the flip-sequence for both \(\mathbf {Rec}_{k}(\mathbf {p})\) and \(\mathsf {GreedyMin}_{k}(n)\). This flip-sequence is a straightforward generalization of the recurrences for non-coloured permutations [27] and signed permutations [20]. Note that \(\sigma _{3,3}\) is shown to the right of the vertical bar in Example 2.
Lemma 2
For \(n \ge 1\) , \(k\ge 1\), and \(\pi \in \mathbb {P}_{k}(n)\), the flip-sequence for \(\mathbf {Rec}_{k}(\pi )\) is \(\sigma _{k,n}\).
Proof
By induction on n. In the base case \(\mathbf {Rec}_{k}(p_1) = p_1, p_1^{+1},p_1^{+2},\ldots , p_1^{+(k-1)}\) and the flip-sequence is \(\sigma _{k,1} = 1^{k-1}\). For \(n \ge 1\) assume that the sequence of flips used to create \(\mathbf {Rec}_{k}(p_1p_2p_3\cdots p_n)\) is given by \(\sigma _{k,n}\). Consider \(\mathbf {Rec}_{k}(\pi )\) where \(\pi = p_1p_2p_3\cdots p_{n+1}\in \mathbb {P}_{k}(n+1)\). By the inductive hypothesis, it suffices to show that the last permutation of \(\mathbf {Rec}_{k}(\rho (\pi )_{i}) \cdot r_{i}\) and the first permutation of \(\mathbf {Rec}_{k}(\rho (\pi )_{i-1}) \cdot r_{i-1}\) differ by a flip of length \(n+1\) for \(i= 2,3,\ldots ,m\ (=k(n+1))\). By definition, \(\rho (\pi )_{i}=r_{i-n}r_{i-(n-1)}\cdots r_{i-2}r_{i-1}\) where the indices are taken modulo m. Therefore, by Lemma 1, the last permutation in \(\mathbf {Rec}_{k}(\rho (\pi )_{i})\) is \((r_{i-1}r_{i-2}\cdots r_{i-(n-1)}r_{i-n})^{+(k-1)}\). Applying a flip of length \(n\,+\,1\) to \(\mathbf {Rec}_{k}(\rho (\pi )_{i})\cdot r_i\) yields
By Lemma 1, the first permutation of \(\mathbf {Rec}_{k}(\rho (\pi )_{i-1})\) is \(r_{i-(n+1)}r_{i-n}\cdots r_{i-3}r_{i-2}\). By the definition of \(\rho (\pi )\), it follows that \(r_{i-(n+1)}=r_i^{+1}\). Thus, from (3), it follows that \(\mathbf {Rec}_{k}(\rho (\pi )_{i}) \cdot r_{i}\) and the first permutation of \(\mathbf {Rec}_{k}(\rho (\pi )_{i-1}) \cdot r_{i-1}\) differ by a flip of length \(n+1\). By applying the inductive hypothesis, the flip-sequence for \(\mathbf {Rec}_{k}(\pi )\) is \( (\sigma _{k,n}, n+1)^{k(n+1)-1}, \sigma _{k,n}\) which is exactly \(\sigma _{k,n+1}\). \(\Box \)
Theorem 1
For \(n \ge 1\), \(k\ge 1\), and \(\pi \in \mathbb {P}_{k}(n)\), \(\mathbf {Rec}_{k}(\pi )\) is a cyclic flip Gray code for \(\mathbb {P}_{k}(n)\), where the first and last permutations differ by a flip of length n.
Proof
From Lemma 2, the flip-sequence for \(\mathbf {Rec}_{k}(\pi )\) is given by \(\sigma _{k,n}\). Inductively, it is easy to see that the length of the flip-sequence \(\sigma _{k,n}\) is \(k^nn!-1\) and that each permutation of \(\mathbf {Rec}_{k}(\pi )\) is unique. Thus, each of the \(k^nn!\) permutations must be listed exactly once and, from Lemma 1, the first and last permutations of the listing differ by a flip of length n, making \(\mathbf {Rec}_{k}(\pi )\) a cyclic flip Gray code for permutations. \(\square \)
Lemma 3
For \(n \ge 1\) and \(k\ge 1\), the flip-sequence for \(\mathsf {GreedyMin}_{k}(n)\) is \(\sigma _{k,n}\).
Proof
By contradiction. Suppose the sequence of flips used by \(\mathsf {GreedyMin}_{k}(n)\) differs from \(\sigma _{k,n}\) and let j be the smallest value such that the j-th flip used to create \(\mathsf {GreedyMin}_{k}(n)\) differs from the j-th value of \(\sigma _{k,n}\). Let these flip lengths be s and t respectively. Since \(\mathsf {GreedyMin}_{k}(n)\) follows a greedy minimum-flip strategy and because \(\sigma _{k,n}\) produces a valid flip Gray code for permutations by Theorem 1 where no permutation is repeated, it must be that \(s < t\). Let \(\pi = p_1p_2p_3\cdots p_n\) denote the j-th permutation in the listing \(\mathsf {GreedyMin}_{k}(n)\), i.e. the permutation immediately prior to the j-th flip. Since \(\sigma _{k,n}\) is the flip-sequence for \(\mathbf {Rec}_{k}(1^02^0\cdots n^0)\) by Lemma 2, from the recursive definition it follows inductively that all other permutations with suffix \(p_tp_{t+1}\cdots p_n\) appear before \(\pi \) in \(\mathbf {Rec}_{k}(1^02^0\cdots n^0)\), since no permutations are repeated by Theorem 1. Since \(\sigma _{k,n}\) and the sequence of flips used by \(\mathsf {GreedyMin}_{k}(n)\) agree until the j-th value, all other permutations with suffix \(p_tp_{t+1}\cdots p_n\) appear before \(\pi \) in \(\mathsf {GreedyMin}_{k}(n)\). Therefore, flipping \(\pi \) by a flip of length \(s<t\) results in a permutation already visited in \(\mathsf {GreedyMin}_{k}(n)\) before index j contradicting the fact that \(\mathsf {GreedyMin}_{k}(n)\) produces a list of permutations without repetition. \(\square \)
By definition, \(\mathsf {GreedyMin}_{k}(n)\) starts with the permutation \(1^02^0\cdots n^0\) and by Lemma 1, \(\mathbf {Rec}_{k}(1^02^0\cdots n^0)\) also starts with \(1^02^0\cdots n^0\). Since they are each created by the same flip-sequence by Lemma 2 and Lemma 3, we get the following corollary.
Corollary 1
For \(n \ge 1\) and \(k\ge 1\), the listings \(\mathsf {GreedyMin}_{k}(n)\) and \(\mathbf {Rec}_{k}(1^02^0\cdots n^0)\) are equivalent.
3.3 Successor Rule
In this section, we will generalize the successor rules found for non-coloured permutations and signed permutations in [21] for \(\mathsf {GreedyMin}_{k}(n)\) for \(k> 2\). We say a permutation in \(\mathbb {P}_{k}(n)\) is increasing if it corresponds to a length n subword of the circular string \(\rho (1^02^0\cdots n^0)\). For example if \(n=6\) and \(k=4\), then the following permutations are all increasing:
A permutation is decreasing if it is a reversal of an increasing permutation. A pre-perm is increasing (decreasing) if it corresponds to a subsequence of an increasing (decreasing) permutation (when the permutation is thought of as a sequence). For example, \(5^16^12^04^0\) is an increasing pre-perm, but \(5^1 2^0 4^0 6^0\) and \(1^2 2^2 3^1 4^0\) are not. Given a permutation \(\pi _2\), let \(\mathsf {succ}(\pi _2)\) denote the successor of \(\pi _2\) in \(\mathbf {Rec}_{k}(\pi )\) when the listing is considered to be cyclic.
Lemma 4
Let \(\pi _2 = q_1q_2\cdots q_n\) be a permutation in the (cyclic) listing \(\mathbf {Rec}_{k}(\pi )\), where \(\pi =p_1p_2\cdots p_n\) is increasing. Let \(q_1 q_2 \cdots q_j\) be the longest prefix of \(\pi _2\) that is decreasing. Then \(\mathsf {succ}(\pi _2) = \mathsf {flip}_{j}(\pi _2).\)
Proof
By induction on n. When \(n=1\), the result follows trivially as only flips of length 1 can be applied. Now, for \(n>1\), we focus on the permutations whose successor is the result of a flip of length n and the result will follow inductively by the recursive definition of \(\mathbf {Rec}_{k}(\pi )\). By Lemma 2, the successor of \(\pi _2\) will be \(\mathsf {flip}_{n}(\pi _2)\) if and only if it is the last permutation in one of the recursive listings of the form \(\mathbf {Rec}_{k}(\rho (\pi )_{\mathbf {i}}) \cdot r_i\). Recall that \(r_i\) is the i-th element in \(\rho (\pi )\) when indexed from \(r_1=p_1^{+(k-1)}\) to \(r_m=p_n\). As it is clear that at most one permutation is decreasing in each recursive sublist, it suffices to show that the last permutation in each sublist is decreasing to prove the successor rule holds for flips of length n. By Lemma 1, the last permutation in \(\mathbf {Rec}_{k}(\rho (\pi )_{\mathbf {i}})\cdot r_i\) is \(\overleftarrow{\mathbf {s}}\cdot r_i\) where \(\mathbf {s}=\rho (\pi )_{\mathbf {i}}^{\mathbf {+(k-1)}}\). Since \(\pi \) is increasing, it is clear that \(\rho (\pi )_{\mathbf {i}}\) is increasing and therefore that \(\mathbf {s}\) is increasing. Hence, \(\overleftarrow{\mathbf {s}}\) is decreasing by definition. Furthermore, by the definition of the circular word \(\rho (\pi )\), the element immediately before \(r_{i-1-(n-1)}^{+(k-1)}\) in \(\rho (\pi )\) is \(r_i\) (note the subscript \(i-1-(n-1)\) is considered modulo nk here). Therefore, \(\overleftarrow{\mathbf {s}}\cdot r_i\) is decreasing. Therefore, the successor rule holds for flips of length n and thus for flips of all lengths by induction. \(\square \)

By applying the previous lemma, computing \(\mathsf {succ}(\pi _2)\) for a permutation in the listing \(\mathbf {Rec}_{k}(\pi )\) can easily be done in O(n)-time as described in the pseudocode given in Algorithm 1.

Theorem 2
Successor(\(\pi \)) returns the length of the flip required to obtain the successor of \(\pi \) in the listing \(\mathbf {Rec}_{k}(1^02^0\cdots n^0)\) in O(n)-time.
Though the worst case performance of Successor(\(\pi \)) is O(n)-time, on average it is much better. Let \(\overline{\sigma }_{k,n}\) denote \((\sigma _{k,n},n)\), i.e. the sequence of flips used to generate the listing \(\mathbf {Rec}_{k}(\pi )\) with an extra flip of length n at the end to return to the starting permutation. Our goal is to determine the average flip length of \(\overline{\sigma }_{k,n}\), denoted avg(k, n). Note that our analysis generalize the results for avg(1, n) [27] and avg(2, n) [20].
Lemma 5
For \(n\ge 1\) and \(k\ge 1\),
Moreover, \(\text{ avg }(k,n)<\root k \of {e}\).
Proof
By definition of \(\sigma _{k,n}\), it is not difficult to see that \(\overline{\sigma }_{k,n+1}\) is equivalent to the concatenation of \((n+1)k\) copies of \(\overline{\sigma }_{k,n}\) with the last element in every copy of \(\overline{\sigma }_{k,n}\) incremented by 1. Therefore, we have
Hence, with the trivial base case that \(\text{ avg }(k,1)=1\), we have
Therefore,
by applying the well-known Maclaurin series expansion for \(e^{x}\). \(\square \)
Observe that the Successor function runs in expected O(1)-time when the permutation is passed by reference because the average flip length is bounded above by the constant \(\root k \of {e}\) as proved in Lemma 5. Thus, by repeatedly applying the successor rule, we obtain a CAT algorithm for generating \(\mathbf {Rec}_{k}(1^02^0\cdots n^0)\).
3.4 Loop-Free Generation of the Flip-Sequence \(\sigma _{k,n}\)
Based on the recursive definition of the flip-sequence \(\sigma _{k,n}\) given in (2), Algorithm 2 will generate \(\sigma _{k,n}\) in a loop-free manner. The algorithm generalizes a similar algorithm presented by Zaks for non-coloured permutations [27]. The next flip length x is computed using an array of counters \(c_1,c_2,\ldots ,c_{n+1}\) initialized to 0, and an array of flip lengths \(f_1,f_2, \ldots , f_{n+1}\) with each \(f_i\) initialized to i. For a formal proof of correctness, we invite the readers to see the simple inductive proof for the non-coloured case in [27], and note the primary changes required to generalize to coloured permutations are in handling of the minimum allowable flip lengths (when \(k=1\), the smallest allowable flip length is 2) corresponding to lines 5–6 and adding a factor of k to line 8.

Theorem 3
The algorithm FlipSeq is a loop-free algorithm to generate the flip-sequence \(\sigma _{k,n}\) one element at a time.
Since the average flip length in \(\sigma _{k,n}\) is bounded by a constant, as determined in the previous subsection, Algorithm 2 can be modified to generate \(\mathbf {Rec}_{k}(\pi )\) by passing the initial permutation \(\pi \) as a parameter, outputting \(\pi \) at the start of the repeat loop, and updating \(\pi \leftarrow \mathsf {flip}_{x}(\pi )\) at the end of the loop instead of outputting the flip length.
Corollary 2
The algorithm FlipSeq can be modified to generate successive permutations in the listing \(\mathbf {Rec}_{k}(\pi )\) in O(1)-amortized time.
4 Summary and Related Work
We presented four different combinatorial algorithms for traversing a specific Hamilton cycle in the k-sided pancake network. The Hamilton cycle corresponds to a flip Gray code listing of coloured permutations. Given such combinatorial listings, it is desirable to have associated ranking and unranking algorithms. Based on the recursive description of the listing in (1), such algorithms are relatively straightforward to derive and implement in \(O(n^2)\)-time. A complete C implementation of our algorithms is available on The Combinatorial Object Server [7].
Notes
- 1.
Some unusual data structures can support flips of any lengths in constant-time [25].
References
Akers, S., Krishnamurthy, B.: A group-theoretic model for symmetric interconnection networks. IEEE Trans. Comput. 38(4), 555–566 (1989)
Athanasiadis, C.A.: Binomial Eulerian polynomials for colored permutations. J. Comb. Theory Ser. A 173, 105214 (2020)
Bagno, E., Garber, D., Mansour, T.: On the group of alternating colored permutations. Electron. J. Comb. 21(2), 2.29 (2014)
Borodin, A.: Longest increasing subsequences of random colored permutations. Electron. J. Comb. 6(13), 12 (1999)
Chen, W.Y.C., Gao, H.Y., He, J.: Labeled partitions with colored permutations. Discret. Math. 309(21), 6235–6244 (2009)
Cohen, D.S., Blum, M.: On the problem of sorting burnt pancakes. Discret. Appl. Math. 61(2), 105–120 (1995)
COS++: The Combinatorial Object Server. http://combos.org/cperm
Duane, A., Remmel, J.: Minimal overlapping patterns in colored permutations. Electron. J. Comb. 18(2), 38 (2011). Paper 25
Dweighter, H.: Problem E2569. Am. Math. Mon. 82, 1010 (1975)
Essed, H., Therese, W.: The harassed waitress problem. In: Ferro, A., Luccio, F., Widmayer, P. (eds.) Fun with Algorithms. FUN 2014. Lecture Notes in Computer Science, vol. 8496. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-07890-8_28
Fertin, G., Labarre, A., Rusu, I., Vialette, S., Tannier, E.: Combinatorics of Genome Rearrangements. MIT Press, Cambridge (2009)
Gates, W.H., Papadimitriou, C.H.: Bounds for sorting by prefix reversal. Discret. Math. 27(1), 47–57 (1979)
Gray, F.: Pulse code communication. U.S. Patent 2,632,058 (1947)
Heydari, M.H., Sudborough, I.H.: On the diameter of the pancake network. J. Algorithms 25(1), 67–94 (1997)
Justan, M.P., Muga, F.P., Sudborough, I.H.: On the generalization of the pancake network. In: Proceedings International Symposium on Parallel Architectures, Algorithms and Networks. I-SPAN 2002, pp. 173–178 (2002)
Kaneko, K.: Hamiltonian cycles and Hamiltonian paths in faulty burnt pancake graphs. IEICE - Trans. Inf. Syst. E90-D(4), 716–721 (2007)
Knuth, D.E.: The Art of Computer Programming, volume 4: Combinatorial Algorithms, Part 1. Addison-Wesley (2010)
Mansour, T.: Pattern avoidance in coloured permutations. Sém. Lothar. Combin. 46, B46g-12 (2001)
Mansour, T.: Coloured permutations containing and avoiding certain patterns. Ann. Comb. 7(3), 349–355 (2003)
Sawada, J., Williams, A.: Greedy flipping of pancakes and burnt pancakes. Discret. Appl. Math. 210, 61–74 (2016)
Sawada, J., Williams, A.: Successor rules for flipping pancakes and burnt pancakes. Theoret. Comput. Sci. 609(part 1), 60–75 (2016)
Sedgewick, R.: Permutations generation methods. ACM Comput. Surv. 9(2), 137–164 (1977)
Shin, H., Zeng, J.: Symmetric unimodal expansions of excedances in colored permutations. Eur. J. Comb. 52(part A), 174–196 (2016)
Singh, S.: Flipping pancakes with mathematics. The Guardian (2013)
Williams, A.: O(1)-time unsorting by prefix-reversals in a boustrophedon linked list. In: Boldi, P., Gargano, L. (eds.) FUN 2010. LNCS, vol. 6099, pp. 368–379. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13122-6_35
Williams, A.: The greedy gray code algorithm. In: Dehne, F., Solis-Oba, R., Sack, J.-R. (eds.) WADS 2013. LNCS, vol. 8037, pp. 525–536. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40104-6_46
Zaks, S.: A new algorithm for generation of permutations. BIT 24(2), 196–204 (1984)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Cameron, B., Sawada, J., Williams, A. (2021). A Hamilton Cycle in the k-Sided Pancake Network. In: Flocchini, P., Moura, L. (eds) Combinatorial Algorithms. IWOCA 2021. Lecture Notes in Computer Science(), vol 12757. Springer, Cham. https://doi.org/10.1007/978-3-030-79987-8_10
Download citation
DOI: https://doi.org/10.1007/978-3-030-79987-8_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-79986-1
Online ISBN: 978-3-030-79987-8
eBook Packages: Computer ScienceComputer Science (R0)


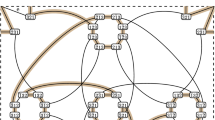



 . (Color figure online)
. (Color figure online)