Abstract
In this review chapter, we present the current state of the art of photovoltaic device technology. We begin with an overview of the fundamentals of solar cell device operation, and the nature of the solar energy spectrum and light absorption in devices. We then go into detail of the basics of solar cell operation, and the effects of various factors on the primary figures of merit, the open circuit voltage, short circuit current, and fill factor. In particular we focus on recombination, both in terms of the photocurrent and the dark current affecting the cell voltage. We then discuss heterojunction solar cells, and the general concept of carrier selective structures, which improve solar cell performance. We summarize the main single junction technologies and their efficiencies historically, starting with Si wafer-based technology and GaAs, then thin film technology, and organic solar cells, ending with recent developments of hybrid perovskite-based solar cells.
The limits of solar cell performance in terms of energy conversion efficiency are discussed, where we introduce the concept of detailed balance to derive the Shockley-Queisser limit for single junction cells. Methods of circumventing this single gap limit are discussed, which set the stage for discussing multijunction or tandem solar cells which currently hold the record for highest conversion efficiency in any solar technology. We then discuss nanotechnology in general, and how it is increasingly incorporated in modern solar cells. In this context, we discuss the use of nanostructures in improving light management in solar cells by enhancing light trapping beyond the classical limit. We discuss quantum dot/nanoparticle-based cells such as dye-sensitized solar cells and nanowire solar cells. Finally, we conclude by discussing advanced concept solar cell structures such as intermediate band, multiexciton generation, and hot carrier solar cells, and their theoretical capability of greatly exceeding the Shockley-Queisser limit.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
1 Background and Basic Operation of Solar Cells
Solar cells are semiconductor-based devices primarily, which convert sunlight directly to electrical energy through the photovoltaic effect, which is the appearance of a voltage and current when light is incident on a material. The photovoltaic effect was first reported by Edmond Becquerel in 1839, who observed a voltage and current resulting from light incident on electrochemical cells. Later in the 1800s, the first solid-state solar cells were developed based on platinum-selenium junctions. The first semiconductor-based pn junction cell was developed in the late 1930s and patented in 1946 by Russell Ohl at Bell Laboratories. The first practical solar cell devices utilizing the solar spectrum were demonstrated in 1954 at Bell Laboratories. While too expensive at the time for terrestrial applications, the burgeoning space industry found the first commercial applications of solar cells, as lightweight and long lifetime power sources replacing traditional battery technology for spacecraft in the late 1950s. Photovoltaics has since developed into the fastest growing source of terrestrial renewable energy, with an installed global capacity of over 600 GW peak energy by the end of 2019. This growth in capacity has been driven by the exponential decrease in the manufacturing cost for photovoltaic panels, which has dropped from $75/watt in the late 1970s to under $0.30/watt today, as a result of continuous improvements in materials, device efficiency, and manufacturing scale-up. Coupled with this dramatic cost reduction, the lifetime of solar panels is in excess of 25 years, which has dramatically reduced the levelized cost of electricity (LCOE) from photovoltaics, with some recent utility-scale installations priced below $0.02/kWhr, cheaper than any other current source of electricity.
Figure 19.1 illustrates the photovoltaic conversion process in a pn homojunction (same material on each side). It shows the energy band diagram (representative of the potential energy of electrons) as a function of position across the junction, where Ec is the minimum energy of the conduction band, which is primarily in unfilled state, and Ev is the maximum energy of the valence band which is almost completely filled. They are separated by an energy gap, Eg (1.12 eV in the case of Si at room temperature, the dominant semiconductor material), where no states exist in the ideal material. The junction occurs between an n-type semiconductor material (intentionally doped with donor atoms that contribute electrons to the conduction band) and a p-type material doped with acceptors, which remove an electron from the valence band, leaving behind a positively charged hole, which behaves as a positive charge carrier. The degree of filling of either the conduction band by electrons or the valence bands by holes is represented by the Fermi energies on the n- and p-sides, denoted Efn and Efp in the figure. At equilibrium, the Fermi energies are the same across the junction. At the junction, because of the huge gradient of positive charge on one side and negative on the other, a space charge region (SCR) is established at the junction, which is devoid of free carriers, and has a high electric field which opposes the flow of free charge from the n-region to the p-region and vice versa. As shown in Fig. 19.1, this results in a potential barrier for electrons on the n-side (right side) to cross the junction, while it is likewise a potential barrier for holes from the p-side (left side) to move across (since the diagram is of electron potential energy, increasing hole potential and kinetic energy is downward).
In the quantum mechanical description of photovoltaics, photons (quanta of electromagnetic radiation) are absorbed if their energy, hν (ν is the frequency of the incident light), exceeds the bandgap, and, in so doing, excite an electron from a filled state in the valence band to an empty state in the conduction band, creating electron-hole pairs (EHPs) as shown. Photons below the bandgap are not absorbed, which is the first major loss mechanism in terms of conversion of optical to electrical energy. The photoexcited electron and hole each have an excess kinetic energy above or below the conduction and valence band edges, respectively, and on a very short time scale (picoseconds), they relax to the their respective band edges through thermal losses to the underlying semiconductor material (through phonon emission, where quantum mechanically, phonons are quanta of the wave-like vibrational motion of the crystal). Hence, all the excess energy of the photon above the bandgap is lost, which is the second major loss mechanism, limiting the conversion efficiency of a solar cell as discussed in Sect. 19.5.
Once an EHP is created by absorption of a photon, what is required is charge separation of the electron and hole to opposite contacts to establish a photocurrent. This process requires some sort of symmetry breaking in the material, which is provided by the SCR shown in Fig. 19.1, where, as shown, the photoexcited electron on the p-side, if it reaches the edge of the SCR through diffusive motion, is swept across by the high electric field contributing to the photocurrent. The corresponding hole of the initial EHP sees a barrier at the junction on the other hand and so preferentially finds its way to the contact in the p-type material where it is extracted. The opposite process occurs for photons absorbed on the n-side but with the result of a photocurrent in the same direction. If the electron or hole created on a given side of the SCR recombines, i.e., the conduction band electron annihilates a hole in the valence band either through being trapped in a defect state (Shockley-Read-Hall recombination) or directly via band to band recombination and light emission (radiative recombination), then that EHP is lost to the photocurrent generation process. Therefore, another contribution to the overall conversion efficiency is the competition between extraction of the carriers and recombination before carriers are separated by the junction.
In terms of the solar cell delivering power to an external load, Fig. 19.2 illustrates the equivalent circuit model for a solar cell and its load. It consists of an ideal current source corresponding to the photocurrent, Iph, in parallel with a diode, representing the pn junction. For a pn junction in the dark, when it is forward biased with a positive voltage applied to the p-side with respect to the opposite side, a large current can flow, due to the lowering of the potential barrier in Fig. 19.1, whereas in reverse bias, this barrier is increased by the bias, creating a large barrier to charge flow and hence small current. The general form of the diode current for junction devices is exponential
where VD is the voltage across the diode (the same as V, the voltage across the load in Fig. 19.2), q is the charge of an electron, n is the ideality factor which varies between 1 and 2 usually, and I0 is the reverse saturation current, which physically is a result of recombination of electrons and holes in and near the junction. As discussed in Sect. 19.3.1, recombination can be radiative, where a photon is emitted when an electron decays into a hole state; it can occur through intermediate trap states in the bandgap, or through Auger processes, and typically has an exponential dependence on the bandgap over the thermal voltage, i.e., −Eg/kT. Eq. 19.1 shows that for positive VD the current increases exponentially whereas in reverse bias, for negative VD, the current goes to a small value, I0. In terms of the equivalent circuit in Fig. 19.2, under short circuit current conditions (RL = 0), the short circuit current equals the photocurrent, Isc = Iph. As the resistance of the load increases from zero, there is an increasing voltage across the diode, VD = V = IRL, due to the photocurrent which forward biases the diode, increasing ID, and hence decreasing the net current to the load. The load current decreases until it goes to zero, corresponding to open circuit conditions when RL = ∞. Under open circuit conditions, ID = Iph = Isc. Equating the diode current with the short circuit current in Eq. (19.1) at open circuit voltage conditions, VD=Voc, leads to
The open circuit voltage depends most importantly on the reverse saturation current, I0, characteristic of the pn junction, and, as mentioned above, decreases exponentially with bandgap. Hence the open circuit voltage scales linearly with bandgap, increasing for increasing bandgap materials, and empirically is found to be about 0.4 V less than the bandgap for a given material in well-developed technologies, i.e., Voc ≈ EG(in volts) − 0.4 V.
Figure 19.2 also illustrates the current-voltage characteristic of the solar cell in the dark, and under illumination, where the convention has been used of defining the net solar cell current, I, as flowing into the device, corresponding to negative power in terms of the product of IV, or power generation. As can be seen, the I-V characteristic under illumination is shifted rigidly downward, which illustrates the assumption of superposition, that the dark current and photocurrent can be treated independently, which is not generally the case. The points A, B, and C along the curve denote the short circuit current, the maximum power point, and open circuit. The maximum power at point B is Pm = ImVm, which is less than the product IscVoc, due to the “roundness” of the I-V curve as seen in Fig. 19.2, characterized by the fill factor (FF), i.e., Pm = FFIscVoc. In terms of the total optical energy incident on the device area, Pin, the optical to electrical conversion efficiency, η, is given by
The optical to electrical conversion efficiency,η, Isc, Voc, and the fill factor, FF, are all figures of merit related to the performance of different photovoltaic technologies, discussed in more depth throughout the rest of this chapter. In what follows, we go into more depth into the materials and physics of present-day photovoltaics technology, starting with the properties of the solar spectrum, and then beginning with Si-based solar cells that are currently the dominant technology worldwide, and continuing through thin film and organic technologies. Due to space limitations, we only provide the basics of solar cell device physics, which are covered in more detail in [1]. We then look at what limits the efficiency of conventional solar cells, and look at more advanced approaches to high efficiency performance in terms of multiple junction solar cells, as well as advanced concept approaches, and implementations thereof using nanotechnology, and some perspectives on future developments in the field.
2 Solar Spectrum and Optical Properties
In the present section, we first introduce the properties of the solar spectrum in terms of its blackbody characteristic from the sun incident on Earth, and atmospheric absorption and scattering effects on the corresponding terrestrial solar spectrum which are relevant for solar energy conversion at different locations on Earth. We then discuss the physics of optical absorption in semiconductors, and some basic design considerations for solar cells in terms of maximizing absorption and the corresponding photocurrent.
2.1 Solar Irradiance
The solar spectrum in space is modeled to a high level of accuracy by Planck’s blackbody radiation law, where the intensity as a function of wavelength is given by
where Rsun is the radius of the sun, D is the distance from the sun, T is the temperature of the sun, λ is the wavelength, c is the speed of light in vacuum, h is Plank’s constant, and k is Boltzmann’s constant. In terms of the photon flux associated with this intensity, the number of photons per unit time per unit area is simply found by dividing by the photon energy.
where N is the photon flux in terms of number per unit time per unit area per unit wavelength.
Figure 19.3 shows the ideal blackbody intensity assuming a temperature of 5250 C in Eq. (19.4) (the solid curve), compared with the solar spectrum at the top of the Earth’s atmosphere, where the difference is quite small. The red curve shows the actual spectrum somewhere on the Earth’s surface, where absorption and reflection losses from atmospheric constituents (water, CO2, etc.) as well as Raleigh scattering (at shorter wavelengths) reduce the intensity of light, particularly at certain preferential absorption wavelengths.
Integration of Eq. (19.4) over all wavelengths (assuming the temperature of the sun is 5762 K) gives a value of 1366 W/m2, referred to as the solar constant, representing the maximum available solar power reaching the Earth. The intensity on Earth is reduced due to atmospheric absorption as evidenced in Fig. 19.3. While local fluctuations in intensity occur due to various local atmospheric effects such as clouds and humidity, in general, the solar intensity at the surface is reduced due to the increasing path length through the atmosphere, and consequent absorption and scattering, which increases with increasing latitude. The increase in path length is characterized by the air mass, which is defined as the ratio of path length through the atmosphere normalized by the shortest path length at the equator. Geometrically, the air mass is approximately given by
where θ is the angle between the sun at a given latitude and the normal to the atmosphere at the equator. Equation (19.6) comes from just the geometrical increase in path length in a rectangular geometry. If the curvature of the atmosphere itself is included, and empirical correction to Eq. (19.6) is given as
AM0 is top of atmosphere, therefore AM = 0. For the sun directly overhead, AM = 1. Given the air mass, AM, the solar intensity at any point is given by the approximate formula [1]
A widely used air mass is AM1.5, corresponding to a latitude of 48.2°, representing an average latitude of temperate zones in either the northern and southern hemispheres. The AM1.5 intensity is approximately 930 W/m2, significantly reduced from the solar constant. Because of atmospheric scattering (Raleigh) as well as dust particles, water vapor, etc., a fraction of the radiation incident on the solar panel is indirect, in the form of diffuse radiation, which comes in from all angles rather than directly from the disk of the sun itself. Both components, diffuse and direct, should be considered in modeling of photovoltaic system performance.
2.2 Optical Properties of Photovoltaic Materials
In the previous section, we discussed the intensity and spectral content of solar radiation. For describing solar cell design and operation, what is critically important is the absorption of the incident photons as a function of wavelength, described by the absorption coefficient of the semiconductor described in more detail below.
Optical absorption in semiconductors depends on band to band transitions from the valence band to the conduction band. Due to the quantum nature of light, the absorption of photons can only occur when hυ > EG (although in fact sub-bandgap photons can be absorbed through impurities and other states in the gap). The nature of such transitions and the strength of absorption depends on whether the semiconductor is a direct or indirect gap material. In the former case, transitions occur directly from valence to conduction band leading to strong absorption when the photon energy exceeds the bandgap. For indirect materials, the conduction and valence band minimum and maximum, respectively, occur at different crystal momentum, and therefore at the bandgap, a second-order phonon-assisted process is required, and hence absorption is reduced until a direct conduction band minimum is bridged by the photon energy.
The quantity characterizing absorption is the absorption coefficient, α, which is basically the inverse of the average depth a photon penetrates a material before being absorbed. Mathematically, this may be written
where Nph(x) is the photon flux at distance x relative to the surface and Ns is the photon flux incident on the surface. The change in the number of photons gives the generation rate, such that
The above equation for the generation rate shows that G varies not only with the wavelength of light but also with distance into the material. Figure 19.4 plots the absorption coefficient as a function of wavelength for several materials. As can be seen, the absorption coefficient for Si is weaker compared to GaAs and InP due to its indirect bandgap for the same relative photon energy to the gap itself (similarly for thin film materials like CdTe), with the consequence that the thickness of Si required for high quantum efficiency (i.e., the number of electrons collected per incident photon) is much higher than for direct gap materials like GaAs.
Absorption coefficient versus wavelength for several direct gap materials (GaAs, InP, CdTe, CdS) and two indirect gap materials (Ge, Si) as well as amorphous Si. (With permission from PVEducation.org)
As illustrated in Fig. 19.4, the absorption coefficient is weakest for a given material for long wavelength photons just above the bandgap in energy, while shorter wavelength photons are absorbed within a short distance from the surface. Thus, the design of a Si solar cell reflects the spectral nature of the absorbed photons. This is illustrated in Fig. 19.5 for a basic Si cell design, where longer wavelength red light has a relatively long absorption depth, whereas short wavelength blue light is absorbed near the surface.
The structure of a commercial Si solar cell device (left panel of Fig. 19.5) typically has a thick base region (here p-type), a narrow emitter layer that is highly doped to minimize lateral resistance, heavy doping near the back contact to reduce recombination of photogenerated electrons there (back surface field), and a grid top contact to the emitter which has narrow fingers to minimize optical reflection (right panel is a top view of the grid structure). The design of the top grid involves a trade-off between the shading due to the area of the grid, which reduces the optical absorption through reflection, and the lateral spreading resistance due to current flow in the emitter (n+) region toward the fingers. Another optical consideration is the reflection of light from the semiconductor surface due to the refractive index difference between the cell and the air (or glass). As shown in Fig. 19.5, the design of the basic cell structure includes an antireflection (AR) coating of a material with refractive index between that of the semiconductor and air (here, e.g., silicon nitride), with the thickness optimized for minimum reflection across the solar spectrum (Fig. 19.3). A number of different wide bandgap insulating materials are used for AR coatings such as SiO2, MgF2, and others. Additionally, transparent conducting oxides (TCOs) are often employed, especially in more advanced solar cell architectures, which are wide bandgap materials (EG > 3 eV) and typically heavily n-type self-doped materials due to defects and other sources. In addition to providing a role as an AR material, they provide a conducting surface layer which mitigates spreading resistance effects. As discussed in more detail in Sects. 19.3.2 and 19.7.3, other schemes under the general category of light management are employed to increase the path length of light within the semiconductor and thus increase absorption, including a back optical reflector and texturing the front surface to deflect normal incident light into random angles inside the absorbing layer.
3 Theory of Operation of Conventional Solar Cells
Homojunction solar cells are basically pn junction solar cells from conventional single crystal or multi-crystalline semiconductor wafer-based materials such as Si and GaAs that some authors [2] have referred to as first generation due to their early appearance in the historical development of photovoltaics discussed earlier. Here we provide a brief introduction to the theory of homojunction solar cells but refer the reader to more in-depth treatments of the subject in a number of textbooks [1, 3,4,5,6].
As discussed in Sect. 19.1, the overall current-voltage (I-V) relationship for a solar cell under illumination is assumed to be a linear superposition of the dark I-V of the underlying pn junction and the light-induced photocurrent which flows in the opposite direction. The dark current is ultimately dependent on minority carrier (i.e., holes in n-type material) recombination (including the contacts themselves), and as such, an understanding and control of this phenomena are critical to high performance. The photocurrent depends on both the optical generation process discussed in the previous section and on collection of the photogenerated carriers at the junction (shown in Fig. 19.1), which converts minority carriers into majority carriers. The collection process itself depends on minimizing recombination before the carriers reach the junction. The superposition approximation turns out to be well obeyed in state-of-the-art Si and III–V technologies, although less so in thin film and organic-based technologies, where the nonlinear dependence of recombination on intensity and other factors leads to a breakdown of this approximation. Nevertheless, we begin by considering recombination and its effect on dark current, followed by the photocurrent and control of series resistance effects, and then look at advances in performance through heterojunctions and carrier selective contacts, ending with a discussion of current performance limits of single crystal and multi-crystalline Si and GaAs technology.
3.1 Dark Current and Recombination
In the following, we discuss the various recombination mechanisms in semiconductors, and the role of recombination in the dark current of conventional junction solar cells.
3.1.1 Recombination and Minority Carrier Lifetime
Solar cells are highly dependent on the effective minority carrier lifetime, such that the minority carrier lifetime is one of the most important parameters in a solar cell. Solar cell technology can be described as maximizing the effective minority carrier lifetime, given practical constraints such as cost or scalability. The minority carrier lifetime affects both the short circuit current and open circuit voltage as mentioned above. Note that the effective minority carrier lifetime includes the effect of surfaces.
The minority carrier lifetime is dependent on multiple parameters, including the processing history of the material, the type and number of defects in the material, the solar cell operating point, and other device parameters. Here we seek to develop equations and values for the minority carrier lifetimes in terms of relevant material parameters.
The term minority carrier lifetime can refer to different physical recombination mechanisms. We define the general term to refer to the effective minority carrier lifetime, which is a combination of both bulk and surface recombination mechanisms. The effective minority carrier lifetime is related to the minority carrier lifetime from individual physical processes by the equation below
where the four lifetimes correspond to Auger recombination, radiative (direct) recombination, trap-based recombination (Shockley-Read-Hall), and surface recombination. The effective minority carrier lifetime is the parameter, which is usually measured and then de-convolved into its individual components by either additional measurements or by fitting calculations.
Radiative recombination is proportional to the density of electrons in the conduction band, and the density of holes in the valence band, expressed as
where Rrad is the radiative recombination rate of electron-hole pairs (EHPs), the proportionality constant, B, is the recombination coefficient, while n and p are the electron and hole concentrations, respectively. The net radiative recombination of excess minority carriers is the total radiative recombination minus the radiative recombination at equilibrium (where np = ni2, with ni the intrinsic concentration of the material)
The minority carrier lifetime for radiative recombination can be found by
Letting n = Δn + n0 and p = Δn + p0, where n0 and p0 are the equilibrium carrier concentrations, and using Δn = Δp (due to charge neutrality) gives
For low-level injection in n-type material (n0 ≫ Δn and n0 ≫ p0), where n0 ≅ ND, the donor concentration, the minority carrier recombination due to radiative recombination becomes τRad = 1/BND, while for the same case in p-type material, τRad = 1/BNA. Thus under low injection conditions, the value of the lifetime depends on the doping, but it does not depend on the number of carriers, which is determined by the injection level (the voltage of the solar cell).
For high-level injection on the other hand, Δn ≫ (n0 + p0), and τRad = 1/BΔn, which means the radiative lifetime decreases with increasing injection level, which is one way to differentiate this type of recombination in experiments such as time-resolved cathodoluminescence in which the injection level is controlled with the pump beam intensity.
Auger recombination is a three-particle interaction which occurs via two similar processes: (i) the recombination of an electron in the conduction band with a hole in the valence band, where the excess energy is given to an electron in the conduction band, and (ii) the recombination of an electron in the conduction band with a hole in the valence band, where the excess energy is given to a hole in the valence band.
In the first case, the particles involved in the recombination process are two electrons and a hole, and in the second, it is two holes and an electron. In each case, we subtract the recombination at equilibrium. The overall Auger recombination rate for these two processes is then
where Cn and Cp are the Auger recombination coefficients. Since Auger is often calculated in highly doped or highly excited material, we can usually neglect the ni2 term to get
Using the simpler form above and substituting \( {U}_{\mathrm{Auger}}\equiv \frac{\Delta n}{\tau_{{{\fontsize{6}{9}\selectfont\mathrm{Auger}}}}} \), and also writing n = Δn + n0 and p = Δn + p0 and using Δn = Δp (due to charge neutrality), gives
We sometimes only need the sum of these terms and this is called the ambipolar Auger coefficient Ca.
Similar to the radiative case above, under low-level injection conditions, the minority carrier recombination due to Auger in low-level injection becomes
for holes in n-type material and electrons in p-type material, respectively. Here the Auger lifetime decreases as the square of the doping concentration, which imposes a limitation in terms of high doping. Under high-level injection conditions, the lifetime depends inversely on the square of the injected carrier concentration (i.e., Δn large)
Finally, Shockley-Read-Hall (SRH)recombination is recombination mediated by traps. It is derived by considering the downward and upward transitions for an electron (hole) in a single trap level located at energy ET with density Nt. Electrons in the conduction band are assumed to be captured with a rate proportional to the capture cross section, σn, traveling with a thermal velocity \( {v}_{\mathrm{th}}=\sqrt{3 kT/{m}^{\ast }} \)
with a similar expression for holes in the valence band. Exponential activation of electrons out of the trap to the conduction band (and electrons from the valence band to the trap level) is assumed as well, leading to the SRH recombination rate
where
where Ei is the intrinsic Fermi energy (approximately midgap). For low-level injection, and assuming the trap is located at the intrinsic level, i.e., midgap, the electron and hole minority carrier lifetimes reduce to τn0 and τp0, respectively.
Surface recombination occurs due to traps at an interface or surface, with a two-dimensional density of trap states. Such states occur intrinsically due to the breaking of the translational symmetry of the crystal, and from dangling or differently bonded states on the surface. Since surface recombination occurs at a plane at a definite location, rather than distributed through the bulk of the solar cell, its effect in terms of the net recombination rate due to surface recombination depends on the distance from the surface. For that reason, the effect of surface recombination is often treated as a boundary condition on the flux due to recombination
where for minority carrier electrons (np), Dn is the diffusion coefficient and Sn is a parameter called the surface recombination velocity, which is a proportionality constant between the excess carrier concentration at the surface, ∆np (the rhs), and the flux toward the surface (lhs). Sn itself is proportional to the density of traps at the surface. An ohmic contact, in which equilibrium is established in the contact, can be thought of as surface recombination with an infinite recombination velocity (i.e., np = np0).
3.1.2 Dark Current
A pn diode is characterized by the presence of a space charge region (SCR) at the junction between the n- and p-regions due to the balance between the forces of carrier drift (due to electric fields) and diffusion (due to concentration gradients) between the different regions. The SCR is ideally assumed to be devoid of free carriers across its width W, with a fixed charged density due to ionized acceptors and donors for the p- and n-regions, respectively. This charge density is responsible for an electric field across the junction, which opposes the diffusion of carriers into the SCR (within the drift diffusion model of carrier transport), which in turn leads to a built-in potential between the two sides
and a corresponding width of the depletion region assuming an abrupt doping profile
where εs is the permittivity of the semiconductor, and we have included for generality the forward voltage, VD, applied to the p-side with respect to the n-side.
Under forward bias conditions in the dark, the conventional description of behavior of a pn junction device is that the equilibrium state of the semiconductor is broken, leading to a quasi-equilibrium in which excess minority carriers are injected across the junction from their corresponding majority carrier n- and p-regions, due to the lowering of the built-in potential across the junction, as given in the equations above. The dark current in a pn junction device then arises from recombination currents due to this excess carrier, both in the bulk of the n- and p-regions through diffusion outside the SCR, as well as recombination within the SCR.
The quasi-equilibrium approximation assumes that the effect of the forward bias is to increase the minority carrier concentrations on either side of the junctions at x = 0 and x′ = 0, as shown in Fig. 19.6, which illustrates an n (emitter) and p (base) structure. Under low-level injection conditions, the concentrations at these two points may be written
where \( {n}_{\mathrm{p}0}={n}_i^2/{N}_{\mathrm{A}} \) and \( {p}_{\mathrm{n}0}={n}_i^2/{N}_{\mathrm{D}} \) are the equilibrium concentrations of minority carrier electrons and holes on the p- and n-sides, respectively.
The regions outside the SCR defined by W in Fig. 19.6 are assumed to be charge neutral with no electric field. Hence, we can solve the semiconductor minority carrier diffusion equations in both regions
where Un,p and Gn,p are the recombination and generation rates for minority carriers, with Gn,p(x) given by Eq. (19.7), and the holes are solved in the x′ coordinate system on the left (positive x′ to the right). The solutions require two boundary conditions (BCs); Eq. (19.24) for the excess carrier concentration injected across the boundary serves as BCs at x, x′ = 0. At the other boundaries, we assumed the surface recombination conditions
For the case of the dark current, Gn,p(x) = 0, the general solutions are in the form of hyperbolic functions due to the combination of exponential solutions to the ordinary differential equations above.
The current densities on either side of the junction are expressed in terms of the diffusion current of charge carriers diffusing away from the junction in terms of the carrier gradients
The total current is the sum of these two in the general form of Eq. (19.1)
where the reverse saturation current density, J0, is given in general by.
where \( {L}_{\mathrm{n,p}}=\sqrt{D_{\mathrm{n,p}}{\tau}_{\mathrm{n,p}}} \) is the diffusion length for electrons (n) and holes (p), which is the average distance they diffuse before recombining, and the equilibrium minority carrier concentrations, np0 and pn0, have been written in terms of the doping concentrations on either side of the SCR, \( {n}_i^2/{N}_{\mathrm{A,D}} \), respectively. Here the form of the diode equation has an ideality factor n = 1. In the more general case including recombination in the space charge region and high-level injection at high bias, the ideality factor can vary between n = 1 and 2 depending on the bias.
The above expression simplifies in two cases, one in which the thicknesses of the emitter and base regions Wn and Wp are much larger than Lp and Ln, respectively (short base/emitter), and the other, which corresponds to the opposite, in which the regions are so short that no recombination occurs (short/base), further assuming ohmic contacts with infinite Sp and Sn (short base/emitter). This may be written generally as
where Xn, p = Wp, n for the short base/emitter case and Xn, p = Ln, p for the long base/emitter case.
The open circuit voltage given in Eq. (19.2) can be rewritten in terms of the current densities as
Clearly Voc depends on minimizing the dark current, characterized by J0, which arises due to recombination in the various regions and surfaces. Several general trends can be observed from the expression for J0. Increasing the doping on both sides increases the built-in potential and correspondingly Voc. However, the diffusion coefficients, Dn,p, are proportional to the carrier mobility, which degrade with increasing doping due to ionized impurity scattering. Further, for very high doping, there is increased recombination due to Auger processes which decreases the diffusion lengths, as well as bandgap narrowing effects, which increase ni due to its exponential dependence on the bandgap. Figure 19.7 shows the dependence of the open circuit voltage on doping in a conventional architecture, where the degradation of the diffusion length with doping correlates with a degradation of Voc.
Dependence of the open circuit voltage and carrier diffusion length on the base doping in a homojunction solar cell. (With permission from PVEducation.org)
The above analysis did not address specifically the role of surface recombination on the open circuit voltage, but looking at Eq. (19.30), with infinite recombination velocity, the dark current is clearly much larger than the case limited by the diffusion length. Thus, reducing Sn,p through passivation of the front and back surfaces is critical in good cell performance, particularly considering that in state-of-the-art Si solar cells, the diffusion length is typically much longer than the entire wafer thickness.
Figure 19.8 illustrates the solution of the minority carrier diffusion equation in the limit that the based width Wp is much less than the diffusion length, Ln, in Fig. 19.6, where the solution is just a straight line. In the case of a conventional ohmic contact, where Sn = ∞, the minority carrier concentration goes to zero at the boundary, and the current is given by the slope of the line times the diffusion coefficient for minority carrier electrons, Dn. As Sn decreases, so does the slope and the corresponding minority carrier current. Asymptotically, the solution goes back to the long base solution as Sn → 0.
Reducing the minority carrier current extracted through the front and back is therefore a major strategy in the design of solar cells for maximizing Voc. However, at the same time, we have to extract majority carriers through low resistance contacts, which is somewhat of a contradiction. Design of contacts which have high majority carrier extraction but low minority carrier extraction is the goal of carrier selective contact design, discussed in more detail in Sect. 19.3.4.
A traditional strategy for reducing minority carrier recombination in the contact region is the use of a back surface field (BSF), which usually involves having a higher doped region in the vicinity of the back contct. The isotope junction formed between a p+ and p-region results in a SCR with a field that opposes the flow of electrons toward the p contact, reducing the effective surface recombination velocity. This results in a Voc increase of several tens of mV.
The above analysis has considered the current density in a one-dimensional analysis, but another approach to reducing the effective recombination on the back is to minimize the contact area laterally through selective contacts to the base with local BSFs, where the rest of the back surface is highly passivated by a dielectric layer. Here the ratio of the passivated area is high compared to the actual contact area, with a commensurate reduction in dark current. This structure is the basic architecture of the PERC (passivated emitter and rear contact) solar cell, which is presently (in 2020) the dominant commercial Si technology, and has demonstrated cell efficiencies greater than 24% [7].
3.2 Photocurrent
The short circuit current density, Jsc, is directly related to the photocurrent density, resulting from light absorption in the solar cell, and is equal to this quantity when nonideal effects such as shunt and series resistance are minimized. Maximizing the short circuit current involves two main design factors: one is absorbing the maximum amount of light above the bandgap, and the other is maximizing the collection of light-generated carriers throughout the volume of the cell.
Maximizing the amount of light absorbed involves minimizing reflection both from the metallic front contact grid and from the surface of the cell where light is transmitted. As mentioned earlier, minimizing the front contact grid shading is a design optimization between the spacing and width of the fingers and the spreading resistance of the top layer which impacts the fill factor of the cell. Minimizing reflectance involves the design of an optimal AR coatings based on the spectral response characteristics of the cell as discussed in Sect. 19.2. In addition to the optical coating, texturing of the front (and back) surfaces is employed in commercial Si solar cells to increase the capture of light into the cell. Finally, either the thickness of the cell has to be sufficiently thick that light is not lost through the back side of the cell due to incomplete absorption, or light trapping techniques have to be employed so that photons make multiple passes through the absorber. The most straightforward approach is simply having an ideal reflecting back side, so that photons make at least two transits of the cell thickness. Texturing of the front surface leads to a high probability of being scattered again back into the cell rather than exiting the front surface. The maximum number of passes is expressed in the classical light trapping limit [8] for the maximum optical path length in the cell, \( \left\langle l\right\rangle =4{n}_{\mathrm{s}}^2W \), where ns is the index of refraction of the absorber and W is its thickness. Light trapping is discussed in more detail in Sect. 19.7.3. Reflection and absorption depend on characteristics of sunlight, solar cell optical properties, EG, and solar cell thickness, so that the optimum design is a nontrivial task.
The second important quantity associated with the short circuit current is the collection probability of the cell for the photoexcited carrier distribution, which is nonuniform and wavelength dependent due the wavelength dependence of the absorption coefficient. The collection probability is illustrated in Fig. 19.9. It represents the probability that an electron generated at some point relative to the SCR will be collected, where in the SCR it is commonly assumed that 100% of the carriers are collected due to the high electric field there.
Sketch of the collection probability versus distance in the device. The shaded region represents the SCR where the collection probability is unity. The panel (a) compares the collection probability with the generation rate, while the panel (b) shows the effect on the collection probability of surface passivation and diffusion length. (With permission from PVEducation.org)
In terms of the collection probability, the short circuit current can be written as an integral
where Eq. (19.7) has been substituted for the generation rate, and we have integrated over all wavelengths. The upper panel of Fig. 19.9 illustrates the overlap of the generation rate and the collection probability for one wavelength. As mentioned earlier, shorter wavelengths have a generation rate profile close to the top surface, whereas longer wavelength photons result in generation throughout the structure. The dependence of the collection probability with distance relative to the SCR depends on recombination, both bulk and surface recombination, through the solution of the minority carrier diffusion equations, as discussed below. Qualitatively, the effects of low and high bulk recombination, as well as low and high surface recombination (often referred to as the degree of surface passivation), are illustrated in Fig. 19.9, where the realization of high short circuit current requires both a high minority carrier lifetime in the bulk and well-passivated front and back surfaces.
A simple case in which analytical expressions can be derived is considering the solution of the minority carrier diffusion equations again on either side of the junction, with a constant G (both in terms of position and wavelength) throughout the device, which would be the case of a light source with a small absorption coefficient relative to the width of the cell. The minority carrier diffusion equations in Eq. (19.25) then have a simple inhomogeneous constant, which, in the limit of the diffusion lengths being much shorter than the widths of the emitter and base regions, gives the analytical form for the current density as the sum of the dark and light currents
where W is the width of the SCR, and it has been assumed that all the carriers generated in the SCR are collected. This analytical model gives the simple interpretation that all the carriers generated within a diffusion length of the edge of the SCR on either side of the junction are collected in addition to those generated within the SCR, and the short circuit current is the sum of these three contributions. Qualitatively, this situation corresponds to the collection probability profile illustrated in Fig. 19.9 for the low diffusion length case. As mentioned earlier, in state-of-the-art crystalline Si solar cells, the diffusion length is actually greater than the width of the base region, and passivation of the front and back surfaces plays a critical role in both the photocurrent and dark current.
An important characterization of the photocurrent response of a solar cell is in terms of its quantum efficiency(QE), which is defined as the ratio of electron-hole pairs collected to incident photons on the cell within a certain wavelength interval. Once the QE is known, the short circuit current density can be obtained from the integration of the QE with the spectrally resolved incident photon flux
The quantum efficiency provides useful information on the limiting mechanisms controlling the short circuit current. Fig. 19.10 shows a typical QE versus wavelength plot. The ideal quantum efficiency is zero below the bandgap and then jumps to unity above the bandgap and remains constant. In reality, there is reflection from the front surface, which depends on wavelength (in addition to the uniform loss due to the grid pattern, which reduces QE). At long wavelengths, the QE degrades due to the increased absorption depth of photons close to the bandgap energy, where they either are lost due to being absorbed further than a diffusion length from the junction or from not being absorbed due to the cell being too thin. For short wavelengths in the blue region, carriers are absorbed very close to the front surface, where surface recombination exists resulting in loss of collection in a traditional Si cell architecture. Thus, the quantum efficiency of a solar cell is an important characterization used in the optimization of the cell design.
Illustration of the quantum efficiency of a solar cell compared with the ideal quantum efficiency illustrating the various factors affecting its wavelength dependence. (With permission from PVEducation.org)
3.3 Series Resistance
The simple equivalent circuit model of a solar cell shown in Fig. 19.2 neglected two important parasitic effects that degrade mainly the fill factor defined in Eq. (19.3), that of shunt and series resistance. Figure 19.11 shows the modified equivalent circuit including these two effects modeled simply as linear lumped parameter elements. In general, these resistances are nonlinear, depending on the operating point of the device, but for analysis of the main effects, the linear model is sufficient.
Solar cell equivalent circuit including both shunt (Rsh) and series resistance (Rs). (With permission from PVEducation.org)
The effect of the shunt resistance is to effectively short the junction, leading to a parallel leakage current component which degrades the ideal diode behavior, with a corresponding degradation of the fill factor. Ideally, the shunt resistance is semi-infinite in a good device. Shunt leakage paths can originate due defects such as dislocations or grain boundaries that bridge SCR leading to a current transport separate from the ideal recombination currents discussed earlier. It can also originate from leakage around the edges of the cell due to poor isolation and potential metallization problems with the final cell design.
Series resistance can arise from the bulk resistance, contact resistance, the resistance of the metal top grid in the fingers, and importantly the spreading resistance in the emitter as the current spreads laterally to reach the fingers of the top contact metallization, illustrated in Fig. 19.12. Typically, the base resistance is small in comparison to the spreading resistance as the cross-sectional area is quite large. The metal contact resistance between the metal and the semiconductor, defined in terms of the specific contact resistance, is usually well behaved in commercial solar cells as well, and not the main source or resistance loss, while the resistance of the metal itself is not problematic if the finger width is sufficiently large. So the main component of series resistance of concern is usually the emitter spreading resistance, and the design of the finger spacing to minimize the power loss due to this resistance.
Illustration of the different components of series resistance in a solar cell. (With permission from PVEducation.org)
The emitter is typically quite thin, and current transport is primarily lateral in this layer. Therefore, it is more usual to talk about the sheet resistance of the emitter in terms of
where ρe is the bulk resistivity of the material, t is the thickness, while L and W are the length and width of the material that current is passing through. The quantity ρsh is the sheet resistance in ohms/square (Ω/□).
The problem requires solving the resistive power loss associated with the distributed current flow problem in which the current density is changing in the y direction relative to the grid finger as illustrated in the geometry shown in Fig. 19.13. The incremental power loss in a section dy is given by
The current flowing into the left finger is zero in the middle and increases linearly as y increases
The total power loss due to the current flowing into the left finger is therefore
At the maximum power point, the generated power is given by
where Jmp and Vmp are the current density and voltage at the maximum power operating point of the current-voltage characteristic of Fig. 19.2. Therefore, the fractional power loss is given by
As S increases as well as the sheet resistance, so does the fractional power loss. For ρsh=40 Ω/□, Jmp = 30 mA/cm2, Vmp = 450 mV, S < 4 mm is necessary for less than 4% total power loss. The optimal grid design minimizes this power loss while simultaneously minimizing shading loss.
Schematic of the finger geometry for calculating the spreading resistance in the emitter of a photovoltaic device. (With permission from the PVEducation.org)
3.4 Heterojunction Cells and Carrier Selective Contacts
Here we discuss heterojunction solar cells and the efficiency improvements due to the heterojunction, followed by a more general discussion of carrier selective contacts, of which heterojunctions can be considered a subset.
3.4.1 Heterojunctions
The highest efficiency solar cell technologies, either single junction or multijunction, employ heterojunctions between dissimilar semiconductor materials. Figure 19.14 illustrates the ideal band alignment between the two materials based on the electron affinity rule or Anderson model. This model assumes that the vacuum level can be treated as a reference level, which is assumed continuous in forming the heterojunction band diagram. The band offset in the conduction band is then the difference between the two electron affinities, χ1 − χ2. The conduction and valence band alignment can either be such to confine both electrons and holes (type I), either electrons or holes (type II), or staggered such that the VB of one material overlaps the CB of the other (e.g., InAs/GaSb). This model works well for some systems, e.g., InAs/GaSb and Si/Ge. However, deviations from Anderson model generally occur due to interface dipoles which allow the electrostatic potential to change discontinuously. Typically the band offsets are determined experimentally from capacitance voltage, photoemission, photoconductivity, and other techniques.
There are a variety of heterojunction structures in photovoltaics used in high performance devices in various technologies. In the context of conventional wafer-based technologies such as Si and GaAs, these include amorphous Si (a-Si)/c-Si (crystalline Si) heterostructures as a passivating as well as carrier selective contact (discussed in the next section), as well as TCO-based heterostructures, for example, ITO (indium tin oxide)/Si structures and a-Si/c-Si structures. GaAs typically employs AlxGa1-xAs ternary compounds as a heterojunction “window” layer to mitigate surface recombination and serve as a carrier selective contact.
From the standpoint of the ideal diode equation for the dark current as discussed in Sect. 19.3.1, the derivation can be slightly modified to account for the difference in bandgaps, which results in different intrinsic carrier concentrations, ni, on either side of the junction. The modified reverse saturation current is then given by
where the parameters have the same definition as Eq. (19.32) except that the intrinsic concentrations are different and significantly reduced in the wider bandgap material by a factor
Hence, one component of the minority carrier reverse saturation current is exponentially reduced by a factor involving the bandgap difference, leading to an increase in Voc. In general, however, reductions in J0 may be realized by selective controlling the minority carrier injection, which is the basis of the general topic of carrier selective contacts in the next section.
3.4.2 Thermodynamic and Detailed Balance Definition of Ideal Contacts
The ideal thermodynamic or detailed balance solar cell structure consists of an absorber material with a given quasi-Fermi-level separation, with the light-generated carriers extracted from the material at the quasi-Fermi-level energy asshown in Fig. 19.15 (see Sect. 19.5).
However, such a structure encounters several practical barriers relating to extracting the light-generated carriers. An ohmic contact (with the band diagram shown in Fig. 19.16) has high recombination for minority carriers, and therefore the carriers are extracted at the Fermi level rather than the quasi-Fermi level. This fact drives the need for a pn junction; we need to have two different Fermi levels in the semiconductor, and hence we need the pn junction used by the majority of solar cell structures.
Band structure of an ohmic contact. (a) The ideal band diagram of an ohmic contact. (b) Practical implementations of an ohmic contact. In all cases, there is a large density of allowed energy states in the contact (a metal), such that there the concentration of minority carrier is low and the quasi-Fermi level is identical to the Fermi level
The thermodynamically ideal contact for a detailed balance structure was termed a selective carrier contact by Würfel [5]. It consists of a contact which allows one type of carrier to be extracted, with the band diagrams shown in Fig. 19.17, consisting of a Fermi level in the contact material aligned with the quasi-Fermi level in the absorber material. The band structure has a large number of allowed energy states above the Fermi level in the contact material, and no allowed energy stated below the Fermi level of the contact material. The band structure diagram shows that a selective carrier structure is the “inverse” of the band structure of an ohmic contact.
Detailed balance and thermodynamic calculations also show that even a carrier selective contact incurs substantial losses in that extracting carriers from a carrier population with an energy given by a quasi-Fermi level loses substantial energy as the quasi-Fermi level is near the bottom of the energy distribution, and hence the higher energy of some carriers is lost. Solar cells which extract carrier at energies above the quasi-Fermi level are generally called hot carrier solar cells, and the contacts to such device are called energy selective contacts. They are discussed in Sect. 19.8.3. Their band structure is similar to a carrier selective contact structure, except that the allowed density of states is a narrow band. Overall, the type of contacts indicated by thermodynamic or detailed balance analyses is shown in Table 19.1.
A substantial optimization in solar cells has centered on minimizing the nonideal recombination associated with an ohmic contact. This involves addressing two features: (1) ensuring that the Fermi level is close to the quasi-Fermi level and (2) minimizing the recombination at the metal-semiconductor interface. Increasing doping, particularly using higher doping near the contacts, is an effective way to minimize both effects. However, high doping itself introduces non-idealities including bandgap narrowing and increased Auger recombination. The introduction of selective carrier contacts, initially through the HIT (heterojunction with thin intrinsic region) and later through a greater variation of structures such as TOPCon, has allowed solar cell efficiencies to more closely approach thermodynamic ideals. The next subsection describes the implementation of a selective carrier contact in the constraints of commercial silicon solar cell technologies, and examples of silicon selective contact solar cells.
3.4.3 Silicon-Based Selective Carrier Contact Solar Cells
The ideal implementation of a carrier selective contact consists of a material with a zero density of states below the Fermi level of the contact material, and a large density of states above it. There are several ways in which we can approximate such a band structure. The conceptually simplest way is to use a very wide bandgap semiconductor with quantum well used to adjust the Fermi level to the quasi-Fermi level in the absorber material. This is similar to a hot carrier contact in which the requirement of a narrow band for the density of states is relaxed to a wide band for the density of states above the lowest energy level, and hence quantum wells can be used instead of quantum dots.
In practice, however, particularly for large area silicon and thin film solar cells, a quantum well contact is not readily commercially feasible. A far simpler implementation is to use a very thin wide bandgap layer. The bandgap of the material needs to be wide enough such that there are theoretically no allowed states near the silicon band edge as shown in Fig. 19.18a. However, adjusting the Fermi level of this wideband material by doping is typically not useful, as the introduction of allowed energy levels from the dopants introduces energy states, which increase recombination. Further, because of the difficulty in doping wide bandgap materials or oxides, even with high doping, such materials are unlikely to have sufficient conductivity to avoid large resistive losses given the large currents from a solar cell. Instead of doping, we adjust the Fermi level in wide bandgap region adjacent to the solar cell by putting a doped wide bandgap semiconductor on top and using band offsets to achieve large band bending. The separation of an ideal selective carrier into two layers introduces the need to examine the transport, usually by tunneling and/or thermionic emission across the thin wide bandgap region.
There are several solar cell architectures which meet the above requirements. One group of solar cell structures uses silicon heterojunctions, initially developed using amorphous Si layers on a crystalline Si solar cell. These approaches are often called HIT solar cells (heterojunction with intrinsic thin layers) or SHJ (silicon heterojunctions). The HIT structure is shown in Fig. 19.20. It achieved an efficiency of 24.7% in 2014 [9], reaching the previously long-standing silicon efficiency record from the pn junction-based PERL solar cell. Since then numerous improvements have allowed solar cells based on silicon heterojunctions to reach 26.6% [10] in an interdigitated back contact structure (Fig. 19.20). Several companies have large-scale commercial production of HIT solar cells, including Panasonic and Tesla Solar. Key challenges for broader adoption of SHJ solar cell relate to the consistency in large-scale manufacturing and more expensive metallization for these solar cells. Metal screen printing for HIT solar cell uses different pastes and processing since SHJ require low temperature processes, and cannot use the high temperature sintering steps in conventional solar cells. A variety of other metallization processes are used to address these issues including using wires (SmartWire), copper plating, or metal stencils.
Overall, a selective carrier contact for a commercial solar cell generally consists of several features (Fig. 19.19): (1) a wide bandgap material often called a membrane with (a) sufficiently low interface defects where the defects have a minimal impact taking into account the band bending at the Si surface and (b) thin enough to support high tunneling/thermionic emission currents; (2) layers on the surface of the wide bandgap to adjust the Fermi level and to support lateral transport to the contacts; and (3) an approach in the silicon absorber to reduce the impact of interface defects.
Another selective contact technology is the TOPCon technology [11]. It is used as a rear contact approach for solar cells in which the emitter already closely approaches the ideal structure shown in Fig. 19.21. In the TOPCon structure, SiO2 is used as the membrane wide bandgap region. The Fermi level is adjusted by a polysilicon doped layer on the SiO2, and reducing the impact of interface states is accomplished by a thin doped layer in the silicon (which is diffused through the oxide). TOPCon solar cells have achieved 25.7% efficiency [12].
Schematic of a TOPCon solar cell. (With permission from [11])
4 Performance Comparison of Single Junction Technologies
In the following, we compare the performance of different single junction technologies, including Si, the III–V materials, II–VI and chalcogenide materials, and finally organic and perovskite-based cells. All are referenced to the conversion efficiency versus time of the various technologies, as discussed below.
4.1 Performance Limits of Si- and GaAs-Based Technologies
A primary performance metric for solar cells is the solar to electrical energy conversion efficiency, defined earlier by Eq. (19.3). The National Renewable Energy Laboratory (NREL) publishes annually a comparison of the efficiencies of all solar cell technologies versus time shown in Fig. 19.22. Silicon solar cell technology dominates 95% of the current world photovoltaic market, through both single crystal and multi-crystalline Si technologies [13], as shown by the various blue curves in Fig. 19.22. The current high efficiency record (as of 2020) reported for single junction Si device technology under 1 sun illumination to date is 26.7%, based on a heterojunction HIT structure (see Sect. 19.3.4) using a crystalline Si substrate with thin layers of amorphous Si (a-Si), which forms a heterojunction due to the larger bandgap of a-Si (∼1.7 eV) [10]. This cell record was demonstrated on a large area device, with an interdigitated back-side contact as shown in Fig. 19.20.
Measured solar cell efficiency records for various technologies versus time (NREL https://www.nrel.gov/pv/) (This plot is courtesy of the National Renewable Energy Laboratory, Golden, CO)
The highest efficiency for any single junction technology was reported by Alta Devices for a heterojunction AlGaAs/GaAs single crystal solar cells where they achieved 28.8%, as shown by the purple curves in Fig. 19.22 (see Ref. [14] for discussion). III–V semiconductor solar cells are normally too expensive for terrestrial flat plate solar applications due to the costs of the substrate materials. However, III–V-based cells, as well as their multijunction realizations (shown in purple below), are standard technologies for space applications, where radiation tolerance and efficiency versus weight are the main performance drivers.
4.2 Thin Film Technology
The Si and III–V technologies described in the previous section are mainly wafer based, which is a major contribution to their cost in terms of materials. Thin film solar cells, in contrast, are deposited using thin film technology onto a low-cost substrate material such as metal or glass. Since the quality (as characterized by its minority carrier lifetime and surface recombination velocity) of the deposited material is inferior to that of single crystal materials, thin film cells typically have lower efficiency but lower fabrication and material costs, thus achieving lower $/W cost, the other main metric of solar cell technology. Amorphous Si (a-Si) thin film solar was the dominant thin film technology several decades ago but has since been supplanted by II–VI CdTe heterostructure technology. A schematic cross section of a CdTe cell is illustrated in Fig. 19.23. Typically a heterostructure is used, with a wider bandgap “window” layer (here CdS with a bandgap of 2.5 eV), while CdTe has a bandgap of 1.32 eV. The structure is an inverted structure in which glass is used as the supporting substrate, followed by a thin transparent conducting oxide as the front contact through which light enters the cell. The wider bandgap CdS layer is deposited first followed by the polycrystalline CdTe layer (typically a few microns thick), and finally rear contacts. As shown in Fig. 19.22 by the green sets of data, CdTe cells have demonstrated over 21% performance by First Solar [15], and this is the basis for a number of large (>200 MW) utility-scale solar installations worldwide. Chalcogenide-based materials such as CIGS (CuInGaSe2) have demonstrated even higher efficiencies >23% [16] and are competing for market share.
4.3 Organic Solar Cells
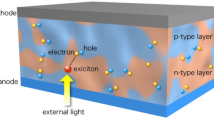
Organic solar cells are basically thin film solar cells based on organic semiconductor materials rather than inorganic semiconductors. In analogy to the energy band diagram of Fig. 19.1, organic materials are defined by their HOMO (highest occupied molecular orbital) and LUMO (lowest unoccupied molecular orbital) levels, which play the same role as the valence and conduction bands in inorganic semiconductors, respectively. A heterojunction is formed due to the lineup of the HOMO/LUMO levels of the two different materials (called donor and acceptor materials), rather than through doping in a pn junction. Excitonic effects play a strong role in organic materials; photoexcitation of an electron from a filled HOMO level to an empty LUMO level creates a strongly bound exciton, which diffuses as a bound (neutral) state to the heterointerface, where it dissociates at the barrier into separate free electrons and holes on either side of the heterojunction, which are then collected at the contacts giving rise to a photocurrent. Typically the lifetime of the exciton is quite short, leading to short diffusion lengths, and hence problems with charge collection. To circumvent this diffusion limitation, blended heterostructures with the donor and accepter materials interdiffused into a random network are employed, which provide better charge collection and short circuit current. A conventional organic solar cell includes P3HT (poly(3-hexylthiophene)), which acts as a donor material, and PCBM (6,6-phenyl-C61 butyric acid methyl ester), which acts as an acceptor material [17]. While efficiencies are generally lower than inorganic thin film approaches, the fabrication process for organic is much less expensive; organic layers can be sprayed or spun on, hence not requiring vacuum deposition or high temperature processing. Recent high performance organic cells have increasingly used more conventional thin film processing, however [18]. The improvement in efficiency with time of conventional organic cells is shown by the solid red circuits in Fig. 19.22 and tandem (discussed in Sect. 19.6) organic cells by the red triangles.
While research work on commercial ventures in niche markets continues on all organic photovoltaics, including incorporation of advanced concept and nanotechnology-inspired approaches discussed in more detail in Sect. 19.7, remarkable advances in performance have been achieved over the past decade on cells fabricated from hybrid organic-inorganic perovskite materials. These hybrid perovskite materials have the general perovskite crystal structure ABX3, most commonly methylammonium lead trihalide, CH3NH3PbX3, where A is the organic methylammonium, B is Pb, and X is a halogen (I, Br, or Cl) [19]. The bandgap ranges from 1.55 eV to 2.3 eV depending on the halide, where CH3NH3PbI3 corresponds to the lower value. This bandgap is well suited for terrestrial photovoltaics in terms of its maximum theoretical efficiency discussed in the next section. Perhaps more importantly, the transport properties of the hybrid perovskites are superior to those of the typical organic materials discussed in the preceding paragraph, with electron and hole mobilities comparable to inorganic semiconductors, and diffusion lengths on the order of microns. Excitonic effects are relatively weak as well. The early high performance results report for perovskite solar cells was based on the nanostructured dye-sensitized solar cell architecture [20], discussed in Sect. 19.7.2, in which the hybrid perovskite is infused into a mesoporous wide bandgap TiO2 structure which acts as an electron acceptor from the perovskite, while holes are extracted in an electrolytic liquid cell structure. This efficiency was greatly improved by replacing the liquid electrolyte with a solid organic hole transport layer (spiro-MeOTAD) [21], which is the basis of the current high efficiency cells shown in Fig. 19.22. In a further breakthrough leading to high efficiency cells, the Cambridge group further demonstrated that high performance devices may be fabricated in a planar structure in which CH3NH3PbI3 is essentially a polycrystalline semiconductor [22], resembling an organic thin film solar cell. As seen in Fig. 19.22, the performance of perovskite solar cells has one of the steepest slopes of any technology over a very short time period, reaching a record as of today of 25.2% at the Korea Research Institute of Chemical Technology (KRICT)/MIT, surpassing that of thin film inorganic technologies such as CdTe and CIGS. The advantage of perovskite technology is the low manufacturing cost, similar to those of organic and thin film processing, where solvent spin coating and vapor deposition are the two main synthesis methods. The main barrier to commercialization presently is issues related to the long-term stability, where degradation occurs due to the sensitivity of the perovskite to water vapor, which can occur over a matter of hours or days. Different approaches to encapsulation and improved materials processing ameliorate these problems, but long-term field testing and accelerated life testing are necessary to assure the longtime reliability of the technology (e.g., commercial Si solar modules are guaranteed for lifetimes in excess of 20 years).
5 Efficiency Limits for Photovoltaic Converter
The record solar to electrical conversion efficiencies shown in Fig. 19.22 are all monotonically increasing with time for different technologies, albeit at different rates, and to date, less than 50%. Thermodynamics provides a guide to what the maximum conversion efficiency of a solar converter can approach. For example, the classical Carnot efficiency, ηc = 1 − Ta/Ts, representing a reversible engine working between the temperature of the Earth, Ta, and that of the sun, Ts, would predict efficiencies close to 95%. However, the Carnot efficiency assumes infinitesimally small amounts of work performed with no entropy production (inherent in the reversible assumption), which does not model a practical converter. de Vos has surveyed various thermodynamic engines for solar energy conversion [23], which have been reviewed by Green (Chap. 3, [2]). Considering the entropy production associated with blackbody radiation and absorption, a more realistic value closer to 85.4% is obtained.
It is clear that there is a substantial gap between the present operating limits of solar cells and their thermodynamic potential, which has driven considerable research on overcoming fundamental barriers to efficiency. In the following, we review the limits of efficiency including the constraints on current technology through an idealized analysis based on the concept of detailed balance, and how to circumvent the assumptions inherent in the derivation of a single gap absorber to reach the potential limits of efficiency.
5.1 Shockley-Queisser Limit
Shockley and Queisser’s (SQ) analysis [24] of the limits of performance of photovoltaic devices, independent from their material parameters other than their energy gap, is the most well-cited work on this topic, although other such analyses appeared around the same time. The approach is based on the thermodynamic hypothesis of detailed balance and considers the only losses from the cell treated as an ideal blackbody absorber/emitter taking into account the chemical potential difference in the absorber due to absorption and external voltage. The idealized description assumes the following: (1) complete collection of all the photons incident on the absorber; (2) radiative recombination only; (3) one bandgap; (4) absorption across the bandgap in which one photon generates one electron-hole pair; (5) constant temperature in which the carrier temperature is equal to the lattice and ambient temperature; and (6) steady state, close to equilibrium.
The current density may be written as the sum of three terms, the first representing the incident photons absorbed above the bandgap of the semiconductor from direct blackbody radiation at the temperature of the sun given by Eq. (19.4), the second the diffuse blackbody radiation collected outside the incident cone of the direct radiation, and finally the third term the blackbody radiation from the solar cell (Eq. (19.4) modified by the quasi-Fermi energy splitting of the absorber equated to the external voltage)
with
Here C is the concentration factor, Eg is the material bandgap, and V is the voltage across the cell. If a solar spectrum other than the ideal blackbody spectrum is used, then the first term is simply replaced by the integral of the photon flux above the bandgap.
In Eq. (19.46), the “dark” current discussed in the previous section is only due to blackbody radiation from the semiconductor absorber, which in effect is due to radiative recombination within the semiconductor generating photons above the bandgap. The power density delivered by the cell is the product of J(V)V, which has a maximum power point corresponding to the maximum conversion efficiency. The calculated results are shown in Fig. 19.24, where the black curve is the calculated efficiency versus bandgap for an AM1.5 terrestrial solar spectrum (hence the multiple maxima due to spectral features). The maximum efficiency without concentration is around 33.7% corresponding to maxima at 1.1 and 1.4 eV (conveniently close to Si and GaAs, respectively), while the effect of concentration is to increase the efficiency. The rest of Fig. 19.24 illustrates the principal losses compared to 100% efficiency. The main losses include loss of photons with energy below the bandgap (transparency) and loss of the excess energy of the photon above the bandgap (thermalization) in terms of energy relaxation of photoexcited carriers back to the band edges, with thermalization being the main loss for small bandgap materials and optical transparency the main loss for high bandgaps. Additionally there are other losses including unavoidable heat loss to the surroundings and irreversible entropy generation [25].
5.2 Overcoming the Shockley-Queisser Limit
The detailed balance efficiency versus bandgap shown in Fig. 19.24 has a number of assumptions built-in that may be circumvented in order to exceed the single gap SQ limit. Here we discuss some of those assumptions and strategies for avoiding them to overcome the single gap limitations.
Broadband Solar Spectrum:
As discussed in Sect. 19.2.1, the solar spectrum is a broadband in nature as described by Planck’s law, which leads to particular shape of the maximum efficiency curve versus bandgap, representing a trade-off in losses between transparency and thermalization. If the input spectrum were monochromatic, for example, then the optimum bandgap would match the photon energy of such a source, and the efficiency would theoretically approach the thermodynamic limit since both transparency and thermalization would be eliminated. Transforming the solar spectrum to a narrower spectrum would therefore circumvent one of the assumptions in Eq. (19.46), and attempts at up/down conversion of portions of the solar spectrum through phosphors or two-photon absorption/emission have been pursued.
OneElectron-hole PairCreated Per Photon Absorbed:
The assumption in Eq. (19.46) is that one EHP is excited per photon. However, if the excess energy of the electron or hole above their respective band edges is more than twice the bandgap, a second EHP may be created through the process of impact ionization, where the excess kinetic energy is transferred to creation of the second EHP. This process reduces the thermalization loss by converting excess photon energy into increased photocurrent. Kolodinski et al. considered carrier multiplication in the SQ limit of conventional Si solar cells [26]; however the effect was negligible due to restrictions on the threshold energy for impact ionization to occur due to momentum conservation in bulk crystals. In more recent years, strong multiplication effects have been measured in nanostructured systems such as quantum dots and nanowires in which momentum conservation is relaxed [27], discussed in more detail in Sect. 19.8.2. There the effect is referred to as multiexciton generation (MEG), as optical absorption occurs primarily through excitonic states in strongly confined systems like quantum dots and nanocrystals.
The Extracted Carrier Energies Correspond to the Band Edges:
Ross and Nozik proposed the concept of hot carrier solar cells in the early 1980s [28], where electrons and holes are not collected at the band edges (and the voltage determined by the bandgap), but through energy selective contacts above and below the conduction and valence band edges, respectively. The operating voltage of the device would then be determined by energy separation of these energy selective contacts, while the photocurrent would be determined by the bandgap itself, thus circumventing the SQ limit. This concept requires that the absorber material has a low carrier energy loss rate to the lattice, so that the carriers can maintain sufficient average kinetic energy to be extracted through the energy selective contacts. Würfel and coworkers further considered the effect of impact ionization and carrier multiplication on the performance [29, 30]. Recent results are discussed in more detail later in Sect. 19.8.3.
Single Bandgap Absorber:
The SQ model only considers a single bandgap material, but by the mid-1950s, it was already recognized that multijunction or tandem solar cells, discussed in more detail below, were capable of efficiencies above that of single gap devices. Tandem cells are most commonly fabricated as a stack of series connected junction cells, with the widest bandgap at the top, where it absorbs the blue portion of the solar spectrum, the next largest gap below, and so forth until the bottom cell which has the smallest bandgap. As shown in Fig. 19.22, III–V compound tandem cells demonstrate the highest efficiencies of any solar cell technology [31], with the record to date in excess of 47.1% in a six-junction metamorphic structure [32], compared to the single gap SQ limit of 33%.
6 Multijunction Solar Cells
Of the abovementioned approaches to circumvent the SQ limit, by far the most successful has been the demonstration and commercial development of multijunction or tandem solar cells. Such cells are the highest efficiency technology presently, particularly at high concentration. In tandem solar technology, multiple bandgap junction devices are connected together or simply grown sequentially on a substrate, where the multiple bandgaps reduce the thermalization loss and transparency issues of a single bandgap solar cell, as discussed in more detail below. The highest efficiency tandem devices are single crystal III–V materials grown epitaxially on top of one another, starting with the lowest bandgap material (which often is a Ge substrate which is lattice matched to GaAs) and ending with the highest bandgap, in terms of the direction of the incident radiation. In this way, the short wavelength light is absorbed in the top wide bandgap material, and the longer wavelength light is absorbed by subsequent layers. The cells are typically connected together in series with tunnel junctions, such that, overall, the current is the same through all the cells and the overall cell voltage is the sum of the voltages of the individual cells. The cost of the substrates and high-quality epitaxial growth (using, e.g., molecular beam epitaxy (MBE) or metal organic chemical vapor deposition (MOCVD)) makes the cost per cell quite high. The high cost of these devices is compensated for by using them in an optical concentrator (where the light intensity is 200× to 400× higher than typical sunlight), such that only very small areas are needed. The optical systems must track the sun, and these large systems are suited primarily for utility-scale applications. Three junction cells based on Ge/GaAs/GaInP or similar combinations have exceeded 40% efficiency as shown by the purple set of curves in Fig. 19.22, and the record as of the time of this writing is 47.1% from NREL in a six-junction structure, which is well in excess of the SQ limit for a single junction.
The detailed balance approach given by Eq. (19.46) can be generalized to consider multiple junctions, each with its own detailed balance equation, and with a modified spectrum according to the number of cells above or below (due to reabsorption of the emitted light) the particular junction in question. Consider an n-layer stack, in which cells are arranged in order of decreasing bandgap, with the highest bandgap closest to the top surface where radiation is incident. Consider the ith cell in the n-layer stack. The net absorption in this layer is due to absorption from incident light through upper layers plus re-emitted light from layers above and below. The current in the ith cell is then given by a generalization of the detailed balance equation for a single junction, Eq. (19.46), as.
where the first two terms represent the light absorbed in the range of photon energies between the bandgap of the layer and the bandgap of the layer above due to both direct and diffuse light, the third term is the radiation emitted from this cell with Vi the voltage across the cell, while the last two terms represent absorption due to reabsorbed photons emitted from the cells above and below, respectively. Eq. (19.48) is then used for all the cells in the stack, in which the upper limits on the top cell go to infinity.
In the usual architecture, the cells are grown epitaxially on top of one another, which imposes stringent constraints in terms of lattice matching of the layers to minimize defect formation due to strain. The current then has to be the same in all the cells as they are series connected
Therefore, the voltage operating point of each of the cells described by Eq. (19.48) has to adjust such that the currents are the same, and the resulting operating voltage is the sum of the voltages of the individual cells when series connected.
The results of this calculation for maximum efficiency of different numbers of bandgaps for normal, low, and high concentration are shown in Fig. 19.25. As can be seen, concentration provides a significant improvement in performance for high number of junctions, which can be explained simplistically in terms of Eq. (19.3) for the open circuit voltage increase with photocurrent (proportional to concentration) and having junctions in series where the effect is additive, multiplying the concentration effect. For maximum concentration (set by étendue limits to 46,050X), one can approach the thermodynamic limit with an arbitrarily large number of junctions, where the thermodynamic limit for a solar energy converter is above 85%, as discussed in the preceding section.
As discussed earlier, commercial tandem cells are grown in series using epitaxial material growth technology, which is generally quite expensive compared to conventional Si solar cell manufacturing and has many material challenges to both optimize the bandgaps and have lattice-matched materials for low defect growth. Si-based tandems leverage the low cost of Si substrates in commercial technology today, with the efficiency advantages of a top cell grown on the underlying Si platform. Fig. 19.26 shows the calculated detailed balance efficiency versus bandgap for a two-terminal (2T), series constrained, top and bottom cell, which is peaked in a narrow bandgap range around 1.7 eV at 46%. A key challenge in tandems is that in series connected tandems, the maximum efficiency is achieved only for a narrow range of bandgaps as shown for a two-terminal structure, giving rise to the search for a 1.7 eV material that can be grown or deposited onto a silicon solar cell without an added substrate and yields stable, high performance. Realizing this bandgap with a material lattice matched to Si is quite challenging. What is also plotted in Fig. 19.26 is the efficiency versus bandgap when the 2T series constraint is relaxed. The dependence on bandgap is much weaker and shifted slightly higher to 1.9 eV, meaning that a range of bandgap options become available when current matching between the two cells is relaxed.
The main approaches to realizing 2J tandems in Si have been through III–V, II–VI, and perovskite top cells. The highest efficiencies have been reported by several groups for III–V cells bonded onto Si in a 4T configuration, with over 32% reported for 2J cells and 35.9% for 3J by EPFL/NREL [33]. However, the 4T approach generally requires a full III–V cell to be fabricated separately and bonded onto a Si substrate, which is most likely not cost competitive in terms of current Si technology. II–VI materials are still in development for Si tandems, with basically only material growth demonstrations at present. The current highest efficiency in a monolithically grown series connected Si-based tandem is using a wider bandgap perovskite cell as the top cell [34]. The low temperature processing of the perovskite top cell is very compatible with integration with an already fabricated Si bottom cell. 2T perovskites on Si cells have recently exceeded 29% [35], the highest 2J performance reported to date for an integrated structure, as shown in Fig. 19.22 by the purple triangles. However, there remain many open questions about long-term stability of perovskites for solar applications, particularly with new higher bandgap materials.
From a stability, efficiency, and cost perspective, the direct growth of III–Vs on Si appears the most promising, with recent advances in the approaches and efficiencies of tandem structures. The key barrier to III–V/silicon solar cell is the lattice mismatch between silicon and most III–V materials. The importance and impact of III–V/Si integration means that many different approaches have been tried to overcome the lattice mismatch between Si and III–Vs. These include insertion of a layer that accommodates the strain [36, 37]; decoupling the III–V material from the Si substrate by limiting the direct contact between the two via techniques such as epitaxial lateral overgrowth [38,39,40] or nanostructures [41]; joining the III–V and Si by mechanical means such as bonding [42]; lattice-matched materials [43,44,45,46,47]; compositionally graded, metamorphic buffer layers; and the development of defect-tolerant materials [48].
GaP is the closest III–V material in terms of lattice constant for monolithic integration on Si; hence most approaches incorporate GaP, either for direct growth or as a grading layer for growth of other III–V materials. Grassman and coworkers have demonstrated 21.8% in a 2T tandem on Si using a GaP buffer and GaPAs grading layer to grow a GaAs top cell on Si [49, 50]. The University of Illinois and Arizona State University have collaborated on a graded junction cell on a GaP buffer, using graded GaAsP to grow a GaAsP top cell demonstrating 20% efficiency [51, 52]. Fraunhofer ISE has also used graded GaAsP growth to demonstrate a triple junction cell with GaAs/GaInP top cells on Si exceeding 22% [53, 54]. Grading Si using a SiGe-based buffer as a template for further III–V devices has reached 20.6% [55]. An alternative option is to capitalize on defect and materials advances to develop a dilute nitride top solar cell [56]. Dilute nitrides are conventional III–V materials in which the introduction of a small amount of substitutional N (on the order of 1 to 2%) can lead to large changes in the bandgap and lattice constant, allowing for tunable materials to satisfy lattice and bandgap requirements in tandem cell applications. Dilute nitride-phosphides such as GaNPAs and GaInNP have been investigated for optoelectronic devices, including Si-integrated lasers and solar cells [57].
7 Nanotechnology-Based Approaches
Besides multijunction approaches, realization of many of the approaches listed for circumventing the Shockley-Queisser limit is difficult to realize in bulk semiconductor materials. For that reason, nanostructured materials have been an area of active investigation for so-called advanced concept or third-generation [2] photovoltaics. The advantages of nanostructured materials are in the ability to tune bandgaps through quantum confinement and surface effects, as well as modify the chemical and reactive properties of materials relative to their bulk forms. From the standpoint of optical properties, absorption is generally enhanced, and nanophotonic structures may be used to manage light in terms of light trapping and reflection losses. As discussed in connection with hot carrier solar cells, nanostructured materials may also have reduced energy loss rates, which help in terms of phenomena such as hot carrier extraction and carrier multiplication through impact ionization. The main detrimental effects are the increased surface to volume ratio, which may lead to increased recombination affecting both the short circuit current and the open circuit voltage as discussed in Sect. 19.3.1.
7.1 Nanomaterials
Nanostructure materials can be fabricated from the top down using nanoscale lithography such as deep UV, electron and ion-beam lithography, as well as direct manipulation of atoms on the surface using atomic force microscopy (AFM). At the same time, self-assembly of materials allows the growth from the bottom up of a variety of structures with atomic perfection. Some of the more interesting materials are summarized in the following. For an extensive review on the subject, see Chap. 2 of reference [58].
Layered Structures and 2D Materials:
Already in the 1980s, epitaxial growth was exploited to realize nanostructure materials in one direction, the growth direction. The advent of molecular beam epitaxy (MBE) [59] and metal organic chemical vapor deposition (MOCVD) allowed atomic layer control of the growth of high-quality, lattice-matched heterojunctions. A quantum well (QW) corresponds to a layered structure of a narrow bandgap material sandwiched between two larger bandgap materials, which, as discussed in Sect. 19.3.4, can be type I or type II depending whether confinement exists for both electrons and holes (type I) or for just one (type II). A multi-quantum well (MQW) system is just a succession of QWs grown with sufficiently thick barrier material such that they are essentially isolated. If the barriers are sufficiently thin, then broadening of the QW states occurs and a superlattice (SL) is formed, with mini-bands. In all such materials, electronic confinement is only in one directly, and the motion in the plane is quasi-two-dimensional (2D), with a two-dimensional density of states.
In more recent years, true 2D materials have been synthesized and extensively characterized, beginning with work on graphene [60, 61], a 2D form of graphitic C, which forms a hexagonal honeycomb structure, and can be synthesized by exfoliation from graphite, chemical vapor deposition, as well vacuum graphitization of SiC. The electronic structure has a unique linear dispersion with no gap, where the conduction and valence bands meet at the so-called Dirac points, the discovery of which was awarded the 2010 Nobel Prize in physics. More recently, of 2D materials have been synthesized from transition metal dichalcogenide (TMD) monolayers, which are generally 2D semiconductors with bandgaps from 1 to 2 eV of the form MX2, where X is a chalcogen atom and X is a transition metal [62]. Different 2D materials can be grown in layered structures called van der Waals heterostructures, which as the name suggests are bonded weakly in the vertical direction to form the equivalent of MQW and SL structures with unique optical and transport properties [63]. Because of their tunable bandgaps in the optimal range for solar energy conversion, there have been a number of demonstrations of photovoltaic effects, and proposals for energy converters based on such materials.
Nanowires and Nanotubes:
These components are quasi-one-dimensional (1D) materials that are usually self-assembled, although they can be fabricated by top-down lithography as well. Carbon nanotubes (CNTs) are the most common nanotube structure, which are basically a rolled form of graphene, whose chirality (related to the direction along which the graphene sheet is rolled) determines whether they are metallic or semiconducting. Semiconductor nanowires (NWs) are solid crystalline, which may be grown using vapor-phase synthesis, in which nanowires self-assemble on from the gas phase onto a semiconductor substrate with a given crystallographic orientation. Vapor-liquid-solid (VLS) epitaxy is the most common method of growth, in which metallic nanoparticles act as catalysts to nucleate the self-assembled growth of NWs, with the diameter of the NW directly related to the droplet size [64]. Fig. 19.27 shows a micrograph of Si NWs grown by the VLS method, where chemical vapor deposition (CVD) was used to generate the semiconductor precursors for VLS growth. The figure below also illustrates that the NWs may be deterministically placed using nanolithography techniques to pattern the catalyst.
Self-assembled growth of NWs using vapor-liquid-solid (VLS) epitaxy. (a) Scanning electron micrograph of Au seeds patterned with electron beam lithography. (b) Ge nanowires after growth on Si (111) [71]
Other methods may also be used for NW growth, however, including laser ablation and MBE. Growth of high-quality nanowires has been demonstrated in III–V (GaN, GaAs, GaP, InP, InAs) and II–VI (ZnS, ZnSe, CdS, CdSe) semiconductor NWs, as well as several different wide bandgap oxides (ZnO, MgO, SiO2, CdO). Samuelsson and coworkers at Lund University have fabricated a variety of nanoscale electronic devices utilizing VLS-grown III–V semiconductor NWs as their active elements [65]. They have demonstrated that heterostructure nanowires of InAs and InP, as well as GaAs and InAs, can be realized that have very sharp heterointerfaces [66], both vertically and laterally (core-shell NWs, similar to core-shell nanoparticles; Fig. 19.28). Such heterostructure NWs have been used to fabricate nanoscale devices such as resonant tunneling diodes [67] and single [68] and multiply coupled [69, 70] quantum dots.
(a) schematic of a core-shell nanoparticle (Wikimedia Commons). (b) micrograph of self-assembled InAs nanoparticles on a GaAs substrate [74]
As discussed in more detail below, NWs can be used directly as the active absorber in solar cells (Sect. 19.7.4) and in terms of optical light management to increase absorption (Sect. 19.7.3).
Nanoparticles, Nanocrystals, and Quantum Dots:
The names nanoparticles (NPs), nanocrystals (NCs), and quantum dots (QDs) are sometimes used interchangeably to denote either lithographically defined or self-assembled structures with characteristic dimensions on the order of 1–100 nm. If the NPs are single crystal structures, they are referred to as nanocrystals [72]. Nanoparticles can be metals, dielectrics, or semiconductors and are synthesized by a variety of techniques. Some mass-produced approaches include ball mill micro-machining, as well as pyrolysis and rf plasma techniques. High-quality NCs are synthesized through chemical solution methods, including sol-gel methods which result in colloidal solutions of nanoparticles. Self-assembled QDs of common III–V semiconductor materials (InAs, InGaAs, etc.) can form during epitaxial growth via the three-dimensional Stranski-Krastanov growth mode [73]. In this mode of growth, a thin layer of InAs is grown on top of a substrate of different lattice constant such as GaAs, where strain results in islanding of the epitaxial layer into 3D QDs, as shown by the micrograph in Fig. 19.28. Similar to NWs, QDs may become active components for realizing advanced concept solar cells discussed in the following sections as well as optical layers for light management beyond the texturing and antireflection coating approaches discussed in Sect. 19.3.2.
7.2 Dye-Sensitized and Quantum Dot Solar Cells
One of the first solar cell architectures that directly incorporated nanostructured materials as an active part of the absorber was the dye-sensitized solar cell (DSSC, or sometimes referred to as a Grätzel cell), which resembles an electrochemical cell in design. The DSSC was first demonstrated by O’Regan and Grätzel in 1991 [75] and, as shown by the open red circles of Fig. 19.22, has reached efficiencies of over 11% with the conventional dye approach shown in Fig. 19.29. Conventional DSSCs have since been superceded by perovskite solar cells as discussed in Sect. 19.4.3, where the first high efficiency perovskite solar cells evolved from the DSSC architecture, and the highest efficiency perovskite cells still incorporate a nanostructured DSSC-like structure, albeit with the electrolyte replaced with a solid hole transport layer that is much more compatible with traditional thin film fabrication techniques.
The schematic of a conventional DSSC architecture is shown in Fig. 19.29. The absorber layer consists of nanoparticle or nanostructured TiO2, which is a wide bandgap semiconductor with a bandgap of approximately 3.2 eV, coated with a dye such as ruthenium (Ru), whose HOMO-LUMO splitting is in the optimum range for the solar spectrum. The dye is usually spun on in liquid form to diffuse into and adhere to the TiO2 nanostructure and is subsequently dried. The large surface to volume ratio of the nanostructured TiO2 leads to an effectively large surface area, increasing light absorption. The whole structure is formed on a glass substrate as shown, coated with a TCO such as ITO or fluorine-doped tin oxide (FTO). When light is incident on the glass/TCO side, it is absorbed by the dye, and the excited e− transfers from the excited LUMO level to the conduction band of the TiO2 as shown. The electron diffuses through the TiO2 matrix to the TCO and the external circuit. The positively charged hole left in the HOMO level reacts via a redox couple in the electrolyte, which is typically iodine based, consisting of I− and \( {I}_3^{-} \) ions in solution. The dye is reduced by an electron being transferred to the dye through an oxidation process in the iodine, \( 3{I}^{-}=2{e}^{-}+{I}_3^{-} \), where two holes in the dye are neutralized by converting three iodine ions into one \( {I}_3^{-} \) singly charged molecule, giving up two electrons to the dye. At cathode, the positively charged ionic species, \( {I}_3^{-}, \)is reduced and converted back to 3I− by the transfer of two electrons from the cathode, completing the circuit.
DSSCs have enjoyed some commercial success, particularly in niche applications such as building integrated PV, where different dyes corresponding to different colors provide some aesthetic benefits. Liquid electrolyte DSSCs suffer from stability issues as well as the complications of a panel structure involving liquid encapsulation. There are a variety of dyes, both natural and synthetic, that are suitable for DSSC applications; however, they typically have a relatively narrow spectral absorption, which has led to the search for new dye materials such as inorganic NP-based dyes with broad absorption. Another problem arises due to recombination process occurring at the dye-TiO2 interface, which lowers Voc.
As discussed earlier in Sect. 19.4.3, a dramatic evolution of the DSSCs occurred with the development of the hybrid perovskite CH3NH3PbI3 replacing traditional dyes, which could be introduced into the nanoporous TiO2 matrix through low temperature processing. The liquid electrolyte was later replaced by a solid organic hole transport layer, which eliminated the issue mentioned above related to liquid-based cells, and a cell geometry more resembling that of a conventional thin film organic solar cell. More recently, the Cambridge group demonstrated that a planar hybrid perovskite thin film replacing the nanostructured TiO2 could reach high efficiencies as well [22], which has increasingly become the dominant architecture, especially for tandem perovskite structures, although the mesoscopic approach continues to be investigated for high performance cells [76].
Quantum dot solar cells (QDSCs) have been of interest since the beginnings of the nanotechnology field [77]. As discussed in Sect. 19.8, QDSCs have many potential advantages in realizing advanced concept architectures in terms of multiexciton generation, hot carrier extraction, intermediate bands, and up-down conversion [78]. Like other nanomaterials, quantum confinement and surface effects allow tunable bandgaps for synthesizing ideal absorbers for single gap and multi-gap (tandem) cell applications. While MBE-grown QDs as described earlier have been used as absorbers in advanced concept architectures described later, colloidal quantum dots (CQDs) have been successful in realizing efficiency advances as shown in Fig. 19.22 by the open red diamonds.
There are several ways of incorporating CQDs into solar cell architectures. One is replacing the organic dyes in the DSSC structure above with semiconducting QDs such as InP, CdSe, CdS, and PbS [78]. More commonly, they are dispersed in an electron or hole conducting polymer forming, or in a ligand network ink, forming an organic solar cell architecture as discussed in Sect. 19.4.3. With the latter approach, the Toronto group in collaboration with KAUST demonstrated an 11.6% efficient PbS CQD-based device [79]. More recently, QDSCs based on inorganic perovskite CQDs (CsPbI3) [80] (NREL) and hybrid perovskite CQDs of FAPbI3 (where FA is formamidinium) (University of Queensland) [81] reached efficiencies of 13.4% and 16.6%, respectively. Of particular note is that the stability of these CQD-based perovskite materials appears superior to the bulk hybrid perovskites discussed earlier. While these recent perovskite-based QDSC results are quite promising, there are still many obstacles to overcome in terms of cost and stability which are active areas of research presently [82].
7.3 Light Management in Photovoltaics
As discussed in Sects. 19.2.2 and 19.3.2, maximizing solar light absorption in the semiconductor is critical in obtaining good short circuit current, which generally means getting photons into the semiconductor (no reflection from the front), and absorbing the photons before they can escape from the back or front of the cell. The necessary path length for absorption is directly related to the inverse of the absorption coefficient, α(hυ), which is a strong function of wavelength, being small for photons just at the bandgap, and increasing strongly for shorter wavelengths. In terms of the path length, the fraction, f, of photons absorbed is given by
where R is the reflection coefficient from the front surface and l is average path length of photons in the absorber. Clearly one wants to minimize reflectance, while at the same time increasing the path length or correspondingly the absorption coefficient, which are the main objectives of light management.
Figure 19.30 illustrates the classical “ray optics” trajectory of light incident on a generic absorber, which has a textured surface which refracts light away from normal incidence, and a back-side reflector, which is in general textured as well to randomize the direction of the light. Due to internal reflection considerations, on the front surface, the ray is reflected and executes a number of bounces between the front and back surface before eventually exiting the front surface again at a small angle relative to the normal. For an absorber of width W, if there was no texturing on the front, and no reflection from the back, the path length is simply l = W. Adding an ideal back reflecting and assuming zero reflection when incident on the front surface leads to l = 2 W.
Illustration of the classical path of light in a general semiconductor absorber structure including texturing of the front, the back, and a back reflector. (With permission from PVEducation.org)
Yablonovitch [8] used statistical arguments assuming ideal diffusive scattering from the front and back surfaces and classical ray optics, to derive the so-called classical light trapping limit for the enhancement of the path length in an absorber such as in Fig. 19.30
where ns is the index of refraction of the absorber. Taking Si as an example, with ns ≈ 3.8 for long wavelengths, a maximum path length enhancement of 58 is predicted. The implication is that one could reduce the thickness of the Si wafer from a typical value close to 200 μm to just a few microns, which would lead to substantial savings in terms of material costs (if one could process such thin Si), and actually lead to a boost in the cell voltage somewhat analogous to the effect of concentration.
Nanostructured materials offer the potential to go beyond the classical light trapping limit given by Eq. (19.51) [83], with characteristic dimensions corresponding to the regime of diffraction-limited optics. In recent years, there has been considerable interest in periodic arrays of optical scatterers forming photonic bandgap materials [84, 85], which are analogues to the band structure in semiconductor materials, in which gaps are opened up in the spectrum due to Bragg scattering. Such modification of the optical dispersion leads to passbands and stopbands for the propagation of electromagnetic radiation at certain frequencies. Such arrays can then be used to reflect or selectively enhance absorption, allowing the classical light trapping limit to be superceded, at least for certain bands of frequencies.
A common way to realize photonic bandgap structures is to grow or fabricate periodic arrays of NWs or nanopillars, as shown on the left side of Fig. 19.31. There, particular nanopillars were fabricated top-down using nanosphere lithography, in which silica nanoparticles are deposited on the surface of Si in a close packed hexagonal structure, followed by reactive ion etching through the nanospheres to form a periodic array [86]. The right side of Fig. 19.31 shows the measured reflectance (dashed curves), comparing the reflectance from different height nanopillars compared to bare Si. The solid curves correspond to full-wave finite difference time domain (FDTD) solutions of Maxwell’s equations, where the ratio of the incident to reflected waves determines the reflectance. As can be seen, the nanopillars significantly decrease the reflectance due to light trapping, and that this reflectance is well described by the full-wave electromagnetic solutions to Maxwell’s equations (as opposed to ray optics). The sharp features in the numerical simulations are due to the sharp features assumed in simulation, whereas experimentally, the nanopillars are somewhat tapered and the edges at the top and bottom are smoothed out. Atwater’s group studied different NW arrays including both periodic and randomly spaced arrays and showed that the absorption properties of the arrays were evidence exceeding the classical light trapping limit over a limited band of optical frequencies [87].
(a) Micrograph of nanopillars fabricated using nanosphere lithography. (b) Measured (dashed) and simulated reflectance from a regular hexagonal array of Si nanopillars with period, p = 600 nm, for cylinder heights of a 100 (red) and 200 nm (blue) [86]
Besides photonic bandgap structures, nanoplasmonic structures are also of interest in terms of enhanced light trapping. Plasmonic structures may correspond to metals adjacent to a dielectric, metal strips, and finally metallic nanoparticles on a surface or interface. Metal nanoparticles are similar to the semiconductor ones discussed in the Sect. 19.7.1 in terms of synthesis, where typically Au or Ag are used due to their low loss. Strong interaction between the incident electromagnetic waves and the collective charge oscillations of the metal structures results in the formation of hybrid surface plasmon polariton (SPP) modes. Such coupling is strongest close to the plasma frequency of the metal, and the SPP modes strongly favor propagation along the surface, which increases the effective path length manyfold, hence increasing absorption. Plasmonic structures may be incorporated at the front or back surface as well as within the absorber itself, and have been investigated in Si, III–V, and organic solar cells, where in particular they are used to try and improve the red response of cells, where absorption is usually weakest. For Si solar cells, for example, path length enhancements of seven to eight times were reported in Si cells [88], while plasmonic nanoparticle arrays of Au NPs on GaAs cells showed increase in short circuit current of 8% [89].
7.4 Nanowire Solar Cells
As discussed in the previous section, NW arrays have demonstrated good light management properties in terms of photonic bandgap properties, with the potential to exceed the classical light trapping limit. Semiconductor NWs may also act as the active optical absorber in photovoltaic applications, in which the effective absorption per volume of material is greatly enhanced compared to the bulk due to the nanophotonic enhancements in array structures. NWs also have the advantage of having good quasi-1D transport properties along the axis of the NW, allowing for separation and collection of photoexcited EHPs. III–V NWs are routinely grown on Si substrates, allowing for the possibility of Si-based tandems discussed in Sect. 19.6. In terms of lattice matching constraints and critical thickness limitations in epitaxially grown layered structures, the finite lateral extent of NWs allows the strain to be accommodated in the lateral direction, allowing much more flexibility in the heterogeneous growth of different lattice constant materials. The ability to grow both vertical and lateral (core-shell) structures allows for the design of material systems to be used to realize advanced concept photovoltaics that cannot be realized with bulk materials. The main disadvantage of NWs (and all nanostructured systems) is that the large surface to volume ratio means that surface recombination effects are enhanced, which is detrimental to solar cell performance as discussed in Sect. 19.3. Surface passivation strategies are therefore critical. In the case of NWs, an effective strategy is growth of a core-shell structure with a large bandgap material as the outer layer, which reduces recombination [90].
There have been a number of studies of optoelectronic devices based on NWs including solar cells, starting in the mid-2000s [91,92,93,94]. The best performance in NW solar cells has been demonstrated in III–V compound semiconductors like GaAs, due to the high absorption associated with a direct bandgap material, and good transport properties. As mentioned above, one of the advantages of NW-based systems is that III–V materials may be grown on Si substrates, providing another approach for Si-based tandem solar cells. A schematic of an InGaAs NW array solar cell architecture is shown in the upper panel of Fig. 19.32. The NWs are core-shell structures, with InGaAs cores, and InP cladding layers, grown on Si (111) substrates. The (111) orientation is usually necessary to grow vertical NWs. This radial core-shell design has been used by the Technical University of Munich group for optoelectronic applications such as NW light-emitting diodes (LEDs) and lasers. [95]. As shown in the bottom panel of Fig. 19.32, regular arrays of NWs with well-defined periodicity are grown using nanolithographic techniques, in this case nanoimprint lithography, which is a low-cost method for nanofabrication. The main difficulty in such NW solar cell approaches is in making both p and n contacts. While the Si substrate serves as one contact, the top must be contacted separately as shown, which must be isolated from the substrate to avoid leakage.
(a) InGaAs core-shell nanowire solar cell structure. (b) SEM picture of arrays of NWs defined by nanoimprint lithography [96]
Besides Si-based tandem solar cells, there is considerable interest in Si-based optoelectronics, integrating III–V-based photonic circuits with Si microelectronics. Chuang et al. [97] demonstrated the first NW GaAs LED and GaAs NW avalanche photodetectors (APD) grown on Si substrates using relatively low temperature processes compatible with CMOS technology. They later demonstrated the first InGaAs/GaAs core-shell NW laser grown on silicon [98].
For NW solar cells, one may either use lateral core-shell junctions or vertical junctions grown vertically along the axis of the NW. Colombo et al. reported a single GaAs core-shell NW p-i-n solar cell [99, 100] with an efficiency of 4.5% and a Voc for GaAs cells of almost 1 V, which is comparable to that of high performance GaAs bulk solar cells. Radial GaAs junction arrays were reported by Mariani et al. [101] with efficiencies of 2.54%. In the past 5 years, remarkable improvement in the performance of NW solar cells has been reported. Axial InP p-i-n junction arrays were reported by Borgström et al. [102] with 13.8% efficiency in 2013. Sol Voltaics and Lund University reported GaAs VLS-grown nanowire solar cells with independently tested efficiencies of 15.3% in 2016 [103]. In the same year, Eindhoven University reported a 17.8% InP vertical junction nanowire solar cell formed by etching and passivation [104]. The improvement in NW solar cell technology has occurred quite rapidly, from a few percent in 2009 to over 17% in 2017, similar to that of perovskite solar cells, although not represented on the NREL efficiency charts.
8 Advanced Concept Photovoltaics
Advanced concept is a term sometimes used to describe novel approaches to exceeding the Shockley-Queisser (QS) limit beyond the demonstrated approach of multijunction solar cells, based on circumventing the implicit assumptions in QS discussed in Sect. 19.5.2. Below we briefly review three such concepts, intermediate band, multiexciton generation, and hot carrier devices. There are also other approaches not discussed here, including up-down conversion using phosphors and nanoparticles to narrow the effective spectrum, as well as hybrid photovoltaic-thermal approaches, such as thermophotovoltaics, or spectral splitting approaches to use both photovoltaics and concentrating solar thermal for electrical energy production. Green’s book on third-generation photovoltaics provides an excellent overview of these various approaches [2].
8.1 Intermediate Bands
Finally, rather than fabricating multiple junctions, another proposed approach to circumvent the SQ single bandgap assumption is to introduce multiple energy levels within the same material. Luque and Martı [105, 106] first proposed the concept of an intermediate band(IB) solar cell, although the same basic concepts were already investigated earlier in connection with MQW solar cells [77, 107, 108]. It consists of an intermediate band between the conduction and valence band of a bulk-like material. The most widely investigated approach is illustrated in Fig. 19.33, where the intermediate band arises from the introduction of either quantum wells or quantum dots into a wider bandgap material. Quantum wells have quantized levels as shown, which broaden in a MWQ or SL structure. However, there remains a continuum of states in the directions parallel to the growth direction, which is a disadvantage in realizing a separate intermediate band. Quantum dots on the other hand have true discrete density of states, which broaden into an intermediate band when grown as a SL. Besides IB QW and QD structures, bulk IB materials may be synthesized, for example, in alloy structures [109], where a narrow band exists between the conduction and valence bands.
Illustration of an intermediate band solar cell architecture based on quantum dot (or quantum wells) levels introduced within a wider bandgap host semiconductor [110]
Figure 19.33 illustrates the processes and energy separations in the IB concept. Here Ec and Ev represent the CB and VB edges of the higher bandgap material with bandgap EG. The center of the IB is an energy EIV above the VB, and EIC below the CB. As shown, the IB allows sub-bandgap photons to be absorbed, promoting electrons from the VB to the IB and promoting electrons in the IB to the CB. The third process is the direct band to band absorption from VB to CB. In order for the IB concept to provide an efficiency increase of the SQ limit, there must be a separate quasi-Fermi energy associated with the IB band which is separate from that of holes in the VB and electrons in the CB. For example, if the Fermi level of the IB is above the IB and close to the CB (the usual case under strong photoexcitation), then the IB states are all filled, and not transitions can occur to the IB. Hence, ideally, it should be half occupied. Likewise, if the IB and CB quasi-Fermi energies are common, then cell will be effectively a cell with a bandgap EIV, with a drop in Voc. Thus, having multiple quasi-Fermi energies is a necessary for efficiency operation.
Detailed balance may again be used to calculate the maximum conversion efficiency as a function of EG and EIC (EIV being simply EG-EIC in this three-level approach). For any particular value of EIC, there exists an optimum EG for maximum efficiency. Luque and Martí used detailed balance to calculate the maximum efficiency versus EIC, where the optimum combination corresponds to EG = 1.95 eV and EIC = 0.71 eV, corresponding to an efficiency of greater than 60% under concentration, clearly well above the SQ single gap limit.
There have been a number of experimental reports that demonstrate the presence of the three individual processes, in a number of different technologies including solar cells, quantum dot lasers, and quantum cascade lasers [111,112,113,114,115]. However, demonstration of independent quasi-Fermi energies necessary for IB cell performance is difficult. Marti et al. have demonstrated the ability to collect carriers at high energy using two low-energy photons [116], which is a necessary process for IB operation. In addition, early results from Nelson et al. in QW solar cells are explained [117] by a different Fermi level inside a QW than in the barrier. Thus there is the suggestion that multiple quasi-Fermi levels can exist in multilevel structures, although the demonstration of a high performance IB cell that convincingly exceeds the SQ limit effect remains elusive.
An extensive review of the state of the art of IB solar cell technology is given by Okada et al. [118], which the interested reader is referred to for more detail. A well-studied system is that of self-assembled multiple layers of InGaAs QDs grown on GaAs as discussed in Sect. 19.7.1 via Stranski-Krastanov strained growth mode. Although the combination of bandgaps and intermediate-level energies is nonideal from the detailed balance calculations mentioned above, single crystal defect-free structures may be grown, where the QDs tend to self-align during between subsequent layers, so that large numbers (10s of layers) may be grown. The main challenge in realizing a viable IB solar cell technology is demonstrating a significant increase in short circuit current due to the sub-bandgap absorption of photons while not degrading the open circuit voltage, which has been hard to simultaneously achieve if the occupancy of the IB level is tied to that of the CB. While this has been demonstrated to some extent in GaAs cells, typically the baseline GaAs cells for comparison have inferior Voc (0.7–0.9 V) compared to the voltages of record GaAs cells which exceed 1.1 V [119]. Various schemes have been introduced such as doping the QDs, strain compensation, and other approaches, to both improve the optical efficiency and minimize recombination. For example, Bailey et al. have demonstrated GaAs-based IB cells with voltages over 1.0 V [114], with improvement in the short circuit current, although the efficiency was still less than the baseline cell.
8.2 Multiple Exciton Generation (MEG)
An energetic electron or hole in a semiconductor with a kinetic energy greater than the bandgap may lose its kinetic energy creating one or more EHPs depending on the energy. This process is generally called impact ionization, since promoting an electron from the VB to CB is equivalent to bond breaking. This may occur through acceleration of a charge carrier to the threshold energy for this process under high electric fields, or it may occur for photoexcited electrons whose excess energies are high enough to create a second EHP. Figure 19.34 illustrates the creation of multiple electron-hole pairs for different photon energies, assuming that electrons near the top of the VB are excited into the CB with an excess energy equal to the difference of the photon energy and the bandgap. As shown, there are different thresholds reached in energy when the photon energy in this picture is hν = 2Eg, 3Eg, 4Eg, etc., resulting in 2 EHPs, 3 EHPs, etc. When present in a solar cell, the quantum efficiency can now be greater than 100%, breaking the assumption of 1 EHP per photon, increasing the photocurrent, and allowing the SQ limit to be overcome.
Creation of multiple electron-hole pairs by energetic photons was already known for Ge in the 1960s. Kolodinski et al. measured the quantum efficiency in bulk silicon solar cells as a function of photon energy, where they showed greater than 100% QE occurring above 3 eV [26]. Such a high photon energy is beyond the useful range for the solar spectrum, due to the fact that the threshold for impact ionization in bulk crystals must simultaneously satisfy both energy and crystal momentum conservation, which shifts the threshold up by a factor of 1.5 using simple effective mass considerations with parabolic bands.
On the other hand, due to quantum confinement in nanomaterials, conservation of crystal momentum is relaxed, in particular for QDs. Experimentally using ultrafast absorption and other spectroscopies, threshold energies for carrier multiplication were found to be close to twice the fundamental gap in PbSe and PbS CQDs with quantum efficiencies in excess of 300% [120, 121]. The optically excited states of QDs are strongly excitonic in nature due to the strong confinement, hence the term multiple exciton generation, or MEG for short. Experiment [122] and theoretical calculations [123] suggest that MEG occurs over very short time scales and may be regarded as a coherent effect, rather than as two successive scattering processes, although there is still not agreement on this interpretation. MEG has now been demonstrated in a variety of nanomaterials, including CQDs of PbSe, PbS, InAs [124], PbTe [125], Si [126], and CdSe [127].
The effect of MEG on the detailed balance efficiency is easily incorporated into Eq. (19.46) [128]. The incident photon flux includes both the direct and diffused terms, which in the SQ analysis is equated to the photocurrent assuming 1 EHP per photon, which in the presence of MEG is weighted inside the energy integrals of the first two terms by the quantum yield (QY) as a function of photon energy, Q(E), which is the number of EHPs produced per incident photon. For the ideal case, carrier multiplication is assumed to jump abruptly with each multiple of the threshold exceeding, represented mathematically by the staircase function
where Θ is the unit step function, m is the number of electron-hole pairs generated per photon, Eg is the threshold energy (ideally the bandgap energy), and M is the maximum number of EHPs per incident photon. Additionally, it is usual to weight the voltage term, qV, by Q(E) in the third integration to account for the inverse process to MEG (Auger recombination in the bulk), i.e., multi-electron recombination [2]. Assuming the blackbody spectrum form with a unity concentration factor in Eq. (19.46), the calculated detailed balance efficiency versus bandgap with different values of M in Eq. (19.52) is shown in Fig. 19.35. The result using the AM1.5 spectrum gives a similar and somewhat higher efficiency but less smooth as was the case in Fig. 19.24 due to spectral features.
The case of M = 1 is just the SQ limit for the blackbody spectrum. Already for M = 2, there is a sizable increase in maximum efficiency, which approaches 44% for the limit of M going to infinity. The optimum bandgap decreases with increasing multiplication factor M, as shown, going from 0.76 eV for large values to 1.05 for M = 2 [129], very close to that of Si.
The ideal quantum efficiency given in Eq. (19.52) is never in practice observed, as in experimental data shown in Fig. 19.36. The idea case assumes the existence of multiple separate, noninteracting MEG processes for excitation of 2 EHPs, 3 EHPs, etc. Also, the assumption that all excess energy of the photon is given to electrons in the CB is only true near the band edge for a high ratio of hole to electron effective masses. In the realistic case of photon energies exceeding twice the bandgap, the density of states of holes and electrons coupled by a high-energy photon is roughly equal, leading to a smearing out of the threshold energy for the onset of MEG.
Measured quantum yield versus photon energy (normalized by the bandgap) for bulk Si and two different diameters of nanoparticles. (With permission from [127])
Ultrafast spectroscopy has been primarily used to measure MEG by monitoring the transient state filling on a picosecond time scale at the bottom of the conduction band for different pulse excitation energies, which provides a measure of the QY in terms of the number of EHPs produced per incident photon. Fig. 19.36 plots experimental QY data for Si NPs measured spectroscopically by NREL [126] in comparison to the experimental internal quantum efficiency data of bulk Si solar cells [130]. As mentioned earlier, the threshold for turn-on (QY > 100%) for bulk Si does not occur until relatively high energy due to energy and momentum conservation constraints, while for Si NPs, the turn-on is much closer to twice the bandgap (including quantum confinement and excitonic effects in NPs). The NP data shows more of a linear slope past threshold rather than an abrupt turn-on, characteristic of most experiments. As mentioned above, the slope is related to the partitioning of the excess energy between electrons and holes, as well as the efficiency of the multi-excitation effect relative to competing energy relaxation effects due to phonons and other processes. While most evidence for MEG comes from ultrafast optical measurements in NPs, recently the internal quantum efficiency of PbSe quantum dot solar cells was reported by the NREL group in which for short wavelength photons above the threshold for MEG, quantum efficiencies greater than 100% were measured [131], which is promising for realizing MEG effects in real devices.
Besides MEG in NPs, other nanostructures have exhibited carrier multiplication effects. Evidence for MEG in CNTs was reported by Gabor et al. in CNT photodiodes [132]. MEG in multiexciton in PbSe nanowire/nanorod structures was demonstrated by Cunningham et al. where the performance of PbSe nanorods was significantly improved compared to PbSe NPs in terms of both the QY threshold and the slope after threshold (steeper) [133]. MEG in NWs would have potential advantages in terms of the NW solar cells discussed in Sect. 19.7.4, as efficient carrier collection may occur along the axis wire for vertical structures or transverse in core-shell structures, in contrast to NP-based structures which require some extraction mechanism such as tunneling for carrier collection.
As mentioned earlier, the efficiency of the MEG process depends on a competition between carrier multiplication processes like impact ionization and inelastic energy loss mechanisms such as electron-phonon scattering, which relax the excess energy of the electrons and holes back to the band edges (thermalization). Such energy relaxation processes are also important for hot carrier solar cells, discussed in the next section. In semiconductors, electrons lose (or gain) energy through acoustic and optical phonon emission (absorption). Due to the relatively large energy associated with optical phonon emission, on the order of 20–50 meV per event, optical phonon energy loss usually dominates, particularly in polar III–V and II–VI materials where the Fröhlich interaction (polar optical scattering) for zone center optical phonons is strong.
Nanostructures such as in QWs, NWs, and NPs have been experimentally observed to have reduced energy relaxation rates by a number of researchers discussed in more detail in the next section, for example, by Pelouch et al. [134]. In reduced dimensionality nanostructures, energy relaxation requires intersubband scattering in order for electrons and holes to reach their lowest energy states in the CB and VB, respectively, i.e., scattering between the quantized states associated with the spatial confinement in one or more directions. Due to this requirement, the optical emission rate may be suppressed due to so-called “phonon bottleneck” effects, when the subband spacing is such that there is no final state to scatter to. In 2D materials like QWs, there is a continuum of states associated with the free transverse motion which usually provides a channel for scattering. However, in 1D (NWs) and 0D (NPs, QDs), such effects become more important due to the spike-like density of states (DOS).
The left panel of Fig. 19.37 shows the simulated energy versus time of a short time pulse of photoexcited electrons in bulk InGaAs compared with narrow core-shell InGaAs/InP nanowires of various core and shell thicknesses using full band ensemble Monte Carlo simulation, a particle-based technique for simulating nonequilibrium carrier dynamics [135]. As shown, the energy loss rate, here limited mainly by polar optical phonon scattering, is significantly slower in the nanowire structures compared to the bulk. Such results are consistent with slow energy relaxation observed in semiconductor NWs. Optical studies in InP NWs using transient Raleigh scattering [136] and steady-state photoluminescence [137] showed energy relaxation times of several hundred ps and high carrier temperatures under steady-state excitation.
(a) Full band Monte Carlo simulation of the average kinetic energy versus time for carriers excited in a short time pulse at an energy 2Eg above the CB edge (bulk) and lowest confined state (NWs) for different diameter NWs. (b) Simulated quantum yield (relative to the initial population) versus excitation energy for a 2 nm InGaAs NW and 1 nm InP cladding [135]
The right panel of Fig. 19.37 shows the simulated carrier multiplication versus photon energy based again on full band NW Monte Carlo simulation, including the calculated QY due to impact excitation rate in NW systems [135]. The blue curve corresponds to the simple assumption of all the excess photon energy going to the electrons, whereas the red curve is a more realistic calculation in which the dipole matrix element for direct band to band absorption is used to generate the electron and hole injected distributions, where the excess energy is more evenly split between the two systems. As can be seen, while the simple model leads to a more ideal (i.e., Eq. (19.52)) step-like QY, the full calculation of the optical absorption leads to a higher threshold and lower slope after threshold.
8.3 Hot Carrier Solar Cells
The final advanced solar cell concept discussed in this chapter is related to circumventing the SQ assumption that the carriers are collected at energies corresponding to the band edges, which are the main source of thermalization loss discussed in Sect. 19.5. The idea is to extract photoexcited carriers at energies well above the band edges before they lose energy to phonons as discussed in the previous section. Figure 19.38 illustrates the concept of a hot carrier solar cell proposed by Ross and Nozik in the 1980s [28]. The structure consists of an ideal absorber with a low energy loss rate for the photoexcited electrons and holes. Energy selective contacts extract electrons only on the left in a narrow energy window, and holes to the right as shown. Realization of such contacts is challenging; one of the main approaches is implementation of a resonant tunneling structure, such as a double barrier heterostructure, or tunneling through an artificial impurity such as a QD in a wide bandgap material [138]. The contacts themselves should be at temperature of the surround ambient as discussed by Würfel et al. [30], requiring that the absorber must be spatially separated from the cold metallic contacts; otherwise there will be strong energy loss mechanism due to cold contact electrons interacting with carriers in the absorber layer.
Hot carrier solar cell architecture consisting of an ideal absorber with energy selective contacts [110]
While the carriers in a hot carrier device ideally do not lose energy through phonon scattering processes, they do exchange energy among themselves through electron-electron, electron-hole, and hole-hole scattering. This can occur through two-particle scattering or scattering between charge carriers and collective excitations such as plasmons. Such scattering drives the distribution function of the carriers toward the equilibrium distribution represented by the Fermi-Dirac (FD) (or for nondegenerate carriers, Maxwell-Boltzmann, MB) distribution, however at an effective temperature, TH, much greater than the lattice temperature, TL.
Ensemble Monte Carlo (EMC) simulation has been used to simulate this nonequilibrium evolution of the carrier distribution [135], as shown in Fig. 19.39. The EMC simulations are for a quasi-2D system (10 nm GaAs/AlGaAs quantum well), which show the evolution of the electron distribution from a highly nonequilibrium distribution shortly after the pulse to a heated FD distribution. Scattering due to polar optical phonons, intervalley deformation potential, and carrier-carrier scattering (electron-electron, hole-hole, electron-hole) are included. Immediately after the optical pulse, the electron distribution is an athermal Gaussian-shaped distribution at the excess carrier energy. Even at these short times, an optical phonon sideband or replica is observed below the peak due to the effectiveness of polar optical phonon scattering. As time progresses, a series of phonon replicas appear showing that the initial cooling occurs through a cascade of optical phonon emission events. During this time, the distribution broadens due to electron-electron scattering, and eventually the phonon replicas vanish and are replaced by a what appears to be a heated FD/MB distribution, whose temperature continues to decrease with increasing time due to phonon emission.
EMC simulation of the time evolution of the electron distribution in the conduction band of a 10 nm GaAs quantum well at 10 K for carriers injected at 150 meV above the band edge, with an injected carrier density of 5 × 1011/cm2 [135]
Ross and Nozik considered the theoretical performance of hot carrier solar cells [28], based on the detailed balance approach discussed in Sect. 19.5. Within this approach, the electrical power delivered from the cell, Pout, may be written.
where Iph is the photocurrent corresponding to photons above the bandgap of the absorber, ΔμH is the quasi-Fermi-level splitting in the absorber, Ta and TH are the ambient and hot carrier temperature in the absorber (assuming a heated FD/MB distribution as discussed earlier), respectively, and εext is the separation of the selective energy contacts or, more precisely, the Fermi energy separation of the metal contacts to the electrons and holes. In the limit that the ambient and hot carrier temperatures are the same, this just reverts to the usual SQ model where the voltage out is the quasi-Fermi energy separation. For high carrier temperatures, the first term is small, and the output voltage is determined by εext, while the photocurrent corresponds to the gap of the absorber, which then favors small gaps. There is a limit on εext set by the total energy available in the solar spectrum, so that assuming no energy loss and small bandgaps, the theoretical detailed balance conversion efficiency approaches the maximum thermodynamic conversion efficiency of 85.4% [139]. Würfel and coworkers later considered the effect of impact ionization on the ultimate efficiency of this concept [140, 141].
For the hot carrier solar cell to exceed the SQ limit, it’s necessary that the energy loss rate in the absorber be very low such that a high carrier temperature may be maintained, as evidenced by Eq. (19.53). This is very challenging, since the energy rate due to optical phonons in the bulk and in quantum wells is subpicosecond. As seen in Fig. 19.39, even at very short times, polar optical phonon emission is already cooling the initial high energy distribution of carriers. As discussed in Sect. 19.8.2, the energy loss rate in NWs is reduced several times compared to bulk, although this rate is still too fast reaching high carrier temperatures under steady-state conditions. In QDs, the energy loss rate is further reduced, due to phonon bottleneck effects. As mentioned in the previous section, pump and probe as well as cw experiments in QWs have demonstrated greatly reduced cooling rates, and high carrier temperatures for high excited carrier densities, despite the fast polar optical phonon energy relaxation rate. Attempts have been made to utlize this in a hot carrier solar cell architectures, where researchers have demonstrated hot carrier transfer from quantum well absorbers to contacts [142], and photovoltaic conversion efficiencies above 10% [143].
One proposed explanation for strong hot carrier effects in nanostructure system is in terms of nonequilibrium optical phonons (hot phonons) [144, 145]. In nanostructures in contrast to bulk systems, the excitation of EHPs occurs in a small volume spatially, and hence energy relaxation and phonon emission also occur in the same small volume. In particular, optical phonons have a very small group velocity, essentially zero at the zone center, and so remain in the excitation volume until they decay into acoustic modes through anharmonic three and four phonon processes, which propagate away from the excitation volume at essentially the sound velocity of the crystal. The nonequilibrium population of optical phonons increases the probability of phonon absorption, it transfers the energy lost back into the electron-hole system, and the excess kinetic energy of the EHP is retained in the coupled charge carrier/optical phonon system, essentially until the hot phonons decay into acoustic modes.
Time-resolved Raman scattering has been used in the past to measure nonequilibrium phonon effects during ultrafast photoexcitation and to directly measure the anharmonic phonon decay time through the time dependence of the anti-Stokes line (which is proportional to Nq, the phonon population at the relevant phonon wave vector). Measurement has been reported for a variety of III–V compound bulk and quantum well materials [146,147,148,149], where typical anharmonic decay times are in the 1–10 ps time scale. The UNSW group has argued that nonequilibrium “hot” phonons may play a critical role in reducing carrier energy loss in hot carrier solar cells, allowing for high electron/hole temperatures in the absorber. Engineering materials as absorbers with long phonon decays (phononics), both in the bulk and in nanostructured structures, are currently being investigated [150, 151].
Ensemble Monte Carlo (EMC) simulation as described in Sect. 19.8.2 has been used to simulate ultrafast carrier dynamics and nonequilibrium phonons in quantum well materials [152, 153], where hot phonon effects have been shown to lead to substantial reduction in carrier cooling. Figure 19.40 shows the simulated effect of phonon lifetime on carrier relaxation using EMC simulation, similar to earlier work on this topic [135, 144, 154]. In these simulations, electrons are injected via a 200-fs-wide 2 eV laser pulse within a 10 nm GaAs/AlAs QW. The injected carrier density is 5 × 1011/cm2 in all cases and the lattice temperature is 5 K. In Fig. 19.40, the simulated carrier temperature versus function of time is plotted, assuming different anharmonic phonon decay times, ranging from 0 (i.e., no hot phonons) to 100 ps.
Without hot phonons, the electrons cool rapidly and decay to the lattice temperature within ∼5 ps. As the phonon lifetime is increased, the decay slows and starts to be governed by the anharmonic decay time rather than the electron-phonon emission rate. The effect is strongly density dependent, similar to experiment, since a higher injected density leads to a higher nonequilibrium phonon population, which increases the strength of the hot phonon effect. Hence, finding absorber materials with long phonon lifetimes is a possible approach to realizing hot carrier solar cell performance.
9 Summary
In this review chapter, we have discussed the state of the art with respect to photovoltaic device technology. We started with an overview of the fundamentals of solar cell device operation, and the nature of the solar energy spectrum and its absorption by the device. We then went into detail into the basics of solar cell operation, and what limits the main figures of merit, the open circuit voltage, short circuit current, and fill factor, where a particular emphasis was given on the role the minority carrier recombination plays. Methods of reducing such effects through passivation and carrier selective structures such as heterostructures were also introduced. We then provided an overview of the main technologies and their reported efficiencies starting with Si wafer-based technology and GaAs, then thin film technology, and organic solar cells, ending with recent developments of perovskite-based solar cells which are a hybrid of organic and inorganic cell architectures.
We then provided a synopsis of the limits of solar cell performance, and the use of detailed balance to derive the Shockley-Queisser limit for single junction cells. Methods of circumventing this single gap limit were discussed, which set the stage for discussing multijunction or tandem solar cells which currently hold the record for highest conversion efficiency in any solar technology, greater than 46%. We then discussed how nanotechnology may play a role in realizing other ways of circumventing the SQ limit in terms of advanced concept architectures. Nanotechnology is playing an increasing role in improving existing devices, as well as new device architectures seeking to improve efficiency while seeking lower cost. We discussed how, for example, nanostructures are playing an increasing role in improving light management in solar cells to improve light collection and allow thinner materials to be used reducing cost. Nanostructured materials play a central role in device architectures such as the dye-sensitized solar cell, which in turn became the basis for perovskite solar cells, which have rapidly overtaken thin film technology in terms of efficiency and approach that of crystalline Si solar cells. Nanowire solar cells have also shown tremendous improvement in recent years, with efficiencies over 15%. Research continues on realizing advanced concept solar cell structures such as multiexciton generation and hot carrier solar cells, and recent results show continued improvement in the design and architectures of such systems.
References
Honsberg, C. B., Bowden, S.: PVCDROM, https://www.pveducation.org/pvcdrom
Green, M.A.: Third Generation Photovoltaics: Advanced Solar Energy Conversion. Springer, Berlin (2003)
Hovel, H.J.: Semiconductor and Semimetals Vol. 11: Solar Cells. Academic Press, New York (1975)
Green, M.A.: Solar Cells: Operating Principles, Technology, and System Applications. Prentice-Hall, New Jersey (1986)
Wurfel, P.: The Physics of Solar Cells. Wiley, New York (2007)
Nelson, J.: The Physics of Solar Cells. Imperial College Press, London (2003)
https://www.pv-magazine.com/2019/01/17/perc-cell-efficiency-records-tumble/
Yablonovitch, E.: Statistical ray optics. J. Opt. Soc. Am. 72, 899–907 (1982)
Taguchi, M., Yano, A., Tohoda, S., Matsuyama, K., Nakamura, Y., Nishiwake, T., Fugita, K., Maruyama, E.: 24.7% record efficiency HIT solar cell on thin silicon wafer. IEEE J. Photovoltaics. 4(1), 96–99 (2014)
Yoshikaw, K., Kawasaki, H., Yoshida, W., Irie, T., Konishi, K., Nakano, K., Uto, T., Adachi, D., Kanematsu, M., Uzu, H., Yamamoto, K.: Silicon heterojunction solar cell with interdigitated back contacts for a photoconversion efficiency over 26%. Nat. Energy. 2, 1–8 (2017)
Richter, A., Benick, J., Feldmann, F., Fell, A., Hermle, M., Glunz, S. W.: n-Type Si solar cells with passivating electron contact: Identifying sources for efficiency limitations by wafer thickness and resistivity variation. Sol. Energy Mater. Solar Cells 173, 96–105 (2017)
Haase, F., Kiefer, F., Krugener, J., Brendel, R., Peibst, R.: IBC Solar cells with polycrystalline on oxide (POLO) Passivating contacts for both polarities. In Proceedings of the 26th International Photovoltaic Science and Engineering Conference (PVSEC-26), Singapore (2016)
“Photovoltaics Report” (PDF). Fraunhofer ISE. 12 July 2017
Yablonovitch, E., Miller, O. D., Kurtz, S. R.: The opto-electronic physics that broke the efficiency limit in solar cells. Proceedings of the 38th IEEE Photovoltaics Specialists Conference, 1556–1559 (2011)
Green, M.A., Dunlop, E.D., Hohl-Ebinger, J., Yoshita, M., Kopidakis, N., Hao, X.: Solar cell efficiency tables (version 56). Prog. Photovolt. Res. Appl. 28, 629–638 (2020)
Nakamura, M., Yamaguchi, K., Kimoto, Y., Yasaki, Y., Kato, T., Sugimoto, H.: Cd-free Cu (In,Ga)(Se,S)2 thin-film solar cell with a new world record efficacy of 23.35%. Proceedings of the 46th IEEE Photovoltaics Specialists Conference, Chicago, IL, (2019)
Dennler, G., Scharber, M.C., Brabec, C.J.: Polymer-fullerene bulk-heterojunction solar cells. Adv. Mat. 21, 1323–1338 (2009)
Timmreck, R., Meyer, T., Gilot, J., Seifert, H., Nueller, T., Furlan, A., Wienk, M.M., Wynands, D., Hohl-Ebinger, J., Warta, W., Janssen, R.A.J., Riede, M., Leo, K.: Characterization of tandem organic solar cells. Nat. Photonics. 9, 478–479 (2015)
Grätzel, M.: The light and shade of perovskite solar cells. Nat. Mater. 13, 838–842 (2014)
Kojima, A., Teshima, K., Shirai, Y., Miyasaka, T.: Organometal halide perovskites as visible-light sensitizers for photovoltaic cells. J. Am. Chem. Soc. 131, 6050–6051 (2009)
Kim, H.-S., Lee, C.-R., Im, J.-H., Lee, K.-B., Moehl, T., Marchioro, A., Moon, S.-J., Humphry-Baker, R., Yum, J.-H., Moser, J.E., Grätzel, M., Park, M.-G.: Lead iodide perovskite sensitized all-solid-state submicron thin film mesoscopic solar cell with efficiency exceeding 9%. Sci. Rep. 2(591), 1–7 (2012)
Liu, M., Johnston, M.B., Snaith, H.J.: Efficient planar heterojunction perovskite solar cells by vapour deposition. Nature. 501, 395–398 (2013)
de Vos, A.: Endoreversible Thermodynamics of Solar Energy Conversion. Oxford University Press, Oxford (1992)
Shockley, W., Queisser, H.J.: Detailed balance limit of efficiency of p-n junction solar cells. J. Appl. Phys. 32, 510–519 (1961)
Hirst, L.C., Ekins-Daukes, N.J.: Fundamental losses in solar cells. Prog. Photovolt. Res. Appl. 19, 286–293 (2010)
Kolodinski, S., Werner, J.H., Wittchen, T., Queisser, H.J.: Quantum efficiencies exceeding unity due to impact ionization in silicon solar cells. Appl. Phys. Lett. 63, 2405 (1993)
Schaller, R., Klimov, V.: High efficiency carrier multiplication in pbse nanocrystals: implications for solar energy conversion. Phys. Rev. Lett. 92, 186601 (2004)
Ross, R.T., Nozik, A.J.: Efficiency of hot-carrier solar energy converters. J. Appl. Phys. 53, 3813 (1982)
Würfel, P.: Solar energy conversion with hot electrons from impact ionization. Sol. Energy Mater. Sol. Cells. 46, 43 (1997)
Würfel, P., Brown, A.S., Humphrey, T.E., Green, M.A.: Particle conservation in the hot-carrier solar cell. Prog. Photovolt. Res. Appl. 13, 277 (2005)
Cotal, H., Fetzer, C., Boisvert, J., Kinsey, G., King, R., Hebert, P., Yoon, H., Karam, N.: III-V multijunction solar cells for concentrating photovoltaics. Energy Environ. Sci. 2, 174–192 (2009)
Geisz, J.F., Steiner, M.A., Jain, N., Schulte, K.L., France, R.M., McMahon, W.E., Perl, E.E., Fridman, D.J.: Building a six-junction inverted metamorphic concentrator solar cell. IEEE J. Photovoltaics. 8, 626–632 (2018)
Essig, S., Allebe, C., Remo, T., Geisz, J.F., Steiner, M.A., Horowitz, K., Barraud, L., Ward, J.S., Schnabel, M., Descoeudres, A., Young, D.L., Woodhouse, M., Despeisse, M., Ballif, C., Tamboli, A.: Raising the one-sun conversion efficiency of III-V solar cells to 32.8% for two junctions and 35.9% for three junctions. Nat. Energy. 2, 17144 (2017)
Bush, K.A., et al.: 23.6%-efficient monolithic perovskite/silicon tandem solar cells with improved stability. Nat. Energy. 2, 17009 (2017)
Hutchins, M.: Perovskite/silicon tandem solar cells approaching 30% efficiency in lab. PV Magazine. 21 (2020) https://pv-magazine-usa.com/2020/01/31/tandem-cells-approaching-30-efficiency/
Alaskar, Y., Arafin, S., Wickramaratne, D., Zurbuchen, M.A., He, L., McKay, J., Lin, Q., Goorsky, M.S., Lake, R.K., Wang, K.L.: Towards van der Waals epitaxial growth of GaAs on Si using a graphene buffer layer. Adv. Funct. Mater. 24, 6629–6638 (2014)
Yamaguchi, M.: Dislocation density reduction in heteroepitaxial III-V compound films on Si substrates for optical devices. J. Mater. Res. 6, 376–384 (1991)
Lourdudoss, S.: Heteroepitaxy and selective area heteroepitaxy for silicon photonics. Curr. Opinion Solid State Mater. Sci. 16, 91–99 (2012)
Mauk, M.G., Curran, J.P.: Electro-epitaxial lateral overgrowth of silicon from liquid-metal solutions. J. Cryst. Growth. 225, 348–353 (2001)
Zytkiewicz, Z.R.: Laterally overgrown structures as substrates for lattice mismatched epitaxy. Thin Solid Films. 412, 64–75 (2002)
Holm, J.V., Jørgensen, H.I., Krogstrup, P., Nygård, J., Liu, H., Aagesen, M.: Surface-passivated GaAsP single-nanowire solar cells exceeding 10% efficiency grown on silicon. Nat. Commun. 4, 1498 (2013)
Tanabe, K., Watanabe, K., Arakawa, Y.: III-V/Si hybrid photonic devices by direct fusion bonding. Sci. Rep. 2, 349 (2012)
Corkish, R.: Some candidate materials for lattice-matched liquid-phase epitaxial growth on silicon. Solar Cells. 31, 537–548 (1991)
Geisz, J. F., Friedman, D. J., Mcmahon, W. E., Ptak, A. J., Kibbler, A. E., Ols, J. M., Metzger, K., Kurtz, S.: GaNPAs solar cells that can be lattice-matched to silicon. Presented at the National Center for Photovoltaics and Solar Program Review Meeting, 24–26 March (2003), Denver, Colorado, https://www.osti.gov/biblio/15004240
Kunert, B., Volz, K., Stolz, W.: Advances in the growth of lattice-matched III-V compounds on Si for optoelectronics. In: The Proceedings of the 22nd International Conference on Indium Phosphide and Related Materials (IPRM), pp. 1–4 (2010)
Bachmann, K.J., Dietz, N., Miller, A.E., Venables, D., Kelliher, J.T.: Heteroepitaxy of lattice-matched compound semiconductors on silicon. J. Vac. Sci. Technol. A. 13, 696–704 (1995)
Zhang, P., Crespi, V.H., Chang, E., Louie, S.G., Cohen, M.L.: Computational design of direct-bandgap semiconductors that lattice-match silicon. Nature. 409, 69–71 (2001)
Yamaguchi, M.: Dislocation density reduction in heteroepitaxial III-V compound films on Si substrates for optical devices. J. Mater. Res. 6, 376–384 (1991)
Grassman, T.J., Derkacs, D., Whipple, S.G., Stavrides, A.P., Bremner, S.P., Ringel, S.A., Lepkowski, D.L., Boyer, J.T., Chmielewski, D.J., Yi, C., Western, N., Mehrvarz, H., Ho-Baillie, A., Kerestes, C.: Toward >25% efficient monolithic epitaxial GaAsP/Si tandem solar cells. In: 2019 IEEE 46th Photovoltaic Specialists Conference (PVSC), Chicago, IL, USA, pp. 0734–0737 (2019)
Lepkowski, D.L., Boyer, J.T., Chmielewski, D.J., Silvaggio, A.C., Ringel, S.A., Grassman, T.J.: Investigation of rear-emitter GaAs0.75P0.25 top cells for application to III–V/Si tandem photovoltaics. IEEE J. Photovoltaics. 9, 1644–1651 (2019)
Fan, S., Lee, M.L., Yu, Z., Sun, Y., Weigand, W., Dhingra, P., Kim, M., Hool, R.D., Ratta, E.D., Holman, Z.C.: Epitaxial GaAsP/Si tandem solar cells with integrated light trapping. In: 2019 IEEE 46th Photovoltaic Specialists Conference (PVSC), Chicago, IL, USA, pp. 0730–0733 (2019)
Fan, S., Yu, Z.J., Suna, Y., Weigand, W., Dhingra, P., Kim, M., Hoola, R.D., Ratta, E.D., Holman, Z.C., Lee, M.L.: 20%-efficient epitaxial GaAsP/Si tandem solar cells. Sol. Energy Mater. Sol. Cells. 202, 110144 (2019)
Feifel, M., Ohlmann, J., Benick, J., Hermle, M., Belz, J., Beyer, A., Volz, K., Hannappel, T., Bett, A.W., Lackner, D., Dimroth, F.: Direct growth of III–V/Silicon triple-junction solar cells with 19.7% efficiency. IEEE J. Photovoltaics. 8, 1590–1595 (2018)
Feifel, M., Lackner, D., Ohlmann, J., Benick, J., Hermle, M., Dimroth, F.: Direct Growth of a GaInP/GaAs/Si Triple-Junction Solar Cell with 22.3% AM1.5g Efficiency. Solar RRL. 3, 1900313 (2019)
Wang, L., Conrad, B., Soeriyadi, A., Zhao, X., Li, D., Diaz, M., Lochtefeld, A., Gerger, A., Perez-Wurfl, I., Barnett, A.: Current matched three-terminal dual junction GaAsP/SiGe tandem solar cell on Si. Sol. Energy Mater. Sol. Cells. 146, 80–86 (2016)
Murali, S., Irvin, N.P., Zhang, C., King, R.R., Honsberg, C.B.: Epitaxial GaP grown on Silicon by MEE and MBE Techniques as a Pathway for Dilute Nitride-Si Tandem Solar Cells. In: 2019 IEEE 46th Photovoltaic Specialists Conference (PVSC), Chicago, IL, USA, pp. 1044–1048 (2019)
Geisz, J.F., Olson, J.M., Friedman, D.J., Jones, K.M., Reedy, R.C., Romero, M.J.: Lattice-matched GaNPAs-on-Silicon Tandem Solar Cells. In: Conference Record of the Thirty-First IEEE Photovoltaic Specialists Conference, 2005, Lake Buena Vista, FL, USA, pp. 695–698 (2005). https://doi.org/10.1109/PVSC.2005.1488226
Ferry, D.K., Goodnick, S.M., Bird, J.: Transport in Nanostructures, 2nd edn, p. 650. Cambridge University Press, Cambridge, UK (2009)
Cho, A.Y., Arthur, J.R.: Molecular beam epitaxy. Prog. Solid State Chem. 10, 157–191 (1975)
Novoselov, K.S., Geim, A.K., Morozov, S.V., Jiang, D., Zhang, Y., Dubonos, S.V., Grigorieva, I.V., Firsov, A.A.: Science. 306, 666 (2004)
Novoselov, K.S., Jiang, D., Schedin, F., Booth, T.J., Khotkevich, V.V., Morozov, S.V., Geim, A.K.: Proc. Nat. Acad. Sci. 102, 10451 (2005)
Manzeli, S., Ovchinnikov, D., Pasquier, D., Yazyez, O.V., Kis, A.: 2D transition metal dichalcogenides. Nat. Rev. Mat. 2, 17033 (2017)
Geim, A.K., Grigoreiva, I.V.: Van der Waals heterostructures. Nature. 499, 419–425 (2013)
Lu, W., Lieber, C.M.: Semiconductor nanowires. J. Phys. D. Appl. Phys. 39, R387 (2006)
Samuelson, L.: Self-forming nanoscale devices. Mater. Today. 6, 22–31 (2003)
Björk, M.T., Ohlsson, B.J., Sass, T., Persson, A.I., Thelander, C., Magnusson, M.H., Deppert, K., Wallenberg, L.R., Samuelson, L.: One-dimensional steeplechase for electrons realized. Nano Lett. 2, 87–89 (2002)
Björk, M.T., Ohlsson, B.J., Thelander, C., Persson, A.I., Deppert, K., Wallenberg, L.R., Samuelson, L.: Nanowire resonant tunneling diodes. Appl. Phys. Lett. 81, 4458–4460 (2002)
Thelander, C., Martensson, T., Björk, M.T., Ohlsson, B.J., Larsson, M.W., Wallenberg, L.R., Samuelson, L.: Single-electron transistors in heterostructure nanowires. Appl. Phys. Lett. 83, 2052–2054 (2003)
Fuhrer, A., Fasth, C., Samuelson, L.: Single electron pumping in InAs nanowire double quantum dots. Appl. Phys. Lett. 91, 052109 (2007)
Fuhrer, A., Froberg, L.E., Pedersen, J.N., Larsson, M.W., Wacker, A., Pistol, M.E., Samuelson, L.: Few electron double quantum dots in InAs/InP nanowire heterostructures. Nano Lett. 7, 243–246 (2007)
Chandra, N., Tracy, C.J., Cho, J.-H., Picraux, S.T., Hathwar, R., Goodnick, S.M.: Vertically grown Ge nanowire Schottky diodes on Si and Ge substrates. J. Appl. Phys. 118, 024301–024307 (2015)
Alivisatos, A.P.: Perspectives on the physical chemistry of semiconductor nanocrystals. J. Phys. Chem. 100, 3226–13239 (1996)
Bimberg, D., Grundmann, M., Ledentsov, N.N.: Quantum Dot Heterostructures. Wiley, Chichester (1999)
Ban, K.-Y., Bremner, S.P., Liu, G., Dahal, S.N., Dippo, P.C., Norman, A.G., Honsberg, C.B.: Use of a GaAsSb buffer layer for the formation of small, uniform, and dense InAs quantum dots. Appl. Phys. Lett. 96, 183101 (2010)
O’Regan, B., Grätzel, M.: A low-cost, high-efficiency solar cell based on dye-sensitized colloidal TiO2 films. Nature. 353, 737–740 (1991)
Seok, S.I., Grätzel, M., Park, N.-G.: Methodologies toward highly efficient perovskite solar cells. Small. 14, 1704177 (2018)
Barnham, K.W.J., Duggan, G.: A new approach to high-efficiency multi-band-gap solar cells. J. Appl. Phys. 67, 3490–3493 (1990)
Nozik, A.J.: Quantum dot solar cells. Phys. E. 14, 115–120 (2002)
Liu, M., et al.: Hybrid organic–inorganic inks flatten the energy landscape in colloidal quantum dot solids. Nat. Mat. 16, 258–264 (2016)
Sanehira, E.M., Marshall, A.R., Christians, J.A., Harvey, S.P., Ciesielski, P.N., Wheeler, L.M., Schulz, P., Lin, L.Y., Beard, M.C., Luther, J.M.: Enhanced mobility CsPbI3 quantum dot arrays for record-efficiency, high-voltage photovoltaic cells. Sci. Adv. 3, 8 (2017)
Hao, M., Bai, Y., Zeiske, S., Ren, L., Liu, J., Yuan, Y., Zarrabi, N., Cheng, N., Ghasemi, M., Chen, P., Lyu, M., He, D., Yun, J.-H., Du, Y., Wang, Y., Ding, S., Armin, A., Meredith, P., Liu, G., Cheng, H.-M., Wang, L.: Ligand-assisted cation-exchange engineering for high-efficiency colloidal Cs1−xFAxPbI3 quantum dot solar cells with reduced phase segregation. Nat. Energy. 80, 79–88 (2020)
Jean, J.: Getting high with quantum dot solar cells. Nat. Energy. 5, 10–11 (2020)
Yu, Z., Raman, A., Fan, S.: Fundamental limit of nanophotonic light trapping in solar cells. PNAS. 107, 17491–17496 (2010)
John, S.: Strong localization of photons in certain disordered dielectric superlattices. Phys. Rev. Lett. 58, 2486–2489 (1987)
Yablonovitch, E.: Inhibited spontaneous emission in solid-state physics and electronics. Phys. Rev. Lett. 58, 2059–2062 (1987)
Vulic, N., Choi, J.-Y., Honsberg, C.B., Goodnick, S.M.: Silica nanosphere lithography defined light trapping structures for ultra-thin Si photovoltaics. MRS Proc. 1770, 31–36 (2015)
Kelzenberg, M.D., Boettcher, S.W., Petykiewicz, J.A., Turner-Evans, D.B., Putnam, M.C., Warren, E.L., Spurgeon, J.M., Briggs, R.M., Lewis, N.S., Atwater, H.A.: Enhanced absorption and carrier collection in Si wire arrays for photovoltaic applications. Nat. Mat. Lett. 9, 239–244 (2010)
Pillai, S., Catchpole, K.R., Trupke, T., Green, M.A.: Surface plasmon enhanced silicon solar cells. J. Appl. Phys. 101, 093105 (2007)
Nakayama, K., Tanabe, K., Atwater, H.A.: Plasmonic nanoparticle enhanced light absorption in GaAs solar cells. Appl. Phys. Lett. 93, 121904 (2008)
Vulic, N., Goodnick, S.M.: Analysis of recombination processes in polytype gallium arsenide nanowires. Nano Energy. 56, 196–206 (2019)
Tian, B., et al.: Coaxial silicon nanowires nanoelectronic power sources. Nature. 449, 889 (2007)
Garnett, E.C., Peidong, Y.: Silicon nanowire radial p-n junctions solar cells. J. Am. Chem. Soc. 130, 9224–9225 (2008)
Tang, J., Huo, Z., Brittman, S., Gao, H., Yang, P.: Solution-processed core-shell nanowires for efficient photovoltaic cells. Nat. Nanotechnol. 6, 568–572 (2011)
Kempa, T.J., Kim, S.K., Day, R.W., Park, H.G., Nocera, D.C., Lieber, C.M.: Facet-selective growth on nanowires yields multi-component nanostructures and photonic devices. J. Am. Chem. Soc. 135, 18354–18357 (2013)
Treu, J., Stettner, T., Watzinger, M., Morkötter, S., Döblinger, M., Matich, S., Saller, K., Bichler, M., Abstreiter, G., Finley, J.J., Stangle, J., Koblmüller, G.: Lattice-matched InGaAs-InAlAs core-shell nanowires with improved luminescence and photoresponse properties. Nano Lett. 15, 3533–3540 (2015)
Popescu, B., Popescu, D., Luppina, P., Julian, T., Koblmüller, G., Lugli, P., Goodnick, S.: Modeling and simulation of InGaAs nanowire solar cells. In: Proceedings of the IEEE International Conference on Nanotechnology, pp. 728–231 (2015)
Chuang, C., Sedgwick, F.G., Chen, R., Ko, W.S., Moewe, M., Ng, W., Tran, T.-T.D., Chang-Hasnain, C.: GaAs-based nanoneedle light emitting diode and avalanche photodiode monolithically integrated on a silicon substrate. Nano Lett. 11, 385–390 (2010)
Chen, R., Tran, T.-T.D., Ng, K.W., Ko, W.S., Chuang, L.C., Sedgwick, F.G., Chang-Hasnain, C.: Nanolasers grown on silicon. Nat. Photonics. 5, 170–175 (2011)
Colombo, C., Heiss, M., Gratzel, M., Fontcuberta, A., Morral, I.: Gallium arsenide pin radial structures for photovoltaic applications. Appl. Phys. Lett. 94, 173108 (2009)
Krogstrup, P., et al.: Single-nanowire solar cells beyond the Shockley-Queisser limit. Nat. Photonics. 7, 206–310 (2013)
Mariani, G., et al.: Patterned radial GaAs nanopillar solar cells. Nano Lett. 11, 2490–2494 (2011)
Wallentin, J., Anttu, N., Asoli, D., Huffman, M., Aberg, I., Magnusson, M.H., Siefer, G., Fuss-Kailuweit, P., Dimroth, F., Witzigmann, B., Xu, H.Q., Samuelson, L., Deppert, K., Borgström, M.T.: InP nanowire array solar cells achieving 13.8% efficiency by exceeding the ray optics limit. Science. 339, 1057–1060 (2013)
Åberg, I., Vescovi, G., Asoli, D., Naseem, U., Gilboy, J.P., Sundvall, C., Dahlgren, A., Svensson, K.E., Anttu, N., Björk, M.T., Samuelson, L.: A GaAs nanowire Array solar cell with 15.3% efficiency at 1 Sun. IEEE J. Photovoltaics. 6, 185–190 (2016)
van Dam, D., van Hoof, N.J.J., Cui, Y., van Veldhovern, P.J., Bakkers, E.P.A.M., Rivas, J.G., Haverkort, J.E.M.: High-efficiency nanowire solar cells with Omnidirectionally enhanced absorption due to self aligned Indium−Tin−Oxide Mie Scatterers. ACS Nano. 10, 11414–11419 (2016)
Luque, A., Martí, A.: Increasing the efficiency of ideal solar cells by photon induced transitions at intermediate levels. Phys. Rev. Lett. 78, 5014–5017 (1997)
Luque, A., Martí, A.: The intermediate band solar cell: Progress toward the realization of an attractive concept. Adv. Mater. 22, 160–174 (2010)
Barnham, K.W.J., Braun, B., Nelson, J., Paxman, M., Button, C., Roberts, J.S., Foxon, C.T.: Short-circuit current and energy efficiency enhancement in a low-dimensional structure photovoltaic device. Appl. Phys. Lett. 59, 135–137 (1991)
Barnham, K.W.J., Ballard, I., Barnes, J., Connolly, J., Griffin, P., Kluftinger, B., Nelson, J., Tsui, E., Zachariou, A.: Quantum well solar cells. Appl. Surf. Sci. 113(114), 722–733 (1997)
Walukiewicz, W., Shan, W., Yu, K.M., Ager III, J.W., Haller, E.E., Miotkowski, I., Seong, M.J., Alawadhi, H., Ramdas, A.K.: Interaction of localized electronic states with the conduction band: band Anticrossing in II-VI semiconductor ternaries. Phys. Rev. Lett. 85, 1552–1555 (2000)
Goodnick, S.M., Faleev, N., Honsberg, C.: Nanoscale photovoltaics and the terawatt challenge. In: Korkin, A., Lockwood, D. (eds.) Nanoscale Applications for Information and Energy Systems. Nanostructure Science and Technology. Springer, New York (2013)
Yao, Y., Charles, W.O., Tsai, T., Wysocki, G., Chen, J., Gmachl, C.F.: Broadband quantum cascade laser gain medium based on a “continuum-to-bound” active region design. Appl. Phys. Lett. 96, 211106 (2010)
Bhattacharya, P., Stiff-Roberts, A.D., Krishna, S., Kennerly, S.: Quantum dot infrared detectors and sources. Int. J. High Speed Electron. Syst. 12, 969–994 (2002)
MacMillan, H.F., Hamaker, H.C., Kaminar, N.R., Kuryla, M.S., Ristow, M.L., Liu, D.D., Virshup, G.F., Gee, J.M.: 28% efficient GaAs concentrator solar cells. In: IEEE Photovoltaic Specialists Conference, pp. 462–468 (1988)
Bailey, C.G., Forbes, D.V., Raffaelle, R.P., Hubbard, S.M.: Near 1 V open circuit voltage InAs/GaAs quantum dot solar cells. Appl. Phys. Lett. 98, 163105 (2011)
Sauvage, S., Boucaud, P., Julien, F.H., Gérard, J.-M., Thierry-Mieg, V.: Intraband absorption in n-doped InAs/GaAs quantum dots. Appl. Phys. Lett. 71, 2785 (1997)
Martí, A., Antolín, E., Stanley, C.R., Farmer, C.D., López, N., Díaz, P., Cánovas, E., Linares, P.G., Luque, A.: Production of photocurrent due to intermediate-to-conduction-band transitions: a demonstration of a key operating principle of the intermediate-band solar cell. Phys. Rev. Lett. 97, 247701 (2006)
Nelson, J., Barnes, J., Ekins-Daukes, N., Kluftinger, B., Tsui, E., Barnham, K., Foxon, C.T., Cheng, T., Roberts, J.: Observation of suppressed radiative recombination in single quantum well p- i- n photodiodes. J. Appl. Phys. 82, 6240 (1997)
Okada, Y., Ekins-Daukes, N.J., Kita, T., Tamaka, R., Yoshida, M., Pusch, A., Hess, O., Phillips, C.C., Farrell, D.J., Yoshida, K., Ahsan, N., Shoji, Y., Sogabe, T., Guillemoles, J.-F.: Intermediate band solar cells: recent progress and future directions. Appl. Phys. Rev. 2, 021302 (2015)
Kayes, B.M., Nie, H., Twist, R., Spruytte, S.G., Reinhardt, F., Kizilyalli, I.C., Higashi, G.S.: 27.6% conversion efficiency, a new record for single-junction solar cells under 1 sun illumination. In: 2011 37th IEEE Photovoltaic Specialists Conference, Seattle, WA, pp. 4–8 (2011)
Schaller, R.D., Klimov, V.I.: High efficiency carrier multiplication in PbSe nanocrystals: implications for solar energy conversion. Phys. Rev. Lett. 92, 186601 (2004)
Ellingson, R.J., Beard, M.C., Johnson, J.C., Yu, P., Micic, O.I., Nozik, A.J., Shabaev, A., Efros, A.L.: Highly Efficient Multiple Exciton Generation in Colloidal PbSe and PbS Quantum Dots. Nano Lett. 5, 865–871 (2005)
Nozick, A.J.: Exciton multiplication and relaxation dynamics in quantum dots: applications to ultrahigh-efficiency solar photon conversion. Inorganic Chem. 44, 6893 (2005)
Shabaev, A., Efros, L., Nozik, A.J.: Multiexciton generation by a single photon in nanocrystals. Nano Lett. 6, 8 (2006)
Schaller, R.D., Pietryga, J.M., Klimov, V.I.: Carrier multiplication in InAs nanocrystal quantum dots with an onset defined by the energy conservation limit. Nano Lett. 7, 3469–3476 (2007)
Murphy, J.E., Beard, M.C., Norman, A.G., Johnson, S.P., Ahrenkiel, J.C., Micic, P., Yu, O.I., Ellingson, R.J., Nozik, A.J.: PbTe colloidal nanocrystals: synthesis, characterization, and multiple exciton generation. J. Am. Chem. Soc. 128, 3241–3247 (2006)
Beard, M.C., Knutsen, K.P., Yu, P., Luther, J.M., Song, Q., Metzger, W.K., Ellingson, R.J., Nozik, A.J.: Multiple Exciton Generation in Colloidal Silicon Nanocrystals. Nano Lett. 7, 2506–2512 (2007)
Schaller, R.D., Petruska, M.A., Klimov, V.I.: Effect of electronic structure on carrier multiplication efficiency: Comparative study of PbSe and CdSe nanocrystals. Appl. Phys. Lett. 87, 253102 (2005)
Werner, J.H., Kolodinski, S., Queisser, H.J.: Novel optimization principles and efficiency limits for semiconductor solar cells. Phys. Rev. Lett. 72, 3851–3854 (1994)
de Vos, A., Desoete, B.: On the ideal performance of solar cells with larger-than-unity quantum efficiency. Sol. Energy Mater. Sol. Cells. 51, 413–424 (1998)
Wolf, M., Brendel, R., Werner, J.H.: Solar cell efficiency and carrier multiplication in Si1-xGex alloys. J. Appl. Phys. 83, 4213–4221 (1998)
Semonin, O.E., Luther, J.M., Choi, S., Chen, H.-Y., Gao, J., Nozik, A.J., Beard, M.C.: Peak external photocurrent quantum efficiency exceeding 100% via MEG in a quantum dot solar cell. Science. 334, 1530–1533 (2012)
Gabor, N.M., Zhong, Z., Bosnick, K., Park, J., McEuen, P.L.: Extremely efficient multiple electron-hole pair generation in carbon nanotube photodiodes. Science. 325, 1367–1371 (2009)
Cunningham, P.D., Boercker, J.E., Foos, E.E., Lumb, M.P., Smith, A.R., Tischler, J.G., Melinger, J.S.: Enhanced multiple exciton generation in quasi-one-dimensional semiconductors. Nano Lett. 11, 3476–3481 (2011)
Pelouch, W.S., Ellingson, R.J., Powers, P.E., Tang, C.L., Szmyd, D.M., Nozik, A.J.: Comparison of hot-carrier relaxation in quantum wells and bulk GaAs at high carrier densities. Phys. Rev. B. 45, 1450–1453 (1992)
Hathwar, R., Zou, Y., Jirauschek, C., Goodnick, S.M.: Nonequilibrium electron and phonon dynamics in advanced concept solar cells. Top. Rev. J. Phys. D Appl. Phys. 52, 093001 (2019)
Wang, Y., Jackson, H.E., Smith, L.M., Burgess, T., Paiman, S., Gao, Q., Tan, H.H., Jagadish, C.: Carrier Thermalization dynamics in single Zincblende and Wurtzite InP nanowires. Nano Lett. 14, 7153–7160 (2014)
Tedeschi, D., De Luca, M., Fonseka, H.A., Gao, Q., Mura, F., Tan, H.H., Rubini, S., Martelli, F., Jagadish, C., Capizzi, M., Polimeni, A.: Long-lived hot carriers in III–V nanowires. Nano Lett. 16, 3085–3093 (2016)
Conibeer, G., Green, M.A., Corkish, R., Cho, Y., Chob, E., Jiang, C., Fangsuwannarak, T., Pink, E., Huang, Y., Puzzer, T., Trupke, T., Richards, B., Shalav, A., Lind, K.: Silicon nanostructures for third generation photovoltaic solar cells. Thin Solid Films. 511-512, 654 (2006)
Landsberg, P.T., Tonge, G.: Thermodynamic energy conversion efficiencies. J. Appl. Phys. 51, R1 (1980)
Würfel, P.: Solar energy conversion with hot electrons from impact ionization. Sol. Energy Mater. Sol. Cells. 46, 43–52 (1997)
Würfel, P., Brown, A.S., Humphrey, T.E., Green, M.A.: Particle conservation in the hot-carrier solar cell. Prog. Photovolt. Res. Appl. 13, 277 (2005)
Dimmock, J.A.R., Day, S., Kauer, M., Smith, K., Heffernan, J.: Demonstration of a hot-carrier photovoltaic cell. Prog. Photovolt. Res. Appl. 22, 151–160 (2014)
Nguyen, D.T., Lombez, L., Gibelli, F., Boyer-Richard, S., Le Corre, A., Durand, O., Guillemoles, J.F.: Quantitative experimental assessment of hot carrier-enhanced solar cells at room temperature. Nat. Energy. 3, 236–242 (2018)
Lugli, P., Goodnick, S.M.: Non-equilibrium LO phonon effects in GaAs/AlGaAs quantum wells. Phys. Rev. Lett. 59, 716–719 (1987)
Conibeer, G., Patterson, R., Huang, L., Guillemoles, J.-F., König, D., Shrestha, S., Green, M.A.: Modelling of hot carrier solar cell absorbers. Solar Energy Mat. Solar Cells. 94, 1516–1521 (2010)
Tsen, K.S., Wald, K.R., Ruf, T., Yu, P.Y., Morkoc, H.: Electron optical phonon interactions in ultrathin GaAs AlAs multiple quantum well structures. Phys. Rev. Lett. 67, 2557–2560 (1991)
Tsen, K.T., Joshi, R.P., Ferry, D.K., Botcharev, A., Sverdlov, B., Salvador, A., Morkoc, H.: Non-equilibrium electron distributions and phonon dynamics in wurtzite GaN. Appl. Phys. Lett. 68, 2990–2992 (1996)
Tsen, K.T., Kiang, J.G., Ferry, D.K., Morkoc, H.: Subpicosecond time-resolved Raman studies of LO phonons in GaN: dependence on photoexcited carrier density. Appl. Phys. Lett. 89, 112111 (2006)
Tsen, K.T., Kiang, J.G., Ferry, D.K., Lu, H., Schaff, W.J., Lin, H.-W., Gwo, S.: Direct measurements of the lifetimes of longitudinal optical phonon modes and their dynamics in InN. Appl. Phys. Lett. 90, 152107 (2007)
Conibeer, G.J., Jiang, C.-W., König, D., Shrestha, S., Walsh, T., Green, M.A.: Selective energy contacts for hot carrier solar cells. Thin Solid Films. 516, 6968–6973 (2008)
Conibeer, G.J., Shrestha, S., Huang, S., Patterson, R., Xia, H., Feng, Y., Zhang, P., Gupta, N., Tayebjee, M., Smyth, S., Liao, Y., Lin, S., Wang, P., Dai, X., Chung, S.: Hot carrier solar cell absorber prerequisites and candidate material systems. Sol. Energy Mater. Sol. Cells. 135, 124–129 (2015)
Goodnick, S.M., Lugli, P.: Hot carrier relaxation in quasi-2D systems. In: Shah, J. (ed.) Hot Carriers in Semiconductor Microstructures: Physics and Applications, pp. 191–234. Academic Press (1992)
Dür, M., Goodnick, S.M., Lugli, P.: Monte Carlo simulation of intersubband relaxation in wide, uniformly doped GaAs/AlxGa1-xAs quantum wells. Phys. Rev. B. 54, 17794 (1996)
Goodnick, S.M., Honsberg, C.: Modeling carrier relaxation in hot carrier solar cells. Proc. SPIE. 8256(82560W), 10.1117/12.910858 (2012)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Goodnick, S.M., Honsberg, C. (2023). Solar Cells. In: Rudan, M., Brunetti, R., Reggiani, S. (eds) Springer Handbook of Semiconductor Devices . Springer Handbooks. Springer, Cham. https://doi.org/10.1007/978-3-030-79827-7_19
Download citation
DOI: https://doi.org/10.1007/978-3-030-79827-7_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-79826-0
Online ISBN: 978-3-030-79827-7
eBook Packages: EngineeringEngineering (R0)