Numerical Modelling Techniques for Wave Energy Converters in Arrays

Abstract

Wave and tidal renewable energy systems have received a great deal of attention in recent years worldwide. A number of Wave Energy Converter (WEC) technologies to harvest wave energy have been proposed, developed, tested and in operation in ocean at different parts of the globe with varying maturity levels. Over the past two decades, a broad range of academic research output has emerged, covering topics that include numerical and physical modelling of WEC arrays systems. However, to date, there have only been limited examples of WEC array installations, and these have been small in terms of the number of devices. Many developments in the future will focus on arrays of devices, as such an improved understanding of how arrays can be modelled is essential. This article attempts to describe the numerical modelling techniques used to study the hydrodynamic interaction of WEC arrays. An understanding of these techniques is necessary for not only device developers and researchers, but also for authorities, investors, insurers and other stakeholders. Such work will provide evidence for the expected energy output, control requirements, array configurations and to evaluate any environmental impact the array deployments may have on the ocean environment.

9.1 Introduction

Wave and tidal renewable energy systems have received a great deal of attention in recent years worldwide. Although several estimates for global wave energy potential are given in the literature, the Intergovernmental Panel on Climate Change (IPCC) in 2012 reported a theoretical potential of around 29,500 terawatt-hours per year (TWh/yr) considering all areas with wave energy densities higher than 5 kW/m [1]. A number of device developers have been endorsed by large utility companies hoping to exploit these resources by developing various Wave Energy Converter (WEC) technologies. Over the past two decades, a broad range of academic research output has emerged, covering topics that include numerical and physical modelling of WEC arrays systems. The foundation for all research, however, remains in the 1970s and ’80s with pioneering work by Salter, Budal, Falnes, Evans, Newman, Mei, Jefferys, Count and others. There are a number of fascinating accounts on the historical developments of wave energy extraction included in Salter [2], Clement et al. [3], Falnes [4], Drew et al. [5], Falcão [6], Langhamer [7], Lindroth [8], Moriarty [9] and Falnes [10]. These articles cover a range of subjects in the context of wave energy conversion. The European Marine Energy Centre (EMEC) in the UK has outlined device type categories [11]. The technology maturity levels of the various devices vary considerably. A degree of early commercial interest in some of the devices has helped identify the relatively advanced proposals. To date, there have only been limited examples of WEC array installations, and these have been small in terms of the number of devices. Many developments in the future will focus on arrays of devices, as such an improved understanding of how arrays can be modelled is essential. This article attempts to describe the numerical modelling techniques used to study the hydrodynamic interaction of WEC arrays. An understanding of these techniques is necessary for not only device developers and researchers, but also for authorities, investors, insurers and other stakeholders alike, to support backing for large scale developments. Such work will provide evidence for the expected energy output, control requirements, array configurations, environmental impact, etc.

9.2 Review of Hydrodynamic Modelling of WEC Arrays

Modelling of hydrodynamic interactions between floating, fixed and constrained rigid bodies with ocean waves and currents has been the focus of many studies in the field of marine systems. This has traditionally been carried out for the design of ships and military vessels, but also applies to oil storage and production platforms, harbours and coastal defence systems, and more recently, wave energy converters (WECs). Folley et al. [12] provide a review of hydrodynamic modelling methods for WEC arrays, giving benefits of each method by evaluating three characteristics: fundamental modelling ability, computational processing requirements and usability. This highlights issues such as code availability, stability and processing time. Folley et al. [12] also score the key numerical methods against their suitability to various types of study, showing relative merits. Another important review is that of Li and Yu [13], who also consider the numerical methods available, specifically for modelling point absorber arrays.

Two distinct groups of modelling approaches are apparent, the first including potential flow based codes (semi-analytical, boundary element method) and CFD solvers, both of which are well suited to addressing the device interaction problem. Diffraction and radiation can be accurately modelled, giving realistic device responses within the scattered and radiated wave fields. What is more, there is a broad range of flexibility in terms of efficiency or accuracy. The potential flow methods include the point absorber (PA) [14,15,16,17,18,19], plane wave (PW) [19,20,21,22], multiple scattering (MS) [19, 23, 24], direct matrix (DM) [25,26,27,28,29] and boundary element methods (BEMs) [30, 31]. These are generally considered semi-analytical methods (with the exception of BEM) in that various assumptions are used to provide expressions for the velocity potential of the incident waves, the diffracted waves and radiated waves. Some of these assumptions that are made can remove or simplify certain components, for example, scattering effect omitted from the PA method.

9.2.1 Point Absorber Method

The point absorber (PA) method has seen a widespread application since it was introduced by Budal in 1977 [14]. The individual body dimensions are assumed to be small compared to incident wavelength allowing the scattering effect on the incoming wave to be ignored. The q-factor can therefore be taken from the solution of the radiation problem alone, which is determined using the excitation forces and damping coefficients. As with the other semi-analytical methods, the linear potential theory is used to formulate expressions to evaluate the velocity potential. It should be noted the term ‘point absorber’ is often used to describe floating buoy type WECs in a more general sense and does not always imply that the point absorber method is used.

The PA approximation has been used by Thomas and Evans [17] to assess the power capture of five and ten-body arrays of spheres, making use of the fact that with the PA approximation, no knowledge of the precise device geometry is required in order to compute the interaction factor q. The work carried out is essentially an array optimisation study, considering variations in wavenumber, device spacing and wave heading. For the range of spacings studied the maximum and minimum q-factors for unconstrained motions of the five-body array are found to be $q = 2.25\text{ and } 0.57$, respectively. These limits occur within a relatively narrow range of conditions (ka = 5.1 and 6.75, respectively, where $k$ is the wavenumber and $a$ is the device radius), confirming a strong variance of q with device spacing. Constrained motions are also studied, as the device displacements are considerably larger than the incident wave amplitude and are in violation of linear wave theory.

Mavrakos and McIver [19] carried out detailed studies on arrays of five equally spaced truncated cylinders using the PA, PW and MS methods. As the ‘exact’ MS approach is known to accurately represent the total wave field around each body, this has been used to benchmark the comparative study. Two values are chosen for the ratio of device spacing over radius, i.e. $d/a =$ 5 and 8, respectively. Mavrakos and McIver found that the results for the PA method show reasonable agreement for longer wavelengths, up to around $ka < 1.0$ and $ka < 1.4$ for $d/a =$ 5 and 8 respectively, and beyond this large discrepancies are found. The better performance of the PA method at wider device separations is to be expected, as the no-scattering approximation applies.

9.2.2 Plane-Wave Method

The plane-wave (PW) method assumes wide device spacing relative to the incident wavelength, it ignores evanescent waves and approximates non-planar outgoing waves as plane waves. This produces a set of simultaneous equations for the plane wave amplitude, allowing straightforward assessment of the hydrodynamic interactions after the scattering and radiation problems are solved for a single device. In this respect, it can be regarded as a simplified variant of the direct method described in Sect. 9.2.4.

Initial work on the PW method emerged from Simon [20], in which simplifications were sought for representations of the scattered component of the wave field. The assumptions that allowed these simplifications were that the bodies were axisymmetric, widely spaced and body motions were in heave only, and the result was a method that allows a compromise between the efficiency of the PA method and accuracy of the MS method.

McIver and Evans [21] modified Simon’s solution by including a correction term and consequently making a marked improvement to the accuracy. The PW method is applicable to a wide range of problems and has demonstrated good performance in evaluations of the wave amplitude down to a surprisingly close device spacing. McIver and Evans confirmed a good correspondence between body forces obtained using their method and that of the “exact” Spring and Monkmeyer method [25]. Linton and Evans [27] then extended the validation of the PW method by comparing the more onerous free-surface elevation with their rework of [22], also finding good agreement down to a relatively close device spacing (unlike the forces, the wave amplitudes are not integrated quantities, making the potential for errors much more significant).

In the comparative study by Mavrakos and McIver [22], the authors showed that the hydrodynamic forces can be accurately calculated using the PW method. Mavrakos and McIver found that the modulus of the complex exciting forces agrees well with the MS method, with small deviations of <5% around the peak forces. The phase of these forces also agrees well with the MS method, with the biggest discrepancies occur around the ‘edge-of-array’ bodies. There may however be errors in the forces measured within the array, with these errors increasing with array size. Erratic behaviour was found for very long wavelengths, due to an inversion procedure applied to the damping matrix. The onset of this instability of the PW method (shown in Fig. 9.7, in [19]) occurs at $ka \approx$ 0.45 and $ka \approx$ 0.275 for $d/a =$ 5 and 8, respectively. By normalising wave number to account for these two device spacings, the value of $ka$ for which instability occurs appears to fall in the range 2.20–2.25. Pending additional work, this may provide a useful working limit for generic PW studies.

9.2.3 Multiple Scattering

The multiple scattering (MS) technique takes the superposition of the various propagating and evanescent waves scattered and radiated by the array. The computations are simplified due to the fact that there is no need to simultaneously retain the spectra of partial wave amplitudes around all the individual bodies, as the boundary conditions for each are satisfied successively. Ohkusu [24] applied it to floating bodies. The effect on a wavefield caused by any number of fixed obstructing objects is not just the sum of the scattering components of this incident wave at each obstruction, but the sum of the scattered incident wave plus the scattering of the scattered waves (first-order scattering), and scattering of these waves (second-order scattering), and so on. Twersky [23] asserted that these effects are not necessarily as insignificant as had been previously believed because phase alignments may cause small scattered interference to superpose into much larger spikes (as confirmed by existing experimental anomalies in the field of acoustics and electromagnetics). This lends itself well to the problem of interactions between closely spaced WECs in water waves where multiple scattering interference is generally significant. Ohkusu adopted this MS approach, adding radiating components for the case of floating (and hence oscillating) bodies. Mavrakos and Koumoutsakos [22] extended this methodology to also include evanescent waves with solutions for arbitrary numbers of vertically axisymmetric bodies (in any array configuration with any individual body geometries). Any number of orders of interactions may be obtained to give the total wave field.

9.2.4 Direct Matrix Method

The term direct matrix (DM) is associated with methods that perform an exact analytical assessment of a problem in which the boundary conditions are applied directly to all bodies simultaneously, allowing all unknowns to be evaluated in a single matrix inversion procedure. The velocity potential for any field point is calculated by taking the superposition of the incident wave and all scattered waves for each of the $N$ bodies in the problem. To evaluate the wave amplitudes at each body, the set of equations that result are split into their real and imaginary parts. The force components on the bodies are finally evaluated after integrating the pressure on the wetted surface of each body.

Spring and Monkmeyer [25] first carried out this technique for a two-cylinder, bottom-mounted problem. They found that, when compared to a single cylinder, forces increase by as much as 60–65%. Spring and Monkmeyer also noted that the force ratios obtained from their studies are periodic with the variation of the device spacing and resemble the Bessel functions that are used to translate local coordinate frames. As the application of this particular method is limited to simple bottom-mounted geometries, it can only contribute to evaluations of certain types of WECs, such as OWCs.

Kagemoto and Yue [26] carried out an exact method (as far as is possible using linearized theory) to give the wave excitation forces, hydrodynamic coefficients and second-order drift forces in a selection of array problems, including that of floating bodies (and is in fact applicable to arbitrary configurations and numbers of arbitrarily shaped objects). This combines the work of Spring and Monkmeyer [25], Simon [20] and Ohkusu [24], becoming applicable to a far wider range of WEC problems due to the inclusion of evanescent waves. It is executed using only the diffraction interactions from a single body and hence removes the need to evaluate all of the n-order scattering components for the other bodies interfering with the incident wave. Kagemoto and Yue found excellent agreement of their solution with the exact hybrid element method (HEM) of Yue et al. [32], in which an entire array is modelled in one assessment.

Other more recent work on the DM method include Linton and Evans’ [27] rework of Spring and Monkmeyer’s method [25] in which a major simplification is identified. This again applies only to bottom mounted cylinders and may find more applications in studies of fixed offshore platforms. Linton and Evans ultimately found very efficient expressions for the free surface amplitude, for both the near-field and far-field regions.

Child and Venugopal [29] also used the direct method and optimised layouts of buoy type WECs by applying a genetic algorithm (GA) and alternative parabolic intersection (PI) approach. Using a partial wave notation, based on the assumption that the components can be combined linearly, a set of discrete expressions are used to describe the scattered and radiated wave fields. As GAs are simply optimisation routines, their application is not limited the DM method. Child and Venugopal demonstrated that the GAs are particularly well suited to problems to which an absolute optimum solution is not deemed essential. It would usually be assumed that this type of problem would take a long time to solve using conventional techniques and in many cases, there would be limited knowledge of the rational optimisation functions. Given the complex nature of interactions within an array of WECs, a GA routine can be used to rapidly generate acceptable solutions. The alternative PI method involves a more analytical approach, positioning devices on the peaks of waves that are diffracted by neighbouring devices. Each WEC is positioned in a way that maximises the constructive interference with its neighbours, so that the scattered waves are in phase with incident waves as they reach the neighbouring device. PI identifies very regular shaped array layouts, which tend to be symmetrical and highly sensitive to changes in incident wave direction. The highest $q$-factors obtained by Child and Venugopal in [29] come from the application of their GA method, rather than PI. In the GA case, it has been accepted that an element of randomness exists with the generation of the array shapes.

The second group of software codes (see Sect. 9.2.5) include those used for evaluating the far-field effects due to the presence of an array of WECs. These codes model wave propagation through a larger geographical scale domain, approximating the effects of energy extraction for a real ocean site with capacity to model ecological and morphological changes around a WEC array. These can be phase resolving or phase averaging techniques and can capture the various coastal processes that are observed on a medium to large scale.

9.2.5 Geographical Scale Studies

Global and regional scale numerical wave modelling are undertaken at various research and commercial institutions for wave forecasting and hindcasting, using models like WAM 4.5, WAVEWATCH III, SWAN, TOMAWAC, MIKE 21 and Delft 3D. More recent applications include the modelling of wave energy extraction processes and the resulting impact on wave climate. The scarcity of field data for this specific purpose means however that validation is problematic. Literature indicates that this methodology might serve as a preliminary assessment tool for energy extraction at real sites and also as a key technique for environmental impact assessments (EIAs). In general wave models can be classified as ‘phase resolving’ or ‘phase averaged’. This section gives an explanation of the various methods and applications with this distinction in mind.

9.2.5.1 Mild-Slope Models

The mild-slope method treats wave diffraction and refraction over a mildly varying water depth, where it is known that wavelengths and amplitudes will also vary. The dependence of wave number $k$ on water depth $h$ can be inferred from the dispersion relation. A new expression is therefore required for the free surface elevation $\eta \left( {x,y} \right)$, on which a number of publications (including an early derivation by Berkhoff [33]) have reported variations of the same result [18]. The form used in the MILDwave solver [34] for example, which emerged from the work of Troch [35], takes the Radder and Dingemans [36] depth-integrated form of the mild-slope equations:

$$\frac{{\partial \eta }}{{\partial t}} = B\phi - \nabla \cdot \left( {A\nabla \phi } \right)~,\quad ~\frac{{\partial \phi }}{{\partial t}} = - g\eta$$

(9.1)

where,

$$A = \frac{{\bar{C}\bar{C}_{g} }}{g},~B = \frac{{\omega ^{2} - k^{2} \bar{C}\bar{C}_{g} }}{g}.$$

Equation (9.1) describes the evolution of the free surface elevation with time, where either the velocity potential $\phi$ or free surface elevation $\eta$ can be eliminated to give a single time-dependent mild-slope expression. Here, $\bar{C}$ is the phase velocity and $\bar{C}_{g}$ is the group velocity.

The provision for the spatial dependency makes the mild-slope equations well suited to near coast problems with traditional application to coastal defence, breakwaters, harbour design and environmental impact assessments. This has been readily extended to applications in wave energy conversion processes, particularly for fixed WECs, e.g. overtopping devices and OWCs. Power extraction is not implicitly solved, however, sponge layers have been shown to give effective representations of WEC absorption characteristics.

Several studies have also applied the mild-slope method to problems with floating bodies. Mendes et al. [37] carried out an assessment of the Pelamis device installed at the offshore pilot zone in Portugal using REF/DIF mild-slope software with some auxiliary modifications. Beels [38] went a step further and carried out an evaluation of a motion-based device (FO3) in MILDwave and included radiated wave inputs from an independent WAMIT solution. This approach takes the radiation outputs from WAMIT and reproduces a corresponding and similar wave train in the MILDwave model from a circular generation line that surrounds the WEC. These results are compared to the full WAMIT diffraction and radiation results for a single FO3 device and show reasonable agreement. Application of the mild-slope solver in this way avoids the unmanageable burden on computational resources that would otherwise be necessary to model a large scale array of multiple-float devices.

A common problem with phase-resolving models is a suitable treatment of the domain boundaries. Conditions must be specified at domain boundaries so that waves are not reflected towards the area of interest. This includes the boundaries that lie behind any wave generation lines (absorption boundaries and generation lines are discrete).

For irregular and omnidirectional long-crested waves, Beels [38] gave a good comparative study of generation line configurations. A U-shaped configuration (two parallel lines with connecting arc) is found to be the most effective at generating wave components in the range $0^\circ < \theta < 90^\circ$. Short crested waves are also considered, with the directionality of the separate components accounted for through application of a spreading factor $s$. The parameter $s_{{max}}$ is used as a limit for the cases of wind-generated seas ($s_{{max}} = 10$), swells with short decay distances ($s_{{max}} = 25$) and swells with long decay distances ($s_{{max}} = 75$).

Finally, Beels includes a single obstruction to represent an array of devices. The power captured by the simplified single interference is shown to be ±40% that of more detailed evaluations of the array. On the basis of this result, Beels suggests that any economic evaluations of proposed schemes should take a more onerous route, modelling discrete WECs in a solver that can account for interactions. Ultimately, these types of mild-slope studies remove the difficult coupling of the reflection and transmission which is present in Boussinesq methods but also allows detailed geometry modelling within the array as a result of the small grid size, something which is not possible with the spectral wave models like SWAN.

9.2.5.2 Boussinesq Models

The linear theory discussed above requires the ratio of wave amplitude and water depth to be small, i.e. the nonlinearity $A/h << 1$. When studying a wave as it approaches a coastal area, the combined effects of reduced water depth and shoaling means $A/h > 1$, thus the hydrodynamics can become highly nonlinear. The Boussinesq equations are well suited to this type of problem as they omit the vertical components of the wave equations. This happens to be a reasonable assumption that addresses the fact that the circular particle motions associated with deep water waves become distorted in shallow water. Another important parameter in the derivation of the Boussinesq equations is the dispersion $\mu^{2}\equiv \left( {kh} \right)^{2}$, wherein the limiting cases $\left( {A/h} \right)\sim0$ and $\mu ^{2} \sim0$, the solution becomes linear. Numerical codes that implement variations of the classical Boussinesq equations include the MIKE21 Boussinesq Wave software, first developed by Madsen and Sørensen [87].

Boussinesq models have been used in the context of wave energy conversion to model interactions around fixed structures such as OWCs or overtopping devices. Venugopal and Smith [39] used a Boussinesq model (MIKE21) to investigate changes to the wavefield around an array of five hypothetical overtopping devices. Sponge layers are configured around the boundary of a domain (measuring $5 \times 4.5~{\text{km}}$) representing a coastal region to the west of Orkney. Waves are generated along lines within the domain, with input conditions provided by a much larger spectral wave model ($130 \times 110\,{\text{km}}$, also validated against buoy data). Venugopal and Smith evaluated the wave disturbance coefficients $h_{{wdc}}$ (local significant wave height, normalised by the input significant wave height) in the direction of wave propagation at each WEC location (waves are irregular and unidirectional). Results showed largely consistent profiles, with discrepancies in part caused by differing bathymetries at each specific location. Venugopal and Smith found that the wave amplitude is between 13 and 69% lower in the lee of the WECs depending on the porosity. The wave amplitudes recover briefly at a distance of around 500–600 m in the lee of the array regardless of porosity, which might suggest a suitable location for a second row of WECs.

Venugopal et al. [40] used the Boussinesq modelling code MIKE 21 to investigate $h_{{wdc}}$ around an array of bottom fixed OWCs. A significant challenge when studying OWCs is the quantification of radiation characteristics. This includes representation of the PTO mechanisms, as it is not possible to model the airside processes of the OWC as an integrated part of the Boussinesq solver. An iterative investigation is carried out at each wave period in order to resolve sponge layer. The authors concluded that the array spacing and peak wave periods are both factors that affect wave disturbance coefficients. The maximum disturbances experienced under the incident JONSWAP wave condition peaked at +39% upstream and −41% downstream of the array. The benefit of using the Boussinesq codes in this type of application is that they are capable of resolving a comprehensive set of hydrodynamic mechanisms. This includes the combined effects of diffraction, refraction, shoaling, wave breaking, nonlinear wave-wave interactions, bottom dissipation, partial wave reflection and transmission from structures, directional wave spreading and internal wave generation. Solid and permeable structures can be modelled, however, objects in the flow domain must be fixed to the ocean floor (e.g. OWCs), as there are no means to account for the dynamics of a moving object.

9.2.5.3 Phase Averaged Spectral Wave Model

Spectral wave models are based on the principle of wave action conservation, where wave action is a ratio of spectral density to intrinsic frequency. In contrast to other methods that focus on predictions of the surface elevation, the spectral wave methods are phase-averaging, predicting how the characteristics of a wave evolve with time. This method originated from the idea that the ocean waves could be decomposed into components of various frequency, amplitude and direction. The JONSWAP [41] project was an important step in the development, with first, and then second-generation models emerging from such work, with the latter including parameterised representations of nonlinear waves generated by the wind.

A later collaboration titled WAM provided the first of the third generation models that explicitly included these nonlinear waves. WAM is still commonly used, along with other global wave prediction models such as WAVEWATCH III, to provide input boundary conditions to other solvers intended for local or coastal interaction studies, such as SWAN (Delft University of Technology) and TOMAWAC (Electricité de France). Global wave models (WAM, WAVEWATCH III, etc.) and local models (SWAN, TOMAWAC, MIKE21 SW, etc.) work on similar principles, with the latter including additional descriptions for shallow water behaviour. Local models can theoretically execute oceanic scale problems however this inevitably proves unnecessary and inefficient.

It is common for both model scales to use a spherical coordinate system however it can be more convenient to work with a Cartesian system at the smaller scale. Discretization of the local domain can be achieved using structured or unstructured grids. Structured grids can feature more refined nested grid(s) in regions of greatest interest, whereas with an unstructured grid it is possible to have a continuously variable cell density. Care must be taken to ensure that the grid captures all relevant seabed features and avoids oversimplify step changes, as model bathymetry is interpolated between grid points. At Wave Hub, Millar et al. [42] and Smith et al. [43] used SWAN to examine the impact on the surrounding wave climate following a reduction in spectral energy density at the array location. Various configurations of barrier and transmission coefficients are used. Millar et al. [42] impose this energy reduction equally across all wave frequencies, while in the subsequent study, Smith et al. [43] employ a frequency-dependent power transfer function (PTF). The latter study is understood to be a significant improvement on [42] in terms of accurately estimating the wave height reduction, but both studies present useful applications of spectral wave models.

9.3 Boundary Element Methods

The boundary element method (BEM) is a well-established technique used to study floating bodies for which again potential flow theory is assumed. Wetted surfaces are panelled, either into planar surface elements curved patches (e.g. Higher Order in WAMIT) using splines. A normal force is then applied at the centre of each element, inducing a body motion as a result of fluid pressure fluctuations around the body. BEMs can be simplified by formulating in the frequency domain, however, use of the time domain enables the inclusion of non-linear external loads and non-linear hydrodynamics.

An outline requirement of BEMs is that there must be an appropriate Green’s function solution to translate the volume problem into a surface problem and hence evaluate the velocity potential in the whole fluid domain. Added complexity when dealing with nonlinear codes includes discretisation of the free surface which changes upon every time step, allowing any floating bodies to reorientate prior to the application of the Green’s function.

Codes such as WAMIT, ANSYS AQWA, Aquaplus and Nemoh operate in the frequency domain, and are generally used to provide matrices for the added mass $A_{{ij}}^{{added}}$, added damping $B_{{ij}}^{{added}}$ and excitation force $F_{i}$. These terms are required to evaluate the complex excursion amplitudes $\xi _{j}$ using the $6 \times 6~$ linear system based on Newton’s law (2).

$$\begin{gathered} \left[ { - \omega ^{2} \left( {M_{{ij}} + M_{{ij}}^{E} + A_{{ij}}^{{added}} \left( \omega \right)} \right) + {\text{i}}\omega \left( {B_{{ij}}^{{added}} \left( \omega \right) + B_{{ij}}^{E} } \right) + \left( {C_{{ij}} + C_{{ij}}^{E} } \right)} \right]\xi _{j} = F_{i} , \hfill \\ {\text{for~}}i,j = 1,2, \ldots ,6 \hfill \\ \end{gathered}$$

(9.2)

where $M_{{ij}}$ is the inertia matrix and $C_{{ij}}$ is the matrix of hydrostatic and gravitational coefficients. The externally applied inertia $M_{{ij}}^{E}$, damping $B_{{ij}}^{E}$ and stiffness $C_{{ij}}^{E}$ matrices in Eq. (9.2) can be tuned to control the motion of the WECs in a desirable way, such that the power output is maximised. It is common to either tune the external damping alone (real tuning) or the external damping and stiffness (reactive tuning). Applicability of the linear BEM codes requires that the hydrodynamic problem is suitably linear, and that the motion of any floating bodies remains small compared to the wave height. Larger excursions that can alter for example the hydrostatics of a WEC, must be captured in the time domain.

The WAMIT is used to determine $A_{{ij}}^{{added}}$, $B_{{ij}}^{{added}}$, $F_{i}$ and response amplitude operators $\bar{\xi }_{j}$ (non-dimensional excursion amplitudes). Equation (9.3) highlights the principle steps required in the procedure that follows, in which the excursion amplitudes are normalised, the auxiliary power $P_{{aux}}$ is evaluated (expressed in $W/m^{2}$), the average absorbed power per farm element $\bar{P}_{n}$ is found and summated to give the average absorbed power by the array.

$$P_{{aux}} = \frac{1}{2}\omega ^{2} B_{{ij}}^{E} \left| {\bar{\xi }_{j} } \right|^{2} ~ \Rightarrow \bar{P}_{n} = \smallint 2P_{{aux}} S\left( \omega \right)d\omega ~ \Rightarrow \bar{P} = \mathop \sum \limits_{n}^{N} \bar{P}_{n}$$

(9.3)

As discussed above, a plethora of methods have been developed and applied in WEC arrays modelling. This article provides the application of two methods, namely the Boundary Element Method and Phase Averaged Spectral Wave Model for evaluating the wave-device array interactions, where the BEM is used in assessing the performance and wave climate of the WEC array in nearfield (Sect. 9.4), whereas the Phase Averaged Spectral Wave Model is used in the ocean scale (Sect. 9.5).

9.3.1 Problem Definition

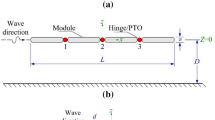
This paper considers arrays of two different types of WECs, i.e. the terminators (e.g. Oyster WEC) and attenuators (e.g. Pelamis WEC). The terminator type WEC is shown in Fig. 9.1(a), which comprises a flap-type floating body hinged at the bottom to a foundation, hence only allowing for the rotational motion about the hinge (pitch, $\Theta _{y}$). Note that the local-coordinate ($x,y,z$) is located at the hinge. The flap has a width $a_{f}$, immersion depth $d_{f}$, thickness $h_{f}$ and the hinge is located at a height $c_{f}$ from the seafloor. The attenuator type WEC is shown in Fig. 9.1(b), which comprises four modules connected by three hinges. The modules are allowed to pitch ($\Theta _{y}$, rotation about $y$-axis) and yaw ($\Theta _{z}$, rotation about $z$-axis) at their connected hinges. Note that the local-coordinate ($x,y,z$) is located at the hinge 2 (see Fig. 9.2b). The attenuator has a total length $L_{a}$, a diameter of $\emptyset _{a}$ and an immersed depth $d_{a} ~ = \emptyset _{a} /2$, where the length of the hinges is assumed to be negligibly small so that each module has an equal length of $L_{a} /4$. The PTO system is modelled by a force represented by the damping coefficient $B^{E}$ to convert the kinetic energy into electricity. The seabed is considered to be flat with a constant water depth of $d$. The principal dimensions for the terminator and attenuator are presented in Table 9.1.

Fig. 9.1

Dimensions for: a Terminator WEC, b Attenuator WEC

Fig. 9.2

Array layout for: a Terminator WEC, b Attenuator WEC

Table 9.1 Principal dimensions and properties for terminator and attenuator WECs

The array layouts for the WECs are presented in Fig. 9.2(a)-(b), in which the waves approach the arrays at an angle $\theta$ from the $Y$-axis. Each terminator and attenuator array has seven WECs and is arranged in a two-row array configuration as shown in Fig. 9.2(a) and (b), with four devices at the front row and three devices at the back row. For the terminator array, the devices are spaced at an equal horizontal distance $d_{x}$ of $2a_{f}$ and vertical distance $d_{y}$ of $a_{f}$. Note that these are the optimal spacings obtained via an optimisation scheme [44] to produce the maximum $q$-factor at the operating wave period $T$. On the other hand, the horizontal spacing $d_{x}$ and vertical spacing $d_{y}$ for the attenuator array are $2L_{a}$ and $L_{a}$, respectively, and these spacings are determined to ensure that the devices do not interfere with each other under oblique wave direction. The rigid body motion of the devices together with the total wave elevation surrounding the arrays are generated by using WAMIT. These values are expressed in terms of the response amplitude operator RAO. The stochastic post-processing is then performed in MATLAB to obtain the average q-factor of the array and the significant wave height of the wave climate under the multi-directional sea. The details of the post-processing will be discussed in Sect. 9.3.2.

9.3.2 Mathematical Formulation

9.3.2.1 WEC Under Regular Wave

Consider a generic WEC operating in a constant water depth $d$ as shown in Fig. 9.3. The WEC is subjected to an incoming wave of wave period $T$ and a wave height $2A$, where A is the wave amplitude, which impacts the structure at a wave angle $\theta ~$ measured from the Y-axis (see Fig. 9.2). The motion of the WEC is assumed to be $W = \left( {W_{x} ,W_{y} ,W_{z} ,\Theta _{x} ,\Theta _{y} ,\Theta _{z} } \right),$ where $W_{x}$, $W_{y}$ and $W_{z}$ are the respective translations about the x-, y- and z-axes and $~\Theta _{x} ,~\Theta _{y}$ and $\Theta _{z}$ the respective rotations about the x-, y- and z-axes. The water domain is denoted by $\Omega$ whereas the symbols $S_{F}$, $S_{B}$, $S_{s}$ and $S_{\infty }$ denote the boundary for the free surface, the seabed, the wetted surface of the WEC and the artificial boundary at infinity, respectively, as shown in Fig. 9.3.

Fig. 9.3

Computational domain for a generic wave energy convertor

Governing Equation for Water Motion

The water is assumed to be an ideal fluid with no viscosity, incompressible and the fluid motion is irrotational. Based on these assumptions, the fluid motion may be represented by a velocity potential $\Phi \left( {x,y,z,t} \right)$. We consider the water to oscillate in a steady-state harmonic motion with the circular frequency $\omega$. The velocity potential $\Phi \left( {x,y,z,t} \right)$ could be expressed into the following form

$$\Phi \left( {x,y,z,t} \right) = \text{Re} \left\{ {\phi \left( {x,y,z} \right)e^{{ - i\omega t}} } \right\}$$

(9.4)

The single frequency velocity potential $\phi \left( {x,y,z} \right)$ must satisfy the Laplace equation [45] and the boundary conditions on the surfaces as shown in Fig. 9.3. These boundary conditions are given in Faltinsen [45]. The Laplace equation together with the boundary conditions on the surface S are transformed into a Boundary Integral Element (BIE) by using the Green’s 2^nd Theorem via a free surface Green’s function given in the WAMIT manual [46] that satisfies the surface boundary condition at the free water surface $S_{F}$, the seabed $S_{B}$ and at the infinity $S_{\infty }$. Hence, only the wetted surface of the body $S_{s}$ needs to be discretised into panels so that the boundary element method could be used to solve the diffracted and radiated velocity potentials. For details on the Green’s function used in solving the BIE, refer to the WAMIT manual [46].

Governing Equation for WEC Motion

The WEC with a moment of inertia $I$, Mass $m$, PTO damping $B^{E}$ and hydrostatic stiffness $C$ is assumed to be a rigid body oscillating with six degrees of freedom rigid body motion ${\mathbf{W}}\left( {x,y,z,t} \right)~$ at a frequency $\omega$ and is subjected to wave forces $F$. ${\mathbf{W}}\left( {x,y,z,t} \right)~~$ could then be written as

$${\mathbf{W}} = Re\left\{ {W\left( {x,y,z} \right)e^{{ - i\omega t}} } \right\}$$

(9.5)

where $W = \left( {w_{1} ,w_{2} ,w_{3} ,w_{4} ,w_{5} ,w_{6} } \right)$. It is noted that $w_{1} ,w_{2} ~{\text{and }} w_{3}$ are the WEC translation motion along the $x$, $~y$ and $z$-axes, respectively, whereas $w_{4} ,w_{5}$ and $w_{6} ~$ are the rotational motion about the $x$-, $y$- and $z$-axes, respectively. The corresponding equation of motion for the terminator or attenuator expressed in Einstein summation convention is given by

$$\begin{aligned} &\left[ {\omega ^{2} \left( {M_{{ij}} + A_{{ij}}^{{added}} } \right) - i\omega \left( {B_{{ij}}^{{added}} + B_{{ii}}^{E} } \right) + C_{{ij}} } \right]w_{j} = F_{i} ,\\ &\,{\text{where}}\left\{ {\begin{array}{*{20}l} {i,j = 5} & {{\text{for}}\,{\text{terminator}}} \\ {i,j = 3,5,6} & {{\text{for}}\,{\text{attenuator}}} \\ \end{array} } \right. \end{aligned}$$

(9.6)

where, $M_{{ij}}$ is the inertia matrix for the pitch component as given in the WAMIT manual [46]. For the case of a terminator, the external damping $B_{{55}}^{E}$ in (9.6) is the optimum PTO damping for the rotational (pitch) motion and is obtained from Eq. (9.7) [10]. On the other hand, $B_{{55}}^{E}$ and $B_{{66}}^{E}$ for the attenuator WEC are obtained via a trial and error calibration process with hydrodynamic properties found in the literature,

$$B_{{55}}^{E} = \sqrt {\frac{{\left[ {C_{{55}} - \omega ^{2} \left( {M_{{55}} + A_{{55}}^{{added}} } \right)} \right]^{2} }}{{\omega ^{2} }} + \left( {B_{{55}}^{{added}} } \right)^{2} }$$

(9.7)

where, $A_{{55}}^{{added}}$ and $B_{{55}}^{{added}}$ are the added inertia and radiated damping for the pitch component, respectively whereas $C_{{55}}$ is the rotational stiffness. It is to note that $M_{{55}}$ in (9.7) is the mass moment of inertia $I$ for the terminator given in Table 9.1. Note that $B_{{55}}^{E}$ varies with respect to the wave frequency $\omega$; however, the PTO damping is taken as a constant in WAMIT by taking the minimum value of the $B_{{55}}^{E}$ generated from (9.7). This value is found from calibration with known results published in the open literature as shown later in Sect. 9.4.

The excitation force $F_{i}$ in Eq. (9.6) comprises the wave force components which can be derived from the velocity potential $\phi \left( {x,y,z} \right)$ as,

$$F_{i} = i\rho \omega \mathop \smallint \limits_{S} \phi \cdot n_{i} \cdot dS,~\,{\text{where}}\left\{ {\begin{array}{*{20}c} {i = 5} & {{\text{for}}\,{\text{terminator}}} \\ {i = 3,5,6} & {{\text{for}}\,{\text{attenuator}}} \\ \end{array} } \right.$$

(9.8)

where, $\rho$ is the mass density of the seawater. $n_{5}$ and $n_{6}$ are, respectively, the pitch and yaw components of the unit normal vector to the K-th panel in local coordinate system defined as $\left( {n_{4} ,n_{5} ,n_{6} } \right) = \user2{r} \times \user2{n},$ where $\user2{n} = \left( {n_{1} ,n_{2} ,n_{3} } \right)$ is the unit normal vector which is defined to point out of the fluid domain and $\user2{r}$ is the vector of coordinates of the WEC panel. It is to note that the subscripts $1$, $2$ and $3$ denote the translation motion about the $x,~y$ and $z$-axes, respectively, whereas 4, 5 and 6 denote the rotational motion about the $x,~y$ and $z$-axes, respectively. As the velocity potential $\phi$ in Eq. (9.4) could be further decomposed into the diffracted $\phi _{D}$ and radiated $\phi _{R}$ part, this gives us the exciting moment $F_{i}$ which is derived from the diffracted velocity potential, and the added inertia $A_{{ij}}^{{added}}$ and radiated damping $B_{{ij}}^{{added}} ~$ which are derived from the radiated velocity potential.

For $N$ numbers of WECs, the equation of motion of the terminator body $n$ due to the body $p$ is written as

$$\begin{gathered} \left\{ {\omega ^{2} \left[ {M_{{ij}} + \left( {A_{{ij}}^{{added}} } \right)_{{nn}} } \right] - i\omega \left[ {B^{E} + \left( {B_{{ij}}^{{added}} } \right)_{{nn}} } \right] + C_{{ij}} } \right\}\left( {w_{j} } \right)_{n} ~ \hfill \\ - \mathop \sum \limits_{{\begin{array}{*{20}c} {p = 1} \\ {p \ne n} \\ \end{array} }}^{p} \left[ {\omega ^{2} \left( {A_{{ij}}^{{added}} } \right)_{{pn}} + i\omega \left( {B_{{ij}}^{{added}} } \right)_{{pn}} } \right]\left( {w_{j} } \right)_{p} = \left( {F_{i} } \right)_{n} \hfill \\ \end{gathered}$$

(9.9)

where, $i,j = 5$ for terminator WEC and $i,j = 3,~$ 5,6 for attenuator WEC. It is to note that $W$ in (9.5) can be expanded as a series of product of the complex excursion amplitudes $\xi _{j}$ and rigid body modes, thus, the equation of motion can also be represented by (9.2).

9.3.2.2 WEC Array Under Multi-Directional Sea

The JONSWAP (JS) wave spectrum is developed for limited fetch North Sea by the offshore industry and is given by Goda [47]

$$S_{{JS}} \left( \omega \right) = \beta _{\gamma } \cdot 8.1 \times 10^{{ - 3}} \frac{{g^{2} }}{{\omega ^{5} }}\exp \left[ { - 0.032\left( {\frac{g}{{H_{s} \omega ^{2} }}} \right)^{2} } \right]\gamma ^{b}$$

(9.10)

where, the normalising function $\beta _{\gamma } = 1 - 0.287\ln \gamma$ [48], $b = \exp \left[ { - \frac{{\left( {\omega - \omega _{p} } \right)^{2} }}{{2\sigma ^{2} \omega _{p}^{2} }}} \right]$ and bandwidth parameter $\sigma = \left\{ {\begin{array}{*{20}c} {0.07} & {{\text{for}}~\omega < \omega _{p} } \\ {0.09} & {{\text{for}}~\omega \ge \omega _{p} } \\ \end{array} } \right.$. $\omega$ and $\omega _{p} ~$ are the wave frequency and peak wave frequency, respectively, $g$ the gravitational acceleration and $H_{s}$ is the significant wave height. It is noted here that the shape parameter $\gamma$ is taken as a mean value of 3.3.

The multi-directional wave spectrum $S_{{JS}}^{{MD}} \left( {\omega ,\theta } \right)$ is then obtained by multiplying the wave spectrum $S_{{JS}} \left( \omega \right)$ with a spreading function $D\left( \theta \right)$ as given in Eq. (9.11),

$$S_{{JS}}^{{MD}} \left( {\omega ,\theta } \right) = \mathop \sum \limits_{{i = 1}}^{{mf}} S_{{JS}} \left( {\omega _{i} } \right) \cdot D\left( \theta \right)$$

(9.11)

where, $mf$ is the number of wave frequency $\omega _{j}$ considered in the JONSWAP wave spectrum $S_{{JS}} \left( \omega \right)$. The spreading function $D\left( \theta \right)$ is given by,

$$\begin {aligned} & D\left( \theta \right) = \mathop \sum \limits_{{j = 1}}^{m} \left\{ {\frac{{\sqrt \pi ~\Gamma \left( {\hat{s} + 1} \right)}}{{2\theta _{{\max }} \Gamma \left( {\hat{s} + \frac{1}{2}} \right)}} \cdot \left| {\cos \left( {\frac{{\pi \left( {\theta - \overline{{\theta _{j} }} } \right)}}{{2\theta _{{\max }} }}} \right)} \right|^{{2\hat{s}}} } \right\}, \\& for - \theta _{{\max }} < \left( {\theta - \overline{{\theta _{j} }} } \right) < \theta _{{\max }} \end{aligned}$$

(9.12)

where, $m$ is the number of wave direction $\theta _{i}$ considered in the spreading function $D\left( \theta \right)$, $\bar{\theta }_{j}$ is the mean wave direction, $\hat{s}$ the wave spreading parameter and $\theta _{{\max }} = \pi /2$ in (9.12).

9.3.3 Generated Power and Interaction Factor

By solving the equation of motion (9.9), $w_{j}$ of the WEC can be obtained. This value can then be used to derive the average power generated by the $n$th WEC over the range of wave frequency $\omega$ considered under the multi-directional sea by using the following expression [30],

$$\left( {\overline{{P_{n} }} } \right) = \mathop \smallint \limits_{{ - \pi /2}}^{{\pi /2}} \left( {\omega ^{2} \cdot B^{E} \cdot \left| {w_{i} } \right|_{n}^{2} } \right) \cdot S_{{JS}}^{{MD}} \left( {\omega ,\theta } \right) \cdot ~d\omega ,~~~{\text{where~}}\left\{ {\begin{array}{*{20}c} {i = 5} & {{\text{for}}\,{\text{terminator}}} \\ {i = 5,6} & {{\text{for}}\,{\text{attenuator}}} \\ \end{array} } \right.$$

(9.13)

Noted also that (9.13) provides the average power generation ($\overline{{P_{n} }}$) of the nth WEC in the wave energy farm when subjected to the multi-directional sea in the long term statistical sea state. In order to quantify the interaction between devices, Budal [14] defines the q-factor which is modified here in Eq. (9.14) for the multi-directional sea to facilitate the discussion on the performance of the array.

$$q = \frac{{\sum\nolimits_{{n = 1}}^{N} {\left( {\overline{{P_{n} }} } \right)} }}{{N \times \left( {\overline{{P_{0} }} } \right)}}$$

(9.14)

where, ${\overline{{P_{0} }} }$ is the average generated power of an isolated WEC and the total average generated power in the array $\bar{P} = \mathop \sum \nolimits_{{n = 1}}^{N} \left( {\overline{{P_{n} }} } \right)$. For simplicity, the total average generated power will be referred as $P$ and the hat of the wave spreading parameter $\hat{s}$ is dropped and represented by $s$. Equation (9.14) is used as a performance evaluator for the array where a constructive interaction is denoted by a value greater than 1.0 and a destructive interaction when smaller than 1.0.

9.3.4 Wave Disturbance Under Multi-Directional Sea

The diffracted and radiated wave elevations surrounding the WEC arrays under regular wave could be obtained directly from the WAMIT software. The response amplitude operator for the wave elevation $\bar{\xi }_{\eta }$ are expressed by normalising the wave elevation $\eta$ with the incident wave amplitude $A$, i.e.

$$\bar{\xi }_{\eta } = \frac{\eta }{A}$$

(9.15)

In order to obtain the significant wave height of the wave disturbance under the multi-directional sea, the square of the amplitude for $\bar{\xi }_{\eta }$ is multiplied with the multi-directional wave spectrum to obtain the response spectrum $S_{{res}} \left( {\omega ,\theta } \right)$ as follows

$$S_{{res}} \left( {\omega ,\theta } \right) = \smallint \left| {\bar{\xi }_{j} } \right|^{2} ~ \cdot S_{{JS}} \left( {\omega ,\theta } \right) \cdot ~d\omega$$

(9.16)

The significant wave height of the wave field is obtained as:

$$\left( {H_{s} } \right)_{{wf}} = 4\sqrt {m_{0} }$$

(9.17)

where, $m_{0} ~$ is the moment of order 0 of spectrum $S_{{res}} \left( {\omega ,\theta } \right)$.

9.4 Verification of the Numerical Model

The numerical models for the terminator and attenuator were verified with the hydrodynamic properties found in the literature review. The verification of the numerical model for the terminator WEC was undertaken by Tay and Venugopal [44, 49, 50]. The results obtained from our numerical model were found to be in very good agreement as with those published by Renzi et al. [51] and Retzler [52]. With the numerical model verified with the existing data found in the literature, the hydrodynamic interaction analysis is then performed on the array layouts presented in Fig. 9.2 with the particulars given in Table 9.1. The number of terminator and attenuator WECs formed in the array is the same as those presented in Fig. 9.2. Note that the terminator and attenuator WEC arrays shown in Fig. 9.2 generate an approximately 5 MW of power, where each terminator and attenuator WECs has a rated power of 800 kW and 750 kW, respectively.

The arrays are subjected to multi-directional sea generated using the JONSWAP wave spectra. Three different wave spreading parameters $s$ as given in Eq. (9.12) are considered, i.e. $s~ =$ 4, 15 and 100. It is noted here that the larger $s~$ value, i.e. $s~ = 100$ corresponds to the uni-directional sea whereas the smaller $s$ value, i.e. $s~ =$ 4 corresponds to a combination of wave components approaching from different directions with the most wave coming from $~\bar{\theta }$.

9.4.1 Performance of Arrays

9.4.1.1 Response of WECs Under Multi-Directional Sea

The responses of the individual and arrays of terminator and attenuator WECs when subjected to waves generated by the JONSWAP spectrum with a significant wave height of 3 m are plotted in Fig. 9.4 to study the motion behaviour of the various WECs under the multi-directional sea. It is noted that the response $\theta _{s} ~$ of the attenuator, WEC is presented as the total summation of the magnitude response (pitch $w_{5}$ and yaw $w_{6}$) at the three joints of the WEC. The results shown here are only for the spreading parameter = 4. It is to be noted that the responses of the WECs for $s = 15$ and 100 have similar patterns as their counterparts of $s = 4$, but with higher magnitudes when the wave spreading parameter $s$ increases. This is because of the more concentrated wave energy distribution when waves approach close to the uni-directional sea.

Fig. 9.4

Performance of WECs for JONSWAP spectrum $H_{S} = 3~{\text{m}}$, $~s = 4$. Top: single terminator and attenuator, and, bottom: an array of terminators and attenuators

The response of the terminator WEC is found to increase with the increase of wave period, i.e. wavelength and when the wave approaches from the headsea. Hence, this suggests that the response of the terminator WEC is driven by the exciting torque and could be more effective when operating at harsh environment. On the other hand, the attenuator WEC is effective when the sea state is mild with its optimal performance occurs when the wave period is around 7–12 s. The motion is also found to be the highest when wave approaches from the headsea with decreasing response when wave approaches from the oblique direction. This is because of the higher pitching motion at the connection joints between the connected modules when subjected to the headsea condition, thus making the turret mooring system more preferable for the attenuator WEC as the device is able to weathervane in accordance to the different wave directions.

The average responses of the WECs when deployed in arrays are also presented in Fig. 9.4. It is noted that the average response is obtained by normalizing the sum of the response of the WECs in the array with the numbers of WEC considered in the array, i.e. $\left( {\mathop \sum \nolimits_{{n = 1}}^{N} \bar{\xi }_{n} } \right)/N.$ It is important to note also that the average displacement for each WEC in the array may not be a good measure to quantify the performance of the array as the individual displacement may vary considerably about the average displacement value. Nevertheless the former is able to provide an overall insight to the performance of the WEC array under the multi-directional sea as the average displacement has similar patterns as their individual counterpart presented in Fig. 9.4. Due to the constructive and destructive interferences as a result of the hydrodynamic interaction between the devices, the effectiveness of the array configurations in generating energy could be quantified by using the q-factor (9.14), which is a quantity defined as the ratio of the average total power produced in an array to the power produced by an individual WEC. It is noted that the q-factor is related to the WECs’ response via Eq. (9.13) and is used to quantify the efficiency of the array in producing energy (Fig. 9.5) as compared to its individual counterpart, where constructive interference is denoted by q-factor value larger than 1.0. This is to say that q-factor greater than 1.0 is desirable as it implies that more energy could be generated by each WEC in the array as compared to a single isolated WEC.

Fig. 9.5

Comparison of q-factor for terminator and attenuator WEC arrays for JONSWAP Spectrum for different s and $H_{s}$ = 3 m

The performances of the WEC arrays expressed as the $q$-factor subjected to multi-directional sea are presented in Fig. 9.5. The q-factor is plotted against the mean wave direction $\bar{\theta }$ and the peak wave period $T_{p}$, where $\bar{\theta }~$ ranges from 0 $^\circ$ (headsea) to 90$^\circ$ (beam sea) and $T_{p}$ from 5 to 20 s. The maximum $\bar{\theta }$ for the attenuator is however taken only up to 45$^\circ$ as the attenuator is usually weathervane against the wave direction. Focusing on the multi-directional sea with $s~ =$ 4, it is observed that the terminator WEC has a higher q-factor with its value greater than 1.0 (denoting constructive interference) when the array is subjected to smaller $T_{p}$, i.e. smaller wavelength at headsea condition. At headsea direction, the q-factor is found to reduce with the increase of $T_{p}$. This is because when the terminator WEC is placed across the incoming wave, they behave like a breakwater, and a greater disturbance is generated as waves are diffracted and radiated, which contributes to the constructive wave interference between the wave energy devices.

On the other hand, the q-factor for the attenuator arrays are found to converge to 1.0 with the increase of $T_{p}$ indicating that the hydrodynamic interactions of these types of WEC arrays when operating at a longer wavelength are similar to their counterparts of a single device. This is because the attenuator WECs oscillate at the same phase and amplitude as the incoming wave when the wavelength is large, hence resulting in a smaller relative motion. It is found that the q-factor for the attenuator WEC array is greater than 1.0 when the $T_{p}$ is smaller indicating the occurrence of constructive interference. This is attributed to the larger relative movement between the modules in the attenuator WEC and hence generating greater power when the wavelength is small. It is observed from the time series simulation that the radiated waves generated by the attenuator devices could be as small as 1.0 m (as a result of energy being extracted from the wave) which contribute significantly to the constructive interference between the devices. This shows that the diffracted and radiated waves that arise from the presence of the devices aid in increasing the power absorption of the wave farm. For all the WEC arrays, the maximum q-factor occurs when wave approaches from the headsea direction ($\bar{\theta } =$ 0$^\circ$).

Similar observation on the performance of the WEC arrays is also found when $s$ increases to 15. The q-factors for the terminator WEC array are found to be affected significantly by the changes in $\bar{\theta }$ with the increase of $s$ for the whole range of $T_{p}$ considered whereas the counterpart for the attenuator WEC array is only influenced by the changes in $\bar{\theta }$ when $T_{p}$ is small. This finding is affected by the absorption bandwidth of the WECs where the terminator is known to have a wider bandwidth [10], hence enabling it to generate energy at a wider range of wave frequency, i.e. wave period.

It can be seen from Fig. 9.5 that the terminator and attenuator WEC arrays have a higher q-factor when subjected to uni-directional sea, i.e. s = 100. This is because the encountered waves have a very small spreading and travel in the headsea direction. This also emphasizes the importance of taking into account the realistic sea by using the multi-directional sea and suggests that the q-factor could sometimes be overestimated if the uni-directional sea is assumed instead of the multi-directional sea. The q-factor for the attenuator WEC array has the same trend for varying $s$ value but in general, it is observed that the q-factor varies significantly with the changes in wave directions at smaller $T_{p}$. However, for the attenuator type WECs such as the Pelamis WEC, the device is always weathervane with respect to the incoming waves, thus allowing the WEC to generate maximum wave power at headsea direction.

9.4.1.2 Wave Climate Surrounding Arrays

The wave disturbance is represented by the significant wave height $\left( {H_{s} } \right)_{{wf}}$, which is obtained via post-processing of the regular wave elevations approaching from different directions as given in Eqs. (9.16) and (9.17). Three different spreading parameters $s = 4$, 15 and 100 are considered. The array layout as presented in Fig. 9.2(a) and (b) are used for the terminator and attenuator WEC arrays, respectively, where the terminator WEC array has a computational domain of 600 × 1200 m whereas the attenuator WEC array has a computation domain of 1400 × 3000 m. The computational domain of the arrays for these two types of WEC is different as it depends on the attenuated wave downstream the array which will be presented in the subsequent sections.

The significant wave heights of the wave field $\left( {H_{s} } \right)_{{wf}}$ surrounding the terminator and attenuator WEC arrays subjected to the multi-directional sea are presented in Fig. 9.6. The mean wave propagation direction considered is $\bar{\theta } =$ 0^o and the significant wave height is $H_{s} =$ 3 m. The wave disturbances upstream and downstream of the array depend significantly on the mechanism of wave generation by the WECs. In general, it can be seen from Fig. 9.6 that the maximum wave height of the wave disturbance due to the presence of the WEC arrays is the highest for the attenuator WEC array, followed by the terminator array. It can also be seen that the maximum $\left( {H_{s} } \right)_{{wf}} ~$ occurs at the wave field near the WECs due to the greater interaction of the diffracted and radiated waves, and these wave elevations are found to be attenuated when they are propagating away from the arrays. The presence of the highest $\left( {H_{s} } \right)_{{wf}} ~$ in the wave field surrounding the attenuator array is attributed to the greater intensity of waves being radiated by the attenuator WECs. The intensity of the interaction between the diffracted and radiated waves will affect the wave attenuation at the downstream of the array. For the case when $s~ =$ 4, the wave interaction is the greatest for the attenuator WEC array, hence explains the occurrence of the slowly attenuated waves downstream of the array as compared to their counterparts of the terminator WEC arrays. Note that this phenomenon can be checked by observing the $\left( {H_{s} } \right)_{{wf}} ~$ of the wave disturbance, where the wave is fully attenuated when it approaches $H_{s} =$ 3 m, i.e. the significant wave height of the wave spectrum. This implies that the radiated and scattered waves have diminished and only the incident waves are present.

Fig. 9.6

Comparison of $\left( {H_{s} } \right)_{{wf}}$ for terminator and attenuator WEC arrays for JONSWAP spectrum for different s. $\bar{\theta } =$ 0$^\circ$, $T_{p} = 8s$

Fig. 9.7

Comparison of $\left( {H_{s} } \right)_{{wf}}$ for terminator and attenuator WEC arrays under JONSWAP wave spectrum for different s. $\bar{\theta } =$ $45^\circ$, $T_{p} = 8s$

When comparing the effect of the spreading parameters $s$, it can be seen that the wave disturbances surrounding the terminator WEC arrays are greater when $s~ =$ 100, i.e. when the arrays are subjected to an almost uni-directional sea. However, the opposite is observed for the attenuator WEC array where greater disturbance is noticed when $s~ =$ 4. The difference is attributed to the means of power generation by different types of WECs. As the attenuator generates power via articulation in two degrees of freedom, there are greater interactions with the waves approaching from different directions, which is represented by the multi-directional sea when $s~ =$ 4. On the other hand, the terminator WEC pitches to generate energy with respect to the wave oscillation when the wave approaches in a single direction, i.e. $s~ =$ 100, and thus contributes to a lesser disturbance in the wave field. As the terminator WECs generate energy via a single degree of freedom, their presence in the uni-directional sea i.e. $s~ =$ 100 will produce greater wave disturbance because of the higher wave energy in the governing direction. It can also be seen that due to the geometry of the terminator WEC that is oriented perpendicular to the wave propagation direction, greater waves are being reflected upstream as compared to their counterparts of the attenuator WECs.

In Fig. 9.6, the wave disturbances surrounding the terminator WEC arrays are found to behave in the similar manner with respect to the changes in $s$. However, the opposite trend is found for the WEC array under the oblique sea (see Fig. 9.16) as compared to those presented when $\bar{\theta } =$ 0$^\circ$ (in Fig. 9.15), where the wave disturbance increases with greater $s$ value, i.e. $s~ =$ 100. For the terminator WEC array under oblique sea, larger wave separation occurs when the wave hits on the terminator WEC array, which in a group behaves like a single floating breakwater. This wave separation phenomena result in a larger wave disturbance downstream as observed in Fig. 9.7. It is also found from Fig. 9.7 that the wave attenuates at a slower pace downstream the WEC arrays as compared to their counterparts of the headsea presented in Fig. 9.6. This shows a greater interference of diffracted and radiated waves occur between the devices in the array when subjected to an oblique sea condition.

9.5 WEC Array Modelling by Ocean Scale Numerical Models

The extraction of wave energy from a wave farm produces a wave energy deficit or shadow down region which in turn may affect the downstream sediment transport and may thus result in beach erosion/deposition. The quantification of the wave energy reduction and identification of induced wave height gradients are desired for an accurate assessment of the environmental impact of a Wave Energy Converter (WEC) array on the nearby marine environment. Here we investigate the consequences wave energy extraction by large scale wave arrays in the areas of the Crown Estate Round 1 lease sites in the Pentland Firth and Orkney Waters (PFOW) in the United Kingdom (Fig. 9.8). MIKE 21 Spectral Wave, in association with the wave-structure interaction software tool WAMIT, has been employed to study the impact of energy extraction by large arrays of Wave Energy Converters (WECs) on the wave height alteration in the neighbourhood of WEC arrays. As with Sect. 9.4, two generic types of WEC, one representing surface attenuators (deployed in deep water) and other representing terminators (deployed in shallow waters) are used for numerical modelling. The power extraction performance of the WECs are initially modelled using WAMIT (Sect. 9.4) and validated with data from the literature. As MIKE 21 SW has limited ability in modelling complete dynamics of a moving structure, each WEC has been modelled as a generic structure but with appropriate reflection, transmission and energy absorption properties derived from WAMIT, and this methodology is found to have worked well.

Fig. 9.8

Location of Pentland Firth showing wave and tidal energy leasing sites (http://www.thecrownestate.co.uk/energy-and-infrastructure/wave-and-tidal/the-resources-and-technologies/3)

9.5.1 Numerical Model Set-Up

MIKE 21 SW is a third-generation spectral wind-wave model utilising unstructured meshes [53] to simulate the growth, decay and transformation of the wind-generated sea and ocean swells in offshore and coastal areas. The wind waves are expressed by the wave action density spectrum. The model accounts for the physical phenomenon of wave growth from wind, energy transfer due to non-linear quadruplet or triad wave-wave interaction, and includes energy dissipation terms for white-capping, bottom friction and depth-induced breaking. A cell-centred finite volume method is applied in the discretization of the governing equations in geographical and spectral space and a multi-sequence explicit method is applied for the wave propagation with the time integration carried out using a fractional step approach. The model generates phase averaged wave parameters as output for either the total computational domain or selected parts thereof. Further details can be found in the MIKE 21 wave modelling user guide [53].

An unstructured computational mesh (see Fig. 9.9) was constructed for the North Atlantic region (10^oE–75^oW and 10^oN–70^oN) using bathymetry data compiled from General Bathymetric Chart for Oceans (GEBCO, http://www.gebco.net/) and Marine Scotland Science [54]. Finer mesh resolutions were produced for Pentland Firth and Orkney Waters with a mesh area of 0.0005 square degrees (approx. 1700 m²), for the Hebrides and northwest Scotland of 0.001 square degrees and 0.75 square degrees (approx. 2.5 km²) for the North Atlantic Ocean. Further details on the model domain and setup are available in Venugopal and Nemalidinne [55]. The model was forced with wind data obtained from the operational model of the European Centre for Medium-Range Weather Forecasts (ECMWF, http://www.ecmwf.int/) at 6 hourly intervals with a spatial resolution of 0.125° × 0.125°. To ensure fetch unlimited wave growth, decay and transformation of wind sea and swells, the model was run in ‘fully spectral’ mode with ‘Instationary formulation’. The number of frequencies used for the model was 25 with f_min = 0.04 Hz and a logarithmic frequency distribution with a frequency factor of 1.1. The directional discretisation had 24 directional bins, each with 15° resolution. A low order fast algorithm has been chosen as the solution technique with the ‘maximum number of levels in the transport calculation’ set as 32. A quadruplet-wave interaction has been applied. No current, ice coverage and diffraction were included into the model. Dissipation due to whitecapping, bottom friction and depth-induced wave breaking were considered in the simulations and the energy transfer was activated. For a detailed description of the above source terms and the basis for selection of the appropriate values, the reader is referred to the MIKE 21 SW user guide [53] and [55]. Measured wave data from scientific buoys deployed around Scotland was used to calibrate and validate the model. The successful calibration and validation of the model are described in detail in [55].

Fig. 9.9

Computational domain for North Atlantic wave model

9.5.2 Predictions Without Energy Extraction

The efficiency of WECs depends on the characteristics of the site-specific resource, and key parameters are the wave height and period of the different sea states. Power matrices are a standard way of expressing WEC performance against particular sea states and the selection of the most appropriate site and technology for wave farm operation in a specific region should be based on a thorough analysis of the energy production of different combinations of different types of WECs at a range of sites. To be able to undertake such an assessment an accurate and detailed resource characterisation at each location of interest has to be conducted. The approach taken here is to run the MIKE 21 Spectral Wave model for the year 2010, with and without WECs, and to subtract the results from each other to produce maps of the differences in wave parameters following the inclusion of WECs. The significant wave height and conditions simulated for the year 2010 are shown in Figs. 9.10 and 9.11. The evolution of mean significant wave height for the pre-device model, for the study area around Orkney, is shown in Fig. 9.12 for the period January to December 2010, which is extracted from the validated model described in Sect. 9.3.1. Note that this is one of the strategic deployment zones identified by the Crown Estate in Fig. 9.8. As expected, the wave height decreases as the wave progresses from a westerly direction across the domain into reduced water depths. The annual average wave height varies from about 1.6 m to about 2.5 m at the sites where nearshore arrays are proposed.

Fig. 9.10

Comparison of significant wave height, between measurements (black line) and model (red line) for Orkney Islands wave deployment site (58.970200°N–3.390900°W)

Fig. 9.11

Wave rose diagram of the model data at Orkney location: left hand—significant wave height (Hm0) and right hand—peak wave period Tp

Fig. 9.12

Mean significant wave height for the period January to December–2010 without energy extraction

9.5.3 Implementation of Energy Extraction

Marine Scotland Science developed possible array layout scenarios from Environmental Statements submitted by developers. Two generic types of WEC are used, a surface-based line attenuator and terminators (Oscillating Wave Surge Converters, OWSC). The first device is based on the Pelamis WEC. The second device, an OWSC, used in this study is based on the Oyster 800 by Aquamarine Power. The WEC arrays proposed by the developers are:

• (i) Marwick Head: An array of 66 terminator type devices with a 350 x 400 m staggered spacing across 4 rows was considered.

• (ii) West Orkney: Arrays of 132 terminator devices with a 400 x 400 m distance between the WECs in two staggered rows, and 10 times the device length between the arrays (1800 m) were considered.

• (iii) Brough Head: Single row of 120 attenuator devices (26 m wide and 45 m spacing) was distributed as 4 arrays along the 12.5 m depth contour.

For the detailed methodology used for the array layouts see O’Hara Murray and Gallego [56]. These array configurations are modelled using MIKE 21 (see Fig. 9.13). This study explores a new method of removing energy from the model domain as the MIKE 21 SW model has no built-in algorithm for simulating WECs. By including individual WECs or WEC arrays as additional source terms representing the energy extracted and redistributed by the WECs in spectral wave models as used in this study, it is possible to assess the hydrodynamic behaviour and power performance of WEC array. Such an approach in the representation of WECs in the most commonly used coastal modelling packages has significant practical implications on the development of software tools for the planning of wave farms. Since the horizontal dimensions of WECs are usually smaller than the mesh resolution used in the computational grid, the generic wave energy device in the MIKE 21 SW are modelled using a sub-grid scaling technique. Further details may be found in [57]. The location of a WEC is given by a number of geo-referenced points which together make up a polyline. The location and geometry of these polyline structures are included when the mesh is created. The values of the wave energy transmission factors are still not completely understood (due to a lack of installed systems for validation) or openly disclosed by the WEC developers. Moreover, these values depend not only on the farm geometry, but on a wider range of factors, and they often appear to have a dynamic behaviour relationship with the impacting wave conditions.

Fig. 9.13

Map of the Orkney showing the layout of 300 WEC devices

Given that this work is concerned with surface attenuator and terminator type technology as represented by Pelamis and Oyster devices respectively, the values of the reflection, transmission and energy loss coefficients were obtained from the software tool WAMIT as presented in Sect. 9.3.2, to represent various scenarios.

Although the MIKE21 SW model does not have the ability to model the entire dynamics of a floating wave energy device, it can model wave propagation accurately over varying complex bathymetry in coastal to ocean scale regions, thus it makes a highly suitable tool to study wave forecasting or hindcasting. On the other hand, the wave structure interaction tool WAMIT, as demonstrated through various studies is powerful and accurate in modelling any type of fixed and floating offshore structures, but its downside is that it cannot be applied to varying bathymetry or wave forecasting or hindcasting and therefore its use in modelling realistic oceanic scale array to assess environmental impact is less proved. Hence the method to use WAMIT to determine the energy absorption, reflection and transmission characteristics of WECs and then transfer these into MIKE 21 for large scale array modelling and at the same time for studying WECs interaction with the marine environment on a wider scale is chosen. The facility available with MIKE 21 allows one to model the WEC as a line or point structure, and the former was chosen for this study to model the WECs. MIKE 21 also allows the structure to be modelled as a submerged, emergent, or sub-aerial structure.

The following methodology was adopted in modelling the devices. The energy transmission through any WEC structure can be represented by the energy balance equation,

$$C_{R}^{2} + C_{T}^{2} + C_{L}^{2} = 1$$

(9.18)

where, $C_{T}$ is the transmission coefficient, $C_{R}$ is the reflection coefficient and $C_{L} ~$ is the energy loss coefficient. The reflection and transmission coefficients are calculated in normalised form as ratios of reflected wave height to incident wave height, and, transmitted wave height to incident wave height respectively.

The information on energy loss or energy absorbed by a device could be obtained from the power matrix produced by developers. The power matrices for Pelamis and Oyster devices are extracted using the data from [58] and a metric known as Power Capture Ratio (PCR) is produced. The PCR which is a measure of wave power absorbed by a device can be calculated for the different range of significant wave heights (Hm0) and energy periods (T_e) as,

$$PCR = \frac{{P_{m} }}{{P_{{flux}} }}$$

(9.19)

where, $P_{m}$ is the power produced by a device based on its power matrix for a chosen pair of wave height and energy period and $P_{{flux}}$ is theoretical energy flux calculated for the same pair of wave parameters, using Eqs. (9.20) and (9.21),

$$P_{{flux}} \approx \rho g\frac{{H_{{m0}}^{2} }}{{16}}C_{g} \left( {T_{e} ,d} \right)$$

(9.20)

$$C_{g} \left( {T_{e} ,d} \right) = \frac{1}{2}\left[ {1 + \frac{{2kd}}{{\sinh 2kd}}} \right]\sqrt {\frac{{g\lambda }}{{2\pi }}\tanh \left( {kd} \right)}$$

(9.21)

where, $C_{g} \left( {T_{e} ,d} \right)$ is the group velocity corresponding to the energy period $T_{e}$, $\rho ~$ is the seawater density taken as 1025 kg/m³, $g$ is the gravitational constant, $k$ and $\lambda$ are the wavenumber and wavelength respectively, computed with $T_{e}$ for the depth $d$ using the linear wave ‘dispersion relationship’. Now the energy conservation Eq. (9.18) may be rewritten as,

$$C_{R}^{2} + C_{T}^{2} + \left( {PCR} \right)^{2} = 1$$

(9.22)

While $C_{T}$, $C_{R}$ and $C_{L}$ (or $PCR$) are wave period dependent which means they change with sea states, determining the energy coefficients for every wave frequency, while it is possible to do, is laborious, and considering the time and resources available, the wave periods that correspond to the maximum power output from both the attenuator and terminator have been selected and corresponding energy coefficients have been chosen to model the WECs in MIKE 21 SW model. This approach may be justified as the main interest is to evaluate the impacts on the environment when the devices operate at its best.

However, before using these coefficients in MIKE 21, the WAMIT results are to be validated which were done by comparing the results produced from WAMIT with published literature and from Sect. 9.3. To verify the validity of the above coefficients and method, wave climate modification for an array of devices from both WAMIT and MIKE 21 have been compared in Fig. 9.14, for significant wave height $H_{{m0}}$ = 3 m and peak wave period $T_{p}$ = 7.5 s. In total, three attenuator type devices and five terminators were simulated using JONSWAP wave spectrum with a peak enhancement factor of 3.3 and a directional standard deviation = 5°. Despite some differences in wave height distribution, the general wave propagation pattern in MIKE 21 agreed well with WAMIT. It is also clear that MIKE 21 shows a large reduction in wave height immediately downstream of the device and no alteration to the upstream wave field; this is expected as the wave diffraction which was included in WAMIT was not considered in MIKE 21. Nevertheless, as the far-field wave conditions being less affected in MIKE 21, and no other single software tool that can model both WEC and wave environments, it was decided to accept this solution for further modelling. A maximum difference of up to 30% in wave heights between WAMIT and MIKE 21 results are seen, particularly very close to downstream of the WECs, however, this difference is found to be minimum further downstream. Thus the WAMIT model has been verified, further simulations were carried out for the wave conditions corresponding to the maximum power production for each device and the values of transmission and reflection coefficients have been obtained. The values of the wave transmission/reflection coefficients for attenuator type devices selected were $C_{T} = 0.99$ and $C_{R} = 0.01$, and for terminator OWSC, $C_{T} ~ = 0.75$ and $C_{R} ~ = 0.25$.

Fig. 9.14

Comparison of WEC performance between WAMIT and MIKE21 SW models for a attenuator and b terminator. Wave conditions: H_m0 = 3 m, T_p = 7.5 s and $\bar{\theta }$ = 0°

Fig. 9.15

Mean significant wave height for the period January to December 2010 with energy extraction

Fig. 9.16

Absolute difference of mean significant wave height with and without energy extraction for the period January to December 2010

The WEC array models were simulated for the same time period as the baseline model (as in Fig. 9.12), to be able to evaluate the wave farm impact by comparing model outputs with and without WECs. Following the implementation of the WEC arrays (both attenuator and terminators) in the model for the year 2010, it is observed that the mean significant wave height is decreased downwave of the arrays and this is visible in Fig. 9.15. Further, the absolute mean difference in the significant wave height as a result of the inclusion of the WEC arrays is shown in Fig. 9.16. A clear reduction of wave height is observed downwave following the inclusion of WEC arrays with the largest differences being visible in the region immediately behind the wave array. At the point of maximum impact, i.e., downstream of array close to the coast, a large decrease in wave height based on the annual mean wave conditions is noticed and this constitutes a reduction of a maximum of up to 1 m or just above (i.e. difference in mean wave height computed with WEC minus no WEC) of the incident wave height. The wave height is decreased because of the energy extraction by the WEC array, which is indicated by a negative value in the downstream of the arrays (Fig. 9.16). Furthermore, the results show that as the downstream distance increases the individual effects of each device reduces and an evenly distributed reduction in wave height is observed. The impact of the wave farms decreases with increasing distance, and this is due to restoring processes e.g. diffracted wave energy penetrating into the lee of the wave farm from both sides.

A comparison of the baseline data time series against the WEC array scenario is shown in Fig. 9.17 for a location indicated by the red coloured point to the west of the Bay of Skaill in a water depth of 8 m. Significant wave height, peak wave period and mean wave direction of both cases are presented for the year 2010, and, it is clear that a significant reduction in wave height is obvious. The fact that the wave heights are reduced and the wave directions and wave periods are less affected, which demonstrates that changes to sediments and beach erosion at this site might be less significant, however, this needs further research.

Fig. 9.17

Comparison of time series of wave height, wave period and wave direction at Bay of Skaill between Baseline and WEC scenarios

To provide a detailed analysis of energy extraction, the percentage change in significant wave height for each node is calculated and shown in Fig. 9.18. The location of each device is indicated by a large reduction in wave height leeward of the device as indicated in the theoretical test in Fig. 9.14. The maximum percentage height difference results from a situation where a very small original wave height undergoes a substantial change due to wave farm even though the absolute difference is minimal. These changes of significant wave height represent the net change of wave conditions due to energy absorption by WECs, the interaction between devices within an array and between adjacent arrays, scattering by the array and local bathymetry effect. The magnitude of reduction clearly varies with both the number of devices installed in each row and their alignment. It is to be kept in mind that the results presented above are purely numerical simulation-based and no validation with real scale deployments has been done, hence the usage of this data to be treated with caution.

Fig. 9.18

Percentage change in significant wave height

9.6 Concluding Remarks

The possibilities of modelling wave energy converter arrays by using two different numerical models were illustrated in this article. Hydrodynamic performance of two types of energy converter arrays, i.e. a terminator and an attenuator was successfully investigated. These arrays were subjected to multi-directional realistic seas.

The arrays’ performance determined by the Boundary Element Method, presented in terms of the q-factor, was obtained by using stochastic analysis. The seas close to uni-directional wave conditions ($s = 100)$ tend to produce a much larger q-factor because of the greater energy density in the single wave component approaching from one direction. The q-factor differs in a relatively greater magnitude with respect to the peak wave period as compared to the wave direction, when subjected to multi-directional sea. Also, the q-factor of the terminator and attenuator WEC arrays are greater when the peak wave period is small. Comparison of the significant wave height of the wave field showed that the wave patterns upstream and downstream of the arrays depends significantly on the type of WECs where the WEC that generates greater diffracted and radiated waves tend to produce greater wave disturbance. Thus, the attenuator WEC generates a greater wave disturbance followed by the terminator; and these phenomena are even more obvious when waves approach from the oblique wave direction. The intensity of the wave disturbance was very much affected by the changes in the wave spreading parameters used in defining the spreading function and encountering wavelength (peak wave period) but not much by the variation in wave direction. In general, this depends on the diffracted and radiated waves generated by the WECs where greater wave disturbances are created when the WECs are subjected to smaller wavelength or when two uni-directional waves interfere with each other.

The array’s performance simulated using ocean scale numerical model demonstrated that the WEC arrays altered the wave climate within an array and also the neighbouring array. Cumulative wave height reduction downstream of the WEC array and farther down the coastline appears to be significant, and, its magnitude depends on the array layout and number of co-located arrays. The average yearly reduction in wave height immediately to the lee side of the array was observed to be very high, and its magnitude varies from arrays to arrays. With increasing distance from the arrays towards the shoreline, a recovery in wave heights or energy restore is evident, and energy progresses into the downwave shadow region of the arrays from the sides. The devices modelled for this article used frequency-independent transmission coefficients, rather than using a more detailed approach, due to unavailability of precise device-specific data. Further work is required in investigating frequency-dependent behaviour and dynamic response characteristics of coefficients for absorption, transmission and reflection.

The hydrodynamic interaction of the WEC arrays presented here has added values for WEC designers working on optimising the performance of the array. Also, the wave disturbance upstream and downstream of the arrays can be used as a guideline to coastal engineers in investigating the effect of the presence of the WEC arrays on the environment.