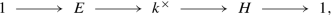Abstract
Here we give a proof of the ambiguous class number formula for quadratic number fields and show that it implies the quadratic reciprocity law.
Access provided by Autonomous University of Puebla. Download chapter PDF
It is quite difficult to determine class numbers, even in the simplest case of quadratic number fields, for fields with large discriminant. It is, however, possible to make several rather precise statements concerning the parity of class numbers of quadratic number fields. The theory behind these statements is called genus theory and goes back to Gauss, who worked with quadratic forms rather than quadratic number fields. Genus theory may be generalized to cyclic extensions, and in fact the question we will answer is how the Galois group of an extension acts on the ideal classes. In this chapter we will only scratch the surface of genus theory by proving the ambiguous class number formula.
The essential idea behind the proof is to reduce the action of the Galois group on ideal classes to the action on ideals, then on principal ideals and finally on elements, where everything can be done explicitly. Once more we will be studying a difficult object, namely the class group, by studying homomorphisms into simpler structures.
9.1 Ambiguous Ideal Classes
Let A be a finite abelian group. Then A can be written as a direct sum of cyclic groups, say A = A 1 ⊕⋯ ⊕ A n. If A is a finite 2-group, i.e., a group whose order is a power of 2, then the 2-rank of A is the number n of cyclic components. Since it is easy to see that \(A/A^2 \simeq A_1/A_1^2\oplus \cdots \oplus A_n/A_n^2\), and since \(A_j/A_j^2 \simeq {\mathbb Z}/2{\mathbb Z}\) for cyclic groups A j, the 2-rank of A is n if and only if #A∕A 2 = 2n.
The determination of the order of the quotient group Cl(k)∕Cl(k)2, i.e., of the 2-rank of the ideal class group, goes back to Gauss, who solved this problem in the language of binary quadratic forms. It is almost impossible to miss the central questions of this theory when studying the operation of the Galois group G = {1, σ} of \(k/{\mathbb Q}\) on the ideal class group.
For an ideal class \(c = [\mathfrak a]\) we set \(c^\sigma = [\mathfrak a^\sigma ]\); of course we have to show that this action is well defined (see Exercise 9.1). Clearly an ideal class c and its conjugate c σ always have the same order. Moreover, since \(c \cdot c^{\sigma } = [\mathfrak a][\mathfrak a^\sigma ] = [(N\mathfrak a)] = (1)\) is the principal class, c σ = c −1 is always the inverse class of c.
We call an ideal class c ∈Cl(k) ambiguous if c σ = c. Similarly, an ideal \(\mathfrak a\) is called ambiguous, if \(\mathfrak a^\sigma = \mathfrak a\).
Lemma 9.1
The nontrivial automorphism\(\sigma : \sqrt {m} \to - \sqrt {m}\)of\(k = {\mathbb Q}(\sqrt {m})\)acts as − 1 on the class group Cl(k). In particular, an ideal class c is ambiguous if and only if c 2 = 1.
Proof
We have already seen that \(\mathfrak a^{1+\sigma } = \mathfrak a\mathfrak a' = (N\mathfrak a)\) is principal, and that this implies that c σ = c −1.
If c is ambiguous, i.e., if c = c σ, then c 2 = c 1+σ = 1. Conversely, if c 2 = 1, then c σ = c −1 = c. □
If k is a number field with class number 2, then the nontrivial ideal class c is always ambiguous. For \(k = {\mathbb Q}(\sqrt {-5})\), the nontrivial ideal class is generated by the prime ideal \((2, 1+\sqrt {-5})\); since this ideal is ambiguous because of \((2, 1+\sqrt {-5})^\sigma = (2, 1-\sqrt {-5}) = (2, 1+\sqrt {-5})\). The ideal class c is also generated by \((3, 1+\sqrt {-5})\), and here \((3, 1+\sqrt {-5})^\sigma = (3, 1-\sqrt {-5}) \ne (3, 1+\sqrt {-5})\). In \({\mathbb Q}(\sqrt {-5})\), each ideal class contains an ambiguous ideal (the principal class contains the ambiguous ideal (1)), as well as many non-ambiguous ideals.
For ideal class groups of order 4, the number of ambiguous classes determines the structure. If \(\mbox{Cl}(k) \simeq {\mathbb Z}/2{\mathbb Z} \oplus {\mathbb Z}/2{\mathbb Z}\) is elementary abelian, then the number of ambiguous ideal classes is 4 since in this case, every ideal class is ambiguous. If \(\mbox{Cl}(k) \simeq {\mathbb Z}/4{\mathbb Z}\), on the other hand, then the two classes with order 4 are not ambiguous, whereas the class with order 2 and the principal class are ambiguous, Thus there are only 2 ambiguous ideal classes in this case.
If an ideal \(\mathfrak a\) is ambiguous, then so is the ideal class \(c = [\mathfrak a]\) it generates; the converse is not true in general: Since \(k ={\mathbb Q}(\sqrt {34})\) has class number 2, the ideal class c of order 2 is ambiguous. This ideal class is not generated by an ambiguous ideal for the simple reason that all ambiguous ideals in k are principal. As we will see below, each ambiguous ideal is a product of ramified prime ideals and ideals generated by ordinary integers. But in k we have \((2,\sqrt {34}) = (6 + \sqrt {34})\) and \((17,\sqrt {34}) = (17+3\sqrt {34})\).
The ambiguous ideal classes form a group \(\operatorname {Am}(k)\), in which the ideal classes generated by ambiguous ideals form a subgroup, namely the group \(\operatorname {Am}_{\operatorname {st}}(k)\) of strongly ambiguous ideal classes . Our goal is determining the structure of the group \(\operatorname {Am}(k)\).
This will allow us to deduce information about the elements of order 2 in the class group. In fact, since c σ = c −1 we have c 1−σ = c 2, and therefore the homomorphism c↦c 1−σ maps the class group Cl(k) of a quadratic number field k to the group Cl(k)1−σ = Cl(k)2 of ideal classes that are squares, and this homomorphism is onto. Its kernel consists of the ideal classes c with c 1−σ = 1, i.e., of the ambiguous ideal classes. This implies that the order of the group \(\operatorname {Am}(k)\) of ambiguous ideal classes is equal to the order of Cl(k)∕Cl(k)2:
Proposition 9.2
Let k be a quadratic number field. Then
and, in particular, the class number of k is odd if and only if the number of ambiguous ideal classes is 1.
Actually, since both groups are elementary abelian, equal cardinality implies isomorphism. The last claim follows from the observation that squaring is an isomorphism on a finite group if and only if it has odd order.
9.1.1 Exact Sequences
The calculations below are far easier to digest by using exact sequences. A short sequence of abelian groups A, B, C consists of group homomorphisms α : A→B and β : B→C, which are composed as follows:

The map 1→A (which is often denoted by 0→A if A is written additively) sends the element of the trivial group {1} to the neutral element of A. Similarly, C→1 is the homomorphism sending each element of C to the element of the trivial group {1}.
A sequence of abelian groups is called exact if the kernel of each map in the sequence is equal to the image of the preceding map (if there is one). Thus the sequence (9.1) is exact if and only if the following conditions are satisfied:
-
\(\ker \alpha = \mbox{im}\,\, (1 \longrightarrow A) = \{1\}\); in other word, α must be injective;
-
\(C = \ker (C \longrightarrow 1) = \mbox{im}\,\, \beta \); in other words, β must be surjective;
-
\(\ker \beta = \mbox{im}\,\, \alpha \).
Essentially, this short exact sequence contains the same information as the homomorphism theorem C ≃ B∕im A, but it has the advantage that all the maps occur explicitly in the diagram. Perhaps this advantage will only become clear by studying homological algebra more carefully. One goal of this chapter is showing that this is a useful thing to do for those who are interested in algebraic number theory.
The proof of Proposition 9.2 consisted in verifying the exactness of the sequence

The definitions of principal ideals and the ideal class group Cl(k) of a number field k provide us with two exact sequences, namely

where E k is the unit group, H k the group of (fractional) principal ideals ≠(0), and I k the group of all fractional ideals ≠(0).
9.1.2 Ambiguous Ideal Classes
The group \(\operatorname {Am}_{\operatorname {st}}(k)\) of strongly ambiguous ideal classes is, by definition, equal to \(\operatorname {Am}_{\operatorname {st}}(k) = AH/H \simeq A/A \cap H\), where A denotes the group of nonzero ambiguous ideals and H the group of nonzero principal ideals. Clearly A ∩ H = H G is the group of ambiguous principal ideals, and so we have \(\operatorname {Am}_{\operatorname {st}}(k) \simeq A/H^G\). This observation gives us the exact sequence

The group P of all fractional ideals (a) with \(a \in {\mathbb Q}^\times \) is a subgroup of both H G and A; this allows us to modify the exact sequence slightly and turn it into

Since \(\operatorname {Am}(k)\) is elementary abelian, i.e., since c 2 = 1 for each ambiguous ideal class c, for determining the structure of \(\operatorname {Am}(k)\) and \(\operatorname {Am}_{\operatorname {st}}(k)\) it is sufficient to compute the orders of these groups. The exact sequence (9.2) is a first step in this direction. The next steps consist in the computation of the order of H G∕P and of A∕P. Before we do so we present a simple but very effective tool.
9.1.3 Hilbert’s Theorem 90
Hilbert’s Theorem 90 (in Hilbert’s report on algebraic numbers, his famous Zahlbericht, the theorems were numbered, and this one had the number 90) comes in two versions, one for elements and one for ideals.
Theorem 9.3 (Hilbert’s Theorem 90 for Elements)
Let k be a quadratic number field and α ∈ k × . Then Nα = 1 if and only if α has the form α = β 1−σ . Here β is determined uniquely up to rational factors.
Equivalent formulations of Hilbert’s Theorem 90 are the following:
-
1.
There is an exact sequence

where N denotes the norm map \(N_{k/{\mathbb Q}}: k^\times \longrightarrow {\mathbb Q}^\times \).
-
2.
The group k ×[N]∕(k ×)1−σ is trivial. Here k ×[N] denotes the kernel of the norm map \(N: k^\times \longrightarrow {\mathbb Q}^\times \).
Proof
The proof of “⇐= ” is trivial. Assume therefore that Nα = 1. If α = −1, we set \(\beta = \sqrt {m}\); if α≠ − 1, we set β = α σ + 1; then \(\beta ^{\sigma -1} = \frac {\alpha +1}{\alpha '+1} = \frac {\alpha (\alpha +1)}{\alpha \alpha '+\alpha } = \frac {\alpha (\alpha +1)}{1+\alpha } = \alpha \). □
The corresponding result for ideals is
Theorem 9.4 (Hilbert’s Theorem 90 for Ideals)
If\(\mathfrak a\)is a fractional ideal Footnote 1in\(\mathcal O_k\) , then we have\(N\mathfrak a = (1)\)if and only if\(\mathfrak a\)has the form\(\mathfrak a = \mathfrak b^{\sigma -1}\)for some (integral) ideal\(\mathfrak b\).
Proof
As in the case of elements, the proof of “⇐= ” is trivial. Assume therefore that \(N\mathfrak a = 1\) (hence \(\mathfrak a = \mathfrak c\mathfrak d^{-1}\) is the quotient of two integral ideals \(\mathfrak c\) and \(\mathfrak d\) with the same norm). By the uniqueness of prime ideal factorization we may assume that \(\mathfrak c\) and \(\mathfrak d\) are coprime. This immediately implies that \(\mathfrak c\) and \(\mathfrak d\) are not divisible by any inert prime ideals: If, for example, we had \((q) \mid \mathfrak c\), then q 2 would occur in the factorization of \(N\mathfrak d\), hence \(\mathfrak d\) would also be divisible by (q), and this contradicts our assumption that \(\mathfrak c\) and \(\mathfrak d\) are coprime. For the same reason, no ramified prime ideals can divide \(\mathfrak c\). Thus \(\mathfrak c\) and \(\mathfrak d\) are products of split prime ideals. If \(\mathfrak c = \mathfrak p_1^{e_1} \cdots \mathfrak p_r^{e_r}\) is the prime ideal factorization of \(\mathfrak c\), then we must have \(N\mathfrak c = p_1^{e_1} \cdots p_r^{e_r} = N\mathfrak d\). Since \(\mathfrak c\) and \(\mathfrak d\) are coprime, none of the \(\mathfrak p_j\) can divide \(\mathfrak d\), hence the only possibility is that \(\mathfrak d = {\mathfrak p_1^{\prime }}^{e_1} \cdots {\mathfrak p_r^{\prime }}^{e_r} = \mathfrak c'\). But then \(\mathfrak a = \mathfrak c \mathfrak d = \mathfrak d' \mathfrak d^{-1} = \mathfrak d^{\sigma -1}\). □
9.2 The Ambiguous Class Number Formula
As a warm-up we construct a few exact sequences involving the following groups:
-
\(E = \mathcal O_k^\times \) is the unit group of \(\mathcal O_k\);
-
\(E[N] = \{\varepsilon \in E: N_{k/{\mathbb Q}}(\varepsilon ) = 1\}\) is the kernel of the norm map on the unit group, that is, the subgroup of units with norm + 1;
-
E 1−σ = {ε 1−σ : ε ∈ E};
-
H G = {(α) : (α)σ = (α)} is the group of ambiguous principal ideals;
-
\(P = \{(a): a \in {\mathbb Q}^\times \}\) is the subgroup of A consisting of all nonzero ideals generated by rational numbers.
Now we claim
Proposition 9.5
There is an exact sequence

Proof
The map E 1−σ→E[N] is the inclusion map: Each unit ε 1−σ has norm 1 and thus is an element of E[N]. For constructing λ : E[N]→H G∕P assume that ε ∈ E[N], i.e., Nε = 1. By Hilbert’s Theorem 90 there is an α ∈ k × such that ε = α 1−σ; clearly (α) ∈ H G since (α)σ = (α σ) = (εα) = (α). The map ε↦(α) is not well defined, however, since with α each element αa for any \(a \in {\mathbb Q}^\times \) has the property (αa)1−σ = ε. For this reason we set λ(ε) = (α)P, and this map now is well defined. Clearly \(\varepsilon \in \ker \lambda \) if and only if λ(ε) = P; this is equivalent to (α) = (a), i.e., to α = aη for some unit η. This implies ε = α 1−σ = η 1−σ, which shows that \(\ker \lambda = E^{1-\sigma }\).
The surjectivity of λ is clear: If (α) is ambiguous, then (α)σ = (α) and thus εα σ = α for some unit ε, hence ε = α 1−σ. □
The content of this proposition may also be expressed by the isomorphism
The quotient group H −1(G, E) = E[N]∕E 1−σ is a cohomology group. We have come across such a group already in Hilbert’s Theorem 90, which says that H −1(G, k ×) = k ×[N]∕(k ×)1−σ = 1. Hilbert’s Theorem 90 for ideals claims accordingly that \(H^{-1}(G,I_k) = I_k[N]/I_k^{1-\sigma } = 1\), where I k denotes the group of nonzero fractional ideals in a quadratic number field. Such cohomology groups for cyclic Galois groups G = 〈σ〉 are all over the place in class field theory, the theory of abelian extensions of number fields.
Galois cohomologyFootnote 2 gives the exact sequence in Proposition 9.5 in the other direction (Exercise 9.10).
The order of the group E[N]∕E 1−σ can be determined quickly. If Δ < 0, then E consists only of roots of unity with norm 1. Thus ε σ = ε −1, hence E 1−σ = E 2 and \(E[N]/E^{1-\sigma } = E/E^2 \simeq {\mathbb Z}/2{\mathbb Z}\). If Δ > 0, then let ε denote the fundamental unit. If Nε = +1, then again E[N] = E and E 1−σ = E 2, hence \(E[N]/E^{1-\sigma } = E/E^2 = \langle -1, \varepsilon \rangle / \langle \varepsilon ^2 \rangle \simeq ({\mathbb Z}/2{\mathbb Z})^2\). If Nε = −1, on the other hand, then E[N] = 〈−1, ε 2〉 and E 1−σ = E 2 = 〈ε 2〉, hence \(E[N]/E^{1-\sigma } = E/E^2 \simeq {\mathbb Z}/2{\mathbb Z}\).
Lemma 9.6
Let k be a quadratic number field whose unit group E is generated by the fundamental unit ε (and − 1). Then
It remains to determine the order of A∕P. To this end we will use the following lemma.
Lemma 9.7
An ideal\(\mathfrak a\)is ambiguous if and only if\(\mathfrak a\)is the product of ramified prime ideals and an ideal (a) with\(a \in {\mathbb Q}^\times \) . More exactly we have
where t is the number of primes that ramify in \(k/{\mathbb Q}\) , in other words, the number of distinct prime factors of the discriminant of k.
Proof
We may assume that \(\mathfrak a\) is an integral ideal (otherwise we multiply it by a suitable rational integer). Among all decompositions \(\mathfrak a = (a) \mathfrak b\) with an integral ideal \(\mathfrak b\) we pick one in which \(a \in {\mathbb N}\) is maximal.
Let \(\mathfrak p\) denote a prime ideal with \(\mathfrak p^\sigma \ne \mathfrak p\); if \(\mathfrak p\) divides \(\mathfrak b\), then we must have \(\mathfrak p^\sigma \mid \mathfrak b\). In fact by applying σ to \(\mathfrak p \mid \mathfrak a\) we see that \(\mathfrak p^\sigma \mid \mathfrak b^\sigma = \mathfrak b\). Thus \((p) \mid \mathfrak b\), where \((p) = \mathfrak p \mathfrak p^\sigma \), which contradicts the maximality of a. This shows that \(\mathfrak b\) is not divisible by a split prime ideal.
For the same reason, \(\mathfrak b\) is not divisible by any inert prime ideal (p). Thus \(\mathfrak b\) is a product of ramified prime ideals. If \(\mathfrak p\) is such a prime ideal, then \(\mathfrak p^2 = (p)\), and the maximality of a implies that we can write \(\mathfrak a\) uniquely in the form
where \(\mathfrak p_j\) runs through the ramified prime ideals and where e j ∈{0, 1}. Now we set
and show that ϕ is a group isomorphism, which is left as an exercise. □
If we collect everything, then the exact sequence (9.2) now implies
Corollary 9.8
In the quadratic number field k with discriminant Δ and fundamental unit ε we have
where t denotes the number of primes that ramify in k.
Thus it remains only to determine the difference between the group of ambiguous ideal classes \(\operatorname {Am}(k)\) and that of strictly ambiguous ideal classes \(\operatorname {Am}_{\operatorname {st}}(k)\):
Proposition 9.9
There is an exact sequence

In particular,\(\operatorname {Am}(k) = \operatorname {Am}_{\operatorname {st}}(k)\)except when − 1 is the norm of an element, but not of a unit. In this case,\(\# \operatorname {Am}(k) = 2 \cdot \, \# \operatorname {Am}_{\operatorname {st}}(k)\).
Proof
Let \(c = [\mathfrak a]\) be ambiguous. Then \(\mathfrak a^\sigma \sim \mathfrak a\), hence \(\mathfrak a^\sigma = \alpha \mathfrak a\). Taking norms yields (Nα) = (1), that is \(N\alpha = \pm 1 \in E_{\mathbb Q} \cap Nk^\times \). We set μ(c) = Nα ⋅ NE k and claim that μ is well defined. In fact if we start from \(c = [\mathfrak b]\), then \(\mathfrak b = \gamma \mathfrak a\), and \(\mathfrak b^\sigma = \gamma ^\sigma \mathfrak a^\sigma = \gamma ^\sigma \alpha \mathfrak a = \gamma ^{\sigma -1} \alpha \mathfrak b\) shows that N(γ σ−1 α) ⋅ NE k = Nα ⋅ NE k since elements of the form γ σ−1 have norm 1. Thus μ is well defined.
If \(c \in \ker \mu \), then Nα = Nη, d.h. N(αη) = 1. According to Hilbert’s Theorem 90, we have αη = β 1−σ, and now \(\mathfrak a^\sigma = \alpha \mathfrak a\) implies \((\beta \mathfrak a)^\sigma = (\beta ) \mathfrak a\). Thus \(\mathfrak b = \beta \mathfrak a\) is an ambiguous ideal equivalent to \(\mathfrak a\), and therefore \(c = [\mathfrak b]\) is strongly ambiguous. Conversely, strongly ambiguous ideal classes are clearly contained in \(\ker \mu \).
In order to prove the surjectivity of μ we have to show that − 1NE k lies in the image of μ if − 1 is the norm of an element from k. Assume therefore that Nα = −1 for \(\alpha = x + y \sqrt {m}\). Then x 2 − my 2 = −1, hence − 1 is a quadratic residue modulo each odd prime divisor p of m. We know from elementary number theory (or from the arithmetic of Gaussian integers) that this holds if and only if m = a 2 + b 2 is a sum of two squares; here we may assume that a is odd. Now we verify that \(\mathfrak a = (a, b + \sqrt {m})\) generates an ambiguous ideal class \(c = [\mathfrak a]\), and that μ(c) = −1. In fact we have
because of \(\gcd (a^2, 2b) = 1\) and \((b+\sqrt {m})(b-\sqrt {m}) = b^2 - m = -a^2\). Thus \(\mathfrak a^2 = (b+\sqrt {m})\) and \(\mathfrak a\mathfrak a^\sigma = N\mathfrak a = (a)\), and therefore \(\mathfrak a^{1-\sigma } = \mathfrak a^2/\mathfrak a^{1+\sigma } = \frac 1a(b+\sqrt {m})\). This yields \(\mu (c) = N(\frac {b+\sqrt {m}}a) = \frac {b^2-m}{a^2} = -1\) as claimed. □
The group \((E_{\mathbb Q} \cap Nk^\times )/NE_k\) is small, because even \(E_{\mathbb Q} = \{\pm 1\}\) has only two elements. In fact we have \((E_{\mathbb Q} \cap Nk^\times )/NE_k = 1\) unless − 1 is the norm of an element from k or if Nε = −1, and \((E_{\mathbb Q} \cap Nk^\times )/NE_k \simeq {\mathbb Z}/2{\mathbb Z}\) if − 1 is the norm of an element, but not the norm of a unit. As we just have seen, − 1 is the norm of an element if and only if \(\varDelta = \square + \square \) is the sum of two squares. Thus we have
Theorem 9.10 (Ambiguous Class Number Formula)
In quadratic number fields k with discriminant Δ and fundamental unit ε we have
where t denotes the number of primes ramified in k.
Examples

As an additional consequence of the ambiguous class number formula we claim:
Corollary 9.11
The class number of the quadratic number field with discriminant Δ is odd if and only if we are in one of the following cases; there p denotes prime numbers ≡ 1 mod 4 and q, q′ prime numbers ≡ 3 mod 4:
-
(1)
Δ is a prime discriminant, i.e., Δ = −4, ±8, p, −q;
-
(2)
Δ is a product of two negative prime discriminants: Δ = 4q, Δ = 8q or Δ = qq′.
Proof
The class number of k is even if and only if \(\# \operatorname {Am}(k) \ne 1\), thus if the number of ambiguous ideal classes is even. The other claims follow directly from the ambiguous class number formula. □
9.3 The Quadratic Reciprocity Law
The quadratic reciprocity law is a corollary of Corollary 9.11. We begin by proving the two supplementary laws.
Theorem 9.12 (First Supplementary Law)
For all odd prime numbers p, the following assertions are equivalent:
-
(1)
\((\frac {-1}p) = +1\) , i.e., the congruence x 2 ≡−1 mod p is solvable.
-
(2)
p = a 2 + 4b 2is sum of two squares.
-
(3)
We have p ≡ 1 mod 4.
The equivalence of (1) and (3) may also be expressed by the equation
Proof
(1) ⇒ (2): If (−1∕p) = 1, then p splits in \(k = {\mathbb Q}(i)\). Multiplying through by i we may assume that the coefficient of i is even. Thus p = (a + 2bi)(a − 2bi), and taking the norm yields p = a 2 + 4b 2.
(2) ⇒ (3): Since p and a are odd, p = a 2 + 4b 2 implies p ≡ 1 mod 4.
(3) ⇒ (1): If p ≡ 1 mod 4, then \((\frac {-1}p) = (-1)^{(p-1)/2} = 1\) according to Euler’s Criterion. □
Similarly we can prove
Theorem 9.13 (Second Supplementary Law)
For all odd prime numbers p, the following assertions are equivalent:
-
(1)
\((\frac {2}p) = +1\) , i.e., the congruence x 2 ≡ 2 mod p is solvable.
-
(2)
We have p = e 2 − 2f 2for integers\(e, f \in {\mathbb Z}\).
-
(3)
We have p ≡±1 mod 8.
The equivalence of (1) and (3) can also be expressed by the equation
Proof
(1) ⇒ (2): If \((\frac 2p) = +1\), then p splits in \({\mathbb Q}(\sqrt {2})\), and we have ± p = x 2 − 2y 2; multiplying \(x+y\sqrt {2}\), if necessary, by the unit \(1+\sqrt {2}\) we can make sure that p = e 2 − 2y 2.
(2) ⇒ (3): Reduction modulo 8 yields p ≡±1 mod 8 in all cases.
(3) ⇒ (1): Let h denote the class number of \(k={\mathbb Q}(\sqrt {p})\), which is odd by Corollary 9.11. If p ≡±1 mod 8, then 2 splits in \(k/{\mathbb Q}\), hence \(2\mathcal O_k = \mathfrak p\mathfrak p'\) for prime ideals \(\mathfrak p, \mathfrak p'\). Since \(\mathfrak p^h = \frac 12(x+y\sqrt {p})\) is a principal ideal, taking the norm yields x 2 − py 2 = ±4 ⋅ 2h. Reduction modulo p shows that ± 2h and thus ± 2 is a quadratic residue modulo p; the claim now follows from the first supplementary law. □
The quadratic reciprocity law for odd prime numbers is the content of the following theorem.
Theorem 9.14 (Quadratic Reciprocity Law)
If p and q are odd primes, then
Proof
We first discuss the case where one of the primes, say p, is congruent to 1 mod 4. We will show that in this case we have \(\big (\frac {p}{q}\big ) =+1 \iff \big (\frac {q}{p}\big ) =+1 \).
Since \(\big (\frac {p}{q}\big ) = +1\), the prime q splits in \(k = {\mathbb Q}(\sqrt {p})\). Thus \(q\mathcal O_k = \mathfrak q\mathfrak q'\) and \(\mathfrak q^h = \frac 12(x+y\sqrt {p})\) is a principal ideal, where h is the class number of k, which is odd by Corollary 9.11. Taking the norm yields ± 4q h = x 2 − py 2. This in turn provides us with the congruence ± 4q h ≡ x 2 mod p, and then \(\big (\frac {-1}{p}\big ) = +1\) implies \(\big (\frac {q}{p}\big ) = + 1\) as claimed.
If \(\big (\frac {q}{p}\big ) = +1\), on the other hand, then we use the number field \(k = {\mathbb Q}(\sqrt {q})\), which also has odd class number h. Again the fact that p splits in \(\mathcal O_k\) yields the equation ± 4p h = x 2 − qy 2 and thus \(\big (\frac {\pm p}{q}\big ) = +1\). Since either q ≡ 1 mod 4 and \((\frac {-1}{q}) = +1\) or q ≡ 3 mod 4 and the sign is necessarily positive (Exercise 9.15), we obtain \(\big (\frac {p}{q}\big ) = +1\).
Finally assume that p ≡ q ≡ 3 mod 4. Consider the field \(k = {\mathbb Q}(\sqrt {pq})\). According to Corollary 9.11, the class number h of k is odd. Thus the prime ideal \(\mathfrak p = (p,\sqrt {pq})\) above p must be principal: In fact we have \(\mathfrak p^2 \sim (1)\) and \(\mathfrak p^h \sim 1\), and since h = 2j + 1 we get \(\mathfrak p = \mathfrak p^{h-2j} \sim (1)\). Assume therefore that \(\mathfrak p = \frac 12(x+y\sqrt {pq})\). Then ± 4p = x 2 − pqy 2, hence x = pz and ± 4 = pz 2 − qy 2. If the positive sign holds, then reduction modulo q and p shows that \((\frac {p}{q}) = +1\) and \((\frac qp) = -1\). If the negative sign holds, then we find accordingly that \((\frac {p}{q}) = -1\) and \((\frac qp) = +1\). This completes the proof. □
9.3.1 Summary
In this chapter we have proved the ambiguous class number formula for quadratic number fields, and derived the quadratic reciprocity as a corollary.
9.4 Exercises
-
9.1.
Show that the operation \([\mathfrak a]^\sigma = [\mathfrak a^\sigma ]\) on the ideal class group of a quadratic number field is well defined, i.e., that \([\mathfrak a] = [\mathfrak b]\) implies \([\mathfrak a^\sigma ] = [\mathfrak b^\sigma ]\).
-
9.2.
Show that the ideal class of order 2 in \({\mathbb Q}(\sqrt {10})\) contains the ideals \((2,\sqrt {10})\), \((3, 1+\sqrt {10})\) and \((5, 1+\sqrt {10})\). Which of these ideals are ambiguous?
-
9.3.
Let p ≡ 5 mod 8 be prime. Show that the ideal class \({\mathbb Q}(\sqrt {2p})\) generated by the ambiguous ideal \((2,\sqrt {2p})\) has order 2.
-
9.4.
Let p ≡ 1 mod 8 be prime. Show that the ambiguous ideal \((2,\sqrt {2p})\) is principal in \(k = {\mathbb Q}(\sqrt {2p})\) if and only if the norm of the fundamental unit in k is + 1.
In this case write 2p = a 2 + b 2 with a > b > 0 and show that the ideal \(\mathfrak a = (a,b+\sqrt {m})\) generates an ambiguous ideal class of order 2.
-
9.5.
Show that if k is a quadratic number field with class number 2, then \(\operatorname {Am}(k) = \mbox{Cl}(k)\).
-
9.6.
Show that if k is a quadratic number field with odd class number, then \(\operatorname {Am}(k) = 1\).
-
9.7.
Show: If A and B are subgroups of an abelian group, then AB∕B ≃ A∕A ∩ B. Hint: Show that A ∩ B is the kernel of the natural map A→AB∕B.
-
9.8.
Show that the inclusion ι : H G∕P→A∕P in (9.2) is injective and that the map \(\pi : A/P \longrightarrow \operatorname {Am}_{\operatorname {st}}(k)\) defined by \(\pi (\mathfrak a P) = [\mathfrak a]\) is well defined and surjective. Also show that \(\ker \pi = \mbox{im}\,\, \iota \).
-
9.9.
(O. Taussky) Solve the Pythagorean equation x 2 + y 2 = z 2 using Hilbert’s Theorem 90. Hint: \(\alpha = \frac {x+yi}{z} \in {\mathbb Q}(i)\) satisfies the equation Nα = 1. Write \(\alpha = \frac {m+ni}{m-ni}\) and rationalize the denominator.
Generalize this exercise to all equations of the form x 2 − my 2 = z 2 for squarefree values \(m \in {\mathbb Z} \setminus \{0, 1\}\).
-
9.10.
Show that there is an exact sequence

where H denotes the group of nonzero principal ideals.
-
9.11.
Let m = a 2 + b 2 be a sum of two squares. Then the ideals \((a,b+\sqrt {m})\) do not necessarily lie in the same ideal class for each choice of a and b. Verify this for m = 10 = 12 + 32 = 32 + 12.
For the distribution of these ideals over the ideal classes see [82] and [9].
-
9.12.
Let p be a ramified prime in \(k = {\mathbb Q}(\sqrt {m})\), where m≠ ± p, and assume that the prime ideal \(\mathfrak p\) above p is principal, say \(\mathfrak p = (\pi )\). Show that \(\varepsilon = \frac 1p \pi ^2\) is a unit in \(\mathcal O_k\), and that neither ε nor − ε is a square. Generalize this to products of ramified prime ideals. Use this to compute the fundamental unit of \({\mathbb Q}(\sqrt {30})\).
-
9.13.
Let p ≡ 1 mod 4 be a prime number. Show that \(\big (\frac {q}{p}\big ) =+1\) implies \(\big (\frac {p}{q}\big ) =+1\).
Hint: Use \(k = {\mathbb Q}(\sqrt {q^*})\) for \(q^* = (\frac {-1}q) q\) instead of \({\mathbb Q}(\sqrt {q})\).
-
9.14.
Show that the solvability of the Pell equation implies that the norm of the fundamental unit ε p of \({\mathbb Q}(\sqrt {p})\) for primes p is equal to \(N\varepsilon _p = -(\frac {-1}p)\). Show also that Nε pq = −1 if p ≡ q ≡ 1 mod 4 are primes with \((\frac pq) = -1\).
-
9.15.
Let ± 4p h = x 2 − qy 2 for prime numbers p ≡ 1 mod 4 and q ≡ 3 mod 4. Show that x and y are both even, and that the plus sign must hold.
-
9.16.
Let \(k = {\mathbb Q}(\sqrt {m})\) be a quadratic number field with fundamental unit ε m. Show: If Nε m = +1, then there is an ambiguous principal ideal \(\mathfrak a = (\alpha )\) with \(\mathfrak a \ne (1)\), \((\sqrt {m})\).
Hint: By Hilbert’s Theorem 90 we have ε = α′∕α.
-
9.17.
Show that the norm of the fundamental unit ε of \({\mathbb Q}(\sqrt {p})\) is negative if p ≡ 1 mod 4 is prime.
Hint: Use the preceding exercise.
-
9.18.
The idea behind Kummer’s ideal numbers was the construction of ring homomorphisms \(\mathcal O_k \longrightarrow {\mathbb F}_q\) of the ring of integers of number fields into finite fields. Restrict these homomorphisms to the multiplicative group, that is, consider the group homomorphism \(\psi : \mathcal O_k^\times \longrightarrow {\mathbb F}_q^\times \). Find examples of real quadratic number fields and primes q for which this homomorphism is trivial, or where it is surjective.
-
9.19.
Let p be a prime number such that \((\frac {10}{p}) = +1\). Then there exist two possibilities:
-
1.
\((\frac 2p) = (\frac 5p) = +1\); in this case p = x 2 − 10y 2.
-
2.
\((\frac 2p) = (\frac 5p) = -1\); in this case ± 2p = X 2 + 10y 2 and, using X = 2x, ± p = 2x 2 − 5y 2.
Show that this implies that each element \(x + y \sqrt {10} \in {\mathbb Z}[\sqrt {10}\,]\) can be written uniquely as a product of a unit and irreducible elements of the form \(a+b\sqrt {10}\) or \(c\sqrt {2} + d\sqrt {5}\).
-
1.
-
9.20.
Let q ≡ 3 mod 8 be a prime number. Show that the class number of \({\mathbb Q}(\sqrt {2q})\) is odd and deduce that the equation 2x 2 − qy 2 = −1 is solvable. Deduce that \((\frac 2q) = -1\).
Notes
- 1.
For integral ideals, the statement is trivial since then \(N\mathfrak a = (1)\) is equivalent to \(\mathfrak a = (1)\).
- 2.
Those who are familiar with the first principles of cohomology get the sequence for free: The trivial sequence
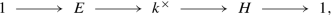
in which H denotes the group of nonzero fractional principal ideals, provides the long exact sequence
$$\displaystyle \begin{aligned}1 \longrightarrow E^G \longrightarrow (k^\times)^G \longrightarrow H^G \longrightarrow H^{1}(G,E) \longrightarrow H^1(G,k^\times),\end{aligned} $$from which the claim follows using Hilbert’s Theorem 90 (H 1(G, k ×) = 1), the periodicity H 1(G, A) ≃ H −1(G, A) for cyclic groups G, as well as \((k^\times )^G = {\mathbb Q}^\times \), E G = {±1} and \({\mathbb Q}^\times /E^G \simeq P\).
References
E. Benjamin, C. Snyder, Elements of order four in the narrow class group of real quadratic fields. J. Aust. Math. Soc. 100, 21–32 (2016)
F. Lemmermeyer, Relations in the 2-class group of quadratic number fields, J. Austr. Math. Soc. 93, 115–120 (2012)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2021 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Lemmermeyer, F. (2021). Ambiguous Ideal Classes and Quadratic Reciprocity. In: Quadratic Number Fields. Springer Undergraduate Mathematics Series. Springer, Cham. https://doi.org/10.1007/978-3-030-78652-6_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-78652-6_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-78651-9
Online ISBN: 978-3-030-78652-6
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)