Abstract
One of the aims of proof theory is to calibrate the strength of axiom systems by invariants. According to Gödel’s discoveries these invariants will in general not be finite but rather transfinite objects. Pioneering work in this direction had been done by Gerhard Gentzen who characterized the axiom system for Peano arithmetic by the transfinite ordinal \({\varepsilon _0}\). In this paper we try to develop a general framework for characterizing ordinals of axiom systems and study to what extend these ordinals embody a measure for their performance.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
1 Introduction
Hilbert’s advocacy of the “axiomatic method”, as presented in his 1917 lecture in Zurich (reprinted in [18]) has had a lasting influence on research and teaching in mathematics. Nowadays, even beginners’ lectures are based on precisely introduced axioms. Also in his Zurich lecture Hilbert emphasized the importance of the consistency of the axiom systems used in the different areas of mathematics and explained that this finally requires an axiomatization of number theory and set theory and the underlying logic. But the quest for consistency, already expressed in Hilbert’s second problem in [17], arose much earlier and formed the root of Hilbert’s program which aimed at a finitistic confirmation of the axiom systems for number theory and logic. Gödel’s incompleteness theorems, published in [16], wrecked Hilbert’s dream of a finitistic consistency proof for axiom systems comprising the theory of natural numbers. Nevertheless, Gerhard Gentzen in [13, 14] succeeded in giving a consistency proof for an axiom system of Peano arithmetic by use of infinitary means which can be merged into a single transfinite induction of height \({\varepsilon _0}\). It thus follows by Gödel’s second incompleteness theorem that transfinite induction up to \({\varepsilon _0}\) cannot be provable in Peano arithmetic. In a subsequent paper [15] Gentzen gave a direct proof of this unprovability and showed that, conversely, transfinite induction can be proved up to any proper initial segment of \({\varepsilon _0}\) by the Peano axioms. This was the birth of ordinal analysis and established \({\varepsilon _0}\) as the proof-theoretic ordinal of Peano arithmetic.
Due to their genesis proof-theoretic ordinals are connoted with the problem of consistency. The problem of consistency, however, is a problem which is provably unsolvable. To prove the consistency of a (sufficiently strong) axiom system \(\textsf{T}\) we, by Gödel’s second incompleteness theorem, necessarily need an axiom system \(\textsf{T}'\) which is “stronger” than \(\textsf{T}\). To secure the consistency of \(\textsf{T}'\) we need an axiom system \(\textsf{T}''\) stronger than \(\textsf{T}'\) and so on. This leads to an “argumentum ad infinitum”. Of course one can try to reduce \(\textsf{T}\) to an axiom system \(\textsf{T}'\) whose proof-theoretic strength is in principle that of \(\textsf{T}\) but whose consistency is intuitively more plausible. This form of “reductive proof theory” is still flourishing.
Nevertheless, nowadays the problem of consistency no longer seems to play a role in “everyday” mathematical discussions. Experience tells us that up to now the assumption of the existence of abstract structures did not lead us to unsolvable inconsistencies.
In this paper we will therefore put abstract structures in the centre and try to study the role of proof-theoretic ordinals from this perspective. This puts their connection to consistency in the background.
Characterizing properties of abstract structures by specific ordinals (and vice versa) is a well-established tool in definability theory and generalized recursion theory. One of the best-known examples is the ordinal \(\omega _1^{\hbox {\tiny CK}}\), the first ordinal which cannot be represented by a recursive well-ordering on the natural numbers. So \(\omega _1^{\hbox {\tiny CK}}\) is the supremum of the order-types of well-orderings that are primitive-recursively, elementarilyFootnote 1 or even \(\Sigma _1^1\)-definable in the structure \({\mathfrak N}\) of the natural numbers. It is moreover the closure ordinal of the structure \({\mathfrak N}\), in the sense defined by Moschovakis in [24], and the first ordinal above \(\omega \) at which the stage \(\mathord {\textsf{L}}_{\omega _1^{\hbox {\tiny CK}}}\) in the constructible hierarchy becomes an admissible set, etc.
Investigating abstract structures by Hilbert’s axiomatic method requires an axiomatization \(\textsf{T}\) for \({\mathfrak M}\), i.e. a set \(\textsf{T}\) of sentences in the language of \(\mathfrak {M}\) which we consider to be characteristic for \({\mathfrak M}\) and thus are assumed to be valid in the structure \({\mathfrak M}\).
In Sect. 3.2.2 we define the \(\Pi _{1}^{1}\)-ordinal \(\pi ^{\mathfrak M}\) of a countable abstract structureFootnote 2 and its counterpart \(\pi ^{\mathfrak M}(\textsf{T})\) for an axiomatization \(\textsf{T}\) of \({\mathfrak M}\). Since we regard \(\pi ^{\mathfrak M}\) as characteristic for \({\mathfrak M}\) and \(\pi ^{\mathfrak M}(\textsf{T})\) as characteristic for \(\textsf{T}\), it is obvious to consider the distance between \(\pi ^{\mathfrak M}(\textsf{T})\) and \(\pi ^{\mathfrak M}\) as a possible measure for the performance of the axiom system \(\textsf{T}\). It is one of the aims of this paper to find out to what extend this is actually the case.
The main tool in our investigations are semi-formal systems, i.e. systems of formal inference rules which allow for inferences with infinitely many premises. Semi-formal systems are introduced in Sect. 3.2.1.2. The Boundedness TheoremFootnote 3 in Sect. 3.2.4 shows that the ordinal \(\pi ^{\mathfrak M}(\textsf{T})\) is an upper bound for the ordinal \(\delta ^{\mathfrak M}(\textsf{T})\), which is the supremum of the order-types of elementarily definable orderings whose well-foundedness is provable in \(\textsf{T}\). If \(\delta ^\mathfrak {M}(\textsf{T})=\pi ^{\mathfrak M}(\textsf{T})\) we call \(\delta ^\mathfrak {M}(\textsf{T})\) the proof-theoretic ordinal of \(\textsf{T}\). This coincides (at least in all cases that are known to us) with the familiar definition of the proof-theoretic ordinal.
In Sect. 3.2.5 we apply these definitions to the example of an acceptable countable structure and first-order axiomatizations for it. The lessons learned from these examples are twofold. First it shows the importance of pseudo \(\Pi _{1}^{1}\)-sentencesFootnote 4 in the axiomatization. Secondly it tells us that augmenting an axiom system by true elementary sentences will not improve its performance. For example, there is no difference between the performance of the Peano axioms and an axiom system which, besides Mathematical Induction, contains the full elementary diagram of \({\mathfrak N}\), although the elementary diagram should know everything about \({\mathfrak N}\). The conclusion drawn from these observations is that the ordinal \(\pi ^{\mathfrak M}(\textsf{T})\) is rather a measure for the performance of the axiom system \(\textsf{T}\) with respect to a universe above \({\mathfrak M}\) than for \({\mathfrak M}\) itself.Footnote 5 This is corroborated by the “No Enhancement Theorem” (Theorem 3.21) which states that even the addition of true \(\Sigma ^1_1\)-sentences to an axiom system will not enhance its performance.
The focus of the paper therefore concentrates on universes above a structure \({\mathfrak M}\) which have to be axiomatized by sentences “beyond” \(\Sigma ^1_1\) (e.g. by pseudo \(\Pi _{1}^{1}\)-sentences).
If a universe above \(\mathfrak {M}\) is supposed to contain only subsets of and functions on \(\mathfrak {M}\), the largest possible universe above \({\mathfrak M}\) is apparently the full power set of \({\mathfrak M}\). A different option is to allow arbitrary sets above \({\mathfrak M}\) and to regard the objects in \(\mathfrak {M}\) as urelements (or sets in the universe). Since Analysis, i.e. the theory of sets and functions on the reals \(\mathbb R\), lives in the powerset of the natural numbers we refer to the first form of universes as analytical universes while in the second form we talk about set-theoretic universes. Our original plan was to investigate both forms of universes in the present paper, but it quickly turned out that such a paper would become much too long. So we decided to postpone the set-theoretic universes to a forthcoming paper and to concentrate on analytical universes. Even here we had to cut back and to concentrate on universes with characteristic ordinals below the first recursively inaccessible ordinal. We feared that otherwise the necessary overhead could bury the idea of our approach.Footnote 6 Another argument is that for universes with characteristic ordinals above the first inaccessible ordinal the set-theoretic approach is much more natural such that they should better be treated there.
The full powerset \(\mathscr {P}({{\mathfrak M}})\) of a countable structure \({\mathfrak M}\) is uncountable and thus outside of the reach of our methods. Therefore we restrict ourselves to universes that are countable subsets of \(\mathscr {P}({{\mathfrak M}})\). Clearly not every subset of \(\mathscr {P}({{\mathfrak M}})\) is a suitable universe above \({\mathfrak M}\). Only sets that fulfill certain closure properties are potential universes.
Good candidates are countable Spector classes above \({\mathfrak M}\) as introduced in [24]. Spector classes above \({\mathfrak M}\) are collections of relations on \({\mathfrak M}\) whose properties are modeled on the paradigmatic example of recursively enumerable relations. Their origin is the attempt to generalize computability theory.Footnote 7 A partial function  is partial \(\Gamma \)-recursive iff its graph is in the Spector class \(\Gamma \) above \(\mathfrak {M}\).
is partial \(\Gamma \)-recursive iff its graph is in the Spector class \(\Gamma \) above \(\mathfrak {M}\).
Among other properties, Spector classes are normed, which is one of their salient properties. For every relation R in a Spector class \(\Gamma \) there is an ordinal \(\lambda \) and a \(\Gamma \)-norm  satisfying certain conditions. This entails that for every relation R in a Spector class \(\Gamma \) we have an ordinal o(R) which is the supremum of all possible \(\Gamma \)-norms on R. Putting \(o(\Gamma )\) as the supremum of all the \(\Gamma \)-norms for relations in \(\Gamma \) we obtain a characteristic ordinal for a Spector class above a structure \({\mathfrak M}\) which generalizes the ordinal \(\pi ^\mathfrak {M}\).Footnote 8
satisfying certain conditions. This entails that for every relation R in a Spector class \(\Gamma \) we have an ordinal o(R) which is the supremum of all possible \(\Gamma \)-norms on R. Putting \(o(\Gamma )\) as the supremum of all the \(\Gamma \)-norms for relations in \(\Gamma \) we obtain a characteristic ordinal for a Spector class above a structure \({\mathfrak M}\) which generalizes the ordinal \(\pi ^\mathfrak {M}\).Footnote 8
The new and central notion of this paper is the spectrum of an axiom system which already has been touched in a very preliminary form in [26] and in a bit more elaborated form in [33].
Given a basis structure \({\mathfrak M}\) we construct a hierarchy of Spector classes \({\mathfrak M}_{\mu }\) above \({\mathfrak M}\) and thus obtain a hierarchy \(\kappa _{\mu }^{{\mathfrak M}}\) of characteristic ordinals. Spector classes in general are difficult to axiomatize. Fortunately the least Spector class above a structure \({\mathfrak M}\) can be obtained as a positive fixed-point structure. Axiomatizing a hierarchy of Spector classes above a countable structure \({\mathfrak M}\) thus leads to iterated positive inductive definitions which are well studied in proof theory.Footnote 9 If \(\textsf{T}\) is an axiomatization for the basis structure \({\mathfrak M}\) we extend \(\textsf{T}\) to an axiom system \(\textsf{ID}_{\nu }({\textsf{T}})\) which axiomatizes the hierarchy \({}{\{{{\mathfrak M}_{\mu }}\,|\,{\mu \le \mathrm{\nu }}\}}\) above \(\mathfrak {M}\).
We then obtain a whole spectrum of characteristic ordinals for \(\textsf{ID}_{\nu }({\textsf{T}})\). If \({\mathfrak M}_{\mu }\) for \(\mu \le \nu \) is a Spector class we define \(o^{{\mathfrak M}_{\mu }}(\textsf{ID}_{\nu }({\textsf{T}}))\) as the supremum of all \({\mathfrak M}_{\mu }\)-norms \(\sigma _R(x)\) such that \(R\in {\mathfrak M}_{\mu }\) and  . Then \(\textit{Spec}^{\mathfrak {M}}({\textsf{ID}_{\nu }({\textsf{T}})})\) is the set of all ordinals \(o^{{\mathfrak M}_{\mu }}(\textsf{ID}_{\nu }({\textsf{T}}))\) such that \({\mathfrak M}_{\mu }\) is a Spector class above \({\mathfrak M}\).Footnote 10
. Then \(\textit{Spec}^{\mathfrak {M}}({\textsf{ID}_{\nu }({\textsf{T}})})\) is the set of all ordinals \(o^{{\mathfrak M}_{\mu }}(\textsf{ID}_{\nu }({\textsf{T}}))\) such that \({\mathfrak M}_{\mu }\) is a Spector class above \({\mathfrak M}\).Footnote 10
If \({\mathfrak M}\) is an acceptable structure, i.e. a structure which contains an elementarily definable copy of the natural numbers and an elementarily definable coding machinery, and \(\textsf{T}\) an acceptable axiomatization for \({\mathfrak M}\) which proves all the properties of the coding machinery, then the spectral points in \(\textit{Spec}^{{\mathfrak M}}({\textsf{ID}_{\nu }({\textsf{T}})})\) represent exactly the range of the \({\mathfrak M}_{\mu }\)-recursive functions, whose totality is provable in \(\textsf{ID}_{\nu }({\textsf{T}})\).
The main technique used is that of collapsing operator controlled semi-formal derivations.Footnote 11 The controlling operators are obtained by iterations of Skolem-hull operators on ordinals as introduced in Sect. 3.3.3.1. The main result is the Collapsing Theorem (Theorem 3.68).
In Sect. 3.4.1 we apply the Collapsing Theorem to an axiom system \(\textsf{T}\) for \({\mathfrak M}\) which only contains Mathematical Induction as a non-elementary axiom. For such an axiom system we obtain \(o^{{\mathfrak M}_{\nu }}(\textsf{ID}_{\nu }({\textsf{T}})) =\pi ^{{\mathfrak M}_{\nu }}(\textsf{ID}_{\nu }({\textsf{T}}))\le \varepsilon _{\kappa _{\nu }^{\mathfrak {M}}+1}\). If \(\mathcal{H}\) is the operator which closes the set \({}{\{{\kappa _{\mu }^{{\mathfrak M}}}\,|\,{\mu \le \nu }\}}\) under \(+\) and the Veblen function \(\varphi \) we obtain the iteration \(\mathcal{H}^\alpha \) for \(\alpha :={\pi ^{{\mathfrak M}_{\nu }}(\textsf{ID}_{\nu }({\textsf{T}}))}\) as a suitable operator for the collapsing procedure. Upper bounds for the spectral points of \(\textsf{ID}_{\nu }({\textsf{T}})\) are then uniformly generated as \(o^{{\mathfrak M}_{{\mu +1}}}(\textsf{ID}_{\nu }({\textsf{T}}))= \mathcal{H}^\alpha \left( {\kappa _{\mu }^{{\mathfrak M}}}\right) \cap \kappa _{\mu +1}^{{\mathfrak M}}\).
In Sect. 3.4.2 we show that for acceptable axiom systems \(\textsf{T}\) these are the exact points.
We end the paper by the remark that a refinement of the collapsing techniques can be used to characterize the recursive functions on \({\mathfrak M}\) which are provably total in \(\textsf{ID}_{\nu }({\textsf{T}})\) even for the case \(\nu =0\). However, space did not allow to go into more details.Footnote 12
2 Characteristic Ordinals
2.1 Semi-formal Systems
The central tools in our research are semi-formal systems. Semi-formal systems form a bridge between proofs and semantics with a certain emphasis on the proof-theoretic side. In designing semi-formal system we follow the pattern introduced in [31] and start with a brief overview on semi-formal systems.
2.1.1 The Verification Tree
Given a countable abstract structure \(\mathfrak {M}\) with language \({{\mathscr {L}}(\mathfrak {M})}\) we denote by \({{\mathscr {L}}(\mathfrak {M})}_M\) its extension by names \(\underline{m}\) for all elements m in the domain M of \(\mathfrak {M}\). The verification of \({{\mathscr {L}}(\mathfrak {M})}_M\) -sentences F can be arranged in countably branching well-founded trees \(\mathscr {V}_{F}\), labeled by subsentences of F. The verification of atomic sentences in \(\mathscr {V}_{F}\) is given by the diagram \(\mathscr {D}(\mathfrak {M})\) of \(\mathfrak {M}\), which consists of all true atomic \({{\mathscr {L}}(\mathfrak {M})}_M\)-sentences. Composed sentences G in \(\mathscr {V}_{F}\) are verified logically by recurrence to a characteristic sequence \(\text {CS}~G\) of subsentences of G which depends on the language \({{\mathscr {L}}(\mathfrak {M})}\). If all sentences of \(\text {CS}~G\) are needed in the verification of G we say that G belongs to \(\bigwedge -{\mathord {\textsf {type}}}\,\) (conjunction type), if some of the sentences in \(\text {CS}~G\) suffice then G belongs to \(\bigvee -{\mathord {\textsf {type}}}\,\) (disjunction type). For composed sentences we thus have
and
For atomic sentences G we have \(\text {CS}~G={\langle \ \rangle }\) and \(\mathscr {D}(\mathfrak {M})\subseteq \bigwedge -{\mathord {\textsf {type}}}\,\) since the sentences in \(\mathscr {D}(\mathfrak {M})\) need no logical verification.
The verification tree \(\mathscr {V}_{F}\) is, in principle, determined by F. The heights of well-founded countable trees are measured by countable ordinals. For an ordinal \(\alpha \) we thus denote briefly by
 that the verification tree \(\mathscr {V}_{F}\) for F has a height \(\le \alpha \).
that the verification tree \(\mathscr {V}_{F}\) for F has a height \(\le \alpha \).
We assume that a language \({{\mathscr {L}}(\mathfrak {M})}\) is characterized by its \(\bigwedge -{\mathord {\textsf {type}}}\,\), \(\bigvee -{\mathord {\textsf {type}}}\,\) and the characteristic sequences \(\text {CS}~F\) for \({{\mathscr {L}}(\mathfrak {M})}_M\)-sentences F. Under this assumption there is an inductive definition of the verification relation
 by the two rules:
by the two rules:
- (\(\bigwedge \)):
-
If
 and \(\alpha _G<\alpha \) holds true for all \(G\in \text {CS}~F\) then conclude
and \(\alpha _G<\alpha \) holds true for all \(G\in \text {CS}~F\) then conclude
 .
. - (\(\bigvee \)):
-
If
 holds true for some \(G\in \text {CS}~F\) then
holds true for some \(G\in \text {CS}~F\) then
 holds true for all \(\alpha >\alpha _0\).
holds true for all \(\alpha >\alpha _0\).
The paradigmatic example for \({{\mathscr {L}}(\mathfrak {M})}\) is the first-order language of \(\mathfrak {M}\). Since dealing with negations causes technical inconveniences we generally do not count negation among the logical symbols. Instead we assume that for every relation in \(\mathfrak {M}\) there is also a symbol for its complement. Using de Morgan’s rules, negation of \({{\mathscr {L}}(\mathfrak {M})}_M\)-sentences becomes definable by pushing the negation symbol in front of atomic sentences and there using complements. We also restrict the propositional symbols to conjunction and disjunction. Nevertheless we keep writing \(A\rightarrow B\) which is supposed to be a “shorthand” for \(\lnot A\,\vee \,B\) where \(\lnot A\) is assumed to be defined in the just mentioned way. For the first-order language we then get
-
\(\text {CS}~F=\langle \ \rangle \), if F is atomic,
-
\(\text {CS}~{A\,\wedge \,B}=\text {CS}~{A\,\vee \,B}=\langle A,B\rangle \),
-
\(\text {CS}~{(\forall x) F(x)}=\text {CS}~{F(x)}={}{\big \langle {F(\underline{m})}\,|\,{m\in M}\big \rangle }\), where we anticipate a given enumeration of the elements of M,
and
-
the \(\bigwedge -{\mathord {\textsf {type}}}\,\) comprises all sentences in \(\mathscr {D}(\mathfrak {M})\), all sentences of the form \((A\,\wedge \,B)\) and \((\forall ~x) A(x)\),
-
\(\bigvee -{\mathord {\textsf {type}}}\,:={}{\{{\lnot F}\,|\,{F\in \bigwedge -{\mathord {\textsf {type}}}\,}\}}\), where \(\lnot F\) is understood as defined in the above sense.
A canonical complexity measure \(\textit{rnk}(F)\) for first-order formulae F can be obtained by counting the number of logical symbols occurring in F. This yields \(\textit{rnk}(G)<\textit{rnk}(F)\) for all \(G\in \text {CS}~F\).
For more complex languages the complexity \(\textit{rnk}(F)\) may require a more sophisticated definition. It is, however, essential that the complexity definition always fulfills the requirement
By an easy induction on the complexity of an \({{\mathscr {L}}(\mathfrak {M})}_M\)-sentence F using (3.1), (3.2) and (3.3) we then obtain in general

2.1.2 The Semi-formal System for Countable Structures
Equation (3.4) shows that
 is just a redefinition of the familiar truth definition for the sentences in \({{\mathscr {L}}(\mathfrak {M})}_M\) which is usually defined by induction on \(\textit{rnk}(F)\). The situation changes if we allow free second-order variables in the language. We call an \({{\mathscr {L}}(\mathfrak {M})}_M\)-formula a pseudo \(\Pi _{1}^{1}\)-sentence if it does not contain free object variables but may contain free second-order variables. For convenience we sometimes denote by \({\mathscr {L}}^{\scriptscriptstyle +}(\mathfrak {M})\) the set of pseudo \(\Pi _{1}^{1}\)-sentence of \({{\mathscr {L}}(\mathfrak {M})}_M\).
is just a redefinition of the familiar truth definition for the sentences in \({{\mathscr {L}}(\mathfrak {M})}_M\) which is usually defined by induction on \(\textit{rnk}(F)\). The situation changes if we allow free second-order variables in the language. We call an \({{\mathscr {L}}(\mathfrak {M})}_M\)-formula a pseudo \(\Pi _{1}^{1}\)-sentence if it does not contain free object variables but may contain free second-order variables. For convenience we sometimes denote by \({\mathscr {L}}^{\scriptscriptstyle +}(\mathfrak {M})\) the set of pseudo \(\Pi _{1}^{1}\)-sentence of \({{\mathscr {L}}(\mathfrak {M})}_M\).
The semantics for pseudo \(\Pi _{1}^{1}\)-sentences is defined by

We thus treat pseudo \(\Pi _{1}^{1}\)-sentences semantically as \(\Pi _{1}^{1}\)-sentences.
The point is that we can extend the verification relation
 to a semi-formal system which includes pseudo \(\Pi _{1}^{1}\)-sentences. We do that in form of a one-sided sequent calculus à la Tait. That means that the semi-formal system derives finite sets of \({\mathscr {L}}^{\scriptscriptstyle +}(\mathfrak {M})\)-sentences which are to be interpreted as finite disjunctions. We still do not count the negation symbol among the logical symbols but regard negation as defined. Finite sets of pseudo \(\Pi _{1}^{1}\)-sentences are denoted by upper case Greek letters and we freely use the notions which are common in proof theory. So we write \(\Delta ,\Gamma \) for \(\Delta \cup \Gamma ,\quad \Delta ,G\) for \(\Delta \cup \{G\}\) etc.
to a semi-formal system which includes pseudo \(\Pi _{1}^{1}\)-sentences. We do that in form of a one-sided sequent calculus à la Tait. That means that the semi-formal system derives finite sets of \({\mathscr {L}}^{\scriptscriptstyle +}(\mathfrak {M})\)-sentences which are to be interpreted as finite disjunctions. We still do not count the negation symbol among the logical symbols but regard negation as defined. Finite sets of pseudo \(\Pi _{1}^{1}\)-sentences are denoted by upper case Greek letters and we freely use the notions which are common in proof theory. So we write \(\Delta ,\Gamma \) for \(\Delta \cup \Gamma ,\quad \Delta ,G\) for \(\Delta \cup \{G\}\) etc.
Since atomic pseudo \(\Pi _{1}^{1}\)-sentences \(\vec s\in X\) and \(\vec s\notin X\) are neither logically verifiable nor possess a truth value in \(\mathfrak {M}\) they belong neither to \(\bigwedge -{\mathord {\textsf {type}}}\,\) nor to \(\bigvee -{\mathord {\textsf {type}}}\,\). However. observations (3.1) and (3.2) can be generalized.
Let \(S_1,\dots ,S_{n}\) be a tuple of relations on M whose arities match the arities of the second-order variables occurring in a pseudo \(\Pi _{1}^{1}\)-sentence, \(F\equiv F(X_1,\dots ,X_{n})\).
Definition 3.1
Let \(\Delta \) be a finite set of pseudo \(\Pi _{1}^{1}\)-sentences. We define the semi-formal proof relation  by the following clauses
by the following clauses
- (X):
-
If \(\vec s=s_1,\dots ,s_{n}\) and \({\vec t}=t_1,\dots ,t_{n}\) are tuples of \({\mathscr {L}}(\mathfrak {M})_M\)-terms such that \(\mathfrak {M}\models s_i = t_i\) for \(i=1,\dots , n\) and \(\{\vec s\in X,{\vec t}\notin X\}\subseteq \Delta \) then
 holds true for all ordinals \(\alpha \) and \(\rho \).
holds true for all ordinals \(\alpha \) and \(\rho \). - (\(\bigwedge \)):
-
If \(F\in \Delta \cap \bigwedge -{\mathord {\textsf {type}}}\,\) and
 holds true for all \(G\in \text {CS}~F\) then
holds true for all \(G\in \text {CS}~F\) then 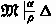 holds true for all \(\alpha \ge \sup {}{\{{\alpha _G+1}\,|\,{G\in \text {CS}~F}\}}\).
holds true for all \(\alpha \ge \sup {}{\{{\alpha _G+1}\,|\,{G\in \text {CS}~F}\}}\). - (\(\bigvee \)):
-
If \(F\in \Delta \cap \bigvee -{\mathord {\textsf {type}}}\,\) and
 holds true for some \(G\in \text {CS}~F\) then
holds true for some \(G\in \text {CS}~F\) then 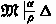 holds true for all \(\alpha >\alpha _0\).
holds true for all \(\alpha >\alpha _0\). - (Cut):
-
If
 ,
,  and \(\textit{rnk}(F)<\rho \) then
and \(\textit{rnk}(F)<\rho \) then  holds true for all \(\alpha >\alpha _0\).
holds true for all \(\alpha >\alpha _0\).
Theorem 3.2
 implies \(\mathfrak {M}\models \bigvee {}{\{{F}\,|\,{F\in \Delta }\}}\) in the sense of (3.6).
implies \(\mathfrak {M}\models \bigvee {}{\{{F}\,|\,{F\in \Delta }\}}\) in the sense of (3.6).
Proof
This follows from (3.7) and (3.8) by induction on \(\alpha \). \(\square \)
The obvious next observation shows that the semi-formal system is a straightforward extension of the verification relation.
Observation 3.3
For every \({\mathscr {L}}(\mathfrak {M})_M\)-sentence we have  iff
iff
 . Hence
. Hence  holds true for every true \({\mathscr {L}}(\mathfrak {M})_M\)-sentence F.
holds true for every true \({\mathscr {L}}(\mathfrak {M})_M\)-sentence F.
Lemma 3.4
Let \(\Delta \) be a finite set of pseudo \(\Pi _{1}^{1}\)-sentences such that its disjunction is logically valid. Then there is a finite ordinal n such that  .
.
Proof
We just motivate the proof.Footnote 13 It relies on the well-known fact that there are finite sequent calculi in which every logically valid formula is cut-free derivable. These finite derivations are easily translated into  -derivations with a finite \(\alpha \). \(\square \)
-derivations with a finite \(\alpha \). \(\square \)
The next theorem embraces the outstanding feature of the semi-formal system.
Theorem 3.5
For any countable structure \(\mathfrak {M}\) we get  iff there is a countable ordinal \(\alpha \) such that
iff there is a countable ordinal \(\alpha \) such that  .
.
Proof
The direction from right to left is Theorem 3.2. For the opposite direction assume  for all countable ordinals \(\alpha \) and construct a search tree for a semi-formal proof of F(X) by inverting the rules \((\bigwedge )\) and \((\bigvee )\). By assumption the search cannot be successful and the search tree thus contains an infinite path f. Assigning the relation
for all countable ordinals \(\alpha \) and construct a search tree for a semi-formal proof of F(X) by inverting the rules \((\bigwedge )\) and \((\bigvee )\). By assumption the search cannot be successful and the search tree thus contains an infinite path f. Assigning the relation  to the second-order variable X we obtain \(\mathfrak {M}\not \models G[S]\) for all formulae occurring in f. This shows \(\mathfrak {M}\not \models (\forall ~X)F(X)\). For a detailed proof see [31] Sect. 3. \(\square \)
to the second-order variable X we obtain \(\mathfrak {M}\not \models G[S]\) for all formulae occurring in f. This shows \(\mathfrak {M}\not \models (\forall ~X)F(X)\). For a detailed proof see [31] Sect. 3. \(\square \)
We close the section by listing some of the obvious properties of the semi-formal system which all follow by an easy induction on \(\alpha \). Call two \({\mathscr {L}}^{\scriptscriptstyle +}(\mathfrak {M})\)-formulae \(\mathfrak {M}\)-equivalent it they at most differ in \({{\mathscr {L}}(\mathfrak {M})}_M\)-terms \(s_1,\dots ,s_{n}\) and \(t_1,\dots ,t_{n}\) such that \(\mathfrak {M}\models (s_i=t_i)\) holds true for \(i=1,\dots ,n\).
Observation 3.6
- (Weakening):
-
 , \(\alpha \le \beta \), \(\rho \le \sigma \) and \(\Delta \subseteq \Gamma \) imply
, \(\alpha \le \beta \), \(\rho \le \sigma \) and \(\Delta \subseteq \Gamma \) imply  .
. - (\(\bigwedge \)-Inversion):
-
 and \(F\in \bigwedge -{\mathord {\textsf {type}}}\,\) implies
and \(F\in \bigwedge -{\mathord {\textsf {type}}}\,\) implies  for all \(G\in \text {CS}~F\).
for all \(G\in \text {CS}~F\). - (\(\vee \)-Exportation):
-
 implies
implies  .
. - (Tautology):
-
 holds true for all \(\mathfrak {M}\)-equivalent \({\mathscr {L}}^{\scriptscriptstyle +}(\mathfrak {M})\)-formulae F and G.
holds true for all \(\mathfrak {M}\)-equivalent \({\mathscr {L}}^{\scriptscriptstyle +}(\mathfrak {M})\)-formulae F and G.
Remark 3.7
The rules (\(\bigwedge \)), \((\bigvee )\) and (Cut) represent the logical part of the verification calculus and the semi-formal system, respectively. Their non-logical part is represented by the condition \(\mathscr {D}(\mathfrak {M})\subseteq \bigwedge -{\mathord {\textsf {type}}}\,\).
2.2 The Ordinals \(\pi ^\mathfrak {M}\) and \(\pi ^\mathfrak {M}(\textsf{T})\)
We use the \(\Pi _{1}^{1}\)-completeness (Theorem 3.5) to define the \(\Pi _{1}^{1}\)-ordinal of a countable structure \(\mathfrak {M}\).
Definition 3.8
Let \(\mathfrak {M}\) be a countable structure and F a pseudo \(\Pi _{1}^{1}\)-sentence in the language \({\mathscr {L}}(\mathfrak {M})_M\). Then we define

where \({\omega _1}\) denotes the first uncountable ordinal. The \(\Pi _{1}^{1}\)-ordinal of \(\mathfrak {M}\) is defined by
\(\quad \pi ^\mathfrak {M}:=\sup {}{\{{{\mathord {\text {tc}}(F)}}\,|\,{F \text { is a pseudo } \Pi _{1}^{1}\text {-sentence and }\mathfrak {M}\models F}\}}\)
where we again understand \(\mathfrak {M}\models F\) in the sense of (3.6).
Let \(\textsf{T}\) be an axiomatization of the structure \(\mathfrak {M}\).Footnote 14 We define the \(\Pi _{1}^{1}\)-ordinal of \(\textsf{T}\) with respect to \(\mathfrak {M}\) by
 .
.
There is an obvious observation.
Observation 3.9
An axiom system \(\textsf{T}\) for a countable structure \(\mathfrak {M}\) is consistent iff \(\pi ^\mathfrak {M}(\textsf{T})\le \pi ^\mathfrak {M}\).
Remark 3.10
Observation 3.9 is a triviality since we require \(\mathfrak {M}\models \textsf{T}\) for any axiom system \(\textsf{T}\) for \(\mathfrak {M}\) (otherwise it would not be an axiom system for \(\mathfrak {M}\)). Let us—putting for the moment consistency in the foreground—assume that \(\textsf{T}\) is just a set of \({\mathscr {L}}(\mathfrak {M})\)-sentences.Then it may happen that  but \(\mathfrak {M}\not \models F\). In that case we would get \(\pi ^\mathfrak {M}(\textsf{T})={\omega _1}\) even if \(\textsf{T}\) is consistent. For a consistent set \(\textsf{T}\), however, there would be a countable model \(\mathfrak {S}\) of \(\textsf{T}\) for which we would get \(\pi ^{\mathfrak {S}}(\textsf{T})\le \pi ^{\mathfrak {S}}<{\omega _1}\). The consistency of an arbitrary set of sentences is thus secured if we succeed to show \(\pi ^{\mathfrak {S}}(\textsf{T})<{\omega _1}\) for some structure \(\mathfrak {S}\) which matches the language of \(\textsf{T}\).Footnote 15 The definition of \(\pi ^\mathfrak {M}(\textsf{T})\) thus depends on the intended structure \(\mathfrak {M}\).
but \(\mathfrak {M}\not \models F\). In that case we would get \(\pi ^\mathfrak {M}(\textsf{T})={\omega _1}\) even if \(\textsf{T}\) is consistent. For a consistent set \(\textsf{T}\), however, there would be a countable model \(\mathfrak {S}\) of \(\textsf{T}\) for which we would get \(\pi ^{\mathfrak {S}}(\textsf{T})\le \pi ^{\mathfrak {S}}<{\omega _1}\). The consistency of an arbitrary set of sentences is thus secured if we succeed to show \(\pi ^{\mathfrak {S}}(\textsf{T})<{\omega _1}\) for some structure \(\mathfrak {S}\) which matches the language of \(\textsf{T}\).Footnote 15 The definition of \(\pi ^\mathfrak {M}(\textsf{T})\) thus depends on the intended structure \(\mathfrak {M}\).
In the following parts we want to study to what extend the distance between \(\pi ^\mathfrak {M}(\textsf{T})\) and \(\pi ^\mathfrak {M}\) represents a measure for the performance of the axiom system \(\textsf{T}\) with respect to the structure \(\mathfrak {M}\). To simplify notations we will mostly restrict ourselves to acceptable structures which allow for an elementarily definable coding machinery. We can therefore consider all second-order variables as unary and thus simply talk about set variables.
2.3 Basics of Ordinal Arithmetic and Cut-Elimination
In Theorem 3.5 and Sect. 3.2.2 we have seen that cut-free semi-formal proofs and their heights play a distinguished role. The essential feature of the semi-formal system is that it allows for a cut-elimination procedure with computable increase of the derivation height as stated in the Cut Elimination Theorem below. Though we will not prove the theorem here—its proof is widespread and can be found in practically all textbooks on proof theory—its understanding needs a rudimentary knowledge of ordinal arithmetic which we are going to recap roughly.
We understand ordinals in the set-theoretic sense as hereditarily transitive sets which are well-ordered by the membership relation \(\in \). Every ordinal is the set of all its predecessors.
An ordinal is either 0, a successor ordinal of the form \(\alpha \cup \{\alpha \}\), or a limit ordinal \(\lambda \) such that for every \(\xi <\lambda \) there is an \(\eta <\lambda \) such that \(\xi <\eta \). By \(\omega \) we denote the least limit ordinal. It represents the order-type of the natural numbers.
Every class \(A\subseteq \mathord { On}\) of ordinals possesses an enumerating function \(\mathord {\textit{en}}_{A}\) which enumerates the ordinals in A according to their natural ordering.
The enumerating function of a class which is closed and unbounded is a normal-function, i.e. a function that is order-preserving and continuous with respect to the canonical order topology of the ordinals.
The fixed points of the enumerating function of a closed and unbounded class of ordinals form again a closed and unbounded class.
Let \(\lambda \xi .\ \beta +\xi \) be the enumerating function of the class \({}{\{{\xi }\,|\,{\beta \le \xi }\}}\).
Then we obtain \(\alpha +0=\alpha ,\quad \alpha +1=\alpha \cup \{\alpha \}, \quad \alpha +(\beta +1)=(\alpha +\beta )+1\) and \(\sup {}{\{{\alpha +\xi }\,|\,{\xi <\lambda }\}}=\alpha +\lambda \) for limit ordinals \(\lambda \).
An ordinal \(\beta \) is additively indecomposable if it is closed under ordinal addition, i.e. \(\xi ,\eta <\beta \) imply \(\xi +\eta <\beta \). The class \(\mathbb H\) of additively indecomposable ordinals is closed and unbounded. The first ordinals in \(\mathbb H\) are \(1=\{\emptyset \}\) and \(\omega \).
Let \(\lambda \xi .\ \omega ^\xi \) denote the enumerating function of the class \(\mathbb H\). Then \(\omega ^0=1\), \(\omega ^1=\omega \) and \(\omega ^\lambda =\sup {}{\{{\omega ^\xi }\,|\,{\xi <\lambda }\}}\) for limit ordinals \(\lambda \). If \(\alpha \) is additively indecomposable and \(\beta <\alpha \) then \(\beta +\alpha =\alpha \).
An ordinal is an \(\varepsilon \)-number if it is closed under \(\omega \)-powers, i.e. if \(\alpha <\varepsilon \) entails \(\omega ^\alpha <\varepsilon \).
The Veblen functions \(\varphi _{\xi }\) are defined by \(\varphi _{0}({\xi }):=\omega ^\xi \) and for \(\xi >0\) the function \(\varphi _{\xi }\) enumerates the common fixed points of the functions \(\varphi _{\eta }\) for \(\eta <\xi \). Then \(\alpha <\beta \) implies \(\varphi _{\xi }({\alpha })<\varphi _{\xi }({\beta })\), since \(\varphi _{\xi }\) is an enumerating function, and \(\xi <\eta \) implies \(\varphi _{\xi }({\varphi _{\eta }({\alpha })})=\varphi _{\eta }({\alpha })\), since \(\varphi _{\eta }({\alpha })\) is a fixed point of \(\varphi _{\xi }\).
The function \(\varphi _{1}\) thus enumerates the \(\varepsilon \)-numbers. Therefore we sometimes write \(\varepsilon _{\xi }\) instead of \(\varphi _{1}({\xi })\).
An ordinal \(\gamma \) is strongly critical if it is closed under the Veblen functions viewed as a binary function, i.e. if \(\alpha ,\beta <\gamma \) also implies \(\varphi _{\alpha }({\beta })<\gamma \). Let \(\lambda \xi .\ \Gamma _\xi \) enumerate the strongly critical ordinals. An ordinal \(\gamma \) is strongly critical iff \(\varphi _{\gamma }({0})=\gamma \).
Theorem 3.11
(Cut-Elimination)  entails
entails  .
.
Remark 3.12
The case \(\rho =0\) in the cut-elimination theorem shows that the decrease of the cut rank by one means an increase of the derivation hight by one \(\omega \)-power. This can be improved to an increase by only a power of 2, i.e. to  , which may become important when it comes to not leaving the realm of the finite.
, which may become important when it comes to not leaving the realm of the finite.
2.4 Boundedness
Another important feature of semi-formal systems is expressed in the Boundedness Lemma and the resulting Boundedness Theorem. As a preparation we need some notions.
Let \(\prec \) be a well-ordering on the domain M of a structure \(\mathfrak {M}\), B a finite subset of \(\mathord {\hbox {{ field}}}(\prec )\) and \(\textit{ coen}_{B}\) enumerate the complement of \({}{\{{\mathord {\mathord {\text {otyp}}_{\prec }(x)}}\,|\,{x\in B}\}}\) in the ordinals.
Put  and \(B^{<\alpha }=B\cup \bigcup _{\xi <\alpha }B^\xi \).
and \(B^{<\alpha }=B\cup \bigcup _{\xi <\alpha }B^\xi \).
Then we obtain
Proof
Equation (3.8) is obvious for \(x\in B\). Otherwise there is an ordinal \(\alpha _0\) such that \(\mathord {\mathord {\text {otyp}}_{\prec }(x)}=\textit{coen}_{B}(\alpha _0)\). For \(\alpha <\alpha _0\) it is \(\textit{coen}_{B\cup \{x\}}(\alpha )=\textit{coen}_{B}(\alpha )\). For \(\alpha = \alpha _0+\xi \) we get \(\textit{coen}_{B\cup \{x\}}(\alpha _0 +\xi )\le \textit{coen}_{B}(\alpha _0+1+\xi )\) and \(\alpha _0+1+\xi \le \alpha +1.\)
Equation (3.9) follows directly from (3.8).
To show (3.10) observe that by the transitivity of the relation \(\prec \) we get for every \(\alpha <\mathord {\mathord {\text {otyp}}_{\prec }(x)}\) a \(y\prec x\) such that \(\mathord {\mathord {\text {otyp}}_{\prec }(y)}=\alpha \). Claim (3.10) is trivial for \(x\in B\). Otherwise there is a \(\xi \) such that \(\mathord {\mathord {\text {otyp}}_{\prec }(x)}=\textit{coen}_{B}(\xi )\). If \(\xi \le \alpha \) we are done. If \(\alpha <\xi \) then \(\textit{coen}_{B}(\alpha )<\textit{coen}_{B}(\xi )\) and there is a \(y\prec x\) such that \(\mathord {\mathord {\text {otyp}}_{\prec }(y)}=\textit{coen}_{B}(\alpha )\). Since \(\mathord {\mathord {\text {otyp}}_{\prec }(y)}=\textit{coen}_{B}(\alpha )\) excludes \(y\in B\) we get the contradiction \(\textit{coen}_{B}(\alpha )=\mathord {\mathord {\text {otyp}}_{\prec }(y)}<\textit{coen}_{B}(\alpha )\). \(\square \)
The Boundedness Lemma and the Boundedness Theorem provide statements about the order-types of well-orderings that are definable in \(\mathfrak {M}\). The well-foundedness of an order relation \(\prec \) can be expressed by the pseudo \(\Pi _{1}^{1}\)-sentence 
By \(\textit{ Prog}(\prec ,X)\) we abbreviate the formula \((\forall ~x)[(\forall ~y)[y\prec x\rightarrow y\in X]\rightarrow x\in X]\).
Lemma 3.13
(Boundedness Lemma) Let \(\mathfrak {M}\) be a countable acceptable structure and \(\prec \) a well-ordering that is elementarily definable in \(\mathfrak {M}\). If

for a finite set of X-positive pseudo \(\Pi _{1}^{1}\)-sentences \(\Delta (X)\) then \(\mathfrak {M}\models \bigvee \Delta (X)[B^{<\alpha }]\) for \(B:=\{x_1,\dots ,x_{n}\}\).
Proof
Since this is one of the central lemmas of the paper we sketch the crucial case of its proof.Footnote 16 We induct on \(\alpha \).
Assume that the critical formula of the last inference is \(\lnot \!\textit{ Prog}(\prec ,X)\). Then we have the premise
(i)  .
.
By \(\bigwedge \)-inversion this entails
(ii) 
and
(iii)  .
.
Assume \(\mathfrak {M}\not \models \bigvee \Delta (X)[B^{<\alpha }].\) By X–positivity this entails \(\mathfrak {M}\not \models \bigvee \Delta (X)[B^{<\alpha _0}].\) Then we obtain by (ii) and the induction hypothesis
(iv) \(\mathfrak {M}\models (\forall ~x)[y\prec x\rightarrow y\in B^{<\alpha _0}]\) which by (3.10) implies \(x\in B^{\alpha _0}\subseteq B^{<\alpha }\).
By (iii) and the induction hypothesis it follows
(v) \(\mathfrak {M}\models \Delta (X)[(B\cup \{x\})^{<\alpha _0}]\) and by (3.9) we have \((B\cup \{x\})^{<\alpha _0}\subseteq B^{<\alpha }\cup \{x\}\).
Since \(B^{<\alpha }\cup \{x\}=B^{<\alpha }\) by (iv) we have the contradiction \(\mathfrak {M}\models \bigvee \Delta (X)[B^{<\alpha }]\).
\(\square \)
Since \(\textit{coen}_{\emptyset }(\xi )=\xi \) we obtain the next theorem as a corollary of Lemma 3.13.
Theorem 3.14
(Boundedness Theorem) Let \(\mathfrak {M}\) be a countable structure and assume that \(\prec \) is an \({\mathscr {L}}(\mathfrak {M})\)-definable ordering on \(\mathfrak {M}\) such that  . Then \(\mathord {\mathord {\text {otyp}}({\prec })}\le \alpha \).
. Then \(\mathord {\mathord {\text {otyp}}({\prec })}\le \alpha \).
The Boundedness Theorem makes the connection of \(\pi ^\mathfrak {M}\) to better known characteristic ordinals of a structure \(\mathfrak {M}\), e.g. the supremum of the order-types of well-orderings that are definable in \(\mathfrak {M}\).
Definition 3.15
For a structure \(\mathfrak {M}\) and a language \({\mathscr {L}}\subseteq {{\mathscr {L}}(\mathfrak {M})}_M\) define
We briefly put \(\delta ^\mathfrak {M}:=\delta ^{{{\mathscr {L}}(\mathfrak {M})}}\).
For an axiomatization \(\textsf{T}\) of \(\mathfrak {M}\) let

and
From the Boundedness Theorem we get immediately
and
If \(\delta ^\mathfrak {M}(\textsf{T})=\pi ^\mathfrak {M}(\textsf{T})\) we put

and call  the proof-theoretic ordinal of T with respect to \(\mathfrak {M}\).
the proof-theoretic ordinal of T with respect to \(\mathfrak {M}\).
By an ordinal analysis of an axiom system \(\textsf{T}\) we understand the computation of its proof-theoretic ordinal. An ordinal analysis of \(\textsf{T}\) usually follows the pattern that we first compute \(\pi ^\mathfrak {M}(\textsf{T})\) to obtain an upper bound and then show that for every ordinal \(\alpha <\pi ^\mathfrak {M}(\textsf{T})\) there is an \({{\mathscr {L}}(\mathfrak {M})}_M\)-definable well-ordering \(\prec \) of order-type \(\alpha \) such that  .
.
Note 3.16
If \(\mathfrak {M}\) is the structure \({\mathfrak N}\) of natural numbers, we have \(\delta ^{\Delta ^0_0}\le \delta ^{\Delta ^1_0}=\delta ^{\mathfrak N}\le \delta ^{\Sigma ^1_1}\le \pi ^{\mathfrak N}\le \delta ^{\Delta ^0_0}\) and likewise  . Hence \(\delta ^{\mathfrak N}=\pi ^{\mathfrak N}\) and \(\delta ^{\mathfrak N}(\textsf{T})=\pi ^{\mathfrak N}(\textsf{T})\).
. Hence \(\delta ^{\mathfrak N}=\pi ^{\mathfrak N}\) and \(\delta ^{\mathfrak N}(\textsf{T})=\pi ^{\mathfrak N}(\textsf{T})\).
In [31] we claimed that \(\delta ^\mathfrak {M}=\pi ^\mathfrak {M}\) holds true for all acceptable structures \(\mathfrak {M}\). This is false in the there claimed generality. There are counterexamples which are countable elementary “Skolem” substructures of uncountable structures in which well-foundedness is elementarily (i.e. first order) definable (cf.[24] Sect. 8D). These are structures which allow for an elementarily definable coding machinery but in which the characteristic sequences of elementary sentences are not elementarily definable.
Call a structure strictly acceptable if there is not only an elementarily definable coding machinery but also all characteristic sequences for elementary sentences are elementarily definable. This requires an elementary coding
 for all \({\mathscr {L}}(\mathfrak {M})\)-sentences such that
for all \({\mathscr {L}}(\mathfrak {M})\)-sentences such that
 can be expressed by an elementary \({\mathscr {L}}(\mathfrak {M})\) -formula.Footnote 17 Then the search tree for a pseudo \(\Pi _{1}^{1}\)-sentence becomes elementarily definable which entails \(\delta ^\mathfrak {M}=\pi ^\mathfrak {M}\) as shown in [31].Footnote 18 The paradigmatic example for strictly acceptable structure are structures above the natural numbers. In general, strictly acceptable structures are even more “standard like” and therefore constitute a restriction of generality. However, since strictly acceptable structures are not in the centre of this paper we will not go into further details.
can be expressed by an elementary \({\mathscr {L}}(\mathfrak {M})\) -formula.Footnote 17 Then the search tree for a pseudo \(\Pi _{1}^{1}\)-sentence becomes elementarily definable which entails \(\delta ^\mathfrak {M}=\pi ^\mathfrak {M}\) as shown in [31].Footnote 18 The paradigmatic example for strictly acceptable structure are structures above the natural numbers. In general, strictly acceptable structures are even more “standard like” and therefore constitute a restriction of generality. However, since strictly acceptable structures are not in the centre of this paper we will not go into further details.
Remark 3.17
It should be noted that there is a certain parallel between pseudo \(\Pi _{1}^{1}\)-sentences and \(\Pi ^0_1\)-sentences of the first-order language of \(\mathfrak {M}\). For a recursive axiom system \(\textsf{T}\) we can construct the Gödel sentence G(x) such that \(\textsf{T}\vdash G(\underline{z})\) holds true for every numeral z but \(\textsf{T}\not \vdash (\forall ~x)G(x)\). For an arbitrary axiom system \(\textsf{T}\), for which we have an ordinal analysis, there is an \({{\mathscr {L}}(\mathfrak {M})}\)-definable well-ordering \(\prec \)—whose order-type is  —and the pseudo \(\Pi _{1}^{1}\)-sentence \({G(\underline{z},X):\equiv \underline{z}\in \mathord {\hbox {{ field}}}(\prec )\rightarrow \textit{ WO}(\mathord \prec \mathord {\restriction }\underline{z},X)}\) such that \(\textsf{T}\vdash G(\underline{z},X)\) for every \(z\in M\) but \(\textsf{T}\not \vdash (\forall ~x)G(x,X)\).
—and the pseudo \(\Pi _{1}^{1}\)-sentence \({G(\underline{z},X):\equiv \underline{z}\in \mathord {\hbox {{ field}}}(\prec )\rightarrow \textit{ WO}(\mathord \prec \mathord {\restriction }\underline{z},X)}\) such that \(\textsf{T}\vdash G(\underline{z},X)\) for every \(z\in M\) but \(\textsf{T}\not \vdash (\forall ~x)G(x,X)\).
Note 3.18
To avoid second-order variables the proof-theoretic ordinal of an axiom system is occasionally defined by a scheme

where F is any first-order sentence. This is not without problems. Let \(\textit{Def}\,({\mathfrak {M}})\) denote the collection of all subsets of \(\mathfrak {M}\) which are \({{\mathscr {L}}(\mathfrak {M})}\)-definable from \(\mathfrak {M}\). Then the scheme \(\textsf{T}\vdash \textit{ WO}(\prec ,F)\) entails that \((\mathfrak {M},\textit{Def}\,({\mathfrak {M}}))\models (\forall ~X)\textit{ WO}(\prec ,X)\). But \((\mathfrak {M},\textit{Def}\,({\mathfrak {M}}))\) is in general not a \(\beta \) -model. So \(\textsf{T}\vdash \textit{ WO}(\prec ,F)\) in general will not entail that \(\prec \) is well-founded. Therefore we must assume “from outside” that \(\prec \) is a well-ordering. Since \(\textsf{T}\vdash \textit{ WO}(\prec ,X)\) implies \(\textsf{T}\vdash \textit{ WO}(\prec ,F)\) for all \({{\mathscr {L}}(\mathfrak {M})}\)-sentences F we get under this assumption  . On the other hand we can show that for a strictly acceptable structure \(\mathfrak {M}\) there is an \({{\mathscr {L}}(\mathfrak {M})}\)-sentence G and a well-ordering \(\prec \) of order-type \(\pi ^\mathfrak {M}(\textsf{T})\) such that \(\textsf{T}+\textit{ WO}(\prec ,G)\) proves the consistency of \(\textsf{T}\). Hence \(\textsf{T}\not \vdash \textit{ WO}(\prec , G)\) by Gödel’s second incompleteness theorem which entails
. On the other hand we can show that for a strictly acceptable structure \(\mathfrak {M}\) there is an \({{\mathscr {L}}(\mathfrak {M})}\)-sentence G and a well-ordering \(\prec \) of order-type \(\pi ^\mathfrak {M}(\textsf{T})\) such that \(\textsf{T}+\textit{ WO}(\prec ,G)\) proves the consistency of \(\textsf{T}\). Hence \(\textsf{T}\not \vdash \textit{ WO}(\prec , G)\) by Gödel’s second incompleteness theorem which entails  and both ordinals coincide.
and both ordinals coincide.
2.5 An Example
We give an example for an ordinal analysis. Let \(\mathfrak {M}\) be a countable strictly acceptable structure, \({{\mathscr {L}}(\mathfrak {M})}\) its first-order language and \(\textsf{T}\) be an axiom system for \(\mathfrak {M}\). Then F is a logical consequence of \(\textsf{T}\) if there are finitely many axioms \(T_1,\dots ,T_{n}\) in \(\textsf{T}\) such that the formula
is logically valid. By Lemma 3.4 we thus obtain

Let us first assume that \(\textsf{T}\subseteq {{\mathscr {L}}(\mathfrak {M})}_M\). Since \(\textit{rnk}(G)<\omega \) holds true for all sentences G in \({{\mathscr {L}}(\mathfrak {M})}_M\) we get by Observation 3.3  with \(m_i=\textit{rnk}(T_i)<\omega \) for \(i=1,\dots ,n\) . For \(m:=\max \{m_1,\dots ,m_{n}\}+1\) we therefore obtain together with Lemma 3.4 by n cuts followed by cut-elimination (cf. Remark 3.12)
with \(m_i=\textit{rnk}(T_i)<\omega \) for \(i=1,\dots ,n\) . For \(m:=\max \{m_1,\dots ,m_{n}\}+1\) we therefore obtain together with Lemma 3.4 by n cuts followed by cut-elimination (cf. Remark 3.12)

If we assume that there is an upper bound for the complexities of the sentences in \(\textsf{T}\) we thus get \(\pi ^\mathfrak {M}(\textsf{T})<\omega \). If there is no such upper bound we get \(\pi ^\mathfrak {M}(\textsf{T})=\omega \).
If we allow pseudo \(\Pi _{1}^{1}\)-sentences among the axioms of \(\textsf{T}\) we can no longer apply Observation 3.3 to obtain upper bounds for the truth complexities of the sentences in \(\textsf{T}\). In this case we need additional computations. As an example we compute the truth complexity of the axiom of Mathematical Induction
in the structure \({\mathfrak N}\) of natural numbers. We show

by induction on n. For \(n=0\) we obtain (3.16) by tautology (Observation 3.6). By induction hypothesis we have

and by tautology

By an inference \((\bigwedge )\) followed by an inference \((\bigvee )\) we get (3.16) with n replaced by \(n+1\). From (3.16) we finally get

hence

Call an axiomatization of an acceptable structure acceptable if it proves all the properties of the coding machinery. We especially require that an acceptable axiomatization comprises a form of Mathematical Induction. The truth complexity of this axiom may be a bit greater than \(\omega +4\)—depending on the complexity of the elementarily definable copy\((N^{\mathscr {C}},\le ^{\mathscr {C}})\) of \({\mathfrak N}\)—but it will always remain smaller than \(\omega +\omega \). If we assume that all other axioms in \(\textsf{T}\) are \({{\mathscr {L}}(\mathfrak {M})}_M\)-sentences and thus have finite truth complexities we obtain with the same procedure as above

for every pseudo \(\Pi _{1}^{1}\)-sentence which is provable from \(\textsf{T}\). This shows \(\pi ^\mathfrak {M}(\textsf{T})\le \sup {}{\{{2^{(m)}(\omega +\omega )}\,|\,{m\in \omega }\}}={\varepsilon _0}\), where \({\varepsilon _0}\) is the first ordinal \(\alpha \) such that \(\omega ^\alpha =\alpha \), i.e. \({\varepsilon _0}=\varphi _{1}({0})\). Call such axiom systems Peano-like.
On the other hand already Gentzen in [15] has shown that the Peano axioms \(\mathord {\textsc {PA}}\) suffice to show that for any ordinal \(\alpha <{\varepsilon _0}\) there is a well-ordering \(\prec \) of order-type \(\alpha \) which is elementarily (even primitive-recursively) definable in \({\mathfrak N}\)—and thus also in every acceptable countable structure \(\mathfrak {M}\)—such that  . So \({\varepsilon _0}\le \delta ^{\mathfrak N}(\mathord {\textsc {PA}})\). Since the critical axiom in the Gentzen proof is Mathematical Induction this proof can be mimicked in any acceptable axiomatization of a countable acceptable structure. So we have the following theorem.
. So \({\varepsilon _0}\le \delta ^{\mathfrak N}(\mathord {\textsc {PA}})\). Since the critical axiom in the Gentzen proof is Mathematical Induction this proof can be mimicked in any acceptable axiomatization of a countable acceptable structure. So we have the following theorem.
Theorem 3.19
Let \(\mathfrak {M}\) be an acceptable countable structure and \(\textsf{T}\) an acceptable axiomatization of \(\mathfrak {M}\) in which all axioms except Mathematical Induction are of finite complexity. Then  and \(\textsf{T}\) is Peano-like.
and \(\textsf{T}\) is Peano-like.
Remark 3.20
Usually the Peano axioms \(\mathord {\textsc {PA}}\) are formulated in the first-order language \({\mathscr {L}}({\mathfrak N})\) of \({\mathfrak N}\) with the scheme of Mathematical Induction. This means that we have \(\mathord {\textsc {PA}}\subseteq {\mathscr {L}}({\mathfrak N})\) which—according to our above considerations—leads to \(\pi ^{\mathfrak N}(\mathord {\textsc {PA}})=\omega \). This is irritating since it is well known that the proof-theoretic ordinal of \(\ \mathord {\textsc {PA}}\) is \({\varepsilon _0}\). The reason for this irritation is the fact that the presence of the free second-order variable X in \(\textit{ WO}(\prec ,X)\) is essential for the validity of the Boundedness Theorem. We cannot conclude \(\mathord {\mathord {\text {otyp}}({\prec })}\le \alpha \) from the scheme  Even if we extend the language of \(\mathord {\textsc {PA}}\) conservatively to \(\mathord {\textsc {PA}}(X)\) by adding second-order variables. We cannot infer \(\mathord {\textsc {PA}}(X)\vdash \textit{ WO}(\prec ,X)\) from the scheme \(\mathord {\textsc {PA}}(X)\vdash \textit{ WO}(\prec ,F)\), where F only varies over \({\mathscr {L}}(\mathord {\textsc {PA}})\)-sentences. The Boundedness Theorem is therefore not applicable. Moreover we get \(\delta ^{\mathbb N}(\textsf{T})=0\) in absence of second-order variables. Without second-order variables, we thus have to rely on Gödel’s second incompleteness theorem and to argue as in Note 3.18.
Even if we extend the language of \(\mathord {\textsc {PA}}\) conservatively to \(\mathord {\textsc {PA}}(X)\) by adding second-order variables. We cannot infer \(\mathord {\textsc {PA}}(X)\vdash \textit{ WO}(\prec ,X)\) from the scheme \(\mathord {\textsc {PA}}(X)\vdash \textit{ WO}(\prec ,F)\), where F only varies over \({\mathscr {L}}(\mathord {\textsc {PA}})\)-sentences. The Boundedness Theorem is therefore not applicable. Moreover we get \(\delta ^{\mathbb N}(\textsf{T})=0\) in absence of second-order variables. Without second-order variables, we thus have to rely on Gödel’s second incompleteness theorem and to argue as in Note 3.18.
According to Observation 3.3 we generally have \({\mathord {\text {tc}}(F)}=\textit{rnk}(F)\) for \({{\mathscr {L}}(\mathfrak {M})}_M\)-sentences which shows that \({\mathord {\text {tc}}(F)}\) only carries additional information for pseudo \(\Pi _{1}^{1}\)-sentences. In absence of free second-order variables the ordinal \(\pi ^\mathfrak {M}\) carries no additional information. Thus second-order variables are essential for the definition of \(\delta ^\mathfrak {M}\).
However, Theorem 3.19 leads to another oddity. Let \(\textsf{T}\) be any Peano-like axiomatization for a strictly acceptable countable structure \(\mathfrak {M}\). If we denote by \(\textit{ Th}({\mathfrak {M})}:={}{\{{F}\,|\,{F \text { is an } {{\mathscr {L}}(\mathfrak {M})}_M-\text {sentence and }\mathfrak {M}\models F}\}}\) the elementary diagram of \(\mathfrak {M}\) and by \(\mathsf{(Ind)}\) the pseudo \(\Pi _{1}^{1}\)-sentence which expresses Mathematical Induction we obtain

A surprising fact because \(\textit{ Th}({\mathfrak {M})}\) should know everything about \(\mathfrak {M}\). This shows that  cannot serve as a measure of the performance of \(\textsf{T}\) with respect to the ground structure \(\mathfrak {M}\) but is rather a measure of its performance with respect to a “universe” above \(\mathfrak {M}\).Footnote 19 This observation is corroborated by the next theorem.Footnote 20
cannot serve as a measure of the performance of \(\textsf{T}\) with respect to the ground structure \(\mathfrak {M}\) but is rather a measure of its performance with respect to a “universe” above \(\mathfrak {M}\).Footnote 19 This observation is corroborated by the next theorem.Footnote 20
Theorem 3.21
(No Enhancement Theorem) Let \(\mathfrak {M}\) be an acceptable countable structure and \(\textsf{T}\) an acceptable axiomatization of \(\mathfrak {M}\) such that  . Let \(F(Y)\) be a \(\Sigma ^1_1\)-sentence which is true in \(\mathfrak {M}\) and \(\textsf{T}':=\textsf{T}+ F(Y)\). Then
. Let \(F(Y)\) be a \(\Sigma ^1_1\)-sentence which is true in \(\mathfrak {M}\) and \(\textsf{T}':=\textsf{T}+ F(Y)\). Then  .
.
Proof
From  we get
we get  . Therefore there is an ordinal \(\alpha <\pi ^\mathfrak {M}(\textsf{T})\) such that
. Therefore there is an ordinal \(\alpha <\pi ^\mathfrak {M}(\textsf{T})\) such that

By the Boundedness Lemma (Lemma 3.13) we thus obtain

Since \(\mathfrak {M}\not \models \lnot F(Y)\) this entails  . Hence \(\delta ^\mathfrak {M}(\textsf{T}')\le \pi ^\mathfrak {M}(\textsf{T})=\delta ^\mathfrak {M}(\textsf{T})\). The converse inequality holds trivially. \(\square \)
. Hence \(\delta ^\mathfrak {M}(\textsf{T}')\le \pi ^\mathfrak {M}(\textsf{T})=\delta ^\mathfrak {M}(\textsf{T})\). The converse inequality holds trivially. \(\square \)
3 Analytical Universes Above \(\mathfrak {M}\)
Taking the distance between \(\pi ^\mathfrak {M}(\textsf{T})\) and \(\pi ^\mathfrak {M}\) as a measure for the performance of an axiom system \(\textsf{T}\), the considerations of the previous section have shown that the performance of an axiom system for \(\mathfrak {M}\) can only be increased by additional axioms for universes above \(\mathfrak {M}\).Footnote 21
There are in principle two possibilities to build universes above a structure \(\mathfrak {M}\). Set universes with the elements of M as urelements or “analytical” universes which only talk about sets which are subsets of M. The more general and also more promising approach are set universes. However, historically older is the concept of analytical universes, which we think is also of interest for itself. For reasons of space we cannot treat both approaches in this paper. Therefore we decided to postpone the approach via set theoretical universes to another paper and to concentrate on analytical universes.
Axioms for universes above \(\mathfrak {M}\) need an extension of the first-order language of \(\mathfrak {M}\). Already the introduction of pseudo \(\Pi _{1}^{1}\)-sentences constitutes such an extension. The most obvious way is to expand the language to a second-order language \({\mathscr {L}}^2(\mathfrak {M})\). The second-order quantifiers in full second-order logic vary over the full power set of M. Since real numbers can be identified with subsets of natural numbers, “Real Analysis” can be formulated within second-order logic. Hence the term “analytical universe”. There is, however, no completeness theorem for full second-order logic and therefore no formal calculus for full second-order logic which is sound and complete.
There are calculi which are sound for second-order logic, which, however, are in fact two sorted first-order calculi. We refer to such calculi as weak second-order calculi. A second-order sentence is valid in weak second-order logic, if it holds in all structures \({\mathscr {U}({\mathfrak {M}})}=(M,{\mathscr {U}({M})},\cdots )\), where the range \({\mathscr {U}({M})}\) of second-order quantifiers is supposed to be any subset of the full power set \(\mathscr {P}({M})\). However, we count only such subsets \({\mathscr {U}({M})}\subseteq \mathscr {P}({M})\) that satisfy certain closure conditions among possible candidates for “analytical universes”.
The full structure \((M,\mathscr {P}({M}),\cdots )\) is uncountable and therefore not accessible to the methods introduced in Sect. 3.2. The largest structure which could possibly be accessible to these methods is \(\mathfrak {M}_2:=(M,{\mathscr {D}}(M),\cdots )\) where \({\mathscr {D}}(M)\) is the set of all subsets of M which are definable in the second-order language \({\mathscr {L}}^2(\mathfrak {M})\). For countable structures \(\mathfrak {M}\) this is again a countable structure.
Any axiomatization \(\textsf{T}\) for the structure \(\mathfrak {M}\) can be extended to an axiomatization \(\textsf{T}_2\) for \(\mathfrak {M}_2\) by adding the comprehension scheme
- (CA):
-
\((\forall ~x)[x\in X\leftrightarrow F(x)]\),
where F is any formula in the second-order language \({\mathscr {L}}^2(\mathfrak {M})\) not containing the variable X.
Remark 3.22
Since “Real Analysis”, i.e. the theory of real numbers can be formalized in this axiom system, which is based on classical logic, it is often referred to as “Classical Analysis”.Footnote 22 Another common—perhaps even better—name for the system is “Second-Order Number Theory” which we abbreviate by SONT.
Note 3.23
An extensive study of axiom systems for Analysis, i.e. subsystems of SONT, can be found in [38]. However, Simpson’s studies in [38] go in a different direction. He begins with a collection of essentially five axiom systems—formulated in second-order language—and examines which analytical universes fulfill these axioms and which known mathematical theorems are theorems—or even equivalents—of these axiom systems.
Today we are still far away from an ordinal analysis of \(\textsf{T}_2\). The reason is the impredicativity of second-order logic. The decoration for a second-order quantification \(({\mathord {\textsf {Q}}}{X})F(X,\underline{m})\) can only be the sequence \({}{\big \langle {F(S,\underline{m})}\,|\,{S\in {\mathscr {D}}(M)}\big \rangle }\) and the set \(S:={}{\{{x}\,|\,{({\mathord {\textsf {Q}}}{X})F(X,x)}\}}\) is a member of \({\mathscr {D}}(M)\). So we run into a vicious circle which shows that the condition \(\textit{rnk}(G)<\textit{rnk}(F)\) can hardly be met for all \(G\in \text {CS}~F\). But this condition is crucial for \(\Pi _{1}^{1}\)-completeness as well as for cut-elimination. Therefore, we do not even have a definition of \(\pi ^{\mathfrak {M}_2}\), let alone a computation of \(\pi ^{\mathfrak {M}_2}(\textsf{T}_2)\) or \(\delta ^{\mathfrak {M}_2}(\textsf{T}_2)\).
3.1 Spector Classes
To come to structures which are within the reach of our methods we must further restrict the “universe” \({\mathscr {D}}(M)\). Clearly only universes with sufficiently good closure properties are interesting. Examples for such universes are Spector classes above \(\mathfrak {M}\).
Definition 3.24
A Spector class above an abstract structure \(\mathfrak {M}=(M,{\mathscr {F}},{\mathscr {R}})\) is a collection \(\Gamma =\bigcup _{n\in {\mathbb N}}{\Gamma ^n}\) of relations on M which satisfy the following conditions.Footnote 23
- (C):
-
\(\Gamma \) is closed under the positive Boolean operations, first-order quantification and trivial combinatorial substitutions.
- (U):
-
\(\Gamma \) is universal, i.e. for any \(n\in {\mathbb N}\) there is a \(n+1\)-ary relation \(U\in \Gamma ^{n+1}\) such that for every n-ary \(R\in \Gamma ^n\) there is an element \(e\in M\) such that \(\mathfrak {M}\models (\forall ~{\vec x})[R({\vec x})\leftrightarrow U(e,{\vec x})]\).Footnote 24
- (N):
-
\(\Gamma \) is normed, i.e. for every \(R\in \Gamma \) there is an ordinal \(\lambda \) and a norm
 such that the stage comparison relations
such that the stage comparison relations- (N1):
-
\({\vec m}\mathrel {\preceq ^*_{\sigma }}\vec n{}\quad :\Leftrightarrow \quad R({\vec m})\,\wedge \,[R(\vec n)\rightarrow \sigma _R({\vec m})\le \sigma _R(\vec n)]\)
and
- (N2):
-
\({\vec m}\mathrel {\prec ^*_{\sigma }}\vec n{}\quad :\Leftrightarrow \quad R({\vec m})\,\wedge \,[R(\vec n)\rightarrow \sigma ({\vec m})<\sigma (\vec n)]\)
are both in \(\Gamma \). Call such a norm a \(\Gamma \)-norm on R.
- (A):
-
Every \(f\in {\mathscr {F}}\) and every \(R\in {\mathscr {R}}\) belongs to the self-dual class \(\Delta =\Gamma \cap \breve{\Gamma }\) where
$${\breve{\Gamma }:=\bigcup {}{\{{X\mathord \subseteq M^n}\,|\,{(M^n\setminus X)\in \Gamma ^n}\}}}$$denotes the dual of \(\Gamma \).
Here \(f\in \Delta \) means \({}{\{{({\vec x},f({\vec x}))}\,|\,{{\vec x}\in \textit{dom}(f)}\}}\in \Delta \).
As remarked above, second-order quantifiers are difficult to decorate. Therefore it might be difficult to define the \(\Pi _{1}^{1}\)-ordinal \(\pi ^\mathfrak {M}\) for structures which comprise an analytical universe. For Spector classes, however, there is a canonical replacement for the ordinal \(\pi ^{\mathfrak M}\).
Definition 3.25
For a Spector class \(\Gamma \) and \(R\in \Gamma \) we define the ordinal
and for a subset \(\Lambda \subseteq \Gamma \)
We define the Spector spectrum of an abstract structure \(\mathfrak {M}\) by
and the ordinal spectrum of \(\mathfrak {M}\)
The intersection of Spector classes above \(\mathfrak {M}\) is clearly again a Spector class above \(\mathfrak {M}\). Therefore there exists a least Spector class
above \(\mathfrak {M}\) and we put
Lemma 3.26
Let \(\Gamma \) be a Spector class above a countable acceptable structure \(\mathfrak {M}\) and \(\prec \) a well-ordering in \(\Delta \). Then \(\mathord {\mathord {\text {otyp}}({\prec })}\le o(\Gamma ).\) Hence \(\delta ^\mathfrak {M}\le \kappa ^\mathfrak {M}\).
Proof
Let \(U^2\) parameterize the binary relations in \(\Gamma \) and  be a norm for \(U^2\). Then, given a well-ordering \(\prec \ \in \Delta \), the relation
be a norm for \(U^2\). Then, given a well-ordering \(\prec \ \in \Delta \), the relation
is a relation in \(\Gamma ^2\) which, in turn, is parameterized by a fixed element \(a\in M\). Hence
which shows \(\mathord {\mathord {\text {otyp}}_{\prec }(x)}\le \mathord {\mathord {\text {otyp}}_{\prec _{\tau }^{*}}((a,a,x))}\) and thus also \(\mathord {\mathord {\text {otyp}}({\prec })}\le o(\Gamma )\) by \(\prec \)-induction on x. \(\square \)
Remark 3.27
For a Spector class \(\Gamma \) and \(R\in \Gamma \) we have \(R\in \Delta \) iff \(o(R)<o(\Gamma )\). (Cf. [24] Theorem 9C.4).
3.1.1 A Hierarchy of Spector Classes Above \({\mathfrak M}\)
The existence of a least Spector class above \(\mathfrak {M}\) opens the possibility to built a hierarchy of Spector classes above \(\mathfrak {M}\). Call a structure of the form \((M,\Gamma ,\cdots )\), where \(\Gamma \) is a Spector class above \(\mathfrak {M}=(M,\cdots )\), a Spector structure. Augmenting a structure \(\mathfrak {M}=(M,\cdots )\) by the relations in \({\mathbb {S}}{\mathbb {P}}_{\mathfrak {M}}\) we obtain a Spector structure \(\mathfrak {M}_1:=(M,{\mathbb {S}}{\mathbb {P}}_{\mathfrak {M}},\cdots )\). Iterating this procedure yields a hierarchy \(\mathbb S\mathbb P_{\mathfrak {M}}^{n}\) of Spector classes above \(\mathfrak {M}\) and Spector structures \(\mathfrak {M}_n=(M,\mathbb S\mathbb P_{\mathfrak {M}}^{n},\cdots )\). This hierarchy can be continued into the transfinite by defining
-
\(\mathbb S\mathbb P_{\mathfrak {M}}^{0}=\emptyset \),
-
\(\mathbb S\mathbb P_{\mathfrak {M}}^{\mu +1}:={\mathbb {S}}{\mathbb {P}}_{\mathfrak {M}_\mu }\) for \(\mathfrak {M}_{\mu }:=(M,\mathbb S\mathbb P_{\mathfrak {M}}^{\mu },\cdots )\) and
-
\(\mathbb S\mathbb P_{\mathfrak {M}}^{\lambda }=\bigcup _{\xi <\lambda }{\mathbb {S}}{\mathbb {P}}_{\mathfrak {M}}^\xi \) for limit ordinals \(\lambda \).
Let \(\kappa _{\mu }^{\mathfrak {M}}\) denote the corresponding closure ordinals of the Spector classes \(\mathbb S\mathbb P_{\mathfrak {M}}^{\mu }\), i.e.
\( \quad \kappa _{0}^{\mathfrak {M}}:=0,\quad \kappa _{\mu +1}^{\mathfrak {M}}:=o(\mathbb S\mathbb P_{\mathfrak {M}}^{\mu +1})\, \text { and } \kappa _{\lambda }^{\mathfrak {M}}:=o(\mathbb S\mathbb P_{\mathfrak {M}}^{\lambda })=\sup {}{\{{\kappa _{\xi }^{\mathfrak {M}}}\,|\,{\xi <\lambda }\}}\).
Remark 3.28
All the structures \({\mathfrak M}_{{\mu +1}}\) are Spector structures. For limit ordinals \(\lambda \) this is not true in general. If \({\mathfrak M}_{\lambda }\) happens to be a Spector structure, we call \(\kappa _{\lambda }^{{\mathfrak M}}\) a \({\mathfrak M}\)-recursively inaccessible ordinal (mostly omitting the \(\mathfrak {M}\)). Recursively inaccessible ordinals play an important role in the study of set universes above \(\mathfrak {M}\). In this paper, however, we will not study these aspects. Therefore we just neglect recursively inaccessible ordinals which amounts to considering only ordinals \(\mu \) below the first recursively inaccessible ordinal.
3.1.2 The Ordinal Spectrum of an Axiom System
Definition 3.29
Let \(\textsf{T}\) be an axiomatization for a universe above \(\mathfrak {M}\).
For \(\Gamma \in \textit{SPEC}({\mathfrak {M}})\) let

where \(\sigma _R\) again varies over the \(\Gamma \)-norms for R. Let
The distance between \(\kappa ^\mathfrak {M}(\textsf{T})\) and \(\kappa ^\mathfrak {M}\) represents a measure for the performance of the axiom system \(\textsf{T}\) with respect to \({\mathbb {S}}{\mathbb {P}}_{\mathfrak {M}}\). We have \(\delta ^\mathfrak {M}(\textsf{T})\le \kappa ^\mathfrak {M}(\textsf{T})\) and in case that \(\delta ^{\mathfrak {M}}({\textsf{T}})=\kappa ^{\mathfrak {M}}(\textsf{T})\) we put  and call
and call  the proof-theoretic ordinal of \(\textsf{T}\) in relation to \({\mathfrak M}\).Footnote 25
the proof-theoretic ordinal of \(\textsf{T}\) in relation to \({\mathfrak M}\).Footnote 25
Note 3.30
Spector classes are introduced and studied in [24] Chap. 9 and [25]. Spector classes are designed to generalize computability in an abstract way. The archetype of a Spector class is the collection \(\mathscr {R}\mathscr {E}\) of recursively enumerable sets. Clearly, in \(\mathscr {R}\mathscr {E}\) we have to replace closure under first-order quantification by closure under bounded quantification. The universal set is \(U={}{\{{\langle {x,e}\rangle }\,|\,{T(e,x,y)}\}}\), where T denotes the Kleene predicate, and for \(m\in P=U_e\) we get the norm \(\sigma _e(m):=\min {}{\{{n}\,|\,{T(e,m,n)}\}}\). Then we get
and
which are both recursively enumerable.
So the class \(\mathscr {R}\mathscr {E}\) of recursively enumerable sets could be viewed as Spector class with \(o(\mathscr {R}\mathscr {E})=\omega \). Nevertheless, because of its restricted closure properties, we do not count \(\mathscr {R}\mathscr {E}\) among \(\textit{SPEC}({\mathfrak {M}})\). So we always have \(\omega <\kappa ^\mathfrak {M}\).
The analogy of Spector classes to recursively enumerable sets forms the background for the definition of partial \(\Gamma \)-recursive functions. If \(\Gamma \) is a Spector class above a structure \(\mathfrak {M}\) we call a partial function  partial \(\Gamma \)-recursive iff its graph \(G_f\) belongs to \(\Gamma \).
partial \(\Gamma \)-recursive iff its graph \(G_f\) belongs to \(\Gamma \).
3.2 Fixed-Point Theories
3.2.1 General Fixed-Point Theories
The notion of a Spector class is very general. Consequently the Spector spectrum of a countable acceptable structure \(\mathfrak {M}\) is huge, even when we restrict it to countable Spector classes above \(\mathfrak {M}\). Moreover, because of the ordinals needed in condition (N) Spector classes cannot be directly axiomatized in \({\mathscr {L}}^2(\mathfrak {M})\).Footnote 26 Therefore we need a more specific characterization of Spector classes.
The essential examples for Spector classes are obtained by fixed points of \({{\mathscr {L}}(\mathfrak {M})}\)-definable operators on M. We briefly recap some of their key properties.Footnote 27 Again we restrict ourselves to countable acceptable structures \(\mathfrak {M}\). We thus can regard Spector classes above \(\mathfrak {M}\) as subsets of \(\mathscr {P}({\mathfrak {M}})\).
Any formula F(X, x) in the language of \({\mathscr {L}}(\mathfrak {M})\), which contains only the shown free variables, defines an operator

A set \(S\subseteq M\) is a fixed point of \(\Phi _F\) iff \(\Phi _F(S)=S\). Let us denote by \(\Phi ^\alpha _F\) the \(\alpha \)-th inflationary iteration of \(\Phi _F\), i.e. \(\Phi ^\alpha _F:=\Phi _F^{<\alpha }\cup \Phi _F(\Phi _F^{<\alpha })\) for \(\Phi _F^{<\alpha }:=\bigcup _{\xi <\alpha }\Phi ^\xi _F\). For cardinality reasons there is a countable ordinal \(\sigma \) such that \(\Phi ^\sigma _F=\Phi _F^{<\sigma }\). Let  be the least such ordinal, the closure ordinal of F. Clearly
be the least such ordinal, the closure ordinal of F. Clearly  is a fixed point of \(\Phi _F\). Defining \(\sigma _F(a):=\min {}{\{{\alpha }\,|\,{a\in \Phi _F^\alpha }\}}\) we obtain a norm
is a fixed point of \(\Phi _F\). Defining \(\sigma _F(a):=\min {}{\{{\alpha }\,|\,{a\in \Phi _F^\alpha }\}}\) we obtain a norm  whose stage comparison relations are given by
whose stage comparison relations are given by
and
Let \({\mathfrak F}\) be a complexity class for the formulae in \({\mathscr {L}}(\mathfrak {M})\). A set \(A\subseteq M\) is \({\mathfrak F}\)-inductive iff there is a formula F(X, x) in \({\mathfrak F}\) and an element \(m\in M\) such that \(A={}{\{{x}\,|\,{\langle x,m\rangle \in I_F}\}}\). For \(F(X,x)\in {\mathfrak F}\,\) let \(\, F^{*}(X,x){}\quad :\Leftrightarrow \quad F((x)_{0},{}{\{{(x')_{0}}\,|\,{x'\in X}\}})\,\wedge \, (x)_{1}\notin {}{\{{(x')_{1}}\,|\,{x'\in X}\}}.\) It easily follows that \(\langle m,n\rangle \in \Phi _{F^{*}}^\xi {}\quad \Leftrightarrow \quad m\in \Phi _F^\xi \,\wedge \,n\notin \Phi _F^\xi \). Provided that \(F^{*}(x,X)\) still belongs to \({\mathfrak F}\) this shows that \(\mathrel {\prec ^*_{F}}\) is \({\mathfrak F}\)-inductive and similarly we obtain that also \(\mathrel {\preceq ^*_{F}}\) is \({\mathfrak F}\)-inductive. So \(\mathrel {\prec ^*_{F}}\) and \(\mathrel {\preceq ^*_{F}}\) satisfy condition (N). Under certain (mild) additional conditions on \({\mathfrak F}\) also conditions (C) and (U) are fulfilled and the class \( {{\mathfrak F}}-\textsf{IND}\) of \({\mathfrak F}\)-inductive sets then forms a Spector class.Footnote 28
However, we still have the problem that the definition of fixed points needs ordinals. This can be circumvented by the use of prewellorderings as suggested by Möllerfeld in [23]. The triple \((I_{F},\mathrel {\preceq ^*_{F}},\mathrel {\prec ^*_{F}})\) forms a prewellordering with \(I_{F}={}{\{{x}\,|\,{x\mathrel {\preceq ^*_{F}} x}\}}\) satisfying
Let \(\textsf{FIX}_{F}(X)\) express that \(({}{\{{x}\,|\,{\langle x,x\rangle \in (X)_{0}}\}},(X)_{0},(X)_{1})\) is a prewellordering which fulfills (*) with \(\mathrel {\preceq ^*_{F}}\) replaced by \((X)_{0}\) and \(\mathrel {\prec ^*_{F}}\) replaced by \((X)_{1}\). The scheme \((\textsf{FIX}_{F}(X))\) is expressible in second-order logic. If \(\textsf{T}\) is a strictly acceptable axiomatization for a countable strictly acceptable structure \(\mathfrak {M}\) then the scheme
axiomatizes the Spector class \( {{\mathfrak F}}-\textsf{IND}\) above \(\mathfrak {M}\).
Note 3.31
In [29] (reprinted in [30]) we gave an ordinal analysis of the theory \( {\Pi ^0_1}-\textsf{IND}\) above the structure of natural numbers which is based on the axiomatization outlined above. In general, however, \( {\Pi ^0_1}-\textsf{IND}\) is not a full Spector class above arbitrary countable acceptable structures but only a semi-Spector class which lacks full closure under first-order existential quantification.Footnote 29 For countable strictly acceptable structures \(\mathfrak {M}\) the search tree for pseudo \(\Pi _{1}^{1}\)-sentences is elementarily definable. Since the well-foundedness of the search tree can be expressed by a \(\Pi ^0_1\) inductive definition this entails that \( {\Pi ^0_1}-\textsf{IND}\) and the \(\Pi _{1}^{1}\)-relations on \(\mathfrak {M}\) coincide. This makes \( {\Pi ^0_1}-\textsf{IND}\) a full Spector class above strictly acceptable structures.
Whilst \( {\Pi ^0_1}-\textsf{IND}\) equals the collection of \(\Pi _{1}^{1}\)-relations above \({\mathfrak N}\) and thus \(o({ {\Pi ^0_1}-\textsf{IND}})=\pi ^{\mathfrak N}=\omega _1^{\hbox {\tiny CK}}\), the ordinals \(o( {{\mathfrak F}}-\textsf{IND})\) for complexities classes \({\mathfrak F}\) above \(\Pi ^0_1\) are much larger.Footnote 30 There are—at least to my knowledge—also no direct ordinal analyses of axiom systems for such \( {{\mathfrak F}}-\textsf{IND}\)-theories.Footnote 31
3.2.2 Positive Fixed-Point Theories
From a proof-theoretic point of view the structures \( {{\mathfrak F}}-\textsf{IND}\) are difficult to handle. Fortunately the construction of the hierarchy \(\mathbb S\mathbb P_{\mathfrak {M}}^{\alpha }\) can be obtained by a more restricted class of fixed-point theories.
An operator \(\Phi _F\) is X-positively definable if its defining formula F(X, x) contains no occurrence of X in the negated form \(s\notin X\). Due to the X-positivity of F(X, x) such operators are monotone, i.e. \(X\subseteq Y\) entails \(\Phi _F(X)\subseteq \Phi _F(Y)\) for all subsets X, Y of M. For an X-positive formula F(X, x) the formula \(F^{*}(X,x)\), as defined above, is of course no longer X-positive. This makes it a bit harder to prove that \(\mathrel {\preceq ^*_{F}}\) and \(\mathrel {\prec ^*_{F}}\) are positively definable inductive sets. A proof can be found in [24] Thm. 2A.2.
Of distinguished importance is Corollary 9A.3 of [24] which we state as theorem.
Theorem 3.32
Let \(\mathfrak {M}\) be an acceptable structure. Then the collection of positively definable inductive relations on \(\mathfrak {M}\) form the least Spector class above \(\mathfrak {M}\).
Given a relation \(R\in {\mathbb {S}}{\mathbb {P}}_{\mathfrak {M}}\) and a \({\mathbb {S}}{\mathbb {P}}_{\mathfrak {M}}\)-norm \({}{{\sigma :\, R \, \longrightarrow \, }\lambda }\) on R, the associated relation \(\prec ^{*}_\sigma \) belongs to \({\mathbb {S}}{\mathbb {P}}_{\mathfrak {M}}\) and is thus a positively definable inductive relation on \(\mathfrak {M}\). If \(\prec ^{*}_\sigma \) is a slice of a fixed point which is defined by an X-positive formula F(X, x) we obtain  , where
, where  denotes the closure ordinal of F. In order to obtain upper bounds for \(o({\mathbb {S}}{\mathbb {P}}_{\mathfrak {M}})\) and \(o^{{\mathbb {S}}{\mathbb {P}}_{\mathfrak {M}}}(T))\) it therefore suffices to compute upper bounds for
denotes the closure ordinal of F. In order to obtain upper bounds for \(o({\mathbb {S}}{\mathbb {P}}_{\mathfrak {M}})\) and \(o^{{\mathbb {S}}{\mathbb {P}}_{\mathfrak {M}}}(T))\) it therefore suffices to compute upper bounds for  .
.
Remark 3.33
It follows from Theorem 3.32 that the ordinal \(\kappa ^{\mathfrak M}_{\mu +1}\) coincides with the closure ordinal of \({\mathfrak M}_{\mu }\) in the sense of [24] Chpt. 2B.Footnote 32 For the structure \({\mathfrak N}\) of the natural numbers it is a folklore result that \(\kappa ^{\mathfrak N}=\omega _1^{\hbox {\tiny CK}}\) which is the initial ordinal of the second constructive number class.Footnote 33 Therefore we obtain \(\kappa _\mu ^{{\mathfrak N}}={\omega _{\mu }^{\hbox {\tiny CK}}}\) and the ordinals \(\kappa _\mu ^{{\mathfrak N}}\) coincide with the initial ordinals of the constructive number classes.
Because of the monotonicity of a positively defined operator \(\Phi _F\) its fixed point can easily be obtained as the intersection of all \(\Phi _F\)-closed subsets of M, i.e.
For a fixed point \(I_{F}\in {\mathbb {S}}{\mathbb {P}}_{\mathfrak {M}}\) we can express \(s\in I_{F}\) by the pseudo \(\Pi _{1}^{1}\)-sentence \((\forall ~x)[F(X,x)\rightarrow x\in X]\rightarrow s\in X\). Therefore we have
There is also a modificationFootnote 34 of the Boundedness Theorem for fixed points which provides a link to the ordinal \(\pi ^\mathfrak {M}\).
Theorem 3.34
Let \(\mathfrak {M}\) be a countable structure and F(X, x) an X-positive \({{\mathscr {L}}(\mathfrak {M})}\)-formula. Then  implies \({\mathbb {S}}{\mathbb {P}}_{\mathfrak {M}}\models s\in \Phi _F^{<{2^\alpha }}\), where \(\Phi _F\) denotes the operator defined by F(X, x).
implies \({\mathbb {S}}{\mathbb {P}}_{\mathfrak {M}}\models s\in \Phi _F^{<{2^\alpha }}\), where \(\Phi _F\) denotes the operator defined by F(X, x).
As an immediate consequence of Theorem 3.34 we obtain
and for strictly acceptable structures \({\mathfrak M}\) even equality.
Remark 3.35
As shown in [31] Theorem 5.32 we have \(\pi ^\mathfrak {M}=\kappa ^{\mathfrak M}\) for structures \({\mathfrak M}\) which allow for an inductive pairing, especially for acceptable structures. This shows that already the ordinal \(\pi ^{\mathfrak M}\) and thus also the ordinal \(\pi ^{\mathfrak M}(\textsf{T})\) refers to the least Spector class above \({\mathfrak M}\).
As an example let \({\mathfrak M}_{\mu }\) be our basis structure and \({\textsf{D}_{\mu }}\) be the elementary diagram \(\textit{ Th}({{\mathfrak M}_{\mu })}\) plus Mathematical Induction. Since \(o(\mathbb S\mathbb P_{\mathfrak {M}}^{\mu })=\kappa _{\mu }^{\mathfrak {M}}\) we may assume that all sentences in \({\mathscr {L}}({\mathfrak M}_{\mu })\) have complexities less than \(\kappa _{\mu }^{\mathfrak {M}}\).Footnote 35 If we now follow the pattern of the example in Sect. 3.2.5 we obtain the ordinal \(\varepsilon _{\kappa _{\mu }^{\mathfrak {M}}+1}\), the first \(\varepsilon \)-number above \(\kappa _{\mu }^{\mathfrak {M}}\), as an upper bound for \(\pi ^{{\mathfrak M}_{\mu }}({{\textsf{D}_{\mu }}})\). For \(R\in {\mathbb {S}}{\mathbb {P}}_{{\mathfrak M}_{\mu }}={\mathfrak M}_{{\mu +1}}\) there is an X-positive formula F(X, x) in \({\mathscr {L}}({\mathfrak M}_{\mu })\) and an \(n\in M\) such that \(s\in R\Leftrightarrow \langle {s},{n}\rangle \in I_{F}\Leftrightarrow {(\forall ~x)[F(X,x)\rightarrow x\in X]}\rightarrow \langle {s},{n}\rangle \in X\). So if  and \({}{\{{y}\,|\,{G(y)}\}}\in {\mathfrak M}_{{\mu +1}}\) we can assume that G(s) is a pseudo \(\Pi _{1}^{1}\)-sentence \((\forall ~y)[F(X,y)\rightarrow y\in X]\rightarrow s\in X\). Together with Theorem 3.34 this shows that \(o^{{\mathfrak M}_{\mu }}({\textsf{D}_{\mu }})\le \varepsilon _{\kappa _{\mu }^{\mathfrak {M}}+1}\), the first \(\varepsilon \)-number above \(\kappa _\mu \). Gentzen’s accessibility proof for \({\varepsilon _0}\), the first \(\varepsilon \)-number above \(0=\kappa ^{\mathfrak N}_0\), can easily be relativized to show also \(\varepsilon _{\kappa _{\mu }^{\mathfrak {M}}+1}\le o^{{\mathfrak M}_{\mu }}({\textsf{D}_{\mu }})\). Hence \(o^{{\mathfrak M}_{\mu }}({\textsf{D}_{\mu }})= \varepsilon _{\kappa _{\mu }^{\mathfrak {M}}+1}\). If
and \({}{\{{y}\,|\,{G(y)}\}}\in {\mathfrak M}_{{\mu +1}}\) we can assume that G(s) is a pseudo \(\Pi _{1}^{1}\)-sentence \((\forall ~y)[F(X,y)\rightarrow y\in X]\rightarrow s\in X\). Together with Theorem 3.34 this shows that \(o^{{\mathfrak M}_{\mu }}({\textsf{D}_{\mu }})\le \varepsilon _{\kappa _{\mu }^{\mathfrak {M}}+1}\), the first \(\varepsilon \)-number above \(\kappa _\mu \). Gentzen’s accessibility proof for \({\varepsilon _0}\), the first \(\varepsilon \)-number above \(0=\kappa ^{\mathfrak N}_0\), can easily be relativized to show also \(\varepsilon _{\kappa _{\mu }^{\mathfrak {M}}+1}\le o^{{\mathfrak M}_{\mu }}({\textsf{D}_{\mu }})\). Hence \(o^{{\mathfrak M}_{\mu }}({\textsf{D}_{\mu }})= \varepsilon _{\kappa _{\mu }^{\mathfrak {M}}+1}\). If  then \({}{\{{s}\,|\,{F(s)}\}}\) is a set in at most \({\mathfrak M}_{{\mu +1}}\). Therefore we get \(\textit{Spec}^{{\mathfrak M}_{\mu }}({{\textsf{D}_{\mu }}})=\{\varepsilon _{\kappa _{\mu }^{\mathfrak {M}}+1}\}\), hence
then \({}{\{{s}\,|\,{F(s)}\}}\) is a set in at most \({\mathfrak M}_{{\mu +1}}\). Therefore we get \(\textit{Spec}^{{\mathfrak M}_{\mu }}({{\textsf{D}_{\mu }}})=\{\varepsilon _{\kappa _{\mu }^{\mathfrak {M}}+1}\}\), hence  . For a Peano-like basis structure \({\mathfrak M}\) and \(\mu =0\) we get \(\textit{Spec}^{\mathfrak {M}}({{\textsf{D}_{0}}})=\{{\varepsilon _0}\}\) which shows that Definition 3.25 generalizes Definition 3.8 at least for Peano-like structures \(\mathfrak {M}\).
. For a Peano-like basis structure \({\mathfrak M}\) and \(\mu =0\) we get \(\textit{Spec}^{\mathfrak {M}}({{\textsf{D}_{0}}})=\{{\varepsilon _0}\}\) which shows that Definition 3.25 generalizes Definition 3.8 at least for Peano-like structures \(\mathfrak {M}\).
3.2.3 An Axiomatization of the Structures \({\mathfrak M}_{\mu }\)
Although we can express \(s\in I_{F}\) by a pseudo \(\Pi _{1}^{1}\)-sentence we would have to leave the first-order language if we wanted to express \(s\notin I_{F}\). This can be circumvented by introducing constants \(I_{F}\) for fixed points defined by X-positive formulae F(X, x) together with their defining axioms
- \((\text {ID}^1)\):
-
\((\forall ~x)[F(I_{F},x)\rightarrow x\in I_{F}],\)
- \((\text {ID}^2)\):
-
\((\forall ~x)[F(X,x)\rightarrow x\in X]{}\quad \rightarrow \quad (\forall ~x)[x\in I_{F}\rightarrow x\in X]\)
into the language of \({\mathbb {S}}{\mathbb {P}}_{\mathfrak {M}}\). This leaves us in the realm of first-order logic.
Given an axiomatization \(\textsf{T}\) of a structure \(\mathfrak {M}\) we thus get an axiomatization \({\textsc {ID}({\textsf{T}})}\) for the least Spector class \({\mathbb {S}}{\mathbb {P}}_{\mathfrak {M}}\) above \(\mathfrak {M}\) by augmenting \(\textsf{T}\) by the schemes \(\text {ID}^1\) and \(\text {ID}^2\). Finding a decoration and thus a semi-formal system for the structure of \({\mathbb {S}}{\mathbb {P}}_{\mathfrak {M}}\) is, however, not so easy. We need a decoration for the formulae \(s\in I_{F}\) and \(s\notin I_{F}\). The only option is to define
Since both characteristic sequences have only one element the type of these atomic sentences is irrelevant. However, this decoration violates the condition \(\textit{rnk}(G)<\textit{rnk}(F)\) for \(G\in \text {CS}~F\) and this condition is crucial for both \(\Pi _{1}^{1}\)-completeness and cut elimination. Nevertheless we obtain for the resulting semi-formal system  a modified version of \(\Pi _{1}^{1}\)-completeness.
a modified version of \(\Pi _{1}^{1}\)-completeness.
Theorem 3.36
Let \(\mathfrak {M}\) be a (strictly acceptable) countable structure and G(X) be a pseudo \(\Pi _{1}^{1}\)-sentence in the language of \({\mathbb {S}}{\mathbb {P}}_{\mathfrak {M}}\) which contains at most positive occurrences of constants \(I_{F}\). Then \({\mathbb {S}}{\mathbb {P}}_{\mathfrak {M}}\models (\forall ~X) G(X)\) iff there is a countable ordinal \(\alpha (<\kappa ^{\mathfrak {M}})\) such that  .
.
Proof
We sketch the proof. The soundness direction follows easily by induction on \(\alpha \). For the completeness direction we generalize the singleton \(\{G(X)\}\) to a finite set \(\Delta (X,I_{F})\) of \(\Pi _{1}^{1}\)-sentences which contain at most positive occurrences of constants \(I_{F}\) and define a search tree for \(\Delta (X,I_{F})\) by inverting the \((\bigwedge )\) and \((\bigvee )\) rules (including the rules generated by \(\text {CS}~{s\in I_{F}}\)). If \({\mathfrak M}\) is strictly acceptable then \(S_\Delta \) is \({{\mathscr {L}}(\mathfrak {M})}\)-elementarily definable. If the search tree is well-founded we have a semi-formal proof for \(\Delta (X,I_{F})\) of countable height which is less than \(\kappa ^{\mathfrak {M}}\) if \({\mathfrak M}\) is strictly acceptable. Otherwise there is an infinite path f through \(S_\Delta \) and we assign to the variable X the set  . Then we prove by main induction on \(\xi \) with side induction on \(\textit{rnk}(H(X,Y))\) that \({\mathfrak M}_{\nu }\not \models H(X,Y)[S,I_{F}^{\xi }]\) holds true for all formulae \(H(X,I_{F})\) occurring in f and all ordinals \(\xi \). Observe that the X-positivity of the defining formula F(X, x) for \(I_{F}\) is essential for the positive occurrence of \(I_{F}\) in the characteristic sequence of \(s\in I_{F}\). \(\square \)
. Then we prove by main induction on \(\xi \) with side induction on \(\textit{rnk}(H(X,Y))\) that \({\mathfrak M}_{\nu }\not \models H(X,Y)[S,I_{F}^{\xi }]\) holds true for all formulae \(H(X,I_{F})\) occurring in f and all ordinals \(\xi \). Observe that the X-positivity of the defining formula F(X, x) for \(I_{F}\) is essential for the positive occurrence of \(I_{F}\) in the characteristic sequence of \(s\in I_{F}\). \(\square \)
Unfortunately we cannot gain much information from Theorem 3.36. One fact that we can learn from it is that allowing positive occurrences of constants for fixed points in the defining X-positive formula F(X, x) of an operator \(\Phi _F\) will not extend its closure ordinal  beyond \(\pi ^{{\mathfrak M}_{{\mu +1}}}\). This is in accordance with the known fact that positive inductive definitions are closed under “positive inductive in”. (Cf. [24] Theorem 1C.3.)
beyond \(\pi ^{{\mathfrak M}_{{\mu +1}}}\). This is in accordance with the known fact that positive inductive definitions are closed under “positive inductive in”. (Cf. [24] Theorem 1C.3.)
Iterating the passage from \(\textsf{T}\) to \({\textsc {ID}({\textsf{T}})}\) we obtain axiomatizations for all finite levels \({\mathfrak M}_{n}\) in the hierarchy of Spector classes. To obtain also axiomatizations for the transfinite hierarchy we need ordinal notations in \(\mathfrak {M}\). So assume that there is an elementarily definable set \(\mathord { On}\subseteq M\) together with an elementarily definable transitive, irreflexive, and linear “less than” relation \(\prec \) on \(\mathord { On}\). To emphasize that the elements in \(\mathord { On}\) are ordinal notations we use lower case Greek letters as syntactical variables for ordinal notations and write \(\mu <\eta \) instead of \(\mu \prec \eta \). To ensure that \(\mathord { On}\) is in fact an ordinal notation system for the ordinals \(<\nu \) we need the axiom of transfinite induction
- (\({\textbf {TI}}_\nu \)):
-
\((\forall ~\xi )[(\forall ~\rho )[\rho <\xi \rightarrow \rho \in X]\rightarrow \xi \in X]{}\quad \rightarrow \quad (\forall ~\mu )[\mu \in X]\)
where we already use the convention that lower case Greek letters vary over \(\mathord { On}\). By the subscript \(\nu \) we indicate that \((\mathord { On},\prec )\) is supposed to be a well-ordering of order-type \(\nu \). In abuse of notation we occasionally even use the same letter \(\mu \) for the element \(\mu \in \mathord { On}\subseteq M\) and the ordinal \(\mu \) which represents the order-type of \(\mu \) in the well-ordering \(\prec \). It should always be clear from the context to which object we refer.
Every inductive set in \({\mathfrak M}_{\mu }\) is either already in \({\mathfrak M}_{\xi }\) for some \(\xi <\mu \) or a slice of a fixed point of an positive operator \(\Phi _F\) with defining formula \(F(X,T_1,\dots ,T_{n},x)\) where \(T_1,\dots ,T_{n}\) are inductive sets belonging to some \({\mathfrak M}_{\xi }\) for \(\xi <\mu \). Because of the universality of Spector classes we can replace \(T_1,\dots ,T_{n}\) by n-slices of an universal set U and thus assume \(n=1\). Moreover we may assume that universal sets \(U_\xi \) for every Spector class \(\mathbb S\mathbb P_{\mathfrak {M}}^{\xi }\) can be uniformly generated by an X-positive \({{\mathscr {L}}(\mathfrak {M})}\)-formula U(X, Y, x) with no further occurrence of free variables. So we arrive at the following axiomatization for the structure \({\mathfrak M}_{\nu }\):
For any X-positive \({{\mathscr {L}}(\mathfrak {M})}\)-formula F(X, Y, x) without further free variables we introduce a constant \(I_{F}\). To formulate the defining axioms for the constants \(I_{F}\) we use the abbreviation \(s\in I_{F_\mu }\) for \(\langle s,\mu \rangle \in I_{F}\) and define \(s\in I_{F_{<\mu }}\) to denote the formula  .
.
The defining axiom schemes for the constants are
- \((\text {ID}^1_\nu )\):
-
\((\forall ~\mu )(\forall ~x)[F(I_{F_\mu },I_{F_{<\mu }},\langle {x},{\mu }\rangle )\rightarrow x\in I_{F_\mu }]\),
- \((\text {ID}^2_\nu )\):
-
\((\forall ~\mu ) (\forall ~x)[F(X,I_{F_{<\mu }},\langle {x},{\mu }\rangle )\rightarrow x\in X]{}\quad \rightarrow \quad (\forall ~x)[x\in I_{F_\mu }\rightarrow x\in X]\)
For an axiomatization \(\textsf{T}\) for \(\mathfrak {M}\) let \({\textbf { ID}}_\nu (\textsf{T})\) denote \(\textsf{T}\) together with the axiom schemes \(({\textbf {TI}}_\nu \)), \((\text {ID}^1_\nu )\) and \((\text {ID}^2_\nu )\).Footnote 36
Note 3.37
Axiomatizations for iterations of positive inductive definitions have been introduced by Georg Kreisel in [21, 22] for foundational investigations. There was hope that suitable inductive definitions could generate the bar recursive functionals of higher types required by C. Spector in a consistency proof for Second-Order Number Theory ([39]). To cite Sol Feferman from [9] “Kreisel wanted to see whether iterated inductive definitions (of classes of lawlike sequences ...) could serve to model the bar recursive functionals of higher types” This hope did not materialize as only bar recursive functionals of types \(\le 2\) could be generated.Footnote 37 Nevertheless iterated inductive definitions started to become a relevant topic in the foundations of mathematics.Footnote 38
On the other hand inductive definitions on abstract structures were also studied from a purely mathematical point of view. Yannis Moschovakis summarized these studies in his monograph [24] and the subsequent paper [25]. There he also introduced the notion of Spector classes and investigated their connections to inductive definitions. The emphasis of the present paper is on iterated inductive definitions as abstract structures.
3.2.4 The Structures \({\mathfrak M}_{\nu }^{*}\)
In Remark 3.35 we sketched an ordinal analysis of \({\textsf{D}_{\mu }}\) as an axiom system for \({\mathfrak M}_{\mu }\) and suggested in Sect. 3.3.2.3 a decoration for the language of \({\mathfrak M}_{{\mu +1}}=(M,{\mathbb {S}}{\mathbb {P}}_{{\mathfrak M}_{\mu }},\dots )\). But the semi-formal system for \({\mathfrak M}_{{\mu +1}}\) induced by this decoration cannot help us to an ordinal analysis of \({\textsc {ID}({{\textsf{D}_{\mu }}})}\) or \({\textsc {ID}({\textsf{T}})}\) for another axiom system \(\textsf{T}\) for \({\mathfrak M}_{\mu }\). All we can conclude from  is \({\mathfrak M}_{{\mu +1}}\models s\in I_{F}\), hence \({\mathfrak M}_{{\mu +1}}\models (\forall ~x)[F(X,x)\rightarrow s\in X]\rightarrow s\in X]\), hence
is \({\mathfrak M}_{{\mu +1}}\models s\in I_{F}\), hence \({\mathfrak M}_{{\mu +1}}\models (\forall ~x)[F(X,x)\rightarrow s\in X]\rightarrow s\in X]\), hence  for some ordinal \(\alpha <\kappa _{{\mu +1}}^{\mathfrak {M}}\), which finally implies
for some ordinal \(\alpha <\kappa _{{\mu +1}}^{\mathfrak {M}}\), which finally implies  . But this already follows by the definition of \(\kappa _{{\mu +1}}^{\mathfrak {M}}\) (which we in fact used in the proof of Theorem 3.36). What is lacking is a cut elimination procedure for the semi-formal system which allows a computation of the increase (or decrease) of the derivation-height during the procedure and thus gives a better estimation of the ordinal \(\alpha \). For an ordinal analysis of \({\textsc {ID}({{\textsf{D}_{\mu }}})}\) we thus need a decoration for the formulae in \({\mathfrak M}_{{\mu +1}}\) which satisfies \(\textit{rnk}(G)<\textit{rnk}(F)\) for \(G\in \text {CS}~F\).
. But this already follows by the definition of \(\kappa _{{\mu +1}}^{\mathfrak {M}}\) (which we in fact used in the proof of Theorem 3.36). What is lacking is a cut elimination procedure for the semi-formal system which allows a computation of the increase (or decrease) of the derivation-height during the procedure and thus gives a better estimation of the ordinal \(\alpha \). For an ordinal analysis of \({\textsc {ID}({{\textsf{D}_{\mu }}})}\) we thus need a decoration for the formulae in \({\mathfrak M}_{{\mu +1}}\) which satisfies \(\textit{rnk}(G)<\textit{rnk}(F)\) for \(G\in \text {CS}~F\).
The standard structures \({\mathfrak M}_{\nu }\) for \(\nu >0\) are apparently not sufficiently fine grained to allow for a decoration of the language of \({\mathscr {L}}(\mathfrak {M}_\nu )\) with this property. To obtain a finer graining we have to resolve the fixed points in \({\mathfrak M}_{\nu }\) into their stages. This needs ordinal constants in the language. Every fixed point \(I_{F}\) in \(\mathbb S\mathbb P_{\mathfrak {M}}^{\mu }\) is the union \(\bigcup _{\xi <\kappa _{\mu +1}^{\mathfrak {M}}}I_{F}^{\xi }\) of its stages. Let \({\mathbb {S}}{\mathbb {P}}_{\mathfrak {M}^*}^{\mu }\) denote the set of all stages of fixed points in \(\mathbb S\mathbb P_{\mathfrak {M}}^{\mu }\) and put \({\mathfrak M}^{*}_\mu :=(M,{\mathbb {S}}{\mathbb {P}}_{\mathfrak {M}^*}^{\mu },\cdots )\). The language of \({\mathfrak M}_\mu ^{*}\) thus contains also constants for ordinals. These ordinal constants must not be confused with the ordinal notations in \(\mathord { On}\) which are just elements in M. However, ordinal notations and ordinals are connected in so far that for every ordinal notation \(\mu \in \mathord { On}\) (whose order-type is represented by the ordinal \(\mu \)) there is an ordinal constant \(\kappa _{\mu }^{\mathfrak {M}}\) and thus also constants for all ordinals less than \(\kappa _{\mu }^{\mathfrak {M}}\).
To facilitate the decoration for the language \({\mathscr {L}}({\mathfrak M}_{\mu }^*)\) it is preferable to introduce constants \(I_{F_{\mu }}^{<\xi }\) for the union of stages below \(\xi \) instead of constants \(I_{F_{\mu }}^{\xi }\) for the stage \(\xi \) and constants \(I_{F_{<\mu }}\) for the union of fixed points below \(\mu \). The formula \(s\in I_{F_{\mu }}^{\xi }\) is then simply an abbreviation for \(F(I_{F_{\mu }}^{<\xi },I_{F_{<\mu }},\langle {s},{\mu }\rangle )\) and we get the fixed point \(I_{F_{\mu }}\) as \(I_{F_{\mu }}^{<\kappa _{\mu +1}^{\mathfrak {M}}}\).
Definition 3.38
Formally we define the language \({\mathscr {L}}({\mathfrak M}_{\nu }^*)\) by the following clauses:
-
Every pseudo \(\Pi _{1}^{1}\)-sentence in \({{\mathscr {L}}(\mathfrak {M})}\) is an \({\mathscr {L}}({\mathfrak M}_{\nu }^*)\)-formula.
-
Every free second-order variable is a set term.
-
For every ordinal notation \(\mu \in \mathord { On}\) of order-type \(\mu \) there are ordinal constants \(\xi \) for all \(\xi \le \kappa _{\mu }^{\mathfrak {M}}\).
-
For every X-positive \({{\mathscr {L}}(\mathfrak {M})}\)-formula F(X, Y, x) without further free variables, every ordinal notation \(\mu \in \mathord { On}\) and every ordinal constant \(\xi \le \kappa _{{\mu +1}}^{\mathfrak {M}}\) there are set constants \(I_{F_{\mu }}^{<\xi }\) and \(I_{F_{<\mu }}\). Every set constant is a set term.
-
If s is a closed \({{\mathscr {L}}(\mathfrak {M})}_M\)-term and S a set term then \(s\in S\) and \(s\notin S\) are \({\mathscr {L}}({\mathfrak M}_{\nu }^*)\) formulae.
-
The \({\mathscr {L}}({\mathfrak M}_{\nu }^*)\)-formulae are closed under the positive Boolean operations \(\wedge \), \(\vee \) and quantification over elements of M.
Using the translation \(A\mapsto A^{*}\), which maps \(I_{F_{\mu }}\) to \(I_{F_{\mu }}^{<\kappa _{\mu +1}^{\mathfrak {M}}}\) and then proceeding inductively, we obtain
3.2.5 The Semi-formal System for \({\mathfrak M}_{\nu }^*\)
To decorate the language \({\mathscr {L}}({\mathfrak M}_{\nu }^*)\) we first fix the notions of \(\bigwedge -{\mathord {\textsf {type}}}\,\) and \(\bigvee -{\mathord {\textsf {type}}}\,\).
Definition 3.39
(\(\bigwedge -{\mathord {\textsf {type}}}\,\) and \(\bigvee -{\mathord {\textsf {type}}}\,\) of \({\mathscr {L}}({\mathfrak M}_{\nu }^*)\))
- \((\bigwedge -{\mathord {\textsf {type}}}\,)\):
-
The \(\bigwedge -{\mathord {\textsf {type}}}\,\) comprises all true atomic \({{\mathscr {L}}(\mathfrak {M})}_M\)-sentences, all formulae of the form \((A\,\wedge \,B)\), all formulae of the form \((\forall ~x)F(x)\), all formulae of the form \(s\notin I_{F_{<\mu }}\) and all formulae of the form \(s\notin I_{F_{\mu }}^{<\xi }\).
- \((\bigvee -{\mathord {\textsf {type}}}\,)\):
-
The \(\bigvee -{\mathord {\textsf {type}}}\,\) comprises all false atomic \({{\mathscr {L}}(\mathfrak {M})}_M\)-sentences, all formulae of the form \((A\,\vee \,B)\), all formulae of the form \(F(x)\), all formulae of the form \(s\in I_{F_{<\mu }}\) and all formulae of the form \(s\in I_{F_{\mu }}^{<\xi }\).
- (No Type):
-
Atomic formulae of the form \(s\in X\) and \(s\notin X\) belong neither to \(\bigwedge -{\mathord {\textsf {type}}}\,\) not \(\bigvee -{\mathord {\textsf {type}}}\,\).
The finer graining of the structure \({\mathfrak M}_{\nu }^*\) now allows for a decoration of \({\mathscr {L}}({\mathfrak M}_{\nu }^*)\)-formulae, which is summed up by the clauses
-
\(\text {CS}~F=\langle \ \rangle \), if F is atomic,
-
\(\text {CS}~{s\in I_{F_{<\mu }}}={}{\big \langle {s\in I_{F_{\sigma }}^{<\kappa _{{\sigma +1}}^{\mathfrak {M}}}}\,|\,{\sigma <\mu }\big \rangle }\),
-
\(\text {CS}~{s\notin I_{F_{<\mu }}}={}{\big \langle {s\notin I_{F_{\sigma }}^{<\kappa _{{\sigma +1}}^{\mathfrak {M}}}}\,|\,{\sigma <\mu }\big \rangle }\),
-
\(\text {CS}~{s\in I_{F_{\mu }}^{<\xi }}={}{\big \langle {F(I_{F_{\mu }}^{<\eta },I_{F_{<\mu }},\langle {s},{\mu }\rangle )}\,|\,{\eta<\xi }\big \rangle }=:{}{\big \langle {s\in I_{F_{\mu }}^{\eta }}\,|\,{\eta <\xi }\big \rangle }\),
-
\(\text {CS}~{s\notin I_{F_{\mu }}^{<\xi }}={}{\big \langle {\lnot F(I_{F_{\mu }}^{<\eta },I_{F_{<\mu }},\langle {s},{\mu }\rangle )}\,|\,{\eta<\xi }\big \rangle }=:{}{\big \langle {s\notin I_{F_{\mu }}^{\eta }}\,|\,{\eta <\xi }\big \rangle }\),
-
\(\text {CS}~{A\,\wedge \,B}=\text {CS}~{A\,\vee \,B}=\langle A,B\rangle \),
-
\(\text {CS}~{(\forall ~x) F(x)}=\text {CS}~{F(x)}={}{\big \langle {F(\underline{m})}\,|\,{m\in M}\big \rangle }\), where we anticipate a given enumeration of the elements of M.
We define the rank of a set term by \(\textit{rnk}(I_{F_{\mu }}^{<\xi })=\kappa _{\mu }^{\mathfrak {M}}+\omega \mathrel {\cdot }\xi \) and \(\text {rnk} (I_{F_{<\mu }}):=\kappa _{\mu }^{\mathfrak {M}}+1\). Since second-order variables X stand for arbitrary set terms we define \(\textit{rnk}(X)=\kappa _{\nu }^{\mathfrak {M}}\). For a formula \(A(S_1,\dots ,S_{n})\) let \(\textit{rnk}(A(S_1,\dots ,S_{n})):=\max \{\textit{rnk}(S_1),\dots ,\textit{rnk}(S_n)\}+\#{A(S_1,\dots ,S_{n})},\) where \(\# A\) counts the number of logical symbols occurring in A.
Lemma 3.40
For all \(H\in \text {CS}~G\) we have \(\textit{rnk}(H)<\textit{rnk}(G)\).
Proof
This is obvious for atomic formulae G. For \(G\equiv {s\in (\notin )I_{F_{<\mu }}}\) this follows from \(\kappa _{\sigma +1}^{\mathfrak {M}} <\kappa _{\mu }^{\mathfrak {M}}+1\) for all \(\sigma <\mu \). For \(G\equiv s\in (\notin )I_{F_{\mu }}^{<\xi }\) this follows from the fact that \(\kappa _{\mu }^{\mathfrak {M}}+\omega \mathrel {\cdot }\eta + n<\kappa _{\mu }^{\mathfrak {M}}+\omega \mathrel {\cdot }(\eta +1)\le \kappa _{\mu }^{\mathfrak {M}}+\omega \mathrel {\cdot }\xi \) holds true for all \(\eta <\xi \) and finite n. The remaining cases follow easily be induction on \(\# G\). \(\square \)
However, the decoration has a weakness. Only the direction from right to left in condition (3.2) is satisfied. The induced verification calculus
 therefore only satisfies
therefore only satisfies

which is only one half of Eq. (3.4). The opposite implication, which commonly follows by induction on \(\textit{rnk}(F)\), does not hold. The problem is caused by the ordinals \(\kappa _{\mu +1}^{\mathfrak {M}}\), which are abstractly defined by their closure properties
These closure properties are not canonically reflected in the verification calculus. To extend the verification calculus to a semi-formal system which is suited for an analysis of the systems \(\textsf{ID}_{\nu }({\textsf{T}})\) we therefore need additional non-logical rules \((\text {Cl}_{\mu })\) for all ordinal notations \(\mu <\nu \) which axiomatize the ordinals \(\kappa _{{\mu +1}}^{\mathfrak {M}}\).
- (\(\text {Cl}_{\mu }\)):
-
If \(\mu \in \mathord { On}\), \((s\in I_{F_{\mu }}^{<\kappa _{\mu +1}^{\mathfrak {M}}}) \in \Delta \) and
 then
then  holds true for all \(\alpha >\alpha _0\).
holds true for all \(\alpha >\alpha _0\).
The semi-formal system  thus comprises the rules \((\bigwedge )\), \((\bigvee )\), (Cut), \((\text {Cl}_{\mu })\) for all \(\mu < \nu \) and the (X)-rule, where we, in view of the definition \(\textit{rnk}(X):=\kappa _{\nu }^{\mathfrak {M}}\) for second-order variables X, only allow ordinals \(\ge \kappa _{\nu }^{\mathfrak {M}}\) as derivation heights in the (X)-rule.
thus comprises the rules \((\bigwedge )\), \((\bigvee )\), (Cut), \((\text {Cl}_{\mu })\) for all \(\mu < \nu \) and the (X)-rule, where we, in view of the definition \(\textit{rnk}(X):=\kappa _{\nu }^{\mathfrak {M}}\) for second-order variables X, only allow ordinals \(\ge \kappa _{\nu }^{\mathfrak {M}}\) as derivation heights in the (X)-rule.
Despite of these alterations the semi-formal system has all the properties of semi-formal systems as described in Sect. 3.1. The alteration of the (X)-rules is needed to ensure the validity of substitution.
Theorem 3.41
(Substitution) If  then
then  holds true for every set constant S in the language of \({\mathfrak M}_{\nu }^*\).
holds true for every set constant S in the language of \({\mathfrak M}_{\nu }^*\).
Proof
The proof is a simple induction on \(\alpha \). In case that the last inference is an (X)-rule and S a set constant we replace the (X)-rule by tautology (cf. Observation 3.6). Since \(2\mathrel {\cdot }\textit{rnk}(S)\le \kappa _{\nu }^{\mathfrak {M}}\le \alpha \) holds true for any set term or set variable the claim follows by weakening. \(\square \)
Inspecting some basis properties of the semi-formal system  we start with a useful observation.
we start with a useful observation.
Lemma 3.42
(Detachment Lemma) Let \(\Gamma \) be a finite set of false \({\mathscr {L}}({\mathfrak M}_{\nu }^*)\)-sentences. If  we can detach \(\Gamma \) and obtain
we can detach \(\Gamma \) and obtain  .
.
Proof
Straightforward by induction on \(\alpha \). \(\square \)
The Detachment Lemma provides a small bridge from the semi-formal system  to the system
to the system  as a semi-formal system above the structure \({\mathfrak M}_{\nu }\).
as a semi-formal system above the structure \({\mathfrak M}_{\nu }\).
Theorem 3.43
Let \(\Delta \) be a finite set of pseudo \(\Pi _{1}^{1}\)-sentences in the language \({\mathscr {L}}({\mathfrak M}_{\nu })\). Then  entails
entails  .
.
Proof
We induct on \(\alpha \) and sketch the main cases. The case of an (X)-rule is obvious. If the last inference is a an \((\bigwedge )\) rule with main formula \(s\notin I_{F_{\mu }}^{<\kappa _{{\mu +1}}^{\mathfrak {M}}}\) then \(\mu <\nu \) and we have the premises  for all \(\xi <\kappa _{{\mu +1}}^{\mathfrak {M}}\). If \((s\notin I_{F_{\mu }})\in \mathscr {D}({\mathfrak M}_{\nu })\) we obtain the claim by an inference \((\bigwedge )\) with empty premise. Otherwise we have \({\mathfrak M}_{\nu }^*\not \models s\notin I_{F_{\mu }}^{<\xi _0}\) for some \(\xi _0<\kappa _{{\mu +1}}^{\mathfrak {M}}\). By detachment we obtain
for all \(\xi <\kappa _{{\mu +1}}^{\mathfrak {M}}\). If \((s\notin I_{F_{\mu }})\in \mathscr {D}({\mathfrak M}_{\nu })\) we obtain the claim by an inference \((\bigwedge )\) with empty premise. Otherwise we have \({\mathfrak M}_{\nu }^*\not \models s\notin I_{F_{\mu }}^{<\xi _0}\) for some \(\xi _0<\kappa _{{\mu +1}}^{\mathfrak {M}}\). By detachment we obtain  , hence
, hence  by induction hypothesis and the claim by weakening. The other \(\bigwedge \)-cases follow immediately from the induction hypothesis.
by induction hypothesis and the claim by weakening. The other \(\bigwedge \)-cases follow immediately from the induction hypothesis.
If the last inference is an \((\bigvee )\)-rule or \((\text {Cl}_{\mu })\)-rule with main formula \(s\in I_{F_{\mu }}^{<\kappa _{{\mu +1}}^{\mathfrak {M}}}\) then again \(\mu <\nu \) and we have the premise  for some \(\xi \le \kappa _{{\mu +1}}^{\mathfrak {M}}\). Again we are done if \((s\in I_{F_{\mu }})\in \mathscr {D}({\mathfrak M}_{\nu })\). Otherwise we have \({\mathfrak M}_{\nu }^*\not \models s\in I_{F_{\mu }}^{\xi }\) for all \(\xi \le \kappa _{{\mu +1}}^{\mathfrak {M}}\) and proceed as in the previous case.
for some \(\xi \le \kappa _{{\mu +1}}^{\mathfrak {M}}\). Again we are done if \((s\in I_{F_{\mu }})\in \mathscr {D}({\mathfrak M}_{\nu })\). Otherwise we have \({\mathfrak M}_{\nu }^*\not \models s\in I_{F_{\mu }}^{\xi }\) for all \(\xi \le \kappa _{{\mu +1}}^{\mathfrak {M}}\) and proceed as in the previous case.
If the last inference is a cut with cut formula F we have \(\textit{rnk}(F)<\kappa _{\nu }^{\mathfrak {M}}\). Therefore F cannot contain a free set variable, hence is an \({\mathscr {L}}({\mathfrak M}_{\nu }^*)\)-sentence. So either \({\mathfrak M}_{\nu }^*\models F\) or \({\mathfrak M}_{\nu }^*\not \models F\). We detach the false sentence from the corresponding premise and obtain the claim by induction hypothesis and weakening. \(\square \)
The purpose of the semi-formal system  is to find upper bounds for the points in \(\textit{Spec}^{{\mathfrak M}}({\textsf{ID}_{\nu }({\textsf{T}})})\) of an axiom system \(\textsf{ID}_{\nu }({\textsf{T}})\) where \(\textsf{T}\) is an axiomatization for \(\mathfrak {M}\). Theorem 3.43 enables us to find an upper bound for the largest point \(o^{{\mathbb {S}}{\mathbb {P}}_{{\mathfrak M}_{\nu }}}(\textsf{ID}_{\nu }({\textsf{T}}))\) in \(\textit{Spec}^{\mathfrak {M}}({\textsf{ID}_{\nu }({\textsf{T}})})\). Given an X-positive formula F(X, Y, x) in the language of \(\mathfrak {M}\) we express by the formula
is to find upper bounds for the points in \(\textit{Spec}^{{\mathfrak M}}({\textsf{ID}_{\nu }({\textsf{T}})})\) of an axiom system \(\textsf{ID}_{\nu }({\textsf{T}})\) where \(\textsf{T}\) is an axiomatization for \(\mathfrak {M}\). Theorem 3.43 enables us to find an upper bound for the largest point \(o^{{\mathbb {S}}{\mathbb {P}}_{{\mathfrak M}_{\nu }}}(\textsf{ID}_{\nu }({\textsf{T}}))\) in \(\textit{Spec}^{\mathfrak {M}}({\textsf{ID}_{\nu }({\textsf{T}})})\). Given an X-positive formula F(X, Y, x) in the language of \(\mathfrak {M}\) we express by the formula
the closure of X under the operator \(\Phi _{F_\mu }\).
Theorem 3.44
If  then \(\sigma _{F_\nu }(s)<2^\alpha \).
then \(\sigma _{F_\nu }(s)<2^\alpha \).
Proof
From  we obtain
we obtain  by Theorem 3.43 which in turn entails \(s\in \Phi _{F_\nu }^{<2^\alpha }\) by Theorem 3.34. \(\square \)
by Theorem 3.43 which in turn entails \(s\in \Phi _{F_\nu }^{<2^\alpha }\) by Theorem 3.34. \(\square \)
Remark 3.45
To obtain an upper bound for \(o^{{\mathbb {S}}{\mathbb {P}}_{{\mathfrak M}_{\nu }}}(\textsf{T})\) we can follow the technique described in Sect. 3.2.5. We translate the formal \(\textsf{T}\) proof of a pseudo \(\Pi _{1}^{1}\)-sentence into a semi-formal proof, then eliminate all cuts with complexities above \(\kappa _{\nu }^{\mathfrak {M}}\) and finally apply Theorems 3.43 and 3.44 to obtain \(\varepsilon _{\kappa _{\nu }^{\mathfrak {M}}+1}\) as an upper bound.
For the points below \(o({\mathbb {S}}{\mathbb {P}}_{{\mathfrak M}_{\nu }}(\textsf{T}))\), however, we need finer tools. An important tool is provided by the following lemma.
Lemma 3.46
(Boundedness Lemma for \({\mathscr {L}}({\mathfrak M}_{\nu }^*)\)) Assume  holds true for some \(\alpha ,\xi \le \kappa _{\mu +1}^{\mathfrak {M}}\). Then
holds true for some \(\alpha ,\xi \le \kappa _{\mu +1}^{\mathfrak {M}}\). Then  holds true for all \(\eta \in [\alpha ,\xi ]\).
holds true for all \(\eta \in [\alpha ,\xi ]\).
Proof
We induct on \(\alpha \) and just sketch the main cases. If the main formula of the last inference is \(s\in I_{F_{\mu }}^{<\xi }\), then we have the premise  for some \(\zeta <\xi \) or, in case of a \((\text {Cl}_{\mu })\)-rule, for \(\zeta =\xi =\kappa _{{\mu +1}}^{\mathfrak {M}}\). By induction hypothesis we get
for some \(\zeta <\xi \) or, in case of a \((\text {Cl}_{\mu })\)-rule, for \(\zeta =\xi =\kappa _{{\mu +1}}^{\mathfrak {M}}\). By induction hypothesis we get  . Since \(\alpha _0<\alpha \le \eta \) we obtain the claim by an inference \((\bigvee )\). In the case that the main formula is \(s\notin I_{F_{\mu }}^{<\xi }\) we have the premises
. Since \(\alpha _0<\alpha \le \eta \) we obtain the claim by an inference \((\bigvee )\). In the case that the main formula is \(s\notin I_{F_{\mu }}^{<\xi }\) we have the premises  for all \(\zeta <\xi \). By induction hypothesis and \(\eta \le \xi \) we thus get
for all \(\zeta <\xi \). By induction hypothesis and \(\eta \le \xi \) we thus get  for all \(\zeta <\eta \) and the claim follows by an inference \((\bigwedge )\). In case of a cut we have to observe that \(\eta \le \xi \) implies \(\textit{rnk}(I_{F_{\mu }}^{<\eta })\le \textit{rnk}(I_{F_{\mu }}^{<\xi })\) which ensures that the cut rank cannot increase. \(\square \)
for all \(\zeta <\eta \) and the claim follows by an inference \((\bigwedge )\). In case of a cut we have to observe that \(\eta \le \xi \) implies \(\textit{rnk}(I_{F_{\mu }}^{<\eta })\le \textit{rnk}(I_{F_{\mu }}^{<\xi })\) which ensures that the cut rank cannot increase. \(\square \)
The Boundedness Lemma and Eq. (3.21) have an obvious corollary.
Theorem 3.47
(Boundedness Theorem for \({\mathscr {L}}({\mathfrak M}_{\nu }^*)\))  for some \(\alpha <\kappa _{{\mu +1}}^{\mathfrak {M}}\) implies \(s\in I_{F_{\mu }}^{<\alpha }\), hence \(\sigma _{F_\mu }( s)<\alpha \).
for some \(\alpha <\kappa _{{\mu +1}}^{\mathfrak {M}}\) implies \(s\in I_{F_{\mu }}^{<\alpha }\), hence \(\sigma _{F_\mu }( s)<\alpha \).
While Theorem 3.44 requires the elimination of all cuts above \(\kappa _{\nu }^{\mathfrak {M}}\), Theorem 3.47 apparently works without cut elimination. This is corroborated by the fact that cut-elimination below \(\kappa _{\nu }^{\mathfrak {M}}\) nearly comes for free.
Theorem 3.48
Let \(\Delta \) be a finite set of \({\mathscr {L}}({\mathfrak M}_{\nu }^*)\)-sentences such that  . Then we already have
. Then we already have  .
.
Proof
The proof is by induction on \(\alpha \). The critical case it that of a cut which is treated as the cut in the proof of Theorem 3.43. \(\square \)
3.2.6 Embedding
For the remainder of this section assume that \(\textsf{T}\) is an axiom system for \(\mathfrak {M}\). We have to check that the axioms \({\textbf {ID}}_{\nu }({\textsf{T}})\) are indeed semi-formally provable.
First we observe that the semi-formal system proves the monotonicity of positively definable operators.
Lemma 3.49
(Monotonicity Lemma) Assume  for all \(s\in M\) and let A(X) be an X-positive formula in the language \({\mathscr {L}}({\mathfrak M}_{\nu }^*)\). Then we obtain
for all \(s\in M\) and let A(X) be an X-positive formula in the language \({\mathscr {L}}({\mathfrak M}_{\nu }^*)\). Then we obtain  for \(\beta =2\mathrel {\cdot }\#A\).
for \(\beta =2\mathrel {\cdot }\#A\).
Proof
This is an easy induction on \(\#A\), the number of logical symbols occurring in A. \(\square \)
The Monotonicity Lemma is needed to prove a generalization of transfinite induction.
Lemma 3.50
For \(\mu <\nu \) we get  for every ordinal \(\xi <\kappa _{{\mu +1}}^{\mathfrak {M}}\).
for every ordinal \(\xi <\kappa _{{\mu +1}}^{\mathfrak {M}}\).
Proof
The proof is by induction on \(\xi \), using monotonicity and tautology which is responsible for the \(\kappa _{\nu }^{\mathfrak {M}}\) in the derivation height. It should be noted that the proof never uses one of the non-logical rules \((\text {Cl}_{\mu })\). \(\square \)
Observe that for \(F(X,\eta ){}\quad :\Leftrightarrow \quad (\forall ~\xi )[\xi \prec \eta \rightarrow \xi \in X]\) the formula \(\textit{Cl}_{F_{0}}(X)\) is the formula \(\textit{ Prog}(\prec ,X)\) which we introduced in Sect. 3.2.4 to express well-foundedness. Therefore we obtain with the same proof.
Lemma 3.51
We have  for every ordinal notation \(\mu \in \mathord { On}\).
for every ordinal notation \(\mu \in \mathord { On}\).
LemmataFootnote 39 3.51 and 3.50 show the semi-formal provability of \({\textbf {TI}}_\nu \) and \(({{\textsc {ID}}}^{2}_\nu )^{*}\).
Theorem 3.52
(Embedding of transfinite induction) We have

for an ordinal \(\alpha <\kappa _{\nu }^{\mathfrak {M}}+\nu +\omega \).
Theorem 3.53
(Embedding of \(({{\textsc {ID}}}^{2}_\nu )\)) For any \(\mu <\nu \) we get

with \(\alpha <\kappa _{\nu }^{\mathfrak {M}}+\kappa _{{\mu +1}}^{\mathfrak {M}}+\omega \). Hence

None of these embedding theorems needs one of the non-logical rules \((\text {Cl}_{\mu })\). For the embedding of axiom \(({{\textsc {ID}}}^{1}_\nu )\), however, \((\text {Cl}_{\mu })\) is inevitable.
Theorem 3.54
(Embedding of \(({{\textsc {ID}}}^{1}_\nu )\)) For any \(\mu <\nu \) we have

Proof
By tautology we have 
with \(\alpha _\mu <\kappa _{{\mu +1}}^{\mathfrak {M}}+\omega \) for all \(\mu \in \mathord { On}\) and \(s\in M\). Applying a \((\text {Cl}_{\mu })\)-rule and two \((\bigvee )\) rules we obtain

for all \(\mu \in \mathord { On}\) and \(s\in M\). The claim follows by two clauses \((\bigwedge )\). \(\square \)
3.3 Collapsing
It follows from Theorems 3.52, 3.54, and 3.53 that all the additional axioms in \(\textsf{ID}_{\nu }({\textsf{T}})\) are semi-formally provable. But we also have to observe that the derivations have heights above \(\kappa _{\nu }^{\mathfrak {M}}\). In Theorems 3.52 and 3.54 this may be due to the technical peculiarities of our system. It is not absolutely necessary to assign the complexity \(\kappa _{\nu }^{\mathfrak {M}}\) to free set variables. We could even get along with schemes instead of pseudo \(\Pi _{1}^{1}\)-sentences. Also alternative complexity measures are thinkable that allow for semi-formal derivations of tautologies with heights below \(\kappa _{\nu }^{\mathfrak {M}}\) and thus decrease the derivation heights in Lemma 3.51 and Theorem 3.54. In Lemma 3.50, however, and thus also in Theorem 3.53 the height above \(\kappa _{\nu }^{\mathfrak {M}}\) is inevitable. Our standard procedure, as we had described it in Sect. 3.2.5, will therefore not be of use here, as it would deliver too big upper limits.
What is needed is a procedure to collapse derivations of the form  into derivations of heights below \(\kappa _{{\mu +1}}^{\mathfrak {M}}\). Such a procedure is not obvious and forces us to leave our still predominantly semantical point of view in favour of a more proof-theoretically oriented standpoint. The translation of a formal derivation of a sentence \(s\in I_{F_{\mu }}^{<\kappa _{{\mu +1}}^{\mathfrak {M}}}\) will in general require the detour through semi-formal derivations of heights above \(\kappa _{{\mu +1}}^{\mathfrak {M}}\). The key idea is that the ordinals generated by the embedding procedure should leave gaps, which are sufficiently large to allow for a collapsing procedure. Therefore a reasonable idea is only to use those ordinals as a measure for the heights of semi-formal derivations which are generated by the embedding procedure and the necessary subsequent manipulations and then to try to find a collapsing procedure for these ordinals. This generation process can be described by an operator applied to the ordinal constants occurring in the derivation. Therefore we need controlling operators for semi-formal derivations which we will develop in the next sections.Footnote 40
into derivations of heights below \(\kappa _{{\mu +1}}^{\mathfrak {M}}\). Such a procedure is not obvious and forces us to leave our still predominantly semantical point of view in favour of a more proof-theoretically oriented standpoint. The translation of a formal derivation of a sentence \(s\in I_{F_{\mu }}^{<\kappa _{{\mu +1}}^{\mathfrak {M}}}\) will in general require the detour through semi-formal derivations of heights above \(\kappa _{{\mu +1}}^{\mathfrak {M}}\). The key idea is that the ordinals generated by the embedding procedure should leave gaps, which are sufficiently large to allow for a collapsing procedure. Therefore a reasonable idea is only to use those ordinals as a measure for the heights of semi-formal derivations which are generated by the embedding procedure and the necessary subsequent manipulations and then to try to find a collapsing procedure for these ordinals. This generation process can be described by an operator applied to the ordinal constants occurring in the derivation. Therefore we need controlling operators for semi-formal derivations which we will develop in the next sections.Footnote 40
3.3.1 Iterated Skolem-Hull Operators
The Skolem-hull operator \(\mathcal{S}\) generated by a collection \(\mathcal{F}\) of ordinals and ordinal functions assigns to any set X of ordinals the least set \(\mathcal{S}(X)\) of ordinals which contains X, all ordinals in \(\mathcal{F}\) and is closed under the functions in \(\mathcal{F}\).
Observe that for Skolem-hull operators we always have \(X\subseteq \mathcal{S}(X)=\mathcal{S}^2(X)\). They are monotone which entails that with \(X\subseteq \mathcal{S}(Y)\) we also have \(\mathcal{S}(X)\subseteq \mathcal{S}(Y)\). A useful notation is \(\mathcal{S}[X,\mathcal{F}]\) for a set X of ordinals and a collection \(\mathcal{F}\) of functions. It denotes the Skolem-hull operator obtained from \(\mathcal{S}\) by extending its generators by the elements of X and the functions in \(\mathcal{F}\).
The functions which are indispensable in proof theory are ordinal addition and the Veblen functions as introduced in Sect. 3.2.3. Our basic operator will therefore be the operator \(\mathcal{A}\) whose generating functions are \(+\) and \(\varphi \), viewed as binary functions.
Our aim is to extend \(\mathcal{A}\) to an operator \(\mathcal{H}\) which is suited to control the \({\mathfrak M}_{\nu }^*\)-derivations which arise as translations of formal \(\textsf{ID}_{\nu }({\textsf{T}})\)-derivations.
Since we assume that the ordinals less than \(\nu \) are given “from outside”, we have to assume that \(\nu +1={}{\{{\xi }\,|\,{\xi \le \nu }\}}\) is among the generators of \(\mathcal{H}\).
The landmarks in \(\textit{Spec}^{\mathfrak {M}}({\textsf{ID}_{\nu }({\textsf{T}})})\) are apparently the ordinals \(\kappa _{\mu }^{\mathfrak {M}}\). These are ordinals which are abstractly defined by their model theoretic closure properties as displayed in (3.22). These closure properties are complicated and thus difficult to handle. Therefore we introduce names \(\Omega _{\mu }\) for the ordinals \(\kappa _{\mu }^{\mathfrak {M}}\) and axiomatize them by simpler closure conditions. The intended interpretation for \(\Omega _{\mu }\) is of course \(\kappa _{\mu }^{\mathfrak {M}}\) but other interpretations are possible.
We thus define \(\mathcal{H}:=\mathcal{A}[\nu +1,{}{\{{\Omega _{\mu }}\,|\,{0\le \mu \le \nu }\}}]\). Since \(\mathcal{H}^2(X)=\mathcal{H}(X)\) all iterations of \(\mathcal{H}\) become already stationary in the first step. To get really growing iterations \(\mathcal{H}^\alpha \) we have to augment the generating functions of \(\mathcal{H}^\alpha \) in every iteration step. We will start with an informal description how such functions can be obtained.
If we apply the Skolem-hull operator \(\mathcal{H}\) to a transitive subset X of the ordinals—which for proper subsets \(X\subsetneq \textit{ Ord}\) automatically is an ordinal, say \(\xi \)—it will in general not return a transitive subset, i.e. an ordinal. In general \(\mathcal{H}(\xi )\) will not even fill the gap between \(\xi \) and \(\xi ^+:=\min {}{\{{\Omega _{{\mu +1}}}\,|\,{\xi <\Omega _{{\mu +1}}}\}}\). Assuming that we already defined the iterations \(\mathcal{H}^\beta \) for all \(\beta \le \alpha \), the idea is now to give for \(\Omega _{\mu }\le \xi <\Omega _{{\mu +1}}\) the first ordinal in the gap \(\mathcal{H}^\alpha (\xi )\cap \Omega _{{\mu +1}}\) the name \(\Psi _{\Omega _{{\mu +1}}}({\alpha })\). In this way we obtain new functions \(\Psi _{\Omega _{{\mu +1}}}\) for all \(\mu <\nu \) by which we augment the generators of \(\mathcal{H}^{\alpha +1}\). This allows us to iterate the operator \(\mathcal{H}\) stepwise to a Skolem-hull operator \(\mathcal{H}^{\alpha }\) which, besides \(+\) and \(\varphi \), also has the functions \(\Psi _{\Omega _{{\mu +1}}}\mathord {\restriction }\alpha \) among its generators and to extend the functions \(\Psi _{\Omega _{{\mu +1}}}\mathord {\restriction }\alpha \) to the argument \(\Psi _{\Omega _{{\mu +1}}}({\alpha }):=\min {}{\{{\xi }\,|\,{\Omega _{{\mu +1}}\le \xi \notin \mathcal{H}^{\alpha }(\xi )}\}}\). For \(\alpha \notin \mathcal{H}^{\alpha }(\xi )\), however, this strategy would imply \(\mathcal{H}^{\alpha }(\xi )=\mathcal{H}^{\alpha +1}(\xi )\) and thus would make \(\Psi _{\Omega _{{\mu +1}}}\) many one. In order to obtain \(\Psi _{\Omega _{{\mu +1}}}\) as a one-one function we restrict \(\Psi _{\Omega _{{\mu +1}}}\) to those \(\alpha \) for which there is a \(\xi \) such that \(\alpha \in \mathcal{H}_{\alpha }(\xi )\) and \(\Omega _{{\mu +1}}\le \xi \notin \mathcal{H}^{\alpha }(\xi )\). The price to pay is that \(\Psi _{\Omega _{{\mu +1}}}\) becomes partial.
Formally we characterize the set \({}{\{{\Omega _{\mu }}\,|\,{0\le \mu \le \nu }\}}\) of initial ordinals together with the functions \(\Psi _{\Omega _{{\mu +1}}}\) and the iterated Skolem-hulls \(\mathcal{H}^{\alpha }\) by the following axioms:
Definition 3.55
- (A0):
-
\(\Omega _{0}=0\), \(\nu <\Omega _{1}\).
- (A1):
-
\((\forall ~{\mu \mathord \le \nu })(\forall ~\xi )(\forall ~\eta )[\xi ,\eta<\Omega _{\mu }\rightarrow \xi +\eta<\Omega _{\nu }\,\wedge \,\varphi _{\xi }({\eta })<\Omega _{\mu }]\).
- (A2):
-
 .
. - (A3):
-
\(\Omega _{\lambda }=\sup {}{\{{\Omega _{\sigma }}\,|\,{\sigma <\lambda }\}}\) holds true for all limit ordinals \(\lambda \).
- (B0):
-
\(\mathcal{H}^{0}:=\mathcal{H}\).
- (B1):
-
\(\Psi _{\Omega _{{\mu +1}}}({\alpha }):=\min {}{\{{\xi }\,|\,{\alpha \in \mathcal{H}_{\alpha }(\xi )\,\wedge \,\Omega _{\mu }\le \xi \notin \mathcal{H}^{\alpha }(\xi )}\}}\).
- (B3):
-
\(\mathcal{H}^{\alpha }(X)\) is the least set that comprises \(\mathcal{H}(X)\) and is closed under \(+\), \(\lambda \xi \eta . \varphi _{\xi }({\eta })\) and \(\Psi _{\Omega _{{\mu +1}}}\mathord {\restriction }\alpha \) for all \(\mu <\nu \).
- (B4):
-
 .
.
Theorem 3.56
The axiom system in Definition 3.55 is consistent.
Proof
The sequence \(\langle 0\rangle ^\frown {}{\big \langle {\aleph _\mu }\,|\,{0<\mu \le \nu }\big \rangle }\)Footnote 41 obviously fulfills axioms (A0) through (A3). Constructing \(\mathcal{H}^{\alpha }\) and \(\Psi _{\Omega _{{\mu +1}}}\) according to (B0)–(B3) we obtain that the cardinality of \({\mathcal{H}^{\alpha }(\xi )}\) is the maximum of \(\aleph _0\) and the cardinality of \(\xi \). A simple cardinality argument now shows that also (B4) is fulfilled. \(\square \)
Remark 3.57
Whenever we write \(\Psi _{\Omega _{{\mu +1}}}({\alpha })\) we tacitly assume \(\alpha \in \textit{dom}(\Psi _{\Omega _{{\mu +1}}})\), often without mentioning it explicitly.
The definition of the operators \(\mathcal{H}^{\alpha }\) depends of course on \(\nu \). We have refrained from expressing this through another index, as we will have to introduce this index later anyway.
Instead of \(\mathcal{H}\) as the starting point of the iteration we could use \(\mathcal{H}[\Omega _{\mu }]\). Then we of course only allow the functions \(\Psi _{\Omega _{{\sigma +1}}}\mathord {\restriction }\alpha \) for \(\mu \le \sigma <\nu \) and initial ordinals \(\Omega _{\sigma }\) for \(\mu <\sigma \le \nu \) as generators of \(\mathcal{H}[\Omega _{\mu }]^\alpha \). Since \(\mathcal{H}[\Omega _{\mu }](0)=\mathcal{H}(\Omega _{\mu })\) we easily obtain \(\mathcal{H}[\Omega _{\mu }]^\alpha (0)=\mathcal{H}{(\Omega _{\mu })}\).
We collect the main properties of the Skolem-hull operators \(\mathcal{H}^{\alpha }\) and the associated collapsing functions \(\Psi _{\Omega _{{\mu +1}}}\) in the following Lemma.
Lemma 3.58
For \(\alpha ,\beta \in \textit{dom}(\Psi _{\Omega _{{\mu +1}}})\) we have
-
(i)
\(\mathcal{H}^{\alpha }{(\Psi _{\Omega _{{\mu +1}}}({\alpha }))}=\mathcal{H}^{\alpha }{(\Omega _{\mu })}\),
-
(ii)
\(\Psi _{\Omega _{{\mu +1}}}({\alpha })=\mathcal{H}^{\alpha }{(\Omega _{\mu })}\cap \Omega _{{\mu +1}}={}{\{{\xi }\,|\,{\alpha \in \mathcal{H}^{\alpha }{(\Omega _{\mu })}\,\wedge \,\mathcal{H}^{\alpha }(\xi )\cap \Omega _{{\mu +1}}=(\xi )}\}}\),
-
(iii)
\(\Psi _{\Omega _{\mu }+1}({\alpha })<\Psi _{\Omega _{{\sigma +1}}}({\beta })\) iff \(\mu <\sigma \), or \(\mu =\sigma \) and \(\alpha \in \mathcal{H}^{\beta }{(\Omega _{\sigma })}\cap \beta \), and
-
(iv)
\(\Psi _{\Omega _{\mu +1}}(\alpha )=\Psi _{\Omega _{\sigma +1}}(\beta )\) iff \(\mu =\sigma \) and \(\alpha =\beta \).
Proof
We sketch the proofs. Let \(\eta :=\min {}{\{{\xi }\,|\,{\alpha \in \mathcal{H}^{\alpha }{(\Omega _{\mu })} \,\wedge \,\Omega _{\mu }\le \xi \notin \mathcal{H}^{\alpha }{(\Omega _{\mu })}}\}}\). Then \(\eta \subseteq \mathcal{H}^{\alpha }{(\Omega _{\mu })}\), hence \(\mathcal{H}^{\alpha }{(\Omega _{\mu })}=(\mathcal{H}^{\alpha }\eta )\), which in turn implies \(\Psi _{\Omega _{\mu +1}}(\alpha )=\eta \). Then we show by induction on \(\alpha \) that \(\mathcal{H}^{\alpha }{\Omega _{\mu }}\cap \Omega _{{\mu +1}}\) is transitive. If not, let \(\delta \) be the least ordinal in \(\mathcal{H}^{\alpha }{(\Omega _{\mu })}\) which is bigger than \(\Psi _{\Omega _{\mu +1}}(\alpha )\). By minimality \(\delta \) is strongly critical, hence of the form \(\Psi _{\Omega _{\mu +1}}(\rho )\) for some \(\rho <\alpha \). By induction hypothesis we have \(\Psi _{\Omega _{\mu +1}}(\alpha )<\Psi _{\Omega _{\mu +1}}(\rho )=\mathcal{H}^{\rho }{(\Omega _{\mu })}\cap \Omega _{{\mu +1}}\subseteq \mathcal{H}^{\alpha }{(\Omega _{\mu })}\cap \Omega _{{\mu +1}}\) which contradicts the definition of \(\Psi _{\Omega _{\mu +1}}(\alpha )\). So we have (i) and (ii). Claims (iii) and (iv) are immediate consequences of (ii). \(\square \)
By (ii) of Lemma 3.58 we see that \(\nu <\Psi _{\Omega _{1}}({\alpha })\) holds true for any \(\alpha \in \textit{dom}(\Psi _{\Omega _{1}})\).
We already mentioned that interpreting \(\Omega _{\mu }\) by \(\aleph _\mu \) for \(\mu >0\) is for cardinality reasons a sound interpretation. However, we aim at an interpretation of \(\Omega _{\mu }\) by the initial ordinals \(\kappa _{\mu }^{\mathfrak {M}}\) in the spectrum of \(\textsf{ID}_{\nu }({\textsf{T}})\). As a preparation we need a lemma.
Lemma 3.59
For an acceptable structure \(\mathfrak {M}\) we have \(\mathcal{H}^{\alpha }{(\kappa _{\mu }^{\mathfrak {M}})}\cap \Omega _{{\mu +1}}<\kappa _{{\mu +1}}^{\mathfrak {M}}\).
Proof
The idea of the proof is to show that there is an elementarily definable copy of \(\mathcal{H}^{\alpha }{\kappa _{\mu }^{\mathfrak {M}}}\) in \({\mathfrak M}_{\mu }\) which entails that the order-type of \(\mathcal{H}^{\alpha }{(\kappa _{\mu }^{\mathfrak {M}})}\cap \Omega _{{\mu +1}}=\Psi _{\Omega _{\mu +1}}(\kappa _{\mu }^{\mathfrak {M}})\) is less than \(\kappa ^{{\mathfrak M}_{\mu }}=\kappa _{{\mu +1}}^{\mathfrak {M}}\). We just outline the main arguments.
First we observe that the sets \(\mathcal{H}^{\alpha }{(X)}\) are almost syntactically definable by the clauses
-
\(X\cup (\nu +1)\subseteq \mathcal{H}^{\alpha }{(X)},\)
-
\(\rho \le \nu \) implies \(\Omega _{\rho }\in \mathcal{H}^{\alpha }{(X)},\)
-
\(\alpha ,\beta \in \mathcal{H}^{\alpha }{(X)},\) imply \(\{\alpha +\beta ,\varphi _{\alpha }({\beta })\}\subseteq \mathcal{H}^{\alpha }{(X)}\)
-
\(\gamma \in \mathcal{H}^{\alpha }{(X)}\cap \alpha \) and \(\gamma \in \textit{dom}(\Psi _{\Omega _{{\rho +1}}})\) imply \(\Psi _{\Omega _{\rho +1}}(\gamma )\in \mathcal{H}^{\alpha }{(X)}\).
The only “non-syntactical” condition in this inductive definition is \(\gamma \in \textit{dom}(\Psi _{\rho +1})\). According to Lemma 3.58 (i) this condition is equivalent to \(\alpha \in \mathcal{H}^{\alpha }{\Omega _{\rho }}\). From the above inductive definition we can read off the definition of a set \(K_{\mu }(\gamma )\) of ordinals such that \(\gamma \in \mathcal{H}^{\alpha }{(\Omega _{\mu })}\) holds true iff \(\xi <\alpha \) holds true for all ordinals in \(K_{\mu }(\gamma )\). We put
So we can replace the non-syntactical condition \(\gamma \in \textit{dom}(\Psi _{\Omega _{{\mu +1}}})\) by the more syntactical condition \(K_{\mu }(\gamma )<\gamma \). This condition is more syntactical in the sense that if we represent the ordinals in \(\mathcal{H}^{\alpha }{(X)}\) by terms built up according to the above induction steps, the ordinals in \(K_{\mu }(\gamma )\) are represented by previously defined terms.
Since \(\Omega _{\nu }\) is the largest initial ordinal in any \(\mathcal{H}(X)\) and all ordinals \(\Psi _{\Omega _{\rho +1}}(\alpha )\) are less than \(\Omega _{\nu }\) no iteration of \(\mathcal{H}\) will reach beyond \(\Gamma _{\Omega _{\nu }+1}\), the first strongly critical ordinal bigger than \(\Omega _{\nu }\). This implies that the set \(\mathcal{H}^{\Gamma _{\Omega _{\nu }+1}}{(\kappa _{\mu }^{\mathfrak {M}})}\cap \Gamma _{\Omega _{\nu }+1}\) is the largest set of ordinals which we can reach from \(\kappa _{\mu }^{\mathfrak {M}}\). It should be obvious from the above considerations that we can represent the ordinals in \(\mathcal{H}^{\Gamma _{\Omega _{\nu }+1}}{(\kappa _{\mu }^{\mathfrak {M}})}\cap \Gamma _{\Omega _{\nu }+1}\) by ordinal terms which are recursively definable in parameters from \(\kappa _{\mu }^{\mathfrak {M}}\) and \(\nu +1\).
According to Lemma 3.58 (iii) we obtain \(\Psi _{\Omega _{\rho +1}}(\alpha )<\Psi _{\Omega _{\sigma +1}}(\beta )\) iff \(\rho <\sigma \) or \(\alpha \in \mathcal{H}^{\beta }{(\Omega _{\sigma })}\cap \beta \) which in turn holds true iff \(\{\alpha \}\cup K_{\sigma }(\alpha )<\beta \). Together with the well-known fact that size comparison between ordinal terms of the form \(\alpha +\beta \), \(\varphi _{\alpha }({\beta })\) is recursively describable we thus obtain the set \(\mathcal{H}^{\Gamma _{\Omega _{\nu }+1}}{\kappa _{\mu }^{\mathfrak {M}}}\cap \Gamma _{\Omega _{\nu }+1}\) and the size comparison on this set recursive in \(\kappa _{\mu }^{\mathfrak {M}}\).
The remaining problem is that there are no ordinals in \({\mathfrak M}_{\mu }\). However, for \(\mu \) a successor ordinal \(\rho +1\) there is a set \(O_\mu \in {\mathbb {S}}{\mathbb {P}}_{{\mathfrak M}_{\rho }}\) whose complement is not in \({\mathbb {S}}{\mathbb {P}}_{{\mathfrak M}_{\rho }}\).Footnote 42 Let \(\sigma _\mu \) be an associated \({\mathbb {S}}{\mathbb {P}}_{{\mathfrak M}_{\rho }}\)-norm for \(O_\mu \). Since \(O_\mu \) is self-dual iffFootnote 43 \(o(O_\mu )<\kappa ^{{\mathfrak M}_\rho }=\kappa ^{\mathfrak M}_\mu \): and \(O_\mu \) is not self-dual, we have \(o(O_\mu )=\kappa ^{{\mathfrak M}_{\rho }}=\kappa _{\mu }^{\mathfrak {M}}\) and the relations \(\prec _{\sigma _\mu }^{*}\) and \(\preceq _{\sigma _\mu }^{*}\) are in \({\mathbb {S}}{\mathbb {P}}_{{\mathfrak M}_{\rho }}\) and thus elementary in \({\mathfrak M}_{\mu }\). For a limit ordinal \(\mu \) we may therefore assume that for all \(\rho <\mu \) there is an elementarily definable set \(O_\rho \) and an elementarily definable relation \(\prec _\rho \) on \(O_\rho \) of order-type \(\kappa _{\rho }^{\mathfrak {M}}\). We can then take the disjoint union \(O_\mu \) of the sets \(O_\rho \) to obtain an elementarily definable well-founded relation of order-type \(\kappa _{\mu }^{\mathfrak {M}}\) in \({\mathfrak M}_{\mu }\).
Taking the elements in the prewellordering \(O_\mu \) as representatives for the ordinals below \(\kappa _{\mu }^{\mathfrak {M}}\) we can elementarily define a copy of \(\mathcal{H}^{\Gamma _{\Omega _{\nu }+1}}{\kappa _{\mu }^{\mathfrak {M}}}\) in \({\mathfrak M}_{\mu }\). This entails that for \(\alpha \in \mathcal{H}^{\Gamma _{\Omega _{\nu }+1}}{(\kappa _{\mu }^{\mathfrak {M}})}\) the order-type of \(\mathcal{H}^{\alpha }{(\Omega _{\mu })}\cap \Omega _{{\mu +1}}\) and thus the ordinal \(\Psi _{\Omega _{\mu +1}}(\alpha )\) is less than \(\kappa _{{\mu +1}}^{\mathfrak {M}}\). \(\square \)
We define an interpretation \({\mathscr {I}}_{\mu }^{\mathfrak M}\) by
Theorem 3.60
For an acceptable structure \(\mathfrak {M}\) the interpretation \({\mathscr {I}}_{\mu }^{\mathfrak M}\) is for all \(\mu \le \nu \) a sound interpretation for the variables \(\Omega _{\mu }\).
Proof
We proceed by induction on \(\mu \). As already remarked, the interpretation \({\mathscr {I}}_{0}^{\mathfrak M}\) is a sound interpretation for cardinality reasons.
Clearly all the ordinals \(\kappa _{\mu }^{\mathfrak {M}}\) are strongly critical, such that \(\kappa _{\rho }^{\mathfrak {M}}<\kappa _{\mu }^{\mathfrak {M}}\) holds true for \(\rho <\mu \). Moreover we have \(\nu +1<\kappa _{1}^{\mathfrak {M}}\), since \(\nu \) is elementarily represented in \(\mathfrak {M}\). If we assume that \({\mathscr {I}}_{\mu }^{\mathfrak M}\) is a sound interpretation we obtain \(\Psi _{\Omega _{\mu +1}}(\kappa _{\mu }^{\mathfrak {M}})<\kappa _{{\mu +1}}^{\mathfrak {M}}\) by Lemma 3.59. Interpreting \(\Omega _{{\mu +1}}\) by \(\kappa _{{\mu +1}}^{\mathfrak {M}}\) satisfies axiom (B4) in Definition 3.55. Thus \({\mathscr {I}}_{\mu }^{\mathfrak M}\) is a sound interpretation. For limit ordinals \(\lambda \) we get the claim from the induction hypothesis and \(\kappa _{\lambda }^{\mathfrak {M}}=\sup {}{\{{\kappa _{\mu }^{\mathfrak {M}}}\,|\,{\mu <\lambda }\}}\). \(\square \)
Corollary 3.61
Interpreting \(\Omega _{\mu }\) standardly by \(\kappa _{\mu }^{\mathfrak {M}}\) is sound for acceptable structures \(\mathfrak {M}\).
In view of Corollary 3.61 we stick to the standard interpretation of the constants \(\Omega _{\mu }\). Nevertheless we continue to write \(\Omega _{\mu }\) instead of \(\kappa _{\mu }^{\mathfrak {M}}\) (it is easier to type and looks typographically better).
Note 3.62
The development of iterated Skolem-hull operators has a long history. It goes back to an unpublished idea of Sol Feferman around 1970. This idea has been pursued (among others) by Peter Aczel, Jane Bridge (Kister) ([3]) and especially Wilfried Buchholz in a series of papers.Footnote 44
3.3.2 Operator Controlled Derivations
Assume that \({\mathfrak M}\) is a countable structure which contains constants for ordinals in its language. For an \({{\mathscr {L}}(\mathfrak {M})}\)-formula F we denote by \(\mathord {\text {par}}(F)\) the set of ordinal constants occurring in F. For a finite set \(\Delta \) of \({{\mathscr {L}}(\mathfrak {M})}\)-formulae we put \(\mathord {\text {par}}(\Delta ):=\bigcup {}{\{{\mathord {\text {par}}(F)}\,|\,{F\in \Delta }\}}\). Let \(\mathcal{S}\) be a Skolem-hull operator extending \(\mathcal{A}\). We call the language \({{\mathscr {L}}(\mathfrak {M})}\) \(\mathcal{S}\)-regular if \(\textit{rnk}(F)\in \mathcal{S}(\mathord {\text {par}}(F))\) holds true for all \({{\mathscr {L}}(\mathfrak {M})}\)-formulae F. For \(\mathcal{S}\)-regular languages we extend Definition 3.1 to a definition  of an operator controlled derivation.
of an operator controlled derivation.
Definition 3.63
Let \(\mathfrak {M}\) be an acceptable countable structure and \(\mathcal{S}\) be a Skolem-hull operator such that \({{\mathscr {L}}(\mathfrak {M})}\) is \(\mathcal{S}\)-regular. For a finite set of pseudo \(\Pi _{1}^{1}\)-sentences we define the operator controlled semi-formal proof relation  by the following clauses
by the following clauses
- (X):
-
If \(\vec s=s_1,\dots ,s_{n}\) and \({\vec t}=t_1,\dots ,t_{n}\) are tuples of \({\mathscr {L}}(\mathfrak {M})_M\)-terms such that \(\mathfrak {M}\models s_i = t_i\) for \(i=1,\dots , n\) and \(\{\vec s\in X,{\vec t}\notin X\}\subseteq \Delta \) then
 holds true for all ordinals \(\rho \) and \(\Omega _{\nu }\le \alpha \in \mathcal{S}(\mathord {\text {par}}(\Delta ))\).
holds true for all ordinals \(\rho \) and \(\Omega _{\nu }\le \alpha \in \mathcal{S}(\mathord {\text {par}}(\Delta ))\). - (\(\bigwedge \)):
-
If \(F\in \Delta \cap \bigwedge -{\mathord {\textsf {type}}}\,\) and
 hold true for all \(G\in \text {CS}~F\) then
hold true for all \(G\in \text {CS}~F\) then  holds true for all \(\alpha \ge \sup {}{\{{\alpha _G+1}\,|\,{G\in \text {CS}~F}\}}\) such that \(\alpha \in \mathcal{S}(\mathord {\text {par}}(\Delta ))\).
holds true for all \(\alpha \ge \sup {}{\{{\alpha _G+1}\,|\,{G\in \text {CS}~F}\}}\) such that \(\alpha \in \mathcal{S}(\mathord {\text {par}}(\Delta ))\). - (\(\bigvee \)):
-
If \(F\in \Delta \cap \bigvee -{\mathord {\textsf {type}}}\,\) and
 holds true for some \(G\in \text {CS}~F\) such that \(\mathord {\text {par}}(G)\subseteq \mathcal{S}(\mathord {\text {par}}(\Delta ))\) then
holds true for some \(G\in \text {CS}~F\) such that \(\mathord {\text {par}}(G)\subseteq \mathcal{S}(\mathord {\text {par}}(\Delta ))\) then  holds true for all \(\alpha >\alpha _0\) such that \(\alpha \in \mathcal{S}(\mathord {\text {par}}(\Delta ))\).
holds true for all \(\alpha >\alpha _0\) such that \(\alpha \in \mathcal{S}(\mathord {\text {par}}(\Delta ))\). - (Cut):
-
If
 ,
,  , \(\mathord {\text {par}}(F)\subseteq \mathcal{S}(\mathord {\text {par}}(\Delta ))\) and \(\textit{rnk}(F)<\rho \) then
, \(\mathord {\text {par}}(F)\subseteq \mathcal{S}(\mathord {\text {par}}(\Delta ))\) and \(\textit{rnk}(F)<\rho \) then  holds true for all \(\alpha >\alpha _0\) such that \(\alpha \in \mathcal{S}(\mathord {\text {par}}(\Delta ))\).
holds true for all \(\alpha >\alpha _0\) such that \(\alpha \in \mathcal{S}(\mathord {\text {par}}(\Delta ))\).
We obviously have \(\omega +1\subseteq \mathcal{S}(\{\emptyset \})\) and with \(\alpha \in \mathcal{S}(\{\emptyset \})\) also \(\omega \mathrel {\cdot }\alpha \in \mathcal{S}(\{\emptyset \})\) for any Skolem-hull operator \(\mathcal{S}\) that extends \(\mathcal{A}\). The first and main observation is that tautologies of the form \(\lnot F\,\vee \,F\) are operator controlled derivable.
Lemma 3.64
(Controlled Tautology) Let \(\mathcal{S}\) be a Skolem operator extending \(\mathcal{A}\), \({{\mathscr {L}}(\mathfrak {M})}\) an \(\mathcal{S}\)-regular language and F and \(F'\) be \({{\mathscr {L}}(\mathfrak {M})}\) formulae which at most differ in \({{\mathscr {L}}(\mathfrak {M})}_M\)-terms which have the same value in \(\mathfrak {M}\). Then we obtain  for \(\alpha =2\mathrel {\cdot }\textit{rnk}(F)\).
for \(\alpha =2\mathrel {\cdot }\textit{rnk}(F)\).
Proof
We sketch the main case. W.l.o.g. let \(F\in \bigwedge -{\mathord {\textsf {type}}}\,\). For \(G\in \text {CS}~F\) let \(G'\) be the corresponding formula in \(\text {CS}~{F'}\) which differs from G at most in the same \({{\mathscr {L}}(\mathfrak {M})}_M\) terms as F and \(F'\). We have  with \(\beta _G=2\mathrel {\cdot }\textit{rnk}(G)\) for every \(G\in \text {CS}~F\) by induction hypothesis. By an inference \((\bigvee )\) we get
with \(\beta _G=2\mathrel {\cdot }\textit{rnk}(G)\) for every \(G\in \text {CS}~F\) by induction hypothesis. By an inference \((\bigvee )\) we get  for all \(G\in \text {CS}~{F}\) which is applicable since \(\mathord {\text {par}}(G')\subseteq \mathcal{S}(\mathord {\text {par}}(\Delta ,\lnot F,F',G))\). Because of \(\beta _G+1<2\mathrel {\cdot }\textit{rnk}(F)\in \mathcal{S}(\mathord {\text {par}}(\Delta ,\lnot F,F'))\) we obtain the claim by an inference \((\bigwedge )\). \(\square \)
for all \(G\in \text {CS}~{F}\) which is applicable since \(\mathord {\text {par}}(G')\subseteq \mathcal{S}(\mathord {\text {par}}(\Delta ,\lnot F,F',G))\). Because of \(\beta _G+1<2\mathrel {\cdot }\textit{rnk}(F)\in \mathcal{S}(\mathord {\text {par}}(\Delta ,\lnot F,F'))\) we obtain the claim by an inference \((\bigwedge )\). \(\square \)
Based on Controlled Tautology we can show that all the embeddings of Sect. 3.3.2.6 are \(\mathcal{H}\)-controlled derivable. In detail we obtain




Remark 3.65
Since the elements of \(\mathord { On}\) are not counted among the parameters of an \({\mathscr {L}}({\mathfrak M}_{\nu }^*)\)-formula we need the set \(\nu +1\) among the generators of \(\mathcal{H}\) to obtain (3.24) in full generality.Footnote 45 Put, for the moment, \(\mathcal{H}_0 :=\mathcal{A}[{}{\{{\Omega _{\mu }}\,|\,{0\le \mu \le \nu }\}}]\). Then \(\mathcal{H}^{\alpha }=\mathcal{H}_0^\alpha \) holds true whenever \(\nu +1\subseteq \mathcal{H}_0^{\Gamma _{\Omega _{\nu }+1}}(0)\cap \Omega _{1}=: \Psi ^{\mathcal{H}_0}_{\Omega _{1}}(\Gamma _{\Omega _{\nu }+1})\). For \(\nu <\Psi ^{\mathcal{H}_0}_{\Omega _{1}}(\Gamma _{\Omega _{\nu }+1})\) the generator \(\nu +1\) for \(\mathcal{H}\) is thus dispensable.
For an axiom system \(\textsf{T}\) for \(\mathfrak {M}\), containing the axiom of Mathematical Induction, the extension \(\textsf{ID}_{\nu }({\textsf{T}})\) proves induction up to all ordinals less than \(\Psi _{\Omega _{1}}^{\mathcal{H}_0}(\varepsilon _{\Omega _{\nu }+1})\)Footnote 46 which—in principle—makes \((\text {TI}_\nu )\) superfluous for \(\nu <\Psi _{\Omega _{1}}^{\mathcal{H}_0}(\varepsilon _{\Omega _{\nu }+1})\).
As remarked in Note 3.37 iterated inductive definitions have their origin in foundational problems. From a foundational point of view it makes little sense to iterate inductive definitions along ordinals \(\nu >\Psi _{\Omega _{1}}^{\mathcal{H}_0}(\varepsilon _{\Omega _{\nu }+1})\) without having additional information about the foundational meaning of \(\nu \).
Of greater interest are iterations which generate the initial ordinals by a bootstrap procedure. An example is the operator \(\mathcal{I}:=\mathcal{A}[\{I\},\{\lambda \xi . \Omega _{\xi }\}]\), where I is a symbol whose intended interpretation is the first recursively inaccessible ordinal. Defining the iterations \(\mathcal{I}^\alpha \) simultaneously with an axiomatization of I we obtain a model by using cardinals instead of initial ordinals. By a slight generalization of the method sketched here, we then obtain that also the intended interpretation is a correct one. However, this method develops its strength rather in the investigation of set universes above \(\mathfrak {M}\), which we will not pursue further in this paper. An overview of such systems and their connections to axiom systems for Analysis and set theory is given in [28] and its aftermath paper [12].
Note 3.66
The idea to control semi-formal derivations by ordinal operators goes back to a paper by Wilfried Buchholz ([4]) in which he proposed this method as a simplification of the original method of local predicativity which depended on special notation systems for ordinals.
3.3.3 The Collapsing Procedure
The main concern of operator controlled derivations is to enable a procedure to convert a derivation of the form  into a derivation
into a derivation  such that the ordinal \(\beta <\Omega _{{\mu +1}}\) is computable from the data \(\alpha \), \(\rho \) and \(\mu \). If
such that the ordinal \(\beta <\Omega _{{\mu +1}}\) is computable from the data \(\alpha \), \(\rho \) and \(\mu \). If  has been obtained by transforming a formal \(\textsf{ID}_{\nu }({\textsf{T}})\)-proof this, according to the Boundedness Theorem (Theorem 3.47), yields \(\beta \) as an upper bound for \(\kappa ^{{\mathfrak M}_{\mu }}(\textsf{ID}_{\nu }({\textsf{T}}))=o^{{\mathfrak M}_{{\mu +1}}}(\textsf{ID}_{\nu }({\textsf{T}}))\).
has been obtained by transforming a formal \(\textsf{ID}_{\nu }({\textsf{T}})\)-proof this, according to the Boundedness Theorem (Theorem 3.47), yields \(\beta \) as an upper bound for \(\kappa ^{{\mathfrak M}_{\mu }}(\textsf{ID}_{\nu }({\textsf{T}}))=o^{{\mathfrak M}_{{\mu +1}}}(\textsf{ID}_{\nu }({\textsf{T}}))\).
In Lemma 3.50 we have shown that  with negative occurrences of \((I_{F_{\mu }}^{<\Omega _{\mu }})\) requires an \(\alpha \ge \Omega _{{\mu +1}}\). So it is hardly likely that we can collapse such derivations into derivations of heights below \(\Omega _{{\mu +1}}\). Therefore we say that an \({\mathscr {L}}({\mathfrak M}_{\nu }^*)\)-sentence belongs to \({\bigvee ^{\Omega _{\mu +1}}-\textsf{type}}\) if it only contains constants \(I_{F_{<\rho }}\) with \(\rho <\mu \), constants \(I_{F_{\rho }}^{<\xi }\) with \(\rho \le \mu \) and \(\xi <\Omega _{{\mu +1}}\) and at most positive occurrences of \(I_{F_{\mu }}^{<\Omega _{{\mu +1}}}\). Only for sentences in \({\bigvee ^{\Omega _{\mu +1}}-\textsf{type}}\) we can expect semi-formal derivations with heights below \(\Omega _{{\mu +1}}\).
with negative occurrences of \((I_{F_{\mu }}^{<\Omega _{\mu }})\) requires an \(\alpha \ge \Omega _{{\mu +1}}\). So it is hardly likely that we can collapse such derivations into derivations of heights below \(\Omega _{{\mu +1}}\). Therefore we say that an \({\mathscr {L}}({\mathfrak M}_{\nu }^*)\)-sentence belongs to \({\bigvee ^{\Omega _{\mu +1}}-\textsf{type}}\) if it only contains constants \(I_{F_{<\rho }}\) with \(\rho <\mu \), constants \(I_{F_{\rho }}^{<\xi }\) with \(\rho \le \mu \) and \(\xi <\Omega _{{\mu +1}}\) and at most positive occurrences of \(I_{F_{\mu }}^{<\Omega _{{\mu +1}}}\). Only for sentences in \({\bigvee ^{\Omega _{\mu +1}}-\textsf{type}}\) we can expect semi-formal derivations with heights below \(\Omega _{{\mu +1}}\).
Although we do not need a cut-free derivation to apply the Boundedness Theorem, cut-elimination still plays an important role in the collapsing procedure. We therefore have to reformulate cut-elimination for operator controlled derivations.
Theorem 3.67
Assume that there is no initial ordinal in the interval \((\beta ,\beta +\omega ^\rho ]\). If  holds true for \(\rho \in \mathcal{H}(\mathord {\text {par}}(\Delta ))\) then we obtain
holds true for \(\rho \in \mathcal{H}(\mathord {\text {par}}(\Delta ))\) then we obtain  .
.
Proof
The proof is the standard one with some extra care to get \(\varphi _{\rho }({\alpha })\in \mathcal{H}(\mathord {\text {par}}(\Delta ))\).
For the main theorem we define \(\Omega _{\rho }':={\left\{ \begin{array}{ll}\Omega _{\rho }&{}\text {if}\, \rho \, \text {is a limit ordinal,}\\ \Omega _{\rho }+1&{}\text {if}\, \rho \, \text {is a successor ordinal}. \end{array}\right. }\)
Theorem 3.68
(Collapsing Theorem) Let \(\Delta \) be a finite set of \({\mathscr {L}}({\mathfrak M}_{\nu }^*)\) formulae belonging to \({\bigvee ^{\Omega _{\mu +1}}-\textsf{type}}\). If  holds true for some \(\gamma \in \mathcal{H}^{\gamma }(\mathord {\text {par}}(\Delta ))\) and \(\mathcal{H}_{{\mathfrak M}_{\nu }^*}^{\gamma +1}(\mathord {\text {par}}(\Delta ))\subseteq \mathcal{H}_{{\mathfrak M}_{\nu }^*}^{\gamma +1}(\Omega _{\mu })\) then
holds true for some \(\gamma \in \mathcal{H}^{\gamma }(\mathord {\text {par}}(\Delta ))\) and \(\mathcal{H}_{{\mathfrak M}_{\nu }^*}^{\gamma +1}(\mathord {\text {par}}(\Delta ))\subseteq \mathcal{H}_{{\mathfrak M}_{\nu }^*}^{\gamma +1}(\Omega _{\mu })\) then  holds true for \(\beta =\gamma +\omega ^{\Omega _{\rho }+\alpha }\).
holds true for \(\beta =\gamma +\omega ^{\Omega _{\rho }+\alpha }\).
Proof
This follows by main induction on \(\rho \) with side induction on \(\alpha \). We just indicate the most spectacular case of a cutFootnote 47
- (C):
-
 and
and 
with \(\Omega _{\mu }<\Omega _{\rho }'=\Omega _{{\sigma +1}}+1\). and \(\textit{rnk}(G)=\Omega _{{\sigma +1}}\). Then G is a formula \(s\in I_{F_{\sigma }}^{<\Omega _{{\sigma +1}}}\). Here we have the problem that \(\lnot G\notin {\bigvee ^{\Omega _{\sigma +1}}-\textsf{type}}\). However, for any \(\xi <\Omega _{{\sigma +1}}\) we have \((s\notin I_{F_{\sigma }}^{<\xi })\in {\bigvee ^{\Omega _{\sigma +1}}-\textsf{type}}\). We therefore obtain by induction hypothesis and \(\bigwedge \)-inversion
 and
and 
for \(\delta =\gamma +\omega ^{\Omega _{{\sigma +1}}+\alpha _0}\) and all \(\xi <\Omega _{{\sigma +1}}\). By Boundedness we thus get
 and by cut
and by cut
 . Hence
. Hence
 for \(\eta =\varphi _{\Psi _{\Omega _{{\sigma +1}}}({\delta })+1}({\Psi _{\Omega _{{\sigma +1}}}({\delta })+1})\)
for \(\eta =\varphi _{\Psi _{\Omega _{{\sigma +1}}}({\delta })+1}({\Psi _{\Omega _{{\sigma +1}}}({\delta })+1})\)
by cut-elimination. By the main induction hypothesis we obtain
 for \(\zeta =\delta +\omega ^{\Omega _{\sigma }+\eta }\). We have
for \(\zeta =\delta +\omega ^{\Omega _{\sigma }+\eta }\). We have
\(\quad \alpha _0\in \mathcal{H}^{{\delta +1}}{(\mathord {\text {par}}(\Delta ,G))}\subseteq \mathcal{H}^{{\delta +1}}{(\mathord {\text {par}}(\Delta ))}\subseteq \mathcal{H}^{{\delta +1}}{(\Omega _{\mu })}\subseteq \mathcal{H}_{\beta }(\Omega _{\mu })\)
as well as
\(\quad \gamma \in \mathcal{H}^{\gamma }{(\mathord {\text {par}}(\Delta ))}\subseteq \mathcal{H}^{{\gamma +1}}{(\mathord {\text {par}}(\Delta ))}\subseteq \mathcal{H}^{{\gamma +1}}{(\Omega _{\mu })}\subseteq \mathcal{H}^{\beta }{(\Omega _{\mu })}\).
This implies \(\delta =\gamma +\omega ^{\Omega _{{\sigma +1}}+\alpha _0}\in \mathcal{H}^{\beta }{(\Omega _{\mu })}\cap \beta \), hence \(\Psi _{\Omega _{{\sigma +1}}}({\delta })\in \mathcal{H}^{\beta }{(\Omega _{\mu })}\cap \beta \) and thus also \(\eta \in \mathcal{H}^{\beta }{(\Omega _{\mu })}\cap \beta \) which, in turn, implies \(\zeta \in \mathcal{H}^{\beta }{(\Omega _{\mu })}\cap \beta \). So \(\Psi _{\Omega _{{\mu +1}}}({\zeta })<\Psi _{\Omega _{{\mu +1}}}({\beta })\) and the claim follows from (i) by weakening. \(\square \)
4 Ordinal Analysis for Arithmetical Universes
4.1 Upper Bounds
The Collapsing Theorem together with the results of Sect. 3.3.3.2 allow us to compute upper bounds for the points in \(\textit{Spec}^{{\mathfrak M}_{\mu }}({\textsf{ID}_{\nu }({\textsf{T}})})\) where \(\textsf{T}\) is an axiomatization for the structure \({\mathfrak M}_{\mu }\) for \(0\le \mu \le \nu \). As an example we assume that \(\textsf{T}\) is a subset of \({\textsf{D}_{\mu }}\), which is the elementary diagram of \({\mathfrak M}_{\mu }\) plus the axiom for Mathematical Induction, and compute upper bounds for the points in \(\textit{Spec}^{{\mathfrak M}_{\mu }}({\textsf{ID}_{\nu }({{\textsf{D}_{\mu }}})})\). As indicated in Remark 3.35 the spectrum \(\textit{Spec}^{{\mathfrak M}_{\mu }}({{\textsf{D}_{\mu }}})\) is the singleton \(\{\varepsilon _{\Omega _{\mu }+1}\}\).
If \(\textsf{T}\) is an axiom system for \({\mathfrak M}_{\mu }\) we do not need axioms for fixed points already belonging to \({\mathfrak M}_{\mu }\). We therefore specify the axioms of \(\textsf{ID}_{\nu }({\textsf{T}})\) as follows.
- \((\text {ID}^1_\nu )\):
-
\((\forall ~\sigma )(\forall ~x)[\mu \le \sigma \,\wedge \,F(I_{F_\sigma },I_{F_{<\sigma }},\langle {x},{\sigma }\rangle )\rightarrow x\in I_{F_\sigma }]\),
- \((\text {ID}^2_\nu )\):
-
\((\forall ~\sigma ) (\forall ~x)[\mu \le \sigma \,\wedge \,F(X,I_{F_{<\sigma }},\langle {x},{\sigma }\rangle )\rightarrow x\in X]\rightarrow (\forall ~x)[x\in I_{F_\sigma }\rightarrow x\in X]\).
For an axiomatization \(\textsf{T}\) for \(\mathfrak {M}\) let \({\textbf {ID}}_\nu (\textsf{T})\) denote \(\textsf{T}\) together with the axiom schemes \(({\textbf {TI}}_\nu \)), \((\text {ID}^1_\nu )\) and \((\text {ID}^2_\nu )\).
We have \(\textit{rnk}(F^{*}) <\Omega _{\mu }+\omega \subseteq \mathcal{H}(\Omega _{\mu })=\mathcal{H}[\Omega _{\mu }](0)\) for every \({\mathscr {L}}({\mathfrak M}_{\mu })\)-sentence F and therefore by induction on \(\textit{rnk}(F^{*})\)

As in the example in Sect. 3.2.5—recall that \(\textit{rnk}(X):=\Omega _{\nu }\)—we obtain

Together with (3.23)–(3.26) we thus obtain

which by cut-elimination entails

By Theorem 3.44 this shows
For \(\mu \le \sigma <\nu \) we obtain from (3.29) by the Collapsing Theorem

which entails by Boundedness \(\sigma _F(s)\le \Psi _{\Omega _{{\sigma +1}}}({\alpha })<\Psi _{\Omega _{{\sigma +1}}}({\varepsilon _{\Omega _{\nu }+1}})\) and therefore
Remark 3.69
The technique used for the example \({\textsf{D}_{\mu }}\) seems to work for any axiom system \(\textsf{T}\) whose spectrum contains exactly one point. Call such axiom systems simple.Footnote 48 The ordinal obtained from Eq. (3.28) has to be replaced by the ordinal which is needed to derive the pseudo \(\Pi _{1}^{1}\)-sentences in \(\textsf{T}\). To illustrate this let \(\mu =0\) and assume that the proof-theoretic ordinal  has a notation in the, say fixed-point free, n-ary Veblen functions and let \(\alpha ^{(\nu )}\) be the notation which is obtained when replacing 0 by \(\Omega _{\nu }\). Then we conjecture that the technique just shown will give
has a notation in the, say fixed-point free, n-ary Veblen functions and let \(\alpha ^{(\nu )}\) be the notation which is obtained when replacing 0 by \(\Omega _{\nu }\). Then we conjecture that the technique just shown will give  and the operator \(\mathcal{H}^{\alpha ^{(\nu )}}\) as a generator of the ordinals \({\mathcal{H}^{\alpha ^{(\nu )}}}\!{(\Omega _{\mu })}\cap \Omega _{{\mu +1}}\) which represent upper bounds for the points in \(\textit{Spec}^{{\mathfrak M}}({\textsf{ID}_{\nu }({\textsf{T}})})\).Footnote 49 Clearly such a conjecture can hardly be proved in the stated generality. For many systems already the computation of
and the operator \(\mathcal{H}^{\alpha ^{(\nu )}}\) as a generator of the ordinals \({\mathcal{H}^{\alpha ^{(\nu )}}}\!{(\Omega _{\mu })}\cap \Omega _{{\mu +1}}\) which represent upper bounds for the points in \(\textit{Spec}^{{\mathfrak M}}({\textsf{ID}_{\nu }({\textsf{T}})})\).Footnote 49 Clearly such a conjecture can hardly be proved in the stated generality. For many systems already the computation of  often needs a subtle procedureFootnote 50 which has to be mirrored in the computation of
often needs a subtle procedureFootnote 50 which has to be mirrored in the computation of  . Such cases need to be checked individually.
. Such cases need to be checked individually.
Even more subtle is the situation if \(\textsf{T}\) is not simple. Here it has to be checked whether the definition of the iterations \(\textsf{ID}_{\nu }({\textsf{T}})\) makes sense at all, or whether we are not trying better to find an embedding of \(\textsf{T}\) into \(\textsf{ID}_{\nu }({\textsf{T}'})\) for a simpler axiom system \(\textsf{T}'\) and an appropriate \(\nu \). An obvious example is an axiom system \(\textsf{T}\) for \({\mathfrak M}_{\mu }\) which could be replaced by an axiom system \(\textsf{ID}_{\mu }({\textsf{T}'})+T_0\), where \(\textsf{T}'\) is an axiom system for \({\mathfrak M}\) and \(T_0\) is an appropriate subset of \({\textsf{D}_{\mu }}\) covering the additional first-order properties of \({\mathfrak M}_{\mu }\) as expressed in \(\textsf{T}\). A more complex example is the axiom system (\(\Pi _{1}^{1}\)-CA) for \(\Pi _{1}^{1}\)-comprehension formulated in (weak) second-order logic, which can be reduced to \(\textsf{ID}_{<\omega }({\mathord {\textsc {PA}}})\). The problems that may arise here are partly discussed in [8].
Further insights can be expected in the study of set-theoretic universes. First steps in these directions have been made by M. Rathjen in [35] which are based on his dissertation [34].
Another open question is if a simple axiom system coincides with systems which are metapredicative in the sense of the Berne school.Footnote 51 We guess that the answer is yes.
4.2 Lower Bounds
To obtain also lower bounds for the points in the spectrum of an axiom system we have to refer to Sect. 3.3.3.1 where we indicated that there is an elementarily definable copy of \(\mathcal{H}^{\Gamma _{\Omega _{\nu }+1}}{(\Omega _{\mu })}\) in \({\mathfrak M}_{\mu }\). We require that \(\textsf{T}\subseteq {\textsf{D}_{\mu }}\) is an acceptable axiomatization of the structure \({\mathfrak M}_{\mu }\). Then \(\textsf{T}\) is also strong enough to prove all the properties of \(\mathcal{H}^{\Gamma _{\Omega _{\nu }+1}}{(\Omega _{\mu })}\).Footnote 52 We work within the Axiom system \(\textsf{ID}_{\nu }({\textsf{T}})\). For \(\alpha \in \mathcal{H}^{{\Omega _{\nu }+1}}({\Omega _{\mu }})\) we define its strongly critical components above \(\Omega _{{\sigma +1}}\) by
For \(\mu \le \sigma <\nu \) we define
where \(\textsf{W}_{\rho }\) is the fixed point defined by the formula
Then \(\textsf{ID}_{\nu }({\textsf{T}})\) proves for \(\mu \le \sigma <\nu \)
- (A):
-
\(\alpha \in \textsf{W}_{\sigma }\leftrightarrow \alpha \in \textsf{M}_{\sigma }\,\wedge \,\textsf{M}_{\sigma }\cap \alpha \subseteq \textsf{W}_{\sigma }\)
and
- (B):
-
\((\forall ~\alpha )[\alpha \in \textsf{M}_{\sigma }\,\wedge \,\textsf{M}_{\sigma }\cap \alpha \subseteq X \rightarrow \alpha \in X]\rightarrow \textsf{W}_{\sigma }\subseteq X\).
Lemma 3.70
For \(\mu \le \sigma <\nu \) the sets \(\textsf{W}_{\sigma }\) are closed under ordinal addition.
Proof
Let \(B:={}{\{{\alpha }\,|\,{(\forall ~\xi )[\xi \in \textsf{W}_{\sigma }\rightarrow \xi +\alpha \in \textsf{W}_{\sigma }]}\}}\). Then \(\alpha \in \textsf{M}_{\sigma }\,\wedge \,\textsf{M}_{\sigma }\cap \alpha \subseteq B\) entails \(\alpha \in B\) and the claim follows by (B). \(\square \)
Lemma 3.71
For \(\mu \le \sigma <\nu \) the sets \(\textsf{W}_{\sigma }\) are closed under the Veblen functions.
Proof
Let \(B={}{\{{\alpha }\,|\,{(\forall ~\xi )[\xi \in \textsf{W}_{\sigma }\rightarrow \varphi _{\alpha }({\xi })\in \Omega _{\sigma }]}\}}\). Then \(\alpha \in \textsf{M}_{\sigma }\,\wedge \,\textsf{M}_{\sigma }\cap \alpha \subseteq B\) entails \(\alpha \in B\) and the claim follows by (B). \(\square \)
Lemma 3.72
For \(\mu \le \sigma <\nu \) and \(\alpha <\Omega _{{\sigma +1}}\) we have \(\textit{SC}_{\sigma }({\alpha })\subseteq \textsf{W}_{\sigma }\) iff \(\alpha \in \textsf{W}_{\sigma }\).
Proof
This follows from the definition of \(\textit{SC}_{\sigma }({\alpha })\) and Lemmata 3.70 and 3.71. \(\square \)
Lemma 3.73
For \(\mu \le \sigma \le \tau <\nu \) we have \(\textsf{W}_{\sigma }\subseteq \textsf{W}_{\tau }\).
Proof
We induct on \(\tau \) and assume \(\alpha \in \textsf{W}_{\sigma }\) and \(\textsf{M}_{\sigma }\cap \alpha \subseteq \textsf{W}_{\tau }\). Then \(\alpha \in \textsf{M}_{\sigma }\), hence \(\textit{SC}_{\rho }({\alpha })\subseteq \textsf{W}_{\rho }\) for \(\mu \le \rho <\sigma \). For \(\sigma \le \rho <\tau \) we get \(\alpha \in \textsf{W}_{\rho }\) by induction hypothesis, hence \(\textit{SC}_{\sigma }({\alpha })\subseteq \textsf{W}_{\rho }\) by Lemma 3.72. So \(\alpha \in \textsf{M}_{\tau }\) holds true. It is \(\textsf{M}_{\tau }\cap \alpha \subseteq \textsf{M}_{\sigma }\cap \alpha \subseteq \textsf{W}_{\tau }\), hence \(\alpha \in \textsf{W}_{\tau }\). By (B) we get \(\textsf{W}_{\sigma }\subseteq \textsf{W}_{\tau }\). \(\square \)
Lemma 3.74
It is \(\textsf{M}_{\nu }\cap \Omega _{\nu }=\bigcup {}{\{{\textsf{W}_{\sigma }}\,|\,{\mu \le \sigma <\nu }\}}\).
Proof
If \(\alpha \in \textsf{M}_{\nu }\cap \Omega _{\nu }\) then \(\alpha <\Omega _{{\sigma +1}}\) and \(\alpha \in \textsf{W}_{\sigma }\) for some \(\mu \le \sigma <\nu \) by Lemmata 3.72 and 3.73. Hence \(\alpha \in \bigcup {}{\{{\textsf{W}_{\sigma }}\,|\,{\mu \le \sigma <\nu }\}}\). If \(\alpha \in \textsf{W}_{\sigma }\subseteq \textsf{M}_{\sigma }\cap \Omega _{{\sigma +1}}\) for some \(\mu \le \sigma <\nu \) then \(\textit{SC}_{\rho }({\alpha })\subseteq \textsf{W}_{\rho }\) for all \(\rho <\sigma \) and \(\textit{SC}_{\rho }({\alpha })\subseteq \textsf{W}_{\rho }\) for all \(\sigma \le \rho <\nu \) by Lemmata 3.73 and 3.72. Hence \(\alpha \in \textsf{M}_{\nu }\cap \Omega _{\nu }\). \(\square \)
Lemma 3.75
For \(\mu \le \sigma <\nu \) we have \(\Omega _{\sigma }\in \textsf{W}_{\sigma }\).
Proof
\(\Omega _{\sigma }\in \textsf{M}_{\sigma }\) holds trivially by definition of \(\textit{SC}_{\sigma }({\Omega _{\sigma }})\). For \(\alpha \in \textsf{M}_{\sigma }\cap \Omega _{\sigma }\) there is a \(\rho <\sigma \) such that \(\alpha <\Omega _{{\rho +1}}\) and \(\textit{SC}_{\rho }({\alpha })\subseteq \textsf{W}_{\rho }\subseteq \textsf{W}_{\sigma }\). Hence \(\Omega _{\sigma }\in \textsf{W}_{\sigma }\) by Lemma 3.72 and (A). \(\square \)
Lemma 3.76
(Condensing Lemma) Let \(\mu \le \rho \le \sigma <\nu \) and \(\alpha \in \textsf{W}_{\sigma }\). Then \(\Psi _{\Omega _{{\rho +1}}}({\alpha })\in \textsf{W}_{\rho }\) holds true for all \(\alpha \in \mathcal{H}^{\alpha }{(\Omega _{\rho })}\).
Proof
Let \(\quad B_\sigma :={}{\{{\alpha }\,|\,{(\forall ~\rho )[\mu \le \rho \le \sigma \,\wedge \,\alpha \in \mathcal{H}^{\alpha }{(\Omega _{\rho })} \rightarrow \Psi _{\Omega _{{\rho +1}}}({\alpha })\in \textsf{W}_{\rho }]}\}}\)
and assume \(\alpha \in \textsf{M}_{\sigma }\) as well as \(\textsf{M}_{\rho }\cap \alpha \subseteq B_\sigma \), i.e.
-
(i)
\((\forall ~\rho )[\mu \le \rho \le \sigma \,\wedge \,\xi \in \textsf{M}_{\rho }\cap \alpha \,\wedge \,\xi \in \mathcal{H}^{\xi }{(\Omega _{\rho })}\rightarrow \Psi _{\Omega _{{\rho +1}}}({\xi })\in \textsf{W}_{\rho }]\).
We want to show \(\alpha \in B_\sigma \), i.e.
-
(ii)
\((\forall ~\rho )[\mu \le \rho \le \sigma \,\wedge \,\alpha \in \mathcal{H}^{\alpha }{(\Omega _{\rho })}\rightarrow \Psi _{\Omega _{{\rho +1}}}({\alpha })\in \ \textsf{W}_{\rho }]\).
By (A) it suffices to show
\(\quad \Psi _{\Omega _{{\rho +1}}}({\alpha })\in \textsf{M}_{\rho }\,\wedge \,\textsf{M}_{\rho }\cap \Psi _{\Omega _{{\rho +1}}}({\alpha })\subseteq \textsf{W}_{\rho }\) for \(\mu \le \rho \le \sigma \).
For \(\tau <\rho \le \sigma \) we have \(\textit{SC}_{\tau }({\Psi _{\Omega _{{\rho +1}}}({\alpha })})=\textit{SC}_{\tau }({\alpha })\subseteq \textsf{W}_{\tau }\), hence \(\Psi _{\Omega _{{\rho +1}}}({\alpha })\in \textsf{M}_{\rho }\). Assume \(\xi \in \textsf{M}_{\rho }\cap \Psi _{\Omega _{{\rho +1}}}({\alpha })\). We prove \(\xi \in \textsf{W}_{\rho }\) by induction on the definition of \(\xi \in \mathcal{H}^{\Gamma _{\Omega _{\nu }+1}}{(\Omega _{\mu })}\). If \(\xi \) is not strongly critical this follows immediately from the induction hypothesis and Lemmas 3.70 or 3.71, respectively. If \(\xi =\Omega _{\zeta }\) then \(\Omega _{\zeta }\le \Omega _{\rho }\) and we can apply Lemma 3.75. If \(\xi =\Psi _{\Omega _{{\tau +1}}}({\beta })\) then \(\tau \le \rho \) and \(\beta \in \mathcal{H}^{\beta }{(\Omega _{\tau })}\cap \alpha \). If \(\tau <\rho \) then \(\xi <\Omega _{\rho }\in \textsf{W}_{\rho }\). If \(\tau =\rho \) then \(\textit{SC}_{\zeta }({\beta })=\textit{SC}_{\zeta }({\Psi _{\Omega _{{\tau +1}}}({\beta })})\subseteq \textsf{W}_{\zeta }\) for all \(\zeta <\rho \). Hence \(\beta \in \textsf{M}_{\rho }\cap \alpha \) and \(\Psi _{\Omega _{{\rho +1}}}({\beta })\in \textsf{W}_{\rho }\) by (i). So we have \(\Psi _{\Omega _{{\rho +1}}}({\alpha })\subseteq \textsf{W}_{\rho }\), hence \(\alpha \in B_\sigma \). If \(\alpha \in \textsf{M}_{\sigma }\) and \(\textsf{M}_{\sigma }\cap \alpha \subseteq B_\sigma \) and \(\rho \le \sigma \) we also have \(\textsf{M}_{\rho }\cap \alpha \subseteq B_\sigma \), hence \(\alpha \in \ B_\sigma \), as we have just seen. By (B) it follows \(\textsf{W}_{\sigma }\subseteq B_\sigma \) which is the claim. \(\square \)
Let
express transfinite induction along \(\textsf{M}_{\nu }\) up to \(\alpha \).
Theorem 3.77
(Condensing Theorem) Let \(\mu \le \sigma <\nu \). Then \(\mathord { TI}({X,\textsf{M}_{\nu }},{\alpha })\) and \(\alpha \in \mathcal{H}^{\alpha }{(\Omega _{\sigma })}\) entail \(\Psi _{\Omega _{{\sigma +1}}}({\alpha })\in \textsf{W}_{\sigma }\).
Proof
By (A) we have \((\forall ~\xi )[\textsf{M}_{\sigma }\cap \xi \subseteq \textsf{W}_{\sigma }\leftrightarrow \xi \in \textsf{W}_{\sigma }]\). Since \(\alpha \in \textsf{M}_{\nu }\cap \Omega _{{\sigma +1}}\) implies \(\alpha \in \textsf{M}_{\sigma }\) we get from \(\mathord { TI}({X,\textsf{M}_{\nu }},{\alpha })\) first \(\textsf{M}_{\nu }\cap \alpha \subseteq \textsf{W}_{\sigma }\) and thus \(\alpha \in \textsf{W}_{\sigma }\). Together with \(\alpha \in \mathcal{H}^{\alpha }{(\Omega _{\sigma })}\) this implies by Lemma 3.76 \(\Psi _{\Omega _{{\sigma +1}}}({\alpha })\in \textsf{W}_{\sigma }\). \(\square \)
Theorem 3.78
\(\mathord { TI}({X,\textsf{M}_{\nu }},{\Omega _{\nu }})\).
Proof
Assume \(\alpha \in \textsf{M}_{\nu }\cap \Omega _{\nu }\) then we have \(\textit{SC}_{\rho }({\alpha })\subseteq \textsf{W}_{\rho }\), hence \(\alpha \in \textsf{W}_{\rho }\), for all \(\mu \le \rho <\sigma \). From \((\forall ~\xi )[\textsf{M}_{\nu }\cap \xi \subseteq X\rightarrow \xi \in X]\) we get by (B) \(\textsf{W}_{\rho }\subseteq X\), hence \(\alpha \in X\). \(\square \)
Let \(\omega ^{(0)}(\Omega _{\nu })={\Omega _{\nu }+1}\) and \(\omega ^{(n+1)}(\Omega _{\nu })=\omega ^{\omega ^{(n)}(\Omega _{\nu })}\). Having the axiom of Mathematical Induction among the axioms of \(\textsf{T}\) we can use the familiar Gentzen technique to prove \(\mathord { TI}({X,\textsf{M}_{\nu }},{\omega ^{(n)}(\Omega _{\nu })})\) for all finite n. This entails \(o^{{\mathfrak M}_{{\mu +1}}}(\textsf{ID}_{\nu }({\textsf{T}}))\ge \Psi _{\Omega _{{\mu +1}}}({\varepsilon _{\Omega _{\nu }+1}})\) for all acceptable axiom systems \(\textsf{T}\) for \({\mathfrak M}_{\mu }\) which contain the axiom of Mathematical Induction. As a summary of Sects. 3.4.1 and 3.4.2 we have the following theorem.
Theorem 3.79
Let \(\textsf{T}\subseteq {\textsf{D}_{\mu }}\) be an acceptable axiomatization for the structure \({\mathfrak M}_{\mu }\). Then we obtain for \(0\le \mu \le \nu \)
Remark 3.80
The proof of the lower bound also may carry over to simple axiom systems.Footnote 53 If \(\textsf{T}\) is a simple axiom system with  then there regularly is a fundamental sequence \({}{\big \langle {\alpha _n}\,|\,{n<\omega }\big \rangle }\), converging to \(\alpha \), such that
then there regularly is a fundamental sequence \({}{\big \langle {\alpha _n}\,|\,{n<\omega }\big \rangle }\), converging to \(\alpha \), such that  implies
implies  . This has to be converted into a sequence \({}{\big \langle {\alpha _n^{(\nu )}}\,|\,{n\in \omega }\big \rangle }\) such that
. This has to be converted into a sequence \({}{\big \langle {\alpha _n^{(\nu )}}\,|\,{n\in \omega }\big \rangle }\) such that  implies
implies  while
while  holds trivially. By condensing this yields lower bounds for the points in the spectrum of \(\textsf{ID}_{\nu }({\textsf{T}})\). Together with Remark 3.69 we may therefore conjecture that
holds trivially. By condensing this yields lower bounds for the points in the spectrum of \(\textsf{ID}_{\nu }({\textsf{T}})\). Together with Remark 3.69 we may therefore conjecture that
holds true for (most?) simple axiom systems \(\textsf{T}\).
Again this is a coarse conjecture which is probably unprovable in full generality. Nevertheless we think that there are good reasons why the computation of the spectral points works in a very general manner. Of course we are aware that there are axiom systems \(\textsf{T}\) for which the “well-ordering proof” (i.e. the computation of the lower bound) is so sophisticated that its conversion into a \(\textsf{ID}_{\nu }({\textsf{T}})\) proof is not straightforward and may need careful checking.
5 Provably Recursive Functions
We return to Note 3.30 in which we have briefly touched generalized recursive functions.
Definition 3.81
Let \({\mathfrak S}\) be a Spector structure above a structure \(\mathfrak {M}\).  a partial n-ary function and \(\mathscr {G}_{f}:={}{\{{\langle {{\vec x}},{y}\rangle }\,|\,{{\vec x}\in M^n\,\wedge \,f({\vec x})\simeq y}\}}\) its graph. We say that f is partial \({\mathfrak S}\)-recursive, if \(\mathscr {G}_{f}\) is a relation in \({\mathfrak S}\). Let \({\mathscr {R}}_p({\mathfrak S})\) denote the set of partial \({\mathfrak S}\)-recursive functions and \({\mathscr {R}}({\mathfrak S})\) denote the set of \({\mathfrak S}\)-recursive functions, i.e. the functions in \({\mathscr {R}}_p({\mathfrak S})\) which are total. For an axiomatization \(\textsf{T}\) of a countable Spector structure \({\mathfrak S}\) let
a partial n-ary function and \(\mathscr {G}_{f}:={}{\{{\langle {{\vec x}},{y}\rangle }\,|\,{{\vec x}\in M^n\,\wedge \,f({\vec x})\simeq y}\}}\) its graph. We say that f is partial \({\mathfrak S}\)-recursive, if \(\mathscr {G}_{f}\) is a relation in \({\mathfrak S}\). Let \({\mathscr {R}}_p({\mathfrak S})\) denote the set of partial \({\mathfrak S}\)-recursive functions and \({\mathscr {R}}({\mathfrak S})\) denote the set of \({\mathfrak S}\)-recursive functions, i.e. the functions in \({\mathscr {R}}_p({\mathfrak S})\) which are total. For an axiomatization \(\textsf{T}\) of a countable Spector structure \({\mathfrak S}\) let

denote the set of \({\mathfrak S}\)-recursive functions whose totality is provable in \(\textsf{T}\). Then \({\mathscr {R}}^{{\mathfrak S}}(\textsf{T})\) is a subset of \({\mathfrak S}\) and we have \(o({\mathscr {R}}^{{\mathfrak S}}(\textsf{T}))\le o({\mathscr {R}}({\mathfrak S}))\le o({\mathfrak S})\) by Definition 3.25.
Given an axiomatization \(\textsf{T}\) of a countable structure \(\mathfrak {M}\) we obviously have for \(\mu \ge 0\) \(o({\mathscr {R}}^{{\mathfrak M}{\mu +1}}(\textsf{ID}_{\nu }({\textsf{T}})))\le o^{{\mathfrak M}_{{\mu +1}}}(\textsf{ID}_{\nu }({\textsf{T}}))\). As a corollary to Eq. (3.32) we obtain for \(\mu \ge 0\)
for any axiom system \(\textsf{T}\subseteq {\textsf{D}_{0}}\). For the proof of Theorem 3.79 we defined a sequence \({}{\big \langle {\alpha _n}\,|\,{n\in \omega }\big \rangle }\) of ordinal terms such that \(\alpha _n\in \mathcal{H}^{\varepsilon _{\Omega _{\nu }+1}}({\Omega _{0}})\) and \(\sup _{n\in \omega }\alpha _n=\varepsilon _{\Omega _{\nu }+1}\). In an acceptable structure \({\mathfrak M}\) we thus obtain by primitive recursion a function F such that
 where \({\mathscr {N}}\) denotes the copy of the natural numbers in \({\mathfrak M}\) and
where \({\mathscr {N}}\) denotes the copy of the natural numbers in \({\mathfrak M}\) and
 codes \(\alpha _n\). Let
codes \(\alpha _n\). Let

Putting
 , we obtain functions \({}{{f_\mu :\, {\mathscr {N}} \, \longrightarrow \, }{\mathfrak M}_{\mu }}\)Footnote 54
, we obtain functions \({}{{f_\mu :\, {\mathscr {N}} \, \longrightarrow \, }{\mathfrak M}_{\mu }}\)Footnote 54

In Theorems 3.79 and 3.76 we have shown that for any acceptable axiom system \(\textsf{T}\subseteq {\textsf{D}_{0}}\) we obtain

and

for \(0\le \mu <\nu \). Since \(\textsf{W}_{\nu }:={}{\{{\xi }\,|\,{\mathord { TI}(X,\textsf{M}_{\nu },\xi )}\}}\in {\mathbb {S}}{\mathbb {P}}_{{\mathfrak M}_{\nu }}={\mathfrak M}_{\nu +1}\)Footnote 55 and \(\textsf{W}_{\mu }\in {\mathfrak M}_{{\mu +1}}\) the functions \(f_\mu \) are \({\mathfrak M}_{{\mu +1}}\)-recursive for \(0\le \mu \le \nu \) and we have
Hence \(o({\mathscr {R}}^{{\mathfrak M}_{\nu +1}}(\textsf{ID}_{\nu }({\textsf{T}})))\ge \varepsilon _{\Omega _{\nu }+1}\) and \(o({\mathscr {R}}^{{\mathfrak M}_{{\mu +1}}}(\textsf{ID}_{\nu }({\textsf{T}})))\ge \Psi _{\Omega _{{\mu +1}}}({\varepsilon _{\Omega _{\nu }+1}})\) for \(0\le \mu <\nu \) and thus
for \(\mu \le \nu \). To sum up we have the following characterization of the \({\mathfrak M}_{{\mu +1}}\)-recursive functions whose totality is provable in \(\textsf{ID}_{\nu }({\textsf{T}})\).
Theorem 3.82
Let \(\mathfrak {M}\) be a countable acceptable structure and \(\textsf{T}\subseteq {\textsf{D}_{0}}\) an acceptable axiomatization of \({\mathfrak M}\). Then \(\textit{Spec}^{{\mathfrak M}}({\textsf{ID}_{\nu }({\textsf{T}})})= {}{\{{o({\mathscr {R}}^{{\mathfrak M}_{{\mu +1}}}(\textsf{ID}_{\nu }({\textsf{T}})))}\,|\,{\mu \le \nu }\}}={}{\{{\mathcal{H}^{\varepsilon _{\Omega _{\nu }+1}}{(\Omega _{\mu })}\cap \Omega _{{\mu +1}}}\,|\,{\mu \le \nu }\}}\).
The combinatorial power of a structure \({\mathfrak M}\) is manifested in the \(\Pi ^0_2\)-sentences which are valid in \(\mathfrak {M}\). The functions in \({\mathscr {R}}(\mathfrak {M})\) comprise the \(\Pi ^0_2\)-Skolem functions of the structure \(\mathfrak {M}\). The combinatorial power of an axiom system \(\textsf{T}\) for \(\mathfrak {M}\) is therefore quite well characterized by the set \({\mathscr {R}}^{{\mathfrak M}}(\textsf{T})\). Theorem 3.82 therefore shows that \(\textit{Spec}^{\mathfrak {M}}({\textsf{ID}_{\nu }({\textsf{T}})})\) is a pretty good measure for the combinatorial strength of \(\textsf{ID}_{\nu }({\textsf{T}})\) in relation to the hierarchy of Spector structures \({\mathfrak M}_{{\mu +1}}\) above \(\mathfrak {M}\) for \(\mu \le \nu \). We moreover see that for axiom systems \(\textsf{ID}_{\nu }({\textsf{T}})\) with \(\textsf{T}\subseteq {\textsf{D}_{0}}\) this spectrum is generated by the operator \(\mathcal{H}^{\varepsilon _{\Omega _{\nu }+1}}\). The conjecture is that this result can be extended to simple axiom systems \(\textsf{T}\) with  , for which the spectrum is generated by \(\mathcal{H}^{\alpha ^{(\nu )}}\). It is therefore a reasonable statement that the operator \(\mathcal{H}^{\alpha ^{(\nu )}}\) is a fairly good measure for the performance of the axiom system \(\textsf{ID}_{\nu }({\textsf{T}})\).
, for which the spectrum is generated by \(\mathcal{H}^{\alpha ^{(\nu )}}\). It is therefore a reasonable statement that the operator \(\mathcal{H}^{\alpha ^{(\nu )}}\) is a fairly good measure for the performance of the axiom system \(\textsf{ID}_{\nu }({\textsf{T}})\).
In computing \(o^{{\mathfrak M}_{{\mu +1}}}(\textsf{ID}_{\nu }({\textsf{T}}))\) we encounter the same phenomenon as in the example in Sect. 3.2.5. The results of Sects. 3.4.1 and 3.4.2 show that
holds true for \(\sigma \le \mu \le \nu \). Therefore it is not possible to enhance the performance of \(\textsf{ID}_{\nu }({\textsf{T}})\) with respect to Spector classes \({\mathfrak M}_{{\mu +1}}\) for \(\mu \ge \sigma \) by adding true \({\mathfrak M}_{\sigma }\)-sentences.Footnote 56
The obvious, not yet answered question is the case \(\mu =0\). In general, \({\mathfrak M}_{0}\) is not a Spector structure but we may ask if \(\mathcal{H}^{\varepsilon _{\Omega _{\nu }+1}}\) may help to characterize the class \({\mathscr {R}}(\textsf{ID}_{\nu }({\textsf{T}}))\) of general recursive functions which \(\textsf{ID}_{\nu }({\textsf{T}})\) proves to be total. The answer is yes. Unfortunately, the remaining space does not allow us to respond fully to it. Therefore we just report the result for a Peano-like axiomatization.Footnote 57
The key notions are again Skolem-hull operators and their iterations. According to Sect. 3.3.3.1 the sets \(\mathcal{H}^{{\Omega _{\nu }+1}}({\Omega _{\mu }})\) are definable by an inductive definition with closure ordinal \(\omega \). Therefore we have an inductive norm \(N_{\mu }(\alpha )<\omega \) for any \(\mathcal{H}^{{\Omega _{\nu }+1}}({\Omega _{\mu }})\). Given a primitive recursive start function \({}{{\Phi :\, {\mathscr {N}} \, \longrightarrow \, }{\mathscr {N}}}\) which is sufficiently strongly increasingFootnote 58 we define the function
For \(\mu =0\) there are only finitely many \(\beta \) such that \(N_{0}(\beta )\le \Phi (N_{0}(\alpha ))\) below \(\alpha \). Hence \(\phi (\alpha ):=\phi ^0(\alpha )<\omega \) holds true for all \(\alpha \in \mathcal{H}^{\varepsilon _{\Omega _{\nu }+1}}(0)\). Any ordinal has the form \(\omega \mathrel {\cdot }\alpha +n\) where \(n<\omega \) is its finite remainder. Defining
we obtain a hierarchy of functions \({}{{\Phi _\alpha :\, {\mathscr {N}} \, \longrightarrow \, }{\mathscr {N}}}\), which for finite \(\alpha \) approximately coincides with the \(\alpha \)th iteration \(\Phi ^\alpha \) of the function \(\Phi \). For \(\alpha <\omega \) we get \(\Phi ^\alpha (x)\le \Phi _\alpha (x)\le \Phi ^\alpha (2x+\alpha )+\alpha \). So \(\Phi _\alpha \) represents a subrecursive hierarchy of functions whose initial part essentially coincides with the so-called “fast growing” hierarchy.Footnote 59
By a refinement of the collapsing procedure in Sect. 3.3.3.3, applied to “fragmented operator controlled derivations” in which we also have to count the constants in \({\mathscr {N}}\) occurring in a formula F among the parameters of F, we can finally show that the provably recursive functions in \({\mathscr {R}}^{\mathfrak {M}}(\textsf{ID}_{\nu }({\textsf{T}}))\) are exactly the functions which are primitive recursive in the functions \({}{\big \langle {\Phi _\alpha }\,|\,{\alpha <\Psi _{\Omega _{1}}({\varepsilon _{\Omega _{\nu }+1}})}\big \rangle }\)Footnote 60 and this includes the case \(\nu =0\), i.e. a characterization of the recursive functions that are provably in \(\textsf{T}\).
The hierarchy \(\Phi _\alpha \) depends upon the starting function \(\Phi \). But this dependence is not very sensitive. Thus, for example, the hierarchies for different (sufficiently increasing) primitive recursive starting functions quickly catch up and yield the same hierarchies at ordinals far below \({\varepsilon _0}\). Nevertheless, the “No Enhancement Theorem” is not applicable for \({\mathscr {R}}(\textsf{ID}_{\nu }({\textsf{T}}))\). For example, while \({\mathscr {R}}(\textsf{ID}_{\nu }({\mathord {\textsc {PA}}}))\) consists of the functions that are primitive recursive in the hierarchy \({}{\big \langle {\Phi _\alpha }\,|\,{\alpha <\Psi _{\Omega _{1}}({\varepsilon _{\Omega _{\nu }+1}})}\big \rangle }\), already the set \({\mathscr {R}}({\textsf{D}_{0}})\), and thus also \({\mathscr {R}}(\textsf{ID}_{\nu }({{\textsf{D}_{0}}}))\), contains all the recursive functions on the natural numbers although \(\textit{Spec}^{{\mathfrak N}}({\textsf{ID}_{\nu }({{\textsf{D}_{0}}})})\) and \(\textit{Spec}^{{\mathfrak N}}({\textsf{ID}_{\nu }({\mathord {\textsc {PA}}})})\) coincide.
So \({\mathscr {R}}(\textsf{ID}_{\nu }({\textsf{T}}))\) depends upon the \({{\mathscr {L}}(\mathfrak {M})}\)-sentences in \(\textsf{T}\). Let us assume for the moment that the structure \(\mathfrak {M}\) (besides equality) only contains functions and \(\textsf{T}\) is an acceptable axiom system for \(\mathfrak {M}\) with  which comprises the defining equations for a subset \({\mathscr {F}}\) of the functions in \(\mathfrak {M}\). Then we can pick any sufficiently increasing starting function \({}{{\Phi :\, M \, \longrightarrow \, }M}\), which is primitive recursive in \({\mathscr {F}}\), to obtain \({\mathscr {R}}(\textsf{T})\) as the set of functions which are primitive recursive in the sequence \({}{\big \langle {\Phi _\xi }\,|\,{\xi <\alpha }\big \rangle }\).
which comprises the defining equations for a subset \({\mathscr {F}}\) of the functions in \(\mathfrak {M}\). Then we can pick any sufficiently increasing starting function \({}{{\Phi :\, M \, \longrightarrow \, }M}\), which is primitive recursive in \({\mathscr {F}}\), to obtain \({\mathscr {R}}(\textsf{T})\) as the set of functions which are primitive recursive in the sequence \({}{\big \langle {\Phi _\xi }\,|\,{\xi <\alpha }\big \rangle }\).
On the other hand the hierarchy \({}{\big \langle {\Phi _\xi }\,|\,{\xi <\alpha }\big \rangle }\) also depends on the norm function on the ordinals. If, however, the proof-theoretic ordinal is obtained by application of a Skolem-hull operator, this norm is canonically given by the inductive definition of the Skolem-hull of 0. It is perhaps a remarkable fact that even for simple axiom systems, which need no collapsing procedure in the computation of their spectra, the characterization of the provably recursive functions can be pretty uniformly obtained via a collapsing technique using a Skolem-hull operator which, of course, in general is weaker than \(\mathcal{H}\). In the case of the Peano axioms, for example, the operator \(\mathcal{A}_0\) would suffice, which is generated by the functions \(\{0\}\), \(+\) and \(\lambda \xi .\ \omega ^\xi \). Then  Footnote 61 and \({\mathscr {R}}(\mathord {\textsc {PA}})\) is the set of functions which are primitive recursive in the sequence \({}{\big \langle {\Phi _\xi }\,|\,{\xi <{\varepsilon _0}}\big \rangle }\) for any sufficiently increasing primitive recursive starting function \(\Phi \).
Footnote 61 and \({\mathscr {R}}(\mathord {\textsc {PA}})\) is the set of functions which are primitive recursive in the sequence \({}{\big \langle {\Phi _\xi }\,|\,{\xi <{\varepsilon _0}}\big \rangle }\) for any sufficiently increasing primitive recursive starting function \(\Phi \).
In this sense we can claim that not the bare proof-theoretic ordinal  but the Skolem-hull operator which is needed in the computation of
but the Skolem-hull operator which is needed in the computation of  carries the information about the performance of \(\textsf{T}\) in relation to the ground structure \({\mathfrak M}\).
carries the information about the performance of \(\textsf{T}\) in relation to the ground structure \({\mathfrak M}\).
6 Conclusion
In this paper we tried to clarify in how far the proof-theoretic ordinal can be regarded as a measure for the performance of an axiom system for a countable acceptable structure \(\mathfrak {M}\). Though \({\mathfrak N}\), the structure of natural numbers, is the paradigmatic example for such structures, we tried to do this in a more general framework. In some cases, however, we had to restrict ourselves to strictly acceptable structures which allow for an elementary definition of their verification tree and thus are even more “standard like” than countable acceptable structures in general. A central observation is the “No Enhancement Theorem” which shows that the proof-theoretic ordinal of \(\textsf{T}\) is rather a measure for the performance of \(\textsf{T}\) in relation to a universe above \(\mathfrak {M}\) than for the basis structure \(\mathfrak {M}\) itself.
For this paper we decided to concentrate on the study of countable “analytic universes” above \(\mathfrak {M}\), which are countable subsets of the powerset of \(\mathfrak {M}\) with sufficient closure properties. Good candidates for universes with sufficient closure properties are Spector classes above \(\mathfrak {M}\) whose closure properties allow for a generalization of computability. We get the least Spector class above \(\mathfrak {M}\) as slices of fixed points of operators on the powerset of \(\mathfrak {M}\) which are positively definable in \(\mathfrak {M}\). In turn, the theory of fixed points of positively definable operators is easily formalizable in first-order logic with additional constants for fixed points. So we were able to concentrate on the study of the formal theories \(\textsf{ID}_{\nu }({\textsf{T}})\) of \(\nu \)-fold iterated inductive definitions. Although these theories have already been extensively studied in the past we have—also for the sake of more completeness—outlined their essential features from the angle of their performance in relation to Spector classes above \(\mathfrak {M}\).
This leads to the definition of a spectrum \(\textit{Spec}^{\mathfrak {M}}({\textsf{ID}_{\nu }({\textsf{T}})})\) of characteristic ordinals which is generated by the \(\alpha \)th iteration \(\mathcal{H}^\alpha \) of a Skolem-hull operator \(\mathcal{H}\) where the ordinal \(\alpha \) is computable from the proof-theoretic ordinal of \(\textsf{T}\) in relation to the basis structure \(\mathfrak {M}\). The spectrum \(\textit{Spec}^{\mathfrak {M}}({\textsf{ID}_{\nu }({\textsf{T}})})\) reflects the combinatorial power of \(\textsf{ID}_{\nu }({\textsf{T}})\) in so far, that it characterizes the \(\textsf{ID}_{\nu }({\textsf{T}})\)-provably \({\mathfrak M}_{\mu }\)-recursive functions on \(\mathfrak {M}\) in terms of their \({\mathfrak M}_{\mu }\)-norms.
By an refinement of the collapsing technique, which is needed in the computation of the spectrum, this can even be extended to a characterization of the \(\textsf{ID}_{\nu }({\textsf{T}})\)-provably recursive function on \({\mathfrak M}\) in terms of a subrecursive hierarchy generated by the operator \(\mathcal{H}^\alpha \).
By a similar refined collapsing technique we can also characterize the recursive functions whose totality is provable from a simple axiom system\(\textsf{T}\), whose spectrum is a singleton and thus does not need a collapsing technique in its computation. Here again the \(\textsf{T}\)-provably recursive functions are characterized by a subrecursive hierarchy which is generated by an operator whose closure ordinal, i.e. the first ordinal which cannot be reached by the operator is the proof-theoretic ordinal  . If not the bare proof-theoretic ordinal, so yet the operator which leads to the proof-theoretic ordinal, actually carries some information about the performance of \(\textsf{T}\) in relation to \(\mathfrak {M}\).
. If not the bare proof-theoretic ordinal, so yet the operator which leads to the proof-theoretic ordinal, actually carries some information about the performance of \(\textsf{T}\) in relation to \(\mathfrak {M}\).
The theories \(\textsf{ID}_{\nu }({\textsf{T}})\) can therefore be viewed as a yardstick for axiomatizations of universes above a basic structure \(\mathfrak {M}\). Applications as yardstick are already included in [8]. More examples of embeddings of second-order theories for universes above \({\mathfrak N}\) into iterated inductive definitions have been given in [28] and partially corrected in [12]. There we included already the first steps towards the use of set-theoretic axioms for universes above \(\mathfrak {M}\) as yardsticks. We think that on the long run this is the better and farer reaching perspective. Its basic principles will be compiled in a forthcoming paper.
Notes
- 1.
By the elementary language of a structure we understand the basis language of \(\mathfrak {M}\). This is in principle always a first-order language. However, it does not exclude many sorted first-order languages, e.g. weak second-order languages.
- 2.
The properties of the ordinal \(\pi ^{\mathfrak M}\) are studied in [31]. In case that the structure \({\mathfrak M}\) is the structure \({\mathfrak N}\) of arithmetic, we get \(\pi ^{\mathfrak N}=\omega _1^{\hbox {\tiny CK}}\).
- 3.
This theorem, in a different formulation, already appears in [15].
- 4.
By a pseudo \(\Pi _{1}^{1}\)-sentence we understand a formula in the elementary language of \({\mathfrak M}\), which must not contain free first-order variables but may well contain free second-order variables. Semantically pseudo \(\Pi _{1}^{1}\)-sentences are treated as \(\Pi _{1}^{1}\)-sentences.
- 5.
That similarly \(\pi ^\mathfrak {M}\) is characteristic rather for an universe above \(\mathfrak {M}\) than for \({\mathfrak M}\) itself follows from Sect. 5 in [31].
- 6.
Therefore many of the mathematical results presented here are not new. Most of them are already contained in [33] but are presented here in a different context.
- 7.
- 8.
- 9.
Therefore, in some sense, we are selling “old wine in new skins”. Nevertheless we decided to include—at least extended sketches of—many of the old proofs. First, of course, to make the paper more self-contained and thus retain the survey character of the paper. Secondly because in many cases the central ideas of the proofs are helpful (or even needed) to make our approach transparent.
- 10.
Here one should observe that the spectrum of an axiomatization \(\textsf{ID}_{\nu }({\textsf{T}})\) for \({\mathfrak M}_{\nu }\) also comprises the ordinal \(\pi ^{{\mathfrak M}_{\nu }}(\textsf{ID}_{\nu }({\textsf{T}}))\).
- 11.
Introduced in Sect. 3.3.3.
- 12.
A more elaborated sketch is in [33].
- 13.
For a complete proof cf. e.g. [31] Theorem 4.4.
- 14.
By an axiomatization of \({\mathfrak M}\) we understand a set \(\textsf{T}\) of \({\mathscr {L}}(\mathfrak {M})\)-sentences such that \(\mathfrak {M}\models \textsf{T}\).
- 15.
This is just because any axiom system \(\textsf{T}\) is consistent iff there is a formula F such that \(\textsf{T}\not \vdash F\).
- 16.
A full proof is given in [1].
- 17.
This implies that the well-ordering on the countable domain of \({\mathfrak M}\) is elementarily definable.
- 18.
Cf. Sects. 5.3 and 5.4 in [31].
- 19.
To what extend the ordinal
 also has a meaning for the ground structure \(\mathfrak {M}\) will be briefly touched in Sect. 3.5.
also has a meaning for the ground structure \(\mathfrak {M}\) will be briefly touched in Sect. 3.5. - 20.
Rumor has it that this observation is due to Kreisel. Unfortunately I know no reference.
- 21.
This is familiar from “Reverse Mathematics” as, e.g. presented in [38]. The increasing strength of the axiom systems treated there is due to additional set-existence axioms.
- 22.
To distinguish Analysis in the meaning of “Real Analysis” from analysis in concepts such as “ordinal analysis” we capitalize Analysis, whenever we mean it in the former sense.
- 23.
Spector classes are introduced in [24] Chap. 9.
- 24.
In abuse of notation we will often use \({\vec x}\in R\) and \(R({\vec x})\) synonymously.
- 25.
For strictly acceptable structures \(\mathfrak {M}\) and acceptable axiom systems \(\textsf{T}\) which prove Weak König’s Lemma we always have \(\delta ^{\mathfrak M}(\textsf{T})=\kappa ^{\mathfrak M}(\textsf{T})\) (cf. [30] Thm. 6.7).
- 26.
The lack of direct access to ordinals in \({\mathscr {L}}^2(\mathfrak {M})\) is one of the reasons why ordinal analysis shifted from the study of analytical universes to the study of set-theoretic universes in which ordinal numbers occur naturally (cf. [32] for a brief overview).
- 27.
- 28.
- 29.
Cf. [25] Sect. 8.
- 30.
Cf. [36].
- 31.
Although some proof-theoretic ordinals are known via embeddings into set-theoretic universes.
- 32.
Hence the notation \(\kappa ^\mathfrak {M}_{\mu +1}\).
- 33.
Cf. e.g. [27] Sect. 7.2.
- 34.
The proof of the modification follows in principle the same pattern as the proof of Theorem 3.14. Because of the more blurred estimate \(2^\alpha \) it is even a bit easier and does not need the notion of co-enumeration. However, the extra 2-power is indispensable.
- 35.
An assumption that will be substantiated later.
- 36.
This axiom system is essentially the axiom system for iterated inductive definitions as introduced by Sol Feferman in [8].
- 37.
Cf. [22].
- 38.
- 39.
Observe that \(\mu \) in the derived formula stands for the ordinal notation and \(\mu \) in the derivation height for its order-type in \(\prec \).
- 40.
- 41.
By \(\aleph \) we denote the enumerating function of the infinite cardinals. As usual we write \(\aleph _\mu \) instead of \(\aleph (\mu )\).
- 42.
This is the familiar diagonal argument.
- 43.
Cf. e.g. [24] Theorem 2B.1.
- 44.
Cf. [5] for a survey and further citations.
- 45.
- 46.
Cf. Sect. 3.4.2.
- 47.
More details are in [33] Theorem 8.4.
- 48.
One of the “simplest” examples for a theory which is not simple is \({\textsc {ID}}_1\) (i.e. \(\textsf{ID}_{1}({\mathord {\textsc {PA}}})\)). Its spectrum consists of two points \(\{\Psi _{\Omega _1}({\varepsilon _{\Omega _{1}+1}}),\varepsilon _{\Omega _{1}+1}\} \).
- 49.
In case that the notation for \(\alpha \) needs n-ary Veblen functions it is wise to count also these functions among the generating functions of \(\mathcal{H}\). This is, however, not absolutely necessary. Even in our definition of \(\mathcal{H}\) the Veblen functions \(\varphi _{\xi }\) for \(\xi >0\) are dispensable in principle. These Veblen functions can be expressed in terms of the \(\Psi \)-functions. However, the then obtained results look somewhat weird, very unfamiliar and thus much less attractive (and are therefore also more difficult to read and to memorize).
- 50.
Examples could be systems in weak second-order logic, e.g. (\(\Delta ^1_1\)-CA).
- 51.
Cf. [19].
- 52.
As an example the Peano axioms suffice to prove the properties of \(\mathcal{H}^{\Gamma _{\Omega _{\nu }+1}}(0)\).
- 53.
Recall that an axiom system is simple, if its spectrum is a singleton.
- 54.
Recall that in general we have no ordinals in \({\mathfrak M}_{\mu }\) but have to represent them by elements in \(O_\mu \) as discussed in Sect. 3.3.3.1.
- 55.
Cf. Sect. 3.3.2.2.
- 56.
Without having checked that we conjecture that also the “No Enhancement Theorem” can be generalized to this situation.
- 57.
A more detailed proof sketch can be found in [33].
- 58.
E.g. \(\Phi (n):=3^{n+2}\) is sufficiently increasing for the basis structure \({\mathfrak N}\).
- 59.
Cf. [7].
- 60.
- 61.
The intersection with \(\Omega _{1}\) is of course superfluous and should only illustrate the bridge to the previous results.
References
Arnold Beckmann and Wolfram Pohlers. Application of cut–free infinitary derivations to generalized recursion theory. Annals of Pure and Applied Logic, 94: 1–19, 1998.
Benjamin Blankertz and Andreas Weiermann. How to characterize provably total functions by the Buchholz operator method. Number 6 in Lecture Notes in Logic. Springer-Verlag, Heidelberg/New York, 1996.
Jane Bridge. A simplification of the Bachmann method for generating large countable ordinals. Journal of Symbolic Logic, 40: 171–185, 1975.
Wilfried Buchholz. A simplified version of local predicativity. In Peter Aczel, Harold Simmons, and Stanley S. Wainer, editors, Proof Theory, pages 115–147, Cambridge, July 1992. Cambridge University Press.
Wilfried Buchholz. A survey on ordinal notations around the Bachmann–Howard ordinal. In [20], pages 71–100.
Wilfried Buchholz, Solomon Feferman, Wolfram Pohlers, and Wilfried Sieg, editors. Iterated Inductive Definitions and Subsystems of Analysis: Recent Proof-Theoretical Studies. Number 897 in Lecture Notes in Mathematics. Springer-Verlag, Heidelberg/New York, 1981.
Wilfried Buchholz, E. Adam Cichon, and Andreas Weiermann. A uniform approach to fundamental sequences and hierarchies. Mathematical Logic Quarterly, 40: 273–286, 1994.
Solomon Feferman. Formal theories for transfinite iteration of generalized inductive definitions and some subsystems of analysis. In Akiko Kino, John Myhill, and Richard E. Vesley, editors, Intuitionism and Proof Theory, Studies in Logic and the Foundations of Mathematics, pages 303–326, Amsterdam, August 1970. North-Holland Publishing Company.
Solomon Feferman. Preface: How we got from there to here. In [6], pages 1–15.
Solomon Feferman. The proof theory of classical and constructive inductive definitions. A forty year saga, 1968–2008. In [37], pages 79–95.
Solomon Feferman and Wilfried Sieg. Inductive definitions and subsystems of analysis. In [6], pages 16–77.
Kentaro Fujimoto. Notes on some second order systems of inductive definitions and \({\Pi }^1_1\)–comprehensions and relevant subsystems of set theory. Annals of Pure and Applied Logic, 166: 409–463, 2014.
Gerhard Gentzen. Die Widerspruchsfreiheit der reinen Zahlentheorie. Mathematische Annalen, 112: 493–565, 1936.
Gerhard Gentzen. Neue Fassung des Widerspruchsfreiheitsbeweises für die reine Zahlentheorie. Forschungen zur Logik und Grundlegung der exakten Wissenschaften, 4: 19–44, 1938.
Gerhard Gentzen. Beweisbarkeit und Unbeweisbarkeit von Anfangsfällen der transfiniten Induktion in der reinen Zahlentheorie. Mathematische Annalen, 119: 140–161, 1943.
Kurt Gödel. Über formal unentscheidbare Sätze der ‘Prinzipia Mathematica’ und verwandter Systeme. Monatshefte für Mathematik und Physik, 38: 173–198, 1931.
David Hilbert. Mathematische Probleme. Archiv für Mathematik und Physik, 1. 3. Reihe: 44–63, 1901.
David Hilbert. Axiomatisches Denken. Mathematische Annalen, 78: 405–415, 1918.
Gerhard Jäger. Metapredicative and explicit Mahlo: a proof-theoretic perspective. In Rene Cori, Alexander Razborov, Stevo Todorcevic, and Carol Wood, editors, Logic Colloquium ’00, volume 19 of Lecture Notes in Logic, pages 272–293, Wellesley, MA, 2005. AK Peters.
Gerhard Jäger and Wilfried Sieg, editors. Feferman on Foundations, Outstanding Contributions to Logic, Heidelberg, Berlin, 2017. Springer-Verlag.
Georg Kreisel. Generalized inductive definitions. Reports of seminars on the foundation of Analysis. (Stanford Report), mimeographed, section III, 1963a.
Georg Kreisel. Theory of free choice sequences of natural numbers. Reports of seminars on the foundation of Analysis. (Stanford Report), mimeographed, section IV, 1963b.
Michael Möllerfeld. Systems of inductive definitions. PhD Thesis, Münster, 2003.
Yiannis N. Moschovakis. Elementary Induction on Abstract Structures. Number 77 in Studies in Logic and the Foundations of Mathematics. North-Holland Publishing Company, Amsterdam, 1974a.
Yiannis N. Moschovakis. On nonmonotone inductive definability. Fundamenta Mathematicae, 82: 39–83, 1974b.
Wolfram Pohlers. Proof-theoretical analysis of ID\(_{\nu }\) by the method of local predicativity. In [6], pages 261–357.
Wolfram Pohlers. Computability theory of hyperarithmetical sets. Lecture notes (www.uni-muenster.de/imperia/logik/skripte), Westfälische Wilhelms–Universität, Münster, 1996.
Wolfram Pohlers. Subsystems of set theory and second order number theory. In Samuel R. Buss, editor, Handbook of Proof Theory, Studies in Logic and the Foundations of Mathematics, pages 209–335. North-Holland Publishing Company, 1998.
Wolfram Pohlers. Ordinal analysis of non–monotone \(\Pi ^0_1\)–definable inductive definitions. Annals of Pure and Applied Logic, 156: 160–169, 2008.
Wolfram Pohlers. Proof Theory. The first step into impredicativity. Universitext. Springer-Verlag, Berlin/Heidelberg/New York, 2009.
Wolfram Pohlers. Semi–formal calculi and their applications. In Reinhard Kahle and Michael Rathjen, editors, Gentzen’s Centenary: The quest for consistency, pages 317–354. Springer-Verlag, 2015.
Wolfram Pohlers. From subsystems of Analysis to subsystems of set theory. In Reinhard Kahle, Thomas Strahm, and Thomas Studer, editors, Advances in Proof Theory, Progress in Computer Science and Applied Logic 28, pages 319–338. Birkhäuser Verlag, 2016.
Wolfram Pohlers. Iterated inductive definitions revisited. In [20], pages 209–251.
Michael Rathjen. Untersuchungen zu Teilsystemen der Zahlentheorie zweiter Stufe und der Mengenlehre mit einer zwischen \({\Delta }^1_2-CA und {\Delta }^1_2-CA+BI\) liegenden Beweisstärke. Dissertation, Westfälische Wilhelms-Universität, Münster, 1988.
Michael Rathjen. Investigations of subsystems of second order arithmetic and set theory in strength between \({\Pi }^1_1\)–CA and \({\Delta }_2^1\)–CA + BI: Part I. In [37], pages 363–439.
Wayne Richter. Recursively Mahlo ordinals and inductive definitions. In Robin O. Gandy and C. M. E. Yates, editors, Logic Colloquium ’69, number 61 in Studies in Logic and the Foundations of Mathematics, pages 273–288, Amsterdam, August 1971. North-Holland Publishing Company.
Ralf Schindler, editor. Ways of Proof Theory. Number 2 in Ontos Mathematical Logic. Ontos Verlag, Frankfurt, Paris, Lancaster, New Brunswick, 2010.
Stephen G. Simpson. Subsystems of Second Order Arithmetic. Springer-Verlag, Berlin/Heidelberg/New York, 1999.
Clifford Spector. Provably recursive functionals of analysis: a consistency proof of analysis by an extension of principles formulated in current intuitionistic mathematics. In James C. E. Dekker, editor, Recursive Function Theory, number 5 in Proceedings of Symposia in Pure Mathematics, pages 1–27, Providence, April 1962. American Mathematical Society.
Andreas Weiermann. How to characterize provably total functions by local predicativity. Journal of Symbolic Logic, 61: 52–69, 1996.
Acknowledgements
I want to thank the anonymous referee for her or his criticism and the many extremely helpful comments and corrections.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Pohlers, W. (2022). On the Performance of Axiom Systems. In: Ferreira, F., Kahle, R., Sommaruga, G. (eds) Axiomatic Thinking II. Springer, Cham. https://doi.org/10.1007/978-3-030-77799-9_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-77799-9_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-77798-2
Online ISBN: 978-3-030-77799-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)





 and
and  .
. holds true for some
holds true for some  holds true for all
holds true for all  holds true for all ordinals
holds true for all ordinals  holds true for all
holds true for all 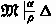 holds true for all
holds true for all  holds true for some
holds true for some 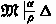 holds true for all
holds true for all  ,
,  and
and  holds true for all
holds true for all  ,
,  .
. and
and  for all
for all  implies
implies  .
. holds true for all
holds true for all  such that the stage comparison relations
such that the stage comparison relations then
then  holds true for all
holds true for all  .
. .
. holds true for all ordinals
holds true for all ordinals  hold true for all
hold true for all  holds true for all
holds true for all  holds true for some
holds true for some 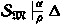 holds true for all
holds true for all  ,
, 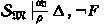 ,
,  holds true for all
holds true for all  and
and 
 also has a meaning for the ground structure
also has a meaning for the ground structure