Abstract
The purpose of this article is to present a new and simplified cut elimination procedure for \(\textsf{KP}\). We start off from the basic language of set theory and add constants for all elements of the constructible hierarchy up to the Bachmann-Howard ordinal \(\psi (\varepsilon _{\Omega {+}1})\). This enriched language is then used to set up an infinitary proof system \(\textsf{IP}\) whose ordinal-theoretic part is based on a specific notation system \(C(\varepsilon _{\Omega +1},0)\) due to Buchholz and his idea of operator controlled derivations. \(\textsf{KP}\) is embedded into \(\textsf{IP}\) and complete cut elimination for \(\textsf{IP}\) is proved.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
1 Introduction
Kripke-Platek set theory \(\textsf{KP}\) (with infinity) is a remarkable subsystems of Zermelo-Fraenkel set theory and had an enormous impact on the interaction between various fields of mathematical logic; see, for example, Barwise [1]. Its proof-theoretic analysis has been carried through in Jäger [11], and it is known that the proof-theoretic ordinal of \(\textsf{KP}\) is the Bachmann-Howard ordinal \(\psi (\varepsilon _{\Omega {+}1})\) and that \(\textsf{KP}\) proves the same arithmetical sentences as the theory \(\textsf{ID}_1\) of positive inductive definitions (cf. Feferman [8] and Buchholz, Feferman, Pohlers, and Sieg [6]). Functional interpretations of \(\textsf{KP}\) have been studied by Burr [7] and Ferreira [9].
The purpose of this article is to present a new and simplified cut elimination procedure for \(\textsf{KP}\). We start off from the basic language of set theory and add constants for all elements of the constructible hierarchy up to the Bachmann-Howard ordinal \(\psi (\varepsilon _{\Omega {+}1})\). This enriched language is then used to set up an infinitary proof system \(\textsf{IP}\) whose ordinal-theoretic part is based on a specific notation system \(C(\varepsilon _{\Omega +1},0)\) due to Buchholz (see, for example, Buchholz [3]) and his idea of operator controlled derivations. \(\textsf{KP}\) is embedded into \(\textsf{IP}\) and complete cut elimination for \(\textsf{IP}\) is proved.
In the older proof-theoretic treatments of theories for admissible sets infinitary systems of ramified set theory play a central role. The build up of the set terms in these systems has always been complicated—requiring a lot of technical intermediate steps to deal with, for example, extensionality and equality—and is now for free.
This article is organized as follows: We begin with a very compact presentation of Kripke-Platek set theory \(\textsf{KP}\) (with infinity) and its Tait-style variant \(\textsf{KP}^T\). Then we discuss the ordinal notation system and the derivation operators needed for our analysis. Here we can confine ourselves to a “slimmed down” version of Buchholz [3]. It follows the presentation of the new infinitary system \(\textsf{IP}\) with its very simple term structure. After some partial soundness and completeness results for \(\textsf{IP}\) we show how to embed \(\textsf{KP}^T\) into \(\textsf{IP}\). The last two sections are dedicated to cut elimination: predicative cut elimination and collapsing. The Hauptsatz then tells us that the Bachmann-Howard ordinal is an upper bound for the cut-free embedding of the \(\Sigma \) fragment of \(\textsf{KP}\) into \(\textsf{IP}\); also, the constructible hierarchy up to the Bachmann-Howard ordinal is a model of the \(\Pi _2\) fragment of \(\textsf{KP}\).
2 Kripke-Platek Set Theory
Let \(\mathcal {L}\) be the standard first-order language of set theory with \(\in \) as the only relation symbol, countably many set variables, and the usual connectives and quantifiers of first-order logic. With regard to the later proof-theoretic analysis we want all formulas of \(\mathcal {L}\) to be in negation normal form. Thus, the atomic formulas of \(\mathcal {L}\) are all expressions \((u \in v)\) and \((u \notin v)\). The formulas of \(\mathcal {L}\) are built up from these atomic formulas by means of \(\vee ,\wedge ,\exists ,\forall \) as usual. We use as metavariables (possibly with subscripts):
-
u, v, w, x, y, z for set-theoretic variables,
-
A, B, C, D for formulas.
As you can see, we have no connective for negation. However, the negation \(\lnot A\) of A is defined via de Morgan’s laws and the law of double negation. In addition, we work with the following abbreviations:
To simplify the notation we often omit parentheses if there is no danger of confusion. Moreover, we shall employ the common set-theoretic terminology and the standard notational conventions. For example, \(A^u\) results from A by restricting all unbounded quantifiers to u. The \(\Delta _0\), \(\Sigma \), \(\Pi \), \(\Sigma _n\), and \(\Pi _n\) formulas of \(\mathcal {L}\) are defined as usual.
The logic of Kripke-Platek set theory is classical first-order logic. The set-theoretic axioms of \(\textsf{KP}\) consist of
- (Equality):
-
\(u \in w \,\wedge \,u=v \;\rightarrow \; v \in w,\)
- (Pair):
-
\(\exists z(u \in z \,\wedge \,v \in z),\)
- (Union):
-
\(\exists z(\forall y \in u)(\forall x \in y)(x \in z),\)
- (Infinity):
-
\(\exists z(z \ne \varnothing \,\wedge \,(\forall x \in z)(x \cup \{x\} \in z)),\)
- (\(\Delta _0\)-Sep):
-
\(\exists z(z = \{x \in u : D[x]\}),\)
- (\(\Delta _0\)-Col):
-
\((\forall x \in u)\exists y D[x,y] \,\rightarrow \,\exists z(\forall x \in u)(\exists y \in z)D[x,y],\)
- (\(\in \)-Ind):
-
\(\forall x((\forall y \in x)A[y] \,\rightarrow \,A[x]) \,\rightarrow \, \forall x A[x].\)
The formulas D in the schemas (\(\Delta _0\)-Sep) and (\(\Delta _0\)-Col) are \(\Delta _0\) whereas the formula A in the schema (\(\in \)-Ind) ranges over arbitrary formulas of \(\mathcal {L}\).
3 A Tait-Style Reformulation of \(\textsf{KP}\)
For the later embedding into the infinitary system \(\textsf{IP}\) it is technically convenient to work with a Tait-style variant \(\textsf{KP}^T\) of \(\textsf{KP}\). In \(\textsf{KP}^T\) we derive finite sets of \(\mathcal {L}\) formulas rather than individual formulas. In the following the Greek letters \(\Gamma ,\Theta ,\Lambda \) (possibly with subscripts) act as metavariables for finite sets of \(\mathcal {L}\) formulas. Also, we write (for example) \(\Gamma , A_1,\ldots ,A_n\) for \(\Gamma \cup \{A_1,\ldots ,A_n\}\); similarly for expressions such as \(\Gamma ,\Theta ,A\). Finite sets of formulas are to be interpreted disjunctively.
Axioms of \(\textsf{KP}^T\).
- (Tnd):
-
\(\Gamma ,\, A,\, \lnot A\quad \text{ for } \text{ all } \,\mathcal {L}\, \text{ formulas } A.\)
- (Equality):
-
\(\Gamma ,\, u \in w \,\wedge \,u=v \;\rightarrow \; v \in w.\)
- (Pair):
-
\(\Gamma ,\, \exists z(u \in z \wedge v \in z).\)
- (Union):
-
\(\Gamma ,\,\exists z(\forall y \in u)(\forall x \in y)(x \in z).\)
- (Infinity):
-
\(\Gamma ,\, \exists z(\varnothing \ne z \,\wedge \,(\forall x \in z)(x \cup \{x\} \in z).\)
- (\(\Delta _0\)-Sep):
-
\(\Gamma ,\, \exists z(z = \{x\in u : D[x]\}). \)
- (\(\Delta _0\)-Col):
-
\(\Gamma ,\, (\forall x \in u)\exists y D[x,y] \,\rightarrow \,\exists z(\forall x \in u)(\exists y \in z)D[x,y].\)
- (\(\in \)-Ind):
-
\(\Gamma ,\, \forall x((\forall y \in x)A[y] \,\rightarrow \,A[x]) \;\rightarrow \; \forall x A[x].\)
The formulas A in the Tertium-non-datur axioms (Tnd) and \(\in \)-induction axioms (\(\in \)-Ind) range over arbitrary \(\mathcal {L}\) formulas whereas the formulas D in (\(\Delta _0\)-Sep) and (\(\Delta _0\)-Col) are supposed to be \(\Delta _0\).
Rules of inference of \(\textsf{KP}^T\).
In the rules \((b\text {-}all)\) and (all) the eigenvariable u of these rules must not occur in their conclusion.
The notions of principal formula and minor formula(s) of an inference and that of cut formula(s) of a cut are as usual. We say that \(\Gamma \) is provable in \(\textsf{KP}^T\) iff there exists a finite sequence of finite sets of \(\mathcal {L}\) formulas
such that \(\Theta _n\) is the set \(\Gamma \) and for any \(i = 0,\ldots ,n\) one of the following two conditions is satisfied:
-
\(\Theta _i\) is an axiom of \(\textsf{KP}^T\);
-
\(\Theta _i\) is the conclusion of an inference of \(\textsf{KP}^T\) whose premise(s) are among \(\Theta _0,\ldots , \Theta _{i{-}1}\).
In this case we write \(\textsf{KP}^T\vdash \Gamma \). It is an easy exercise to show that a formula A is provable in one of the usual Hilbert-style formalizations of \(\textsf{KP}\) iff \(\textsf{KP}^T\vdash A\). We leave all details to the reader.
4 An Ordinal System for the Bachmann-Howard Ordinal
Buchholz has developed several ordinal notation systems based on so called collapsing functions; see, for example Buchholz [2,3,4]. In the following we work with a reduced version, which is sufficient for our purposes. For that we need the following ingredients:
-
(1)
Let \( On \) be the collection of all ordinals and let \(\Omega \) be a sufficiently large ordinal. To simplify matters we set \(\Omega := \aleph _1\), but also \(\omega _1^{ck}\) or even somewhat smaller ordinals could do the job.
-
(2)
The basic ordinal operations \(\lambda \eta ,\xi .(\eta +\xi )\) and \(\lambda \xi .\omega ^\xi \).
-
(3)
The binary Veblen function \(\varphi \), where \(\varphi _\alpha \) is defined by transfinite recursion on \(\alpha \) as the ordering function of the class
$$ \begin{aligned} \{\omega ^\beta : \beta \in On \; \& \; (\forall \xi <\alpha )(\varphi _\xi (\omega ^\beta ) = \omega ^\beta \}. \end{aligned}$$In the following we write \(\varphi \alpha \beta \) for \(\varphi _\alpha (\beta )\).
-
(4)
An ordinal \(\alpha \) is called strongly critical iff \(\alpha = \varphi \alpha 0\).
-
(5)
Every ordinal \(\alpha \) has a normal form
$$\begin{aligned} \alpha =_{NF} \varphi \alpha _1\beta _1 + \ldots + \varphi \alpha _n\beta _n \end{aligned}$$with \(\beta _i < \varphi \alpha _i\beta _i\) for \(i = 1,\ldots ,n\) and \(\varphi \alpha _1\beta _1 \ge \ldots \ge \varphi \alpha _n\beta _n\).
-
(6)
The collection \( SC (\alpha )\) of strongly critical components of an ordinal \(\alpha \) is defined by

Based on that we can now introduce, for all \(\alpha \) and \(\beta \), the ordinals \(\psi (\alpha )\) and the sets of ordinals \(C(\alpha ,\beta )\).
Definition 2.4.1
By recursion of \(\alpha \) we simultaneously define:
-
(1)
\(\psi (\alpha ) \;:=\; \min (\beta : C(\alpha ,\beta ) \cap \Omega = \beta )\).
-
(2)
\(C(\alpha ,\beta )\) is the closure of \(\beta \cup \{0,\Omega \}\) under \(+\), \(\varphi \), and \((\xi \mapsto \psi (\xi ))_{(\xi < \alpha )}\).
Since \(C(\alpha ,\beta )\) is countable, it is clear that \(\psi (\alpha )\) is always defined and less than \(\Omega \) in case that \(\Omega \) is interpreted as \(\aleph _1\). If \(\Omega \) is interpreted as \(\omega ^{ck}\) (or a smaller ordinal), then additional considerations are required.
Now we list a series of properties of the sets \(C(\alpha ,\beta )\). Their proofs are either standard or follow from the results in the articles of Buchholz mentioned above.
Lemma 2.4.2
We have for all ordinals \(\alpha \) and \(\beta \):
-
(1)
\(C(\alpha ,0) = C(\alpha ,\psi (\alpha ))\).
-
(2)
\(C(\alpha ,\psi (\alpha )) \cap \Omega = \psi (\alpha )\).
-
(3)
\(C(\alpha ,\beta ) \cap \Omega \) is an ordinal.
Every set \(C(\alpha ,0)\) is well-ordered by the usual less relation < on the ordinals but is not an ordinal itself. For example,
If we write \( ot (\alpha ,\xi )\) for the order-type of an element \(\xi \) of \(C(\alpha ,0)\) with respect to \(C(\alpha ,0)\), then
-
\( ot (\alpha ,\xi ) = \xi \) for all \(\xi \le \psi (\alpha )\),
-
\( ot (\alpha ,\xi ) < \xi \) for all elements of \(C(\alpha ,0)\) greater than \(\psi (\alpha )\).
In particular, we have \( ot (\alpha ,\Omega ) = \psi (\alpha )\) and the order types \( ot (\alpha ,\xi )\) of all elements \(\xi \) of \(C(\alpha ,0)\) are countable.
We write \(\varepsilon _{\Omega +1}\) for the least ordinal \(\alpha > \Omega \) such that \(\omega ^\alpha = \alpha \). Its collapse \({\boldsymbol{\eta }}:= \psi (\varepsilon _{\Omega +1})\) is called the Bachmann-Howard ordinal. This number gained importance in proof theory since it is the proof-theoretic ordinal of the theory \(\textsf{ID}_1\) of one positive inductive definition and of Kripke-Platek set theory \(\textsf{KP}\); see, for example, Buchholz and Pohlers [5], Jäger [11], and Pohlers [13].
5 Derivation Operators
The general theory of derivation operators and operator controlled derivations has been introduced in Buchholz [3]. His main motivation was to provide a conceptually clear and flexible approach to infinitary proof theory that allows to put the finger on that part of the ordinal analysis of a sufficiently strong formal theory where the uniformity of proofs and a collapsing technique play the central role.
In this article we confine ourselves to that part of the general theory that goes along with the notation system \(C(\varepsilon _{\Omega +1},0)\) described in the previous section.
Definition 2.5.1
Let \( Pow ( On )\) denote the collection of all sets of ordinals. A class function
is called a derivation operator (d-operator for short) iff it satisfies the following conditions for all \(X,Y \in Pow ( On )\):
-
(i)
\(X \subseteq \mathcal {H}(X)\).
-
(ii)
\(Y \subseteq \mathcal {H}(X) \quad \Longrightarrow \quad \mathcal {H}(Y) \subseteq \mathcal {H}(X)\).
-
(iii)
\(\{0, \Omega \} \subseteq \mathcal {H}(X)\).
-
(iv)
For all \(\alpha \),
$$\begin{aligned} \alpha \in \mathcal {H}(X) \quad \Longleftrightarrow \quad SC (\alpha ) \subseteq \mathcal {H}(X). \end{aligned}$$
Hence every d-operator \(\mathcal {H}\) is monotone, inclusive, and idempotent. Every \(\mathcal {H}(X)\) is closed under \(+\) and the binary Veblen function \(\varphi \), and the decomposition of its members into their strongly critical components.
Let \(\mathcal {H}\) be a d-operator. Then we define for all finite sets of ordinals \(\mathfrak {m}\) the operators
by setting for all \(X \subseteq On \):
If \(\mathcal {H}\) and \(\mathcal {K}\) are d-operators, then we set
In this case \(\mathcal {K}\) is called an extension of \(\mathcal {H}\). The following observation is immediate from this definition.
Lemma 2.5.2
If \(\mathcal {H}\) is a d-operator, then we have for all finite sets of ordinals \(\mathfrak {m}, \mathfrak {n}\):
-
(1)
\(\mathcal {H}[\mathfrak {m}]\) is a d-operator and an extensions of \(\mathcal {H}\).
-
(2)
If \(\mathfrak {m}\subseteq \mathcal {H}(\varnothing )\), then \(\mathcal {H}[\mathfrak {m}] = \mathcal {H}\).
-
(3)
\(\mathfrak {n}\subseteq \mathcal {H}[\mathfrak {m}](\varnothing ) \quad \Longrightarrow \quad \mathcal {H}[\mathfrak {n}] \subseteq \mathcal {H}[\mathfrak {m}]\).
Now we turn to specific operators \(\mathcal {H}_\sigma \). They will play a crucial role in connection with the embedding of \(\textsf{KP}\) into the infinitary proof system \(\textsf{IP}\)—to be introduced in the next section—and the collapsing procedure for \(\textsf{IP}\).
Definition 2.5.3
We define, for all ordinals \(\sigma \), the operators
by setting for all \(X \subseteq On \):
The following lemmas summarize those properties of these operators that will be needed later. For their proof we refer to [3], in particular Lemma 4.6 and Lemma 4.7. Assertion (5) is a consequence of Lemma 2.4.2(3).
Lemma 2.5.4
We have for all ordinals \(\sigma , \tau \) and all \(X \subseteq On \):
-
(1)
\(\mathcal {H}_\sigma \) is a derivation operator.
-
(2)
\(\mathcal {H}_\sigma (\varnothing ) = C(\sigma +1,0))\).
-
(3)
\(\tau \le \sigma \;\;\text{ and }\;\; \tau \in \mathcal {H}_\sigma (X) \quad \Longrightarrow \quad \psi (\tau ) \in \mathcal {H}_\sigma (X)\).
-
(4)
\(\sigma < \tau \quad \Longrightarrow \quad \mathcal {H}_\sigma \subseteq \mathcal {H}_\tau \).
-
(5)
\(\mathcal {H}_\sigma (X) \cap \Omega \) is an ordinal.
Lemma 2.5.5
Let \(\mathfrak {m}\) a finite set of ordinals and \(\sigma \) an ordinal such that the following conditions are satisfied:
Then we have for \({\widehat{\alpha }}:= \sigma + \omega ^{\Omega + \alpha }\) and \({\widehat{\beta }}:= \sigma + \omega ^{\Omega +\beta }\):
-
(1)
\(\alpha \in \mathcal {H}_\sigma [\mathfrak {m}](\varnothing ) \quad \Longrightarrow \quad {\widehat{\alpha }}\in \mathcal {H}_\sigma [\mathfrak {m}](\varnothing ) \;\;\text{ and }\;\; \psi ({\widehat{\alpha }}) \in \mathcal {H}_{\widehat{\alpha }}[\mathfrak {m}](\varnothing )\).
-
(2)
\(\alpha \in \mathcal {H}_\sigma [\mathfrak {m}](\varnothing ) \;\;\text{ and }\;\; \alpha< \beta \quad \Longrightarrow \quad \psi ({\widehat{\alpha }}) < \psi ({\widehat{\beta }})\).
-
(3)
\(\mathcal {H}_\sigma [\mathfrak {m}](\varnothing ) \cap \Omega \subseteq \psi (\sigma +1)\).
From now on the letter \(\mathcal {H}\) will be used as a metavariable that ranges over d-operators.
6 The Infinitary Proof System \(\textsf{IP}\)
Henceforth, all ordinals used on the metalevel range over the set \(C(\varepsilon _{\Omega +1},0)\) if not stated otherwise. In this section we introduce an infinitary proof system whose terms are constants for the elements of the initial segment of the constructible hierarchy \({{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\) and whose proofs are controlled by derivation operators. Later we show that \(\textsf{KP}\) can be embedded into \(\textsf{IP}\) and that \(\textsf{IP}\) permits cut elimination and collapsing.
Definition 2.6.1
The language of \(\textsf{IP}\) is the following extension \(\mathcal {L}[{\boldsymbol{\eta }}]\) of \(\mathcal {L}\):
-
(1)
For each element a of \({{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\) we fix a fresh constant \(\bar{a}\). These constants are the terms of \(\textsf{IP}\). The letters r, s, t (possibly with subscripts) act as metavariables for the terms of \(\textsf{IP}\).
-
(2)
The level \(|\bar{a}|\) of \(\bar{a}\) is the least \(\xi \) such that \(a \in {\boldsymbol{L}}_{\xi {+}1}\).
-
(3)
The formulas of \(\textsf{IP}\) are now easily obtained from the formulas of \(\mathcal {L}\) by simply replacing all their free variables by terms of \(\textsf{IP}\); i.e. the formulas of \(\textsf{IP}\) are the sentences of \(\mathcal {L}[{\boldsymbol{\eta }}]\).
Accordingly, the \(\Delta _0\), \(\Sigma \), \(\Pi \) \(\Sigma _n\), and \(\Pi _n\) formulas of \(\textsf{IP}\) are the \(\Delta _0\), \(\Sigma \), \(\Pi \) \(\Sigma _n\), and \(\Pi _n\) sentences of \(\mathcal {L}[{\boldsymbol{\eta }}]\), respectively.
Definition 2.6.2
Every \(\textsf{IP}\) formula is an expression of the form \(F[\bar{a}_1,\ldots ,\bar{a}_n]\) where \(F[u_1,\ldots ,u_n]\) is a formula of \(\mathcal {L}\) with the free variables indicated and \(a_1,\ldots , a_n\) are elements of \({{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\). The set
is called the parameter set of this formula.
Observe that each \(\Delta _0\) sentence of \(\mathcal {L}[{\boldsymbol{\eta }}]\) has a non-empty parameter set. Below it will be necessary to measure the complexities of the cut formulas appearing in a derivation. To this end we assign a rank to each \(\mathcal {L}[{\boldsymbol{\eta }}]\) sentence.
Definition 2.6.3
The rank \( rk (F)\) of an \(\mathcal {L}[{\boldsymbol{\eta }}]\) sentence F is defined by induction on the number of symbols occurring in F as follows.
-
(1)
\( rk (\bar{a}\in \bar{b}) \;:=\; rk (\bar{a}\notin \bar{b}) \;:=\; \omega {\cdot } \max (|\bar{a}|, |\bar{b}|)\).
-
(2)
\( rk (F \vee G) \;:=\; rk (F \wedge G) \;:=\; \max ( rk (F), rk (G)) +1\).
-
(3)
\( rk ((\exists x \in \bar{a})F[x]) \;:=\; rk ((\forall x \in \bar{a})F[x]) \;:=\; \max (\omega {\cdot } |\bar{a}|, rk (F[\bar{\varnothing }])+1)\).
-
(4)
\( rk (\exists x F[x]) \;:=\; rk (\forall x F[x]) \;:=\; \max (\Omega , rk (F[\bar{\varnothing }])+1)\).
Finally, we define the level \( lev (F)\) of an \(\textsf{IP}\) formula F by
Some important properties of the ranks of \(\mathcal {L}[{\boldsymbol{\eta }}]\) sentences are summarized in the following lemma. Its proof is straightforward and left to the reader.
Lemma 2.6.4
We have for all \(\textsf{IP}\) formulas F, G and all \(a,b \in {{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\);
-
(1)
\( rk (F) = rk (\lnot F)\).
-
(2)
\( rk (F) < \omega {\cdot } lev (F) + \omega \).
-
(3)
\( rk (F), rk (G) < rk (F \vee G)\).
-
(4)
\(|\bar{b}| < lev (F[\bar{\varnothing }]) \quad \Longrightarrow \quad rk (F[\bar{b}]) = rk (F[\bar{\varnothing }])\).
-
(5)
\(b \in a \quad \Longrightarrow \quad rk (F[\bar{b}]) < rk ((\exists x \in \bar{a})F[x])\).
-
(6)
\( rk (F[\bar{b}]) < rk (\exists x F[x])\).
-
(7)
\( rk (F) \in \mathcal {H}[ par (F)](\varnothing )\).
-
(8)
\(\alpha \in par (F) \quad \Longrightarrow \quad \alpha \le rk (F)\).
The proof system for \(\textsf{IP}\) will be Tait-style. From now on we let the Greek letters \(\Gamma ,\Theta ,\Lambda \) (possibly with subscripts) also range over finite sets of \(\mathcal {L}[{\boldsymbol{\eta }}]\) sentences.
For a finite set \(\mathfrak {S}= \{F,\ldots ,F_m,r_1,\ldots ,r_n\}\) of formulas and terms of \(\textsf{IP}\) we set
Accordingly,
Variants of this notation may also be used. However, it will always be clear from the context what is meant.
Axioms of \(\textsf{IP}\). The axioms of \(\textsf{IP}\) are all finite sets
with \(a_1,a_2,b_1,b_2 \in {{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\), \(a_1 \in b_1\), and \(a_2 \notin b_2\).
So the axioms of \(\textsf{IP}\) are the finite sets that contain true atomic sentences of \(\mathcal {L}[{\boldsymbol{\eta }}]\). The next definition introduces the derivability relation, controlled by derivation operators.
Definition 2.6.5
 iff \( par (\Gamma ) \cup \{\alpha \} \,\subseteq \, \mathcal {H}(\varnothing )\) and one of the following cases holds:
iff \( par (\Gamma ) \cup \{\alpha \} \,\subseteq \, \mathcal {H}(\varnothing )\) and one of the following cases holds:

We now list a series of properties of operator controlled derivations before we turn to embedding, cut elimination, and collapsing in the following sections. The first is the Weakening Lemma, and its proof is by straightforward induction on \(\alpha \).
Lemma 2.6.6
(Weakening) Assume that \(\mathcal {H}\subseteq \mathcal {H}'\), \(\alpha \le \beta \), \(\rho \le \sigma \), and that \( par (\Lambda ) \cup \{\beta \} \,\subseteq \, \mathcal {H}'(\varnothing )\). Then

In the following, we will frequently make use of Weakening without making specific reference to it. An important such use is described in the next remark.
Remark 2.6.7
The inference rules formulated above are somewhat special in the sense that it is assumed that the principal formula of each rule (R) is an element of the premise(s) of (R). In general, however, this is not a severe limitation. Assume that we have a rule (R) with the principal formula F and the minor formulas \((F_i)_{(i{:}I)}\). Suppose further that F does not belong to \(\Gamma \) and that we have

where \(\mathcal {H}_i\) is either of the form \(\mathcal {H}\) or \(\mathcal {H}[\bar{b}_i]\), and possibly further side conditions. If \( par (F) \cup \{\alpha \} \subseteq \mathcal {H}(\varnothing )\)—and this requirement will be satisfied below in all relevant cases—then we can apply Weakening and obtain

Now the premises have the right form to conclude

In the following, this intermediate step will often be omitted, and we go directly over from (*) to (**).
Also the next lemma presents some basic properties of \(\textsf{IP}\); its proof is again by induction on \(\alpha \).
Lemma 2.6.8
(Inversion)
-
(1)
 .
. -
(2)
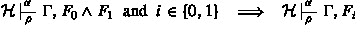 .
. -
(3)
 .
. -
(4)
 .
. -
(5)
 .
. -
(6)
 .
.
We end this section with a third structural lemma. It will be essential in connection with the Collapsing Theorem of Sect. 2.10.
Lemma 2.6.9
(Boundedness) Let F be a \(\Sigma \) sentence of \(\mathcal {L}[{\boldsymbol{\eta }}]\) and assume that \(\alpha \le \beta \in \mathcal {H}(\varnothing ) \cap \Omega \) and that r is the constant \(\bar{{\boldsymbol{L}}}_\beta \). Then we have

Proof
We show this assertion by induction on \(\alpha \) and assume  . First observe that this derivation contains no instances of \((\textsf{Ref})\) since \(\alpha < \Omega \). If \(\Gamma , F\) is an axiom, then \(\Gamma , F^r\) is an axiom as well, and we are done. Otherwise we distinguish cases according to the last inference of
. First observe that this derivation contains no instances of \((\textsf{Ref})\) since \(\alpha < \Omega \). If \(\Gamma , F\) is an axiom, then \(\Gamma , F^r\) is an axiom as well, and we are done. Otherwise we distinguish cases according to the last inference of  .
.
(i) The last inference was \((\exists )\) with principal formula F. Then F is of the form \(\exists x G[x]\) and there exist an \(\alpha _0 < \alpha \) and a set \(b \in {\boldsymbol{L}}_\alpha \) such that

where \(\Lambda := \Gamma \setminus \{F\}\). By two applications of the induction hypothesis we obtain

Since \(b \in {\boldsymbol{L}}_\alpha \subseteq {\boldsymbol{L}}_\beta \) and \((\exists x \in r)G^r[x]\) is the formula \(F^r\), an inference \((b\exists )\) yields

(ii) In all other cases we apply the induction hypothesis to the premise(s) of this inference (once or twice depending on whether F was the principal formula of this inference), and then apply it again.
7 Partial Soundness and Completeness of \(\textsf{IP}\)
The design of the infinitary proof system \(\textsf{IP}\) is so that all its axioms and rules of inference—with the exception of \((\textsf{Ref})\)—are correct with respect to \({{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\). This gives us the following result.
Theorem 2.7.1
(Partial soundness of \(\textsf{IP}\)) For any \(\Gamma \), any d-operator \(\mathcal {H}\) and all \(\alpha ,\rho \) we have that

Proof
By straightforward induction on \(\alpha \). Observe that because of \(\alpha < \Omega \), the inference rule \((\textsf{Ref})\) has not been used in this derivation.
It is clear that \((\textsf{Ref})\) is not correct in \({{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\). For proofs of depths greater than \(\Omega \), which use the rule \((\textsf{Ref})\), more subtle considerations are needed. We will see what to do with such derivations in Sect. 2.10.
Let us now turn to (partial) completeness. We will show that all \(\Pi \) sentences that are true in \({{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\) can be derived in \(\textsf{IP}\). To prove that we need the following auxiliary consideration. Recall the introduction of the derivation operator \(\mathcal {H}_0\) in Definition 2.5.3.
Lemma 2.7.2
If a and b are elements of \({{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\) with \(b \in a\), then we have for all \(\mathcal {L}[{\boldsymbol{\eta }}]\) sentences \(G[\bar{\varnothing }]\) that
Proof
Let \(\mathcal {K}\) be the d-operator \(\mathcal {H}_0[(\forall x \in \bar{a})G[x]]\). Then we clearly have
By Lemma 2.5.4, the set \(\mathcal {K}(\varnothing ) \cap \Omega \) is an ordinal. Therefore, \(|\bar{b}| \in \mathcal {K}(\varnothing )\). Consequently,
Thus Lemma 2.5.2 yields our assertion.
Theorem 2.7.3
(Partial completeness of \(\textsf{IP}\)) If F is a \(\Pi \) sentence of \(\mathcal {L}[{\boldsymbol{\eta }}]\), then

Proof
First observe that \( par (F) \cup \{ rk (F)\} \,\subseteq \, \mathcal {H}_0[F](\varnothing )\); see Lemma 2.6.4(7). The proof is by induction on \( rk (F)\).
(i) F is atomic. Then F is an axiom and, therefore,  .
.
(ii) F is of the form \((\exists x \in \bar{a})G[x]\). Then there exists a \(b \in a\) such that \({{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\, \models \, G[\bar{b}]\). By the induction hypothesis we thus have

for \(\alpha _b := rk (G[\bar{b}])\). From the previous lemma (and Weakening) we see that

An application of \((b\exists )\) implies the assertion; that \(|\bar{b}| < rk ((\exists x \in \bar{a})G[x])\) follows from Lemma 2.6.4(8).
(iii) (ii) F is of the form \(\forall x G[x]\). Then
for all \(b \in {{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\) and the induction hypothesis implies

for \(\alpha _b := rk (G[\bar{b}])\). Since \( par (G[\bar{b}]) \subseteq par (F,|\bar{b}|)\) we obtain (Weakening)

for all \(b \in {{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\). It only remains to apply an \((\forall )\) inference.
(iv) All other cases are similar or even simpler.
It is worth pointing out that the above approach does not work for \(\Sigma \) sentences true in \({{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\): Assume that \({{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\, \models \, \exists x G[x]\) for a, say, \(\Delta _0\) sentence \(G[\bar{\varnothing }]\). Then there exists a \(b \in {{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\) for which \({{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\, \models \, G[\bar{b}]\). With the induction hypothesis we would get

leading then, by an application of \((\exists )\), to

But \( \mathcal {H}_0[G[\bar{b}|]\) may depend on \(\bar{b}\), and can this dependency be avoided?
8 Embedding of \(\textsf{KP}^T\) into \(\textsf{IP}\)
In order to show that \(\textsf{KP}^T\) can be embedded into \(\textsf{IP}\) we first deal with the axioms of \(\textsf{KP}^T\). We show—step by step—how they can be proved in \(\textsf{IP}\).
Lemma 2.8.1
(Tertium-non-datur) For all \(\Gamma \), all F, and all d-operators \(\mathcal {H}\),

where \(\alpha := \omega ^{ rk (F)} \mathrel {\#} \omega ^{ rk (F)}\).
Proof
In view of Lemma 2.6.4(7) the ordinal condition
is clearly satisfied. We prove our assertion by induction on \( rk (F)\).
(i) If F is atomic, the \(\Gamma ,F,\lnot F\) is an axiom since either \({{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\, \models \, F\) or \({{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\, \models \, \lnot F\).
(ii) F is of the form \(\exists x G[x]\). Pick an arbitrary \(b \in {{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\). Then we define
Obviously, \( par (\Gamma ,F,G[\bar{b}]) \subseteq par (\Gamma ,F,\bar{b})\), and by some simple ordinal computatons we obtain
The induction hypothesis implies

and using an inference \((\exists )\) we arrive at

Therefore, an application of \((\forall )\) gives the desired result.
(iii) All other cases are similar.
Lemma 2.8.2
(Equality) For all \(\Gamma \) and all \(a,b,c \in {{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\),

where \(\alpha := \max (\omega {\cdot } |\bar{a}| + 4, \omega {\cdot } |\bar{b}| + 4, \omega {\cdot } |\bar{c}| + 2)\).
Proof
This is an immediate consequence of Theorem 2.7.3 since \(\alpha \) is the rank of the formula \((\bar{a}=\bar{b}\,\wedge \,\bar{a}\in \bar{c}\;\rightarrow \; \bar{b}\in \bar{c})\).
Lemma 2.8.3
(Pair) For all \(\Gamma \), all \(a,b \in {{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\), and all d-operators \(\mathcal {H}\),

where \(\alpha := \max (|\bar{a}|,|\bar{b}|)\).
Proof
We know that \(a, b \in {\boldsymbol{L}}_{\alpha +1} \in {{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\) and, if r is the constant for \({\boldsymbol{L}}_{\alpha +1}\),
Since \(\bar{a}\in r\) and \(\bar{b}\in r\) are axioms of \(\textsf{IP}\) we have

and an application of \((\exists )\) yields our assertion.
Lemma 2.8.4
(Union) For all \(\Gamma \), all \(a \in {{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\), and \(\alpha := |\bar{a}|\)

Proof
Let r be the constant for \({\boldsymbol{L}}_\alpha \). Then
Now we set
Then it is clear that
Therefore, Theorem 2.7.3 and Lemma 2.6.4(2) (plus Weakening) imply that

for a suitable \(n < \omega \). An application of \((\exists )\) yields our assertion.
Lemma 2.8.5
(Infinity) For all \(\Gamma \),

Proof
Clearly, \(\omega \in \mathcal {H}_0(\varnothing )\) and
Hence we already know, cf. Theorem 2.7.3 and Lemma 2.6.4(2), that

for some \(n < \omega \). Thus an application of \((\exists )\) finishes our proof.
Lemma 2.8.6
(\(\Delta _0\) Separation) Let \(A[x,y_1,\ldots ,y_n]\) be a \(\Delta _0\) formula of \(\mathcal {L}\) with all free variables indicated and assume \(a,b_1,\ldots ,b_n \in {{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\). If we set
then we have that, for all \(\Gamma \),

Proof
Under the above assumptions it is clear that there exists a set \(c \in {\boldsymbol{L}}_{\alpha +2}\) such that
Moreover, we have for
-
\( rk (F) = \omega {\cdot }(\alpha {+}1) + n\) for some \(n < \omega \),
-
\(\mathcal {H}_0[F,G](\varnothing ) \cup \{\omega {\cdot }(\alpha {+}2)\} \,\subseteq \, \mathcal {H}_0[\mathfrak {m}](\varnothing )\).
Therefore, Theorem 2.7.3 (plus Weakening) gives us

and after an application of \((\exists )\) we are done.
Lemma 2.8.7
(\(\in \)-Induction) Given the \(\textsf{IP}\) formula \(F[\bar{\varnothing }]\), we let G be the formula \( \exists x((\forall y \in x)F[y] \wedge \lnot F[x])\) and set
where \(a \in {{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\). For all \(\Gamma \) and all d-operators \(\mathcal {H}\) we then have:
-
(1)
 .
. -
(2)
 .
.
Proof
We prove (1) by \(\in \)-induction. From Lemma 2.6.4(6) we immediately obtain that \( rk (F[\bar{a}]) < \gamma \) for all \(a \in {{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\). Pick any \(a \in {{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\). Then the induction hypothesis (plus Weakening) implies

for all \(b \in a\). Therefore, an application of \((b\forall )\) yields

On the other hand, Lemma 2.8.1 (together with Lemma 2.6.4(6,7) and Weakening) tells us that

Hence by \((\wedge )\),

From the latter we obtain our assertion (1) by an application of \((\exists )\). Assertion (2) is an immediate consequence of (1).
Lemma 2.8.8
(\(\Delta _0\) Collection) Let \(A[x,y, z_1,\ldots ,z_n]\) be a \(\Delta _0\) formula of \(\mathcal {L}\) with the indicated free variables and assume \(a,b_1,\ldots ,b_n \in {{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\). If we set
then we have

for all \(\Gamma \) and all d-operators \(\mathcal {H}\).
Proof
From Lemma 2.8.1 we know that

Now we apply \((\textsf{Ref})\) and obtain

Then two applications of \((\vee )\) finish our proof.
Now we know that all axioms of \(\textsf{KP}^T\) can be embedded into \(\textsf{IP}\). Before turning to the embedding theorem we need some further notation. If \(\Gamma [x_1,\ldots ,x_k]\) is the finite set of \(\mathcal {L}\) formulas
whose free variables are among \(x_1,\ldots ,x_k\) and if \(r_1,\ldots ,r_k\) are terms of \(\textsf{IP}\) (i.e. constants for elements of \({{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\)), then \(\Gamma [r_1,\ldots ,r_k]\) stands for the set of \(\textsf{IP}\) formulas
Theorem 2.8.9
(Embedding) If \(\textsf{KP}^T\) proves \(\Gamma [u_1,\ldots ,u_k]\), then there exist \(m, n <\omega \) such that

for all \(\textsf{IP}\) terms \(r_1,\ldots ,r_k\).
Proof
Note that
-
\( par ( \Gamma [r_1,\ldots ,r_k]) \cup \{\omega ^{\Omega {+}m}\} \,\subseteq \, \mathcal {H}_0[r_1,\ldots ,r_k](\varnothing )\).
-
If \(A[u_1,\ldots ,u_k]\) is a formula of \(\mathcal {L}\) with at most the indicated free variables, then there exists an \(n_A < \omega \) such that
$$\begin{aligned} rk (A[r_1,\ldots ,r_k]) < \Omega +n_A \end{aligned}$$for all terms \(r_1,\ldots ,r_k\) of \(\textsf{IP}\); see Lemma 2.6.4. Since every derivation in \(\textsf{KP}^T\) contains only finitely many formulas A, we simply choose n to be the maximum of all such \(n_A\).
Now we proceed by induction on the length of the derivation of \(\Gamma [x_1,\ldots ,x_k]\) in \(\textsf{KP}^T\).
(i) \(\Gamma [u_1,\ldots ,u_k]\) is an axiom of \(\textsf{KP}^T\). By Lemmas 2.8.1–2.8.8 we then have

for all \(\textsf{IP}\) terms \(r_1,\ldots ,r_k\).
(ii) The last inference was (ex). Then \(\Gamma [u_1,\ldots ,u_k]\) contains a formula \(\exists x F[x,u_1,\ldots ,u_k]\) and the premise of this inference is
for some variable v. By the induction hypothesis there exists an \(m_0 < \omega \) such that

for all \(\textsf{IP}\) terms \(r_1,\ldots ,r_k\). Here s is the term \(r_i\) if v is the variable \(u_i\) for some \(i \in \{1,\ldots ,k\}\) and the term \(\bar{\varnothing }\) if v is different from all \(u_1,\ldots ,u_k\). An application of \((\exists )\) yields our assertion for \(m:= m_0+1\).
(ii) The last inference was (cut). Then the two premises of (cut) are
-
(1)
\(\Gamma [u_1,\ldots ,u_k],\, A[u_1,\ldots ,u_k,v_1,\ldots v_\ell ]\),
-
(2)
\(\Gamma [u_1,\ldots ,u_k],\, \lnot A[u_1,\ldots ,u_k,v_1,\ldots v_\ell ]\),
with cut formula \(A[u_1,\ldots ,u_k,v_1,\ldots v_\ell ]\), where \(v_1,\ldots ,v_\ell \) lists its free variables not belonging to \(u_1,\ldots ,u_k\). By the induction hypothesis we have \(m_0,m_1 < \omega \) such that
-
(3)
 ,
, -
(4)
 .
.
\((\textsf{Cut})\) applied to (3) and (4) yields our assertion for \(m := \max (m_0,m_1)+1\).
(iii) All other cases can be treated accordingly.
9 Predicative Cut Elimination
The rules of inference of \(\textsf{IP}\) can be divided into two classes: (i) In all rules with the exception of \((\textsf{Ref})\) the principal formula is more complex (or complicated if you want) than the respective minor formula(s). We, therefore, consider rules of this sort as predicative rules. (ii) On the other hand, in \((\textsf{Ref})\) we transform a \(\Sigma \) sentence into a (generally) less complex \(\Sigma _1\) sentence. This is a sort of impredicativity and, consequently, we consider \((\textsf{Ref})\) as an impredicative inference. This distinction is also reflected in the elimination of cuts from proofs in \(\textsf{IP}\); it proceeds in two steps.
In this section we show that all cut formulas, that come from a predicative inference rule, can be eliminated by standard methods as described, for example in Schütte [16]. The principal formula of an \((\textsf{Ref})\) inference has rank \(\Omega \) and so we do not touch, in this section, cut formulas of rank \(\Omega \).
Lemma 2.9.1
(Reduction) Let F be an \(\mathcal {L}[{\boldsymbol{\eta }}]\) sentence of the form \((G_0 \vee G_1)\), \((\exists x \in \bar{a})G[x]\), or \(\exists x G[x]\) and assume that \(\rho := rk (F)\) is different from \(\Omega \). Then we have, for all \(\Gamma , \Lambda , \alpha , \beta \) and all d-operators \(\mathcal {H}\),

Proof
One easily checks that
follows from (a) and (b). The proof is by induction on \(\beta \), and we distinguish the following cases.
(i) \(\Lambda , F\) is an axiom of \(\textsf{IP}\). Then \(\Lambda , F\) contains an atomic formula true in \({{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\), and this formula must be different from F. Hence \(\Gamma , \Lambda \) contains this formula as well and so is an axiom of \(\textsf{IP}\).
(ii) The last inference was \((\exists )\) with principal formula F. Then F has the form \(\exists x G[x]\) and there exist a \(b \in {\boldsymbol{L}}_\beta \) and a \(\beta _0 < \beta \) such that

By the induction hypothesis we have

From (2.1) we also obtain
(a) and (2.3) yield by Inversion that

and therefore, by (2.4) and Weakening,

Since \( rk (G[\bar{b}]) < \rho \) it only remains to apply \((\textsf{Cut})\) to (2.2) and (2.5).
(iii) All other last inferences with principal formula F are treated analogously. F cannot be the principal formula of \((\textsf{Ref})\) because of \( rk (F) \ne \Omega \).
(iv) Finally, if F was not the principal formula of the last inference, we apply the induction hypothesis the premise(s) of this inference and then carry it out again.
As mentioned above, we restrict ourselves in this section to eliminate all cuts whose cut formulas do not have rank \(\Omega \). With the help of the previous lemma the proof of the following theorem is standard.
Theorem 2.9.2
(Predicative elimination) We have for all \(\Gamma \) and all derivation operators \(\mathcal {H}\):
-
(1)
 .
. -
(2)
 .
.
For details see Buchholz [3] and/or Schütte [16]. Recall that \(\omega _0(\alpha ) := \alpha \) and \(\omega _{n{+}1}(\alpha ) := \omega ^{\omega _n(\alpha )}\).
10 Collapsing Theorem
We begin this section by showing how to eliminate cut formulas of rank \(\Omega \). More precisely, we will show that any operator controlled proof of a set \(\Gamma \) of \(\Sigma \) sentences in which all cut formulas have ranks \(\le \Omega \) can be collapsed into a proof of depth and cut rank less than \(\Omega \). This technique—called collapsing technique—is the corner stone of impredicative proof theory.
Together with the results of the previous sections this collapsing theorem will then lead to the Hauptsatz of this article.
Theorem 2.10.1
(Collapsing) Let \(\Gamma \) be a finite set of \(\Sigma \) sentences of \(\mathcal {L}[{\boldsymbol{\eta }}]\) and \(\gamma \) an ordinal such that
Then we have, for all \(\alpha \),

where \({\widehat{\alpha }}\,:=\, \gamma + \omega ^{\Omega + \alpha }\).
Proof
We show this assertion by induction on \(\alpha \) and assume  . Then we have (see Lemmas 2.5.4 and 2.5.5):
. Then we have (see Lemmas 2.5.4 and 2.5.5):
Now we proceed with a distinction by cases according to the last inference of  and note that this cannot be \((\forall )\). In the following we confine our attention to the interesting cases; all others can be dealt with in a similar manner.
and note that this cannot be \((\forall )\). In the following we confine our attention to the interesting cases; all others can be dealt with in a similar manner.
(i) \(\Gamma \) is an axiom. Then  follows from (2.1) and (2.2).
follows from (2.1) and (2.2).
(ii) The last inference was \((b\forall )\). Then \(\Gamma \) contains a formula \((\forall x \in \bar{a})F[x]\) and we have

with \(\alpha _b < \alpha \) for all \(b \in a\). We also know that \(|\bar{a}| \in \mathcal {H}_\gamma [\Gamma ](\varnothing )\). Since \(|\bar{b}| < |\bar{a}|\) for all \(b \in a\), Lemma 2.5.2, Lemma 2.5.4(5), and (2.1) yield
Hence (2.3) gives us

and by the induction hypothesis we obtain that

and, therefore,

always for all \(b \in a\). Furthermore, from (2.3) and (2.4) we can also deduce that \(\alpha _b \in \mathcal {H}_\gamma [\Gamma ](\varnothing )\) for all \(b \in a\). In view of Lemma 2.5.5(2) we thus have \(\psi ({\widehat{\alpha }_b}) < \psi ({\widehat{\alpha }})\) for all \(b \in a\). An application of \((b\forall )\) yields  .
.
(iii) The last inference was \((\exists )\). Then \(\Gamma \) contains a formula \(\exists x F[x]\) such that

for some \(\alpha _0 < \alpha \) and some set \(b \in {\boldsymbol{L}}_\alpha \). Now set
In view of (2.6) we have \(\alpha _0, |r| \in \mathcal {H}_\gamma [\Gamma ](\varnothing )\). The induction hypothesis yields

thus also

Now recall that from Lemma 2.5.5(3) that
and conclude that \(|r| < \psi ({\widehat{\alpha }})\). In addition, \(\psi ({\widehat{\alpha }_0}) < \psi ({\widehat{\alpha }})\) follows from Lemma 2.5.5(2). Therefore, \((\exists )\) applied to (2.5) yields  .
.
(iv) The last inference was \((\textsf{Ref})\). Then \(\Gamma \) contains a formula \(\exists x F^x\), where F is a \(\Sigma \) sentence, and there exists an \(\alpha _0 < \alpha \) such that

and \(\alpha _0 \in \mathcal {H}_\gamma [\Gamma ](\varnothing )\). Now the induction hypothesis yields

hence

We know \(\psi ({\widehat{\alpha }_0}) \in \mathcal {H}_{\widehat{\alpha }}[\Gamma ](\varnothing )\) and therefore, since F is a \(\Sigma \) sentence, the Boundedness Lemma gives us

where r is the constant for the set \({\boldsymbol{L}}_{\psi ({\widehat{\alpha }_0})}\). In view of \(\alpha _0 \in \mathcal {H}_\gamma [\Gamma ](\varnothing )\) and Lemma 2.5.5(2) we also have \(\psi ({\widehat{\alpha }_0}) < \psi ({\widehat{\alpha }})\). Hence we can apply \((\exists )\) to (2.7) and obtain  .
.
(v) The last inference was \((\textsf{Cut})\). Then there exist an ordinal \(\alpha _0 < \alpha \) and a sentence F with \( rk (F) \le \Omega \) such that

and \( par (F) \cup \{\alpha _0\} \subseteq \mathcal {H}_\gamma [\Gamma ](\varnothing )\). We distinguish two cases:
(v.1) \( rk (F) < \Omega \). Then from Lemma 2.6.4(7) and Lemma 2.5.5(3) we conclude that \( rk (F) < \psi (\gamma +1) \le \psi ({\widehat{\alpha }})\). Also, F and \(\lnot F\) are \(\Sigma \) sentences. Therefore the induction hypothesis applied to (2.8) yields

As before, \(\psi ({\widehat{\alpha }_0}) < \psi ({\widehat{\alpha }})\). Hence \((\textsf{Cut})\) gives us  .
.
(v.2) \( rk (F) = \Omega \). Then F or \(\lnot F\) is of the form \(\exists x G[x]\) with \(G[\bar{\varnothing }]\) being a \(\Delta _0\) sentence. We assume that F is \(\exists x G[x]\). The induction hypothesis applied to the left hand side of (2.8) yields

Since \(\psi ({\widehat{\alpha }_0}) \in \mathcal {H}_{\widehat{\alpha }_0}[\Gamma ](\varnothing )\) we can apply the Boundedness Lemma and obtain

where r is the constant for the set \({\boldsymbol{L}}_{\psi ({\widehat{\alpha }_0})}\). By applying Lemma 2.6.8 to the right hand side of (2.8), we get

We also have \({\widehat{\alpha }_0}\in \mathcal {H}_\gamma [\Gamma ](\varnothing ) \subseteq \mathcal {H}_{\widehat{\alpha }_0}[\Gamma ](\varnothing )\) and
Hence, since \(\lnot F^r\) is a \(\Sigma \) sentence, we are in the position to apply the induction hypothesis, yielding

where \(\alpha _1 := \widehat{{\alpha }_{0}} + \omega ^{\Omega +\alpha _0} = \gamma + \omega ^{\Omega +\alpha _0} + \omega ^{\Omega +\alpha _0} < \gamma + \omega ^{\Omega +\alpha } = {\widehat{\alpha }}\) and, in addition, \(\alpha _1 \in \mathcal {H}_\gamma [\Gamma ](\varnothing );\) see Lemma 2.5.5(1).
Clearly, \( rk (F^r) < \Omega \) and, according to (2.9), we have \( par (F^r) \subseteq \mathcal {H}_{\widehat{\alpha }_0}[\Gamma ](\varnothing )\). Hence \( rk (F^r) < \psi ({\widehat{\alpha }_0}+1)\) by Lemma 2.6.4(7) and Lemma 2.5.5(3). Furthermore, \(\psi ({\widehat{\alpha }_0})< \psi (\alpha _1) < \psi ({\widehat{\alpha }})\). Therefore, we can apply \((\textsf{Cut})\) to (2.9) and (2.10) and obtain  .
.
Theorem 2.10.2
(Hauptsatz) Let \(A[u_1,\ldots ,u_k]\) be a \(\Sigma \) formula of \(\mathcal {L}\) with at most the indicated free variables and suppose that it is provable in \(\textsf{KP}^T\). For all \(a_1,\ldots , a_k \in {{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\) there exist a d-operator \(\mathcal {H}\) and an ordinal \(\alpha < {\boldsymbol{\eta }}\) such that
-
(1)
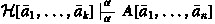 .
. -
(2)
 .
.
Proof
By Theorem 2.8.9 there are \(m,n < \omega \) with

for all \(\textsf{IP}\) terms \(r_1,\ldots ,r_k\). By a first application of predicative cut elimination, cf. Theorem 2.9.2(1), we obtain

for \(\beta := \omega _{n+1}(\Omega + m)\) and all \(\textsf{IP}\) terms \(r_1,\ldots , r_k\).
Now we pick specific \(a_1,\ldots , a_n \in {{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\). Then there exits an \(\ell <\omega \) such that
It follows that
and from (2.1) we obtain

Because of (2.2) and (2.3) we can apply Theorem 2.10.1, yielding

for \({\widehat{\beta }}:= \gamma + \omega ^{\Omega {+}\beta }\). A simple calculation shows that \(\alpha := \psi ({\widehat{\beta }})\) is smaller than \(\eta \) and thus the required ordinal for (1).
By making use of Theorem 2.9.2, the second assertion is an immediate consequence of (1). It only has to be verified with the help of Lemma 2.5.5 that \(\psi ({\widehat{\beta }}) \in \mathcal {H}_{\widehat{\beta }}[\bar{a}_1,\ldots ,\bar{a}_k](\varnothing )\).
The notion of \(\Pi _2\) ordinal of a theory T has been introduced in Jäger [12]. It is defined there as the least ordinal \(\alpha \) such that \({\boldsymbol{L}}_\alpha \, \models \, A\) for all \(\Pi _2\) consequences of T. One of the most prominent results along these lines and a direct consequence of Jäger [11] states that \({\boldsymbol{\eta }}\) is the \(\Pi _2\) ordinal of \(\textsf{KP}\). Besides that [12] contains a series of results about \(\Pi _2\) ordinals of theories for iterated admissible sets.
\(\Pi _2\) ordinals have also been considered in Rathjen [15] and Pohlers [14]. Some remarks have been made in these articles and in [12] about the relationship between proof-theoretic ordinals and \(\Pi _2\) ordinals. It is planned to come back to this topic from a more general perspective in Jäger [10].
It is not surprising that our Hauptsatz directly implies that \({\boldsymbol{\eta }}\) is the \(\Pi _2\) ordinal of \(\textsf{KP}\).
Corollary 2.10.3
(\(\Pi _2\) ordinal of \(\textsf{KP}\)) If A is a \(\Pi _2\) sentence of \(\mathcal {L}\), the we have
Proof
A has the form \(\forall x \exists yB[x,y]\) such that B[x, y] is a \(\Delta _0\) formula of \(\mathcal {L}\) with at most x, y free. Since \(\textsf{KP}\) proves A, it is clear that \(\textsf{KP}^T\) proves \(\exists yB[u,y]\) for any u. Now pick an arbitrary \(a \in {{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\). Then the Hauptsatz tells us that

for some d-operator \(\mathcal {H}\) and some \(\alpha < {\boldsymbol{\eta }}\). Therefore,
according to Theorem 2.7.1. Since this is so for any element a of \({{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\), we have \({{\boldsymbol{L}}}_{{\boldsymbol{\eta }}}\, \models \, A\).
References
J. Barwise. Admissible Sets and Structures. Number 7 in Perspectives in Mathematical Logic. Springer, 1975.
W. Buchholz. A new system for proof-theoretic ordinal functions. Annals of Pure and Applied Logic, 32: 195–207, 1986.
W. Buchholz. A simplified version of local predicativity. In P. Aczel, H. Simmons, and S.S. Wainer, editors, Proof Theory, pages 115–147. Cambridge University Press, 1992.
W. Buchholz. Assigning ordinals to proofs in a perspicious way. In W. Sieg, R. Sommer, and C. Talcott, editors, Reflections on the Foundations of Mathematics: Essays in Honor of Solomon Feferman., volume 15 of ASL Lecture Notes in Logic, pages 37–59. Association for Symbolic Logic, 2002.
W. Buchholz and W. Pohlers. Provable wellorderings of formal theories for transfinitely iterated inductive definitions. The Journal of Symbolic Logic, 43 (1): 118–125, 1978.
W. Buchholz, S. Feferman, W. Pohlers, and W. Sieg. Iterated Inductive Definitions and Subsystems of Analysis: Recent Proof-Theoretical Studies, volume 897 of Lecture Notes in Mathematics. Springer, 1981.
W. Burr. A Diller-Nahm-style functional interpretation of \(\sf {KP}\omega \). Archive for Mathematical Logic, 39 (8): 599—604, 2000.
S. Feferman. Formal theories for transfinite iterations of generalized inductive definitions and some subsystems of analysis. In A. Kino, J. Myhill, and R.E. Vesley, editors, Intuitionism and Proof Theory, volume 60 of Studies in Logic and the Foundations of Mathematics, pages 303–326. North-Holland, 1970.
F. Ferreira. A new computation of the \({\Sigma }\) ordinal of \(\sf {KP} \omega \). The Journal of Symbolic Logic, 79 (1): 306–324, 2014.
G. Jäger. Proof-theoretic ordinals, \({\Pi }_2\) ordinals, and all that. in preparation.
G. Jäger. Zur Beweistheorie der Kripke-Platek-Mengenlehre über den natürlichen Zahlen. Archive for Mathematical Logic, 22 (3-4): 121–139, 1982.
G. Jäger. Some proof-theoretic contributions to theories of sets. In The Paris Logic Group, editor, Logic Colloquium ’85, volume 122 of Studies in Logic and the Foundations of Mathematics, pages 171–191. North-Holland, 1987.
W. Pohlers. Cut-elimination for impredicative infinitary systems part I. ordinal-analysis for \({{\sf ID}_1}\). Archive for Mathematical Logic, 21 (1): 113–129, 1981.
W. Pohlers. Proof Theory. The First Step into Impredicativity. Universitext. Springer, 2009.
M. Rathjen. Fragments of Kripke-Platek set theory. In P. Aczel, H. Simmons, and S.S. Wainer, editors, Proof Theory, pages 251–273. Cambridge University Press, 1992.
K. Schütte. Proof Theory, volume 225 of Grundlehren der mathematischen Wissenschaften. Springer, 1977.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2022 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Jäger, G. (2022). Simplified Cut Elimination for Kripke-Platek Set Theory. In: Ferreira, F., Kahle, R., Sommaruga, G. (eds) Axiomatic Thinking II. Springer, Cham. https://doi.org/10.1007/978-3-030-77799-9_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-77799-9_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-77798-2
Online ISBN: 978-3-030-77799-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)





 .
.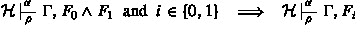 .
. .
. .
. .
. .
. .
. .
. ,
, .
. .
. .
.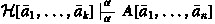 .
. .
.