Keywords

1 Introduction

Tensegrity domes, Geiger’s type (Ouni and Ben Kahla 2014) for instance, are innovative lightweight space reticulated pre-stressed systems composed of a network of continuous tensile cables and discontinuous compressive bars. They are employed as large span roofs of structures including arenas, stadiums and sport centers. These structures are very flexible and have low damping and thus they are sensitive to vibrations induced by wind or earthquakes. In order to control these induced vibrations, several studies have been carried out and the focus was particularly made on active control techniques (Ouni and Ben Kahla 2014). Although actives control techniques showed effectiveness, their implementation in real large scale structures remains of particular complexity. An alternative to these techniques is the use of passive techniques such as mounting TMD devices into vibrating structure (Mrabet et al. 2016).

TMD devices are very reliable and efficient in vibration control of structures and have been widely used for their low cost and design simplicity. Nevertheless, the parameters of such devices should be carefully optimized in order to effectively reduce the vibrations. Several optimization strategies can be found in the literature and among them the reliability based optimization (RBO) (Mrabet et al. 2016) that has been efficiently used in the passive control (using TMD) of earthquakes induced vibrations, for instance. In the present work a TMD device, optimized using the RBO strategy, is used for the control of a Geiger’s structure. The RBO strategy has been compared to other strategies and the obtained results showed its superiority in reducing the global vibration of a Geiger’s structure.

2 Governing Equations, Optimization of the TMD Parameters

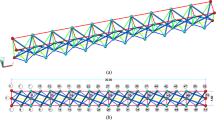
Figure 1 shows the considered tensegrity dome of Geiger’s type with its components of strings and struts. In Fig. 1(a) the nodes are numbered whereas in Fig. 1(b) the location of the TMD device (on node 2) is showed in a typical section view. The TMD is characterized by its natural frequency \(\omega_{T}\) and its damping ratio \(\xi_{T} = c_{T} /2m_{T} \omega_{T}\), where \(c_{T}\) is the damping coefficient and \(m_{T} = \mu \times m_{s}\) is its mass; \(\mu\) and \(m_{s}\) are the mass ratio and the mass of the tensegrity structure, respectively.

Let \({\mathbf{x}} = (x_{1} ,y_{1} ,z_{1} ,..,x_{31} ,y_{31} ,z_{31} ,z_{T} )^{T}\) be the (78 + 1) × 1 displacement vector of the nodes and the TMD device, where \(z_{T}\) is the TMD displacement and the superscript notation T denotes transpose. Assuming that the deformations of the structure is linear elastic (Feng et al. 2018), the governing equation of motion, around an equilibrium configuration, of the cable dome equipped with a TMD can be written as follows,

$$ \overline{{\mathbf{M}}} {{\ddot{\mathbf{x}} + }}\overline{{\mathbf{C}}} {{\dot{\mathbf{x}} + }}\overline{{\mathbf{K}}} {\mathbf{x = W}}_{excit} $$
(1)

where \(\overline{{\mathbf{M}}} = \left[ {\begin{array}{*{20}c} {\mathbf{M}} & 0 \\ 0 & {m_{T} } \\ \end{array} } \right]\), \(\overline{{\mathbf{C}}} = \left[ {\begin{array}{*{20}c} {\mathbf{C}} & {\mathbf{0}} \\ {\mathbf{0}} & 0 \\ \end{array} } \right] + c_{T} {\mathbf{b}}{\mathbf{.b}}^{T}\), \(\overline{{\mathbf{K}}} = \left[ {\begin{array}{*{20}c} {\mathbf{K}} & {\mathbf{0}} \\ {\mathbf{0}} & 0 \\ \end{array} } \right] + k_{T} {\mathbf{b}}{\mathbf{.b}}^{T}\), \({\mathbf{W}}_{excit}\) is the (78 + 1) × 1 vector of the point forces that are assumed to be uncorrelated stationary zeros mean Gaussian white noise; the point forces are applied on the top nodes (1, 3, 5, 8, …., 28, 30) of the structure along the z-axis (vertical forces). Besides, \({\mathbf{b}} = (0,0,0,.., - 1,0,..,1)^{{\text{T}}}\) is the location vector of the TMD; \({\mathbf{M}}\), \({\mathbf{C}}\) and \({\mathbf{K}}\) are the mass, damping and the tangent stiffness matrices, respectively. The expressions of these matrices are given in Feng et al. (2018).

Fig. 1.
figure 1

(a) The tensegrity dome of a Geiger’s type made up of 13 vertical struts and 60 strings (Ouni and Ben Kahla 2014), (b) typical section view with the TMD mounted on node2

Full size image

Equation (1) can be recast in space state form and the covariance responses of the structure can be obtained, in stationary conditions, using the Lyapunov equation (Wijker 2009) as follows:

$$ {\mathbf{AR + RA}}^{{\text{T}}} + {\mathbf{B = }}0 $$
(2)

where \({\mathbf{R}} = \left\langle {{\mathbf{XX}}^{{\text{T}}} } \right\rangle\) is the covariance matrix, \({\mathbf{X}} = ({\mathbf{x,\dot{x}}})^{{\text{T}}}\), \(\left\langle . \right\rangle\) denotes the mathematical expectation, \({\mathbf{A}} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{I}} \\ { - \overline{{\mathbf{M}}}^{ - 1} \overline{{\mathbf{K}}} } & { - \overline{{\mathbf{M}}}^{ - 1} \overline{{\mathbf{C}}} } \\ \end{array} } \right]\), \({\mathbf{B}} = {\mathbf{GS}}_{0} {\mathbf{G}}^{{\text{T}}}\), \({\mathbf{G}} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & { - \overline{{\mathbf{M}}}^{ - 1} } \\ \end{array} } \right]^{{\text{T}}}\) and \({\mathbf{S}}_{0}\) is the constant power spectral density (PSD) matrix of the white noise excitations.

In the present work the optimization strategy consists in minimizing the failure probability \(P_{f}\) characterized by the out-crossing, for the first time, of a given threshold value β of the vertical displacement of node 2 during some interval time T. The failure probability can be approximated, using the Rice’s formula based on the Poisson assumptions (Mrabet et al. 2016), as follows:

$$ P_{f} = 1 - \exp [ - {\text{T}} \times (\sigma_{{\dot{z}_{2} }} /\pi \sigma_{{z_{2} }} ) \times \exp ( - \beta^{2} /2\sigma_{{z_{2} }}^{2} )] $$
(3)

where \(\sigma_{{z_{2} }}\) and \(\sigma_{{\dot{z}_{2} }}\) are the root mean square (RMS) displacement (z-axis) and velocity of node 2 of the dome structure, respectively; these quantities can be obtained using Eq. (2).

Let \({\mathbf{d}} = (\omega_{T} ,\xi_{T} )^{T}\) be the design vector, the optimization problem can be formulated as follows:

$$ {\text{Find}}\;\;{\mathbf{d}} = (\omega_{T} ,\xi_{T} )^{T} \;\;{\text{to}}\;{\text{minimize}}\;\;P_{f} $$
(4)

3 Numerical Example

Tables 1 and 2 show the geometric characteristics of the Tensegrity dome. The elastic modulus and density of all the elements are equal to 160 GPa and 7.85 × 10−3kg/cm3, respectively. The cable elements have yield strength of 0.6 GPa and a breaking strength of 0.8 GPa. The struts are round tubes (diameter = 2.13 cm and thickness = 0.16 cm) and they have a cross section area equal to 1 cm2. The natural damping of the structure is assumed equal to 1% for all modes.

A modal analysis of the uncontrolled structure has been conducted and the first three flexural mode shapes that are sensitive to the vibrations induced by vertical random excitations are shown in Fig. 2 where their corresponding resonant frequencies are also presented.

For the sake of comparisons, the performance of the TMD, optimized using the RBO strategy, has been compared with three other strategies from the literature. The first strategy is that established by Den Hartog (Warburton 1982), which is a deterministic strategy, the two other are that of Leung (Leung and Zhang 2009) and that of Warburton (Warburton 1982) which are stochastic optimization strategies, since they involve white noise excitations.

Table 1. Initial coordinates of the Geiger’s dome.
Full size table
Table 2. Cross-section area and initial pre-tension of different cable families.
Full size table

The corresponding tuning formulas are shown in Table 3 where \(\xi_{s}\) is the modal damping ratio of the structure (the mode to be controlled), \(\varpi\) is the target frequency and \(\mu_{eff}\) is the effective mass ratio as defined by Warburton (Warburton 1982). For the RBO strategy, the mass ratio is taken μ = 2%, T = 10 s, β = 0.25 m and the PSD intensity of the forces is taken S0 = 1N2/Hz.

The targeted mode was the first flexure mode of the structure corresponding to the natural frequency \(\varpi\) = 31.95 rad/s and the optimization (RBO) has been carried out. The optimal parameters are found \({\mathbf{d}}_{\mathrm{RBO}}^{\mathbf{*}}\) = (30.62, 0.26)T and \({P}_{f}^{*}\) = 9.910–4 whereas for the other strategies \({\mathbf{d}}_{\mathrm{Leung}}^{\mathbf{*}}\) = (29.86, 0.20)T, \({\mathbf{d}}_{\mathrm{Warburton}}^{\mathbf{*}}\) = (29.90, 0.15)T and \({\mathbf{d}}_{\mathrm{Den Hartog}}^{\mathbf{*}}\) = (29.22, 0.18)T.

Fig. 2.
figure 2

Flexural mode shapes sensitive to vibrations induced by a vertical excitation on the upper nodes of the dome (Ouni and Ben Kahla 2014)

Full size image

The performances of the TMD are shown in Figs. 3, 4, 5 where the frequency response functions (FRF) are plotted for three different nodes. Indeed, because of the symmetry in the dome structure, the FRFs of nodes 4, 9, 14, 19, 24 and 29 are similar and those of nodes 6, 11, 16, 21, 26 and 31 are also similar.

The inspection of Fig. 3 shows good performance of the RBO strategy where significant reduction has been recorded (19.5 dB) in the vicinity of the targeted frequency. In addition, although the Leung’s tuning provided better performance (20.5 dB), the RBO strategy has performed better in the vicinity of the off-target frequencies. Indeed, one can observe that for the third resonant mode, for instance, the RBO provided a reduction of 18.1 dB in the FRF magnitude whereas it has been 16.1 dB when the Leung’s tuning (which is the better among the other strategies) is applied.

Table 3. The tuning formulas of the TMD parameters.
Full size table

Figures 4 and 5 show the FRFs of nodes 4 and 6 where significant reductions of 20.6 dB and 20.4 dB are obtained, respectively, in the vicinity of the targeted frequency. This fact implies that the RBO strategy provide better global attenuation performances since all displacement nodes are better controlled. For the other strategies, the best performance is obtained when the Leung’s tuning has been applied.

Fig. 3.
figure 3

FRF (observation node 2)

Full size image
Fig. 4.
figure 4

FRF (observation node 4)

Full size image
Fig. 5.
figure 5

FRF (observation node 6)

Full size image

4 Conclusion

In the present work, a passive control of a tensegrity structure using TMD is investigated. The TMD parameters are obtained using a reliability based optimization and the TMD showed good performance in the vicinity of the targeted frequency as well as the off-targeted ones. Compared to other optimization strategies, the reliability based optimization strategy has shown its superiority especially in the global attenuation of structural vibrations. Although it needs to be investigated in real scale structures, such strategy is a promising tool for the TMD design for the passive vibration control of such types of spatial structures.