Deformation Mechanisms in Tool–Workpiece Asperity Contact in Metal Forming

Abstract

The contribution to friction stemming from dissipation of plastic energy is studied by numerical simulations and experiments. The geometrical setup consists of a single model asperity, which is first flattened against a tool with grooves on a smaller length scale. Relative, tangential sliding between the model asperity and the tool is induced subsequently until a steady state is reached. The flank angle of the grooves on the tool is varied. Comparison between the simulations and the experiments leads to validation of the simulations at low tool flank angles, while the current numerical implementation cannot handle the complicated flow around the tool grooves with a large flank angle. At low flank angles, the simulated tangential tool force is in agreement with experiments when keeping one determined friction factor. This proves that the change in tangential force, corresponding to a change in apparent friction factor, is only due to the dissipated energy from the plastic waves. The validated numerical model can be used to determine a wider range of apparent friction factors for strain hardening materials.

1 Introduction

Bowden and Tabor [3] described the influence of asperity contact on friction and started the intense analysis on asperity flattening among several research groups over the following decades. One path goes through Shaw et al. [12], who suggested a smooth transition from Amontons–Coulomb’s friction model to the constant friction model due to asperity flattening being individual at low normal pressures while being interacting at higher normal pressures, and Wanheim and Bay [17] who quantified the development of real contact area by slip-line analysis under frictional sliding. Sutcliffe [14] also analyzed asperity flattening by slip-line analysis taking into account subsurface deformation but not the asperity interaction at high normal pressures. Lately, Wang et al. [15] and Nielsen et al. [10, 11] analyzed asperity flattening while taking both strain hardening and subsurface deformation into account by a combined experimental and numerical study.

Common for the majority of research on asperity flattening is the focus on model asperities that are scaled up for practical reasons when evaluating real contact area. The real contact area resulting from these analyses is, however, overestimating the true real contact area due to the existence of multiple orders of asperities. In fact, the typical flat plateaus of the first-order asperities contain second-order asperities, and hence, the true real contact area is smaller than that estimated by first-order asperities. Such an approach can continue on the flat plateaus of the second-order asperities, and so forth. Steffensen and Wanheim [13] did such an analysis and concluded that the reduction of the true real contact area due to second-order asperities on the first-order plateaus is rather insensitive to normal pressure and friction on the plateaus. This is justifying the analyses that are being done on model asperities, which represent the first-order asperities of a real surface. It is justified by the higher order effects on the real contact area being rather constant, which leaves the possibility of having this effect hidden in the friction factor that is assumed on the flat plateaus of the first-order asperities.

A number of mechanisms have been proposed as contributions to the friction that appears in the real contact. Bay and Wanheim [1] presented an overview of the origins of friction. Bowden and Tabor [3] identified the shearing of layers due to adhesion and micro welds as well as dragging or plowing of a harder material through a softer material. Wanheim and Abildgaard [16] later added the mechanism of plastic waves in the softer material induced by the roughness of the harder tool material upon relative sliding. They showed the existence of the plastic wave mechanism by an experiment and gave by slip-line analysis the apparent friction factor as function of the real friction factor along the tool grooves and the groove angle on the harder tool material.

Plastic waves have also been analyzed by other groups. Challen and Oxley [4] modeled one hard asperity in relative sliding against a softer material. Depending on the angle of the hard asperity, this gave rise to a steady-state standing wave, wear, or cutting. Challen et al. [5] presented experiments verifying the modeling, and Challen and Oxley [6] presented slip-line analyses with more than one hard asperity and in the full range from zero to full filling of the grooves in the hard material.

Luo et al. [8] applied upper bound analysis to the moving wave mechanism by assuming contact with the tool only on one side. They found that for low flank angles, the wave may disappear after some sliding and confirmed that by experiments. Bin and Luo [2] applied finite element analysis to the analysis of one hard asperity sliding against a softer workpiece material and found good agreement with their simulation and experiments previously published by Challen and Oxley [4].

In the present paper, the focus is on the deformation mechanisms due to plastic waves on top of workpiece asperities that are flattened by a hard tool and subjected to relative sliding against it. First-order asperity flattening is considered by imposing the plastic waves on top of a model asperity. The deformation mechanisms are analyzed by experiments, numerical simulation, and metallurgical analysis.

2 Experimental Setup

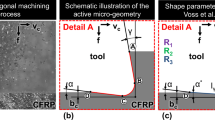
The tool–workpiece contact in metal forming is considered by taking into account first-order asperities on the workpiece surface and a tool surface, which in comparison to the workpiece, is smooth. Such an interface is illustrated in Fig. 1a with the identification of a single asperity that is taken out for analysis. The single asperity is shown in a schematic illustration of an experiment in Fig. 1b. At this scale, the tool surface is assumed to have asperities as well, but with a wavelength much smaller than that of the workpiece surface. The experiment illustrated in Fig. 1b has a single model asperity (A) with flank angle $\gamma$ in contact with a tool (T) with many, smaller asperities with flank angle $\beta$. A normal pressure between the asperity and the tool can be induced by the punch (P) resulting in asperity flattening against the tool under plane strain deformation (zero strain perpendicular to the figure due to tool blocks that are not shown in the illustration).

Fig. 1

Schematic illustration of the asperity contact. a Workpiece and tool interface represented by first-order workpiece asperities in contact with a smooth tool with relative movement given by the arrow. The dashed rectangle identifies a single asperity (A) and the contacting tool (T). b Experimental setup with a single model asperity (A) supported against rotation by (S) and pressed towards a tool (T) by the punch (P). Notice that the tool in this magnification also has asperities. The tool (T) is separated from the base (B) by a layer of Teflon (L) to minimize friction when moved tangentially to the asperity

The tool (T) can move tangentially to emulate relative sliding in the tool–workpiece interface. The tangential force will be the sum of the apparent friction against the model asperity and the friction against the base (B), which is minimized by a separating layer of Teflon (L). The apparent friction against the model asperity is due to true friction, where workpiece material is in relative sliding along the tool asperities, and due to plastic power dissipation in the plastic waves that the tool induces in the workpiece model asperity.

Figure 2 shows a photograph of the real experiment after having removed a few supporting blocks to allow the photograph to show the model asperity and tool contact. The photograph is taken after an experiment and therefore Fig. 2 shows a flattened model asperity. The normal load applied by the punch (P) is measured by a piezoelectric load cell above the punch. The tangential load on the tool (T) is measured through a pre-compressed piezoelectric load cell connected to the rigging screw (R). Both load cells are outside the photograph.

Fig. 2

Experimental setup with labels corresponding to Fig. 1 with the addition of (R) identifying the rigging screw connected to a movable horizontal axis that is used to pull the tool (T). The support is given by four blocks surrounding the model asperity. The two blocks indicated by white dashed lines were removed for taking the photograph. Of the two other blocks, which are used to ensure plane strain deformation, one was also removed for taking the photograph. (Color figure online)

The model asperity (A) is machined with a flank angle $\gamma = 10^{ \circ }$ and a width $w = 60\,{\text{mm}}$ representing the model asperity wavelength. The thickness of the specimen is $t = 10\,{\text{mm}}$ (in the direction of plane strain). The model asperities are made from aluminum 1050, while the tool (T) is made of cold work tool steel, hardened and tempered to 58–60 HRC. Three tools were made with flank angles $\beta = 5^{ \circ }$, $\beta = 10^{ \circ }$, and $\beta = 15^{ \circ }$, respectively. The wavelength of the tool asperities is $l = 1.5\,{\text{mm}}$. The tool asperities were polished to a roughness $R_{a} \le 0.25\,\mu {\text{m}}$ and the tool asperity tip radii were measured to around $R = 1.4\,{\text{mm}}$. Zinc stearate was used for lubrication by applying a thin layer to both the workpiece and tool surfaces. The aluminum workpieces were pickled in a NaOH bath prior to rubbing zinc stearate to the surface.

Aluminum 1050 used for the model asperities is characterized by the flow stress curve shown in Fig. 3. The flow stress has been tested at large strains due to heavy local deformation in the experiments. The flow stress curve is based on simple upsetting until an equivalent strain of 0.5. In order to achieve experimental data at large strains, the original 1050 plate was rolled with different thickness reductions and tensile samples were cut from the rolled plates. The yield stress found by tensile testing gave rise to a flow stress at the equivalent strain dictated by the amount of rolling. The data points stemming from rolling and subsequent tensile testing have been multiplied by an estimated factor of 1.18 [7] taking into account the strength anisotropy of the lamellar structure, especially formed at the medium and large strains in the present study. The strength in the normal direction is typically higher than that of the lamellar direction when a lamellar microstructure forms with surface deformation by different processing methods, e.g. due to friction or particle bombardment [18]. By doing this, comparison to compression stress from aluminum 1050 cylinders in our previous research [19] revealed good agreement with the compression stress from the aluminum 1050 cylinders at strains up to 2. The flow stress between equivalent strains of 0.5 and 3.9, which was the maximum strain obtained by rolling, is a best fit by a second-order polynomial through the end point of the upsetting test and the experimental data points at large strains after scaling. Above an equivalent strain of 3.9, the flow stress is assumed constant. The flow stress curve used for numerical modeling can be summarized as

Fig. 3

Flow stress curve based on simple upsetting below an equivalent strain of 0.5 and scaled tensile tests of rolled samples above 0.5

$$ \sigma \left[ {MPa} \right] = \left\{ {\begin{array}{*{20}c} {141\varepsilon^{0.21} } & {\text{for}} & {\varepsilon \le 0.5} \\ {96.1 + 54.7\varepsilon - 6.31\varepsilon^{2} } & {\text{for}} & {0.5 < \varepsilon \le 3.9} \\ {214} & {\text{for}} & {\varepsilon > 3.9} \\ \end{array} } \right. $$

(1)

3 Numerical Model

The deformation mechanisms on the flattened model asperity are simulated by the numerical model shown in Fig. 4. The initial mesh for one model asperity with flank angle $\gamma = 10^{ \circ }$ is shown in Fig. 4a with boundary conditions on the sides that only allow vertical movement and with a nominal normal pressure $q$ stemming from the applied load by the punch. After plain strain asperity flattening against the tool, which is shown for the case having tool asperities with flank angle $\beta = 15^{ \circ }$ and wavelength $l = 1.5\,{\text{mm}}$, relative sliding by a constant velocity $v = 1\,{\text{mm}}/{\text{s}}$ is imposed. The mesh refinement on the asperity tip allows an initial element size being 3% of the tool asperity wavelength.

Fig. 4

Finite element mesh consisting of 26,084 quadrilateral elements for simulation of model asperity shown a in initial condition and b after flattening due to normal pressure $q$ and after sliding with relative velocity $v$ against the hard, rough tool

The numerical calculations are based on discretization by quadrilateral finite elements and an underlying irreducible flow formulation by minimization of the following functional

$$ \varPi = \int\limits_{V} {\dot{\overline{\sigma \varepsilon }}dV} + K\int\limits_{V} {\dot{\varepsilon }_{v}^{2} dV} + \int\limits_{{S_{f} }} {\left( {\int_{0}^{{\left| {u_{r} } \right|}} {\tau du_{r} } } \right)dS} $$

(2)

where the energy rate due to plastic deformation is integrated over volume $V$ in the first term consisting of the effective stress $\bar{\sigma }$ and the effective strain rate $\dot{\bar{\varepsilon }}$. Incompressibility is enforced by penalizing volumetric strain rate $\dot{\varepsilon }_{v}$ by the penalty factor $K$ in the second term. The last term includes the frictional stress $\tau$ between the workpiece and the tool by integration over relative sliding velocity $u_{r}$ on the shared surface $S_{f}$. The applied finite element computer program is iform, which is an in-house numerical code shared between the University of Lisbon and the Technical University of Denmark. Additional information is given by Nielsen et al. [9].

4 Results and Discussion

The resulting tangential load from the experiments with flank angle $\beta = 5^{ \circ }$ is shown in Fig. 5 as function of the sliding length. Corresponding simulation results are included in the figure for a variation of the friction factor $m$ in the sliding along the tool grooves. A friction factor $m = 0.1$ in the simulations is found appropriate when comparing to the experiments. Increasing the tool flank angle $\beta$, while keeping the friction factor constant will increase the necessary tangential load due to additional dissipation of plastic energy by plastic waves. This is shown by the results in Fig. 6 by simulation results and experiments. The results for $\beta = 5^{ \circ }$ are the same as in Fig. 5. The simulations with $m = 0.1$ are seen also to match the experiments well for $\beta = 10^{ \circ }$, indicating that the only contribution to the increase of the tangential force is the plastic waves. When increasing the tool flank angle further to $\beta = 15^{ \circ }$ the simulation does not match the experiments any longer. This difference is explained by a difference in the local flow along the grooves. The finite element discretization still results in a smooth and continuous flow, while the experiments reveal workpiece material sheared off and deformed as a third body between the remaining workpiece and the tool. This gives rise to a higher tangential force than the ideal force predicted by simulation of an ideal flow.

Fig. 5

Tangential load as function of sliding length in case of tool asperity flank angle $\beta = 5^{ \circ }$ for experiments and numerical simulation with variation of the friction factor $m$. The error bars correspond to one standard deviation based on three repetitions, except for the last point which was only obtained in one of the experiments. (Color figure online)

Fig. 6

Tangential load as function of sliding length for different flank angles including experimental results and numerical simulation with friction factor $m = 0.1$. The error bars correspond to one standard deviation based on three repetitions, except for the last point with $\beta = 5^{ \circ }$ which was only obtained in one of the experiments. (Color figure online)

All cases show that the tangential force is building up to a rather constant level corresponding to steady-state sliding. From Fig. 6 it is noticed that steady state is obtained later for larger tool flank angle due to larger extend of the deformation field. During the initial transient build-up of the tangential force, the first-order real contact area increases due to the change in stress state. The induced shear on the flattened workpiece asperity reduces the necessary yield pressure, which is compensated by further deformation of the overall asperity as the normal load is kept constant. For the different tool flank angles, Fig. 7a shows the first-order real contact area ratio after deformation due to the applied normal load (dashed curves) and after additional sliding until steady state (solid curves). Both experimental results (blue curves) and simulated results (black curves) are included in the figure for comparison. A slight overestimation of the contact area is noticed for all the simulations. In order to focus on the effect of the additional sliding, Fig. 7b shows the relative change in first-order contact area for the three tool flank angles. Here, the simulations match the experiment for the tool flank angles $\beta = 5^{ \circ }$ and $\beta = 10^{ \circ }$, while the simulation underestimates the relative change for $\beta = 15^{ \circ }$ in agreement with the differences between simulation and experiment discussed in relation to Fig. 6.

Fig. 7

First-order real contact area between model asperity and tools with three different flank angles by experiments and numerical simulations. The contact area corresponding to stationary contact and to the developed contact area during sliding are shown in (a), while the change from stationary to sliding contact area is shown in (b). (Color figure online)

Cross-sectional photographs of the deformed workpiece surfaces are shown in Fig. 8 based on light optical microscopy (LOM). For each tool flank angle, a corresponding cross section of the workpiece is shown from the center of the flattened plateau of the first-order asperity. The photographs span just above one wavelength of the tool asperity, while the enlarged photos span around 40% of a tool asperity wavelength near a local tip of the workpiece (valley of the tool). The edges are unfortunately unclear after the grinding, polishing, and etching. White dashed lines have therefore been added manually along the edges. The identified edges for the cases with tool flank angles $\beta = 5^{ \circ }$ and $\beta = 10^{ \circ }$ are smooth waves, while the edge identified for the tool flank angle $\beta = 15^{ \circ }$ is a non-smooth wave due to a flow with much more shear and also induced cracks in the surface. This difference supports the above discussion, where simulations represent the results for the low tool flank angles, $\beta = 5^{ \circ }$ and $\beta = 10^{ \circ }$, while the simulations cannot be validated for the larger tool angle, $\beta = 15^{ \circ }$. It would require both further mesh refinement and handling of microcracks with resulting new contacts in the simulations to deal with the larger flank angle.

Fig. 8

Cross-sectional LOM pictures of the workpiece material after reaching steady state sliding for tool flank angles a $\beta = 5^{ \circ }$, b $\beta = 10^{ \circ }$ and c $\beta = 15^{ \circ }$. Enlarged pictures are shown from the workpiece tips of the pictures above. Tool movement is in this figure from left to right

5 Conclusions

Plastic waves, as a suggested deformation mechanism in the contact between workpiece asperities and tool surfaces by Wanheim and Abildgaard [16], have been studied by numerical simulations and experiments by an enlarged asperity which is flattened against a tool with smaller grooves representing tool surfaces asperities. The simulations have been successfully validated for low tool flank angles, $\beta = 5^{ \circ }$ and $\beta = 10^{ \circ }$, while the metal flow around the tool grooves for the larger tool angle, $\beta = 15^{ \circ }$, was too complicated for the present numerical implementation as it involved heavy shear and microcracks with new surfaces getting under compression. This paper leaves the numerical model ready for studying a wider range of friction factors along the tool grooves, a wider range of workpiece materials in terms of strain hardening behavior and a higher resolution of tool flank angles up to at least 10°. Wanheim and Abildgaard [16] already mapped the apparent friction factor as a function of the local friction factor and the tool flank angle for ideal plastic materials. Further work with the presented numerical model allows extending that mapping to include strain hardening materials. Variations of workpiece flank angle is another future extension to the present work. Experiments at smaller scales and numerical modeling based on crystal plasticity with effects of grain sizes and orientation to account for real surface scales are also future work.