Keywords

1 Introduction

The process of optimization is a basic cycle in numerous businesses, executives, and designing tools and applications. An optimization problem generally manages to look through the best solution set from all the attainable solution sets, and it is known as an optimal solution. A significant piece of exploration and application in the region of enhancement is consider as a solitary goal while practically viable tasks think about at least two or more than two destinations. The presence of a few opposing or conflicting destinations is ordinary in bunches of issues and which makes the advancement issues further captivating to illuminate. Most genuine choice and arranging circumstances include numerous conflicting measures that ought to be considered all the while. In these fields, numerous and frequently conflicting targets should be satisfied. They are known as multi-objective optimization problems (MOOPs), and their answer has pulled in consideration of analysts for a long time.

There are mainly three goals to seek after for solving a MOOP: (1) the act of convergent, (2) the assorted variety in the solution set, and (3) the solution set’s dissemination consistency. Moreover, the received non-dominated solution sets must be as close as conceivable to the Pareto optimal front of the MOOP. For the single-objective optimization problem (SOOP), this objective is like the interest to convergent at global optimum. Many times, there are uncountable solution sets which are Pareto optimal. Normally, just a finite number of solution sets is created throughout the process of optimization. Moreover, for reducing the computational expense, the quantity of created solution sets must be restricted. In any case, the biggest conceivable opportunity of decision ought to be put up on a Decision Maker (DM). Hence, a very much dispersed approximation set is requested, which is an objective that comprises itself of two demands: (1) the set that is as extensive as could be expected under the circumstances and (2) a distribution that is as uniformly divided as could reasonably be expected. Pareto optimal fronts may not be continuous, so all the things considered, a precisely uniform circulation of solution sets, is preposterous. In any case, the non-dominated solution sets must spread over the complete area of the Pareto front and reconstruct the fundamental curve of Pareto front as effectively as could be expected under the circumstances. These requirements don’t have a counterpart in SOOP since all things considered, just a single optimum solution is produced.

MOOPs are solved with two types of approaches, specifically known as classical and evolutionary approaches. In classical approaches, we substitute overall goals into an equivalent solitary goal that means the MOOP converts into SOOP. The final objective is to search the solution set that maximizes or minimizes this single objective while keeping up the framework’s physical constraints or cycle. The optimization solution set brings about a solitary worth that returns a trade-off between all goals. The craftsmanship in this cycle is to generate the function to accomplish this ideal trade-off solution.

Transformation of the MOOP into a SOOP is typically done by amassing every goal in a weighted function or converting everything except one of the destinations into constraints. This way to deal with unraveling MOOP has many restrictions: (1) it requires from the earlier information about the overall significance of the destinations, and the restrictions on the destinations that are transformed over into constraints (2) from the amassed function derives just a single solution set; (3) compromise solutions among destinations can’t be search out effortlessly, (4) the solution set can’t be feasible except for the convex space of search.

This basic optimization theory is not, at this point, worthy of frameworks with numerous conflicting destinations. Simultaneously, specialists may want to know every potential solution set of all the destinations. For the real world, it is called trade-off analysis. In the real world scenario, there are many instances of the demand to execute trade-off analysis. For instance, structuring appropriated regulators while decreasing expenses are two conflicting goals. Correspondingly, to put more utilitarian squares on a chip while limiting that chip region or potentially power dissemination are conflicting goals. To search the automobile that travels the largest length in a particular fixed time, although expecting the minimum energy, is a MOOP. Limiting the working expense of business, although keeping up a steady work power, is conflicting. Thus it is a MOOP [1,2,3]. There are so numerous standard life’s issues that go under the MOOP, for example, CPM, assignment problem, transportation problem, COTS selection problem, and so forth [4,5,6,7].

2 Multi-objective Optimization Problem

The goal of MOOP is to search the arrangement of satisfactory solution sets and provide them to the DM, which will pick among them at that point. Extra requirements or standards are prescribed either previously or after the DM’s search process can help direct, refine, or limit the pursuit. Yet, we will take a gander at the conventional situation where there is no earlier DM data.

2.1 Model of MOOP

Think about the issue of buying the most proficient merchandise. Assume here we have accepted it as we need to purchase the couch. Expect two rules are utilized to decide this effectiveness: (a) cost secured to make a specific couch, and (b) nature of the material that is utilized simultaneously. The presence of the mind can be utilized to get every likely arrangement. For instance, if we need a couch with too quality and remarkable look, at that point our spending plan must be high, and if we have an essential spotlight on spending plan and our financial plan is low, at that point we need to compromise with the nature of the couch.

2.2 Formulation of MOOP

The general formulation of MOOP which has \(K\) objective functions is described as below:

$$\begin{aligned}& \mathrm{Min}\, Z(x)=[{z}_{1}(x),{z}_{2}(x),\ldots ,{z}_{K}(x)]^{T}\\ & \text{Subject to constraints},\\ & {g}_{j}(x)\ge 0, \quad j=\mathrm{1,2},\ldots m.\\ & {h}_{k}(x)=0, \quad k=\mathrm{1,2},\ldots o.\\ & {x}_{i}^{L}\le {x}_{i}\le {x}_{i}^{U}, \quad i=\mathrm{1,2},\ldots n.\end{aligned}$$

where \({x}_{i}^{U}\), and \({x}_{i}^{L}\) represents the upper and lower bounds for the \(i\)-th decision variable. \(m\) stands for total number of inequality constraint; \(o\) stands for total number of equality constraint. The solution set \({x}_{i}\) that satisfies the \((m+o)\) constraints is called the feasible solution set, and a collection of every feasible solution sets represents a feasible region and symbolized as \(\Omega\). For the general formulation of MOOP, we consider the minimize MOOP as the maximize problem can be easily transferred to minimize according to the principle of duality through multiply every goal by −1 and constraints are changed according to the rules of duality.

2.3 Basic Definitions

  • Take a pair of solution sets \(x,y\in {\mathbb{R}}^{k}\), then \(x\) dominates \(y\) and symbolized as \(x\prec y\), when \({z}_{i}(x)\le {z}_{i}(y)\) \(\forall\) \(i=1,\dots ,K\), and \({z}_{i}(x)<{z}_{i}(y)\) for at least one \(i\).

  • The solution set \(x\in X\subset {\mathbb{R}}^{k}\) is non-dominate wrt \(X\), when \(\nexists\) another \({x}^{\mathrm{^{\prime}}}\) in \(X\) such that \(z({x}^{\mathrm{^{\prime}}})\prec z(x)\).

  • The solution set \(x\in X\subset {\mathbb{R}}^{k}\) is weakly non-dominate wrt \(X\), when \(\nexists\) another \({x}^{\mathrm{^{\prime}}}\) in \(X\) such that \({z}_{i}({x}^{\mathrm{^{\prime}}})<{z}_{i}(x)\) \(\forall\) \(i=1,\dots ,K\).

  • The solution sets \({x}^{*}\in F\subset {\mathbb{R}}^{k}\) is Pareto-optimal when \({x}^{*}\) is non-dominate wrt \(F\), where \(F\) is feasible region.

  • The Pareto optimal set \({P}^{*}\) is expressed as: \({P}^{*}=\{{x}^{*}\in F|{x}^{*}\,{\text{is Pareto-optimal}}\}\) .

  • The Pareto front \(p{f}^{*}\) is expressed as: \(p{f}^{*}=\{f({x}^{*})\in {\mathbb{R}}^{k}|{x}^{*}\in {P}^{*}\}\).

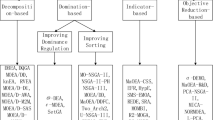
3 Evolutionary Approaches (EAs)

3.1 Non-Pareto EAs

Vector Evaluate Genetic Algorithm: VEGA

In 1985, Schaffer [8] developed one of the first choices to conform EAs to deal with MOOPs known as VEGA. The fundamental thought is to subdivide the population into \(n\) equal parts as there are \(n\) goals, and it is called \(n\) sub-populations. After that, the selection operator performed on each of the solutions set by considering the related goals. Then, to perform the other evolutionary operators, the whole population is gathered when the selection mechanism was completed. This procedure is replicated in every iteration. The discernible VEGA issue is that it inclines toward the best solution sets of every goal independently; however, it doesn’t advance the endurance of good trade-off solution sets. This issue is called speciation (by its similarity in hereditary qualities). Schaffer has searched this issue and attempted to solve by utilizing the mating limitations (i.e., not permitting recombination between solution sets of a similar sub-population). Also, some more heuristic rules were applied to the mechanism of selection. Despite VEGA’s restrictions, a few analysts, in the long run, discovered applications in which such a plan could be more powerful (see, for instance, [9]). In the work of Richardson et al. [10], it was also exhibited that the VEGAs strategy is similar to the linear combination of goals if you utilized the proportional selection that implies VEGA has restrictions concerning non-convex Pareto fronts.

Vector Optimized Evolutionary Strategy: VOES

After VEGA proposed, the Kursawe [11] developed the VOES for handling the MOOPs in 1990. The assignment mechanism of fitness in VOES is similar to VEGA. Additionally, Kursawe utilized some genetic facts with the help of nature. The solution set is presented through the diploid chromosome, and every chromosome has two strings: one is dominant, and the other is recessive in VOES. Two distinct solution sets (both have a design variable \(y\) and the related procedure vector \(\delta\)) are utilized, particularly in a population. Subsequently, the solution set \(y\) is measured through computing: (1) \({Z}^{d}\) dependent on the genotype of dominant string and (2) \({Z}^{r}\) dependent on the genotype of recessive string. Here, we have given the mechanisms of evolution and selection. The selection procedure is carried out in \(N\) levels. The probability vector provided by the client is utilized for choosing a goal at each level. This vector can be varied or fixed throughout the iterations. Suppose the \(n\)-th goal is chosen, the fitness of individual solution set \(y\) is counted as the weighted sum of recessive and dominant goal measure as below:

$$Z(y)=\frac{2}{3}{Z}_{n}^{d}(y)+\frac{1}{3}{Z}_{n}^{r}(y)$$
(20.1)

The population is sorted according to the goal and \((\frac{N-1}{N})\)-th part is chosen as parent from the population at each selection level. Every time we utilized the survived population from past sorting, this process replicated \(N\) times. Hence, the connection among the no. of children \(\gamma\) and no. of parents \(\eta\) can be represented below:

$$\eta =\left(\frac{N-1}{N}\right)^{N}\gamma$$
(20.2)

For example, we get \(\eta =0.25\gamma\) for the bi-objective OP. An external archive that keep a non-dominate solution sets received from the starting of the simulation run and in which every new \(\eta\) solution sets are copied. The verification of non-domination is created on the archive after adding the new solution sets, and just the new non-dominated solution sets are held. The mechanism of niching is utilized to uplift the diversity among solution sets by eliminating the solution sets from the crowded region, and it is performed when the external archive size becomes more than the size of the archive.

VOES utilizes the non-domination verification for ensuring the convergence of solution sets and niching for supporting the diversity of solution sets. These highlights are fundamental to the structure of great MOEA. Sadly, Kursawe evaluated the exhibition of his approach on a solitary test issue, and then further no test appraisals were sought after since Kursawe’s unique examination.

Weight-Based GA: WBGA

WBGA is also known as HLGA, which means Hajela and Lin Genetic Algorithm. In 1992, Hajela and Lin presented the WBGA [12]. For every goal, the coefficient of weighted is allocated. Every population’s solution set has its vector of weight coefficient coded in its string concatenate with its decision variables, not like the classical weight sum method. Thus, the WBGA was capable of searching the multiple non-dominate solution sets in a single simulation run. This approach’s main problem is how to preserve the variety of weight coefficients for the solution sets of population. Two methods were proposed for this purpose. One method utilized the mechanism of niching over the substring, representing the vector of the weight coefficient. Whereas other methods picked, sub-populations are assessed for distinct pre-specified vectors of weight likewise to VEGA. As WBGA is the method depends on weight, subsequently, the solution sets lying on the non-convex portion of the Pareto front cannot search through this approach.

3.2 Pareto EAs

3.2.1 Non-elitist Approaches

Multi-objective GA: MOGA

In 1993, Fonseca and Fleming developed a first Pareto-based evolutionary approach, and it is known as MOGA [13]. To motivate the search in the direction of real Pareto front and keep the diversity among the population, MOGA unitedly utilized the concept of Pareto-based position and niching mechanism. Every solution set has provided a position that is represented as a function of the no. of solution sets dominated by it. Suppose the \(n{d}^{s}\) is the no. of solution sets dominating a specific solution sett \(y\) at the iteration \(s\), then the position at \(s\) of \(y\) solution set is defined as follow:

$$po{s}^{s}(y)=1+n{d}^{s}$$
(20.3)

By the mechanism of position, all the non-dominated solution sets are assigned at position 1 see the Fig. 20.1. The technique of MOGA is according to the position of the solution set and an average fitness value of the population. The procedure for calculating the fitness value is described below. Initially, the population is arranged by position. After that, the fitness value is provided to every solution set according to the interpolation of best to the worst position by some predefined function. At last, the solution sets which provided the same position got the average value of the fitness. That guarantees the every solution sets which has the same position is examined with an indistinguishable frequency. This data is utilized to keep up consistent global population fitness with a suitable measure of specific weight. Moreover, MOGA applies the niching concept and utilizes the niche radius parameter, and here it is defined by \({\sigma }_{rd}\) that should be assigned carefully. For generating the uniform distribution of the approximate Pareto front, the mechanism of niching is carried out on the objective space. Figure 20.2 gives the illustration of the niching mechanism. The solution sets occupying under the area of niching radius are given a penalty in their fitness value. Even though in MOGA, the assigned fitness value is depends on the Pareto dominant concept, it is possible that the solution sets having the same position may not have the same fitness value. That may create an undesirable inclination for the specific area of search space. Especially, MOGA might be effective with the Pareto front geometry, along with the solution sets density on the search space. Besides, the niching mechanism shows kindness towards the solution sets with lower positions over the solution sets with higher positions when these last are more crowded.

Fig. 20.1
figure 1

Ranking process of MOGA

Full size image
Fig. 20.2
figure 2

Mechanism of niching

Full size image

Niche Pareto GA: NPGA

Horn et al. [14] developed NPGA that contrasts from the earlier proposed MOEAs in the operator of selection. The VEGA and MOGA utilized the proportional selection method rather than this approach utilizes the binary tournament selection. In the tournament selection, the randomly two solution sets \(y\), and \(z\) are chosen among the parent population \(J\). Afterward, both the solution sets are examined dependent on Pareto dominance with every solution set of an arbitrarily chosen sub-population \(I\) whose size is \(id\), where \(id\ll |J|\). When anyone from the two solution sets is non-dominate for all solution sets of sub-population and another solution set is dominant through at least one solution set, then the non-dominated solution set is kept. The mechanism of niching is applied to choose the solution set from \(y\) and \(z\) that lies in the least crowded region in the scenarios where both or neither solution sets are dominated through the solution sets of sub-population \(I\).

The process of NPGA is related to the value of \({\sigma }_{rd}\) along with the \(id\). From the numerical results reported in the article of Horn et al. [14], we can conclude that the size of the population is greater than the \(id\). Whereas, when \(id\) is excessively enormous, the non-dominate solution set is well-emphasized, yet its complexity will be its top level. Then again, when \(id\) is excessively little, then the verification of non-domination can boisterous that it can’t focus on the non-dominate solution set sufficiently. Furthermore, \(jd\) relies upon the number of goals that to be optimizing.

Non-dominate Sorting GA: NSGA

NSGA [15] depends on the technique of non-dominated sorting, which is demonstrated in Fig. 20.3. This technique characterizes the solution sets of the population into many positions. The technique of non-dominated sorting starts through searching the non-dominate solution sets among the population. All these solution sets are assigned at position one and provide the largest dummy value of fitness. These solution sets are then deleted among the population, then again search the non-dominate solution sets among the remaining population. Moreover, the non-dominate solution sets of this time are assigned at position two, and the dummy value of fitness is assigned smaller than the previous one. This procedure is repeated until all the solution sets of the population are positioned. For maintaining the diversity of solution sets, the mechanism of niching is applied to a decision space rather than an objective space to reduce the value of fitness according to the value of \({\sigma }_{rd}\). The sharing in each position is accomplished by counting the value of sharing function among two solution sets, \(m\) and \(n\), in a similar position as below:

Fig. 20.3
figure 3

Mechanism of non-dominate sorting

Full size image
$$\left\{\begin{array}{ll}S{h}_{{e}_{mn}}=1-\left(\frac{{e}_{mn}}{{\sigma }_{rd}}\right)^{2},& \mathrm{if}{e}_{mn}<{\sigma }_{rd},\\ 0,& \mathrm{otherwise}.\end{array}\right.$$
(20.4)

where \({e}_{mn}\) denotes the Euclidean distance connecting \(m\) and \(n\). Afterward, the above value of sharing function for every solution sets is added in their respective position to calculate the parameter of niche count. Finally, the value of shared fitness for every solution set is calculated via divide the value of dummy fitness through niche count. Best solution sets are prioritized ever above the other solution sets. Thus, the new solution sets that are nearer to the non-dominate solution sets are more preferred. The mechanism of niching provides the approach to spread the non-dominate solution sets over the Pareto front. At the same time, the more affectability regarding the parameter \({\sigma }_{rd}\) provides the lesser productive execution of NSGA.

3.2.2 Elitist Approaches

Elitism implies that the elite solution sets can’t be removed from the population’s archive gene pool in favor of worse solution sets [16]. In the accompanying, we survey the most popular elitist MOEAs [17].

Strength Pareto EA: SPEA/SPEA2

In 1999, Zitzler and Thiele [18] developed the SPEA that utilizes two populations: (1) the principle populace \(J\), and (2) an archive population \(C\), that is consist of the non-dominated solution sets in the whole process. At first, randomly, the population \(J\) is produced, and the archive population \(C\) is vacant. Afterward, the \(C\) is loaded up by the non-dominate solution sets from \(J\). Then, the solution sets from \(C\), that dominate through any of the solution set from \(C\) are erased. Furthermore, if the quantity of non-dominate solution sets surpasses the size of archive \(|C|\), \(C\) is rationalizing with the help of cluster technique that will be discussed later on. When every population and the archive’s solution sets have allocated the value of fitness, the selection of binary tournament and substitution put for satisfying pool mating. Subsequently, apply the genetic operators and formulate the new population \(J\). When the stopping criterion is achieved, then procedure will be stopped, otherwise, the non-dominate solution sets from \(J\) are transferred to the archive \(C\), and the whole procedure will be replicated.

The assigning of fitness value in SPEA has a two-phase procedure. Initially, the non-dominate solution sets from the archive \(C\) are positioned. Afterward, the solution sets from the \(J\) population is evaluated. Moreover, each solution set \(m\) from archive \(C\) has provided the strength value \({g}_{m}\in [\mathrm{0,1}[\), that is relative to number of solution sets in \(J\), that dominate through \(m\). The strength \({g}_{m}\) is defined as below:

$${g}_{m}=\frac{I}{|J|+1}$$
(20.5)

where \(I\) signifies the no. of solution sets in \(J\) that are cover through \(m\) and \(|J|\) is the population’s total size. The fitness value of solution set \(n\in J\) is received by adding the strength of every non-dominate solution sets \(m\in C\) that dominates \(n\). The received amount is added by 1 to ensure that archive solution sets have preferred execution over \(J\) solution sets. Minimize the fitness value, and it is defined as follow:

$${Z}_{n}=1+\sum_{m,m\le n}{g}_{m}$$
(20.6)

The technique of cluster is applied to decrease the archive size by preserving its features. The basic concept is to divide the archive into \(A\) clusters, where \(A<|C|\) and every solution sets of the same cluster have similar features. The clusters’ process starts with generating the cluster of every component of the initial non-dominate solution set of the archive. Following this, the two groups are picked through the measurement of the distance to be consolidated in single group. A distance is counted as the mean Euclidean distance among the two solution sets over the groups. At the time of accomplishing the cluster technique, the new non-dominate solution sets from the archive contain the centroid solution sets for every group. The authors have also provided the outcomes in favor of SPEA as compared to other MOEAs.

Zitzler et al. [19] have studied and distinguished the three shortcomings for SPEA. The first one is occurred at assigning the fitness value. The solution sets that dominate through the same solution sets of the archive have the same fitness value. Thus, when the archive comprised just one solution set, then every solution set of the population has a similar position that doesn’t depend on whether they dominate one another. Therefore, the selection pressure is diminished considerably, and thus the SPEA executes like the random search method. The second is for the estimation of density. When the numerous solution sets of the recent iteration are Pareto equal, then none or almost no data can be acquired depending on the partial order characterized by dominance. In this circumstance, which will probably happen when the quantity of destinations surpasses two, the information of density must be utilized to direct the search the more efficaciously. Grouping utilizes this knowledge, yet just concerning with the archive, not with primary population-the third for archive truncation scheme. Even though grouping technique utilized in SPEA can decrease the non-dominate solution set avoid destruction in features, it might lose outrageous (external) solution sets. Moreover, these solution sets must be placed with the archive for receiving the well-distributed non-dominate solution sets. To deal with the SPEA’s shortcomings, Zitzler et al. [19] have developed the SPEA2, which is the updated version of SPEA. Rather than SPEA, SPEA2 utilizes the fine-grain fitness assigning scheme, that integrates with data of density. Moreover, the size of archive is constant, which means When the quantity of non-dominate solution set is smaller over the archive’s predefined size, then dominant solution sets fill up the archive; with SPEA, the size of the archive might be shift after some time. Moreover, mechanism of cluster, that is summoned for non-dominate solution sets, surpasses the size of the archive. It is changed by the substitutive method of truncation, which has the same characteristics yet maintain the boundary solution sets. In SPEA2, just the solution sets from the archive are performing the process of mating selection not like SPEA.

The SPEA2 assignment of fitness for a specific solution set \(m\) considers the number of solution sets that dominate the \(m\); moreover, the number of solution sets dominate through \(m\). Every solution set \(m\) of the population \(J\). The archive \(C\) has provided the strength value \({g}_{m}\) defines the number of solution sets is dominant through \(m\):

$${g}_{m}=|n|n\in J\cup C\wedge m\le n|$$
(20.7)

Then raw fitness \({R}_{m}\) is calculated as below:

$${R}_{m}=\sum_{n\in J+C,n\le m}{g}_{n}$$
(20.8)

The \({R}_{m}\) is found out through its dominators’ strengths from the main population and archive instead of SPEA, where just solution sets from the archive are taken in this specific situation. Note that, here, we have to minimize the fitness, i.e., \({R}_{m}=0\) related with solution set which is non-dominate. Simultaneously, the higher worth of \({R}_{m}\) implies that numerous solution sets dominate \(m\). Figure 20.4b represents this technique.

Fig. 20.4
figure 4

Comparison between SPEA and SPEA2 for the technique of fitness assignment [19]

Full size image

The scheme of raw fitness provides the niching sort dependents on concept of Pareto dominant. Moreover, this technique turns ineffective if a major amount of solution sets are non-commanded with one another. Consequently, more data regarding density is consolidated to segregate among the solution sets with indistinguishable raw fitness values. SPEA2 adapted the method of \(l\)-th nearest neighbor in technique of density estimation. Moreover, for every solution set \(m\), calculated the distances of each solution set \(n\) from the \(J\cup C\) in the space of objective. Then, arranged in increasing order and stored. Then, the \(l\)-th closest neighbor provides the looked for distance and indicated by \({\mu }_{m}^{l}\). The \(l\) parameter is typically defined as \(\sqrt{|J|+|C|}\). The density \({\delta }_{m}\) of the solution set \(m\) is:

$${\delta }_{m}=\frac{1}{{\mu }_{m}^{l}+2}$$
(20.9)

Here, two is add in denominator, for guarantee its worth is more prominent than \(0\) and \({\delta }_{m}<1\). At last, the fitness of a specific solution set \(m\) is acquired by adding density information and raw fitness as below:

$${T}_{m}={R}_{m}+{\delta }_{m}$$
(20.10)

The environmental selection mechanism for SPEA2 is different from SPEA one by maintaining the solution sets of a boundary. Also, the number of solution sets is stored in external is fixed throughout the time.

Non-dominate Sorting GA II: NSGA-II

The updated version of NSGA is known as NSGA-II [20, 21]. The less computation complexity, elitist method, and a strategy for diversity which doesn’t require any extra parameter are the noticeable highlights of NSGA-II. The basic concept of NSGA-II is defined as below. In NSGA-II, first, produce the offspring population \({O}_{o}\) through utilizing the genetic operators on an arbitrarily formulated parent population \({J}_{o}\). The fundamental iteration of NSGA-II is distinct from the first generation award. Initially, both the populations \({J}_{s}\) and \({O}_{s}\) are consolidated to shape a population \({T}_{s}\) whose size \(2*M\), where \(|{J}_{s}|=|{O}_{s}|=M\). After that, the sorting of non-dominate solution sets is executed to characterize whole population \({T}_{s}\). When sorting of non-dominate solution set is accomplished, population \({T}_{s}\) becomes similarly partitioned into a few classes as NSGA. Then, the new parent populace \({J}_{s+1}\) is formulated by the solution sets of the best non-dominate fronts, each in turn. As the size of the total population is \(2*M\), so it might not be every front lie in \(M\) spaces as it is the size of the new population \({J}_{s+1}\). When the final permitted front is taken, it might consist of more solution sets then the leftover spaces accessible in \({J}_{s+1}\). Rather than deleting the random solution sets from the last front, NSGA-II utilizes the mechanism of niching to pick solution set from the last front, that lie in the least crowded area. Moreover, for every positioning stage, the value of crowding distance is calculated by adding Euclidean distance among both neighborhood solution sets from either side of the solution set on every objective function, as represented by Fig. 20.5. For maintaining the boundary solution sets, these latter provide the infinite crowding distance. The concept of crowding distance value discussed later on along with the concept of non-dominate sorting and many more.

Fig. 20.5
figure 5

Crowding distance

Full size image

Pareto Archived ES/Pareto Envelope based Selection Algorithm: PAES/PESA

Knowles and Corne [22, 23] developed the \(a(1+1) - \text{ES}\) \(((1+1)-ES)\), known as PAES, for estimate entire Pareto front. The basic idea of PAES is taken from the achievement of \((1+1)-ES\) for solving SOOP. This is the fact that authors have conformed this approach of the search for MOOPs. Initially, in PAES, the child \(c{h}_{o}\) is formulated from the arbitrarily generated parent \({J}_{0}\). At every iteration \(i\), the obtained non-dominated solution sets are kept in a pre-defined archive size. Initially, both the solution sets, \({J}_{i}\) and \(c{h}_{i}\), are analyzed. When one solution set is non-dominate, and the other solution set is the dominant one. The dominant one is deleted, and non-dominate solution set is kept as a parent for the next iteration. Suppose both the solution sets \({J}_{i}\) and \(c{h}_{i}\) are non-dominate. In that case, the new solution set is compared with the reference population of previous archive non-dominate solution sets, i.e., solution sets from the archive. If the comparison with the solution set from the archive is failed to provide a better solution set, then the solution set, which lies in the least crowd area, is preferred. DM has defined the maximum size of the archive that provides the wanted number of final solution sets. Every child \(c{h}_{i}\) that isn’t dominant through its parent \({J}_{i}\), then compared with every solution set from the archive. After that, the solution set, which dominates the archive’s solution sets, is always kept as parents for the next iteration and put in the archive. If the solution set is dominant through the archive’s solution sets, are eliminated, and those who are non-dominate are kept and/or archived according to the CDV. The significant characteristic of PAES is its methodology for advancing diversity in the approximation set. PAES utilizes a versatile hyper-gridding framework in the objective space to partition it into \(O\) non-covering hyper-boxes. Having a place of a specific solution set for a specific area in the hyper-box is dictated through the value of objectives that determines a coordinates of solution sets. For the situation where the solution set is non-dominate according to the solution sets of an archive, then the concept of crowding distance applied on the number of solution sets that are lying in a specific hyper-box for deciding the solution set is rejected or not.

The specific benefit of a technique of diversity preservation is that it doesn’t need any additional parameters like niche radius \({\sigma }_{rd}\). Yet, the principle core of PAES is the sensitiveness of the execution of this approach to the \(O\) parameter of the hyper-gridding framework Fig. 20.6.

Fig. 20.6
figure 6

PAES hyper-gridding system with d = 6

Full size image

The modified version of PAES was developed by the same authors [24], which is named as PESA. It has the same archive and technique of diversity maintenance as the PAES. In PESA, only the solution sets of the archive are performing the genetic operations such as SPEA2. Initially, generate the arbitrarily little internal population \(IJ\). It utilizes a huge external population \(EJ\). Initially, \(EJ\) is vacant. Afterward, archive \(EJ\) is improved by the elite solution sets in a similar way as performed in PAES. Suppose that the stopping criterion is achieved, then the approach gives back the solution sets of \(EJ\); otherwise, \(IJ\) is occupied by the new solution sets through the following operations. By using the probability \(b\), both parents are chosen from \(EJ\). Subsequently, a single child is generated through a crossover. The mutation is applied to this child. By using the probability \((1-b)\), the chosen parent among \(EJ\) is mutated. Afterward, archive \(EJ\) is improved, and the complete procedure is replicated.

The PAES, PESA, requires adjusting the archive’s size and the parameter \(O\) of the gridding framework. By modifying the value of \(O\), exponentially, the hyper-boxes total number varies that effects the distribution of the final population. PESA-II is the updated version of PESA. It was developed by Corne et al. [25], in which selection is according to area, and the selection subject is currently a hyper-box, not just the solution set, which means 1st choose the hyper-box, afterward the solution set browsed among a chosen hyper-box. An inspiration driving PESA is to decrease a total expense of Pareto positioning.

Indicator-Based EA: IBEA

Zitzler and Künzli [26] developed the IBEA in which selection according to the contribution of a solution set for a specific quality indicator. Thus, IBEA can be view as the 3rd evaluation of MOEA. In IBEA, first, generate a random population \(J\). Then, every solution \(t\) of the population \(J\) is consecutively removed from the population \(J\). The approach calculates the fitness value of \(t\) related to the loss in quality. Then, the solution set, which has the poorest fitness value, is deleted from the population. Then fitness value of each solution set is again calculate as population is shortened. This scheme of selection is utilized for generating the mating pool and in the selection of the environment. The most important part of IBEA is its sensitiveness towards the parameter \(l\), which is utilized for scaling the value of fitness function as the execution of this approach is very much related to this parameter, which is studied to relate with the taken MOOP. Some other IB selection approach is named as \(S\) Metric Selection-based EMOA: SMS-EMOA [27], that is a collaboration of sorting of non-dominate and the mechanism of indicator-based selection. The crucial factor in this kind of approaches is effort in computation to calculate the values of a quality indicator for the specific non-dominate solution set [28].

Multi-objective EA Based on Decomposition: MOEAD

Zhang and Li [29] developed a most famous approach depends on decomposition. The essential concept of MOEAD is to break down the MOOP into \(M\) sub-problems, where \(M\) is the size of population. All of these sub-problems are solved turn by turn. To perform the MOEAD, the set of weight vectors \({w}_{i}\) is needed. Thus, the \({w}_{i}\) is formulated with the aim of solution sets that will be spread over the complete Pareto front. In MOEAD, Euclidean distance between weighted vectors is utilized for deciding the neighborhood of \(S\) weight vectors for every vector \({w}_{i}\). Afterward, every solution set of the population has provided a weight vector, and the dependent sub-problem is optimized according to the function of scalarizing. After that, both the solution sets among the neighborhood weighted vectors are mate and generate the offspring solution set. Then, with the help of a scalarizing function, an offspring solution set is evaluated. When the created new solution set was performed, it could also take over the many present solution sets of its neighboring sub-problems. There are three variants of scalarizing functions that are received for MOEAD: (1) weight sum method, (2) weight Tchebycheff method, and (3) boundary intersection method. The diversity of MOEAD has been tackled according to the similarity among the set of weighted vectors, i.e., depends on the related solution sets of a neighborhood. MOEAD is a very good approach for searching a few consistently distribute Pareto solution sets with a little expense of computation. Also, MOEAD has exhibited intriguing outcomes on many issues that have a large number of goals. Yet, its primary weakness is the decomposition of diversity and the distribution of solution sets when the problem deal with the bad scale.

3.3 New EAs

All the swarm intelligence based approaches and evolutionary approaches required for solving the SOOPs and MOOPs are probabilistic. They need standard controlling parameters such as no. of iterations, population size, elite size, etc. Other than the standard control parameters, distinct approaches need their self approach specific control parameters. For instance, GA utilizes selection operator, crossover probability, mutation probability; the PSO utilizes cognitive and social parameters, inertia weight; ABC utilizes the no. of scout bees, onlooker bees, employed bees, and breaking point; HS utilizes rate of pitch adjusting, rate of harmony memory consideration, and the no. of improvisations. Correspondingly, different approaches, for example, EP, DE, ACO, FF, CSA, GSA, BBO, FPA, ALO, IWO, and so forth require the adjustment of their algorithm-specific parameters. The best possible adjustment of the algorithm-specific parameters is a pivotal part that influences the approaches’ execution, as referenced previously. The inappropriate adjustment of parameters further expands a computation attempts or gives the local optimal solution set. Thinking about this reality, in 2011, Rao et al. [30] presented the teaching learning-based optimization (TLBO) algorithm, that doesn’t require even single algorithm-specific parameter. The TLBO requires standard control parameters such as population size and no. of iterations for its functioning. The TLBO has increased broad acknowledgment surrounded by the optimization researchers [31]. By analyzing the achievement of the TLBO, one more approach that is independent of the algorithm-specific parameter was developed by Rao [32] and named the Jaya algorithm (JA). Although, in contrast to two stages means learner stage and teacher stage of the TLBO, the JA has just a single stage. The JA is basic in an idea and has indicated better execution when contrasted with other optimization approaches.

Teaching–Learning-Based Optimization Algorithm: TLBO

In 2011, Rao et al. [30] built up the TLBO, that doesn’t need adjustment of any algorithm-specific parameters for its functioning. An approach expresses two essential ways of updating: (i) by the educator (called a teacher stage) and (ii) by the association with different students (called a student stage). In this optimization approach, student’s clustering is taken as population, and distinct subjects suggested to the students are taken as distinct decision variables of the SOOP or MOOP. A student’s outcome is corresponding to fitness estimation of a considered problem. The best solution set in whole population is assigned as instructor. Each decision variable is a parameter associated with the goals of the provided problem, and best solution set is best estimation of a goal work.

The functioning of TLBO is separated by two sections, the Learner stage and the Teacher stage. The process of both these stages is clarified below [31].

  • Teacher stage: The first part of the TLBO is the Teacher stage, where students learn through the educator. Along this stage, an educator attempts to expand the class’s overall outcome in the subject taught by that person is dependent upon their potential. For any iteration \(t\), expect that there is \(n\) no. of sub. (i.e., decision variables), \(m\) no. of students (i.e., population size, \(l=\mathrm{1,2},\cdots ,m\)) and \({M}_{s,t}\) is average outcome of the students in a specific sub. \(s\) (\(s=\mathrm{1,2},\cdots ,n\)). A best general outcome \({Y}_{total-lbest,t}\) taken every subject to combine acquired in a whole population of students, is taken as outcome of best student \(lbest\). Although, as an instructor is typically assumed as an exceptionally learn individual who trains students to have better outcomes, the best student searched taken through the approach as the educator. The variation among the recent mean outcome of each subject and the instructor’s parallel outcome for each subject is provided as follows:

    $$Var{M}_{s,l,t}={r}_{t}({Y}_{s,lbest,t}-{T}_{f}{M}_{s,t})$$
    (20.11)

    where, \({Y}_{s,lbest,t}\) is the outcome of the best student in sub. \(s\). \({T}_{f}\) stands for teaching factor that chooses the estimation of the average to be modified, and \({r}_{t}\) stands for arbitrary no. lies in between \(0\) and \(1\). The estimation of \({T}_{f}\) could be 1 or 2. The estimation of \({T}_{f}\) is chosen haphazardly by equivalent likelihood as,

    $${T}_{f}=round[1+rand(\mathrm{0,1})\{2-1\}]$$
    (20.12)

    The estimation of \({T}_{f}\) isn’t provided as an input to an approach, and the approach arbitrarily chooses its worth from the Eq. (20.12). After directing several examinations on numerous benchmark functions, it is observed that the approach achieves good outcomes if the estimation of \({T}_{f}\) is somewhere in the range of 1 and 2. In any case, the approach is established to execute much better if estimation of \({T}_{f}\) can be 1 or 2. Consequently, to make an easier approach, the \({T}_{f}\) is recommended to consider as 1 or 2, relying upon the measures provided from the Eq. (20.12). Because of a \(Var{M}_{s,l,t}\), the current solution set is updated in the teacher stage as per the accompanying expression.

    $$Y_{{s,l,t}}^{{\text{'}}} = Y_{{s,l,t}} + VarM_{{s,l,t}}$$
    (20.13)

    where, \({Y}_{s,l,t}^{\mathrm{^{\prime}}}\) represents updated estimation of \({Y}_{s,l,t}\). \({Y}_{s,l,t}^{\mathrm{^{\prime}}}\) is considered whether it provides better esteem. At the end of the teacher stage, every considered esteem is kept up because they are the input for the learner stage. The learner stage relies on the educator stage.

  • Learner stage: The second aspect of the TLBO is the learner stage, where students improve their skills through communication among themselves. A student associates haphazardly with different students to improve their skills. A student learns more when other student has more information over her/him. Taking \(m\) as the population size, the learning process of this stage is clarified below.

    Arbitrarily select two students \(A\) and \(B\) with the end goal that \({Y}_{total-A,t}^{\mathrm{^{\prime}}}\ne {Y}_{total-B,t}^{\mathrm{^{\prime}}}\) Where, \({Y}_{total-A,t}^{\mathrm{^{\prime}}}\) and \({Y}_{total-B,t}^{\mathrm{^{\prime}}}\) represents updated estimations of \({Y}_{total-A,t}\) and \({Y}_{total-B,t}\) of \(A\) and \(B\) individually toward the accomplished of educator stage.

    $$\begin{array}{ll}\mathrm{If} & {Y}_{total-A,t}^{\mathrm{^{\prime}}}<{Y}_{total-B,t}^{\mathrm{^{\prime}}}\\ \mathrm{then}& \\ & {Y}_{s,A,t}^{\prime\prime}={Y}_{s,A,t}^{\mathrm{^{\prime}}}+{r}_{t}({Y}_{s,A,t}^{\mathrm{^{\prime}}}-{Y}_{s,B,t}^{\mathrm{^{\prime}}}),\end{array}$$
    (20.14)
    $$\begin{array}{ll}\mathrm{If} & {Y}_{total-B,t}^{\mathrm{^{\prime}}}<{Y}_{total-A,t}^{\mathrm{^{\prime}}}\\ \mathrm{then}& \\ & {Y}_{s,A,t}^{\prime\prime}={Y}_{s,A,t}^{\mathrm{^{\prime}}}+{r}_{t}({Y}_{s,B,t}^{\mathrm{^{\prime}}}-{Y}_{s,A,t}^{\mathrm{^{\prime}}}).\end{array}$$
    (20.15)

    \({Y}_{s,A,t}^{\prime\prime}\) is considered whether it provides a better esteem.

    Equations (20.14) and (20.15) are for minimizing problem. In the case of maximizing problem, Eqs. (20.16) and (20.17) are utilized.

    $$\begin{array}{ll}\mathrm{If} & {Y}_{total-B,t}^{\mathrm{^{\prime}}}<{Y}_{total-A,t}^{\mathrm{^{\prime}}}\\ \mathrm{then}& \\ & {Y}_{s,A,t}^{\prime\prime}={Y}_{s,A,t}^{\mathrm{^{\prime}}}+{r}_{t}({Y}_{s,A,t}^{\mathrm{^{\prime}}}-{Y}_{s,B,t}^{\mathrm{^{\prime}}}),\end{array}$$
    (20.16)
    $$\begin{array}{ll}\mathrm{If} & {Y}_{total-A,t}^{\mathrm{^{\prime}}}<{Y}_{total-B,t}^{\mathrm{^{\prime}}}\\ \mathrm{then}& \\ & {Y}_{s,A,t}^{\prime\prime}={Y}_{s,A,t}^{\mathrm{^{\prime}}}+{r}_{t}({Y}_{s,B,t}^{\mathrm{^{\prime}}}-{Y}_{s,A,t}^{\mathrm{^{\prime}}}).\end{array}$$
    (20.17)

Non-dominate Sorting TLBO: NSTLBO

NSTLBO is produced to deal with MOOPs. The extension of TLBO is known as NSTLBO. The NSTLBO comes under the posterior approach to deal with MOOPs and keeps up a various solution sets. NSTLBO contains the teacher stage and learner stage, likewise the TLBO. Moreover, to deal with various goals efficaciously and expeditiously, the NSTLBO is integrated by a crowding distance computations and non-dominated sorting approach.

Initially, start with the random initial population’s generation as the \(J\) number of solution sets. Then sorted the initial population and positioned depends on concept of non-dominant and constraint dominance. The prevalence between the solution sets is decided as follows: The priority given to the concept of constraint dominance (CD) and afterward concept of non-dominance (ND), and afterward on the crowding distance value (CDV) of the solution sets. The student with a most elevated position (rank = 1) is chosen as a class educator. By chance that there be two or more than two students with a similar position, at that point, the student with the most elevated CDV is chosen as an instructor for a class. That provides guarantees which an educator is chosen among a scanty area of the search space (SS).

When an educator is chosen, students are updated as described in teacher stage of TLBO, i.e., as per Eqs. (20.11)–(20.13). Then, the solution sets of updated students (new students) are combined with the initial population to acquire \(2J\) solution sets (students). Again, these students are arranged and positioned dependent on the concept of CD, ND, and CDV for every student is calculated. The student with a higher position is viewed as better than the other students. If both the students hold a similar position, at that point, the student with a higher CDV is viewed as better than the other. Established on the concept of new positioning and value of crowding distance, the \(J\) no. of best students are chosen. These students are additionally update through student stage of TLBO, i.e., as indicated by Eqs. (20.14) and (20.15) or (20.16) and (20.17).

The student’s priority is decided according to the concept of CD, the concept of ND, and the CDV of the students. The student with the most elevated position is viewed as better than the other student. On the off chance that both the students hold a similar position, at that point, the student with a larger CDV is viewed as better than the other. At accomplishing the learner stage, all new students are joined with an old students and repeatedly sorted and positioned. Because of the new positioning and CDV, \(J\) no. of best students are chosen, and these students are straightforwardly update dependent on a teacher stage for next iteration [31, 33].

Non-dominated Sorting of the Population

In this methodology, population is arranged at many positions according to the concept of dominance given as bellow: the \({y}_{s}\) solution set is called to dominate \({y}_{t}\) solution set provided the \({y}_{s}\) solution set is no longer poor than \({y}_{t}\) solution set regarding every goal and besides the \({y}_{s}\) solution set is strictly good over \({y}_{t}\) solution set for at least single goal. When one of the above two terms are break, at that point \({y}_{s}\) solution set doesn’t dominate \({y}_{t}\) solution set.

For the \(J\) solution sets, the solution sets that ain’t dominated through any of the \(J\) solution sets are known as the non-dominate solution sets. Every non-dominate solution set recognized in a first sorting run is defined as position one and is erased from the set \(J\). The rest of the solution sets in \(J\) solution sets are again sorted, and the strategy is rehashed until every solution sets of the \(J\) solution sets are sorted and positioned. For constrained MOOPs, the concept of constrained-dominance is utilized. The total no. of function evaluation for the NSTLBO is the two times of total no. of iterations multiply with size of population.

Crowding Distance Value (CDV)

The destination is to calculate density of solution sets around a specified solution set \(m\) is the basic concept of CDV. CDV defined for every solution set of the population. Subsequently, the crowding distance (\(c{d}_{m}\)) is defined as the average distance of a pair of solution sets on either side of the solution \(m\) is calculated along with all \(N\) goals. For computing the CDV of the solution \(m\) in the front \(f\), the accompanying procedure is followed: Step 1: Determine the no. of solution sets lying on front \(f\) as \(k=|f|\). For every solution set \(m\) has provide the \(c{d}_{m}=0\). Step 2: For every goal \(n=\mathrm{1,2},\ldots ,N,\) sort the set in the worst order of \({z}_{n}\). Step 3: For \(n=\mathrm{1,2},\ldots ,N\), provide biggest CDV to limit solution sets \((c{d}_{1}=c{d}_{k}=\infty\)), and for the remaining solution sets \(s=2\) to \((k-1)\), CDV is calculated as below:

$$c{d}_{s}=c{d}_{s}+\frac{{z}_{n}^{s+1}-{z}_{n}^{s-1}}{{z}_{n}^{max}-{z}_{n}^{min}}$$
(20.18)

where, \(s\) stands for the order of solution set, \({z}_{n}\) provides the value of \(n\)-th goal, \({z}_{n}^{min}\) and \({z}_{n}^{max}\) are the values of population minimum and maximum for \(n\)-th goal.

Crowding-Comparison Operator

For finding the solution which is better than the other, the crowding comparison operator is utilized. It is established on the two precious factors: (1) Non-domination position, and (2) CDV of each solution \(s\) of the population. It is denoted by this \({\prec }_{n}\) symbol and it is described as below: \({\prec }_{n}\), if (\(Ran{k}_{s}<Ran{k}_{t}\)) or [(\(Ran{k}_{s}=Ran{k}_{t}\)) and (\(c{d}_{s}>c{d}_{t}\))]. i.e., For the \(s\) and \(t\) two solution sets, which has contrasting non-domination positions, the solution set, which has a better or lower position, is prioritized. Whereas, suppose that the two solution sets have the same position (\(Ran{k}_{s}=Ran{k}_{t}\)), at that point, the solution set situated in the lesser crowded area (\(c{d}_{s}>c{d}_{t}\)) is chosen.

Constraint-Dominance Concept

The concept of constraint dominance is defined as follows: Consider the two solution sets \(s\) and \(t\), the solution set \(s\) is called to constraint dominate solution set \(t\), only when the prescribed events occur. The solution set \(t\) is not feasible and the solution set \(s\) is feasible. Both the solution sets \(s\) and \(t\) are infeasible, yet the solution set \(s\) has the total less constraint violation than solution set \(t\). Both the solution sets \(s\) and \(t\) are feasible and moreover the solution set \(t\) is dominated by the solution set \(s\). Thus, we can say that the concept of constraint dominance guarantees that the infeasible solution sets achieved a lower position than the feasible solution sets. For the infeasible solution sets, the solution sets with a total more constraint violation are defined at the lower position. For the feasible solution sets, the dominated feasible solution sets are defined at a lower position as compared to the non-dominated feasible solution sets.

Jaya Algorithm: JA

Recently, Rao [32] proposed the JA in 2016, which is easy to execute and doesn’t need adjustment of any particular algorithm parameters. In JA, randomly \(J\) initial solution sets are formulated between decision variable’s lower and upper limits. After that, every decision variables of each solution set is updated by utilizing Eq. (20.19). Suppose \(z\) be a goal that is optimized. Assume that \(v\) no. of decision variables. The value of objective function related to best solution set is denoted as \({z}_{best}\), and similarly, the value of objective function related to the worst solution set is denoted as \({z}_{worst}\).

$$V_{s + 1,t,u} = V_{s,t,u} + R_{s,t,1} \left( {V_{s,t,B} - \left| {V_{s,t,u} } \right|} \right) - R_{s,t,2} \left( {V_{s,t,W} - \left| {V_{s,t,u} } \right|} \right)$$
(20.19)

where \(W\) and \(B\) defines the index of worst and best solution sets from the present population. The index of decision variable, iteration, and the solution set is represented as \(t,s,u\), respectively. \({V}_{s,t,u}\) implies the \(t\)th decision variable of \(u\)th solution set at \(s\)th iteration. The random numbers are denoted as \({R}_{s,t,1}\) and \({R}_{s,t,2}\). They are lying in a range of \([\mathrm{0,1}]\). They work as the factor of scaling and provides better diversity. The primary goal of JA is to increase the value of fitness for every solution set of the population. Thus, JA attempts to transfer the value of an objective function of every solution set in the direction of the best solution set through uplifting the decision variables. When the decision variables are updated, there is a comparison between the updated one and the corresponding old one. Whichever provides the better value carried forward, i.e., that solution sets are taking part in the next iteration. In each iteration, the solution sets move closer to a better solution set by the JA, and also the solution set moves far from the worst solution set. In this way, a decent strengthening and broadening of the search space are accomplished. The JA consistently attempts to move nearer to progress (i.e., arriving at the best solution set) and attempts to dodge disappointment (i.e., transferring ceaselessly from the worst solution set). The JA endeavors to get successful through arriving at the best solution set, and thus it is named as Jaya which is a Sanskrit word whose meaning is triumph or win.

There are also a few variations of JA that are found in the literature. These variations are Self-Adaptive JA (SAJA) [34], Quasi-oppositional JA (QOJA) [35], Self-Adaptive multi-population JA (SAMPJA) [36], Self-Adaptive multi-population elitist JA (SAMPEJA) [37].

Multi-objective Jaya Algorithm: MOJA

In 2017, Rao et al. [38], has produced MOJA for tackling the MOOPs. The MOJA is a posteriori form of the JA for tackling MOOPs. According to the Eq. (20.19), the MOJA solution sets are uplifted likewise as in the JA. Yet, to deal with numerous goals efficaciously and expeditiously, the MOJA is integrated with the concept of non-dominated sorting and mechanism of crowding distance.

In SOOP, it is simple to search which one solution set is good than another solution set related to the objective function’s corresponding value. On the other hand, it is a very difficult task to search the solution sets, which is the best and worst among the whole population in the case of MOOP. In the MOJA, the worst and best solution sets find out through the comparison of a position that is provided to the solution sets. The position of the solution sets depends on the concept of CD, ND, and CDV.

Initially, the random initial population is formulated \(J\) number of solution sets. This initial population is then sorted and assigned the position to each solution set according to the concept of CD and ND. The prevalence between solution sets is basically decided according to the concept of constraint-dominance. After that, the concept of ND and CDV of solution sets. The solution set, which has a greater position (position = 1), is viewed as better than the other solution set. However, if both the solution sets have the same position, then the solution set, which has a greater CDV, is prior to other solution set. This guarantees the solution set is chosen from the scanty area of the SS. A solution set which has most lower position is chosen as worst solution set. Similarly, a solution set which has most elevated position (position = 1) is chosen as best solution set. When the worst and best solution sets are chosen, then the solution sets are updated according to the Eq. (20.19).

When every solution set is updated, then the updated solution set is combined with the initial population, and we receive \(2J\) solution sets. Again, these solution sets are sorted and provided the position according to the concept of CD, ND, and CDV. With the help of a new position and CDV, the \(J\) number of better solution sets are chosen. The solution set’s prevalence between the solution sets is resolved according to their position and the CDV. The solution set, which has a greater position, is taken prior to the other solution sets. If some solution sets have the same position, then the solution set, which has a higher value of crowding distance, is preferred over the other solution sets. For each solution set, the MOJA finds the objective function’s value just a single time at every iteration. Consequently, the total no. of function evaluates needed through the MOJA = Size of population * no. of iterations. Moreover, computationally if the approach is run more than a single time, at that point, by multiplying the population size with total number of iterations and runs, we could obtain the total number of function evaluations.

There are also a few variations of MOJA that are found in the literature. These variations are elitist JA (EJA) [39], Binary JA (BJA) [40], Improved JA (IJA) [41] and Multi-objective Quasi-oppositional JA (MOQOJA) [42].

Like wise the TLBO and JA, Rao has also develop the Rao algorithms which are three metaphor-less simple algorithms for solving unconstrained and constrained optimization problems [43, 44].

4 Conclusion

In this chapter, the fundamentals of MOOP are characterized. We divided MOEAs dependent on two fundamental scenario: (1) Utilization of the Pareto dominant for the selection operator, (2) elitism. First evaluation of MOEAs is viewed as the Non-Elitist methods, while the subsequent second evaluation relates to the elitist approaches. The utilization of performance indicators for the selection operator and scalarizing functions for breaking the first MOOP into the collection of sub-problems can be viewed as the third evaluation of MOEA. After that, the algorithms work independently of an algorithm-specific parameter is the forth evaluation of MOEA. Nowadays, there has been more concern for hybridization evolutionary approaches, which combines the original optimization approach with some different ideas to enhance its quality. The result of the acquired methodologies generally consistently gives preferred outcomes over the first one.