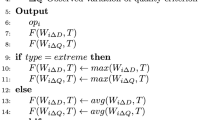A Fast Converging Evolutionary Algorithm for Constrained Multiobjective Portfolio Optimization

Abstract

Portfolio optimization is a well-known problem in the domain of finance with reports dating as far back as 1952. It aims to find a trade-off between risk and expected return for the investors, who want to invest finite capital in a set of available assets. Furthermore, constrained portfolio optimization problems are of particular interest in real-world scenarios where practical aspects such as cardinality (among others) are considered. Both mathematical programming and meta-heuristic approaches have been employed for handling this problem. Evolutionary Algorithms (EAs) are often preferred for constrained portfolio optimization problems involving non-convex models. In this paper, we propose an EA with a tailored variable representation and initialization scheme to solve the problem. The proposed approach uses a short variable vector, regardless of the size of the assets available to choose from, making it more scalable. The solutions generated do not need to be repaired and satisfy some of the constraints implicitly rather than requiring a dedicated technique. Empirical experiments on 20 instances with the numbers of assets, ranging from 31 to 2235, indicate that the proposed components can significantly expedite the convergence of the algorithm towards the Pareto front.

1 Introduction and Background

Portfolio optimization is a prominent application problem in the field of finance. A number of studies have been reported on this subject since 1952, as reviewed in [9]. The core task is to find the optimal allocation of limited capital among certain given assets so that two conflicting goals, minimizing risk and maximizing returns, can be achieved. Mean-Variance (MV) model is an original portfolio optimization model, which estimates the expected return by mean of the profit and measures the risk by variance of the profit [11]. This model is a quadratic problem since it assumes that the risk of an investment should be assessed by a covariance matrix based on the variance and the correlation among the assets. As a general quadratic problem, it is not difficult to solve using contemporary optimization techniques [14]. However, practical portfolio problems involve a range of constraints, such as cardinality, minimum lot size, pre-selected assets, etc. Incorporating these constraints result in mixed integer/combinatorial models. There are also some exact algorithms, which have been designed and utilized to tackle the constrained portfolio optimization problems [1]. Nonetheless, there is no polynomial-time algorithm for the case when a cardinality constraint is involved [13].

Therefore, meta-heuristic algorithms such as Evolutionary Algorithms (EAs) have gained attention to solve complex instances of portfolio optimization problems. Moreover, population-based metaheuristics are also inherently suited for solving multiobjective optimization problems, since the optimum of such problems consists of a trade-off solution set (Pareto optimal front). They have been used to solve different constrained portfolio optimization problems based on the mean-variance (MV) model, with different numbers of objectives and various different types of constraints. For single-objective problems, Chang et al. [2] used three different meta-heuristics, namely genetic algorithms, tabu search, and simulated annealing, to handle the problem with a fixed amount of invested assets. Gaspero et al. [8] proposed a hybrid algorithm with a local search and a quadratic programming solver. The numerical experiments on a portfolio optimization problem with three constraints (cardinality, quantity, and pre-assignment) showed that it performed better than some of the widely used softwares such as CPLEX and MOSEK. As for the constrained multi-objective problems, Pouya et al. [15] transformed the problem into a single-objective form with a fuzzy normalization. Subsequently, they used a metaheurstic method to solve the transformed problem and obtained improved results over Particle Swarm Optimization [15]. Deb et al. [6] solved the problem using a customized hybrid algorithm with specialized evolutionary operators, repair, local search and clustering. Lwin et al. [10] proposed a learning-guided multi-objective evolutionary algorithm (MODEwAwL), utilizing the information about selection of assets from previous generation to guide the search. It was based on a multiobjective Differential Evolution (DE) algorithm and the study compared results obtained with four well known Multi-Objective Evolutionary Algorithms (MOEAs). The simulation results on a MV model based problem, including four constraints such as cardinality, quantity, pre-assignment, and round lot constraints, indicated that the proposed algorithm improved the performance over the others. Yi et al. [3, 4] introduced a tailored representation, Compressed Coding Scheme (CCS) for the same problem as that in [10]. This representation used one gene fragment to represent both the selection and allocation of one asset. The comparison between CCS and the direct representation illustrated that this tailored representation was superior for this problem with regard to the obtained efficient front since it could reduce the interaction between the selection and allocation elements of the problem.

In the methods available to solve constrained multiobjective optimization problems, including those discussed above, the representation of a solution vector is typically done using a binary vector that indicates whether a particular asset is selected or not. Consequently, the length of the solution vector increases significantly as the number of assets increases; resulting in a corresponding (exponential) increase in the solution search space. Therefore, in this paper, we propose and show initial results on a new representation scheme that remains of a fixed size (equal to the cardinality of the portfolio) regardless of the number of assets available to choose from. Moreover, we also propose a customized initialization which guarantees one of the global extremities of the true Pareto front (PF). An evolutionary algorithm constructed with the proposed components shows a commendable speed-up in convergence, delivering a good PF approximation in relatively small number ($\approx$20%) of evaluations compared to the peer algorithms. The mathematical model for the problem is detailed next in Sect. 2, followed by the proposed method in Sect. 3. Numerical experiments and conclusions are presented in Sects. 4 and 5, respectively.

2 Mathematical Model

The constrained portfolio optimization problem studied here has two conflicting objectives (minimum risk, maximum return) and is subject to four constraints: cardinality, quantity, pre-assignment, and round lot constraints [10]. The following notations are used in the formulation:

N:

      the number of available assets

K:

      the number of assets in a portfolio, i.e., the cardinality

L:

      the number of assets in the pre-assignment set

$w_i$:

      the proportion of capital invested in the $i^{th}$ asset

$\rho _{ij}$:

      the correlation coefficient of the returns of $i^{th}$ and $j^{th}$ assets

$\sigma _{i}$:

      the standard deviation of $i^{th}$ asset

$\sigma _{ij}$:

      the covariance of $i^{th}$ and $j^{th}$ assets

$\mu _i$:

      the expected return of the $i^{th}$ asset

$\upsilon _i$:

      the minimum trading lot of the $i^{th}$ asset

$\epsilon _i$:

      the lower limit on the investment of the $i^{th}$ asset

$\delta _i$:

      the upper limit on the investment of the $i^{th}$ asset

$y_i$:

      the multiple of the minimum trading lot in the $i^{th}$ asset

$$\begin{aligned}&\sigma _{ij} = \rho _{ij}\sigma _{i}\sigma _{j} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad&\end{aligned}$$

$$\begin{aligned}&s_i= {\left\{ \begin{array}{ll} 1, &{}\mathbf{if} \text { the } i^{th}\, (i=1,\ldots ,N) \text { asset is chosen} \\ 0, &{}\text {otherwise} \end{array}\right. }&\end{aligned}$$

$$\begin{aligned}&z_i= {\left\{ \begin{array}{ll} 1, &{}\mathbf{if} \text { the } i^{th}\, \text {asset is in the pre-assigned set} \\ 0, &{}\text {otherwise} \end{array}\right. }&\end{aligned}$$

With above notations, the problem can be formulated as:

$$\begin{aligned}&\text {Minimize} \quad f_1=\sum _{i=1}^{N}\sum _{j=1}^{N}w_{i}w_{j}\sigma _{ij},&\end{aligned}$$

(1)

$$\begin{aligned}&\text {Maximize} \quad f_2=\sum _{i=1}^{N}w_{i}\mu _{i},&\end{aligned}$$

(2)

$$\begin{aligned}&\text {subject to} \quad \sum _{i=1}^{N}w_{i}= 1,\qquad 0\le w_{i}\le 1,&\end{aligned}$$

(3)

$$\begin{aligned}&\qquad \qquad \quad \,\, \sum _{i=1}^{N}s_{i}=K,&\end{aligned}$$

(4)

$$\begin{aligned}&\qquad \qquad \quad \,\,\epsilon _{i}s_{i}\le w_{i}\le \delta _{i}s_{i},\qquad i=1,...,N,&\end{aligned}$$

(5)

$$\begin{aligned}&\qquad \qquad \quad \,\, s_{i}\ge z_{i},\qquad i=1,...,N,&\end{aligned}$$

(6)

$$\begin{aligned}&\qquad \qquad \quad \,\, w_{i}=y_{i}\upsilon _{i},\qquad i=1,...,N,\quad y_{i}\in \mathbb {Z}_{+},&\end{aligned}$$

(7)

$$\begin{aligned}&\qquad \qquad \quad \,\, s_{i},z_{i}\in \{0,1\},\qquad i=1,...,N,&\end{aligned}$$

(8)

The Eqs. (1) and (2) represent the two conflicting objectives, i.e., risk minimization and return maximization. Equation (3) ensures that all available capital should be invested. Equation (4) is the cardinality constraint enforcing that exactly K assets are selected. Equation (5) is the floor and ceiling constraint, it defines that investment in the $i^{th}$ asset should lie between $\epsilon _{i}$ to $\delta _{i}$. Further, Eq. (6) designates the pre-assignment constraint that certain asset(s) must be selected ($z_i=1$) in the portfolio, eg, based on investors’ preferences. Equation (7) defines the round lot constraint, specifying a minimum number of lots to be traded for a selected asset. Finally, Eq. (8), discrete constraint, limits both $s_i$ and $z_{i}$ to be binary. In this study, these constraints are set in consistency with the past study [3] as follows:

• Cardinality ${K=10}$, floor $\epsilon _i=0.01$, ceiling $\delta _i=1.0$, pre-assignment ${z_{30}=1}$ and round lot $\upsilon _i=0.008$.

The goal in solving the above problem is to seek a set of portfolios that lie close to/on the Pareto front, with a good diversity to cater to the investors with different risk-return appetite.

3 Proposed Method

The proposed approach follows a canonical evolutionary framework as shown in Algorithm 1. The algorithm uses customized representation and operators (including initialization, offspring generation) to suit the constrained multiobjective portfolio optimization problem considered. The intent behind the customization is to improve the convergence rate, and they assume no more prior knowledge about the problem than already given in the existing works (e.g. [3]). The key components of the algorithm are discussed in the following subsections.

3.1 Solution Representation

From Sect. 2, one can observe that the solution vector under the standard notations includes 2N decision variables. The first N variables $s_i, i=1,\ldots , N$, are binary, indicating whether $i^{th}$ is selected or not; whereas the next N variables $w_i, i=1,\ldots , N$, are discrete, indicating the proportion of the capital invested in $i^{th}$ asset. Given that the given number of assets (N) may often comprise a large set, this representation gives rise to a large number of variables.

In this work, we propose and investigate a compact representation, which consists of merely 2K variables. The first K variables $a_i, i=1,\ldots , K, 1\le a_i \le N$, are categorical, indicating the labels (ids) of the chosen assets. The next K variables $q_i, i=1,\ldots , K$, are discrete (positive integers), representing the lot size acquired of these K assets.

Note that the above representation helps in implicitly satisfying some of constraints and avoiding repair operators. Since the round lot $\upsilon _i=0.008$, the total number of trading lots can be calculated as $p=\sum _i^Nq_i=1/0.008=125$. Now, since, floor $\epsilon _i=0.01$ and ceiling $\delta _i=1.0$, therefore, $2\le q_i\le 125$. Thus, having $q_i$ as integers in the given range automatically satisfy the round lot and floor-ceiling constraints. Moreover, the problem converts to a form akin to distributing the available capital (given number of lots ($p=125$)) lots to a selected number (K) of assets. Such types of problems commonly occur in probability theory, and there is an opportunity to leverage some of the existing techniques to solve them (as detailed in further subsections).

3.2 Initialization

The initialization of the solutions occurs in two parts. First half is a customized initialization to obtain solutions close to the solution with the best return. Of these the one with the maximum return is guaranteed globally for the problem, while the others are created by perturbing it. The second half is generated randomly.

Initializing the Best Return Solution(s): In order to maximize the overall return, one would need to buy the maximum quantity of the asset with highest return, while satisfying the prescribed constraints discussed in Sect. 2. We do so in these steps:

• Sort the assets in the decreasing order of their expected return

• Identify the top K assets in the sorted list, and assign the minimum trading lot ($q_i=2$) to each. This list is referred to as $S_K$

• If the pre-assigned asset ($z_{30}$) already exists in the above list, move to next step, otherwise replace the last asset in $S_K$ by the pre-assigned asset.

• Thereafter, assign $q_i=p-2\times (K-1)$ lots to the first asset in $S_K$ (the one with the largest return) and assign $q_i=2$ lots to the remaining $K-1$ assets. This assignment satisfies all constraints, sums up to p lots traded, and assigns maximum possible lots to the highest return asset. Thus, it constitutes the solution with maximum overall return, denoted by $x_{maxR}$

• For generating the rest of the $N_p/2-1$ solutions of the first half, the quantity of the first asset in $S_k$ is decreased by 1, while that of the second asset is increased by 1 to construct each subsequent solution.

Initializing the Remaining Solutions: The remaining $N_p/2$ solutions are initialized randomly. For generating each solution, $K-1$ assets are selected randomly, and the pre-assigned asset $z_{30}$ is appended to the list to complete the selection. As for their lot sizes, the total p round lots are divided among K assets using the stars and bars (SaB) approach in probability theory [7]. This particular instance is equivalent to dividing n indistinguishable objects into m partitions. SaB approach solves this problem using a graphical aid by representing n objects as indistinguishable symbols (‘stars’) in a single row, and placing $m-1$ separators (‘bars’) between them to specify the number assigned to each bin. For example, for dividing 5 objects in 3 bins, 2 bars can be placed between the them in different positions. Assuming each bin needs to have at least 1 object, the bars cannot be placed at either of the ends of the row. Thus, a total of ${n-1}\atopwithdelims (){m-1}$ possibilities exist for such an assignment. Correspondingly, for the given portfolio problem, there are ${p-2K-1}\atopwithdelims (){K-1}$ distributions possible where each chosen asset has the minimum round lot $q_i=2$ allocated. One of such combinations is chosen randomly, that satisfies the minimum round lot constraint.

3.3 Creating Offspring Solutions

The method proposed to create of the offspring solutions attempts to generate offspring solutions targeting different parts of the PF approximation, i.e., some toward low risk solutions, some towards high return solutions, and some across whole PF. The probability of generating the solution in either of these parts is controlled via a set of self-adapting parameters $\{pr_1, pr_2,pr_3\}$, such that $\sum pr_i=1$. The values are initialized to be equal at the beginning of the run, i.e., $\{1/3, 1/3,1/3\}$.

The offspring solutions are generated through pairwise recombination among the current population. For two parent solutions $px_1$ and $px_2$, the recombination proceeds as follows:

• Let us denote the assets in $px_1$ and $px_2$ as $apx_1$ and $apx_2$, respectively. The common assets between the two parents are identified as $ap_c = apx_1 \cap apx_2$ Correspondingly, the assets that are not common between the two parents can be identified as $ap_{u1} = apx_1{\setminus }ap_c$ and $ap_{u2} = apx_2{\setminus }ap_c$.

• The assets of the offspring solutions are then assigned as follows. The common assets ($ap_c$) are kept in both offspring solutions. The remaining $K-|ap_c|$ assets are chosen randomly from $ap_{u1} \cup ap_{u2}$, while ensuring no asset is assigned to both offspring solutions.

• The lot size for each asset for the offspring solutions are assigned as follows. The lot sizes of the common assets are directly inherited from the parent solutions. For the remaining (not common) assets, first of all, the lot sizes vector $q_i, i=1 \ldots |K-|ap_c||$, are generated using the same approach as used in initialization (i.e., SaB approach). Then,

  • With probability $pr_1$, the lot sizes are assigned in decreasing order to the assets with highest to lowest return. This is to encourage generation of solutions towards the PF extremity with high return.

  • With probability $pr_3$, the lot sizes are assigned in decreasing order by picking the assets with lowest expected risk based on the risk covariance matrix $\sigma$. This is to encourage generation of solutions towards the extremity of the PF with lowest risk.

  • With probability $pr_2$, the lot sizes are assigned randomly, to encourage the solutions across the PF with no bias.

Adjustment of Probabilities ${\varvec{\{pr_1, pr_2,pr_3\}}}$: After each generation, the probabilities $\{pr_1, pr_2,pr_3\}$ are adjusted by the algorithm to allow focus on unexplored regions as per the above conditions. The adjustment is done as follows:

• The curve length $C_l$ of the current non-dominated set (in the objective space) is calculated assuming it to be piece-wise linear among the non-dominated points.

• The number of solutions in the left (min. risk), middle, and right (max return) are identified as $n_1$, $n_2$, $n_3$ are counted as those within length $l \le C_l/3$, $C_l/3 \le l \le 2C_l/3$ and $2C_l/3 \le l \le C_l$ from the one extremity (say min. risk) along the curve. These numbers are then normalized as $\{N_1, N_2, N_3\} = exp(\{n_1, n_2, n_3\} /(n_1+ n_2+ n_3))$. In the final step, the probabilities are calculated as $\{pr_1, pr_2, pr_3\} = \frac{\{1/N_1, 1/N_2, 1/N_3\}}{{1/N_1+ 1/N_2+ 1/N_3}}$.

The rationale behind the above adjustments is to simply map the sections of the non-dominated set with fewer solutions to high probability of exploration and vice-versa. Other mathematical forms that achieve similar mapping can also be used.

3.4 Ranking and Reduction

For ranking the population, the widely used non-dominated sorting and crowding distance are used [5]. The former targets convergence towards the PF and the latter helps promote diversity among the non-dominated solutions during the search process.

4 Empirical Study

In this section, we discuss the experimental set-up and the results of the benchmarking.

4.1 Experiment Configuration

Two sets of test problems are considered here. One is established recently based on the data from Yahoo Finance website (D1−15) with the number of available assets as high as 2235. The other one is a classic but small scale (D16−20) benchmark suite¹. Their details are given in Table 1.

Table 1. Twenty benchmark instances considered in this study

For benchmarking with peer algorithms, the popularly used multiobjective performance metric, Hypervolume (HV) [16], is used in a normalized objective space. HV measures the volume of dominated space by a non-dominated set Q relative to a reference point r. The reference point needs to be carefully chosen for computing HV, to ensure that the contributions of the extreme points are counted but do not overwhelmingly contribute more than those of the other points in the set. Thus it is recommended to set r slightly dominated by the nadir point of the true PF (where known). In this work, we have set $r=(1.2,1.2)$ for this reason in the normalized space. Note that while calculating HV, the second objective (maximize return) is also converted to minimization by negating the values. The second key aspect is to select the normalization bounds. For the datasets from OR-Library (D16–D20), the true PFs can be obtained with a quadratic approach using CPLEX and a mathematical multiobjective method [12]. Therefore, true ideal and nadir points of the true PF are used as normalization bounds for these cases. However, the true PFs are unavailable for some problems in NGINX dataset (D1–D15) due to large number of assets. For these cases, the best known unconstrained Pareto fronts (UCPFs) are considered with the following modification. They are truncated by the best return solution (known to be feasible and globally optimal from Sect. 3). This truncated version of the UCPF is referred to as TUCPF. The PFs, UCPFs and TUCPFs for selected problems are depicted in Fig. 1. It can be seen that PFs and TUCPFs are significantly different from the UCPFs for both instances. Many solutions of UCPFs are infeasible. For instance, on D6, the return for UCPF ranges from 0 to 4, however, the solutions with return higher than 3 are all unavailable. On the other hand, although PFs are very close to TUCPFs on D6, the differences are distinct on D17. These results demonstrate the necessity of utilizing the PFs (where available) or TUCPFs (where PFs are not available) instead of the UCPFs contrary to some past studies that have used UCPFs. Since true PFs are unknown for some problems, we utilize the bounds of TUCPFs for normalizing the obtained PF approximations in those cases.

The proposed method is compared with two recent peer algorithms, namely MODEwAwL [10] and CCS [3]. The number of objective function evaluations are limited to 5000, and each algorithm is run 31 times with a population size of 100 for gathering the statistics of performance (HV).

Fig. 1.

The three different PFs.

4.2 Results and Comparisons

The statistics of HV obtained using the three algorithms are shown in Table 2. The rank and mean rank of each algorithm on all instances is listed in parenthesis $[*]$ and last row, respectively; where lower value indicates better performance. The best result of each instance is highlighted in gray. The symbol “+/−/=" indicates better, worse, and equal performance relationship between paired algorithms in terms of Wilcoxon rank-sum test (5% significant level). Lastly, if a PF is unavailable (for HV normalization bounds calculation) after running the mathematical approach for 7 days, the datasets are shown with a star(*). In such cases, TUCPFs are used for HV normalization bounds during benchmarking. We note that the problems are unsolvable with a 7 days time limit for the mathematical approaches when the available number of assets exceed 225.

Table 2. HV obtained using the three algorithms. Note: for brevity, we denote MODEwAwL, CCS and proposed method with ‘A’, ‘B’ ‘C’ respectively here.

Fig. 2.

PF approximations and the corresponding HV convergence curves.

The results show that the proposed algorithm performs first or second in all problems with an exception of D18. Furthermore, it achieves the best mean rank (1.4) among the three approaches. With regards to the Wilcoxon rank-sum tests, the proposed algorithm outperforms the others on most problems. For example, it shows better performance over MODEwAwL and CCS for large number of instances (9 and 16 times respectively), while it is worse on small number of instances (4 and 1 respectively). Furthermore, the differences are also clear from Fig. 2 in terms of the PF approximations obtained corresponding to the median HV. Due to space limitations, we only show the results for two instances, D3 and D19; but others show a similar trend. The figures show the improved PF approximation obtained by the proposed algorithm. It is able to find solutions covering most regions of the PF, especially the high return end. For example, in Fig. 2(a), the PF approximations of MODEwAwL and CCS only focus on the low risk area, whereas the proposed algorithm achieves much better coverage. Furthermore, the HV convergence plots indicate the significant speedup using the proposed method. It converges to the near-final PF within 1000 fitness evaluations, while the other two algorithms require 5000 fitness evaluations to get to equivalent stage.

On the other end of the spectrum, one relative shortcoming of the proposed algorithm also seems apparent, which is in obtaining the solutions on the low-risk end. For instance, in Fig. 2(c), the PF approximation of CCS can achieve much better low-risk solutions (below 2.5e−4). Moreover, we also observed in preliminary experiments that when large number of evaluations are made available (say 40,000–100,000), the relative advantage of the proposed algorithm is not as significant as its performance for lower evaluation budgets.

To summarize, initial experiments establish that the proposed algorithm is competitive to the state-of-the-art forms and shows significant promise in achieving fast convergence. However, a more in-depth investigation, extensive experimentation and parametric studies need to be further conducted to understand the impact of each component individually, and to improve their performance.

5 Conclusion and Future Work

This paper proposes a new compact representation and initialization for multiobjective portfolio optimization problem. The proposed approach can implicitly satisfy some of the constraints, avoiding the need for specialized repair operators, and can guarantee to obtain one of the extremities (highest return) of the PF. Numerical experiments are conducted on a range of problems with assets up to 2235, and results compared with two other established algorithms. The proposed algorithm shows favorable results for most problems, especially demonstrating remarkable fast convergence rate when compared to the peer algorithms. While the performance is promising, there is further scope for improving performance in terms of obtaining low-risk solutions and further improving its performance for higher computational budgets, which will be studied in the future work.