DNS Study of the Turbulent Inflow Effects on the Fluid Dynamics and Heat Transfer of a Compressible Impinging Jet Flow

Abstract

We present a DNS of a compressible impinging jet flow with Reynolds and Mach numbers of 8134 and 0.71, respectively. The jet is vertically confined between two isothermal walls and issues from a circular orifice of diameter D in the uppermost wall. The lowermost wall, placed at a distance of 5D from the other, serves as impingement plate. The temperature of the walls is constant and ${85\,\text {K}}$ higher than the average total temperature of the jet at inlet. In order to resemble engineering configurations where the inflow will certainly not be laminar, we prescribe fully turbulent inlet conditions. To this end, the impinging jet simulation is coupled with an auxiliary fully developed turbulent pipe flow DNS. This approach circumvents the calibration issues that arise when a synthetic turbulence generator is used. Because of their relevance in cooling applications, the analysis focuses on the heat transfer at the impingement wall and its spatial distribution, whose peculiar shape is determined by the vortex dynamics in the proximity of the wall. Aiming at identifying the effects of the turbulent inflow, results are compared with those of previous computations performed with comparable configuration but laminar inflow.

1 Introduction

Impinging jets are widely used in various engineering configurations for the high heat flux they can generate at the impingement plate. They provide an indispensable cooling technique for gas turbine components, electronic parts and stock materials during material forming processes. Despite their importance and decades of research, the physical mechanism that governs the heat and mass transfer in proximity of the plate is yet not fully understood. This is due to the very small time and length scales involved in the phenomenon, which are often not detectable in experiments or are not at all resolved in Reynolds-averaged Navier–Stokes (RANS) or large eddy simulations (LES). Furthermore, it is still unclear how these small-scales feature of the flow are affected by parameters such as compressibility, nozzle-to-plate distance, Reynolds number, inflow conditions etc.

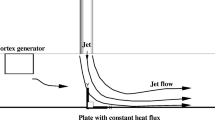
As summarized by Gauntner et al. [1], early experimental studies have been mainly devoted to identifying the characteristic flow regions and regimes of an impinging jet flow. These zones, each of which exhibits distinctive properties, are: the free jet region, the stagnation zone and the wall jet region. The free jet region is characterized by a shear layer that originates between the jet and the surrounding quiescent fluid. The shear layer gives rise to vortical structures, known as primary vortices, which are transported downstream while rolling up on themselves. In the stagnation zone, the flow is deflected radially, causing the primary vortex to break up. In the wall region, the flow evolves mainly radially and a boundary layer with a velocity profile similar to that observable in a wall jet flow originates. Near the wall, the shear layer between the wall jet flow and the quiescent fluid above produces new vortical structures, referred to as secondary vortices. By a LES, Hadžiabdić and Hanjalić [2] identified the vortex roll-up occurring above the impingement plate as the flow feature that influences most the fluid dynamics.

Gardon and Akfirat [3] observed that the mean heat flux distribution at the wall increases as the Reynolds number grows while exhibiting a similar qualitative shape if the nozzle-to-plate distance H is kept constant. Of particular interest has been the occurrence of a secondary peak in the heat flux distribution at a radial distance spanning between one and two jet diameters from the jet axis, in the proximity of which the primary peak is predictably observed. Among others, Jambunathan et al. [4] reported how several parameters affect the heat exchange at the impingement plate. The secondary peak is clearly visible for nozzle-to-plate distances lower than 3 diameters, whereas an inflection point is observed in the same region as H becomes larger. Several attempts of explaining the causes of such peak (or inflection point) have been made in the past decades. Wilke and Sesterhenn [5] showed that in the wall jet region primary and secondary vortices pair and produce concentric rings of alternatively high and low local heat flux travelling downstream on the wall. The area where these vortex rings originate corresponds to the high-heat-transfer area, suggesting that the second peak appears because cold fluid is transported towards the wall with the high velocity induced by the vortex pair in this particular region. Dairay et al. [6] indicate that the toroidal vortex ring structures undergo an azimuthal distortion that instantaneously drives cold fluid closer to the wall. This phenomenon occurs statistically more often in the high-heat-transfer region, giving a possible explanation to the existence of the secondary peak.

Despite the continued interest, most of the numerical studies existing in literature rely upon turbulence modelling for the closure of RANS (e.g. [7]) or LES (e.g. [8]). As previously mentioned, these approaches are inherently unable to explain the impingement heat transfer, because they model the process near the wall, which is exactly what one needs to understand prior to modelling. For instance, Dairay et al. [9] showed that even state-of-the-art large eddy simulations are still not able to satisfactorily predict the impingement heat flux. On the other hand, all previous direct numerical simulation (DNS) studies have specific shortcomings: they are either two-dimensional (e.g. [10]), consider low Reynolds numbers (e.g. [11]), exhibit an inadequate grid resolution (e.g. [12]) or do not implement turbulent inflow conditions (e.g. [5]). Certainly, the inflow in engineering configurations will not be laminar. Therefore, we perform a DNS in which we prescribe turbulent inflow conditions by coupling the impinging jet simulation with an auxiliary fully developed turbulent pipe flow DNS. When compared with synthetic turbulence generation methods as the one used by Dairay et al. [6], this procedure, which has never been used before for the simulation of an impinging jet flow, offers the advantage of not requiring any external calibration parameter and of giving a very accurate representation of all turbulence scales. To the best of the authors’ knowledge, we report here on the first study addressing a compressible impinging jet flow with fully turbulent inflow conditions. We will consider, in particular, the effects of the turbulent inflow on the global flow features and on the heat transfer at the impingement plate. To this end, results will be compared with those obtained by Wilke and Sesterhenn [5], who simulated a comparable configuration with laminar inlet conditions.

2 Flow Configuration

We investigate the impinging jet flow between two horizontal flat plates. The jet issues from a straight pipe through an orifice in the uppermost wall and impinges on the lowermost one (target plate). The distance between the two plates is equal to 5D, being D the diameter of the orifice. The plates are isothermal walls, the temperature of which is approximately 85 K higher than the average total temperature of the jet at the inlet. We consider, in particular, the flow of a compressible Newtonian fluid that obeys the ideal gas law. The characteristic Reynolds and Mach numbers are respectively defined as

$$\begin{aligned} {\textit{Re}}=\frac{\rho _{\infty } U_{\infty } D}{\mu (T_\infty )}, \qquad {\textit{M}}= \frac{U_{\infty }}{\sqrt{\gamma R T_{\infty }}}, \end{aligned}$$

(1)

where $\rho _\infty$, $T_\infty$ and $U_\infty$ are the density, temperature and velocity at the centreline of the jet inlet, R is the specific ideal gas constant and $\mu (T_\infty )$ the gas dynamic viscosity at the temperature $T_\infty$. Prandtl number and heat capacity ratio of the gas are ${\textit{Pr}}=\mu c_p/\lambda = 0.7$ and $\gamma =c_p/c_v=1.4$, where $c_p$ is the specific heat capacity at constant pressure, $c_v$ the specific heat capacity at constant volume and $\lambda$ the heat conductivity of the gas. The dynamics of the flow is described in Cartesian coordinates by the following formulation of the Navier–Stokes equations, introduced by Reiss and Sesterhenn [13]:

$$\begin{aligned}&\qquad \qquad \qquad \qquad \qquad \qquad \quad ~ 2\sqrt{\rho }\frac{\partial \sqrt{\rho }}{\partial t} + \nabla \cdot \left( \rho \mathbf {u} \right) = 0, \end{aligned}$$

(2a)

$$\begin{aligned}&\qquad \qquad \quad ~ \sqrt{\rho } \frac{\partial \sqrt{\rho } \mathbf {u}}{\partial t} + \dfrac{1}{2} \left[ \nabla \cdot (\rho \mathbf {u}\otimes \mathbf {u}) + \rho \mathbf {u}\cdot \nabla \mathbf {u}\right] + \nabla p - \nabla \cdot \boldsymbol{\tau } = \mathbf {0}, \end{aligned}$$

(2b)

$$\begin{aligned}&\dfrac{1}{\gamma -1}\frac{\partial p}{\partial t} + \dfrac{\gamma }{\gamma -1} \nabla \cdot (p\mathbf {u}) - \mathbf {u}\cdot \nabla p + \mathbf {u}\cdot (\nabla \cdot \boldsymbol{\tau }) - \nabla \cdot (\boldsymbol{\tau }\mathbf {u})-\nabla \cdot (\lambda \nabla T) = 0, \end{aligned}$$

(2c)

$$\begin{aligned}&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \rho T - \dfrac{1}{R}p = 0, \end{aligned}$$

(2d)

where $\mathbf {u}(\mathbf {x},t)$ is the fluid velocity, $p(\mathbf {x},t)$ the pressure, $\rho (\mathbf {x},t)$ the density, $T(\mathbf {x},t)$ the temperature,

$$\begin{aligned} \boldsymbol{\tau } = \mu \left( \nabla \mathbf {u}+\nabla \mathbf {u}^\text {T}- \dfrac{2}{3} (\nabla \cdot \mathbf {u})\boldsymbol{I} \right) \end{aligned}$$

(3)

the viscous stress tensor and $R=287.058\ \text {J}/(\text {kg}\,\text {K})$ the specific gas constant. The dependency of the viscosity on the temperature is taken into account by means of the Sutherland’s law [14]. Accordingly, the dynamic viscosity of the fluid is given by:

$$\begin{aligned} \mu = \mu _0 \left( \dfrac{T}{T_S}\right) ^{3/2} \dfrac{T_S+C_S}{T+C_S}, \end{aligned}$$

(4)

with coefficients $\mu _0 = 1.716 \cdot 10^{-5}\,\text {kg}/(\text {m}\,\text {s})$, $T_S=273.15\,\text {K}$ and $C_S=110.4\,\text {K}$.

Here we consider a configuration with a characteristic Reynolds number ${{\textit{Re}}=8134}$ and characteristic Mach number ${{\textit{M}}=0.71}$. This choice allows a direct comparison of the results with those of the study by Wilke and Sesterhenn [5], who addressed the same configuration, except the fact that laminar inflow conditions were used. Herein, Wilke and Sesterhenn’s case is referred to as reference case or laminar inflow case, whereas the present as turbulent inflow case. More specifically, we consider the laminar inflow case with ${\textit{Re}}=8000$ and ${\textit{M}}=0.8$, so that Reynolds number, average total temperature at the inlet and average injected mass flux differ with the turbulent inflow case by less than 2%.

3 Numerical Methods

Direct numerical simulation (DNS) of the above-described flow configuration is performed by means of the in-house solver NSF developed over the years at the CFD group of the TU Berlin. The computational domain chosen for the solution of the fluid dynamics is shown in Fig. 1. It consists of two blocks: an uppermost block, which corresponds to the terminal part of the injection pipe, and the lowermost block, where the impinging jet flow is computed. The length of the uppermost block, equal to 3D, is deemed sufficient to make the influence of the pipe outlet on its inlet not relevant. Both blocks are discretized by use of rectilinear grids with $1024\times 1024\times 1024$ points in the lower block and $144\times 756\times 144$ in the upper block. Equations (2a)–(2c) are discretized in space by using explicit 4th-order skew-symmetric finite differences, whereas a classical low-storage 4th-order Runge–Kutta method is adopted to advance in time. The use of a skew-symmetric scheme, in conjunction with the chosen formulation of the Navier–Stokes equations, results in a fully conservative finite-difference scheme [13].

Fig. 1

Sketch of the computational domain, representing both the Cartesian and cylindrical reference systems adopted in this paper. Walls are colored in grey, whereas the injection pipe in orange. D indicates the orifice or pipe diameter

The grid is refined in proximity of lowermost wall in order to ensure a $y^+ < 0.6$ at the first nodes above the wall, with $y^+$ the dimensionless wall coordinate. A grid refinement around the jet axis is also applied so that the grid spacing in x and z directions normalized with the orifice diameter D spans between 0.0099 and 0.0296. Figure 2 shows the turbulent energy spectra resulting from the present simulation. Given the axisymmetry of the geometry, it is sufficient to compute them on a xy-plane through the symmetry axis in both x and y direction. The monotonicity of the curve at large wave numbers indicates that no energy accumulation occurs at the smallest resolved scales, because the grid is sufficiently fine to dissipate it. Since identical grid refinement and resolution were used, the reader is referred to Wilke and Sesterhenn [5] for a validation of the grid in terms of Kolmogorov length scale.

Fig. 2

Impinging jet flow simulation. Spectra of the x component (a), y component (b) and z component (c) of the turbulent kinetic energy normalized with $U_\infty$ versus the dimensionless wave number in x and y direction: , x-direction (DNS data); , y-direction (DNS data); , line with $-5/3$ slope

As mentioned above, isothermal, non-slip boundary conditions are enforced at the walls. Inflow conditions for the upper block are discussed in Sect. 3.1. At the outlets, which laterally delimit the computing domain, non-reflecting characteristic outflow conditions are implemented. Having the uppermost block the shape a rectangular cuboid, a volume penalization method is used to obtain the cylindrical injection pipe. This method allows to apply non-slip boundary conditions at the wall of the pipe by modelling the solid as a porous media with a small permeability. In particular, the additional forcing term acts on the entire volume of the solid an not just at its interface with the fluid. Proof of convergence to the solution of the Navier–Stokes equations has been given by Feireisl et al. [15].

3.1 Turbulent Inflow Conditions

Turbulent inflow conditions are prescribed at the inlet of the injection pipe by enforcing time-deponent flow data previously recorded from an auxiliary turbulent pipe flow DNS. The pipe flow is computed on a cylindrical structured grid with $192\times 512\times 4096$ points in the radial, azimuthal and axial direction. The auxiliary pipe length is equal to 18D. Boundary conditions in axial direction are non-periodic, thus a recycling technique is implemented in order to maintain the flow in turbulent regime. This technique consists in copying velocity fluctuations from a recycling station downstream of the inlet of the auxiliary pipe. The recycling station is located in the auxiliary pipe at a distance of 15D from its inlet. This distance is deemed sufficient to avoid feedback-loop phenomena.

In order to validate the turbulent pipe DNS, the turbulent kinetic energy spectra of the turbulent kinetic energy components is calculated along the axial direction z. By looking at Fig. 3, it is possible to confirm the appropriateness of the grid resolution, because no energy accumulation at low scales can be observed. On the other side, the typical $-5/3$ slope of the inertial subrange is not wide enough to be detected because of the relatively low Reynolds number considered.

4 Computing Details

Investigating the fluid dynamics by means of direct numerical simulation requires significant computing resources, which can be solely made available by modern high performance computing centres. The direct solution of the Navier–Stokes equations is inherently the only viable method to gain insights into the physical phenomena while resting assured that the observations do not stem from a flaw in the turbulence model adopted. The needful grid resolutions, apt to detect the smallest scales of turbulence, are such that millions of core-hours per computation are needed. Such simulations are therefore always parallelized on a large number of computing cores so that results can be obtained in reasonable times.

Fig. 3

Pipe flow simulation. Spectra of the radial component (a), azimuthal component (b) and axial component (c) of the turbulent kinetic energy normalized with the bulk velocity $U_b$ versus the dimensionless wave number in axial direction: , DNS data; , line with $-5/3$ slope

In the present case, the parallelization is achieved through a block decomposition. This technique consists in partitioning the total load between a number of computing processes, each of which operates on a fractional part of the computational domain (block). In particular, the partitioning is here realized at two different levels: the injection pipe and the domain within the two plates are main blocks, which are in turn subdivided into smaller sub-blocks. In order to compute derivatives, information from adjacent blocks (either main or sub-blocks) is needed. This information is made available with the aid of ghost points between the main blocks, or by changing the domain decomposition between the sub-blocks, so that each of them receives grid lines that span the entire (main) block in the direction along which the derivative is being computed. The required inter-process communication is implemented through Message Passing Interface (MPI). For further details regarding the domain decomposition and parallelization in NSF, refer to [16].

Fig. 4

Strong and weak scaling behavior of NSF on CRAY XC40 (Hazel Hen) at HLRS. The scalability tests were performed respectively on a grid with $1024^3$ points and $64^3$ points per core

The NSF solver has been successfully ported and executed on the Cray XC40 (Hazelhen) supercomputer, on which scalability tests were performed for a computing configuration similar to the present one. As mentioned above, the uppermost block (injection pipe) has a grid resolution of $144\times 756\times 144$ points and is typically parallelized on 162 (or 324) cores. The lowermost block has a grid resolution of $1024\times 1024\times 1024$ points and is typically parallelized on 8192 (or 16,384) cores. In Fig. 4 strong and weak scaling plots for the lowermost block are displayed. The code performs well in both the weak and strong scaling tests, exhibiting in the latter case a nearly linear scaling. It should be noted that, although a setup with $64^3$ grid points per core differs from the production setup, where $40^3$ to $50^3$ points per core are used, we consider the result of the weak scaling test conservative. Keeping constant the number of cores, an increment of points per core will indeed result in less memory requirements and a lower amount of data transferred via MPI. Therefore, we expect in a production setup even more performant weak scaling results.

5 Results and Discussion

In this section, results are presented and discussed in comparison with those obtained by Wilke and Sesterhenn [5] (case with ${\textit{Re}}=8000$ and ${\textit{M}}=0.8$, see Sect. 3). As concerns the present case, statistics have been collected for a time equal to approximately $39\,t_r$, being $t_r=D/U_\infty$ the characteristic time of the simulation. Thanks to the homogeneity in $\theta$ (Fig. 1), averages are taken both in time and in the azimuthal direction. This makes it possible to compute statically converged averages in a relatively short simulated time.

Fig. 5

Contours on a xy-plane passing through the jet axis of the second invariant of the velocity gradient tensor Q normalized with $U^2_\infty /D^2$. The x-axis spans from $r/D=0$ to 4.4, whereas the y-axis form $y/D=0$ to 5

Figure 5 shows a snapshot of instantaneous Q contours on a xy-plane through the jet axis for both the laminar and turbulent inflow cases, being Q an indicator of the flow vorticity [17]. We observe that the typical Kelvin–Helmholtz structures in the shear layer region of the free jet are no longer easily discernible when a turbulent inflow is used. In this case, also the wall-jet region appears more chaotic, making the vortex pairing mechanism not clearly observable.

Fig. 6

Contours of the instantaneous temperature on a xy-plane through the jet axis and of the instantaneous Nusselt number on the impingement plate

In order to get more insight into the modified physics induced by the turbulent inflow, the instantaneous temperature contours on a xy-plane through the jet axis are plotted along with the Nusselt number at the impingement plate (Fig. 6), being the latter defined as the normalized local heat flux:

$$\begin{aligned} {\textit{Nu}}= \dfrac{\dot{q}D}{\lambda \Delta T}, \end{aligned}$$

(5)

with $\dot{q}$ the heat flux, $\lambda$ the thermal conductivity of the fluid and $\Delta T$ the difference between the total temperature of the jet at the inlet and the temperature of the isothermal plate.¹ It can be noted that high spots of ${\textit{Nu}}$, which indicate strong heat removal from the plate, are distributed in a disorderly manner and high-heat-transfer annuli, generated by the vortex rings, are not visible.

In Fig. 7, the velocity and temperature wall boundary layers of the laminar and turbulent inflow case are shown by plotting the mean dimensionless radial velocity $\overline{u^+}$ and the mean dimensionless temperature $\overline{T^+}$ as a function of the wall coordinate $y^+$ at different distances from the jet axis, with

$$\begin{aligned} y^+ = \dfrac{y\,u_\tau }{\nu },\quad u_\tau =\sqrt{\dfrac{\tau _w}{\rho }}, \quad u^+=\dfrac{\overline{u_r}}{u_\tau }, \end{aligned}$$

(5a-c)

$$\begin{aligned} T^+=\dfrac{T_w-T}{T_\tau } \quad \text {and} \quad T_\tau = \dfrac{\dot{q}}{\rho c_p u_\tau }, \end{aligned}$$

(5d,e)

where $\tau _w$ is the wall shear stress, $\rho$ the fluid density at the wall, $\nu$ the fluid kinematic viscosity at the wall and $T_w$ the wall temperature. We note that in the near-wall region (for small $y^+$), the turbulent inflow $\overline{u^+}$ profile better approximates the law $\overline{u^+}=y^+$ at all radial distances. Moreover, the turbulent inflow velocity boundary layer shows a smaller thickness in the turbulent inflow case. The temperature boundary layers of the turbulent and laminar inflow cases match closely up to $y^+\simeq 10$. Further away from the wall, $\overline{T^+}$ recovers quicker in the turbulent inflow case.

Fig. 7

Radial velocity (a–d) and temperature (e–h) boundary layer at $r/D=0.3$ (a, e), $r/D=0.8$ (b, f), $r/D=1.4$ (c, g) and $r/D=3.5$ (d, h): , laminar inflow; , turbulent inflow. As reference, the curves $\overline{u^+}=y^+$ and $\overline{T^+}=y^+$ are shown ()

The wall shear stress can be analyzed by looking at the skin friction factor $C_f$, defined as:

$$\begin{aligned} C_f = \dfrac{2\mu }{\rho U_\infty ^2}\frac{\partial u_r}{\partial y}. \end{aligned}$$

(6)

Figure 8a shows the mean skin friction factor on the impingement plate. We observe that at $r/D=0$, $\overline{C_f} \simeq 0$ in the turbulent inflow case, whereas $\overline{C_f} \simeq 0.01$ in the laminar inflow case. In both cases the maximum skin friction is attained at $r/D \simeq 0.6$, albeit the peak value in the laminar inflow case is approximately $20\%$ higher than in the turbulent inflow case.

Fig. 8

Mean skin friction coefficient $\overline{C_f}$ (a), mean Nusselt number $\overline{{\textit{Nu}}}$ (b): , laminar inflow; , turbulent inflow

Figure 8b shows the mean Nusselt number $\overline{Nu}$ on the impingement plate. We note that the characteristic shoulder, which in the laminar inflow case appears at ${r/D \simeq 1.4}$, is no longer observable in the turbulent inflow case. In the latter case, the Nusselt number is approximately 20% higher in the region $r/D\lesssim 1.2$, whereas the laminar inlet case features a 5% larger heat flux at $r/D\simeq 1.8$. The heat flow rate in the region $r/D<4$ expressed in terms of average Nusselt number is approximately equal to 12.55 in both laminar and turbulent inflow cases. This is due to the fact that the region where the turbulent inflow jet has a higher $\overline{{\textit{Nu}}}$, being located at a small radial distance r, is about 2.5 times smaller than the area where the turbulent inflow $\overline{Nu}$ is lower than in the laminar inflow case.

6 Conclusions

Direct numerical simulation of a compressible impinging jet with fully turbulent inflow conditions has been performed at ${\textit{Re}}=8134$ and ${\textit{M}}=0.71$. Results were compared with those reported by Wilke and Sesterhenn [5] who analyzed the same configuration by using laminar inlet conditions.

We found that the use of a turbulent inflow hinders the formation of the Kelvin–Helmholtz instabilities in the free-jet region and hence prevents the formation of vortex rings at the wall, which were found responsible for producing high local heat flux at the wall [18]. As a consequence, the shoulder in the mean heat flux profile that was found for the laminar inflow case in the region where the vortex rings form is no longer observable. Even though the local heat flux is sensibly higher in the turbulent inflow case up to $r/D\simeq 1.2$, both jets surprisingly provide about the same heat transfer, because the region where the turbulent inflow jet has much better cooling rate is much smaller, too. Nonetheless, the local changes in $\overline{Nu}$ indicate that for the correct design of an impingement cooling device, attention shall be paid to the inflow conditions.

In order to further clarify these aspects, higher order statistics are object of current research. This will give a complete understanding of the physics involved, required to improve the current heat-transfer models.