Radar Target Detection Based on Information Theory

Abstract

In this paper, the information theory method (ITM) is applied to radar detection system in the presence of complex additive white Gaussian noise (CAWGN). We introduce the target existence parameter into the radar detection system, which realize the unification of detection and estimation. We define the detection information in the radar as the mutual information between the received signal and the existence state of the target, and then use the ITM to derive the theoretical expression of target detection information. Meanwhile, we obtain corresponding expressions of the probability of false alarm and detection and get the relationship between the two probabilities approximately. Detection information and the probability of detection probability and false alarm are presented according to Neyman-Pearson (N-P) criterion based on existing methods. The numerical simulation results show that the theoretical detection performance of ITM can be obviously better than that of N-P criterion, which confirms that it is effective to use mutual information as a measure to evaluate the detection performance of the system.

1 Introduction

The purpose of radar target detection is to obtain information about the distance, amplitude, phase and velocity of the target in the echo signal. However, access to this information presupposes that the target must exist, so determining the existence of the target is particularly important in the field of radar detection.

The traditional radar target detection needs to find the threshold value to detect the presence of the target signal, but does not numerically describe the information content of the target by information theory. Woodward and Davies [1,2,3] applied information theory to radar detection system for the first time and obtained the relationship between location information and SNR after information theory [4] published in 1948 by Shannon. Bell first studied the application of information theory in radar waveform design [5], giving the method of obtaining the best estimation waveform and the effect of energy distribution on the mutual information between the target and the receiving waveform.

Based on research of Woodward and Davies and Bell, some research-ers have studied [6] the relationship between information theory and parameter estimation in radar detection. Y. Yang and R.S. Blum [7] find that maximize the mutual information between the random target impulse response and the reflected waveforms and minimize the mean-square error (MSE) in estimating the target impulse response, which could lead to the same solution in optimum waveform design. Recently, Xu’s team focus on research of targets’ location information and amplitude-phase information in the field of radar and sensor radar based on information theory [8,9,10], and estimate the target parameters of interest by maximum likelihood estimation (MLE) [8] and MSE [9] and so on.

Most of the radar system utilize the N-P criterion to realize the detection mission [11], many researchers have a number of ways to detect targets, but none without the N-P criterion [12, 13]. However, they only gave the judgment of the existence of the target and the relationship between false alarm rate and detection rate under their respective models. In [14], the presence or absence of a target is judged by the difference in the covariance matrix in the clutter environment. In [15], Michimasa Kondo maximizes the mutual information between the received signal and the estimated parameter, and the detection performance can be obtained roughly.

In [6,7,8,9,10, 12,13,14], parameter estimation and target detection are studied separately. In [16] and [17], a combination of Bayesian and N-P criterion methodology is developed, which could achieve the unification of detection and estimation. Although the two method is the best on their respective directions, their coalition does not result in optimal federation performance. Recently, some researches on performance, proposing new algorithms to achieve superior network throughput performance over existing schemes [18], proposing IRS-assisted secure strategy to significantly boost the secrecy rate performance [19].

In this paper, we introduce the target existence parameter into the radar detection system, which can use information theory to study both target detection and parameter estimation. Firstly, on the basis of the previous research [5, 6] on radar spatial information, the detection information under complex Gaussian scattering is discussed from the perspective of information theory. Then, the expressions of detection probability and false alarm probability are derived by using ITM under corresponding model, and the relationship between the two probabilities is obtained approximately. In addition, in order to evaluate the performance of information theory method, we also give the receiver operating characteristics (ROC) curves and detection information of N-P criterion, and conclude that the ITM is effective.

This paper is organized as follows. The system model of single target detection system for single antenna radar is presented in Sect. 2. In Sect. 3, the expression of target detection information is derived under complex Gaussian scattering model. Relation between false alarm probability and detection probability under information theory method and N-P criterion are derived in Sect. 4, respectively. In Sect. 5, on the basis of [15], the relationship between detection probability and falsealarm probability is deduced by using N-P criterion, and we got the corresponding detection information. In Sect. 6, the numerical results and analysis are presented, finally, in Sect. 7, the main results of this paper are discussed and concluded.

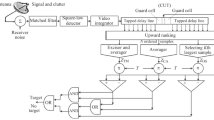
2 System Model

For the target detection in this paper, we focus on the existence of the target, so we introduce the target existence parameter into the radar detection system. In order to facilitate the analysis, we assume that if there is a target within the range of radar detection, it is a single target. To convert the received signal down to the baseband and passing through an ideal low-pass filter with a bandwidth of $B/2$, then the received signal is given by

$$\begin{aligned} z(t)=vys(t-\tau )+w(t), \end{aligned}$$

(1)

where v denotes coefficient of existence, where $v\in \{0,1\}$, $v=0$ and $v=1$ represent the target does not exists and target exist, respectively. $s\left( t \right)$ denotes baseband signal, y is scattering coefficient of target, which is modeled as

$$\begin{aligned} y=\alpha {{e}^{j\varphi }}, \end{aligned}$$

(2)

where $\alpha$ is the amplitude of the scattering coefficient and $\varphi$ is the phase of scattering coefficient. The scattering model of the target depends on the distribution of $\alpha$ and $\varphi$.

Assuming that d represents the distance between the rarget and receive, c denotes the signal propagation velocity, $\tau =2d/c$ represent time delay of the target, $w\left( t \right)$ stand for the additive noise, which is modeled as a complex Gaussian zero-mean with noise power ${{N}_{0}}$. Suppose the reference point is at the detection interval and the detection range is $[-D/2,D/2)$, the time delay interval is $[-T/2,T/2)$, where $T=2D/c$.

Given the radar transmitted signal is an ideal low-signal with bandwidth of B/2, i.e. the baseband signal is

$$\begin{aligned} s\left( t \right) =\sin c\left( Bt \right) =\frac{\sin \left( \pi Bt \right) }{\pi Bt}. \end{aligned}$$

(3)

We sample the received signal $z\left( t \right)$ according to Shannon-Nyquist sampling theory, namely, $t=n/B$, the sampling sequence is

$$\begin{aligned} z\left( n/B \right) =v\alpha {{e}^{j\varphi }}s\left( \left( n-B\tau \right) /B \right) +w\left( n/B \right) . \end{aligned}$$

(4)

Let $x=B\tau$ denotes the normalized time delay of target, we have

$$\begin{aligned} z\left( n \right) =v\alpha {{e}^{j\varphi }}s\left( n-x \right) +w\left( n \right) , \end{aligned}$$

(5)

where $n=-N/2,...,N/2$, $N=TB$ is regard as the time bandwidth product. (5) notes that N points sequence $z\left( n \right)$ can completely reconstruct $z\left( t \right)$.

Concisely, (5) can be rewritten in vector form

$$\begin{aligned} \mathbf {Z}=VY\mathbf {U}\left( \mathbf {x} \right) +\mathbf {W}, \end{aligned}$$

(6)

where $\mathbf {Z}={{\left[ z\left( -\frac{N}{2} \right) ,...z\left( \frac{N}{2}-1 \right) \right] }^{T}}$, $Y=y=\alpha {{e}^{j\varphi }}$, $\mathbf {W}=[ w\left( -\frac{N}{2} \right) ,...,w\left( \frac{N}{2}-1 \right) ]^{T}$, $V=v\in \{0,1\}$ and $\mathbf {U}\left( \mathbf {x} \right) ={{\left[ \sin c\left( -\frac{N}{2}-x \right) ,...,\sin c\left( \frac{N}{2}-1-x \right) \right] }^{T}}$.

Assuming that target is uniformly distributed in the detection, the prior probability density of $\mathbf {X}$ is therefore given by

$$\begin{aligned} p\left( x \right) =\frac{1}{N}. \end{aligned}$$

(7)

Here, we define the ratio of the power of useful signal to the noise power as SNR, namely

$$\begin{aligned} {{\rho }^{2}}=\frac{E\left[ {{\alpha }^{2}} \right] }{{{N}_{0}}}. \end{aligned}$$

(8)

3 Detection Information

The mutual information between the received signal and the existence state of the target is called detection information. Let mutual information $I\left( \mathbf {Z};V \right)$ denotes existence information. According to the mutual information identity, we have

$$\begin{aligned} I\left( \mathbf {Z};V \right) =H\left( V \right) -H\left( V|\mathbf {Z} \right) . \end{aligned}$$

(9)

Note that $H\left( V \right)$ and $H\left( V|\mathbf {Z} \right)$ denote the prior and the posterior entropy of V, respectively.

Where

$$\begin{aligned} H\left( V \right) =-p\left( 1 \right) {{\log }_{2}}p\left( 1 \right) -p\left( 0 \right) {{\log }_{2}}p\left( 0 \right) \end{aligned}$$

(10)

and

$$\begin{aligned} H\left( V|\mathbf {Z} \right) =-{{E}_{\mathbf {Z}}}\left[ \sum \limits _{v}{p\left( v|\mathbf {z} \right) }{{\log }_{2}}p\left( v|\mathbf {z} \right) \right] . \end{aligned}$$

(11)

The $p\left( 1 \right)$ and $p\left( 0 \right)$ is prior probability density of v, which represent the probability of target exist or not, respectively. $p\left( v|\mathbf {z} \right)$ denotes the posterior probability density function of v.

Therefore, we can rewrite the existence information as

$$\begin{aligned} \begin{aligned} I\left( {\mathbf{{Z}};V} \right)&= - p\left( 1 \right) {\log _2}p\left( 1 \right) - p\left( 0 \right) {\log _2}p\left( 0 \right) \\&\begin{array}{*{20}{c}} {}{} & {} {}&+ \end{array}{E_\mathbf{{Z}}}\left[ {\sum \limits _v {p\left( {v|\mathbf{{z}}} \right) } {{\log }_2}p\left( {v|\mathbf{{z}}} \right) } \right] . \end{aligned} \end{aligned}$$

(12)

Next, we study the calculation of complex Gaussian scattered target detection information.

3.1 Complex Gaussian Scattering

Complex Gaussian scattering means the y follows the complex Gaussian distribution, in which the $\alpha$ follows the Rayleigh distribution and the $\varphi$ is uniformly distributed over the interval $[0,2\pi ]$, namely

$$\begin{aligned} p\left( \varphi \right) =\frac{1}{2\pi }. \end{aligned}$$

(13)

As noted previously, $\mathbf {W}$ is the comples Gaussian noise vector whose elements are independent identically distributed (i.i.d) complex Gaussian variables with mean zero and variance ${{N}_{0}}$. Using (6), we can know the received vector $\mathbf {Z}$ is also complex Gaussian, and its covariance matrix $\mathbf {R}$, we have

$$\begin{aligned} \begin{aligned}&\mathbf {R}={{E}_{V,Y,\mathbf {W}}}\left[ \mathbf {Z}{{\mathbf {Z}}^{\text {H}}} \right] \\&=E\left[ \left( VY\mathbf {U(x)}+\mathbf {W} \right) {{\left( VY\mathbf {U(x)}+\mathbf {W} \right) }^{\text {H}}} \right] \\&=\mathbf {U}\left( \mathbf {x} \right) E\left[ VY{{Y}^{\text {H}}}{{V}^{H}} \right] {{\mathbf {U}}^{\text {H}}}\left( \mathbf {x} \right) +E\left[ \mathbf {W}{{\mathbf {W}}^{\text {H}}} \right] \\&={{N}_{0}}\mathbf {I}+Pv\mathbf {U}\left( \mathbf {x} \right) {{\mathbf {U}}^{\text {H}}}\left( \mathbf {x} \right) . \end{aligned} \end{aligned}$$

(14)

Where $P=E\left[ {{\alpha }^{2}} \right]$ represents the power of target.

The determinant

$$\begin{aligned} \left| \mathbf {R} \right| ={{\left( {{N}_{0}} \right) }^{N}}\left( 1+v{{\rho }^{2}} \right) \end{aligned}$$

(15)

doesn’t matter the location of target. The inverse of the covariance matrix can be obtained by the matrix inverse formula

$$\begin{aligned} {{\mathbf {R}}^{-1}}=\frac{1}{{{N}_{0}}}\left( I-\frac{v{{\rho }^{2}}\mathbf {U}(\mathbf {x}){{\mathbf {U}}^{H}}(\mathbf {x})}{1\text {+}v{{\rho }^{2}}} \right) . \end{aligned}$$

(16)

The multi-dimensional probability density of $\mathbf {Z}$ conditioned on $\mathbf {X}$ and V is given by

$$\begin{aligned} p(\mathbf{{Z}}|v,x) = \frac{\mathrm{{1}}}{{{\pi ^N}\left| \mathbf{{R}} \right| }}\exp \left( { - {\mathbf{{Z}}^H}{\mathbf{{R}}^{ - 1}}{} \mathbf{{Z}}} \right) . \end{aligned}$$

(17)

Therefore

$$\begin{aligned} p(\mathbf {Z}|v,x)=\frac{\text {1}}{{{\left( \pi {{N}_{0}} \right) }^{N}}\left( 1+v{{\rho }^{2}} \right) }\exp \left( -\frac{1}{{{N}_{0}}}{{\mathbf {Z}}^{H}}\mathbf {Z} \right) \exp \left( \frac{1}{{{N}_{0}}}\frac{v{{\rho }^{2}}}{v{{\rho }^{2}}\text {+}1}{{\left| {{\mathbf {Z}}^{H}}\mathbf {U}(\mathbf {X}) \right| }^{2}} \right) . \end{aligned}$$

(18)

Since the random variables $\mathbf {X}$ and V are independent of each other, we have

$$\begin{aligned} p\left( \mathbf {Z},v \right) =\int _{-{}^{N}/{}_{2}}^{{}^{N}/{}_{2}}{p\left( \mathbf {Z}|v,x \right) p\left( x \right) p\left( v \right) dx}. \end{aligned}$$

(19)

The posterior probability distribution $p\left( v|\mathbf {Z} \right)$ can be obtained by Bayes formula

$$\begin{aligned} p\left( v|\mathbf {Z} \right) =\frac{p(\mathbf {Z},v)}{p(\mathbf {Z})}, \end{aligned}$$

(20)

where

$$\begin{aligned} p\left( \mathbf {Z} \right) =p\left( \mathbf {Z},v=0 \right) +p\left( \mathbf {Z},v=1 \right) . \end{aligned}$$

(21)

Substituting (18), (19), (21) into (20),

$$\begin{aligned} p(v|\mathbf {Z})=\frac{p(v)\frac{1}{N}\int _{-{}^{N}/{}_{2}}^{{}^{N}/{}_{2}}{\frac{1}{1+v{{\rho }^{2}}}\exp \left\{ \frac{\text {1}}{{{N}_{0}}}\frac{v{{\rho }^{2}}}{1+v{{\rho }^{2}}}{{\left| {{\mathbf {Z}}^{H}}\mathbf {U}(\mathbf {x}) \right| }^{2}} \right\} }dx}{p(0)+p(1)\frac{1}{N}\int _{-{}^{N}/{}_{2}}^{{}^{N}/{}_{2}}{\frac{1}{1+{{\rho }^{2}}}\exp \left\{ \frac{\text {1}}{{{N}_{0}}}\frac{{{\rho }^{2}}}{1+{{\rho }^{2}}}{{\left| {{\mathbf {Z}}^{H}}\mathbf {U}(\mathbf {x}) \right| }^{2}} \right\} }dx}. \end{aligned}$$

(22)

Then, substituting (22) into (12), we can obtain detection information under complex Gaussian scattering model.

4 False Alarm and Detection

We can know that target signal exists or does not exist in received signal depends V from (6). There are two hypotheses to detect target’s existence, ${{H}_{0}}$ corresponds to $V=0$, target does not exist; and ${{H}_{1}}$ corresponds to $V=1$, target exists. The received signal under the two hypotheses are given respectively as follows:

$$\begin{aligned} \begin{aligned}&{{H}_{0}}:\mathbf {Z}=\mathbf {W} \\&{{H}_{1}}:\mathbf {Z}=Y\mathbf {U}\left( \mathbf {x} \right) +\mathbf {W}. \\ \end{aligned} \end{aligned}$$

(23)

Two probabilities of interes to evaluate detection performance. One is probability of detection ${{P}_{D}}$, that is, at hypothesis ${{H}_{1}}$, the probability having detected the target; the other probability of false alarm ${{P}_{FA}}$, the probability having detected the target at hypothesis ${{H}_{0}}$.

Next, we will discuss false alarm probability and detection probability from the perspective of information theory and N-P criterion respectively.

4.1 Information Theory Method

Two probabilities we interest are obtained from perspective of information theory, so we call this method studied in this paper information theory method (ITM).

For simplicity, following ${{\mathbf {Z}}_{1}}$ and ${{\mathbf {Z}}_{0}}$ represent the presence and absence of the target in the actual received signal, respectively.

Theorem 1

If the observation interval is long enough, the probability of false alarm can be approximated as

$$\begin{aligned} {{P}_{FA}}\approx p(1). \end{aligned}$$

(24)

Proof

Under complex Gaussian scattering model, according to (22) and the definition of false alarm probability, we get false alarm probability as

$$\begin{aligned} {{P}_{FA}}=\frac{p(1)\frac{1}{N}\int _{-{}^{N}/{}_{2}}^{{}^{N}/{}_{2}}{\frac{1}{1+{{\rho }^{2}}}\exp \left\{ \frac{\text {1}}{{{N}_{0}}}\frac{{{\rho }^{2}}}{1+{{\rho }^{2}}}{{\left| \mathbf {Z}_{0}^{H}\mathbf {U}(\mathbf {x}) \right| }^{2}} \right\} }dx}{p(0)+p(1)\frac{1}{N}\int _{-{}^{N}/{}_{2}}^{{}^{N}/{}_{2}}{\frac{1}{1+{{\rho }^{2}}}\exp \left\{ \frac{\text {1}}{{{N}_{0}}}\frac{{{\rho }^{2}}}{1+{{\rho }^{2}}}{{\left| \mathbf {Z}_{0}^{H}\mathbf {U}(\mathbf {x}) \right| }^{2}} \right\} }dx}, \end{aligned}$$

(25)

or

$$\begin{aligned} {{P}_{FA}}=\frac{p(1)\varUpsilon \left( 1,{{\mathbf {Z}}_{0}} \right) }{p(0)+p(1)\varUpsilon \left( 1,{{\mathbf {Z}}_{0}} \right) }, \end{aligned}$$

(26)

where

$$\begin{aligned} \varUpsilon \left( 1,{{\mathbf {Z}}_{0}} \right) =\frac{1}{1+{{\rho }^{2}}}\frac{1}{N}\int _{-N/2}^{N/2}{\exp \left( \frac{1}{{{N}_{0}}}\frac{{{\rho }^{2}}}{{{\rho }^{2}}\text {+}1}{{\left| w(x) \right| }^{2}} \right) dx}. \end{aligned}$$

(27)

It represents the time average of the exponential function of the white noise stochastic process in the observation interval. Assuming that the observation interval is long enough, the time average of the stationary process is equal to the ensemble average, then

$$\begin{aligned} \varUpsilon \left( 1,{{\mathbf {Z}}_{0}} \right) ={{E}_{w}}\left[ \frac{1}{{{\rho }^{2}}\text {+}1}\exp \left( \frac{1}{{{N}_{0}}}\frac{{{\rho }^{2}}}{{{\rho }^{2}}\text {+}1}{{\left| w(x) \right| }^{2}} \right) \right] . \end{aligned}$$

(28)

Given that $\xi ={{\left| w(x) \right| }^{2}}$ obeys the exponential distribution with parameter ${{N}_{0}}$, then

$$\begin{aligned} \begin{aligned} \varUpsilon \left( 1,{{\mathbf {Z}}_{0}} \right)&=\int _{0}^{\infty }{\frac{1}{{{\rho }^{2}}\text {+}1}{{{\text {e}}}^{\frac{1}{{{N}_{0}}}\frac{{{\rho }^{2}}}{{{\rho }^{2}}\text {+}1}\xi }}\frac{1}{{{N}_{0}}}{{e}^{-\xi /{{N}_{0}}}}d\xi } \\&=\frac{1}{{{N}_{0}}}\frac{1}{{{\rho }^{2}}\text {+}1}\int _{0}^{\infty }{{{{\text {e}}}^{-\frac{1}{{{N}_{0}}}\frac{1}{{{\rho }^{2}}\text {+}1}\xi }}d\xi } \\&=1.\\ \end{aligned} \end{aligned}$$

(29)

Consequently, substituting (26) into (29), then we obtain (24) which means that the probability of false alarm ${{P}_{FA}}$ equals approximately to the probability that the target actually exists.

According to (22) and the definition of detection probability, we get detection probability as

$$\begin{aligned} {{P}_{D}}=\frac{p(1)\frac{1}{N}\int _{-{}^{N}/{}_{2}}^{{}^{N}/{}_{2}}{\frac{1}{1+{{\rho }^{2}}}\exp \left\{ \frac{\text {1}}{{{N}_{0}}}\frac{{{\rho }^{2}}}{1+{{\rho }^{2}}}{{\left| \mathbf {Z}_{1}^{H}\mathbf {U}(\mathbf {x}) \right| }^{2}} \right\} }dx}{p(0)+p(1)\frac{1}{N}\int _{-{}^{N}/{}_{2}}^{{}^{N}/{}_{2}}{\frac{1}{1+{{\rho }^{2}}}\exp \left\{ \frac{\text {1}}{{{N}_{0}}}\frac{{{\rho }^{2}}}{1+{{\rho }^{2}}}{{\left| \mathbf {Z}_{1}^{H}\mathbf {U}(\mathbf {x}) \right| }^{2}} \right\} }dx}. \end{aligned}$$

(30)

It is obvious that ${{P}_{D}}$ and p(1) are related in (30). By substituting (24) into (30), we can easily obtain the relationship between detection probability${{P}_{D}}$ and false alarm probability ${{P}_{FA}}$ as follow

$$\begin{aligned} {{P}_{D}}\approx \frac{{{P}_{FA}}\frac{1}{N}\int _{-{}^{N}/{}_{2}}^{{}^{N}/{}_{2}}{\frac{1}{1+{{\rho }^{2}}}\exp \left\{ \frac{\text {1}}{{{N}_{0}}}\frac{{{\rho }^{2}}}{1+{{\rho }^{2}}}{{\left| \mathbf {Z}_{1}^{H}\mathbf {U}(\mathbf {x}) \right| }^{2}} \right\} }dx}{1-{{P}_{FA}}+{{P}_{FA}}\frac{1}{N}\int _{-{}^{N}/{}_{2}}^{{}^{N}/{}_{2}}{\frac{1}{1+{{\rho }^{2}}}\exp \left\{ \frac{\text {1}}{{{N}_{0}}}\frac{{{\rho }^{2}}}{1+{{\rho }^{2}}}{{\left| \mathbf {Z}_{1}^{H}\mathbf {U}(\mathbf {x}) \right| }^{2}} \right\} }dx}. \end{aligned}$$

(31)

4.2 N-P Criterion

In radar detection, N-P criterion is often used. The purpose of N-P criterion is to optimize the detection performance under the condition that the probability of false alarm does not exceed the tolerance range.

Basing on (17) and (23), we can get the probability density function of $\mathbf {Z}$ under the two hypothesis as follows:

$$\begin{aligned} \begin{aligned}&P(\mathbf {Z}|{{H}_{0}})=\frac{1}{{{\pi }^{N}}N_{0}^{N}}\exp \left\{ {-}\frac{1}{{{N}_{0}}}{{\mathbf {Z}}^{H}}\mathbf {Z} \right\} \\&P(\mathbf {Z}|{{H}_{1}})=\frac{1}{{{\pi }^{N}}N_{0}^{N}(1+{{\rho }^{2}})}\exp \left\{ \text {-}\frac{1}{{{N}_{0}}}\left( {{\mathbf {Z}}^{H}}\mathbf {Z}-\frac{{{\rho }^{2}}}{1+{{\rho }^{2}}}{{\left| {{\mathbf {Z}}^{H}}\mathbf {U}(\mathbf {x}) \right| }^{2}} \right) \right\} ,\\ \end{aligned} \end{aligned}$$

(32)

The result of log-likelihood ratio test is

(33)

where T denotes the threshold value, $\lambda$ denotes the Lagrange multiplier, $\gamma$ denotes sufficient statistics.

In order to get the maximum output SNR, assume that the baseband signal $\mathbf {U}\left( \mathbf {x} \right)$ and the receive signal $\mathbf {Z}$ are completely matched, we can deduce that the relation expression between the probability of false alarm and detection

$$\begin{aligned} {{P}_{D}}=\text {=}{{P}_{FA}}^{\frac{1}{{{\rho }^{2}}\text {+}1}} \end{aligned}$$

(34)

5 Detection Information Under N-P Criterion

When the target location is know, this paper adopts relationship between the detection information of the N-P detector and false alarm probability and the prior probability proposed in [15]

$$\begin{aligned} \begin{aligned}&I\left( V;\hat{V} \right) =H\left( V \right) -H\left( V\left| {\hat{V}} \right. \right) \\&=H\left( V \right) -{{P}_{{\hat{V}}}}(0)H\left( A \right) -\left[ 1-{{P}_{{\hat{V}}}}(0) \right] H\left( D \right) , \end{aligned} \end{aligned}$$

(35)

where V indicates whether a source is really exist or not and $\overset{\scriptscriptstyle \frown }{V}$ indicates receiving signal expressed in stochastic process. ${{P}_{{\hat{V}}}}(0)$ represents the probability that the target is detected as non-existent, then $1-{{P}_{{\hat{V}}}}(0)$ represents the probability that the target is detected as existing,

$$\begin{aligned} {{P}_{{\hat{V}}}}(0)=p(1){{P}_{D}}-p(1){{P}_{FA}}+{{P}_{FA}} \end{aligned}$$

(36)

A represents the actual existence probability of the target under the condition of the decision signal “target exists”, D represents the probability of the target non-existence under the condition of the decision signal “target does not exist”.

where

$$\begin{aligned} A=\frac{p(1){{P}_{D}}}{{{P}_{{\hat{V}}}}(0)} \end{aligned}$$

(37)

and

$$\begin{aligned} D=\frac{\left( 1-p(1) \right) \left( 1-{{P}_{FA}} \right) }{1-{{P}_{{\hat{V}}}}(0)}. \end{aligned}$$

(38)

6 Numerical Results and Analysis

In this section, we present the simulation results about the detection information and ROC curves in the CAWGN environment using ITM and N-P criterion.

We assume that the sampling point N is 64, the detection internal is $\left[ -N/2,N/2 \right)$, and the noise power ${{N}_{0}}$ is set as 1. In addition, if the single target exists, it locates in the far-field with the true location $x=0$.

6.1 Detection Information with Respect to SNR

In Fig. 1, the detection information is plotted with respect to SNR under complex Gaussian models. For convenience, the probability of target’s real existence $p\left( 1 \right) =0.5$ is used. As can be seen from Fig. 1, the solid curve represents the detection information curve of ITM, and the virtual curve represents the reachable region of detection information and SNR for any false alarm probability according to the detection information expression of N-P criterion. With the increase of SNR, the more information is obtained.

The detection information of ITM and N-P criterion increases from 0 to 1 with the increase of SNR, which verifies the correctness of the theoretical derivation. However, under the same SNR, the detection information of ITM is always greater than that of N-P criterion, which indicates that the detection performance of ITM is better than that of N-P criterion with the change of SNR.

Fig. 1.

Detection information with respect to SNR.

6.2 The ROC Curves Based on ITM and N-P Criterion

Figure 2 depicts the ROC curves based on ITM and N-P criterion under complex Gaussian scattering model, respectively, and the SNR is set as 0 dB, 5 dB. It can be seen that the probability of detection increases with the increase of probability of false alarm. On the condition of constant false alarm probability, the probability of detection increases with the increase of SNR. The probability of detection based on N-P criterion is always higher than that of ITM, which indicates that the performance of ITM is worse than that of N-P criterion from perspective of ROC.

Fig. 2.

The ROC curves based on ITM and N-P criterion.

6.3 Detection Information with Respect to Prior Probability

Figure 3 and Fig. 4 depict the relationship between detection information and prior probability. 0 dB and 5 dB respectively represent the low and medium SNR studied in this paper. The solid curve represents the detection information curve of ITM, and the virtual curve represents the reachable region of detection information and prior probability $p\left( 1 \right)$ for any false alarm probability ${{P}_{FA}}$ according to the detection information expression of N-P criterion.

As we can see from the two figures, the detection information of ITM is aways much higher than that based on N-P criterion, which indicates that the detection performance of ITM is better than that of N-P criterion. The amount of detection information with respect to prior probability on the condition of a certain SNR could be see from Fig. 1, which further verifies its correctness.

Fig. 3.

0 dB, detection Information with respect to prior probability.

Fig. 4.

5 dB, detection Information with respect to prior probability.

7 Conclusion

In this paper, we introduce the target existence parameter into the radar detection system, which could use the same method for target detection and estimation. The detection information in radar is investigated, and the detection performance based on ITM and N-P criterion is discussed. In single target scenario, we derive the theoretical expression of detection information under complex Gaussian scattering model. Moreover, we find that the probability of false alarm is equal to the probability of target’s real existence $p\left( 1 \right)$ by the approximation. And then we derive relational expression between the probability of detection and false alarm based on ITM and N-P criterion. Simulation results show that the detection information of ITM is better than that of N-P criterion from perspective of information theory, however, from the ROC curve, the result is opposite. At present, there is no final conclusion on which of the two criteria is the best, but our research work breaks the situation that N-P criterion dominates the whole country and opens up a new direction for the field of source detection. Finally, some issues such multi-target detection with interference are worthy of further investigations.