Problem of Overbooking for a Case of a Random Environment Existence

Abstract

An overbooking supposes that a booking of some product or service exceed given possibilities. It takes into consideration that a part of the booking will be cancelled. This situation is considered following to example of aviation ticket booking. It is supposed that an external random environment exists. The environment is described as a continuous-time finite irreducible Markov chain. A demand on the booking depends on the state of the random environment. An using of economical criterion supposes a consideration of such indices as costs of engaged seats of the aircraft and the penalty for the refusal of passenger with sold tickets. This criterion is optimized by means of dynamic programming method. A numerical example is considered.

1 Introduction

An overbooking policy assumes that a sale and a booking of some product or service exceed given possibilities. It takes into consideration that a part of the sale or the booking will be cancelled. The overbooking is used in different spheres of a transport, hotel’s businesses etc. Numerous publications are devoted to this problem [1,2,3,4,5,6,7,8].

In this paper we consider the problem of the overbooking in the case of an external random environment existence. Airline overbooking will be considered for concreteness. Notably we use one word “to buy” both as for “to buy” and for “to book”.

At the beginning the following positing of the problem will be considered following to the text [8].

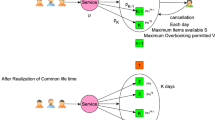
It is considered one aircraft trip, having the capacity $n^*$ passengers. The preddeparture time, when passengers buy tickets, is a random variable with the density $f(x), x\ge 0$. The passengers buy tickets independently of each other. There is the probability q that the passenger with the ticket, doesn’t come for the trip.

Then an external random environment exists, having k states with numbers $1, \ldots , k$. The environment is described as a continuous-time finite irreducible Markov chain J(t) with the matrix $\lambda =(\lambda _{i,j})_{k\times k}$ of transition probabilities between states.

An average demand for a considered trip depends on the state of the random environment and equals $d_i$ for the i-state, $i = 1, \ldots ,k$. Therefore the intensity of customer’s arrivals at time t till a departure, if the i-th state occurs, is calculated as follows:

$$\begin{aligned} \tilde{d_i}(t) = d_i f(t), t \ge 0. \end{aligned}$$

At every moment of time t, the number of the sold tickets n and the state i of the environment J are known. A decision on overbooking is adopted with intervals $\varDelta$, at the instants $s\varDelta$, $s = 1, 2, \ldots$, until departure. The i-th stage is called the time interval $(s\varDelta ,(s-1)\varDelta )$. The average number of the passengers, whose buy tickets on the s-th stage, if $J((s^*-s)\varDelta ) = i$, is

$$\begin{aligned} \alpha _i(s) = \int _{t=\varDelta (s-1)}^{\varDelta s} \tilde{d_i}(t) dt, s=s^*, s^*-1, \ldots , 1. \end{aligned}$$

(1)

Additionally we are guided by the maximal value of the overbooking. Let it be $m_{n,i}(s)$: the maximal value of overbooking at instant $t = s\varDelta$, if n place are busy and $J(t)=i$. Here $m_{n,i}(\varDelta ) \le m^*$, where $m^*$ is given.

From the beginning we suppose that the values $m_{n,i}(s)$ are given. Then we look for the following functions $m_{n,i}(s)$, that optimizes some effectiveness criteria. For example, the average aircraft load. The application of economical criteria implies considering of indices such as the costs of engaged seats of the aircraft and the penalty for refusing a passenger with sold tickets. Let c and r be the cost of one engaged seat and the penalty for one refusal respectively.

At the beginning we consider the first case, then the second case.

2 Main Results

We will consider the described process with the step $\varDelta > 0$. Let $\tau$ be the time, when all seats are occupied, $s^* = \tau /\varDelta$ be an integer, so the step number s of the step belongs to the set $\{s^*, s^* - 1,\ldots ,0\}$. The s-th step corresponds to the time interval $(\varDelta s, \varDelta (s - 1))$.

The random environment is represented by means of the continuous-time irreducible finite Markov chain J(t) with k states and matrix $\lambda (t)=(\lambda _{i,j}(t))$ of transition intensities between states. Let $P_{i,j}(t)$ be the probability that chain J(t) will be in state j at instant t if the initial state is i, $P(t) = (P_{i,j}(t))$ be the corresponding matrix. This matrix is calculated as follows [9, 10].

Let $\begin{pmatrix} 1&\ldots&1 \end{pmatrix}_{k\times 1}^T$ be the column-vector from the units, $\varLambda = \lambda \begin{pmatrix} 1&\ldots&1 \end{pmatrix}_{k\times 1}^T$ be the column-vector, $diag(\varLambda )$ be the diagonal matrix with vector $\varLambda$ on the main diagonal. The $k\times k$-matrix $A=\lambda -diag(\varLambda )$ is called generator of the Markov chain. We denote eigenvalues and eigenvectors of this matrix by $\chi _1, \chi _2, \ldots , \chi _k$ and $\beta _1, \beta _2, \ldots , \beta _k$ correspondingly. It is supposed that all values $\chi _1, \chi _2, \ldots , \chi _k$ are different.

Let $B=(\beta _1, \ldots , \beta _k)$ be the matrix, whose columns are eigenvectors $\beta _1, \ldots , \beta _k$ of the generator A, $\tilde{\beta _1}, \ldots , \tilde{\beta _k}$ be rows of the inverse matrix $B^{-1}$, so that $B^{-1}=(\tilde{\beta }_1^T, \ldots , \tilde{\beta }_k^T)^T$, $diag(\exp {(t \chi )})$ be the diagonal matrix with the vector $\exp {(t \chi )}=(\exp {(t \chi _1)}, \ldots , \exp {(t \chi _k)})$ on the main diagonal. Then

$$\begin{aligned} P(t) = \sum _{i=1}^k\exp {(\chi _i t)}\beta _i \tilde{\beta _i} = B diag(\exp {(t \chi )})B^{-1}, t \ge 0. \end{aligned}$$

(2)

Now we can calculate the average value $E T_{i,\nu ,j}(\varDelta )$ of sojourn time in the state $\nu$ on interval $(0, \varDelta )$ jointly with probability $P\{J(\varDelta ) = j\}$, if $J(0) = i$:

$$\begin{aligned} E T_{i,\nu ,j}(\varDelta ) = \int _0^\varDelta P_{i,\nu }(u)P_{\nu ,j}(\varDelta -u)du, \quad i, \nu , j \in \{1, \ldots , k \}. \end{aligned}$$

(3)

Further let us calculating the probability $\tilde{P}r_{\eta ,i,j}(s)$, that $\eta$ new requests on tickets are received during stage s and the final state $J(\varDelta (s-1))$ equals j, if the i–th state take place at instant $\varDelta s$. With respect to the paper [8] we use the following formula:

$$\begin{aligned} \tilde{P}r_{\eta ,i,j}(s) = \frac{1}{n!} \biggl ( \sum _{\nu =1}^k \alpha _{\nu }(s) E T_{i,\nu ,j}(\varDelta )\biggr )^{\eta } \exp {\biggl (-\sum _{\nu =1}^k \alpha _{\nu }(s) E T_{i,\nu ,j}(\varDelta )\biggr )}, \eta =0,1,\ldots . \end{aligned}$$

(4)

Let $Pr_{n,i}(s)$ be the probability that at beginning of the s–th stage the following situation occurs: n claims are gotten, the state of MC $J(\varDelta s)$ equals i. We will consider the following values of n: $n \in \{0, 1, \ldots , n^*+m^*+1 \}$. If values $n \le n^*$ then $Pr_{n,i}(s)$ means the probability that n places are busy. If value n belong to interval $[n^*+1, n^*+m^*]$ then $Pr_{n,i}(s)$ means the probability of corresponding overbooking. The probability $Pr_{n^*+m^*+1,i}(s)$ means the probability that the number of claims exceeds $n^* + m^*$.

We know values of $n=n^*$ and $i=i_0$ for the initial stage with number $s^*$, therefore

$$\begin{aligned} Pr_{n,i}(s^*) = \left\{ \begin{aligned}&1 \quad \textsf {if } n=n^*, i=i_0, \\&0 \quad \textsf {otherwise}. \end{aligned} \right. \end{aligned}$$

(5)

Further for $s=s^*-1, s^*-2, \ldots , 0$, $n \ge n^*$,

$$\begin{aligned} Pr_{n,j}(s) = \left\{ \begin{aligned}&\sum _{i=1}^k\sum _{\eta =n^*}^n Pr_{\eta ,i}(s+1)\tilde{P}r_{n-\eta ,i,j}(s+1), \textsf { if } n^* \le n \le n^*+m^*(s+1); \\&P_{i_0,j}((s^*-s)\varDelta )-\sum _{n=n^*}^{n^*+m^*(s+1)}Pr_{n,j}(s), \textsf { if } n= n^*+m^*(s+1)+1. \end{aligned} \right. \end{aligned}$$

(6)

The part of the last formula, corresponding to the case $n= n^*+m^*(s+1)$, follows from the equality

$$\begin{aligned} P_{i_0,j}((s^*-s)\varDelta ) = \sum _{n=n^*}^{\infty }Pr_{n,j}(s). \end{aligned}$$

The zero stage $s=0$ corresponds to the instant of the trip beginning. Now n means the number of all booked or sold tickets. Each of the corresponding passengers can not arrive to the trip with probability q, independently on the other passengers. Therefore, the probability that n passengers are in front of the take off

$$\begin{aligned} PP_{n}=\sum _{\eta =n}^{n^*+m^*}\frac{\eta !}{n!(\eta -n)!}(1-q)^n q^{\eta -n}\sum _{j=1}^k Pr_{\eta ,j}(0), n \le n^*+m^*. \end{aligned}$$

(7)

Finally the probability that n passengers have flown away is as follows:

$$\begin{aligned} PFA_{n}= \left\{ \begin{aligned}&PP_n,&\textsf { if } n<n^*, \\&\sum _{n=n^*}^{n^*+m^*} PP_n,&\textsf { if } n=n^*. \end{aligned} \right. \end{aligned}$$

(8)

The represented formulas allow to calculate various efficiency indices. Firstly, the average number of engaged seats:

$$\begin{aligned} Avr = \sum _{n=1}^{n^*}n \times PFA_n. \end{aligned}$$

(9)

Secondly, the probability that n passengers with bought or booked tickets meet with refusal equals $P_{n+n^*}, n=1, \ldots , m^*$. Average number of those passengers AvrR is calculated as follows:

$$\begin{aligned} AvrR = \sum _{n=1}^{m^*}n P_{n+n^*}. \end{aligned}$$

(10)

Finally, the probability that a customer encounters a refusal to purchase the ticket equals $\sum _{i=1}^k \sum _{s=1}^{s^*}Pr_{n^*+m^*+1,i}(s)$.

3 Numerical Example

Our example has the following input data. The Markov chain has three states $(k=3)$ and the transition intensities matrix

$$\begin{aligned} \lambda =\begin{pmatrix} 0 &{} 0.3 &{} 0.4 \\ 0.5 &{} 0 &{} 0.4 \\ 0.5 &{} 0.6 &{} 0 \end{pmatrix} . \end{aligned}$$

The initial state of Markov chain is known and fixed: $J(0) = i_0 = 1$. The capacity of the aircraft $n^*$ equals 20. A time before departure, when passengers buy tickets, has Erlang distribution with parameters $\mu = 0.5$ and $\theta =3$, and the density

$$\begin{aligned} f(x)=\frac{1}{4} (0.5 x)^2 \exp {(-0.5x)}, x \ge 0. \end{aligned}$$

(11)

Further we assume, that the average demand for given trip depends on the state of the random environment and equals $d_1=22.5$, $d_2=18$, $d_3=13.5$ for the first, second and third states. Now the arrivals intensity of passengers at time t until departure, if the i-th state occurs, is calculated by formula (1).

Let $\tau =3$ be the time, when all 20 seats are occupied. We consider the selling and the booking process with the step $\varDelta =1$. Therefore we have $s^* = \tau /\varDelta = 3$ stages. At last we suppose that the probability q, that a passenger doesn’t come to a trip, equals 0.15.

The results for these initial data are given below. Firstly, the case $m_{n,i}(s)=m^*=3$ for all n and s is considered, when the maximal number of additional overbooking equals 3 and doesn’t depend on the number s of the step and the number n of booked and sold tickets. Figure 1 contains graph of density (11).

Fig. 1.

Graph of density (11)

The expression (2) for the transition probabilities between states J(t) has the following form:

$$\begin{aligned} P(t) =\begin{pmatrix} -0.704 &{} 0.577 &{} -0.323 \\ 0.503 &{} 0.577 &{} -0.323 \\ 0.503 &{} 0.577 &{} 0.889 \end{pmatrix} \begin{pmatrix} e^{-1.2t} &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} e^{-1.5t} \end{pmatrix} \begin{pmatrix} -0.829 &{} 0.829 &{} 0 \\ 0.722 &{} 0.549 &{} 0.462 \\ 0 &{} -0.825 &{} 0.825 \end{pmatrix}. \end{aligned}$$

Tables 1, 2 and 3 contain the conditional average times $\tilde{ET}_{i,\nu ,j}(\varDelta )=ET_{i,\nu ,j}(\varDelta )/P_{i,j}(\varDelta )$ of the sojourn of process J(t) in the state $\nu$ on interval $(0,\varDelta )$, if $J(0) = i, J(t) = j$. The columns of the tables correspond to the final states $j = 0, 1, 2$, the rows correspond to the intermediate states $\nu$. Note that for each column the sum of all its elements equals 1.

Table 1. Conditional average sojourn times $ET_{0,\nu ,j}(\varDelta )$

Table 2. Conditional average sojourn times $ET_{1,\nu ,j}(\varDelta )$

Table 3. Conditional average sojourn times $ET_{2,\nu ,j}(\varDelta )$

Table 4. Probabilities $Pr_{n,j}(3)$

Tables 4, 5, 6 and 7 show the calculation results according to formulas (5)–(6). The probabilities $\{Pr_{n,j}(s)\}$ are given for $s = 3, 2, 1, 0$, $j = 0, 1, 2$ and $n = 20, \ldots , 24$. Let us remind, that: 1) the value for n = 24 means the probability, that the number of claims exceeds $n^* + m^* = 23$; 2) the initial state $J(s^*) = i0 = 1$.

Table 5. Probabilities $Pr_{n,j}(2)$

Table 6. Probabilities $Pr_{n,j}(1)$

Table 7. Probabilities $Pr_{n,j}(0)$

The probabilities (7), that n passengers are in front of the take-off, are presented in Table 8.

Table 8. Probabilities $PP_n$

The probabilities (8) that n passengers have flown away are presented in Table 9.

Table 9. Probabilities $PFA_n$

These tables allow the calculating of various efficiency indices. The average number of engaged seats Avr, calculated by the formula (9), equals 18.853. The probability $PP_{20+n}$ that n passengers with bought or booked tickets encounter a refusal equals 0.158, 0.075, and 0.017 for $n = 1, 2$, and 3. There the average number of such passengers

$$ 1\times 0.158 + 2\times 0.075 + 3\times 0.017 = 0.359.$$

It is noteworthy to compare these results with those whose will be without overbooking, when $m_{n,i}(s)=m^*=0$. Instead of Table 9, Table 10 takes place.

Table 10. Probabilities $PFA_n$ for the case $m_{n,i}(s)=m^*=0$

The average number of engaged places Avr equals 17 instead of 18.853. We see that the difference is significant.

4 Optimization of an Economical Criterion

We need to determine values $m_{n,i}(s)\in (0, \ldots , m^*)$ for each stage $s=s^*,s^*-1, \ldots , 1$, and values n and i so, that to maximize the average reward of engaged seats without penalty for refusal of the passenger with sold or booked tickets. Let $m(s)=(m_{n,i}(s))_{(m^*+1)\times k}$ be the corresponding matrix, $\varvec{m}=(m(s),m(s),\ldots , m(s))^T$ be the block-matrix.

Let c be the cost of one ticket, r is the penalty for one refusal. We take into account an additional index: a company derives income from earlier selling or booking of tickets. So we introduce the function of the treble $\varepsilon (s)$: it is the additional income for one given ticket per one day. The function $\varepsilon (s)$ has the following properties: 1) it is non-negative and decreasing; 2) $\varepsilon (0)=0$.

The average number of the of engaged seats $Avr(\varvec{m})$ is calculated by formula (9). The average number the refusals $AvrR(\varvec{m})$ is calculated by formula (10). Let $\varSigma \varepsilon$ be the total additional income owing to the treble. Therefore average reward is calculated as follows:

$$\begin{aligned} AvReward(\varvec{m})=c\times Avr(\varvec{m})-r\times AvrR(\varvec{m}) + \varSigma \varepsilon . \end{aligned}$$

(12)

We have the typical problem of the dynamic programming [11, 12]. In our case the decision variable on stage s for fixed n and i is $m_{n,i}(s), s=s^*, s^*-1, \ldots , 1$.

Let $\tilde{c}_{n,i}(s)$ be the maximal average reward of the best overall policy for the remaining stages $s, s - 1, \ldots , 1$, given that n tickets are sold and the random environment has state i. Given n and i, let $\tilde{m}_{n,i}(s)$ denote any value of the decision variable $m_{n,i}(s)$ that maximizes $\tilde{c}_{n,i}(s)$.

We begin with zero stage $s=0$ and end by the last stage $s^*$. The zero stage gives the number n of the passengers, whose have bought or booked tickets. As before each of corresponding passengers could come not come to the trip with probability q, independently of the other passengers. The probability that $\eta$ passengers from n are in front of the take-off is calculated with respect to the binomial distribution analogously to formula (7). Therefore

$$\begin{aligned} \tilde{c}_n(0)= & {} \sum _{\eta =0}^n \frac{n!}{\eta !(n-\eta )!} (1-q)^{\eta }q^{n-\eta }(c\times min(\eta ,n^*)-r\times max(\eta -n^*,0)) \nonumber \\&0 \le n \le n^*+m^*, \forall i. \end{aligned}$$

(13)

Values $\tilde{c}_{n,i}(s)$ for the other stages s are calculated recurrently for $s=1, 2, \ldots , s^*$; $0\le n\le n^*+m^*$; $\forall i$:

(14)

The ultimate solution is reached at the end of stage $s^*$ as $\tilde{c}_{0,i}(s^*), i=1,\ldots ,k$.

We see that dynamic programming finds it by successively calculating $\tilde{c}_{n}(0)$, $\tilde{c}_{n,i}(1)$, $\ldots$, $\tilde{c}_{n,i}(s^*-1)$, $\tilde{c}_{n,i}(s^*)$ for all $0\le n\le n^*+m^*$, $\forall i$. Because this procedure involves moving backward stage by stage, some authors also call s the number of remaining stages to the problem’s solution.

The described procedure supposes using matrices $(\tilde{c}_{n,i}(s))$ for every stage s. Analogous matrices are necessary to keep up optimal decisions values $\tilde{m}_{n,i}(s)$. It is possible to act otherwise, using so called forward procedure. Namely, the optimal values $\tilde{m}_{n,i}(s)$ are found after the computing of all $\tilde{c}_{n,i}(\eta )$, $\eta = s^*, s^*-1, \ldots , 0$.

5 Numerical Example (Continue)

Additionally to previous conditions we set $m^*=6$, $c=100$, $r=200$. At beginning we set $\varepsilon (s)=0$ for all s: Table 11 shows results of calculations by formula (13).

Table 11. Values of $\tilde{c}_n(0)$

Table 12. Values of $\tilde{c}_{n,i}(1)$

Table 13. Values of $\tilde{c}_{n,i}(2)$

Table 14. Values of $\tilde{c}_{n,i}(3)$

Tables 12, 13 and 14 contain the calculation results according to formula (14) for $s=1,2,3$.

We see that the state of the random environment influences on the results weakly. The optimal values of the decision are the same for various states. Moreover, they are equally at different stages in our case. Theses optimal decisions are presented in the Table 15.

Table 15. Optimal decisions $m_{n,\cdot }(\cdot )$

From the given tables it follows that optimal value of the overbooking $m_{n,i}(s)$ for all stages s and states i is 2 or 1. This corresponds to $n=20+2=22$, and from given tables we see, that the optimal value of the rewards equals 1821.

Now compare this result with the previous case, where it is supposed, that $m_{n,i}(s)=m^*=3$ for all $n<21$, i and s. In this case the average number of engaged seats $Avr=18.853$, the average number of passengers with bought and booked tickets, whose meet with refusal equals 0.359. It gives the following reward, with respect to formula (12):

$$AvReward(\varvec{m})=c\times Avr(\varvec{m})-r\times AvrR(\varvec{m})=100\times 18.853-200\times 0.359=1813.5.$$

We see that the increment is less.

Now we take into account the function of the treble $\varepsilon (s)$. Let it be the following form:

$$\begin{aligned} \varepsilon (s)=\delta (\exp {(\alpha (s^*-s))}, s \ge 0, \end{aligned}$$

(15)

where $\delta , \alpha \ge 0$.

Graph of this function for $\delta =15$ and $\alpha =2$ is presented on Fig. 2. Now the Tables 12, 13 and 14 look as follows (see Tables 16, 17 and 18).

Table 16. Values of $\tilde{c}_{n,i}(1)$ for the expression (15)

Fig. 2.

Graph of the function (15)

Table 17. Values of $\tilde{c}_{n,i}(2)$ for the expression (15)

Table 18. Values of $\tilde{c}_{n,i}(3)$ for the expression (15)

Table 19. Optimal decisions $m_{n,\cdot }(s)$ for the expression (15)

As earlier the random environment influences on the results weakly, but now the optimal values of the decision depends on different stages. These optimal decisions are presented in the Table 19.

6 Conclusion

The considered model can be generalized in many ways. Firstly to discriminate between sold and booked tickets. Secondly it takes into account a possibility of a cancellation of booked tickets during a period of our consideration. Our future researches will be connected with the realization of these possibilities.