Keywords

1 Introduction

Nowadays, there is a growing interest on cloud technology globally, which informs the efforts by many companies toward implementation of cloud technologies in their business processes. Cloud technology with its own unique feature comprises cloud services, storage, computing, grid computing and distributed computing, among others. Since the idea of cloud technology was projected, there is perpetual attention for research across the world. It has become the hottest research area in the domain of information technology which has been realized as unital of the technology that postures the next-generation computing revolution [1]. Cloud computing offers many opportunities to enterprises for their customers to access and operate computing services as “pay-as-you-go”. Customers saddle with responsibilities of batch processing and web applications explored cloud computing model as an efficient alternative way to acquiring and managing private data centers [2].

Cloud computing as described by US National Institute of Standards and Technology (NIST) as a model that allows and provides convenient ways of accessing unlimited pool of shared resources such as on-demand network access, servers, applications, storage and services categorized as software and hardware that can be rapidly made available to the client as soon as requested through the internet, these resources can be reviewed upward and downward automatically based on client’s demand. Thus, cloud computing has five essential characteristics, three service models and four deployment models such as on-demand self-service, broad network access, resource pooling, rapid elasticity and measured service, software-as-a-service (SaaS), platform-as-a-service (PaaS), and infrastructure-as-a-service (IaaS) and private cloud, public cloud, community cloud and hybrid cloud, respectively, as shown in Fig. 1 [1, 3].

Fig. 1
figure 1

Cloud solutions based on the system’s deployment and service model [1]

Full size image

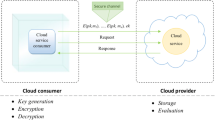
The quick move toward adoption of cloud computing has raised critical fears on an ultimate fact for the success of information systems, communication, virtualization, data availability and integrity, public auditing, scientific application and information security. Despite the demand of businesses and individual organizations to transfer their data to the cloud, security in terms of data integrity and confidentiality, trust in terms of data accessibility and availability, and privacy issue have remained as the challenges for embracing cloud computing [4]. Thus, security anxieties arise when transforming data from locally owned storage to third parties cloud service provider’s (CSP) storage. It is expected of CSP to encrypt user’s data before storing it on their cloud server. Several cryptographic schemes such as encryption and decryption, key exchange and steganography have been used to address the security challenges facing the adoption of cloud computing. Encryption means conversion of plain text to ciphertext, and it can be used in various applications for moving data from one location to another. Encryption algorithms such as DES, AES, RSA, Blow fish and many more are meant for secured storage of data and operations on cloud computing server [5, 6]. The traditional encryption schemes seem to be weak for securing the integrity and confidentiality of stored data in the cloud computing server as it requires secret key to be provided by the users so as to decrypt the data prior to the computations, and this threatens the privacy, confidentiality and integrity of stored data.

Homomorphic encryption (HE) was introduced to overcome this concern. HE is the process of delegating processing of an encrypted data without having access to the raw data, and produces encrypted result when decrypt result matches the result of the same operations carried out on the raw data. It is considered as one of the most efficient solutions for protecting the confidentiality and user’s information privacy in cloud-based services. Also, HE is grouped as partial homomorphic encryption (PHE) and fully homomorphic encryption (FHE) where PHE ropes either to additive or multiplicative operation, whereas FHE supports both operations and seems to be more secured and efficient than PHE as it poses properties of both operations [7].

The concept of FHE scheme was first introduced by Gentry and Boneh [8] and this was used to address cryptography central open issues. The scheme allows arbitrary functions to be computed over an encrypted data with no reference to decryption key [9]. The development of FHE is a revolutionary advancement, greatly extending the scope of the computations, which can be applied to process encrypted data homomorphically. Gentry [10] presented the first version of FHE scheme using ideal lattices; however, his construction was very complex and impracticable. Since then, FHE has been an interesting research area and several developments that centre on the application, implementation and improvement of FHE schemes have also been studied [11]. There are numerous practical applications of FHE in the real world such as buyer privacy in publicity, medical applications (genomics and health), national security, private prediction, private learning, education, monetary privacy and forensic image recognition, among others [12,13,14].

There are three major problems associated with the design and practical implementation of FHE scheme such as security problem, time efficiency problem and cipher expansion problem. However, several researchers [15, 16] have contributed to the improvement of FHE in terms of security that is based on hard mathematical problems, and the cost of breaking such scheme at a given security parameter λ should be at least 2λ. Also, in the last 11 years, progress has been made on time efficiency problem by different researchers such as [17,18,19,20,21], and the proposed schemes were categorized into three generations: FHE based on ideal lattices; the second generation is based on learning with error (LWE) and ring learning with error (RLWE) problems and the third generation is GSW which is also based on RLWE. However, each of these proposed schemes still needs further improvement for it to be efficiently useful in real-world applications.

It is highlighted in [7, 17] that cipher expansion for both asymmetric and symmetric FHE schemes are producing very large ciphertext size between hundreds and tens of thousands as compared to original plaintext size. For instance, ciphertext produced in [17] is till 400,000 times that of the original plaintext and likewise in [7]. These show the growth rate of ciphertext size in an existing FHE schemes which call for serious concern and constitute a major problem of the schemes because it will require large bandwidth to transfer such ciphertext through the network. We proposed scheme conversion concept for encryption scheme originally mentioned in [7] as symmetric-based FHE in order to address the issue. In addition, we provide efficient parallelization in encryption process which produces small ciphertext sizes. However, this study focuses on tackling cipher expansion problem on symmetric-based FHE scheme as proposed by [7] using residue number system.

The organization of this paper is as follows. Section 2 describes the related studies on homomorphic encryption; Sect. 3 discusses the research methodology of the proposed framework. Section 4 presents results findings and discussion. Section 5 is the conclusion to the study.

2 Related Works

HE schemes are classified into three major categories, as shown in Fig. 2 based on supported homomorphism operations and properties which are partial homomorphic encryption (PHE), somewhat homomorphic encryption (SWHE) and fully homomorphic encryption (FHE). This scheme is called PHE when it allows any number of either addition as in [22, 23] or multiplication operation as described in [24, 25]. However, SWHE supports both operations but with limited number of times allowed to evaluate the decryption function because of noise growth as illustrated in [8, 26]. Likewise in [27], the authors presented technique based on SWHE that efficiently secures pre-processing model for dishonest majority in multiparty computation over the ring \({\mathbb{Z}}_{{2_{k} }}\). Finally, improvement over SWHE is FHE which allows unlimited number of operations for both additive and multiplicative homomorphism to be performed on an encrypted data without increase in noise during the computation. This type of schemes is extensively discussed in [8, 10, 21, 28].

Fig. 2
figure 2

Categorization of homomorphic encryption

Full size image

Parallel to conventional cryptography, FHE schemes are also categorized into asymmetric encryption and symmetric encryption. Asymmetric FHE schemes protect the privacy and confidentiality of data by using different pair of keys (public key and private key) to encrypt the data. Recent research on asymmetric-based FHE has been proposed by [10, 17, 19, 20, 23, 28,29,30,31,32,33]. However, these schemes suffer from very high computational overhead, cipher expansion and time efficiency which make it difficult to practice in real-world application. However, researchers such as [7, 27, 34,35,36,37,38,39,40,41] have proposed symmetric-based FHE schemes due to its strength in low computational overhead and practical consideration for real-world deployments. Moreover, some of these symmetric-based FHE schemes [7, 41,42,43,44] still suffer from large cipher expansion and low immunity against attack. This demanded that a robust security resistant and cipher expansion reduction are highly needed for these symmetric-based FHE schemes [40, 45].

3 Research Method

This section discusses the research methodology in relation to homomorphic encryption, N-prime model, residue number system and proposed RNS-based N-prime model for symmetric FHE.

3.1 Homomorphic Encryption

Just after discovery of RSA cryptosystem, HE was introduced by [24] as privacy homomorphism that protects the privacy, integrity and confidentiality of data. Generally, HE scheme allows computations on an encrypted variable without the need for decryption prior to the computation or the use of secret key [14, 46]. HE scheme contains four algorithms such as key generation (KeyGen), encryption (Enc), evaluation function (Eval(f)) and decryption algorithm (Dec) which can be described as follows:

  • KeyGen: (pk, sk) ← KeyGen(k), choose parameter k and the algorithm will generate pk as public key and sk as private key.

  • Enc: c ← Enc(m, pk), where m is the plaintext-message, pk is public key and c is the ciphertext.

  • Dec: m ← Dec(c, sk), where c is the ciphertext, sk is the private key and m is the plaintext message.

  • Eval(f): c* ← Evaluate (f, Enc(m1), Enc(m2), …… Enc(mn))

However, for the scheme to be homomorphic in nature, it must obey the following properties:

  • Dec(c*, sk) = f(m1, m2, ………. mn)

  • Dec(C1 op C2, sk) = M1 op M2

where C1 and C2 are Enc(M1) and Enc(M2), respectively, op is the group operation (addition or multiplication) in the ciphertext and plaintext space, respectively.

3.2 N-Primes Model

In [7], an encryption scheme called N-primes model is investigated for constructing a symmetric-based FHE scheme which converts each plaintext character into ASCII code and passes it to the encryption algorithm \(c = m + r*l*n\) where ct is the ciphertext, m is the plaintext message and m \(\in\) [0, L−1], r is the noise added to the ciphertext, l is a prime big integer and \(n = p1*p2*p3* \ldots pi\) is the multiplication of numerous prime numbers resulting in one ciphertext for each character in the plaintext message. Thus, encryption and decryption are as follows:

Key generation

$${\text{Generate}} n$$
$${\text{Generate}} l \in Z_{n}$$
$$\begin{aligned} {\text{where}}\,n\,{\text{is a multiplication of various prime numbers }}\left( {n = P_{1} * P_{2} * P_{3} * \ldots P_{i} } \right) \hfill \\ {\text{and}}\,l\,{\text{is a big prime integer value }} \hfill \\ \end{aligned}$$

Encryption algorithm

\(c = m + r*l*n\) \({\text{where}} c {\text{is the ciphertext}}, m \in \left[ {0, L - 1} \right] {\text{and}}\,r\,{\text{is random number}}\)

Decryption algorithm

$$m = {\text{c mod l}}$$

Proof of homomorphism

Additive property

$$\begin{aligned} m_{3} &= c_{1} + c_{2} = \left( {m_{1} + r_{1} *l*n} \right) + \left( {m_{2} + r_{2} *l*n} \right) \\ & = \left( {m_{1} + m_{2} } \right) + l*n\left( {r_{1} + r_{2} } \right) \\ & since\,l*n\left( {r_{1} + r_{2} } \right) mod\,l = 0\,then \\ & m_{3} = \left( {m_{1} + m_{2} } \right) \\ \end{aligned}$$

Multiplicative Property

$$m_{3} = c_{1} * c_{2} = \left( {m_{1} + r_{1} *l*n} \right)* \left( {m_{2} + r_{2} *l*n} \right)$$
$$m_{3} = \left[ {\left( {m_{1} * m_{2} + m_{1} * r_{2} *l*n} \right) + \left\{ {\left( {m_{2} *r_{1} *l*n} \right) + \left( {r_{1} *l*n} \right)\left( {r_{2} *l*n} \right)} \right\}} \right]$$
$$m_{3} = \left[ {\left( {m_{1} * m_{2} + m_{1} * r_{2} *l*n} \right) + \left\{ {\left( {m_{2} *r_{1} *l*n} \right) + \left( {r_{1} *r_{2} *l^{2} * n^{2} } \right)} \right\}} \right]$$
$$m_{3} = \left( {m_{1} * m_{2} + m_{1} * l*\left\{ {r_{2} *n + r_{1} *n* m_{2} + r_{1} * r_{2} *l*n^{2} } \right\}} \right)$$
$$\begin{aligned} {\text{Since}}\left[ {l*\left\{ {r_{2} *n + r_{1} *n*m_{2} + r_{1} *r_{2} *l*n^{2} } \right\}} \right]\bmod l = 0 \hfill \\ {\text{and}}\,{\text{multiple}}\,{\text{of}}\,l\bmod l = 0\,{\text{then}} \hfill \\ \end{aligned}$$
$$m_{3} = m_{1} * m_{2} + m_{1} *0$$
$$m_{3} = m_{1} * m_{2}$$

3.3 Residue Number System

The residue number system (RNS) is a non-weighted and carry-free number system that speeds up arithmetic operations by dividing them into smaller parallel operations. It is characterized based on its unique properties which include fault tolerance, modularity, parallelism and carry-free operations, among others. RNS is very efficient in terms of handling arithmetic operations (addition, subtraction and multiplication) [47,48,49,50]. RNS can as well be described as moduli set of positive pairwise relatively prime numbers \(\left( {{m}_{1} ,{ m}_{2} \ldots {m}_{{n}} } \right)\) and the product of all the modulo (M = m1 × m2 × … × mn) that produces the dynamic range (DR) of such moduli set. Any integer X in the range [0, M – 1] can be uniquely represented by an ordered set of residues (x1, x2,…,xn). Each residue xi is represented by xi = X mod mi.

To perform residue arithmetic operations such as addition or multiplication can be achieved by adding or multiplying corresponding digits relative to the modulus for their position [50]. For a given moduli set \(\left\{ {m_{1} , m_{2} , \ldots , m_{N} } \right\}\),

\(X = \left\{ {x_{1} , x_{2} , \ldots , x_{N} } \right\}\) and \(Y = \left\{ {y_{1} , y_{2} , \ldots , y_{N} } \right\}\) such that \(x_{i} = \left| X \right|m_{i}\) and \(y_{i} = \left| Y \right|m_{i}\) where i = 1, 2, …, N, then we may define the residue arithmetic operations as follows:

$$X \otimes Y = Z$$
$$X \otimes Y = \left\{ {x_{1} , x_{2} , \ldots , x_{N} } \right\} \otimes \left\{ {y_{1} , y_{2} , \ldots , y_{N} } \right\} = \left\{ {z_{1} , z_{2} , \ldots , z_{N} } \right\} = Z$$

where \(z_{i} = \left| {x_{i } \otimes y_{i} } \right|m_{i}\) and \(\otimes\) is residue arithmetic operator (+, *, and −). As an example, with the moduli-set \(\left\{ {3, 4, 5} \right\}\), the representation of fifteen is \(\left\{ {0, 3, 0} \right\}\), that of twenty-three is \(\left\{ {2, 3, 3} \right\}\), and adding the two residue numbers yield \(\left\{ {2, 2, 3} \right\}\) which is the representation for thirty-eight and their product is \(\left\{ {0, 1, 0} \right\}\) which is three hundred and forty-five in that system.

3.4 Proposed RNS-Based N-Primes Model for Symmetric FHE

Based on the N-prime model, RNS-based N-primes model is built without altering its homomorphic properties. The steps are illustrated in Fig. 3 and will be explained below.

Fig. 3
figure 3

Proposed RNS-based N-prime model

Full size image

The plaintext in a ring Zn will be checked if it is numeric and pass it to RNS forward conversion module, otherwise, generate ASCII codes for each of the text characters before passing it to RNS forward conversion module.

Key Generation: This produces very big prime integer value as the secret key for the entire scheme and only to be known by owner of data.

Noise Generation: This generates a set of random integer r in a ring Zn as the noise to the entire scheme.

N-Primes Generation: This also generates product of prime numbers \(\left( {np_{i} = \mathop \prod \nolimits_{i = 1}^{n} np_{1} * np_{2} \ldots np_{n} } \right)\)

Moduli Set: It takes in n as the input and generates set of pairwise relatively prime integers and moduli set \(\left\{ {3^{n} - 2, 3^{n} - 1,3^{n} } \right\}\) as proposed in [45] which will be used throughout this study, due to its large dynamic range.

RNS Forward Conversion: It requires five (5) parameters as input argument (plaintext (pi), secret key (ki), noise (ri), n-prime numbers (npi) and the moduli set (mi), where i = 1, 2,…, n), convert pi, ki, ri and npi into residues with respect to mi and send out four outputs into RNS encryption block.

RNS Encryption Block: Based on output received from RNS forward conversion block, the encryption block will perform RNS arithmetic operation in parallel with respect to moduli set mi and produce the ciphertext.

$$\begin{aligned} Ciphertext \left\{ {c_{1} , c_{2} , . . . ., c_{n} } \right\} = & \left\{ {p_{1} , p_{2} , \ldots , p_{n} } \right\} + \left\{ {r_{1} , r_{2} , \ldots , r_{n} } \right\} * \left\{ {k_{1} , k_{2} , \ldots , k_{n} } \right\} \\ & * \left\{ {np_{1} , np_{2} , \ldots , np_{n} } \right\} w.r.t. \left\{ {m_{1} , m_{2} , \ldots , m_{n} } \right\} \\ \end{aligned}$$

However, the ciphertext can then be transmitted to the Cloud as shown in Fig. 3 and possibly, homomorphic bit operations can be carried out at the cloud server using RNS arithmetic operation based on ciphertext residues cxi and cyi with respect to moduli set mi and the result will be sent to decryption block.

Decryption Block: The decryption block adopts Chinese Remainder Theorem as a backward conversion algorithm with the use of ciphertext residues (czi) and moduli set mi to obtain N-prime cipher.

$$X = \left| {\sum\limits_{i = 1}^{k} {\left| {M_{i}^{ - 1} } \right|_{mi} x_{i} } } \right|_{M}$$

where \(M = \varPi_{i = 1}^{k} m_{i} ,M_{i} = \frac{M}{{m_{i} }}and\,M_{i}^{ - 1}\) is the multiplicative inverse of Mi with respect to mi.

Finally, user will now use the generated secret key together with N-prime ciphertext to get the result of the operation.

The following experiments demonstrate the generation of the moduli set, secret key, other corresponding values and to show how these values are used for encryption and ciphertext reduction without loosen homomorphic behavior of the encryption and decryption block.

Experiment 1

Let the big prime number sk = 524287 be the secret key, random numbers r = 687529 as the noise, product of n-primes np = 23 * 73 * 101 = 69579 and moduli set \(\left\{ {3^{n} - 2, 3^{n} - 1,3^{n} } \right\}\). When n = 23, then moduli set mi = [94143178825, 94143178826, 94143178827], let message m1 = 65 and message m2 = 66, the RNS-forward conversion for each of these parameters with respect to mi are:

$$\begin{aligned} & {\text{m1}} = \left[ { 6 5,{ 65},{ 65}} \right] \\ & {\text{m2}} = \left[ { 6 6,{ 66},{ 66}} \right] \\ & {\text{sk}} = \left[ { 5 2 4 2 8 7,{ 524287},{ 524287}} \right] \\ & {\text{r}} = \left[ { 6 8 7 5 2 9,{ 687529},{ 687529}} \right] \\ & {\text{np}} = \left[ { 6 9 5 7 9,{ 69579},{ 69579}} \right] \\ \end{aligned}$$

To calculate the ciphertexts ct1 and ct2.

$$\begin{aligned} {\text{ct1}} &= \left| {{\text{m1}} + {\text{r}}*{\text{sk}}*{\text{np}}} \right|_{\text{mi}} \\ &= |\left[ { 6 5,{ 65},{ 65}} \right] + \left[ { 6 8 7 5 2 9,{ 687529},{ 687529}} \right] \, \\ &\qquad *\,\left[ { 5 2 4 2 8 7,{ 524287},{ 524287}} \right] \, \\ &\qquad *\,\left[ { 6 9 5 7 9,{ 69579},{ 69579}} \right]|_{{[ 9 4 1 4 3 1 7 8 8 2 5,{ 94143178826},{ 94143178827}]}} \\ \end{aligned}$$
$${\text{ct1}} = \left[ { 3 1 3 30 4 3 8 1 5 7,{ 3133}0 1 7 1 7 4 8,{ 313299}0 5 3 3 9} \right]$$
$$\begin{aligned} {\text{ct2}} = & \left| {{\text{m2}} + {\text{r}}*{\text{sk}}*{\text{np}}} \right|_{\text{mi}} = |\left[ { 6 6,{ 66},{ 66}} \right] + \left[ { 6 8 7 5 2 9,{ 687529},{ 687529}} \right] \\ & *\left[ { 5 2 4 2 8 7,{ 524287},{ 524287}} \right] \\ & *\left[ { 6 9 5 7 9,{ 69579},{ 69579}} \right]|_{{[ 9 4 1 4 3 1 7 8 8 2 5,{ 94143178826},{ 94143178827}]}} \\ \end{aligned}$$
$${\text{ct2}} = \left[ { 3 1 3 30 4 3 8 1 5 8,{ 3133}0 1 7 1 7 4 9,{ 313299}0 5 3 40} \right]$$

Proof of Homomorphism Properties

Additive Property

$$\begin{aligned} {\text{ct3}} &= \left| {{\text{ ct1}} + {\text{ct2 }}} \right|_{\text{mi}} \\ &= |\left[ { 3 1 3 30 4 3 8 1 5 7,{ 3133}0 1 7 1 7 4 8,{ 313299}0 5 3 3 9} \right] \\ &\qquad +\, \left[ { 3 1 3 30 4 3 8 1 5 8,{ 3133}0 1 7 1 7 4 9,{ 313299}0 5 3 40} \right]|_{{[ 9 4 1 4 3 1 7 8 8 2 5,{ 94143178826},{ 94143178827}]}} \\ \end{aligned}$$
$${\text{ct3}} = \left[ { 6 2 6 60 8 7 6 3 1 5,{ 6266}0 3 4 3 4 9 7,{ 6265981}0 6 7 9} \right]$$

To decrypt ct3,

$${\text{m3}} = {\text{chinese}}\_{\text{remainder}}\left( {{\text{m}}_{\text{i}} ,{\text{ ct3}}} \right){\text{ mod chinese}}\_{\text{remainder}}\left( {{\text{m}}_{\text{i}} ,{\text{sk}}} \right)$$

m3 = chinese_remainder([94143178825, 94143178826, 94143178827], [62660876315, 62660343497, 62659810679]) mod chinese_remainder([94143178825, 94143178826, 94143178827], [524287, 524287, 524287])

$${\text{m3}} = 1 3 1 {\text{m3}} = 1 3 1$$
$${\text{m3}} = {\text{m1}} + {\text{m2}} = 6 5+ 6 6= 1 3 1$$

Multiplicative Property

$$\begin{aligned} {\text{ct3}} &= \left| {{\text{ ct1}}*{\text{ct2 }}} \right|_{\text{mi}} \\ &= |\left[ { 3 1 3 30 4 3 8 1 5 7,{ 3133}0 1 7 1 7 4 8,{ 313299}0 5 3 3 9} \right] \, \\ & *\left[ { 3 1 3 30 4 3 8 1 5 8,{ 3133}0 1 7 1 7 4 9,{ 313299}0 5 3 40} \right]|_{{[ 9 4 1 4 3 1 7 8 8 2 5,{ 94143178826},{ 94143178827}]}} \\ \end{aligned}$$
$${\text{ct3}} = \left[ { 3 7 6 3 9 6 80 70 6,{ 51114847858},{ 18251522556}} \right]$$

To decrypt ct3,

$${\text{m3}} = {\text{chinese}}\_{\text{remainder}}\left( {{\text{m}}_{\text{i}} ,{\text{ ct3}}} \right){\text{ mod chinese}}\_{\text{remainder}}\left( {{\text{m}}_{\text{i}} ,{\text{sk}}} \right)$$

m3=chinese_remainder([94143178825, 94143178826, 94143178827], [376396807 06, 51114847858, 18251522556]) mod chinese_remainder([94143178825, 94143 178826, 94143178827], [524287, 524287, 524287])

$${\text{m3}} = 4 2 90$$
$${\text{m3}} = {\text{m1}}*{\text{m2}} = 6 5* 6 6= 4 2 90$$

Therefore, the proof shows that the proposed model supports both homomorphic addition and multiplication.

Experiment 2

The experiment is also carried out on a string plaintext that contains message “RNS based techniques for encryption of CAP in 2020” with secret key k = 6700417, random number r = 345957466 and product of n-prime np = 31 * 53 * 71 = 116653 and moduli set \(\left\{ {3^{n} - 2, 3^{n} - 1,3^{n} } \right\}\). When n = 15, then moduli set mi = [14348905, 14348906, 14348907]. Thus, the encryption is as follows:

[[13889688, 9226958, 7190942], [13889684, 9226954, 7190938], [13889689, 9226959, 7190943], [13889638, 9226908, 7190892], [13889704, 9226974, 7190958], [13889703, 9226973, 7190957], [13889721, 9226991, 7190975], [13889707, 9226977, 7190961], [13889706, 9226976, 7190960], [13889638, 9226908, 7190892], [13889722, 9226992, 7190976], [13889707, 9226977, 7190961], [13889705, 9226975, 7190959], [13889710, 9226980, 7190964], [13889716, 9226986, 7190970], [13889711, 9226981, 7190965], [13889719, 9226989, 7190973], [13889723, 9226993, 7190977], [13889707, 9226977, 7190961], [13889721, 9226991, 7190975], [13889638, 9226908, 7190892], [13889708, 9226978, 7190962], [13889717, 9226987, 7190971], [13889720, 9226990, 7190974], [13889638, 9226908, 7190892], [13889707, 9226977, 7190961], [13889716, 9226986, 7190970], [13889705, 9226975, 7190959], [13889720, 9226990, 7190974], [13889727, 9226997, 7190981], [13889718, 9226988, 7190972], [13889722, 9226992, 7190976], [13889711, 9226981, 7190965], [13889717, 9226987, 7190971], [13889716, 9226986, 7190970], [13889638, 9226908, 7190892], [13889717, 9226987, 7190971], [13889708, 9226978, 7190962], [13889638, 9226908, 7190892], [13889673, 9226943, 7190927], [13889671, 9226941, 7190925], [13889686, 9226956, 7190940], [13889638, 9226908, 7190892], [13889711, 9226981, 7190965], [13889716, 9226986, 7190970], [13889638, 9226908, 7190892], [13889656, 9226926, 7190910], [13889654, 9226924, 7190908], [13889656, 9226926, 7190910], [13889654, 9226924, 7190908], [13889652, 9226922, 7190906]].

Experiment 3

In experiment 3, small numbers were used such as 3 for secret key, 5 for random number, 2 * 3 * 5 = 30 for product of n-primes and n = 3 to obtain moduli set =  [25,26,27]. These parameters were used to encrypt message of file size 931 Bytes in 0.47 MS and the ciphertext file is shown in Appendix A. The proposed model has also been tested for 11 different file sizes; encryption execution time and ciphertext file size were recorded and compared with original N-prime model as shown in Table 1.

Table 1 RNS-based N-prime model vs N-prime model
Full size table

4 Results and Discussion

The proposed RNS-based N-prime model and N-prime model implementations are done under Python using Dell Laptop having the following specifications: 64 bits Window 10 operating system, Intel® Core™ i9 processor with 2.90 GHz and 32 GB RAM. The execution time and ciphertext expansion are studied for different plaintext size, and the results are shown in Figs. 4 and 5, respectively. Based on the execution time, the proposed RNS-based N-prime model is taking the lowest execution time, while the N-prime model is taking the highest, and this can be interpreted that during proposed RNS-based N-prime model the encryption is done based on residues number system and also all the computations are performed in parallel without carry propagation which makes the proposed model more efficient and practical. Table 2 shows the improvement of proposed RNS-based N-prime model on the N-prime model in terms of execution time.

Fig. 4
figure 4

Encryption time

Full size image
Fig. 5
figure 5

Ciphertext expansion

Full size image
Table 2 Execution time RATIO (RNS-based N-prime model/N-prime model)
Full size table

Likewise, in Fig. 5, shows the ciphertext expansion between proposed RNS-based N-prime model and N-prime model where the proposed model is able to reduce the growth of ciphertext file size by approximately 72% in comparison to N-prime model as shown in Table 3. This was achieved due to encryption process that was done based on residue number system with respect to moduli set.

Table 3 Ciphertext percentage reduction in N-prime model and RNS-based N-prime model
Full size table

Finally, the security of the proposed model still depends on problem of factorization of integers to their primary numbers as mentioned in [7], such integers are product of multiple N-prime numbers and big prime number that serve as secret key that is unknown to attacker.

5 Conclusion

In this paper, we proposed RNS-based N-prime model as an improvement over N-prime model for real-world applications of symmetric-based FHE scheme that requires lower latency and reduced ciphertext file size. The proposed model is based on residue number system approach and ensures parallel computation at encryption stage which brings about efficiency and robustness in addition to the homomorphic properties. The proposed model also deals explicitly with text after converting it to ASCII value instead of binary system, pass it to RNS forward conversion module in conjunction with moduli set and then pass it to the encryption block. The results show that the proposed model outperform N-prime model in terms of encryption execution time and ciphertext expansion at 72% reduction in ciphertext file size.

Further research can be investigated to gain better decryption execution time, as it is taking larger execution time to decrypting ciphertext file back to the original plaintext or result of the computation than encrypting its corresponding plaintext.