StreamFaSE: An Online Algorithm for Subgraph Counting in Dynamic Networks

Abstract

Counting subgraph occurrences in complex networks is an important analytical task with applicability in a multitude of domains such as sociology, biology and medicine. This task is a fundamental primitive for concepts such as motifs and graphlet degree distributions. However, there is a lack of online algorithms for computing and updating subgraph counts in dynamic networks. Some of these networks exist as a streaming of edge additions and deletions that are registered as they occur in the real world. In this paper we introduce StreamFaSE, an efficient online algorithm for keeping track of exact subgraph counts in dynamic networks, and we explain in detail our approach, showcasing its general applicability in different network scenarios. We tested our method on a set of diverse real directed and undirected network streams, showing that we are always faster than the current existing methods for this task, achieving several orders of magnitude speedup when compared to a state-of-art baseline.

1 Introduction

Complex networks are the mathematical tools that model interaction-based real-world systems, allowing the development of abstract tasks to extract useful information from them. One of these tasks is called Subgraph Census and consists in counting how many induced subgraphs of each isomorphic class exist in the network. However this task is known to be hard, demanding the development of efficient algorithms.

Classical methods for computing Subgraph Census on a network require the whole network to be known beforehand. However, this often not the case, as many real-world systems are constantly undergoing change (e.g. friendships in social networks, financial transactions networks and routes in packet switching networks). Not only that, but analysing dynamic networks has a number of additional challenges when compared to static ones. For example, the number of edges may build up over time to unmanageable dimensions [9].

Here, we present StreamFaSE, an online algorithm that keeps track of subgraph counts in dynamic networks. The core of the our method lies in identifying the region of the network that is affected by each update and restricting the count of subgraphs to that same region.

2 Preliminaries

A graph $G=(V,E)$ is a tuple of vertices $V=\{v_1,v_2,...v_n\}$ and edges E represented as a set of pairs of vertices. In a directed graph, an edge $(v_1,v_2)$ is considered to have its origin in $v_1$. The size of the graph is determined by the number of vertices, denoted as |V(G)|. A k-graph is a graph of size k.

A subgraph $G_k$ of a graph G is a k-graph in which $V(G_k) \subseteq V(G)$ and $E(G_k) \subseteq E(G)$. A subgraph is said to be induced if $\forall v,w \in V(G_k): (v,w) \in E(G) \Rightarrow (v,w) \in E(G_k)$.

Two graphs G and H are isomorphic, denoted as $G \sim H$ if there is a bijection between V(G) and V(H) such that two vertices in G are adjacent if and only if their corresponding vertices are connected in H.

The neighbourhood of a vertex $v \in V(G)$ is the set of all vertices that share an edge with v and is defined as $N(v)\equiv \{w : (v,w) \in E\}$. We say these vertices are adjacent to v. The neighbourhood of a set of vertices is the union of the neighbourhood of each of them and is denoted as $N(\{v_1,v_2,...,v_n\})\equiv \{N(v_1) \cup N(v_2) \cup ... \cup N(v_n)\}$. The k-neighborhood of a vertex v is the subgraph induced by all vertices whose distance to v is less or equal than k. The k-neighbourhood of a set of vertices is the union of the k-neighbourhoods of each vertex in the set.

The exclusive neighbourhood of a vertex v with respect to a subgraph S is defined as $N_{exc}(v,S) = \{ u : u \in N(v) \cap u \not \in N(S) \cap u \not \in S \}$. In simpler terms, it consists of the neighbours of v that are not neither in S nor are adjacent to any vertex in S.

A graph stream consists of an initial graph $G_0$ and a list of updates. These updates can be of four types: vertex addition, vertex removal, edge addition and edge removal. We focus on edge operations, and denote edge additions and removals as $+(v_1,v_2)$ and $-(v_1,v_2)$ respectively.

2.1 Problem Definition

Problem 1 (Subgraph Census)

Given a network N and an integer k, determine the frequencies of all its connected induced k-subgraphs. Two occurrences are considered different if they do not share at least one node.

Problem 2 (Streaming Subgraph Census)

Given a network N, an integer k, a solution to Subgraph Census(N, k) and a stream of edge updates $S = (e_1, e_2, ..., e_n)$, compute the Subgraph Census of all networks $S_N = (e_1(N),e_2(e_1(N)),...)$ resulting from successively performing each operation in S to N.

In this paper we propose a solution to Problem 2.

2.2 Related Work

2.2.1 Taxonomy

The concept of subgraphs in static networks can be mapped, at least in two different meaningful ways, to dynamic networks: (1) Dynamic subgraphs consist in incorporating the dynamic property of the network in the subgraphs. Although the addition of temporal information can bring additional challenges, like unmanageable numbers of temporal edges and the need to account for patterns that occur at different time scales, the study of dynamic subgraphs can bring further insights into temporal phenomena [9]. (2) The second mapping path consists in unfolding the dynamic network into a series of static snapshots. In this model, static subgraphs keep their traditional meaning. In this paper, we address the problem of counting static subgraphs in dynamic networks.

Extensive work has been done to solve the static subgraph census problem. We refer to a survey by Ribeiro et al.  [11] for a better insight. The authors propose a taxonomy that accounts for the existing variations of the problem:

Regarding the cardinality of subgraphs counted, algorithms exist to solve three variations of the subgraph census. (1) Subgraph centric algorithms count the number of occurrences of a single subgraph. (2) Set centric approaches count the occurrences of a given set of subgraphs, and (3) Network centric algorithms count the occurrences of all existing subgraphs. Note that any subgraph centric approach can be computed for every subgraph, resulting in a network centric algorithm. Similarly, set centric approaches are trivially reduced to network centric ones by considering the set of all possible subgraphs.

Precision wise, algorithms follow one of two approaches. (1) Exact counting algorithms compute the exact frequencies of the subgraphs, while (2) approximation based algorithms use sampling and analytical estimators to compute approximated solutions. Note that approximation based solutions deal with a simpler version of the subgraph census problem since they scale differently with the size of the network.

We propose that the same taxonomy be used when considering the streaming subgraph census problem. Taking this into account, in this paper we present StreamFaSE, a network centric, exact counting algorithm for the streaming subgraph census problem.

2.2.2 Relevant Static Algorithms

Wernicke developed a network-centric, exact-counting and enumeration-based algorithm, called ESU  [14], that enumerates subgraphs in a network through a backtracking approach, by performing a depth-first search on each network node. ESU uses two vertex sets: $V_{subgraph}$ or $V_{sub}$, where each vertex is added up to a size of k, upon which the set contains k vertices that form a connected induced subgraph; $V_{extension}$ or $V_{ext}$ which contains vertices that can be added to $V_{sub}$. Whenever ESU finishes enumerating a subgraph, a tool called nauty  [7] is used to compute the isomorphic class of the enumerated subgraph. When a vertex is added to $V_{sub}$, all of its neighbours are added to $V_{ext}$, guaranteed they are not already in $V_{ext}$ . Vertices are labeled with integers, so that no vertex can be added to $V_{sub}$ if its label is less than $V_{sub}[0]$. These two conditions avoid duplicates and repeated computation. ESU implicitly creates a recursion tree.

FaSE  [10], developed by our group, is another network-centric, exact-counting and enumeration-based algorithm that takes advantage of the recursion tree implicitly created by ESU. FaSE combines this enumeration with a data structure called G-Trie  [12], a structure that can store and compress multiple graphs in a prefix tree manner, by taking advantage of common substructures. Each level i of the tree represents i-graphs, and descendants of a g-trie node all share a common substructure. Throughout the enumeration process of ESU, FaSE creates paths in a g-trie, up to a depth k. A leaf node in a g-trie represents a k-subgraph. At the end of the enumeration process, isomorphism tests are performed on the leaf nodes of the g-trie using nauty  [7]. By using a g-trie to encapsulate isomorphism information, isomorphism tests only need to take place at the end of the enumeration, which results in large speedups. However, this approach allows for redundant information to be created in the g-trie (many leaf nodes represent the same isomorphic class), and due to the combinatorial explosion of subgraph types as subgraph sizes grow, FaSE is currently limited to subgraphs with size up to 19. For a better understanding of g-tries, we refer to  [12]. FaSE is extendible to many kinds of graphs, like directed and colored, and also provides a sampling option. Our approach is an adaptation of FaSE to streaming networks that accounts for undirected and directed graphs.

2.2.3 Relevant Dynamic Algorithms

Regarding the streaming subgraph census, Xiaowei Chen and John C. S. Lui propose an approximation based algorithm which consists in generating samples by leveraging consecutive steps of random walks and the observation of the neighbours of visited nodes [2]. This algorithm falls out of the scope of this document, since it is an approximate solution. Another approximate solution has been proposed by Al-Thaedan and Carvalho [1], which consists in infering subgraph frequencies through exact frequencies of smaller subgraphs by using the Pascal triangle. An exact subgraph-centric approach has been developed by Mukherjee et al. [8], based on keeping in memory an association between edges and every occurrence of the target subgraph, trading memory for efficiency.

To the best of our knowledge, only one network-centric, exact-counting solution exists. Schiller  [13] presented StreaM-k, an algorithm that updates subgraph frequencies for every update by retrieving the $k-2$-neighbourhood of an updated edge and using a small adjacency matrix-like representation of each affected subgraph in the $k-2$-neighbourhood to identify the isomorphic classes of the subgraph before and after the update. This correspondence between adjacency codes and isomorphic classes is previously computed and stored. The implementation made available only accounts for subgraphs up to size 7. Moreover, the implementation does not account for directed graphs, unlike our approach.

3 Method

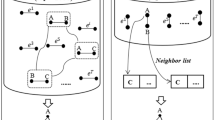
The core of our approach consists in only exploring the area of the network affected by an update. Recomputing subgraph frequencies for the whole network, for every update, is computationally expensive and unnecessary. Therefore, we devised a depth-first search algorithm that only reaches the $(k-2)$-neighbourhood of the vertices of the updated edge. We can guarantee that no additional vertices are needed, since we are counting k-subgraphs, and thus any k-subgraph that includes an edge $(v_1,v_2)$ must be composed of vertices that are at a maximum distance of $k-2$ from either $v_1$ or $v_2$. Figure 1 illustrates this idea.

Fig. 1.

An example of the core idea of StreamFaSE for $k=3$. When adding/deleting the green edge (1, 2), the subgraph induced on the blue vertices is sufficient to compute the topology changes. This corresponds to the 1-neighbourhood of $\{1,2\}$.

Furthermore, even though we are restricting the search space to the affected area, we still need a way to efficiently figure out which isomorphic classes correspond to the subgraphs that existed before and after the update, to correctly update its frequencies. FaSE does this by maintaining a path in the g-trie until a leaf node is reached. However, in a streaming environment, we need an efficient way to determine the isomorphic classes of the affected subgraphs before and after the update. StreamFaSE does both these tasks during the same subnetwork traversal. This translates into verifying if each k -subgraph is connected with and without the (added/deleted) edge.

If a subgraph is connected in both its updated and non-updated versions, then we known that the update (either an edge addition or deletion) changed the topology of the subgraph. As a consequence, we decrease the count of the old subgraph and increase the count of the new one.

If the edge addition (deletion) connects (disconnects) a previously disconnected (connected) subgraph, then we only increment (decrement) the count of the new (old) subgraph.

Our approach lies in verifying if the subgraph is connected with and without the updated edge while enumerating vertices in the $(k-2)$-neighbourhood of the updated edge. This is done through a process we called origin propagation.

Considering the update of an edge $(v_1,v_2)$, we define the origin of a vertex u in the depth-first search as: $O(u) = N(u) \cap \{v_1,v_2\} \cup O(\textit{parent}(u))$. In simpler terms, the origin of a vertex u is the subset of $\{v_1,v_2\}$ that is reachable from u within the subgraph induced on the current enumeration, taking in account that the updated edge may not be used. This is depicted in Fig. 2.

Initially, we define the origin of a vertex v as the set of initial vertices ($v_1$ or $v_2$) from which it was obtained during the search-tree growth. When other vertices are expanded from v, its origin is propagated (i.e. inherited), so these newly expanded vertices will (at least) also have v’ origin.

In summary, we enumerate all k-subgraphs that belong to the $(k-2)$-neighbourhood of the vertices in the updated edge and, by propagating origins, we verify if each subgraph is connected without the updated edge in order to update subgraph frequencies. We keep two paths in a g-trie to deal with the identification of isomorphic classes: one considering the updated edge, and another one not considering it. This is a modification of the original g-trie structure, as disconnected subgraphs will be present in the tree, and more nodes will be created. However, leaf nodes still only represent connected k-subgraphs. Because the g-trie is kept and updated at all times, all possible paths are built early in the computation. Since isomorphism testing is only done once for each leaf node of the tree, as soon as the tree is fully built, no more isomorphic tests need to take place. Empirically, we verified that the total time spent in isomorphism testing is negligible when compared to the total run time.

Fig. 2.

An example of how origin propagation is used to determine the connectedness of subgraphs with $k=3$. S1, S2 and S3 are obtained during the search. Disregarding the updated edge (1, 2), only S2 is connected. We conclude that (1) if the update is an addition S1 and S3 are new occurrences. (2) If the update is a deletion S1 and S3 are no longer connected. (3) Subgraph S2 was connected before and after the update.

3.1 Detailed Description

For every update to an edge $(v_1,v_2)$, the first thing we do is include $v_1$ and $v_2$ in $V_{sub}$ (the vertex set of the current subgraph being enumerated). $v_1$ and $v_2$’s neighbours are added to $V_{ext}$ (a set of vertices that can still be added to the subgraph). While we are adding these neighbours to $V_{ext}$, we also define each vertex’s origin as $v_1$,$v_2$ or $v_1 + v_2$, according to which endpoints they are connected. Furthermore, we initialize two paths in the g-trie like we explained above. A boolean flag $is\_connected$ is used to declare if the current subgraph being enumerated is connected without the updated edge. Initially, this flag is set to false. However, a special verification is needed for directed graphs: if an edge $(v_2,v_1)$ exists, we can be sure that every subgraph enumerated is also a connected subgraph without the edge $(v_1,v_2)$. StreamFaSE enumerates subgraphs on the target graph considering the existence of the updated edge at all times. This means that if the update is an edge addition, we first add the edge and then we run StreamFaSE to enumerate subgraphs. Subgraphs that exist with the edge (and are detected by the normal FaSE procedure) have their frequency incremented; if the subgraphs are connected without the edge, their frequency is decremented (they are detected through origin propagation). If the update is an edge deletion, we first run StreamFaSE and we delete the edge afterwards. The frequencies are updated in an inverse manner regarding edge additions. After this initialization procedure, a recursive function ($DFS\_UPDATE$) that enumerates subgraphs in a depth-first manner is used to explore the $k-2$-neighbourhood of the updated edge. The recursive function’s base case is when $V_{sub}$ has a size of k, meaning we finished enumerating a k-subgraph.

In every recursion of $DFS\_UPDATE$, we iteratively remove every vertex $v_3$ from $V_{ext}$ and add it to the subgraph (to $V_{sub}$). When adding the vertex to the subgraph, we verify if it can be reached by both $v_1$ and $v_2$, by checking if its origin is $v_1 + v_2$. In that case, the flag that indicates the subgraph is connected without the updated edge is set to true. Then, we iterate over $v_3$’s neighbours, in order to propagate origins and verify if they can be added to $V_{ext}$ (if they are already in $V_{ext}$ they are not added again). For every neighbour $v_4$ of $v_3$, we set their origin as $origin(v_4) \leftarrow origin(v_4) \cup origin(v_3)$, as we know that $v_4$ can be reached by $v_3$ and therefore by $v_3$’s origin vertex. $v_4$ is added to $V_{ext}$ if it does not belong to the extension set. Finally, the g-trie path’s are updated, and a new recursive call is made. Changes made to the origins set in each recursion must be undone upon the recursion terminating, as $v_4$ only shares $v_3$’s origin if they are both in the same subgraph. Therefore, when $v_3$ is removed from the subgraph (upon the recursion terminating), $v_4$’s origin must be reset.

When the recursive function reaches its base case ($V_{sub}$ has size k), we only need to retrieve the corresponding isomorphic subgraph class from the g-trie path and update its frequency accordingly, depending on the type of edge update being made. Furthermore, if $is\_connected$ is set to true, we know that the subgraph is connected without considering the updated edge, and we also retrieve the isomorphic class of the subgraph not considering $(v_1,v_2)$ and update its frequency.

4 Experimental Results

All tests were executed on machine using a 16-core AMD Opteron processor with a 2.3 GHz base clock speed, and a total of 252 GB of memory installed.

We used six real-world networks to test the performance of the proposed algorithm, StreamFaSE. Due to the novelty of our work, no data sets were available for testing the performance of StreamFaSE. With that in mind, we adapted networks with timestamped edges by transforming them into a chronological stream of edge additions and deletions. We opted to use a sliding window model, in which an edge is deleted after some predefined amount of time passes since its addition. Table 1 contains a detailed description of the used networks as well as how they were adapted to a stream-friendly format.

Table 1. Real-world networks used in our experiments.

We tested our algorithm by running a thorough experiment in which we iteratively increased the order, k, of the counted subgraphs. Each experiment was ran twice to assure consistency. The following statistics were gathered:

• Types: number of occurring non-isomorphic subgraphs with order k found in the network throughout all updates;

• Time: execution time, measured as elapsed time between launching the program up to computing the frequencies of all possible subgraphs after each update;

• Speedup: Time of other algorithms divided by the time of our own.

We compared the performance of StreamFaSE versus FaSE and StreaM-k. FaSE was chosen, not only because it is the basis for our algorithm, but also because it is a state-of-the-art algorithm for computing the static Subgraph Census; showcasing the importance of taking different approaches to solve the dynamic version of the problem. Table 2 contains the results.

Table 2. Experimental results.

Results are very promising, showing that StreamFaSE outperforms the other algorithms. It is worth noting that FaSE, being the non-native approach to the Streaming Subgraph Census Problem, has a major drop in performance when handling large networks (i.e. mooc, 9/11, mathoverflow, retweets). This is because, unlike StreamFaSE and StreaM-k, FaSE recomputes all subgraph counts after each update.

5 Conclusions and Future Work

In this paper we presented an efficient algorithm for the Streaming Subgraph Census Problem. Our method consists of StreamFaSE, a network-centric approach to perform the exact enumeration of all static subgraphs occurring in a dynamic network. The main novelty of the presented algorithm is that it explores only the regions of the network that have undergone a topology change after each stream update. Also, the main algorithm is the same for edge additions and deletions, varying only in the timing that the update is actually committed to the network.

In the future, we plan to boost the performance of our method when handling real-world stream networks, by developing an online algorithm that can process multiple edge additions and deletions at the same time. This has applications in high-throughput network monitoring systems that demand fast response times, such as detecting anomalies in financial transactions prior to their approval.