Keywords

1 Introduction

Support Vector Machine (SVM) is originally put forward to solve binary classification problem with the idea of maximum-margin hyper-plane separating training samples. The classification hyper-plane is restricted with support vectors, which are used for the decision of a new test sample. Many researchers have successfully applied SVM in many fields   [1, 2]. To solve multi-class classification problem in real applications, binary SVM needs to be extended or combined together to complete the complex classification task. There are many methods extending binary SVM to multi-class classification   [3,4,5], such as one-against-one, one-against-all, hierarchy SVM classifiers, or DAG SVM classifiers. But because at least \(k(k-1)/2\) quadratic programming (QP) optimization problems needs to be combined together to solve k class classification problem, computation cost for these methods is relatively high.

For multi-class classification problem, sphere-structured SVM is one special solution   [6]. Based on one-class SVM, hyper-sphere SVM classifier tries to construct a minimum bounding hyper-sphere restricting all training samples of one class within it as much as possible. The bounding hyper-sphere for each class is restricted with its center and its radius. Similar to binary SVM, this method maximizes the gap between different hyper-spheres by the smallest radius. New test samples are classified depending on the bounding hyper-spheres they falls into. Since this method needs no combination of further computation and solves multi-class classification problem with direct computation of all hyper-spheres together, its computation complexity is less than all the above mentioned combination methods. Sphere-structured SVM has been studied a lot since its presentation. To get good performance for hyper-sphere SVM, Liu et al.   [7, 8] proposed one fuzzy hyper-sphere SVM and one multiple sub-hyper-spheres SVM for multi-class classification. Most of these research focused on one decision rule and few researchers adopted two or more decision rules.

As mentioned above, each training data is bounded within a bounding hyper-sphere. If all bounding hyper-spheres for training data of every class are independent and new test sample falls inside only one hyper-sphere, its classification decision is easy to compute. But real application data are very complicated and relationships between different classification bounding hyper-spheres are very complicated too. When hyper-spheres for each class are intersected or not independent, it is difficult for one simple decision function to get the right classification result. Classification accuracy of test samples falling inside the intersection will influence the final classification performance. Based on the analysis of data distributions for such samples in the intersections, a hybrid decision strategy is put forward in this paper. Section 2 introduces statistical analysis of the intersection data distribution, mathematical description of our hyper-sphere SVM and implementation details of the proposed method. Section 3 discusses the experimental results and Sect. 4 gives the conclusions.

2 Our Method

2.1 Mathematical Description of Hyper-Sphere Support Vector Classifier

Similar with mathematic description of the original binary SVM, mathematic principles of hyper-sphere SVM is as follows. Supposing there is a set of n-dimensional training samples of m classes, the task is to compute the minimum bounding hyper-sphere for each class. Here, the minimum bounding hyper-sphere refers to the smallest hyper-sphere that encloses all the training samples of one class. Referenced by binary SVM, slack variables \(\xi _{ki}\) are introduced by permitting isolated points and a non-linear mapping function \(\phi \) is introduced by transforming the training samples into a high dimensional feature space to solve nonlinear separation problems. So seeking the minimum bounding hyper-sphere for each class is to find the minimum bounding hyper-sphere enclosing all the training examples of that class. This process can be computed by solving the following constrained quadratic optimization problem in Eq. (1).

$$\begin{aligned} \begin{aligned}&\underset{c_{k},R_{k}}{min}\, R_{k}^{2}+C_{k}\sum _{i=1}^{m}\xi _{ki}\\&s.t. \\&\left\| \phi \left( \textit{\textbf{x}}_{\textit{\textbf{ i }}} \right) -c_{k}\right\| ^{2}\le R_{k}^{2}+\xi _{k}\\&\xi _{i}\ge 0,i=1,\cdots ,l_{k} \end{aligned} \end{aligned}$$
(1)

For class k, its minimum bounding hyper-sphere \(S_{k}\) is characterized by its center \(c_{k}\) and radius \(R_{k}\). And \(C_{k}\) is the penalty factor and \(\xi _{ki}\ge 0\) are slack variables.

By introducing Lagrange multipliers, Lagrange polynomial can be written as Eq. (2).

$$\begin{aligned} L(R_{k},c_{k},\xi _{i},\alpha _{i},\beta _{i})=R_{k}^{2}+C_{k}\sum _{i=1}^{l_{k}}\xi _{ki}-\sum _{i=1}^{l_{k}}\alpha _{i}\left( R_{k}^{2}+\xi _{ki}-\left\| \phi (\textit{\textbf{x}}_{i})-c_{k} \right\| ^{2} \right) -\sum _{i=1}^{l_{k}}\beta _{i}\xi _{ki} \end{aligned}$$
(2)

By taking the partial directives of L with respect to \(R_{k}\),\(c_{k}\) and \(\xi _{i}\) and substituting them back to Eq. (2), the original optimization problem becomes its dual optimization problem in the following format as Eq. (3).

$$\begin{aligned} \begin{aligned}&\underset{\alpha _{i}}{min}\, \sum _{i,j=1}^{l_{k}}\alpha _{i}\alpha _{j}K\left( \textit{\textbf{x}}_{i},\textit{\textbf{x}}_{j}\right) -\sum _{i=1}^{l_{k}}\alpha _{i}K\left( \textit{\textbf{x}}_{i},\textit{\textbf{x}}_{i} \right) \\&s.t.\\&\sum _{i=1}^{l_{k}}\alpha _{i}=1\\&0\le \alpha _{i}\le C_{k},i=1,\cdots ,l_{k} \end{aligned} \end{aligned}$$
(3)

In Eq. (3), the kernel trick is adopted to compute inner products in the feature space, that is, \(K(\textit{\textbf{x}}_{i},\textit{\textbf{x}}_{j})=\phi (\textit{\textbf{x}}_{i})\cdot \phi (\textit{\textbf{x}}_{j})\). Support vectors are the vectors \(\textit{\textbf{x}}_{i}\) with \(\alpha _{i}>0\). The Lagrange multipliers get the solutions after solving Eq. (3). So the center can be computed by Eq. (4) and the resulting decision function can be computed as Eq. (5). Then the radius \(R_{k}\) can be computed by equating \(f_{k}(\textit{\textbf{x}})\) to zero for any support vector. For class k, its minimum bounding hyper-sphere \(S_{k}\) is obtained by the solution of its center and radius.

$$\begin{aligned} c_{k}^{2}=\sum _{i,j=1}^{l_{k}}\alpha _{i}\alpha _{j}K(\textit{\textbf{x}}_{i},\textit{\textbf{x}}_{j}) \end{aligned}$$
(4)
$$\begin{aligned} f_{k}(\textit{\textbf{x}})=sgn(R_{k}^{2}-\sum _{i,j=1}^{l_{k}}\alpha _{i}\alpha _{j}K(\textit{\textbf{x}}_{i},\textit{\textbf{x}}_{j}))+2\sum _{i=1}^{l_{k}}K(\textit{\textbf{x}}_{i},\textit{\textbf{x}})-K(\textit{\textbf{x}},\textit{\textbf{x}})) \end{aligned}$$
(5)

Based on Eq. (5), the new point \(\textit{\textbf{x}}\) falls inside of the hyper-sphere if \(f_{k}(\textit{\textbf{x}})>0\). \(\textit{\textbf{x}}\) falls outside of the hyper-sphere if \(f_{k}(\textit{\textbf{x}})<0\) and \(\textit{\textbf{x}}\) lies on the hyper-sphere if \(f_{k}(\textit{\textbf{x}})=0\).

2.2 Analysis of Data in the Intersection of Hyper-Spheres

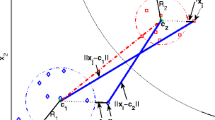
Ideally, all hyper-spheres are independent and each test sample is correctly classified by one hyper-sphere decision function. But it can happen that two or more hyper-spheres intersect, that is, one sample falls inside several hyper-spheres. Or a new test sample falls outside of all hyper-spheres. How to correctly classify these data points influence the accuracy performance of the resulting classifier. In Fig. 1, the minimum bounding sphere for class 1 and class 2 are \(S_{1}\) and \(S_{2}\). \(S_{1}^{{}'}\) of class 1 belongs to sphere \(S_{2}\) and \(S_{2}^{{}'}\) of class 1 belongs to sphere \(S_{1}\). \(\textit{\textbf{x}}_{1}\) belongs to \(S_{1}^{{}'}\) and \(\textit{\textbf{x}}_{2}\) belongs to \(S_{2}^{{}'}\) and they are both support vectors. For example, \(\textit{\textbf{x}}_{2}\) is a support vector of class 2, so \(\textit{\textbf{x}}_{2}\) belongs to class 2. But based on the decision function, \(f_{2}(\textit{\textbf{x}}_{2})=0\) and \(f_{1}(\textit{\textbf{x}}_{2})>0\), so \(\textit{\textbf{x}}\) belongs to class 1. Obviously, it is the wrong classification result. So when two or more hyper-spheres intersect, only Eq. (5) is used as decision rule may lead to wrong decision results.

Fig. 1.
figure 1

Illustration of two hyper-spheres intersecting.

Full size image

To solve this problem, one sub-hyper-sphere support vector machine is put for-ward to classify samples in the intersections in   [9]. In the research, same error data hyper-sphere (data points belong to the same class of the mother hyper-sphere) and different error data hyper-sphere (data points belong to different class of the mother hyper-sphere) are introduced. The decision process is completed by them. In Fig. 1, S-sphere and D-sphere are same error data sub-hyper-sphere and different error data hyper-sphere for class 1. If a new test sample lies in the intersection, S-sphere and D-sphere are used as the classification rule to get the right class.

But by introducing multiple QP optimization problems again, its computation complexity increases. To reduce computation complexity of QP optimization problem, new decision rules are put forward in this paper. Given the training data set, there will be three cases for position of the new test sample, that is, inside one hyper-sphere or in the intersections or outside of all spheres after computing hyper-spheres for all classes. It is easy to get decision class for the inclusion case. If a new test sample \(\textit{\textbf{x}}_{2}\) falls outside of all spheres, Eq. (6) is adopted as its class j decision (\(j=1,\cdots ,m\)).

$$\begin{aligned} min(\frac{d_{xj}^{2}}{R_{j}^{2}}-1),where\, d_{xj}^{2}=\left\| \phi (\textit{\textbf{x}})-c_{j} \right\| ^{2}=K(\textit{\textbf{x}},\textit{\textbf{x}})-2\sum _{i=1}^{l_{k}}\alpha _{i}K(\textit{\textbf{x}},\textit{\textbf{x}}_{i})+\sum _{i,j=1}^{l_{k}}\alpha _{i}\alpha _{j}K(\textit{\textbf{x}}_{i},\textit{\textbf{x}}_{j}) \end{aligned}$$
(6)

If a new test sample belongs to the intersections, there are three cases for different data distribution as following.

(1) For the first case, the intersection hyper-plane can separate samples of two classes directly. Intersection hyper-plane is easy to get from subtraction of two spheres equations.

(2) For the second case, intersection hyper-plane cannot separate samples of two classes directly, so binary optimal plane is used as separation plane for linear and nonlinear cases as shown in Fig. 2.

Fig. 2.
figure 2

Case of binary classification plane as separation plane for linear (left) and nonlinear (right) data.

Full size image

(3) For the third case, there is only one class data in the intersection. For this case, exclusion method is adopted as the decision rule.

As can be seen from the reference   [6, 9], training time complexity for the sphere-structured SVM is O(\(n^{2}\)). Testing time for the sphere-structured SVM is decided by its decision process. For our new hybrid hyper-sphere SVM, its training time complexity is O(\(n^{2}\)). In testing phase, time complexity may be O(1) for case of only one class data in the intersection, O(n) for case of binary classification plane as separation plane and O(\(n^{2}\)) for case of nonlinear classification plane as separation plane. The average time complexity is lower than that of sub-hyper-sphere SVM with O(\(n^{2}\)).

2.3 Implementation Details of the Proposed Method

The proposed hyper-sphere support vector classifier with hybrid decision strategy follows three steps to complete classification process, which are listed as Algorithm 1. And testing process is described as Algorithm 2. Suppose there are m classes needs to be classified.

figure a
figure b

3 Experimental Results and Analysis

In this section some experimental results are given to verify the efficiency of the new improved classification rule and compare it with hyper-sphere SVMs and sub-hyper-sphere SVMs. The first experimental datasets IRIS and glass come from the UCI   [10] Repository of machine learning databases. The second data comes from one real application of action recognition in videos.

Table 1. Comparison result for IRIS classification.
Full size table

For three classes of IRIS data set, all samples are randomly grouped as three parts and one part with number 15 is used as test, the other two 135 as training set. For glass data set, a subset with three classes is selected and the same data pre-processing is adopted as paper   [6]. For hyper-sphere SVMs and sub-hyper-sphere SVMs   [9], \( C=100,\sigma =1.25\) is used. For our new approach, RBF kernel with parameter optimization search are used to get the best classification accuracy. Experimental results are shown in Table 1. All experiments were done for 10 times and data in Table 1 is the average value of each indicator. Experimental results show our new hybrid classification rule is effective and easy to compute for the simple multi-class classification problems.

The second experimental data set is one action recognition system from videos collecting from the Internet. Extracted features consist of foregrounds extraction, morphology operations and shape feature, KLT tracking points and so on. These features are input into the proposed hybrid hyper-sphere SVM classifiers. The dimension of the input image is 20 dimensions, the number of categories is 6, and the size of data set is 9000. Among 9000 samples, data1 consists of 3000 randomly selected samples for each class and 600 testing samples, and data2 with 3000 and 600, data3 with 7800 and 1200 as data1.The experiment was repeated 10 times and the average value was selected as the final experimental result. The accuracy of our method is 86.15, 90.11 and 92.15 for three datasets respectively. For the other two methods, the highest accuracy is fuzzy hyper-sphere SVM, the values are 85.04, 89.19 and 90.67 for three datasets and 83.98, 88.30, 89.33 for sub-sphere SVM. Performance of our new method is better than the other two methods.

4 Conclusions

To improve classification performance of traditional hyper-sphere SVM, one hybrid decision strategy for hyper-sphere support vector classifier is put forward in this paper. To get high classification performance for test samples and decreases computation complexity of QP optimization problems, four decision rules are discussed and detailed algorithm is given. Results on benchmark data and real application data show our hybrid decision rule leads to better generalization accuracy than the existing methods, decreasing computation complexity and saving training time.