Keywords

1 Introduction

Truss structures have been widely used in large-span buildings and constructions due to their advantages as lightweight, robustness, durability. However, because truss structures are intricate and complex with many individual elements, a good design requires a lot of human resources. The conventional process to design truss structures is the “trial and error” method where the result strongly depends on the designer’s experience. Moreover, for large-scale trusses with a wide list of available profiles, the number of candidates becomes too prohibitive. For example, a simple 10-bar truss in which the cross-section of each member must be selected from a set of 42 available profiles has totally 4210 possible options [1]. In such cases, the “trial and error” method is impossible. In order to help a designer find the best choice, another approach called optimization-based design method was invented and has been constantly developed.

In recent decades, many optimization algorithms have been proposed and successfully applied to solve structural problems. Several algorithms are designed based on natural evolution such as Genetic Algorithm (GA) [1], Evolution Strategy (ES) [2], Differential Evolution (DE) [3]. Some other algorithms are inspired by the swarm intelligence like Particle Swarm Optimization (PSO) [4], Ant Colony Optimization (ACO) [5], Artificial Bee Colony (ABC) [6], etc. These algorithms use an effective “trial and error” method to find the minimum. In this way, the global optimum is usually found, but it requires a huge amount of function evaluation. This is further complicated for structural optimization problems where the function evaluation process is usually performed by the finite element analysis (FEA). To demonstrate this, the duration of a single analysis for the tied-arch bridge which consists of 259 members described in [7] is approximately 60 s but the optimization time is nearly 133 h. In recent years, the development of machine learning (ML) has shown a promising solution to this challenge. By building ML-based surrogate models to approximately predict the behavior of structures, the number of FEAs is greatly reduced and the overall computation time is consequently decreased.

The idea of using ML as surrogate models in structural optimization is not new. Many related studies have been previously published [8,9,10,11]. However, due to the recent development in the field of ML, this topic needs to be carefully considered. Among these evolutionary algorithms, DE is preferred because of its advantages [12]. On the other hand, while many ML algorithms exist, the capacity of the NN has been proved [13]. Therefore, an optimization approach that combines NN and DE is proposed in this study. The paper consists of five main sections. The background theory is briefly presented in Sect. 2. Based on the integration between NN and DE, an optimization approach is proposed in Sect. 3. Two computational experiments are performed in Sect. 4. The obtained results are compared with those of other algorithms. Finally, some main conclusions are pointed out in Sect. 5.

2 Background Theory

2.1 Optimization Problem Statement

The weight optimization problem of a truss structure can be stated as follows.

Find a vector of A representing the cross-sectional areas of truss members:

$$ {\mathbf{A}} = \, \left[ {A_{1} ,A_{2} , \ldots ,A_{n} } \right]\,{\text{where}}\,A_{i}^{min} \le A_{i} \le A_{i}^{max} $$
(1)
$$ \begin{array}{*{20}l} {{\text{to}}\,\text{minimize} :} \hfill & {\quad \quad \quad \quad \quad \quad W\left( {\mathbf{A}} \right) = \sum\limits_{i = 1}^{n} {\rho_{i} A_{i} l_{i} } } \hfill \\ \end{array} $$
(2)
$$ \begin{array}{*{20}l} {\text{subject to:}} \hfill & {\quad \quad \quad \quad \quad \quad \left\{ {\begin{array}{*{20}c} {g_{i,s} = {{\sigma_{i} } \mathord{\left/ {\vphantom {{\sigma_{i} } {\sigma_{i}^{allow} }}} \right. \kern-0pt} {\sigma_{i}^{allow} }} - 1 \le 0} \\ {g_{j,u} = {{\delta_{j} } \mathord{\left/ {\vphantom {{\delta_{j} } {\delta_{j}^{allow} }}} \right. \kern-0pt} {\delta_{j}^{allow} }} - 1 \le 0} \\ \end{array} } \right.} \hfill \\ \end{array} $$
(3)

where: 𝜌i, Ai, li are the density, the cross-sectional area and the length of the ith member, respectively; A mini , A maxi are the lower and upper bounds for the cross-sectional area of the ith member; σi, σ allowi are the actual stress and the allowable stress of the ith member; n is the number of members; δj, δ allowj are the actual and the allowable displacements of the jth node; m is the number of nodes.

2.2 Differential Evolution Algorithm

DE was originally proposed by K. Price and R. Storn in 1997 [14]. Like many evolutionary algorithms, the DE comprises four basic operators namely initialization, mutation, crossover, and selection. They are briefly described as follows.

Initialization: a random population of Np individuals is generated. Each individual which is a D-dimensional vector represents a candidate of the optimization problem. Np is the number of candidates in the population and D is the number of design variables. The jth component of the ith vector can be generated using the following express:

$$ x_{ij}^{(0)} = x_{j}^{\hbox{min} } + rand\left[ {0,1} \right]\left( {x_{j}^{\hbox{max} } - x_{j}^{\hbox{min} } } \right) $$
(4)

where: rand[0,1] is a uniformly distributed random number between 0 and 1; x minj and x maxj are the lower and upper bound for the jth component of the ith vector.

Mutation: a mutant vector v (t)i is created by adding a scaled difference vector between two randomly chosen vectors to a third vector. Many different mutation strategies have been proposed like ‘DE/rand/1/’, ‘DE/rand/2’, ‘DE/best/1’, ‘DE/best/2’, etc. In this study, a powerful mutation strategy, called ‘DE/target-to-best/1’ is employed. This variant produces the mutant vector based on the best individual of the population x (t)best and the target individual x (t)i as follows:

$$ {\mathbf{v}}_{i}^{(t)} = {\mathbf{x}}_{i}^{(t)} + F \times \left( {{\mathbf{x}}_{best}^{(t)} - {\mathbf{x}}_{i}^{(t)} } \right) + F \times \left( {{\mathbf{x}}_{r1}^{(t)} - {\mathbf{x}}_{r2}^{(t)} } \right) $$
(5)

where: r1 ≠ r2 are randomly selected between 1 and Np; F is the scaling factor.

Crossover: a trial vector ui is created by getting each variable value from either the mutant vector vi or the target vector xi according to the crossover probability.

$$ u_{ij}^{(t)} = \left\{ {\begin{array}{*{20}c} {v_{ij}^{\left( t \right)} {\text{ if }}j = K{\text{ or }}rand\left[ {0,1} \right] \le Cr} \\ {x_{ij}^{\left( t \right)} {\text{ otherwise}}} \\ \end{array} } \right. $$
(6)

where: u (t)ij , v (t)ij and x (t)ij are the jth component of the trial vector, the mutant vector, and the target vector, respectively; K is any random number in the range from 1 to D, this condition ensures that the trial vector differs the target vector by getting at least one mutant component; Cr is the crossover rate.

Selection: for each individual, the trial vector is chosen if it has a lower objective function value; otherwise, the target vector is retained. The selection operator is described as follows:

$$ {\mathbf{x}}_{i}^{{\left( {t + 1} \right)}} = \left\{ {\begin{array}{*{20}c} {{\mathbf{u}}_{i}^{\left( t \right)} {\text{ if }}f\left( {{\mathbf{u}}_{i}^{\left( t \right)} } \right) \le f\left( {{\mathbf{x}}_{i}^{\left( t \right)} } \right)} \\ {{\mathbf{x}}_{i}^{\left( t \right)} {\text{ otherwise}}} \\ \end{array} } \right. $$
(7)

where: f(u ti ) and f(x ti ) are the objective function value of the trial vector and the target vector, respectively.

For constrained problems, the mutation and crossover operators could produce infeasible candidates. In such case, the selection is based on three criteria: (i) any feasible candidate is preferred to any infeasible candidate; (ii) among two feasible candidates, the one having lower objective function value is chosen; (iii) among two infeasible candidates, the one having lower constraint violation is chosen [15]. For the implementation, the objective function is replaced by the penalty function:

$$ f^{\prime}\left( {\mathbf{x}} \right) = f\left( {\mathbf{x}} \right) + \sum\limits_{i = 1}^{n} {r_{i} \times \hbox{max} \left( {0,g_{i} \left( {\mathbf{x}} \right)} \right)} $$
(8)

where: ri is the penalty parameter; gi is the constraint violation.

The initialization operator is performed only one time at the initial iteration while three last operators are repeated until the termination criterion is satisfied.

2.3 Neural Networks

Neural networks (NNs) are designed based on the structure of the human brain. Many NN architectures have been developed, in which, the feedforward neural network (FFNN) is commonly used in the structural engineering field. In FFNN, the information moves through the network in a one-way direction as illustrated in Fig. 1 [16]. Neurons are organized into multiple layers including the input layer, the hidden layers, and the output layer. The outputs from previous neurons become the inputs of the current neuron after scaling with the corresponding weights. All inputs are summed and then transformed by the activation function.

Fig. 1.
figure 1

Typical architecture of an FFNN

Full size image

It can be expressed as follows. The neuron of jth layer uj (j = 1, 2, …, J) receives a sum of input xi (i = 1, 2, …, I) which is multiplied by the weight wji and will be transformed into the input of the neuron in the next layer:

$$ x_{j} = f\left( {u_{j} } \right) = f\left( {\sum\limits_{i = 1}^{I} {w_{ji} x_{i} } } \right) $$
(9)

where f(.) is the activation function. The most commonly used activation functions are: tanh, sigmoid, softplus, and rectifier linear unit (ReLU). The nonlinear activation function ensures that the network can simulate the complex data.

A NN can has more than one hidden layer, which increases the complexity of the model and can significantly improve prediction accuracy. The loss function is used to measure the error between predicted values and true values. The loss function is chosen depending on the type of task. For regression tasks, the loss functions can be Mean Squared Error (MSE), Mean Absolute Error (MAE) or Root Mean Squared Error (RMSE). To adapts NN for better predictions, the network must be trained. The training process is essentially finding a set of weights in order to minimize the loss function. In other words, it is an optimization process. In the field of machine learning, the commonly used optimization algorithms are stochastic gradient descent (SGD) or Adam optimizer. An effective technique, namely “error backpropagation”, developed by Rumelhart et al. [17] is normally used for training.

3 Proposed Surrogate-Based Optimization Approach

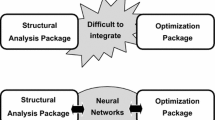
According to the workflow of the conventional DE optimization (Fig. 2(a)), the structural analysis must be performed for every candidate. Consequently, the total number of structural analyses is too large, leading to time-consuming. To deal with this problem, NNs are used to approximately predict the behavior of the structure instead of FEA. The proposed optimization approach, called NN-DE, consists of three phases: sampling, modeling, and optimization as illustrated in Fig. 2(b).

Fig. 2.
figure 2

Optimization workflows

Full size image

First of all, some samples are generated. All samples are then analyzed using FEA. The second phase focuses on constructing accurate NN models. After selecting the suitable NN architecture, the models are trained with the datasets obtained from the sampling phase. The performance of the NN models is strongly influenced by the diversity of the training data, which also means depends on the sampling method. Therefore, a method, called Latin Hypercube Sampling, is used to produce the sample points. The NN models that are already trained will be used to evaluate the constraints in the optimization phase.

In this study, both DE and NN-DE approaches are implemented by Python language. The DE algorithm is written based on the code published on R. Storn’s website [18]. The structural analysis is conducted with the support of the finite element library PyNiteFEA [19]. NN models are build using the library Keras [20].

4 Computational Experiments

4.1 10-Bar Truss

Design Data.

The configuration of the truss are presented in Fig. 3. All members are made of aluminum in which the modulus of elasticity is E = 10,000 ksi (68,950 MPa) and the density is ρ = 0.1 lb/in3 (2768 kg/m3). The cross-sectional areas of truss members range from 0.1 to 35 in2 (0.6 to 228.5 cm2). Constraints include both stresses and displacements. The stresses of all members must be lower than ±25 ksi (172.25 Mpa), and the displacements of all nodes are limited to 2 in (50.8 mm).

Fig. 3.
figure 3

10-bar truss layout

Full size image

Implementation.

Firstly, the truss is optimized based on the conventional DE procedure. The design variables are the cross-sectional areas of the truss members. In this problem, each member is assigned to a different section. It means this problem has ten design variables (D = 10). The optimization parameters are set after a parameter sensitive analysis as follows: F = 0.8; Cr = 0.7, Np = 5×D = 50; maximum iterations n = 1000.

For the NN-DE approach, 1000 sample points are initially produced by LHS. Each sample point is a 10-dimensional vector representing the cross-sectional areas of ten corresponding members. Once the input data were generated, the outputs are determined based on FEA. The obtained results are the internal axial forces of members and the displacements of nodes. From the structural engineering point of view, for some sample points, the truss structures are close to being unstable, leading to the large values of the internal forces and the displacements. These sample points are meaningless and they can negatively affect the accuracy of surrogate models. Therefore, the sample points having maximum constraint violation g(x) > 1.0 are removed from the dataset. The final dataset contains about 700 data points.

In the modeling phase, two surrogate models are developed. The first model named ‘Model-S’ will be used to predict the stresses inside the members while the second model named ‘Model-U’ will be used to predict the displacements of the free nodes. ‘Model-S’ has the architecture (10-40-40-40-10) in which ten inputs of the network are the cross-sectional areas of the ten truss members, ten outputs include stresses of ten members and three hidden layers with 40 neurons per layer. ‘Model-U’ has the architecture (10-20-20-20-4) where four outputs are vertical displacements of four free nodes (1, 2, 3, 4) [21]. ReLU is used as the activation function in this work.

Among available loss functions, MAE is useful if the training data is corrupted with outliers. Therefore, the loss function MAE is used in this work:

$$ E_{MAE} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {y_{i}^{true} - y_{i}^{pred} } \right|} $$
(10)

where: n is the number of training data points; y predi is the predicted value of the network and y truei is the correct value.

Models are trained for 1000 epochs with a batch size of 10. Before training, the input data should be normalized by dividing to the maximum cross-sectional area (35 in2). To prevent overfitting, the data is randomly split into the training and the validation subsets with the ratio of 80/20. The loss curves of the two models during the training process are plotted in Fig. 4. The trained models are then employed to predict the stresses and displacements during the optimization process.

Fig. 4.
figure 4

Loss curves during the training process

Full size image

The optimization parameters for the NN-DE approach are taken the same as in the conventional DE procedure. The computation is performed on a personal computer with the following configuration: CPU Intel Core i5-5257 2.7 GHz, RAM 8.00 Gb.

Results.

Because of the random nature of the search, the optimization is performed for 30 independent runs. The best results of both DE and NN-DE for 30 runs are presented in Table 1 in comparison with other algorithms taken from literature.

Table 1. Comparison of optimum results for 10-bar truss
Full size table

4.2 25-Bar Truss

Design Data.

The layout of the truss is presented in Fig. 5. The mechanical properties are the same as in the 10-bar truss. The allowable horizontal displacement in this problem is ±0.35 in (8.89 mm). Members are grouped into eight groups with the allowable stresses as shown in Table 2. Hence, the number of design variables in this problem D = 8. The cross-sectional areas of the members vary between 0.01 in2 and 3.5 in2. Two loading cases acting on the structure are given in Table 3.

Fig. 5.
figure 5

25-bar truss layout

Full size image
Table 2. Allowable stresses for 25-bar truss - unit: ksi (MPa)
Full size table
Table 3. Loading conditions for 25-bar truss - unit: kips (kN)
Full size table

Implementation.

The DE approach and the proposed NN-DE approach are also implemented with the same parameters: F = 0.8; Cr = 0.7; Np = 5×D = 40; n = 500.

There are totally 5 NN models which are built in this case. Two models namely ‘Model-S-min’ and ‘Model-S-max’ with the architecture (8-50-50-50-25), are used to predict the maximum and the minimum values of stresses inside truss members. Eight inputs of the network are the cross-sectional areas of the eight groups while twenty-five outputs are the stress values of 25 members. Three remaining models, namely ‘Model-Ux’, ‘Model-Uy’, and ‘Model-Uz’, have the architecture (8-20-20-20-6) in which six outputs are displacements of six free nodes (1, 2, 3, 4, 5, 6) along three directions (UX, UY, and UZ). Other parameters are completely similar to the 10-bar truss problem. The optimization is also performed for 30 independent runs.

Results.

The optimization is also performed for 30 independent runs. The best result of DE, NN-DE, and other algorithms is presented in Table 4.

Table 4. Comparison of optimum results for 25-bar truss
Full size table

4.3 Performance Comparisons

The performances of the DE approach and the NN-DE approach are given in Table 5.

Table 5. Comparison of computation time
Full size table

Based on the obtained results, some observations can be summarized as follows.

First of all, it can be noted that the DE algorithm is capable of finding the global optimum. The conventional DE optimization achieves the same results in comparison with other algorithm like GA, PSO, HS, ALSSO, etc. Minor differences in results obtained from different algorithms due to the use of different FEA codes.

Secondly, the computation times of the NN-DE approach are very small compared to the conventional DE optimization. For the 10-bar truss, the computation times of the DE and NN-DE approaches are 1757 s and 324 s, respectively. These values are 4426 s and 575 s for the 25-bar truss. It means the NN-DE approach is more than 5 times faster than the conventional DE approach. It is achieved by a significant reduction in the number of FEAs.

Furthermore, the errors of the optimum weight between DE and NN-DE for two problems are 3.1% and 0.4%, respectively. The reason for the errors is the models’ inaccuracy in predicting structural behavior. However, the coefficient of determination (R2) between the cross-sectional areas found by DE and NN-DE for 10-bar truss and 25-bar truss are 0.981 and 0.971, respectively. It indicates a good similarity and linear correlation between the results of the DE and NN-DE approaches.

5 Conclusions

In this paper, a hybrid approach, called NN-DE, which is combined Neural Networks and Differential Evolution algorithm is proposed. By using Neural Networks as surrogated models instead of FEA, the computation times of the evolutionary optimization is significantly reduced. Thus, the proposed approach has a high potential for large-scale structures. Besides, the optimum results of the proposed approach have still slightly errors compared to the conventional procedure. Therefore, it is important to notice that the results obtained from the proposed approach are not exact, but it can be considered as a good suggestion in the practical design. In the future, the methods to improve the accuracy of the Neural Network models should be studied.