Abstract
In this work we study the topology of complex non-isolated hypersurface singularities. Inspired by work of Siersma and others, we compare the topology of the link L f with that of the boundary of the Milnor fiber, ∂F f. We review the three proofs in the literature showing that for functions \({\mathbb {C}}^3 \to {\mathbb {C}}\), the manifold ∂F f is Waldhausen: one by Némethi-Szilárd, another by Michel-Pichon and a more recent one by Fernández de Bobadilla-Menegon. We then consider an arbitrary real analytic space with an isolated singularity and maps on it with an isolated critical value. We study and define for these the concept of vanishing zone for the Milnor fiber, when this exists. We then introduce the concept of vanishing boundary cycles and compare the homology of L f and that of ∂F f. For holomorphic map germs with a one-dimensional critical set, we give a necessary and sufficient condition to have that ∂F f and L f are homologically equivalent.
To András, in celebration of his first 60th Birthday Anniversary!
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
Subject Classifications
1 Introduction
Given an analytic map-germ \(({\mathbb {R}}^m,0) \overset {{h} } {\to } ({\mathbb {R}}^n,0)\), m > n, with a critical value at 0, a fundamental problem is understanding the way the non-critical levels h −1(t) degenerate to the special fiber V := h −1(0). For instance, when \(f: ({\mathbb {C}}^{m},{ \underline 0}) \to ({\mathbb {C}},0)\) is holomorphic, the celebrated fibration theorem of Milnor [17, 34], says that one has a locally trivial fibration:
where \(\mathbb {B}_{\varepsilon }\) denotes a sufficiently small ball around the origin in \({\mathbb {R}}^m\) and \(\mathbb {D}_\eta \) is a sufficiently small disc around 0 in \({\mathbb {C}}\). The set \(N({\varepsilon },\eta ) := f^{-1}(\mathbb {D}_\eta \setminus \{0\}) \cap \mathbb {B}_{\varepsilon }\) is usually called a Milnor tube for f and the fibers \(F_t := f^{-1}(t) \cap \mathbb {B}_{\varepsilon }\), t≠0, are now called the Milnor fibers. Hence one has a family of diffeomorphic manifolds F t that form a fiber bundle and degenerate to the special fiber V . A lot of interesting work has been done studying how this degeneration process F t ⇝ V takes place for holomorphic map-germs. This has given rise to a vast literature concerning vanishing cycles and vanishing homology.
This article takes an alternative viewpoint, following our previous work [27] that we briefly explain in what follows. This springs from work by R. Randell [43], D. Siersma [47, 48], F. Michel and A. Pichon [28,29,30, 32], A. Némethi and Á. Szilárd [39] and J. Fernández de Bobadilla and A. Menegon [13]. For this we recall that a real analytic map-germ h as above has a link, which by definition is \(L_h:= h^{-1}(0) \cap \mathbb {S}_{\varepsilon }\), the intersection of V with a sufficiently small sphere. The link and its embedding in \(\mathbb {S}_{\varepsilon }\) determine fully the topology of V at 0 and its local embedding in the ambient space (see [34] and [10, Chapter 1, Section 5]).
We shall denote the link by L 0 when we want to emphasize that this is the special fiber in the family {L t := ∂F t} with t in a small disc in \({\mathbb {R}}^n\).
The link L 0 is a real analytic variety and it is non-singular if h has an isolated critical point at 0. In that case, by Ehresmann’s fibration lemma, L 0 is isotopic to the boundary L t of the Milnor fiber F t. Otherwise, when h has a non-isolated critical point on V , the variety L 0 is singular: that is the setting we envisage in this paper.
Given an analytic map-germ h as above, consider a Milnor tube \(N({\varepsilon },\eta ) := h^{-1}(\mathbb {D}_\eta \setminus \{0\}) \cap \mathbb {B}_{\varepsilon }\), and let us assume this is a fiber bundle over \(\mathbb {D}_\eta \setminus \{0\}\) with projection h (unlike the complex setting, this hypothesis is not always satisfied for real analytic map-germs; see for instance [46] for a thorough discussion about that topic). The fibers \(F_t := h^{-1}(t) \cap \mathbb {B}_{\varepsilon }\), t≠0, are compact manifolds with boundary L t. While the family {F t} degenerates to the special fiber \(V := h^{-1}(0) \cap \mathbb {B}_{\varepsilon }\), the corresponding family of boundaries {L t}t≠0, which are smooth compact manifolds, degenerates to the link L 0, which is singular.
The purpose of this work is to study and compare the topology of both L t and L 0 by looking at the degeneration process {L t}t≠0 ⇝ L 0.
We begin this article with a few words about the degeneration of the Milnor fibers to the special fiber, and about the corresponding process as we look at the boundaries (Sect. 2). Then, in Sect. 3, we focus on the case of holomorphic map germs \({\mathbb {C}}^3 \to {\mathbb {C}}\) and describe briefly some of the ideas in András Némethi and Ágnes Szilárd’s excellent book [39], where it is proved that in this setting, the boundary of the Milnor fiber, which is a 3-manifold, is always Waldhausen. That theorem was announced in 2003 by Françoise Michel and Anne Pichon, providing a proof that worked fine for certain families of singularities. Their complete proof was published in 2016. There is also a third proof by Javier Fernández de Bobadilla and Aurélio Menegon that works more generally: for real analytic map-germs of the form \(f \bar g : {\mathbb {C}}^3 \to {\mathbb {C}}\) with a Milnor fibration. Taking g to be constant one gets the previous assertion. In Sect. 3 we briefly discuss these three viewpoints.
Section 4 is a brief summary of [26], and an extension of it to the case of real analytic map-germs \(f: (X,{ \underline 0}) \to ({\mathbb {R}}^n,0)\), m > n, where X is an m-dimensional real analytic space with an isolated singularity at \({ \underline 0}\), f has an isolated critical value at 0 and it has a Milnor fibration in a tube. We introduce the notion of a vanishing zone for f and for the Milnor fibers. This means a regular neighborhood W of the link \(L_{\varSigma } := \varSigma \cap \mathbb {S}_{\varepsilon }\) of the singular set of V = f −1(0), with smooth boundary ∂W, such that for every regular value t with ∥t∥ sufficiently small, one has that the boundary of the Milnor fiber ∂F t meets ∂W transversally, and ∂F t ∖ (F t ∩ W) is diffeomorphic to L f ∖ (L f ∩ W), where \(L_f := V \cap \mathbb {S}_{\varepsilon }\) is the link of V .
Section 5 is part of [1], a work in progress where we look at the homology of the boundary of the Milnor fiber for holomorphic map germs \({\mathbb {C}}^{n+1} \to {\mathbb {C}}\). In analogy with the classical notion of vanishing homology for the Milnor fiber, we introduce the notion of the vanishing boundary homology. For this we observe that there is a specialization morphism from the homology of ∂F f to the homology of the link. We state a theorem from [1] about the homology groups of ∂F f when the critical set is one-dimensional, which is a special case of a more general theorem. As a corollary we give, for holomorphic map-germs with one-dimensional critical set, a necessary and sufficient condition for having that the boundary of the Milnor fiber and the link are homologically equivalent. We give examples of such cases.
In Sect. 6 we conclude with a couple of remarks. One is for map-germs defined on analytic spaces with arbitrary singular locus. Another is for map-germs with non-isolated critical value. We actually look at an example where the critical values have real codimension 1, so they split the target into several connected components. Yet, the singularities in question are all real analytic isolated complete intersections, and this implies that we have a Milnor fibration over each component. Although the topology of the Milnor fibers varies as we change from one sector to another, they all have boundary isotopic to the link. Notice that if the dimension of the link is even, this implies that all Milnor fibers have the same Euler characteristic. If the dimension of the link is odd, we only have that the Euler characteristic of the Milnor fibers coincides modulo 2.
2 From the Non-critical Level to the Special Fiber
The starting point is the classical Milnor’s fibration theorem for holomorphic maps, see [34] and [17]. Consider a holomorphic function-germ with a critical point at \({ \underline 0}\):
Set V = f −1(0) and let \(L_f = V \cap \mathbb {S}_{\varepsilon }\), for ε > 0 sufficiently small, be the link. Given ε, choose δ > 0 small enough with respect to ε, so that every fiber f −1(t) with |t|≤ δ meets transversally the sphere \(\mathbb {S}_{\varepsilon }\); that such a δ exists for every Milnor sphere \(\mathbb {S}_{\varepsilon }\) is a consequence of the fact that f has the Thom a f-property, by Hironaka [14].
Set \(\mathbb {D}_\delta ^* := \mathbb {D}_\delta \setminus \{0\}\), where \(\mathbb {D}_\delta \) is the disc of radius \({\delta } \subset {\mathbb {C}}\) centered at 0, and consider the Milnor tube:
Then part of Milnor’s theorem (which follows from Ehresmann’s fibration theorem extended to manifolds with boundary) says that we have a locally trivial fibration:
The fibers F t are the local regular levels of the function. We denote the Milnor fibers by F t when we emphasize that this corresponds to the value t, or by F f when we look at an arbitrary Milnor fiber of f.
So the Milnor fibers are a family of complex Stein manifolds, the local non-critical levels of the function, that degenerate to the special fiber, the critical level V = F 0 as t tends to 0. A lot of interesting work, particularly in the isolated singularity case, has been done studying how this degeneration process F t ⇝ V takes place (Fig. 1).
When f has an isolated critical point, the fiber F t is diffeomorphic to a 2n-ball to which one attaches μ = μ(f) handles of middle index n, where μ is the Milnor number of f at \({ \underline 0}\), by Lê and Perron [19] and Milnor [34]. This number can be computed as the intersection number:
where Jacf is the Jacobian ideal, generated by the partial derivatives of f. The middle homology group H n(F t) is free of rank μ, generated by μ cycles that “vanish” as F t degenerates into the special fiber, since V is locally a cone. Therefore these are called vanishing cycles and the Milnor number counts how many of these F t has.
The concept of vanishing cycles was first mentioned by Grothendieck in a letter to Serre in 1964 [6, p. 214], where he analyses the difference between the (étale) cohomology of the special fiber and that of the generic fiber in certain families. His theory was developed by Deligne in [9] and has had immense applications.
When f, as above, has non-isolated critical points, the fiber F t, being a Stein manifold, has the homotopy type of a CW-complex of middle dimension, by Andreotti and Frankel [2] and Milnor [34], and it is (n − s − 1)-connected by Kato and Matsumoto [15], where s is the complex dimension of the singular set of V = f −1(0). In this case, by Massey [23], F t is diffeomorphic to a 2n-ball to which one attaches handles of various indices, as indicated by the Lê numbers. The homology groups of F are called groups of vanishing cycles. These have been investigated by several authors; see for instance [23, 24, 48], and [9] for a more general viewpoint. See [44] for a survey on recent results concerning the algebraic computation of vanishing cycles of an algebraic function on a complex quasi-projective variety.
More generally, given an analytic map-germ \(({\mathbb {R}}^m,0) \overset {{h} } {\to } ({\mathbb {R}}^n,0)\), m > n, with an isolated critical value at 0. Under suitable conditions, one still has a locally trivial fibration as above
where \(\mathbb {B}_{\varepsilon }\) denotes a sufficiently small ball around the origin and \(\mathbb {D}_\eta \) is a sufficiently small disc around 0 in \({\mathbb {R}}^n\). The set \(N({\varepsilon },\eta ) := h^{-1}(\mathbb {D}_\eta \setminus \{0\}) \cap \mathbb {B}_{\varepsilon }\) is usually called a Milnor tube for h, and the fibers \(F_t := h^{-1}(t) \cap \mathbb {B}_{\varepsilon }\), t≠0, are the Milnor fibers of h. A fundamental problem is understanding how the non-critical levels h −1(t) degenerate to the special fiber V := h −1(0). We refer to [46, Section 13] for a thorough account on the subject of Milnor fibrations for real and complex singularities.
We now follow [27] and take an alternative viewpoint to the problem of studying how the non-critical levels degenerate to the special fiber. This springs from work by Randell [43], Siersma [47, 48], Michel-Pichon [28,29,30, 32], Némethi-Szilárd [39] and Fernández de Bobadilla-Menegon [13].
For this we recall that a real analytic map-germ h as above has a link, which by definition is \(L_0:= h^{-1}(0) \cap \mathbb {S}_{\varepsilon }\), the intersection of V with a sufficiently small sphere. The link and its embedding in \(\mathbb {S}_{\varepsilon }\) determine fully the topology of V at 0 and its local embedding in the ambient space (cf. [10, 34]).
The link L 0 is real analytic and it is non-singular if h has an isolated critical point at 0. In that case L 0 is a smooth manifold, isotopic to the boundary L t of the Milnor fiber F t. Otherwise L 0 is singular: that is the setting we envisage in this paper.
Given an analytic map-germ h as above, consider a Milnor tube \(N({\varepsilon },\eta ) := h^{-1}(\mathbb {D}_\eta \setminus \{0\}) \cap \mathbb {B}_{\varepsilon }\), and let us assume this is a fiber bundle over \(\mathbb {D}_\eta \setminus \{0\}\) with projection h. The fibers \(F_t := h^{-1}(t) \cap \mathbb {B}_{\varepsilon }\), t≠0, are compact manifolds with boundary L t. While the family {F t} degenerates into the special fiber \(F_0 := h^{-1}(t) \cap \mathbb {B}_{\varepsilon }\), one also has the corresponding family of boundaries {L t}t≠0 degenerating to the link L 0, which may be singular. In the sequel we look at the topology of both L t and L 0, and we study of the degeneration process {L t}t≠0 ⇝ L 0 for both, real and complex singularities.
This is interesting for two reasons. On the one hand, the boundary of the Milnor fiber, being a smooth manifold, is in many ways easier to handle than the link. Understanding the way L t degenerates into L 0 throws light into the topology of the link, and hence into that of V , just as the study of the vanishing cycles on the Milnor fiber throws light into the topology of the special fiber. On the other hand, we can argue conversely: understanding the degeneration L t ⇝ L 0 allows us to get information about L t out from L 0 itself. For instance, this was the approach followed in [13, 28, 30, 39] to show that in the case of holomorphic map-germs in 3 complex variables, and also for map germs of the form \(f \bar g\), the boundary L t is a Waldhausen manifold (see the following section).
3 The Case of Complex Surfaces
Now consider a non-constant holomorphic function-germ,
with a one-dimensional critical set at \({ \underline 0}\). Set V = f −1(0) and Σ = Σ(f) ⊂ V , the singular set. Let \(L_f = V \cap \mathbb {S}_{\varepsilon }\) be the link of V and L Σ = L f ∩ Σ the link of Σ. Notice that L Σ is the singular set of the real analytic three-dimensional variety L f, and L Σ is a disjoint union of circles S 1, one for each branch of V . We denote by F the Milnor fiber of f and ∂F is its boundary,
R. Randell [43] and D. Siersma [47, 48] determined the homology of the boundary ∂F in several cases, finding, among other things, examples where ∂F is a homology sphere. It was also noticed in [47, 48] that the boundary ∂F consists of two parts, which are compact manifolds glued along their common boundary, which is a disjoint union of tori S 1 × S 1, one for each connected component of L Σ. One of these is the portion of ∂F contained within a tubular neighborhood of L Σ; the other is the closure of its complement. Following [30] we call these the vanishing zone of ∂F and the trunk, respectively. The interior of the trunk is diffeomorphic to L f ∖ L Σ. This is discussed with care in the following Sect. 4, so we only say a few words here. This decomposition plays a key role in the work of Némethi-Szilárd [39], Michel-Pichon [30] and Fernández de Bobadilla and Menegon [13]. Those works give three different proofs of the fact that in the setting we now envisage, the boundary ∂F is a Waldhausen manifold. We now say a few words about each of these works.
Recall that a 3-manifold M is a Seifert manifold if it fibers over a surface S with fiber the circle S 1 and this fibration is locally trivial away from a finite number of points in S. The fibers over those points are called the exceptional fibers. So for instance, every circle bundle over a surface is a Seifert manifold with no exceptional fibers.
A 3-manifold M is a Waldhausen manifold if there exist finitely many tori S 1 × S 1 in M, such that cutting M along these torii, the complement is Seifert. And we know from [40] that a 3-manifold M is Waldhausen if and only if it is a graph (or plumbed) manifold.
Plumbing is a construction introduced by Milnor [33] in order to exhibit the existence of exotic spheres. In that construction, the “building blocks”, so to say, are n-dimensional disc bundles E over compact n-manifolds B. The boundary ∂E is an S n−1 bundle over B. Given two of these, say (E 1, B 1) and (E 2, B 2), to perform plumbing on them we choose a small disc D i in each B i, so that E i restricted to this disc is a product of two n-discs, D n × D i. Then we identify the points in E 1 and E 2 contained in \(E_i|{ }_{D_i}\) by identifying a point \((x,y) \in E_1|{ }_{D_1}\) with the point \((y,x) \in E_2|{ }_{D_2}\). What we get is a 2n-dimensional compact manifold E 1 #E 2 with boundary and with corners. But the corners can be smoothed out in an essentially unique way, up to isotopy.
At the level of the boundaries what we are doing is removing from each ∂E i the interior of a product S n−1 × D i, and then identifying the boundaries \(S^{n-1} \times S^{n-1}_i\) by the map (x, y)↦(y, x).
A plumbed manifold is a manifold obtained by iterating this construction a finite number of times. The relevant case in this section is when n = 2, all manifolds and bundles are oriented, and we are plumbing oriented 2-disc bundles over compact 2-manifolds with no boundary. Recall that up to diffeomorphism, every such manifold is classified by its genus. And the oriented 2-disc bundles E over every such manifold B are classified by their Euler class, an integer, which equals the self-intersection number of B in E regarded as the zero-section. Hence in this setting, to every plumbed manifold we can associate a plumbing graph G: to each vertex in G we associate a weight \(w \in {\mathbb {Z}}\) and a genus \(g \in {\mathbb {N}}\). This represents a choice of a closed oriented 2-manifold B of genus g, and a 2-disc bundle E over B with Euler class w. If two vertices are connected by an edge, we do plumbing in the corresponding E i. If we have more than one edge joining two vertices, we repeat this operation several times, choosing disjoint discs.
That is why in singularity theory, in the case n = 2, plumbed manifolds are also called graph manifolds. It is not hard to see that every Waldhausen manifold is a graph manifold and viceversa, cf. [40].
Notice that to every graph manifold one associates naturally a symmetric matrix A = ((E i,j)), called the intersection matrix. The elements in the diagonal are the weights w i of the vertices, and the rest of the coefficients are the number of edges connecting the corresponding vertices.
As an example, let (V, p) be a normal complex surface singularity, and let \(\pi : \widetilde V \to V\) be a good resolution; recall that good means that each irreducible component S i of the exceptional divisor E is non-singular, all S i intersect transversally and no three of them intersect. We may now consider its dual graph: to each S i we associate a vertex v i, with a genus g i which is the genus of E i and a weight, the self-intersection number of S i in \(\widetilde V\). We then join two vertices v i, v j by as many edges as the intersection number S i ⋅ S j. We get a plumbing graph. The result of performing plumbing according to this graph is a 4-manifold, homeomorphic to a tubular neighborhood of the exceptional divisor E in \(\widetilde V\), and its boundary is diffeomorphic to the link L f. Therefore L f is a graph manifold, and we know from [11, 35] that the corresponding intersection matrix is negative definite. In fact the converse is also true: by Grauert’s contractibility criterium, every graph manifold with negative definite intersection matrix, is orientation preserving homeomorphic to the link of a normal complex surface singularity, cf. [40].
Let us consider again a non-constant holomorphic function-germ with a non-isolated critical point at \({ \underline 0}\),
We now say a few words about three different points of view that have been used to establish, among other things, three different proofs of the fact that in this setting, the boundary of the Milnor fiber is a graph manifold.
3.1 A Glance on Némethi-Szilárd’s Work for Surface Singularities
As pointed out in the introduction to [39], the work by András Némethi and Ágnes Szilárd has its roots in several of the milestones in singularity theory, some of these arising from the rich interplay one has between 3-manifolds and isolated complex surface singularities.
The 3-manifolds that arise as links of normal complex surface singularities, which are the graph manifolds with negative definite intersection matrix, are a particularly interesting class of manifolds, with certain properties that make these manifolds provide a ground for a better understanding of important invariants in low dimensional topology.
In fact, given a normal isolated singularity germ \((V,{ \underline 0})\), the link L f can always be regarded as being the boundary of a neighborhood of the special fiber \(\pi ^{-1}({ \underline 0})\) of a resolution \(\widetilde V \overset { {\pi } } {\to } V\). If V is a hypersurface, or more generally a smoothable singularity, then L f can also be regarded as being the boundary of the Milnor fiber. One thus has two natural holomorphic fillings of the link: the resolution and the Milnor fiber, and this gives rise to remarkable index-theoretical relations (see for instance [12, 16] and [45, Ch. IV] for the case where V has dimension two). This has been used by Andras in many articles, to produce remarkable results concerning Seiberg-Witten invariants, Floer homology and many other important 3-manifolds invariants, see for instance [36, 37].
Looking at 3-manifolds that are boundaries of Milnor fibers of non-isolated complex singularities defined by an equation \({\mathbb {C}}^3 \overset { {f} } {\to } {\mathbb {C}}\) extends the class of manifolds that arise from complex singularities. In this setting the Milnor fiber still provides a holomorphic filling for the natural contact structure on the boundary; but one does not have, a priori, the corresponding resolution of the singularity, since the Milnor fiber already is non-singular. A remarkable outcome of the work of Némethi and Szilárd in [39] is that even though these manifolds cannot be in general links of isolated complex singularities, they do appear naturally as links of certain real analytic singularities. Then, resolving these singularities one may regard the boundary of the Milnor fiber as being the boundary of a tubular neighborhood of the resolution, and one gets from this a graph decomposition. In fact the proof in [39] actually provides also an explicit Waldhausen decomposition of it. This is used in [39] to study the topology and geometry of ∂F.
The main algorithm in [39] springs from a Iomdin series associated to f. In fact, given f as above, let g be a holomorphic function germ in \({\mathbb {C}}^3\) such that (f, g) defines an isolated complete intersection. Now consider singularities of the form {f = |g|k} for k > 0. One has that for large k, its link is independent of the choice of k, and it turns out to be diffeomorphic to ∂F. That means that ∂F appears as the boundary of an arbitrary small neighborhood of a real analytic germ. After resolving this real analytic singularity, the tubular neighbourhood of the exceptional set provides a plumbing representation of ∂F.
The way Némethi and Szilárd resolve the above singularities is very interesting, because it not only gives a resolution, but it provides also a lot more information about the singularities in question, and about the boundary ∂F. This springs from their earlier work [38], explained in Chapter 6 of their book, where they introduce a decorated graph Γ to study hypersurface singularities in three variables with one-dimensional singular locus. That is their main tool in [38] for getting resolution graphs of the singularities in question. Starting with a hypersurface germ f as above, choose g so that (f, g) forms an ICIS. Then the graph Γ yields to a resolution of the singularities in the Iomdin series f + g k for k large. Moreover, the same graph Γ also contains enough information to allow them to determine the boundary ∂F. This is done by looking at the aforementioned singularities {f = |g|k} for k large.
The work of Némethi and Szilárd was extended by O. Curmi in [7] to functions defined on an arbitrary ambient space. To be precise, Curmi considers the germ \((X,{ \underline 0})\) of a three-dimensional complex analytic variety, and the germ of a reduced holomorphic function \(f : (X, { \underline 0}) \to ({\mathbb {C}}, 0)\) such that its zero locus V (f) contains the singular locus of X. Then it is proved that the boundary of the Milnor fiber of f is a graph manifold. This is further refined in [8] where the author gives an algorithm for describing the corresponding plumbing graph of the boundary of the Milnor fiber of Newton non degenerate surface singularities.
3.2 On the Work of Michel-Pichon-Weber
The references for this subsection are the articles [28,29,30,31,32] by Françoise Michel, Anne Pichon and Claude Weber. In [28] the authors consider a holomorphic map-germ \(f : ({\mathbb {C}}^3, { \underline 0}) \to ({\mathbb {C}},0)\) and state the theorem that the boundary ∂F of the Milnor fiber is a graph manifold, with a sketch of the proof (with a gap pointed out in [29]). Complete proofs of this theorem are given in [31, 32] for special families of singularities. Shortly after the appearance of the book by A. Némethi and Á. Szilárd [39], F. Michele and A. Pichon provided a complete proof which is in the spirit of the original method they proposed.
The idea is the following. Firstly they split the boundary ∂F f in two parts, as already explained, which essentially are the trunk and the vanishing zone; the work above essentially comes from the fact that in these papers the authors do not work with the singular variety V but with its normalization. That the trunk is Waldhausen follows from the classical theory of complex surface singularities, by taking first a normalization of V and then a good resolution. Since the trunk and the vanishing zone are glued along tori, the hard part is showing that the vanishing zone of ∂F f has a Waldhausen structure compatible with the boundary.
The key point is the use of a “carousel in family”. In fact, recall that given a map-germ \(g: ({\mathbb {C}}^2,{ \underline 0}) \to ({\mathbb {C}},0)\), D. T. Lê developed a remarkable method to construct the corresponding Milnor fiber, known as “the carousel”, see for instance [18] or the expository article [20]. When g is irreducible, so it has only one branch, then we know from [3] that its link is an iterated torus knot determined by the Puiseux pairs of g. Yet, the Puiseux expansions actually give an additional structure near the singular point, observed by D. T. Lê, that gives rise to what he called the carousel associated to the singularity. This is obtained by considering an auxiliary linear form ℓ, general enough for g, and looking at the distribution of points {z j} in the intersection {ℓ = t}∩{g(x, y) = 0}. Then the carousel arises by a careful study of how the Puiseux pairs describe the points in which the line {ℓ = t} meets the Milnor fiber, which are distributed regularly around each point {z j}, and their distribution is determined iteratively by the Puiseux pairs.
In the setting we envisage here, we want to show that the Milnor fiber of the map-germ \(f : ({\mathbb {C}}^3, { \underline 0}) \to ({\mathbb {C}},0)\) has a graph manifold structure within the vanishing zone W. This manifold W has a connected component for each component of the singular set \(L_\varSigma := \varSigma \cap \mathbb {S}_{\varepsilon }\) of the link \(L_f: V \cap \mathbb {S}_{\varepsilon }\), where V = f −1(0). Each component of L Σ is a circle. If at each point z ∈ L Σ we take a small complex two-dimensional disc H z transversal to L Σ what we get in that disc is the germ of a plane curve. The Milnor fiber of the restriction \(f|{ }_{H_z}\) is then described by a carousel. Doing this in a “coherent way” for all points in the corresponding connected component of L Σ, we get a family of carousels, parameterized by the circle S 1. Hence, in order to construct the part of the Milnor fiber contained in the vanishing zone, we may consider, for each connected component of L Σ, a family of carousels parameterized by the circle S 1. After taking care of a number of highly non-trivial subtleties, this shows that the boundary of the Milnor fiber of f is a graph manifold.
3.3 On the Work of Fernández de Bobadilla and Menegon
To finish this section, we say a few words about [13]. This actually considers a more general setting. Let \((X, { \underline 0})\) be a three-dimensional complex analytic germ with an isolated singularity at the origin in some \({\mathbb {C}}^N\), and let f, g be holomorphic function-germs \((X, { \underline 0}) \to ({\mathbb {C}},0)\) such that:
-
V (f) := f −1(0) and V (g) := g −1(0) have no common irreducible components;
-
the real analytic map-germ \(f\bar g: (X, { \underline 0}) \to ({\mathbb {C}}, 0)\) has an isolated critical value; and
-
the real analytic map-germ \(f \bar g : (X,{ \underline 0}) \to ({\mathbb {C}},0)\) has a Milnor fibration. That is, we assume that there exists small positive real numbers ε > 0 and δ > 0 with 0 < δ ≪ ε ≪ 1 such that the restriction
$$\displaystyle \begin{aligned}(f \bar g) |{}_{(f \bar g)^{-1}(D^*_{\delta}) \cap X \cap \mathbb{B}_{\varepsilon}} : (f \bar g)^{-1}(D^*_{\delta}) \cap X \cap \mathbb{B}_{\varepsilon} \longrightarrow D^*_{\delta}\end{aligned}$$is the projection of a locally trivial fibration, where \(\mathbb {B}_{\varepsilon }\) and \(D^*_{\delta }\) are a small enough discs around the origin in \({\mathbb {C}}^N\) and \({\mathbb {C}}\) respectively.
Then it is proved in [13] that the boundary of the Milnor fibre \(\partial F_{f \bar g}:= (f \bar g)^{-1}(t) \cap X \cap \mathbb {S}_{\varepsilon }\), for \(t \in D^*_{\delta }\), is a Waldhausen manifold.
Of course, taking g to be constant one is back in the situation envisaged previously. In other words, this work by Fernández de Bobadilla and Menegon gives a third proof of the theorem that the boundary of the Milnor fiber for holomorphic map germs in three complex variables is a Waldhausen manifold, and that proof works, more generally, for maps \(f \bar g\) and the ambient space X being any three-dimensional complex space which is non-singular away from a point.
The first step in the proof is based on studying the Milnor fibre of a map-germ of the form \(f \bar g\) defined on a complex surface with a an isolated singularity, in terms of an embedded resolution of {fg = 0}. This uses previous work by Pichon and Seade [42] about Milnor fibrations for such maps. Then they proceed to dimension 3. They first split the boundary of the Milnor fibre of \(f \bar g\) into two parts as before: the trunk and the vanishing zone, which are glued together along a finite union of tori. Most of the work goes for showing that the part of the Milnor fibre inside the vanishing zone is a Waldhausen manifold. They do so by means of a slicing argument, and then using their previous results in dimension 2. A key point is noticing that it is sufficient to decompose the transversal Milnor fibre into pieces which are invariant under the corresponding vertical monodromy, and which decompose the vanishing zone into Waldhausen pieces. This is proved by showing that the vanishing zone can be decomposed into pieces that are either fibre bundles over a circle with fibre a cylinder, or it is a finite unramified covering of a Walhausen manifolds, and therefore it is also Waldhausen.
4 The Vanishing Zone
We now consider the germ at \({ \underline 0} \in {\mathbb {R}}^N\) of a real analytic variety X such that \(X \setminus \{{ \underline 0}\}\) is a smooth manifold of real dimension m. We consider real analytic map-germs
with an isolated critical value at 0, which admit a local Milnor fibration in a tube. That is, there is a Milnor ball \(\mathbb {B}_{\varepsilon }\) for f, and δ > 0, depending on ε, such that if we let N(ε, δ) be the Milnor tube \(N({\varepsilon },{\delta }):= f^{-1}(\mathbb {D}_{\delta }^*) \cap \mathbb {B}_{\varepsilon }\), where \(\mathbb {D}_{\delta }^* \) is a punctured ball in \({\mathbb {R}}^n\) around 0 of radius δ, then one has a locally trivial fibration
This is a stringent condition and yet, there are enough examples to make it an interesting setting. For instance, the above conditions are satisfied in all the following examples:
-
(a)
f has an isolated critical value at \({ \underline 0}\) and f −1(0) has positive dimension.
-
(b)
X is complex analytic and f is a \({\mathbb {C}}\)-valued holomorphic map.
-
(c)
X is a complex analytic surface with a normal singularity at 0, and f is of the form \(f = h \bar g\) where h, g are holomorphic with no common branch (see [42]).
-
(d)
f is a polar weighted mixed polynomial \({\mathbb {R}}^{2m} \to {\mathbb {R}}^2\).
Statement (a) essentially follows from the classical Ehresmann’s fibration theorem, using the implicit function theorem (cf. [4, 5]). Statement (b) follows from Hironaka’s theorem in [14], stating that every such map is Thom regular; (c) follows from [42]. For (d) see Oka’s paper [41]: the polar action ensures that the critical value must be isolated, while the radial action ensures the transversality condition.
One has the following folklore theorem (see for instance [5, Theorem 2.7] or [26, Proposition 2.5]).
Theorem 4.1
Let \((X,{ \underline 0})\) be as above and let \( f: (X,{ \underline 0}) \to ({\mathbb {R}}^n,0), m > n > 0, \) be real analytic with an isolated critical value at \(0 \in {\mathbb {R}}^n\) . Assume f satisfies the following transversality condition: for every Milnor sphere \(\mathbb {S}_{\varepsilon }\) there exists δ > 0, depending on ε, such that each fiber f −1(t) with |t|≤ δ intersects transversally the sphere \(\mathbb {S}_{\varepsilon }\) . Then f has a local Milnor-Lê fibration.
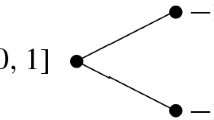
Given f as in this theorem, set V = f −1(0) ∩ X and equip X with a Whitney stratification for which V and its singular set Σ are union of strata. Let \(\mathbb {S}_{\varepsilon }\) be a sufficiently small Milnor sphere for f so that \(L_X:= X \cap \mathbb {S}_{\varepsilon }\) is the link of X, and therefore \(L_f:= V \cap \mathbb {S}_{\varepsilon }\) is the link of V and L Σ is that of Σ. We denote by ∂F t the boundary of a Milnor fiber F t, so:
for \(t \in \mathbb {D}_{\delta } \backslash \{0\}\). Then ∂F t is a smooth submanifold of L X that degenerates to the link L f as |t| goes to 0.
Following the previous discussion, we aim to study and compare the topology of ∂F t with that of L f. For this we want to define and show the existence of a vanishing zone for ∂F t. We follow [27]:
Theorem 4.2
There exists a compact regular neighborhood W of L Σ in L X such that:
-
W has smooth boundary ∂W and this boundary intersects L f transversally;
-
W has L Σ as a deformation retract;
-
for every t sufficiently close to 0 we have
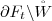 is diffeomorphic to
is diffeomorphic to
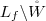 , where
, where
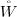 is the interior.
is the interior.
-
If the critical set Σ of f is either smooth or an isolated singularity, then W can be chosen to be a fiber bundle over L(Σ) with fiber a 2(n − k)-dimensional ball, where k is the dimension of Σ.
-
If there is a Whitney stratification of V so that each connected component of Σ∖{0} is a single stratum, then the intersection W t := ∂F t ∩ W is a topological fiber bundle over L Σ , for every t sufficiently near 0.
The proof is exactly like that of [27, Theorem 2.5] and is left to the reader. Notice that in the last statement in Theorem 4.2 the condition that each connected component of Σ∖{0} be a single stratum is rather stringent. This implies the local topological triviality that gives the fiber bundle structure in that statement.
Definition 4.3
A vanishing zone for f is a regular neighborhood W of L Σ in L X as in Theorem 4.2.
5 The Vanishing Boundary Homology
Consider now an irreducible and reduced complex analytic germ \((X,{ \underline 0})\) of pure dimension n + 1 in some \({\mathbb {C}}^m\), and let \(f : (X,{ \underline 0}) \to ({\mathbb C},0)\) be holomorphic. We know from [49] that taking the representative of X to be small enough, f has a unique critical value at 0. And we know from [14] that f has the Thom a f-property, which implies the transversality condition in Theorem 4.1. Hence one has a Milnor fibration in a tube, which is a special case of Lê’s fibration theorem in [17], which holds for X with arbitrary singularities. Notice that if X has a non-isolated singularity at \({ \underline 0}\), then the Milnor fibers of f may not be smooth, due to the singularities of X.
Theorem 4.2 hints on looking at relations between the homology of ∂F f and that of the link L f. In fact one has a specialization morphism (à la Verdier, cf. [25, 50]),
by observing that the vanishing zone W extends to a regular neighborhood \(\widetilde W\) of L f that contains the boundary of F f for all Milnor fibers over points sufficiently near 0. Thus one has a morphism \(H_*(\partial F_f) \to H_* (\widetilde W)\) induced by the inclusion. Also, \(\widetilde W\) has L f as a deformation retract, so one gets an isomorphism \(H_*(\widetilde W) \to H_* (L_f)\). The specialization \({\mathcal S}\) is the composition of these two morphisms.
In [1] we show that \({\mathcal S}\) is surjective whenever the germ \((X,{ \underline 0})\) is an ICIS. It would be interesting to know whether or not \({\mathcal S}\) is always surjective.
We call the kernel of \({\mathcal S}\) the vanishing boundary homology of the Milnor fiber, \(H_*^{\mathcal V}(\partial F_f)\). By Theorem 4.2, \(H_*^{\mathcal V}(\partial F_f)\) has support in the vanishing zone W. Similarly, following [9], the elements in H ∗(∂F f) can be thought of as being the nearby boundary cycles.
In order to study the vanishing and the nearby boundary cycles we prove in [1] the following general theorem:
Theorem 5.1
Let p: E → M be a fibration with fiber F, where E, M, and F are CW-complexes of dimension 2n − 1, 2k − 1, and 2(n − k) respectively. Assume that F ≃∨μ S n−k , M is 0-connected and 2k − 1 ≤ n − k (k > 0). Then:
-
1.
The Leray-Serre spectral sequence of p collapses to the term \(E_{*,*}^2\).
-
2.
The induced homomorphism \(p_*\colon H_\ell (E;\mathbb {Z})\to H_\ell (M;\mathbb {Z})\) , with 0 ≤ ℓ ≤ 2k − 1, has the following properties:
-
a.
If 2k − 1 < n − k, then p ∗ is an isomorphism;
-
b.
If 2k − 1 = n − k, then p ∗ is an isomorphism when ℓ < 2k − 1 and when ℓ = 2k − 1 it is surjective with kernel isomorphic to \((\mathbb {Z}^\mu )_{\pi _1(M)}\) , the group of coinvariants of the action of π 1(M) on the homology of the fiber.
-
a.
Recall that the group of coinvariants is the quotient of H n−k(F) by the subgroup generated by elements of the form g ⋅ a − a, with g ∈ G and a ∈ H n−k(F).
In particular one has the following theorem; some of the statements in it can also be proved using the Wang sequence as Milnor does in [34, Chapter 8].
Theorem 5.2
Let p: E → S 1 be a fiber bundle over the circle with fiber F a compact manifold of dimension 2n − 2 (n ≥ 2), which is homotopically equivalent to a bouquet of μ (n − 1)-spheres (μ > 0). Consider the monodromy action of G ≡ π 1(S 1) on \(H_{n-1}(F)\cong \bigoplus _\mu {\mathbb {Z}}\) . We denote by H n−1(F)G the group of invariants of the action, i.e., the fixed points, and by H n−1(F)G the group of coinvariants. Then:
-
1.
For all n ≥ 2 we have:
-
H q(E)≅0 for all q≠0, 1, n − 1, n, and
-
H n(E)≅H n−1(F)G which is a free abelian group.
-
-
2.
For n = 2 we have:
-
\(H_0(E)\cong {\mathbb {Z}}\) and \(H_1(E)\cong H_1(F)_G\oplus {\mathbb {Z}}\).
-
\( \operatorname {\mathrm {rank}} H_{2}(E) = \operatorname {\mathrm {rank}} H_{1}(E)-1\).
-
p ∗ is an epimorphism with kernel isomorphic to H 1(F)G.
-
-
3.
For n > 2 we have:
-
\(H_0(E)\cong {\mathbb {Z}}\cong H_1(E)\) and H n−1(E)≅H n−1(F)G.
-
\( \operatorname {\mathrm {rank}} H_{n}(E) = \operatorname {\mathrm {rank}} H_{n-1}(E)\).
-
p ∗: H 1(E) → H 1(S 1) is an isomorphism.
-
Similar arguments yield:
Theorem 5.3
With the hypothesis of Theorem 5.2 , let i : F↪E be the inclusion of a fiber in the total space. Then the induced homomorphism i ∗ in homology satisfies:
-
In all cases, its kernel is the image of the homomorphism h ∗− Id : H n−1(F) → H n−1(F), where h ∗ is induced by the monodromy action.
-
If n > 2, i ∗ is surjective.
-
If n = 2, i ∗ is never surjective: its image is isomorphic to the group of coinvariants H 1(F)G.
Now consider a holomorphic function-germ \(({\mathbb {C}}^{n+1},{ \underline 0}) \to ({\mathbb C},0)\) with a non-isolated singularity at \({ \underline 0}\). Notice we know from [27] that in general, the link L f is not homeomorphic to ∂F f. In fact [27, Theorem 2.8] says that if n = 2 and the critical set is one-dimensional, then the boundary of the Milnor fiber is never homeomorphic to the link.
We have the following immediate corollary to the theorems above:
Corollary 5.4
Consider a holomorphic function-germ \(f : ({\mathbb {C}}^{n+1},{ \underline 0}) \to ({\mathbb C},0)\) with a one-dimensional critical set Σ at \({ \underline 0}\) . Assume for simplicity that the singular set Σ of V = f −1(0) is irreducible. Let ε > 0 be small enough so that \(L_f := V \cap \mathbb {S}_{\varepsilon }\) is the link of V and the circle \(L_\varSigma := \varSigma \cap \mathbb {S}_{\varepsilon }\) is the link of Σ. Let z be a point in L Σ, \(F_f^\perp \) a transversal Milnor fiber at z and \(h_*: H_{n-1}(F_f^\perp ; \mathbb Z) \to H_{n-1}(F_f^\perp ; \mathbb Z)\) the corresponding monodromy morphism. Then L f and the boundary ∂F f are integrally homologically equivalent if and only if h ∗− Id is an isomorphism.
Example 5.5
Consider the function f(x, y, z) = x a + y b z where a and b are positive integers with a, b > 1. Then the boundary of the Milnor fiber is homologically equivalent over the integers to the link. To show this, notice first that its critical locus is Σ = {x = y = 0}. We can take in \({\mathbb {C}}^3\) balls with corners \((\mathbb {B}_{{\varepsilon }_1}^4 \times \mathbb {B}_{{\varepsilon }_2}^2) \subset ({\mathbb {C}}^2 \times {\mathbb {C}})\). Then \(L_\varSigma = \{0\} \times \mathbb {S}_{{\varepsilon }_2}^1\)and the vanishing zone \(W= \mathbb {B}_{{\varepsilon }_1}^4 \times \mathbb {S}_{{\varepsilon }_2}^1\) fibers over \(\mathbb {S}^1\) with fiber the ball \(B_z := \mathbb {B}_{{\varepsilon }_1}^4 \times \{z\}\). We have
which fibers over \(\mathbb {S}^1\) with fiber
for \(z \in \mathbb {S}_{{\varepsilon }_2}^1\). Let us denote by \(F_{t,z}^\perp \) the transversal Milnor fiber at a point z ∈ L Σ. One finds (see [1]) that the induced monodromy homomorphism,
is given by the following (a − 1)(b − 1) × (a − 1)(b − 1)-matrix:
where O is the (b − 1) × (b − 1) zero-matrix and M is the (b − 1) × (b − 1)-matrix given by
which appears exactly (a − 1)-times in the matrix [h ∗]. Then
where N is the (b − 1) × (b − 1)-matrix given by
whose determinant is not zero. Therefore the homomorphism h ∗− I ∗ is an isomorphism, so L f and the boundary ∂F f are integrally homologically equivalent.
6 Concluding Remarks
We finish this note with a couple of remarks about more general settings:
Remark 6.1
We may look at germs of holomorphic maps \((X,{ \underline 0}) \overset { {f} } {\to } ({\mathbb {C}},0)\) where X is a complex analytic space with arbitrary singularities. In this general setting, if f has an isolated singularity at \({ \underline 0}\) with respect to some Whitney stratification, by Lê [17] one has a locally trivial fibration
where \(N({\varepsilon },{\delta }):= f^{-1}(\mathbb {D}_{\delta }^*) \cap \mathbb {B}_{\varepsilon }\), \(\mathbb {B}_{\varepsilon } \subset {\mathbb {R}}^m\) is a Milnor ball for f and \(\mathbb {D}_{\delta }^* \) is a punctured ball in \({\mathbb {R}}^n\) around 0, as before. Thus one has the Milnor fibers F t degenerating to the special fiber \(V = f^{-1}(0) \cap X \cap \mathbb {B}_{\varepsilon }\) as t tends to 0, and a degeneration of the boundary ∂F t to the link L f. In this setting one can show the existence of a vanishing zone essentially as in Theorem 4.2. One must replace diffeomorphisms by homeomorphisms, transversality by topological transversality, and Ehresmann’s fibration lemma by the first Thom-Mather isotopy lemma.
Remark 6.2
When considering real analytic map-germs \(({\mathbb {R}}^m,{ \underline 0}) \to ({\mathbb {R}}^n,0)\), generically the discriminant Δ f, i.e., the set of critical values, has codimension 1. In that case Δ f disconnects the target into several connected components, so if one has a fibration, the base space has several components and the fibers over different components can change. Yet, if the variety V = f −1(0), is a complete intersection of dimension m − n in \({\mathbb {R}}^m\) with an isolated singularity at a point, say \({ \underline 0}\), then Theorem 4.1 together with the implicit function theorem imply that we have a Milnor-Lê fibration, which is locally trivial. We still have that the Milnor fibers degenerate to the special fiber. This is obvious when n = 1. In that well-studied case we have the right Milnor fibers, and the left Milnor fibers.
For instance, let us look at the following particularly nice example, investigated thoroughly by S. López de Medrano in various papers, e.g. [21, 22]. Consider the map \({\mathbb {C}}^n \to {\mathbb {C}}\) defined by:
where the λ i are non-zero complex numbers in the Siegel domain. This means that their convex hull contains the origin \(0 \in {\mathbb {C}}\). We further assume that the λ i are generic in the sense that no two of them are in the same line through the origin.
The zero-set V := V (ψ) is a real analytic complete intersection in \({\mathbb {C}}^n\) defined by two quadrics, the real and the imaginary parts of ψ. This has a unique singular point at \({ \underline 0} \in {\mathbb {C}}^n\). The topology of the link of V was determined by López de Medrano and it is homeomorphic to a connected sum of products of spheres (depending on the λ i). For n = 3 the link always is the 3-torus S 1 × S 1 × S 1.
The critical set of ψ consists of the n coordinate axes. The discriminant (the critical values) are the n half-lines \(\mathcal L_1, \cdots , \mathcal L_n\) determined by the λ i. These half-lines split the plane \({\mathbb {C}}\) into n sectors, and the topology of the fibers of ψ changes as we move from one sector to another. Yet one has that all Milnor fibers have the same boundary, which is diffeomorphic to the link. In fact one has:
Theorem 6.3
Let \(f:({\mathbb {R}}^m,{ \underline 0}) \to ({\mathbb {R}}^n,0)\) define a real analytic isolated complete intersection singularity of dimension m − n > 0. Then all Milnor fibers have diffeomorphic boundaries and these are isotopic to the link L f.
The proof is simple and it is left to the reader.
References
Aguilar, M., Menegon, A., Seade, J.: On the topology of the boundary of the Milnor fiber of non-isolated complex singularities (2021). Preprint
Andreotti, A., Frankel, Th.: The Lefschetz theorem on hyperplane sections. Ann. Math. 69, 713–717 (1959)
Brauner, K.: Zur Geometrie der Funktionen zweier komplexen Verändlichen III, IV. Abh. Math. Sem. Hambg. 6, 8–54 (1928)
Cisneros-Molina, J.L., Seade, J., Snoussi, J.: Milnor fibrations and d-regularity for real analytic singularities. Int. J. Math. 21, 419–434 (2010)
Cisneros-Molina, J.L., Menegon, A., Seade, J., Snoussi, J.: Fibration theorems à la Milnor for differentiable maps with non-isolated singularities (2017). Preprint, arXiv:2002.07120
Colmez, P., Serre, J.-P. (eds.): Correspondance Grothendieck-Serre. Documents Mathématiques (Paris) 2. Société Mathématique de France, Paris (2001)
Curmi, O.: Topology of smoothings of non-isolated singularities of complex surfaces. Math. Ann. 377, 1711–1755 (2020)
Curmi, O.: Boundary of the Milnor fiber of a Newton non degenerate surface singularity. Adv. Math. 372, Article 107281 (2020)
Deligne, P., Katz, N.: Groupes de monodromie en géométrie algébrique, SGA7 t. II. LNM, vol. 340. Springer, Berlin (1973)
Dimca, A.: Singularities and Topology of Hypersurfaces. Universitext. Springer, New York (1992)
du Val, P.: On absolute and non-absolute singularities of algebraic surfaces. Rev. Fac. Sci. Univ. Istanb. (A) 91, 159–215 (1944)
Durfee, A.: The signature of smoothings of complex surface singularities. Math. Ann. 232, 85–98 (1978)
Fernández de Bobadilla, J., Menegon, A.: The boundary of the Milnor fiber of complex and real analytic non-isolated singularities. Geom. Dedicata 173, 143–162 (2014)
Hironaka, H.: Stratification and flatness. In: Real and Complex Singularities (Proc. Ninth Nordic Summer School/NAVF Sympos. Math., Oslo, 1976), pp. 199–265. Sijthoff and Noordhoff, Alphen aan den Rijn (1977)
Kato, M., Matsumoto, Y.: On the connectivity of the Milnor fiber of a holomorphic function at a critical point. In: Manifolds Tokyo 1973 (Proc. Internat. Conf., Tokyo, 1973), pp. 131–136. Univ. Tokyo Press, Tokyo (1975)
Laufer, H.B.: On μ for surface singularities. In: “Several Complex Variables”. Proc. Symp. Pure Math. AMS, XXX, Part 1, pp. 45–49 (1977)
Lê, D.T.: Some remarks on relative monodromy. In: Real and complex singularities (Proc. Ninth Nordic Summer School/NAVF Sympos. Math., Oslo, 1976), pp. 397–403. Sijthoff and Noordhoff, Alphen aan den Rijn (1977)
Lê, D.T.: Introduction à la théorie des singularités t. 1 et t. 2. In: Lê, D.T. (ed.) Travaux en cours, pp. 36–37. Hermann Ed., Paris (1988)
Lê, D.T., Perron, O.: Sur la fibre de Milnor d’une singularité isolée en dimension complexe trois. C. R. Acad. Sci. Paris Sé r. A-B 289(2), A115–A118 (1979)
Lê, D.T., Nuño-Ballesteros, J.J., Seade, J.: The topology of the Milnor fiber. In: Cisneros, J.L. et al. (eds.) Handbook of geometry and topology of singularities I. Springer, Verlag (2020)
López de Medrano, S.: Topology of the intersection of quadrics in \({\mathbb {R}}^n\). In: Carlsson et al. (eds.) “Algebraic Topology” (Arcata, CA, 1986). Lecture Notes in Math., vol. 1370, pp. 280–292. Springer, Berlin (1989)
López de Medrano, S.: Singular intersections of quadrics I. In: Cisneros-Molina, J.L. et al. (eds.) Singularities in Geometry, Topology, Foliations and Dynamics. Trends in Mathematics. Birkhäuser, Basel (2017)
Massey, D.B.: Lê Cycles and Hypersurface Singularities. Lecture Notes in Mathematics, vol. 1615. Springer, Berlin (1995)
Massey, D.B.: Notes on Perverse Sheaves and Vanishing Cycles (2016). eprint arXiv:math/9908107, version 7
Maxim, L.: On the Milnor classes of complex hypersurfaces. In: G. Friedman et al. (eds.) Topology of Stratified Spaces, vol. 58. MSRI Publications, Camb. Univ. Press, Cambridge (2011)
Menegon Neto, A., Seade, J.: On the Lê-Milnor fibration for real analytic maps. Math. Nachr. 290(2–3), 382–392 (2017)
Menegon Neto, A., Seade, J.: Vanishing zones and the topology of non-isolated singularities. J. Geom Dedicata 202(1), 321–335 (2019). https://doi.org/10.1007/s10711-018-0415-5
Michel, F., Pichon, A.: On the boundary of the Milnor fiber of non-isolated singularities. Int. Math. Res. Notices 43, 2305–2311 (2003)
Michel, F., Pichon, A.: On the boundary of the Milnor fiber of non-isolated singularities (Erratum). Int. Math. Res. Notices 6, 309–310 (2004)
Michel, F., Pichon, A.: Carousel in family and non-isolated hypersurface singularities in \({\mathbb {C}}^3\). J. Reine Angew. Math. (Crelles J.) 720, 1–32 (2016)
Michel, F., Pichon, A., Weber, C.: The boundary of the Milnor fiber of Hirzebruch surface singularities. In: Cheniot, D. et al. (eds.) Singularity Theory, pp. 745–760. World Sci. Publ., Hackensack (2007)
Michel, F., Pichon, A., Weber, C.: The boundary of the Milnor fiber for some non-isolated singularities of complex surfaces. Osaka J. Math. 46, 291–316 (2009)
Milnor, J.W.: Differentiable structures on spheres. Am. J. Math. 81, 962–972 (1959)
Milnor, J.W.: Singular points of complex hypersurfaces. Ann. Math. Studies, vol. 61. Princeton University Press, Princeton (1968)
Mumford, D.: The topology of normal singularities of an algebraic surface and a criterion for simplicity. Publ. Math.. Inst. Hautes Études Sci. 9, 5–22 (1961)
Némethi, A.: Invariants of normal surface singularities. Contemp. Math. 354, 161–208 (2004)
Némethi, A.: Lattice cohomology of normal surface singularities. Publ. Res. Inst. Math. Sci. 44, 507–543 (2008)
Némethi, A., Szilárd, Á.: Resolution graphs of some surface singularities, II. (Generalized Iomdin series). Contemp. Math. 266, 129–164 (2000)
Némethi, A., Szilárd, Á.: Milnor Fiber Boundary of a Non-isolated Surface Singularity. Lecture Notes in Mathematics, vol. 2037. Springer, Berlin (2012)
Neumann, W.D.: A calculus for plumbing applied to the topology of complex surface singularities and degenerating complex curves. Trans. Am. Math. Soc. 268, 299–344 (1981)
Oka, M.: Topology of polar weighted homogeneous hypersurfaces. Kodai Math. J. 31(2), 163–182 (2008)
Pichon, A., Seade, J.: Fibered multilinks and singularities \(f \bar g\). Math. Ann. 342(3), 487–514 (2008)
Randell, R.: On the topology of non-isolated singularities. In: Proceedings 1977 Georgia Topology Conference, pp. 445–473 (1977)
Sabbah, C.: Vanishing cycles and their algebraic computation. http://www.cmls.polytechnique.fr/perso/sabbah/livres/sabbah_notredame1305.pdf
Seade, J.: On the Topology of Isolated Singularities in Analytic Spaces. Progress in Mathematics, vol. 241. Birkhauser, Basel (2005)
Seade, J.: On Milnor’s Fibration theorem and its offspring after 50 years. Bull. Am. Math. Soc. 56, 281–348 (2019)
Siersma, D.: Variation mappings on singularities with a 1-dimensional critical locus. Topology 30, 445–469 (1991)
Siersma, D.: The vanishing topology of non isolated singularities. In: New Developments in Singularity Theory, Cambridge 2000, pp. 447–472. Kluwer, Dordrecht (2001)
Verdier, J.-L.: Stratifications de Whitney et théorème de Bertini-Sard. Invent. Math. 36, 295–312 (1976)
Verdier, J.-L.: Spécialisation des classes de Chern. Astérisque 82–83, pp. 149–159. Société mathématique de France, Marseille (1981)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 Springer Nature Switzerland AG
About this paper
Cite this paper
Aguilar, M., Menegon, A., Seade, J. (2021). On the Boundary of the Milnor Fiber. In: Fernández de Bobadilla, J., László, T., Stipsicz, A. (eds) Singularities and Their Interaction with Geometry and Low Dimensional Topology . Trends in Mathematics. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-61958-9_14
Download citation
DOI: https://doi.org/10.1007/978-3-030-61958-9_14
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-61957-2
Online ISBN: 978-3-030-61958-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)





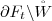 is diffeomorphic to
is diffeomorphic to
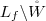 , where
, where
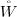 is the interior.
is the interior.