Topological Index Analysis and Its Application to Multi-Physical Systems in System Simulation Software

Abstract

This work is devoted to the topological analysis of multi-physical networks stemming from automated modeling processes in system simulation software. A special focus is on the methodical treatment of multi-physical networks, which can be utilized to develop robust and user-friendly simulation tools. In the multi-physical case, the already available topological criteria of different physics have to be merged and reinterpreted. A general receipt for their analysis is described in terms of a representative example, a fluid-solid network which is thermally coupled. The theoretical results are put in context to a practical realization in a simulation software in terms of modeling and coupling concepts, which help to improve the useability of system simulation software for software application engineers.

1 Introduction and Industrial Background

The importance of system simulation in automotive industry has grown significantly during the past two decades and will grow further. Reasons are the improved power of computer systems and the applied software but also the increasing complexity of multi-physical systems to be modeled. Typical investigation topics related for instance to a hybrid vehicle incorporate mechanical, electrical, fluid dynamical and even chemical domains within one system. Therefore both, the simulation of each separated domain, but also of overall models combining a subset or even all domains is of importance. As a consequence the applied software needs to be based on robust algorithms, which itself requires a structured mathematical and computer scientific basis framework. Based on this framework the according modeling equations and their implementation are build up on.

In this work we consider the analysis of multi-physical dynamical systems stemming from automated modeling processes in system simulation software. In this context, the term multi-physical is used to describe models which are a combination of different physical characteristic equations. For example for fluid and gas flows, those are Navier-Stokes or Euler equations, in electric those are Maxwell’s equations, in translation or rotational mechanics those are Newton’s laws of motion and for solid masses those are heat equations. The different equations are coupled by applying conservation laws on various levels. In system simulation the detailed analysis of the interaction between vehicle dynamics, transient combustion or electric engine performance and the corresponding thermal management systems is of special interest in order to calculate the complete energy and temperature distribution across the entire vehicle. In this work this kind of coupling is referred to as thermal coupling.

Today’s system modeling software typically offers a wide range of basic physical components from several domains (e.g. fluid flow, electric networks, gas flow, heat flow), which can be assembled to customized physical networks simply by drag and drop. The governing equations are derived by representing the network as a linear graph whose edges and nodes correspond to the basic physical components (e.g. pipes, pumps, heat exchangers). Combining the connection structure of the graph with the physical equations of the components, the physical network is modeled as a differential algebraic equation (DAE). Typically those DAEs are of higher index. Hence in order to allow a stable numerical integration, the DAEs need to be reformulated to an index reduced (differential-index (d-index) 1 or strangeness-index (s-index) 0), representation, cf. [15]. Using algebraic graph and DAE theory, the solvability of the mathematical model as well as its index can be analyzed and translated as conditions on the network structure and properties of its elements. Hence topology based index analysis emerges as a suitable tool for the investigation of DAEs stemming from automatic generated system models in system simulations tools, since it combines the scientific disciplines of Analysis for DAEs [8] and Graph Theory [10]. Due to the seamless integration of the network structure in the simulation process, properties of the DAE can be directly reinterpreted on the network structure, allowing for an illustrative modeling paradigm. So far this methodology has been successfully used in various physical domains, including electric circuits [17], gas networks [13] and fluid networks [4,5,6]. The developed methodology focuses on the analysis of one specific physics. The challenges in the development of future topology based methods, do not lie in the analysis of the individual physical networks (electric, gas or fluid networks), but in the assessment of the multi-physical network as a whole (see e.g. [2]). Coupling different physics may lead to a change in the topological criteria of the individual subsystems.

The vice verse question arises, if an automated assembled multi-physical model has to be partitioned into several submodels. This use case is of importance if multi-rate methods (see e.g. [3]) are applied to speed up numerical integration by taking advantage of different time constants of the individual physics. It is not straightforward to decompose a d-index 1 DAE into several DAEs of d-index 1 and guarantee existence and uniqueness of solutions at the same time. In terms of usability the decomposition has to conserve the model structure and consequently the solution. Especially in the constellation of automated generated DAEs the derivation of topological criteria for an appropriate decomposition seems to be promising. Since those decompositions typically cross multi-physical boarders, the topological criteria have to be multi-physical as well.

The structure of the work is the following. In Sect. 2 we formulate a multi-physical network model consisting of a fluid network and a solid network. Section 3 is devoted to the development of an automated partitioning algorithm of the coupled system. For this purpose the global network is divided into its individual physical parts, i.e. into a solid, cf. Sect. 3.1, and a fluid part, cf. Sect. 3.2. For each individual domain the corresponding DAE is stated in input-output form by introducing valid coupling variables (inputs and outputs). For both solvability and index results are provided. In Sect. 3.3 valid coupling conditions are formulated and the coupled system is analyzed with respect to solvability and index constraints. Sections 4 and 5 describe the possible application of the developed theory in commercial system simulation software. While Sect. 4 is devoted to the design of the simulation software in terms of the topological representation of a physical model and the transient solution of the model, Sect. 5 focuses on solver design in terms of transient multi-rate calculations. Section 6 provides an overview of the addressed issues. Therein another major focus is put on the description of open topics and further research requirements.

2 A Multi-Physical Model for Fluid Networks Coupled to Solid Networks

As an example we consider a simple thermal network model, which is an extension of the network model analyzed in [5]. After formulating the full coupled model, consisting of a fluid network and a solid network, we demonstrate, that the combined model obtains a domain specific topological criteria.

We consider a multi-physical network $\mathcal {N}$

$$\displaystyle \begin{aligned} \mathcal{N} = \left \lbrace Pi, Pu, De, Vj, Lj, Re, Ht, Hs, Sw, Lw, Tb \right \rbrace, \end{aligned} $$

(1)

that is composed of pipes Pi, pumps Pu, demands De, volume junctions V j, lumped junctions Lj and reservoirs Re, which are filled with an incompressible fluid and heat transfers Ht, heat sources Hs, solid walls Sw, lumped walls Lw and temperature boundaries Tb. The network is represented by a directed linear graph $\mathcal {G} = \{\mathcal {V}, \mathcal {E}\}$, where the set of vertices $\mathcal {V}$ and edges $\mathcal {E}$ are defined as

$$\displaystyle \begin{aligned} \mathcal{V} &= \left \lbrace Vj, Lj, Re, Sw, Lw, Tb \right \rbrace, \\ \mathcal{E} &= \left \lbrace Pi, Pu, De, Ht, Hs \right \rbrace. \end{aligned}$$

The network $\mathcal {N}$ is assumed to satisfy the following assumptions on its connection structure.

Assumption 1 (Network Assumption)

Let $\mathcal {N}$ be a network as defined in (1).

• 1. The network is connected.

• 2. Two junctions are connected at most by one pipe or one pump.

• 3. Each pipe, pump and demand has an assigned direction.

• 4. Every junction is adjacent to at most one demand branch or heat source.

• 5. Every reservoir is connected at most to one pipe or pump.

• 6. Two walls are connected at most by one heat transfers.

• 7. Each heat transfer and heat source has an assigned direction.

• 8. Every wall is adjacent to at most one heat source.

• 9. Every temperature boundary is adjacent to at most one heat transfer.

• 10. A pair of a wall and a junction is connected at most by one heat transfer.

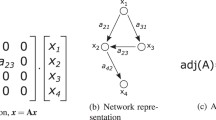
Assumption 1 guarantees, that the network graph $\mathcal G$ is simple, oriented and connected. An example for $\mathcal {N}$ is displayed in Fig. 1.

Fig. 1

Example of a graph $\mathcal {G}$ of a multi-physical network $\mathcal {N}$

The connection structure of the network $\mathcal N$ is described by the incidence matrix $A_{\mathcal N} = (a_{ij})$, which is defined as, cp. e.g. [7, 10, 16],

$$\displaystyle \begin{aligned} a_{ij} = \begin{cases} 1, & \text{if the edge }j\text{ leaves the vertex }i,\\ -1, & \text{if the edge }j\text{ enters the vertex }i,\\ 0, & \text{else}. \end{cases} \end{aligned}$$

This incidence matrix can be further partitioned into blocks considering its involved types of edges $E\in \mathcal {E}$ as well its involved types of vertices $V\in \mathcal {V}$. The corresponding incidence matrices are given by $A_{V,E}\in \{-1,0,1\}^{n_V\times n_E}$, where n _V and n _E denote the number of elements of the relevant type. Using Assumption 1 and sorting the rows and columns of $A_{\mathcal N}$ according to the different element types, the incidence matrix can be representation in the following form:

$$\displaystyle \begin{aligned} A_{\mathcal{N}} = \begin{bmatrix} A_{Vj,Pi} & A_{Vj,Pu} & A_{Vj,De} & A_{Vj,Ht} & A_{Vj,Hs} \\ A_{Lj,Pi} & A_{Lj,Pu} & A_{Lj,De} & A_{Lj,Ht} & A_{Lj,Hs} \\ A_{Re,Pi} & A_{Re,Pu} & 0 & 0 & 0 \\ 0 & 0 & 0 & A_{Sw,Ht} & A_{Sw,Hs} \\ 0 & 0 & 0 & A_{Lw,Ht} & A_{Lw,Hs} \\ 0 & 0 & 0 & A_{Tb,Ht} & 0 \end{bmatrix}. \end{aligned} $$

(2)

Beside the connection structure, each network element is equipped with a characteristic equation, cf. [5, 6], describing the mass flow q _E and/or the enthalpy flow H _E on edge elements $E \in \mathcal {E}$ and the pressure p _V and/or the temperature T _V on vertex elements $V \in \mathcal {V}$. Applying mass and energy conservation laws, the dynamic of the coupled multi-physical network $\mathcal {N}$ is described by the DAE: Find $(q_{Pi}^T, q_{Pu}^T, p_{Vj}^T, p_{Lj}^T, H_{Pi}^T, H_{Pu}^T, T_{Vj}^T, T_{Lj}^T, H_{Ht}^T, T_{Sw}^T, T_{Lw}^T)^T$, such that

$$\displaystyle \begin{aligned} \frac{d q_{Pi}}{dt} &= c_{1,Pi} \left(A_{Vj,Pi}^T p_{Vj} + A_{Lj,Pi}^T p_{Lj} + A_{Re,Pi}^T p_{Re}\right) \\ & \qquad + c_{2,Pi} \text{diag}\left(|q_{Pi}|\right)q_{Pi} + c_{3,Pi} \\ f_{Pu}(q_{Pu}) &= A_{Vj,Pu}^T p_{Vj} + A_{Lj,Pu}^T p_{Lj} + A_{Re,Pu}^T p_{Re} \\ 0 &= A_{Vj,Pi} q_{Pi} + A_{Vj,Pu} q_{Pu} + A_{Vj,De} q_{De} \\ 0 &= A_{Lj,Pi} q_{Pi} + A_{Lj,Pu} q_{Pu} + A_{Lj,De} q_{De} \\ m_{Vj} c_{p, Vj}\frac{d T_{Vj}}{d t} &= A_{Vj,Pi} H_{Pi} + A_{Vj,Pu} H_{Pu} + A_{Vj,De} H_{De} \\ & \qquad + A_{Vj,Ht} H_{Ht} + A_{Vj,Hs} H_{Hs}\\ 0 &= A_{Lj,Pi} H_{Pi} + A_{Lj,Pu} H_{Pu} + A_{Lj,De} H_{De} \\ & \qquad + A_{Lj,Ht} H_{Ht} + A_{Lj,Hs} H_{Hs}\\ H_{Pi} &= B_{Vj}(q_{Pi}) T_{Vj} + B_{Lj}(q_{Pi}) T_{Lj} + B_{Re}(q_{Pi}) T_{Re} \\ H_{Pu} &= B_{Vj}(q_{Pu}) T_{Vj} + B_{Lj}(q_{Pu}) T_{Lj} + B_{Re}(q_{Pu}) T_{Re} \\ m_{Sw} c_{p,Sw} \frac{d T_{Sw}}{d t} &= A_{Sw,Ht} H_{Ht} + A_{Sw,Hs} H_{Hs} \\ 0 &= A_{Lw,Ht} H_{Ht} + A_{Lw,Hs} H_{Hs}\\ H_{Ht} &= c_{Ht} \big(A_{Sw,Ht}^T T_{Sw} + A_{Lw,Ht}^T T_{Lw} \\ & \qquad + A_{Vj,Ht}^T T_{Vj} + A_{Lj,Ht}^T T_{Lj} + A_{Tb,Ht}^T T_{Tb} \big) \\ \end{aligned} $$

(3)

for given boundary conditions $q_{De} = \bar {q}_{De}$, $H_{De} = \bar {H}_{De}$, $H_{Hs} = \bar {H}_{Hs}$ $p_{Re} = \bar {p}_{Re}$, $h_{Re} = \bar {h}_{Re}$, $T_{Tb} = \bar {T}_{Tb}$, positive definite diagonal coefficient matrices c _1,Pi, c _2,Pi, c _3,Pi, c _p,Vj, c _p,Sw, c _Ht, positive definite diagonal mass matrices m _Vj, m _Sw, the pump characteristic f _Pu and the enthalpy function B _⋆ (⋆ ∈{V j, Lj, Re}) as defined in [6].

Under the additional Assumption 2 (cf. [6]), the unique solvability of the DAE (3) can be characterized in Theorem 1.

Assumption 2 (Network Solvability)

Let $\mathcal {N}$ be a network as defined in (1).

• $\mathcal {N}$ contains no cycles of pumps.

• $\mathcal {N}$ contains no paths of pumps between two reservoirs.

• For each junction, the mass flow does not vanish, i.e. $\sum |q_i| > 0$ for all q _i adjacent to the junction.

Theorem 1

Let $\mathcal {N}$ be a network given by (1), meeting the requirements of Assumptions 1 and 2 with positive definite coefficient matrices m _Sw , c _p,Sw and $c_{Ht_S}$ . Let n _Re > 0, where n _Re denotes the number of reservoirs Re in the network. Then, the following statements hold.

• 1. The DAE (3) is regular and has strangeness index μ = 1 (d-index 2).

• 2. The DAE (3) is uniquely solvable for every feasible initial condition condition fulfilling (3) at t = t ₀ and the solution is continuous differentiable.

Proof

In [6] it is shown, that a network consisting only of fluid elements $\mathcal N_F = \left \lbrace Vj, Lj, Re, Pi, Pu, De \right \rbrace$ yields a uniquely solvable system of DAEs with strangeness index 1. Theorem 2 requires a fixed temperature in order to obtain existence and uniqueness of the solution. Since the fixed temperature is provided by the condition n _Re > 0 in the network $\mathcal {N}$, the unique solvability follows for the DAE (3). In [6], it is shown that the mass flow related part q _E ($E\in \mathcal {E}$) and p _V ($V\in \mathcal {V}$) causes the strangeness index 1 condition, while under Assumption 2, the energy flow related part H _E ($E\in \mathcal {E}$), and T _V ($V\in \mathcal {V}$) obtains a strangeness index 0 condition. Since the extension to the thermal elements $\mathcal N_S = \left \lbrace Sw, Lw, Tb, Ht, Hs \right \rbrace$ only effects the energy part due to Assumption 1, and the thermal elements obtain analogous strangeness index 0 conditions (cf. Theorem 2), the proof of [6] can be easily extended to the network $\mathcal {N}$. Hence, the result follows as a natural extension from [6] with the results obtained in the proof of Theorem 2. □

Theorem 1 guarantees existence and uniqueness of solutions for the coupled multi-physical system. Following [6] an index reduced surrogate model can be deduced, which has strangeness index μ = 0 (d-index 1). The surrogate model can be assembled based on the network information only without the need for further algebraic manipulations. Due to strangeness index μ = 0 the surrogate model is suited to be solved with a standard time integration scheme. Having a look at the multi-physical characteristic of the problem it is notable, that the topological criteria only depends on elements in the fluid network $\mathcal {N}_F$ and not on elements of $\mathcal {N}_{S}$. Indeed the original cause of this criteria and its effects on further manipulations in multi-physical context is investigated in the next section.

3 Topology Based Automatic Decomposition of Multi-Physical Networks

In this section the coupled model is decomposed into submodels according to their physical nature. The subsystems are stated in an input-output form, which structure is motivated by standardized approaches like [1, 14] or their software representation in form of a Functional Mock-up Unit [11]. For this purpose, the coupling variables u for the input to the system and y for the output of the system are introduced to enable the exchange of information between the domains. We demonstrate, that the choice of the decomposition has an effect on the solvability of the individual subsystems. Restoring the unique solvability of the individual domains is critical, if individual solvers (standard time integration schemes) are applied, e.g., in a multi-rate or co-simulation procedure, see, e.g., [2, 3]. Furthermore feasible coupling conditions emerge from the analysis as topological criteria based on the input-output structure. Using the derived coupling conditions, a system of coupled DAEs can be stated, which obtains the same solution as the original DAE (3).

3.1 A Solid Network

We consider a solid network

$$\displaystyle \begin{aligned} \mathcal{N}_S = \left \lbrace Ht_S, Hs, Sw, Lw, Tb, \overline{Hs}_S, \overline{Tb}_S \right \rbrace, \end{aligned} $$

(4)

that is composed of heat transfers Ht _S, heat sources Hs, solid walls Sw, lumped walls Lw, temperature boundaries Tb _S, heat source inputs $\overline {Hs}_S$ and temperature boundary inputs $\overline {Tb}_S$. The input elements $\overline {Hs}_S$ and $\overline {Tb}_S$ are introduced to enable generic couplings between different physical domains. Their corresponding variables are denoted by $u_{\overline {Hs}_S}$ and $u_{\overline {Tb}_S}$ and serve as inputs from other domains. Furthermore output variables are introduced where each variable corresponds to an input variable. Temperatures of solid walls y _Sw and lumped walls y _Lw as well as heat transfer elements $y_{Ht_S}$ are exposed and provide their information for other domains. The selection of the possible coupling outputs is shown in Eqs. (5d)–(5f). The basic network assumptions of Assumption 1 carry over to the solid network $\mathcal {N}_S$ as well. The connectivity of the in- and outputs within the thermal network is described with the corresponding incidence matrices, denoted by $A_{Sw,\overline {Hs}_S}, A_{Lw,\overline {Hs}_S}$ and $A_{\overline {Tb}_S,Ht_S}$, which are natural extensions of the incidence matrix (2).

The DAE for the network $\mathcal {N}_S$ in input-output form is given by: For given continuous inputs $(u_{\overline {Hs}_S}^T,u_{\overline {Tb}_S}^T)^T$, find the temperatures $(T_{Sw}^T, T_{Lw}^T)^T$, the heat fluxes $(H_{Ht_S}^T)^T$ and the outputs $(y_{Sw}^T, y_{Lw}^T, y_{Ht_S}^T)^T$, such that

$$\displaystyle \begin{aligned} m_{Sw} c_{p,Sw} \frac{d T_{Sw}}{d t} &= A_{Sw,Ht_S} H_{Ht_S} + A_{Sw,Hs} H_{Hs} + A_{Sw,\overline{Hs}_S}u_{\overline{Hs}_S} {} \end{aligned} $$

(5a)

$$\displaystyle \begin{aligned} 0 &= A_{Lw,Ht_S} H_{Ht_S} + A_{Lw,Hs} H_{Hs} + A_{Lw,\overline{Hs}_S}u_{\overline{Hs}_S} {} \end{aligned} $$

(5b)

$$\displaystyle \begin{aligned} H_{Ht_S} &= c_{Ht_S} \big(A_{Sw,Ht_S}^T T_{Sw} + A_{Lw,Ht_S}^T T_{Lw} \\ &\qquad + A_{Tb,Ht_S}^T T_{Tb} + A_{\overline{Tb}_S,Ht_S}^Tu_{\overline{Tb}_S}\big) {} \end{aligned} $$

(5c)

$$\displaystyle \begin{aligned} y_{Sw} &= |(A_{Sw,\overline{Hs}_S}^T + A_{\overline{Tb}_S,Ht_S} A_{Sw,Ht_S}^T)| T_{Sw} {} \end{aligned} $$

(5d)

$$\displaystyle \begin{aligned} y_{Lw} &= |(A_{Lw,\overline{Hs}_S}^T + A_{\overline{Tb}_S,Ht_S} A_{Lw,Ht_S}^T)| T_{Lw} {} \end{aligned} $$

(5e)

$$\displaystyle \begin{aligned} y_{Ht_S} &= A_{\overline{Tb}_S,Ht_S} H_{Ht_S} {}, \end{aligned} $$

(5f)

for given boundary conditions $H_{Hs} = \bar {H}_{Hs}$ and $T_{Tb} = \bar {T}_{Tb}$ and given diagonal positive definite coefficient matrices m _Sw, c _p,Sw and $c_{Ht_S}$. For practical reasons, the sign of the outputs is controlled via the absolute value of a matrix B = (b _ij), defined via |B| := (|b _ij|). The unique solvability of the network DAE (5) can be characterized via the graph and the input network characteristic.

Theorem 2

Let $\mathcal {N}_{S}$ be a network given by (4) fulfilling Assumption 1 with positive definite coefficient matrices m _Sw , c _p,Sw and $c_{Ht_S}$ . Let $n_{Sw} + n_{Tb} + n_{\overline {Tb}_S} > 0$ , where n _Sw denotes the number of solid walls Sw, n _Tb denotes the number of temperature boundaries Tb, and $n_{\overline {Tb}_S}$ denotes the number of temperature boundary inputs $\overline {Tb}_S$ . Then, the following statements hold:

• 1. The DAE (5) is regular and has strangeness index μ = 0 (d-index 1).

• 2. The DAE (5) is uniquely solvable for every feasible initial condition fulfilling (5) at t = t ₀ and the solution is continuous differentiable.

• 3. The outputs y _Sw and y _Lw are continuous differentiable.

Proof

• 1. To show regularity and strangeness index μ = 0, it is sufficient to transform the DAE (5) to its explicit form. This concerns just the lumped wall characteristic (5b), since all other equations are already given in their explicit representation. First we substitute $H_{Ht_S}$ in the lumped wall equation (5b) by the right hand side of the heat transfer characteristic (5c). The equation reads as

  $$\displaystyle \begin{aligned} 0&= A_{Lw,Ht_S}c_{Ht_S}A^T_{Lw,Ht_S}T_{Lw}+c_{Ht_S} \big(A_{Sw,Ht_S}^T T_{Sw} + A_{Tb,Ht_S}^T T_{Tb} \\ &\qquad + A_{\overline{Tb}_S,Ht_S}^Tu_{\overline{Tb}_S}\big) + A_{Lw,Hs} H_{Hs} + A_{Lw,\overline{Hs}_S}u_{\overline{Hs}_S}. \end{aligned} $$

  This system needs to be solved according to T _Lw, which results in the solvability condition that $A_{Lw,Ht_S} c_{Ht_S} A_{Lw,Ht_S}^T$ needs to be regular. Due to the assumption that $c_{Ht_S}$ is positive definite, it is possible to apply a Cholesky decomposition $c_{Ht_S}=G G^T$ with a regular matrix G. Hence,

  $$\displaystyle \begin{aligned} A_{Lw,Ht_S} c_{Ht_S} A_{Lw,Ht_S}^T = (A_{Lw,Ht_S} G) (A_{Lw,Ht_S} G)^T. \end{aligned}$$

  According to the assumption $n_{Sw} + n_{Tb} + n_{\overline {Tb}_S} > 0$, $A_{Lw,Ht_S}$ is a reduced incidence matrix, cf. [9, p. 141], implying $\operatorname {\mathrm {rank}}(A_{Lw,Ht_S})=n_{Lw}$. Combining the results yields

  $$\displaystyle \begin{aligned} \operatorname{\mathrm{rank}}(A_{Lw,Ht_S} c_{Ht_S} A_{Lw,Ht_S}^T)=\operatorname{\mathrm{rank}}(A_{Lw,Ht_S} G)=\operatorname{\mathrm{rank}}(A_{Lw,Ht_S})=n_{Lw}. \end{aligned}$$

• 2. Since the DAE (5) has been transformed to an explicit formulation, the uniqueness and solvability is covered by the theory of ordinary differential equations, i.e. the Picard-Lindelöf theorem.

• 3. Since y _Sw and y _Lw are linear combinations of continuous differentiable functions, it holds that y _Sw and y _Lw are continuous differentiable as well.

□

Theorem 2 has the consequence, that the topological conditions in order to guarantee existence and uniqueness of a solution for the solid subsystem (5) does not only depend on the actual network structure $\mathcal {N}_S$, but also on the chosen partition via the exposed variables $(u_{\overline {Hs}_S}^T, u_{\overline {Tb}_S}^T)^T$ and $(y_{Sw}^T, y_{Lw}^T, y_{Ht_S}^T)^T$. Indeed, the unique solvability can either be controlled via the coupling variable $u_{\overline {Tb}_S}$, (i.e. $n_{\overline {Tb}_S} > 0$) or via the network configuration n _Sw + n _Tb > 0. In the following this specific restriction of the coupling variables has to be considered for a proper model partitioning.

3.2 A Fluid Network

We consider a fluid network

$$\displaystyle \begin{aligned} \mathcal{N}_F = \left \lbrace Pi, Pu, De, Vj, Lj, Re, Ht_F, \overline{Hs}_F, \overline{Tb}_F \right \rbrace \end{aligned} $$

(6)

that is composed of pipes Pi, pumps Pu, demands De, volume junctions V j, lumped junctions Lj, reservoirs Re, heat transfers Ht _F, heat source inputs $\overline {Hs}_F$ and temperature boundary inputs $\overline {Tb}_F$. As in the solid network special input elements $\overline {Hs}_F$ and $\overline {Tb}_F$ are introduced with their corresponding variables $u_{\overline {Hs}_F}$ and $u_{\overline {Tb}_F}$. In addition the output variables of solid walls, lumped walls and heat transfer elements are given by y _Sw, y _Lw and $y_{Ht_F}$. The basic network assumptions of Assumption 1 carry over to the fluid network $\mathcal {N}_F$ as well. The connectivity in the network is described with the corresponding incidence matrices, denoted by $A_{Vj,\overline {Hs}_F}, A_{Lj,\overline {Hs}_F}$ and $A_{\overline {Tb}_F,Ht_F}$, which are formulated equivalently to the solid network as a natural extension of the incidence matrix (2).

For given continuous inputs $(u_{\overline {Hs}_F}^T,u_{\overline {Tb}_F}^T)^T$, find the pressures $(p_{Lj}^T, p_{Vj}^T)^T$ the mass flows $(q_{Pi}^T, q_{Pu}^T)^T$, the heat fluxes $(H_{Ht_F}^T, H_{Pu}^T, H_{Pi}^T)^T$, the temperatures $(T_{Vj}^T, T_{Lj}^T)^T$ and the outputs $(y_{Vj}^T, y_{Lj}^T, y_{Ht_F}^T)^T$, such that

$$\displaystyle \begin{aligned} \frac{d q_{Pi}}{dt} &= c_{1,Pi} \left(A_{Jc,Pi}^T p_{Jc} + A_{Re,Pi}^T p_{Re}\right) \\ & \qquad + c_{2,Pi} \text{diag}\left(|q_{Pi}|\right)q_{Pi} + c_{3,Pi} \\ f_{Pu}(q_{Pu}) &= A_{Jc,Pu}^T p_{Jc} + A_{Re,Pu}^T p_{Re} \\ 0 &= A_{Jc,Pi} q_{Pi} + A_{Jc,Pu} q_{Pu} + A_{Jc,De} q_{De} \\ m_{Vj} c_{p, Vj}\frac{d T_{Vj}}{d t} &= A_{Vj,Pi} H_{Pi} + A_{Vj,Pu} H_{Pu} + A_{Vj,De} H_{De} \\ & \qquad + A_{Vj,Ht_F} H_{Ht_F} + A_{Vj,\overline{Hs}_F} u_{\overline{Hs}_F}\\ 0 &= A_{Lj,Pi} H_{Pi} + A_{Lj,Pu} H_{Pu} + A_{Lj,De} H_{De} \\ & \qquad + A_{Lj,Ht_F} H_{Ht_F} + A_{Lj,\overline{Hs}_F} u_{\overline{Hs}_F}\\ H_{Pi} &= B_{Jc}(q_{Pi}) T_{Vj} + B_{Jc}(q_{Pi}) T_{Lj} + B_{Jc}(q_{Pi}) T_{Re}\\ H_{Pu} &= B_{Jc}(q_{Pu}) T_{Vj} + B_{Jc}(q_{Pu}) T_{Lj} + B_{Jc}(q_{Pu}) T_{Re}\\ H_{Ht_F} &= c_{Ht_F} \big( A_{Vj,Ht_F}^T T_{Vj} + A_{Lj,Ht_F}^T T_{Lj} + A_{\overline{Tb}_F,Ht_F}^Tu_{\overline{Tb}_F}\big) \\ y_{Vj} &= |(A_{Vj,\overline{Hs}_F}^T + A_{\overline{Tb}_F,Ht_F}A_{Vj,Ht_F}^T)| T_{Vj} \\ y_{Lj} &= |(A_{Lj,\overline{Hs}_F}^T + A_{\overline{Tb}_F,Ht_F}A_{Lj,Ht_F}^T)| T_{Lj} \\ y_{Ht_F} &= A_{\overline{Tb}_F,Ht_F} H_{Ht_F} \end{aligned} $$

(7)

for given boundary conditions $q_{De} = \bar {q}_{De}$, $H_{De} = \bar {H}_{De}$ $p_{Re} = \bar {p}_{Re}$ and $T_{Re} = \bar {T}_{Re}$. Following [5], the solvability of the network DAE (7) can be characterized via the graph structure.

Theorem 3

Let $\mathcal {N}_{F}$ be a network given by (6) which fulfills Assumptions 1 and 2 . Let n _Re > 0. Then, the following statements hold:

• 1. The DAE (7) is regular and has strangeness index μ = 1 (d-index 2).

• 2. The DAE (7) is uniquely solvable for every feasible initial condition fulfilling (7) at t = t ₀ and the solution is continuous differentiable.

• 3. The outputs y _{V j} and y _Lj are continuous differentiable.

Proof

See [5]. □

Theorem 3 shows, that in the fluid network, the choice of the partition with respect to the exposed variables $(u_{\overline {Hs}_F}^T,u_{\overline {Tb}_F}^T)^T$ and $(y_{Vj}^T, y_{Lj}^T, y_{Ht_F}^T)^T$ does not enter the solvability or index condition. This has the consequence, that regarding unique solvability, the coupling conditions can be chosen arbitrary within the specified input and output relations. Furthermore the condition n _Re > 0 is not only crucial for the coupled problem (cf. Theorem 1), but already for the fluid problem. In the following this additional degree of freedom in the coupling variables is utilized for a proper model partitioning.

3.3 The Coupled Network

We consider a coupled network $\mathcal {N}_C$

$$\displaystyle \begin{aligned} \mathcal{N}_C = \left \lbrace \mathcal{N}_F, \mathcal{N}_S \right \rbrace, \end{aligned} $$

(8)

consisting of a single fluid network $\mathcal {N}_F$ and a single solid network $\mathcal {N}_S$. In general Assumption 1 does not imply, that the subnetworks $\mathcal {N}_F$ and $\mathcal {N}_S$ are connected. In this work, we assume that both are connected, i.e., the network $\mathcal {N}_C$ consist of one non-empty connected subnetwork $\mathcal {N}_F$ and one non-empty connected subnetwork $\mathcal {N}_S$. Each element $\mathcal {N}_F$ and $\mathcal {N}_S$ exposes inports $( u_{\overline {Hs}_S}, u_{\overline {Tb}_S}, u_{\overline {Hs}_F}, u_{\overline {Tb}_F})$ and outports $( y_{Sw},y_{Lw}, y_{Ht_S}, y_{Vj}, y_{Lj}, y_{Ht_F})$ according to the definition in (5) and (7). The connection structure of $\mathcal {N}_C$ is assumed to satisfy the following assumptions.

Assumption 3 (Network Coupling Assumption)

Let $\mathcal {N}_C$ be a network as defined in (8).

• 1. Elements of type $\overline {Hs}_S$ are connected to elements of type Ht _F.

• 2. Elements of type $\overline {Hs}_F$ are connected to elements of type Ht _S.

• 3. Elements of type $\overline {Tb}_S$ are connected to elements of type V j or Lj.

• 4. Elements of type $\overline {Tb}_F$ are connected to elements of type Sw or Lw.

An example for $\mathcal {N}_C$ is displayed in Fig. 2. Using Assumption 3 and sorting the inports and outports with respect to their types, we obtain a matrix representation

(9)

Therefore the coupling of the networks is linear.

Fig. 2

Example of a graph of a coupled multi-physical network

Using (5) and (7) as well as the coupling condition (9), the coupled problem can be stated: Find the fluid states $(q_{Pi}^T, q_{Pu}^T, p_{Vj}^T, p_{Lj}^T, H_{Pi}^T, H_{Pu}^T, T_{Vj}^T, T_{Lj}^T, H_{Ht_F}^T)$, the solid states $(H_{Ht_S}^T, T_{Sw}^T, T_{Lw}^T)^T$, the inputs $(u_{\overline {Hs}_S}^T, u_{\overline {Tb}_S}^T, u_{\overline {Hs}_F}^T, u_{\overline {Tb}_F}^T)^T$, and the outputs $(y_{Sw}^T, y_{Lw}^T, y_{Ht_S}^T, y_{Vj}^T, y_{Lj}^T, y_{Ht_F}^T)^T$,such that

$$\displaystyle \begin{aligned} \frac{d q_{Pi}}{dt} &= c_{1,Pi} \left(A_{Jc,Pi}^T p_{Jc} + A_{Re,Pi}^T p_{Re}\right) \\ & \qquad + c_{2,Pi} \text{diag}\left(|q_{Pi}|\right)q_{Pi} + c_{3,Pi} \\ f_{Pu}(q_{Pu}) &= A_{Jc,Pu}^T p_{Jc} + A_{Re,Pu}^T p_{Re} \\ 0 &= A_{Jc,Pi} q_{Pi} + A_{Jc,Pu} q_{Pu} + A_{Jc,De} q_{De} \\ m_{Vj} c_{p, Vj}\frac{d T_{Vj}}{d t} &= A_{Vj,Pi} H_{Pi} + A_{Vj,Pu} H_{Pu} + A_{Vj,De} H_{De} \\ & \qquad + A_{Vj,Ht_F} H_{Ht_F} + A_{Vj,\overline{Hs}_F} u_{\overline{Hs}_F}\\ 0 &= A_{Lj,Pi} H_{Pi} + A_{Lj,Pu} H_{Pu} + A_{Lj,De} H_{De} \\ & \qquad + A_{Lj,Ht_F} H_{Ht_F} + A_{Lj,\overline{Hs}_F} u_{\overline{Hs}_F}\\ H_{Pi} &= B_{Jc}(q_{Pi}) T_{Vj} + B_{Jc}(q_{Pi}) T_{Lj} + B_{Jc}(q_{Pi}) T_{Re}\\ H_{Pu} &= B_{Jc}(q_{Pu}) T_{Vj} + B_{Jc}(q_{Pu}) T_{Lj} + B_{Jc}(q_{Pu}) T_{Re}\\ H_{Ht_F} &= c_{Ht_F} \left( A_{Vj,Ht_F}^T T_{Vj} + A_{Lj,Ht_F}^T T_{Lj} + A_{\overline{Tb}_F,Ht_F}^Tu_{\overline{Tb}_F}\right) \\ y_{Vj} &= |(A_{Vj,\overline{Hs}_F}^T + A_{\overline{Tb}_F,Ht_F}A_{Vj,Ht_F}^T)| T_{Vj} \\ y_{Lj} &= |(A_{Lj,\overline{Hs}_F}^T + A_{\overline{Tb}_F,Ht_F}A_{Lj,Ht_F}^T)| T_{Lj} \\ y_{Ht_F} &= \big(A_{\overline{Tb}_F,Ht_F} + A_{Lj,\overline{Hs}_F}^T A_{Lj,Ht_F}^T \\ & \qquad + A_{Vj,\overline{Hs}_F}^T A_{Vj,Ht_F}^T\big) H_{Ht_F}\\ \end{aligned} $$

(10)

$$\displaystyle \begin{aligned} m_{Sw} c_{p,Sw} \frac{d T_{Sw}}{d t} &= A_{Sw,Ht_S} H_{Ht_S} + A_{Sw,Hs} H_{Hs} + A_{Sw,\overline{Hs}_S}u_{\overline{Hs}_S} \\ 0 &= A_{Lw,Ht_S} H_{Ht_S} + A_{Lw,Hs} H_{Hs} + A_{Lw,\overline{Hs}_S}u_{\overline{Hs}_S}\\ H_{Ht_S} &= c_{Ht_S} \big(A_{Sw,Ht_S}^T T_{Sw} + A_{Lw,Ht_S}^T T_{Lw} \\ & \qquad + A_{Tb,Ht_S}^T T_{Tb} + A_{\overline{Tb}_S,Ht_S}^Tu_{\overline{Tb}_S}\big) \\ y_{Sw} &= |(A_{Sw,\overline{Hs}_S}^T + A_{\overline{Tb}_S,Ht_S} A_{Sw,Ht_S}^T)| T_{Sw} \\ y_{Lw} &= |(A_{Lw,\overline{Hs}_S}^T + A_{\overline{Tb}_S,Ht_S} A_{Lw,Ht_S}^T)| T_{Lw} \\ y_{Ht_S} &= A_{\overline{Tb}_S,Ht_S} H_{Ht_S} \\ u_{\overline{Hs}_F} &= C_{Hs_F,Ht_S} y_{Ht_S}\\ u_{\overline{Tb}_F} &= C_{Tb_F,Sw} y_{Sw} + C_{Tb_F,Lw} y_{Lw}\\ u_{\overline{Hs}_S} &= C_{Hs_S,Ht_F} y_{Ht_F}\\ u_{\overline{Tb}_S} &= C_{Tb_S,Vj} y_{Vj} + C_{Tb_S,Lj} y_{Lj} \end{aligned}$$

for given boundary and initial conditions.

The main result summarizes, that not only the fully coupled problem (10) is uniquely solvable, but also the decomposed problems are unique solvable with respect to the chosen decomposition and the DAE index results are conserved for the decoupled problems.

Corollary 1

Let $\mathcal {N}_C$ be a network as given in (8) with $\mathcal {N}_F$ fulfilling Assumptions 1 and 2 as well as $\mathcal {N}_S$ satisfying Assumption 1 with positive definite coefficient matrices m _Sw , c _p,Sw and $c_{Ht_S}$ . Furthermore let n _Re > 0, $n_{\overline {Tb}_S} > 0$ and $\mathcal {N}_C$ meet the network coupling assumption, i.e. Assumption 3 . Then,

• 1. The coupled DAE (10) is regular and has strangeness index μ = 1 (d-index 2).

• 2. The coupled DAE (10) is uniquely solvable for feasible initial condition fulfilling (10) at t = t ₀ and the solution is continuous differentiable.

• 3. The coupled DAE (10) and the original DAE (3) have the same solution.

4 Application in the Software Design for Multi-Physical System Calculations

System simulation software is typically designed in a way, that the topological representation of a physical model is separated from the transient solution procedure of the model. Considering feasible network DAEs, existence and uniqueness results are already of importance in the topological representation of the model, in order to restrict the set of feasible network models to valid ones. In order to achieve this and limit the full degree of freedom it is convenient to introduce modeling paradigms. Modeling paradigms, determine how a real physical process can be built up in a network-technological way and therefore represent the topological criteria, that have been developed in Sect. 3. Consequently modeling paradigms are an additional extension of the basic network assumption in Assumption 1 and they support the topological representation in a way, that the setup of invalid model topologies is prevented in advance.

On the other hand, coupling paradigms indicate how an existing overall network can systematically be separated into its physical parts without changing the actual model and gaining additional results for the individual physical parts. Therefore coupling paradigms can be used for an automated decomposition of multi-physical networks. Furthermore, they guarantee a stable and robust simulation of the physical model. From a practical point of view it is desirable, that coupling paradigms don’t modify modeling paradigms.

In the following we state certain modeling paradigms and coupling paradigms.

4.1 Modeling Paradigms

In the following two different model paradigms are formulated. The specific choice of the modeling paradigm has a certain effect on the modeling restrictions in the topological representation of the physical model on the one hand and the complexity of the solution procedure on the other hand.

Modeling paradigm 1

If a heat transfer is adjacent to a wall and a junction, then the wall is a solid wall and the junction is a volume or a lumped junction.

Following Modeling paradigm 1, the mass of the solid wall is always taken into account in the solid network. This consideration has a direct consequence on the solvability of the subsystems. Thus in coupled solid systems there is always at least one solid wall, i.e. n _Sw > 0. The assumptions of Theorem 2 are fulfilled and therefore the solid subsystem is uniquely solvable. Since the fluid part only depends on the requirements of the overall network, no special solvability criteria need to be checked during partitioning. This approach guarantees always a valid decomposition for the solution procedure, without taking any coupling considerations into account.

Modeling paradigm 2

If a heat transfer is adjacent to a wall and a junction, then the wall is a lumped wall and the junction is a lumped or a volume junction.

Using Modeling paradigm 2 the existence of a mass is not guaranteed in the solid network. Hence additional constraints imposed on the network structure may arise. In this case, an according coupling is required in order to guarantee a stable decomposition.

4.2 Coupling Paradigms

In this part we state three different coupling paradigms and describe the consequence of their application to the resulting coupled problem.

Coupling paradigm 1

If a heat transfer is adjacent to a wall and a junction, then the heat transfer is considered in the solid network.

A partitioning according to Coupling paradigm 1 means that the solid system is fed by the fluid network by means of the temperature of the junction, i.e. $u_{\overline {Tb}_S}=(y_{Vj}^T, y_{Lj}^T)^T.$ On the other hand, the solid domain provides the heat flow of the heat transfer as input, i.e. $u_{\overline {Hs}_F}=y_{Ht_F}.$ This approach is beneficial regarding the solvability of the decomposed subsystems. As $n_{\overline {Tb}_S}>0$ for each coupled solid system, the assumptions of Corollary 1 are fulfilled. No further topological checks are necessary for the decomposed physical domains. The splitting of the global network given in Fig. 1 with respect to this partitioning strategy is shown in Fig. 3.

Fig. 3

Decoupled version of network $\mathcal N$ from Fig. 1 using coupling paradigm 1

Coupling paradigm 2

If a heat transfer is adjacent to a wall and a junction, then the heat transfer is considered in the fluid network.

In contrast, when dividing according to Coupling paradigm 2, the heat exchange between the two domains is taken into account in the fluid network. Unfortunately following this coupling paradigm the solid model might not be solvable on its own. An example is shown in Fig. 4 where no reference temperature is given in the solid part.

Fig. 4

Decoupled version of network $\mathcal N$ from Fig. 1 using coupling paradigm 2

Coupling paradigm 3

If a heat transfer is adjacent to a wall and a junction, then the heat transfer is considered in both networks.

Following the coupling strategy of Coupling paradigm 3 is special contrary to the first two possibilities. The heat transfer is solved in both domains, i.e. Ht _S = Ht _F, and the temperatures of the attached nodes are passed as outputs to the other domain, cf. Fig. 5. Although additional computational effort is necessary it might be beneficial. If we consider the networks as state transfer patterns, we can interpret the nodes as energy storage whereas the edges as energy flows. In the first two strategies, an energy transfer and an energy state between the circuits has to be handled. In order to allow energy-conserving simulations, the flows must be considered differently to storage. Thus, this approach could be preferred throughout.

Fig. 5

Decoupled version of network $\mathcal N$ from Fig. 1 using coupling paradigm 3

Summarized, the coupling paradigms have different effects on the solvability of the solid system. In addition to the basic solvability, attention must also be paid to their effects on the numerical stability and energy conservation in the overall system.

5 Application to Co-simulation in Multi-Physical System Calculations

Under specific conditions we obtain solvable partitions of equation systems which can clearly be assigned to a specific domain, fluid and solid. Due to their different physical significance and stiffness, these systems therefore require various integration schemes, in particular various step sizes. Since all domains have their predefined input and output variables, all physical subsystems can be parametrized with their own solver settings and form co-simulation components. A crucial point is now handling the interaction of all physical domains and their in- and outputs. First, there exists a broad variety of strategies for exchanging the data. In literature there is a fundamental distinction between event driven or asynchronous and synchronous communication, cf. [3, 12]. Furthermore, it has to be decided whether the overall system should be solved iteratively, i.e. implicit co-simulation, or whether each component should only be evaluated once per time step, i.e. explicit co-simulation. For both constellations, Gauss-Seidel-type or Jacobi-type approaches are possible. Regardless of which strategy is applied, an inter- or extrapolation of the coupling variables is necessary.

State-of-the-art modeling and simulation packages such as AVL CRUISE™M,¹ provide implemented software solutions for co-simulation following different goals. For instance AVL CRUISE™M is adapted to the needs of automotive system simulation based on physical networks.

As an example we consider a BEV (battery electric vehicle) with cooling system as given in Fig. 6. The central part of this model is an electrical network (in orange) responsible for the propulsion and is therefore coupled to a mechanical network (in green). On the other hand the electrical part is coupled to two fluid network, which act as cooling circuits. An oil circuit is used for cooling the electric machine and a water circuit is used for cooling the battery pack and the inverter. In total the model forms a multi-physical network with about 500 network elements. Due to the physical nature of the network elements, the full multi-physical network consists of multiple simply-connected networks of various types. There is one electric network, three mechanic networks, two fluid networks, fourteen gas networks and eight solid networks, which are coupled via thermal or mechanical coupling conditions. Additionally several control components communicate within the multi-physical network via databusses.

Fig. 6

Schematic representation of a BEV with cooling system

The results provided in Sect. 3 can be applied, for example, in the battery pack, cf. Fig. 7. Solid networks (in red) are coupled to a fluid network (in blue) via heat transfer connections. The fluid-solid networks comply with the assumptions of Assumption 1 and Modeling paradigm 1. The solvability of the solid networks is guaranteed and any coupling paradigm out of Coupling paradigm 1–3 can be chosen. In the case, that the fluid-solid network complies with Modeling paradigm 2, the solvability of the solid network can be achieved by choosing an appropriate coupling procedure, i.e. Coupling paradigm 1. Again the solvability of the solid network is guaranteed, since now $n_{\overline {Tb}_S} > 0$. The main result, that any valid network $\mathcal {N}$ can be partitioned into fluid and solid networks, where the solvability of the subnetworks is covered by the developed theory, is summarized in Corollary 2.

Fig. 7

Battery pack model of the BEV with cooling system from Fig. 6

Corollary 2 (Feasible Decomposition)

Let $\mathcal {N}$ be a network given by (1) fulfilling Assumption 1 . Let n _Re > 0, then there exists a decomposition $\lbrace \mathcal {N}_F, \mathcal {N}_s\rbrace$ and a coupling strategy as defined in (9), such that Corollary 1 is applicable.

Corollary 2 implies, that in any case the solvability is guaranteed for both, the coupled multi-physical network DAE and the partitioned solid and fluid network DAEs. No further restrictions on the topology or modifications of the topology for the global model are required. Since Corollary 1 provides the corresponding solvability results, either a single-rate solver can be applied to the coupled DAE or individual (implicit or explicit) time integration schemes can be applied to the solid and fluid DAEs in order to set up a multi-rate co-simulation.

This motivates the following procedure in order to establish feasible single-rate and multi-rate models:

In order to analyze the solvability of the entire model, the theory must be extended to couplings containing additionally electrical, mechanical and gas networks.

6 Conclusion and Outlook

Extending existing topology based methods to multi-physical networks seems to be a promising technique for the analysis of multi-physical systems stemming from automated generated DAEs from system simulation software. The main steps for the analysis of coupled problems have been described in terms of a fluid-solid coupled network. The selection of an appropriate coupling paradigm provides both the solvability of the coupled system and that of the subparts. Hence, both, single-rate and multi-rate approaches are well defined, if the entire network is solvable. Indeed, the thermal coupling of different physical networks is a crucial task in system simulation in order to calculate and optimize the energy distribution within an entire vehicle. Consequently the presented analysis for the fluid-solid coupling has to be extended to electric-solid, gas-solid and mechanic-solid couplings. While the gas-solid coupling is similar to the presented fluid-solid coupling in terms of coupling conditions, the electric-solid and mechanic-solid couplings are more challenging. In those constellations, the coupling is done via material properties (e.g. resistance, capacitance), where additional DAE index problems may arise. Tackling a complete thermal coupled multi-physical system model via topological methods requires further research.