Embedding Augmented Cubes into Grid Networks for Minimum Wirelength

Abstract

Deriving an effective VLSI layout for interconnected network is important, since it increases the cost-effectiveness of parallel architectures. Graph embedding is the key to solving the problems of parallel structure simulation and layout design of VLSI. Wirelength is a criterion measuring the quality for graph embedding. And it is extensively used for VLSI design. Owing to the limitation of the chip area, the total wirelength of embedded network becomes a key issue affecting the network-on-chip communication performance. $AQ_{n}$, the n-dimensional augmented cube, is an important interconnection network topology proposed for parallel computers. In this paper, we first study the minimum wirelength of embedding augmented cube into a linear array based on the maximum induced subgraph problem. Furthermore, we obtain the exact wirelength of embedding augmented cubes into grids and propose a linear embedding algorithm to prepare for further study of efficient layout areas.

1 Introduction

The tremendous engineering advances made in Very Large Scale Integration (VLSI) manufacturing technology has aroused great theoretical interest in VLSI circuit layout issues. Through the effective VLSI layout of the interconnection network, the cost-effectiveness of the parallel architecture can be improved. These efforts have focused on minimizing the layout area of the circuits on the chip. This is partly due to the fact that the layout, which consumes a large amount of chip area, is more expensive to manufacture, less reliable, and more difficult to test, than the VLSI layout which consumes less chip area [2].

In order to meet the requirements of scalability, energy consumption, size, clock asynchronization, reusability etc. in large-scale integrated circuits, the new design method Network-on-Chip (NoC) came into being, which is a new innovation compared to the original design patterns [25]. Grid is one of the most mainstream NoC interconnection structures. It is to connect components together in the form of a matrix. The topology of grid is simple, and it has good scalability and low power consumption. Many researchers early focused on the embedding of simple graphs into complex graphs. They studied the embedding of grids into exchanged crossed cube, crossed cubes, locally twisted cubes, faulty crossed cubes and twisted-cubes [9, 20, 21, 24]. Then, another kind of embedding is to study the embedding of complex graphs into simple graphs. They studied embedding hypercubes, locally twisted cubes, exchanged hypercube and 3-ary n-cubes into grids [1, 5, 6, 18, 19]. There is no research on the embedding of augmented cubes into grid networks. Thus, in this paper, we mainly study the embedding of augmented cubes into grids.

Then, we mainly introduce related work and the contribution of this paper in the following subsections.

1.1 Related Work

Augmented cube, an enhancement to the hypercube, proposed by Choudum and Sunitha [4], not only retains some excellent properties of hypercube but also contains some embedding properties that hypercube does not have. For example, n-dimensional augmented cube $AQ_{n}$ contains cycles of all lengths from 3 to $2^{n}$, but $Q_{n}$ contains only even cycles [14]. Since its introduction, $AQ_{n}$ has attracted the interest of many researchers because of its favorable properties. Hsu et al. studied the fault hamiltonicity and the fault hamiltonian connectivity of the augmented cubes [12]. Ma et al. mainly studied panconnectivity and edge-fault-tolerant pancyclicity of augmented cubes [14]. They also studied the super connectivity of augmented cubes [15]. Edge-independent spanning trees have important applications in networks. Thus, Wang et al. studied the edge-independent spanning trees in augmented cubes and proposed an $O(N\log {N})$ algorithm that constructs $2n-1$ edge-independent spanning trees in $AQ_{n}$ [22]. Mane et al. studied the construction of spanning trees in augmented cubes, and constructed $n-1$ edge-disjoint spanning trees of the augmented cubes [16]. With the development of optical networks, Li et al. studied the routing and wavelength assignment for the augmented cube communication pattern in a linear array wavelength division multiplexing optical network [13].

Graph embedding is the operation of mapping a guest graph into a host graph. Embedding the graph into a linear array is also called linear layout (or linear arrangement) problem. The minimum linear layout problem was first proposed by Harper in 1964 and proved to be NP-Complete [7]. The grid embedding is not only related to the ability of grid to simulate other structures, but also the layout of different structures on the chip. Owing to the limitation of the chip area, the total wirelength of the embedding network has become a key issue affecting the communication performance of the on-chip network. In [1], Bezrukov et al. obtained an approximate result of embedding the hypercube to the grid and lower bound estimate of the wirelength. Rajasingh et al. proposed a minimum wirelength for embedding hypercubes into grid networks [18]. In [19], Shalini et al. proposed a linear algorithm for embedding locally twisted cube into a grid network and obtained the minimum wirelength. In [5], Fan et al. studied embedding exchanged hypercube layout into a grid and obtained an exact formula of minimum wirelength. They also studied the exact wirelength for embedding 3-ary n-cubes into grids [6].

1.2 Contribution

The graph embedding problem is a very worthwhile topic in the field of parallel computing. Regarding the layout of the chip, most researchers let grid be the guest graph because of its simple structure, good scalability and easy to implement on the chip. Augmented cube is an enhancement to the hypercube by adding the complement edge, which makes it more complex than other variants of hypercube. To the best of our knowledge, there are no research results on embedding augmented cubes into grids. In this paper, we study the embedding of n-dimensional augmented cubes into grids with minimum wirelength. The major contributions of the paper are as follows:

• (1) By studying embedding $AQ_{n}$ into linear array $L_{N}$, where $N = 2^{n}$, the minimum wirelength of embedding can be obtained.

• (2) We first study embedding $AQ_{n}$ into grid $M(2^{\left\lfloor \frac{n}{2} \right\rfloor },2^{\left\lceil \frac{n}{2} \right\rceil })$ and calculate the exact wirelength. Then we propose a linear algorithm for the embedding.

• (3) We compare the embedding method mentioned in this paper with the random embedding through simulation experiments.

The rest of this paper is organized as follows: In Sect. 2, some preliminaries are described. In Sect. 3, the wirelength of embedding an augmented cube into a linear array is obtained. Then we study the minimum wirelength of embedding $AQ_{n}$ into a grid. Section 4 gives simulation and experimental results. The last part is the conclusion of this paper.

2 Preliminaries

In this section, we will introduce some definitions and notations used in this paper. Let $G = (V,E)$ be a graph, where V(G) and E(G) denote vertex set and edge set of graph G, respectively. Let (u, v) be an edge with end vertices u and v. And we call $u,\ v$ neighbors for each other. Given a simple graph G, if $V' \subseteq V$, the subgraph of G induced by the vertex subset $V'$ is denoted by $G[V']$.

Let $G = (V(G),E(G))$ and $H = (V(H),E(H))$ be two connected graphs. G is isomorphic to H (represented by $G \cong H$) if and only if there exists a bijection $\psi$ from V(G) to V(H), such that if $(u,v)\ \in E(G)$ then $(\psi (u),\ \psi (v))\ \in E(H)$. For a subset $S \subseteq V(G)$, let $T = \{x \in V(H)|there\ is\ y\in \ S,\ such\ that\ y=\psi (x) \}$. Then, we write $T = \psi (S)$ and $S= \psi ^{-1}(T)$.

For two connected graphs G and H, an embedding $\pi =(\psi ,P_{\psi })$ of G into H is defined as follows [11]:

• (i) $\psi$ is a bijective map from $V(G) \rightarrow V(H)$.

• (ii) $P_{\psi }$ is a one-to-one map from E(G) to $\{ P_{\psi }((u,v))\ :\ P_{\psi }((u,v))\ is\ a\ path\ in\ H between\ \psi (u)\ and\ \psi (v)\ for\ (u,v)\in E(G)\}$.

Definition 1

[17]. The congestion of an embedding $\pi$ of G into H is the maximum number of edges of the graph G that are embedded on any single edge of H. Then the congestion of an edge e in H is the number of paths in $\{P_{\psi }((u,v))\}_{(u,v)\in E(G)}$ such that e is in the path $P_{\psi }((u,v))$ and denoted by $EC_{\pi }(e)$. In the other words:

$$\begin{aligned} EC_{\pi }(e)=|\{(u,v) \in E(G) : e\in P_{\psi }((u,v))\}|. \end{aligned}$$

(1)

Thus, The edge congestion of an embedding $\pi$ of G into H is given by,

$$\begin{aligned} EC_{\pi }(G,H)=max\{EC_{\pi }(e)|e\in E(H)\}. \end{aligned}$$

(2)

$$\begin{aligned} EC(G,H)=min\{EC_{\pi }(G,H)| \pi \ is\ an\ embedding\ from\ G\ to\ H\}. \end{aligned}$$

(3)

Edge congestion is one of the important factors of embedding problem. The wirelength we mainly study in this paper is another important factor. And there is a significant relationship between edge congestion and wirelength.

Definition 2

[17]. The wirelength of an embedding $\pi$ of G into H is given by

$$\begin{aligned} WL_{\pi }(G,H)=\sum _{(u,v)\in G}d(\psi (u),\psi (v)), \end{aligned}$$

(4)

where $d(\psi (u),\psi (v))$ denotes the shortest length of the paths $P_{\psi }((u,v))$ in H.

Lemma 1

[17]. Under the embedding $\pi =(\psi ,P_{\psi })$, the graph H is divided into two subgraph $H_{1}$ and $H_{2}$ if one edge cut S is removed. Let $G_{1}=G[\psi ^{-1}(V(H_{1}))]$ and $G_{2}=G[\psi ^{-1}(V(H_{2}))]$. If S satisfies the following conditions:

• (i) For every edge $(a,b)\in E(G_{i})$, $i=1,2$, $P_{\psi }(a,b)$ has no edges in S.

• (ii) For every edge $(a, b)\in E(G)$ with $a\in V (G_{1})$ and $b\in V (G_{2})$, $P_{\psi }((a, b))$ has exactly one edge in S.

• (iii) $G_{1}$ or $G_{2}$ is a maximum subgraph.

Then $EC_{\pi }(S)$ is minimum and $EC_{\pi }(S) \le EC_{g}(S)$ for any other embedding g of G into H.

Since $EC_{\pi }(S)$ is minimum based on Lemma 1, and according to the definitions of edge congestion and wirelength, the relationship between edge congestion and wirelength is as below.

Lemma 2

[17]. Let $\pi :G\rightarrow H$ be an embedding, and $S_{1}, S_{2}, \ldots , S_{p}$ be p edge cuts of H such that $S_{i}\cap S_{j}=\varnothing ,i\ne j,1\le i,j\le p$. Then

$$\begin{aligned} WL_{\pi }(G,H)=\sum _{i=1}^{p}EC_{\pi }(S_{i}). \end{aligned}$$

(5)

Then, we would introduce the definition of augmented cube in the following. Let $AQ_{n}$ denote the n-dimensional augmented cube [4]. And it has $2^n$ vertices, each of which corresponds to an n-bit binary string. $AQ_{n}$ can be defined recursively as below [13]:

• (1) For $n=1$, $AQ_{1}$ is a complete graph with two vertices labeled 0 and 1, respectively. The edge (0, 1) is called 0-dimensional hypercube edge.

• (2) For $n\ge 2$, an $AQ_{n}$ can be recursively constructed by two copies of $AQ_{n-1}$. We denote the two copies as $AQ_{n-1}^{0}$ and $AQ_{n-1}^{1}$, where $V(AQ_{n-1}^{0}) = \{0u_{n-2}u_{n-3} \ldots u_{0}|u_{i}\in \{0,1\}\ \mathrm{for}\ 0\le i \le n-2\}$ and $V(AQ_{n-1}^{1}) = \{1u_{n-2}u_{n-3} \ldots u_{0}| u_{i}\in \{0,1\}\ \mathrm{for}\ 0\le i \le n-2\}$. Then, we add $2^{n}$ edges between $AQ_{n-1}^{0}$ and $AQ_{n-1}^{1}$, and these edges can be divided into the following two sets:

• (a) $\{(0u_{n-2}u_{n-3} \ldots u_{0}, 1u_{n-2}u_{n-3} \ldots u_{0})|u_{i}\in \{0,1\}\ \mathrm{\ for\ } 0\le i \le n-2 \}$, where the edges in this set are called $(n-1)$-dimensional hypercube edges, denoted by $HE_{n-1}$.

• (b) $\{(0u_{n-2}u_{n-3} \ldots u_{0} , 1\overline{u}_{n-2}\overline{u}_{n-3} \ldots \overline{u}_{0})|u_{i}\in \{0,1\}\ \mathrm{\ for\ } 0\le i \le n-2 \}$, where the edges in this set are called $(n-1)$-dimensional complement edges, denoted by $CE_{n-1}$.

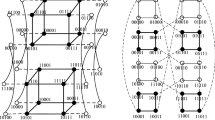
For example, $AQ_{1},\ AQ_{2},\ AQ_{3}$, and $AQ_{4}$ are shown in Fig. 1. We can see that $Q_{n}$ is the subgraph of $AQ_{n}$, thus $AQ_{n}$ retains all favorable properties of $Q_{n}$. It is proved in that $AQ_{n}$ is $(2n-1)$-regular, and $(2n-1)$-connected graph with $2^{n}$ vertices for any positive integer n.

Fig. 1.

$AQ_{n}\ for\ n\ = 1,2,3,4$.

3 Embedding Augmented Cubes into Grids

In this section, we first study embedding $AQ_{n}$ into a linear array and obtain the minimum wirelength of embedding. Then, we further study embedding $AQ_{n}$ into grid to obtain the minimum wirelength of embedding.

3.1 Embedding Augmented Cubes into Linear Arrays

In this section, we will study the minimum wirelength of embedding $AQ_{n}$ into a linear array. Before discussing the issue, we first study maximum induced subgraph of $AQ_{n}$. It is the key to our research on the wirelength problem.

In [3], Chien et al. solved the maximum induced graph for augmented cube. For any positive integer m, it can be uniquely expressed as $m=\sum ^{r}_{i=0}2^{p_{i}}$, where $p_{0}> p_{1}> \ldots >p_{r}$. Chien et al. proposed a useful function [13]:

$$\begin{aligned} f(m) = \left\{ \begin{array}{lcl}0, &{}m \le 1 \\ \sum \nolimits ^{r}_{i=0}(p_{i}+2i-\frac{1}{2})2^{p_{i}},&{}m\ is\ even\ and\ m\ge 2\\ \sum \nolimits ^{r-1}_{i=0}(p_{i}+2i-\frac{1}{2})2^{p_{i}}+2r, &{} m\ is\ odd\ and\ m\ge 2 \end{array}\right. \end{aligned}$$

(6)

Property 1

[13]. $f(2^{k}+m) = f(2^{k})+f(m)+2min\{2^{k},m\} \ if\ k \ge \left\lfloor \log _{2} m \right\rfloor$.

Let $\xi _{AQ_{n}}(m)$ be the number of edges among induced subgraphs with m vertices. The following lemmas can be proved by the function f(m):

Lemma 3

[13]. For any $n \ge 1$ and $0 <m\le 2^{n}$, then $\max \xi _{AQ_{n}}(m) = f(m)$.

Lemma 4

[23]. Let $\{ U_{0},U_{1}, \ldots ,U_{k}\}$ be a partition of U, where $U \subseteq V(G)$. Let $\xi (U)$ denote the number of edges of the graph G[U], and $\xi (U_{i},U_{j})=|\{(u,v)|u\in U_{i}, v\in U_{j} ,\ where\ 0\le i < j\le k \}|$. Then $\xi (U) = \sum _{i=0}^{k}\xi (U_{i})+\sum _{0\le i < j\le k}\xi (U_{i},U_{j})$.

We use $L_{N}$ to represent a linear array graph with the size of N, where $V(L_{N})$ is the vertex set $\{l | 0\le l \le N-1 \}$ and $E(L_{N})$ is the edge set $\{(l-1,l)|1\le l \le N-1 \}$.

Notation 1

Let $lex: V(AQ_{n}) \rightarrow \{1,2, \ldots ,2^{n}\}$ be a mapping, where $N = 2^{n}$ and for arbitrary vertex $u = u_{n-1}u_{n-2} \ldots u_{0}\ in\ AQ_{n}$,

$$\begin{aligned} \begin{aligned} lex(u) = \sum _{i=0}^{n-1}u_{i}*2^{i} +1 . \end{aligned} \end{aligned}$$

(7)

which is actually the decimal number of u.

In [13], Chien et al. studied the wavelengths of embedding augmented cube into linear array by considering the congestion. They proved that the natural embedding is an optimal scheme in embedding augmented cube into linear array. There is a significant relationship between edge congestion and wirelength. So, we can use the similar way to prove the following lemma.

Lemma 5

For each edge $e \in E(L_{N})$, $EC_{lex}(e) =l(2n-1)-2f(l)$. And the embedding lex is an optimal scheme which has minimized the congestion of each edge.

Proof

Let $U_{n,l}$ denote a vertex set of l vertices in $AQ_{n}$ defined by $U_{n,l} = \{u| \sum _{i=0}^{n-1}u_{i}2^{i} < l\}$. Hence $U_{n,l} \subseteq V(AQ_{n})$ consists of l vertices and maps to the first l vertices in $L_{N}$ by the embedding lex. Then $EC_{lex} = l(2n-1)-2\xi (U_{n,l})$, where $e = (l-1,l)$. Then we would prove that $\xi (U_{n,l}) = f(l)$ by induction n. Clearly, the statement holds for $n=1$. Suppose that the claim is true for $n \le k$, i.e., $\xi (U_{k,l}) = f(l)$ for $0 \le l \le 2^{k}$. Then consider that $n = k+1$, that is $0 \le l \le 2^{k+1}$. The cases are as below.

Case 1: $l = 0$. Obviously, $U_{k+1,l} = \varnothing$ and $f(0) = 0$. Hence $\xi (U_{k+1,0}) = f(0)$.

Case 2: $l \not = 0$. We consider the following subcases.

Case 2.1: $1 \le l \le 2^{k}$. It implies that $\sum _{i=0}^{n-1}u_{i}2^{i}<2^{k}$ for $u \in U_{k+1,l}$. So $u_{k} = 0$ for $u \in U_{k+1,l}$, i.e., $U_{k+1,l}$ is a subset of $V(AQ_{k}^{0}).\ U^{1}_{k,l} = \varnothing$ and $U_{k+1,l} = U^{0}_{k,l}$. Since $AQ_{k+1}^{0}$ is isomorphic to $AQ_{k}$ and by the induction hypothesis, $\xi (U^{0}_{k,l}) = f(l)$ which implies $\xi (U_{k+1,l}) = f(l)$.

Case 2.2: $2^{k} < l \le 2^{k+1}$. This implies that $|U^{0}_{k+1,l}| = |V(AQ_{k}^{0})|$ and let $l^{'}=|U^{1}_{k,l}|$ where $l^{'} = l - 2^{k}$. Thus for any vertex $u \in U^{1}_{k,l}$, there are exactly two vertices in $U^{0}_{k,l}$ adjacent to u. This implies that $\xi (U^{0}_{k,l},U^{1}_{k,l}) = 2|U^{1}_{k,l}| = 2l^{'}$. Since $\{U^{0}_{k,l},U^{1}_{k+1,l}\}$ is a partition of $U_{k+1,l}$, by Lemma 4 we have $\xi (U_{k+1,l}) = \xi (U^{0}_{k,l})+\xi (U^{1}_{k,l})+\xi (U^{0}_{k,l},U^{1}_{k,l})$. By the induction hypothesis, we have

$$\begin{aligned} \begin{aligned} \xi (U_{k+1,l})&= \xi (U^{0}_{k,l})+\xi (U^{1}_{k,l})+\xi (U^{0}_{k,l},U^{1}_{k,l})\\&=f(|U^{0}_{k,l}|) + f(|U^{1}_{k,l}|) +\xi (U^{0}_{k,l},U^{1}_{k,l})\\&=f(2^{k})+f(l^{'})+2l^{'} \end{aligned} \end{aligned}$$

Therefore, by Property 1, we have $\xi (U^{l}_{k+1}) = f(l)$.

It is obvious that $EC_{lex} = l(2n-1)-2\xi (U_{n,l}) =l(2n-1)-2f(l)$. Thus we can prove that the embedding lex is an optimal scheme which has minimized the congestion of each edge. $\square$

Lemma 6

Under the embedding lex of $AQ_{n}$ into $L_{N},\ where \ N=2^{n}$, we have

$$\begin{aligned} WL_{lex}(AQ_{n},L_{2^n}) = 2WL_{lex}(AQ_{n-1},L_{2^{n-1}}) + 2^{2n-1}. \end{aligned}$$

(8)

Proof

Let $\pi = lex$. For $n \ge 2,$ $AQ_{n}$ can be partitioned into two disjoint subgraphs $AQ_{n-1}^{0}$ and $AQ_{n-1}^{1}$ by the definition of $AQ_{n}$. Let edge cut $e = (2^{n-1},2^{n-1}+1)\in E(L_{N})$. Let $(u,v) \in E(AQ_{n})$, where $u \in V(AQ_{n-1}^{0})$ and $v \in V(AQ_{n-1}^{1})$, then we consider the hypercube edges and the complement edges between $AQ_{n-1}^{0}$ and $AQ_{n-1}^{1}$, respectively.

Case 1. $(u,v) \in HE(n-1)$. For each vertex $u\in V(AQ_{n-1}^{0})$, there is a vertex v in $AQ_{n-1}^{1}$ adjacent to u. Then the distance of $\psi (u)$ and $\psi (v)$ in linear array is $2^{n-1}$. See Fig. 2. There are $2^{n-1}$ vertices in $AQ_{n-1}^{0}$, so $\sum d(\psi (u),\psi (v)) = 2^{n-1}\times 2^{n-1}$, where $u\in V(AQ_{n-1}^{0})$ and $v \in V(AQ_{n-1}^{1})$.

Fig. 2.

The paths of embedding ($n - 1$)-dimensional hypercube edges into linear array.

Case 2. $(u,v) \in CE(n-1)$. For any vertex u in $AQ_{n-1}^{0}$, there always is a $(n-1)$-complement edge (u, v), where $v \in V(AQ_{n-1}^{1})$. See Fig. 3. Besides, the distance of $\psi (u)$ and $\psi (v)$ in linear array forms an arithmetic sequence with a tolerance of 2. There are $2^{n-1}$ vertices in $AQ_{n-1}^{0}$, so we have $\sum d(\psi (u),\psi (v)) = 1+3+ \ldots +2^{n}-1 = 2^{n-1}\times 2^{n-1}$, where $u \in V(AQ_{n-1}^{0})$ and $v \in V(AQ_{n-1}^{1})$. Therefore

Fig. 3.

The paths of embedding ($n - 1$)-dimensional complement edges into linear array.

$$\begin{aligned} WL_{\pi }(AQ_{n},L_{2^n}) = 2WL_{\pi }(AQ_{n-1},L_{2^{n-1}}) + 2^{2n-1} \end{aligned}$$

   $\square$

Theorem 1

The minimum wirelength of $AQ_{n}$ into $L_{N}$ under embedding lex is:

$$\begin{aligned} WL_{lex }(AQ_{n},L_{2^n}) = 2^{2n} - 3 \times 2^{n-1} \end{aligned}$$

(9)

Proof

We derive this theorem from Lemma 6, then we would prove the result by induction on n. For $n = 1,\ WL_{lex }(AQ_{1},L_{2}) = 2^{2} - 3 \times 2^{0} = 1$. Thus, assume that the result is true for $n=k-1$. Then we prove the result for $n=k$.

$$\begin{aligned} \begin{aligned} WL_{lex }(AQ_{k},L_{2^{k}})&= 2WL_{lex }(AQ_{k-1},L_{2^{k-1}}) + 2^{2(k-1)-1} \\ {}&= 2(2^{2(k-1)} - 3\times 2^{(k-1)-1}) + 2^{2k-1} \\ {}&= 2^{2k} - 3 \times 2^{k-1} \end{aligned} \end{aligned}$$

Then the theorem is proved$.\square$

3.2 Embedding Augmented Cubes into Grids

In this section, we study the minimum wirelength of embedding $AQ_{n}$ into a grid $M[2^{a},2^{b}]$, where $a = \left\lfloor \frac{n}{2} \right\rfloor$, $b = \left\lceil \frac{n}{2} \right\rceil$ and $a+b=n$. Firstly, the definition of grid is given as below:

Notation 2

[5]. An $m \times n$ grid M(m, n) is denoted by an $m \times n$ matrix

$$\begin{aligned} \begin{aligned} \begin{pmatrix} \alpha _{11} &{} \alpha _{12} &{} \cdots &{} \alpha _{1n} \\ \alpha _{21} &{} \alpha _{22} &{} \cdots &{} \alpha _{2n} \\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ \alpha _{m1} &{} \alpha _{m2} &{} \cdots &{} \alpha _{mn} \end{pmatrix} \end{aligned} \end{aligned}$$

Where $V(M) = \{\alpha _{ij}|1 \le i \le m,\ and\ 1 \le j \le n \},\ (\alpha _{i,j}, \alpha _{i,j+1}) \in E(M)$ for $1 \le i \le m,\ and\ 1 \le j \le n - 1$, and $(\alpha _{k,l}, \alpha _{k=1,l}) \in E(M)$ for $1 \le k \le m-1,\ and\ 1 \le l \le n.\ \left\langle \alpha _{11} , \alpha _{12} , \cdots , \alpha _{1n} \right\rangle$ and $\left\langle \alpha _{m1} , \alpha _{m2} ,\cdots , \alpha _{mn} \right\rangle$ are called the row-borders, while $\left\langle \alpha _{11} , \alpha _{21} , \cdots , \alpha _{m1} \right\rangle$ and $\left\langle \alpha _{1n} , \alpha _{2n} , \cdots , \alpha _{mn} \right\rangle$ are called the column-borders.

Definition 3

Let $lex \ :\ AQ_{n} \rightarrow M(2^{a},2^{b })$ be an embedding, where $a = \left\lfloor \frac{n}{2} \right\rfloor$, $b = \left\lceil \frac{n}{2} \right\rceil$ and $a+b=n$. Embedding lex can be defined as follows: The first row is labeled from 1 to $2^{b}$ from top to bottom, and the ith row is labeled as $(i-1)2^{a } + 1,\ (i-1)2^{a} + 2, \ldots ,i2^{a }$ from left to right where $i = 1,2, \ldots ,2^{b }$.

The embedding lex of hypercube into grid has been proved in [18]. And augmented cube is an enhancement on hypercube. Then, we first introduce some lemmas about embedding of hypercube.

Lemma 7

[10]. For $i = 1,2,3, \ldots ,2^{n},\ P_{i} = \{0,1, \ldots ,i-1\}$ is an optimal set in $Q_{n}$.

Let $A_{i}$ be a horizontal edge cut of the grid $M[2^{a},2^{b}]$, where $i = 1,2, \ldots ,2^{a }-1,\ a = \left\lfloor \frac{n}{2} \right\rfloor$, $b = \left\lceil \frac{n}{2} \right\rceil$ and $a+b=n$, such that $A_{i}$ disconnects $M[2^{a},2^{b}]$ into two components $X_{i}$ and $X_{i'}$. For $X_{i}$, there are $i2^{b }$ vertices. Then we let $R_{i}^{lex} = \{1, \ldots ,i2^{b }\}$ denote the vertices of $X_{i}$.

By Lemma 7, the following lemmas can be easily proved.

Lemma 8

$R_{i}^{lex} = \{1, \ldots ,i2^{b }\}$ is an optimal set in $AQ_{n}$ for $i = 1,2, \ldots , 2^{a}$.

Similarly, let $B_{j}$ be a column edge cut of the grid $M[2^{a},2^{b }]$ where $j = 1,2, \ldots ,2^{b }-1,\ a = \left\lfloor \frac{n}{2} \right\rfloor$, $b = \left\lceil \frac{n}{2} \right\rceil$ and $a+b=n$, such that $B_{j}$ disconnects $M[2^{a},2^{b}]$ into two components $Y_{j}$ and $Y_{j'}$. For $Y_{i}$, let $C_{j}^{lex}$ be the vertex set of $Y_{j}$.

Lemma 9

For $j = 1,2, \ldots ,2^{a}$

$$\begin{aligned} \begin{aligned} C_{j}^{lex} = \begin{Bmatrix} 1&1 \times 2^{b } +1&\cdots&(2^{a }-1) \times 2^{b } +1 \\ 2&1 \times 2^{b } +2&\cdots&(2^{a }-1) \times 2^{b} +2 \\ \cdots&\cdots&\cdots&\cdots \\ j&1 \times 2^{b } +j&\cdots&(2^{a}-1) \times 2^{b } +j \end{Bmatrix} \end{aligned} \end{aligned}$$

is an optimal set in $AQ_{n}$, where $a = \left\lfloor \frac{n}{2} \right\rfloor$, $b = \left\lceil \frac{n}{2} \right\rceil$ and $a+b=n$.

Lemma 10

The embedding lex of $AQ_{n}$ into $M(2^{a},2^{b})$ induces a minimum wirelength $WL_{lex}(AQ_{n},M[2^{a },2^{b}])$, where $a = \left\lfloor \frac{n}{2} \right\rfloor$, $b = \left\lceil \frac{n}{2} \right\rceil$ and $a+b=n$.

Proof

Horizontal edge cut$A_{i}$ disconnects $M[2^{a },2^{b}]$ into two components $X_{i}$ and $X_{i'}$. Similarly, column edge cut $B_{j}$ disconnects $M[2^{a },2^{b}]$ into two components $Y_{j}$ and $Y_{j'}$. Let $G_{i}$ and $G_{i'}$ be the inverse images of $X_{i}$ and $X_{i'}$ under lex respectively. The edge cuts $A_{i}$ and $B_{i}$ of the partition, satisfy conditions (i) and (ii) of Lemma 1. In order to show that $EC_{lex}(A_{i})$ is minimum, we just need to prove that $|E(G_{i})|$ is maximum by Lemma 1.

Since $G_{i}$ is a subcube derived from the vertices of $R_{i}^{lex}$ by Lemma 8, it is true that $G_{i}$ is a maximum induced subgraph of augmented cube. Thus by Lemma 1, $EC_{lex}(A_{i})$ is minimum for $i = 1,2, \ldots ,2^{a}-1$.

Similarly, let $G_{j}$ and $G_{j'}$ be inverse images of $Y_{j}$ and $Y_{j'}$ under lex, respectively. By Lemma 9, it is true that $G_{j}$ is a maximum induced subgraph of augmented cube derived from the vertices of $C_{j}^{lex}$. Thus by Lemma 1, $EC_{lex}(B_{j})$ is minimum for $j = 1,2, \ldots ,2^{b }-1$.

Thus by Lemma 2, $WL_{lex}(AQ_{n},M(2^{a},2^{b}))$ is minimum$.\square$

Lemma 11

[17]. $WL_{lex }(Q_{n},P_{2^{n}}) = 2^{2n-1} - 2^{n-1}$, where $P_{2^{n}}$ is a path with $2^{n}$ vertices.

Firstly, we study the paths of embedding hypercube edges into grid, and the ends of each path are in different columns. The problem can be transformed into calculating the wirelength of embedding a hypercube into a linear array. By Lemma 11 Manuel et al. solved the problem of embedding $Q_{n}$ into $M[2^{a},2^{b }]$, and calculated the wirelength of a path. Then the exact wirelength of embedding hypercube edges into grid where the ends of each path are in different columns is $2^{b}(2^{2a -1} - 2^{a - 1})$.

Fig. 4.

The paths of embedding 3-dimensional complement edges of $AQ_{4}$ into M[4 $\times$ 4].

Then, we study the paths of embedding complement edges into grid, and the ends of each path are in different columns. Let the embedding $\pi =lex$. Then for the embedding $\pi (\psi ,P_{\psi })$ of $AQ_{n}$ into $M(2^{a},2^{b})$, where $a = \left\lfloor \frac{n}{2} \right\rfloor$, $b = \left\lceil \frac{n}{2} \right\rceil$ and $a+b=n$, horizontal edge cut $A_{i}$ disconnects $M[2^{a },2^{b}]$ into two components $X_{i}$ and $X_{i'}$. Let $G_{i}$ and $G_{i'}$ be the inverse images of $X_{i}$ and $X_{i'}$ under $\pi$, respectively. Let $e = (u,v)$ be a complement edge of $AQ_{n}$, where $u \in V(G_{i})$ and $v \in V(G_{i'})$, thus $\psi (u) = \alpha _{ij}\in V(X_{i}) \ and\ \psi (v) = \alpha _{i'j'}\in V(X_{i'})$. So $d(\psi (u),\psi (v))) = |i'-i| + |j'-j|$. Then, we use $W_{a}$ to denote the sum of $d(\psi (u),\psi (v)))$, where $2^{a}$ is the number fo rows in grid.

Lemma 12

For embedding m-dimensional complement edges into $M[2^{a },2^{b }]$, where $a<m\le n-1$ and $a = 2^{\left\lfloor \frac{n}{2} \right\rfloor }$, the wirelength of embedding is

$$\begin{aligned} \begin{aligned} W_{a} = 2W_{a-1 }+\ 2^{a+b-2}(2^{a}\ +\ 2^{b }). \end{aligned} \end{aligned}$$

(10)

Proof

Let $i = 2^{a - 1}$, so the horizontal edge cut $A_{i}$ disconnects $M[2^{a },2^{b }]$ into two $M[2^{a - 1},2^{b}]$, $\ M_{1} \ and\ M_{2}$, as depicted in Fig. 4. Let $e = (u,v)$ be a complement edge of $AQ_{n}$, where $\psi (u) = \alpha _{i,j} \in V(M_{1}[2^{a - 1},2^{b}])\ and\ \psi (v) = \alpha _{i'j'} \in V(M_{2}[2^{a - 1},2^{b }])$. Then the distance of e in grid is $d(\psi (u),\psi (v)) = |i - i'| + |j - j'|$. There are $2^{n-1}$ vertices in $M[2^{a- 1},2^{b }]$, so there are $2^{n-1}$ complement edges that one end vertex is in $M_{1}$ and the other end is in $M_{2}$. Let $y_{i}$ be a vertex of the ith row. Then for the first row $R_{1}$, there are $2^{b}$ vertices, so

$$\begin{aligned} \begin{aligned} \sum _{\psi (y_{1})\in V(R_{1}),\psi (v)\in V(M_{2})} d(\psi (y_{1}),\psi (v))&= 2\times (2^{a} + (2^{a} + 2 )+(2^{a} + 4 )+ \ldots \\&+(2^{a}+2^{b } - 2))\\ {}&=2^{b}[2^{a + 1} + 2(2^{b - 1} - 1)] \end{aligned} \end{aligned}$$

It is similar for the rest rows from 2 to $2^{a - 1}$, then the distance of all the paths of embedding complement edges into $M[2^{a },2^{b }]$, where for each path one end is in $M_{1}$ and the other end is in $M_{2}$.

$$\begin{aligned} \begin{aligned}&\sum _{R_{1}}d(\psi (y_{1}),\psi (v)) + \sum _{R_{2}}d(\psi (y_{2}),\psi (v)) + \ldots +\sum _{R_{2^{a-1}}}d(\psi (y_{2^{a-1}}),\psi (v)) \\&= 2^{a+b-2}(2^{a - 1}\ +\ 2^{b }) \end{aligned} \end{aligned}$$

So

$$\begin{aligned} \begin{aligned} W_{a} = 2W_{a-1 }+\ 2^{a+b-2}(2^{a}\ +\ 2^{b }). \end{aligned} \end{aligned}$$

By Lemma 12, we obtain the recursion formula of the wirelength about embedding complement edges into grids. In the following, we will calculate the exact formula of minimum wirelength about embedding augmented cubes into grids.

Theorem 2

The minimum wirelength of embedding $AQ_{n}$ into $M[2^{a},2^{b}]$ under lex is:

$$\begin{aligned} \begin{aligned} WL_{lex}(AQ_{n},M) =&2^{a}( 2^{2b} - 3 \times 2^{b-1}) + 2^{b}(2^{2a -1} - 2^{a - 1}) \\&+ 2^{a+b-2}(a 2^{b} + 2^{a + 1} - 2) \end{aligned} \end{aligned}$$

(11)

where $a = \left\lfloor \frac{n}{2} \right\rfloor$, $b = \left\lceil \frac{n}{2} \right\rceil$, $n\ge 2$ and $a+b=n$.

Proof

There are $2^{a}$ rows in $M[2^{a},2^{b}]$, where $a = \left\lfloor \frac{n}{2} \right\rfloor$, $b = \left\lceil \frac{n}{2} \right\rceil$ and $a+b=n$. Let $H_{i}$ denote the ith row, where $1 \le i \le 2^{a }$, as depicted in Fig. 5. Then the inverse images of $H_{1},H_{2}, \ldots ,H_{2^{a}}$ are disjoint sets in $AQ_{n}$, and $|(H_{i})| = 2^{b }$. Obviously, vertices in $H_{i}$ are mapped to the ith row from left to right. There are $2^{b }$ vertices in each row. Each row can be considered as a linear array. And the embedding for each row can be seen as the embedding of $AQ_{b}$ into $L_{2^{b }}$. So for each row, $WL_{lex}(H_{i},L_{2^{b}}) = WL(AQ_{b },L_{2^{b }}) = 2^{2b} - 3 \times 2^{b-1}$.

Then, we study the paths of hypercube edges and complement edges in grids. And the ends of each path are in different rows. For the hypercube edges, by Theorem 11, we derived that the wirelength along the columns is $2^{b}(2^{2a -1} - 2^{a - 1})$.

For complement edges, we derived the result by the recursion formula in Lemma 12. The wirelength of complement edges in different rows is $2^{a+b-2}(a 2^{b } + 2^{a + 1} - 2)$. We prove the result by induction on a. The base case is trivial. Assume that the result is true for $a=k - 1$. Then we prove the result for $a=k$.

$$\begin{aligned} \begin{aligned} W_{k}&= 2W_{k-1}\ +\ 2^{k+b-2}(2^{k }\ +\ 2^{b }) \\&= 2(2^{k+b-3}((k-1) 2^{b } + 2^{k } - 2)) + 2^{k+b-2}(2^{k }\ +\ 2^{b }) \\&= 2^{k+b-2}(k 2^{b } + 2^{k + 1} - 2) \end{aligned} \end{aligned}$$

Fig. 5.

Mapping vertices of $AQ_{n}$ to the ith row from left to right.

Thus the minimum wirelength of $AQ_{n}$ into $M[2^{a },2^{b }]$ under embedding lex is:

$$\begin{aligned} WL_{lex}(AQ_{n},M) = 2^{a}( 2^{2b} - 3 \times 2^{b-1}) + 2^{b}(2^{2a -1} - 2^{a - 1}) + 2^{a+b-2}(a 2^{b} + 2^{a + 1} - 2) \end{aligned}$$

where $a = \left\lfloor \frac{n}{2} \right\rfloor$, $b = \left\lceil \frac{n}{2} \right\rceil$, $n\ge 2$ and $a+b=n$.

Then the theorem is proved$.\square$

For each vertex $u=u_{n-1}u_{n-2}u_{n-3} \ldots u_{0} \in V(AQ_{n})$, let $j\ (0 \le j \le 2^{n}-1 )$ be a decimal representation of u. Thus we can use $u_{n}^{j}$ to represent each vertex in $AQ_{n}$. We present Algorithm 1 for embedding $AQ_{n}$ into $M(2^{a},2^{b })$, where $a = \left\lfloor \frac{n}{2} \right\rfloor$, $b = \left\lceil \frac{n}{2} \right\rceil$ and $a+b=n$.

4 Simulation and Experiments

Fig. 6.

(a) Wirelength of embedding augmented cubes into linear arrays. (b) Wirelength of embedding augmented cubes into grids

In this section, we compare the result with the other embedding scheme to verify that the proposed embedding is superior to the random embedding [8]. The random embedding (short for Random)is the bijection $f: \{1,.., n\} \rightarrow \{1, \ldots , n\}$ is random.

Firstly, we consider the wirelength of embedding augmented cubes into linear arrays. As seen in Fig. 6(a), compared with the random embedding, the proposed embedding has lower wirelength. With the increasing of the dimension, it also has better performance than random embedding. Besides, the wirelength increases rapidly when we rise the dimension of the augmented cubes. In Fig. 6(a), when n is less than 7, the difference is not obvious. We list the exact wirelength in Table 1. Linear array is a special grid M[1, n], then the comparison of two embedding schemes in gird would be similar to the linear array. In Fig. 6(b), compared with the random embedding, the proposed embedding has lower wirelength. And the exact wirelength is shown in Table 1.

Table 1. Wirelength of embedding augmented cubes into linear arrays and grids in different dimensions

5 Conclusions

In this paper, we study embedding augmented cubes into grid networks and obtain the exact wirelength of embedding. Firstly, we prove that augmented cubes can be embedded into linear arrays with minimum wirelength and obtain the exact wirelength based on the maximum induced subgraph problem. Furthermore, we obtain the minimum wirelength of embedding augmented cubes into grids and propose a linear algorithm.