Keywords

1 Introduction

Vector problems of electrodynamics usually require significant computational resources and are studied using various numerical methods, such as the finite-difference time-domain (FDTD) or Yee’s method, finite element method (FEM), incomplete Galerkin method (IGM) or Kantorovich method, as well as their combinations.

1.1 Purely Numerical Methods

Finite-Difference Methods. Completely numerical methods, e.g., FDTD [1,2,3] and other finite-difference methods, begin from discretization of the continuous variables of the problem and, thereby, offer no possibility of analyzing solutions at the level of symbolic expressions from the very first step.

Finite-difference methods are universal and suitable for the widest class of problems – both linear and nonlinear problems are approximated by finite-difference analogues. However, the price to pay for this versatility is the significant expenditure of computer resources, especially if the object is extended and nonuniform in one or several spatial directions. The success of such methods is directly related to the availability of large computing power.

Finite Element Methods. Finite element methods as well as finite-difference methods are applicable to a wide class of problems  [4,5,6]. Although the solution is represented as a functional dependence, this dependence only ensures smoothness of the solution rather than reflects its physical properties. Due to their versatility, finite element methods are also dependent on computing power.

1.2 Symbolic-Numerical Methods

Galerkin and Kantorovich Methods. In solving electrodynamic problems, there is an “intermediate” class of methods that represent the approximate solution as an expansion in a system of basis functions. The expansion coefficients can be constants (in the classical Galerkin method  [12, 13]) or functions of one or several spatial variables (in the Kantorovich method  [7, 8] and in the incomplete Galerkin method  [9,10,11]). The system of functions in which the solution is expanded must be complete in the functional space to which the desired solution should belong, and some additional conditions (e.g., matching, smoothness, etc.).

As a rule, a fortunate choice of basis functions allows solving the problem with sufficient accuracy even keeping a small number of expansion terms.

The main advantages of this “mixed” approach are:

  1. 1.

    Saving computing resources. The initial problem for multidimensional partial differential equations is reduced at a symbolic level to a system of ordinary differential equations (ODE) with initial or boundary conditions. The problem for the ODE system is solved in reasonable time on a personal computer.

  2. 2.

    Representation of results in the form of symbolic expressions allows a more detailed analysis and provides greater clarity of their physical meaning.

Model of Adiabatic Waveguide Modes. We used the symbolic-numerical approach to develop the adiabatic waveguide modes (AWM) method based on the model of adiabatic waveguide modes described in Refs.  [14, 15].

In Ref.  [15], a symbolic form of the adiabatic waveguide modes in an arbitrary homogeneous layer of a multilayer waveguide was derived, basing on which it is possible to construct waveguide modes of multilayer smoothly-irregular waveguide structures. With further use of the symbolic-numerical approach, these modes can serve as a basis for Kantorovich decomposition.

1.3 Formulation of the Problem

The problem of finding the phase of a waveguide mode in a regular waveguide (by the example of a three-layer regular waveguide) was considered and numerically solved in  [15]. This problem reduces to finding zeros of the characteristic determinant of the matrix of boundary equations, which yields the phase deceleration coefficients of the guided modes \(\beta _j\). The phase of each of the guided modes \({{\varphi }_{j}}\left( z \right) \) is trivially determined given the phase deceleration coefficient: \({{\varphi }_{j}}\left( z \right) ={{\beta }_{j}}\left( z-{{z}_{0}} \right) +{{\varphi }^{0}}\), where \({{\varphi }^{0}}\) is the initial phase, corresponding to \(z={{z}_{0}}\).

The next stage of the study is to formulate the problem of finding the phase of an adiabatic waveguide mode in an irregular waveguide (by the example of a four-layer waveguide with one irregular layer) and to solve it numerically. In this case the presence of a layer with variable thickness violates the linear behaviour of the phase, so that if the layer irregularity depends on both y and z, the phase will also be a function of y and z.

The formulation of this problem and the development of an approximate method for solving it is the subject of the present paper. As an irregular structure, we consider the Luneburg waveguide lens, which is a three-layer regular waveguide with a fourth layer having variable thickness depending on y and z.

The structure choice was not accidental: it is an object rather complicated for modeling, however, its basic properties are known from physical experiments. So, we will carry out numerical calculations using the example of a Luneburg waveguide lens.

2 Methods and Approaches

2.1 AWM Model, the Form of the Solution

The AWM model approximately describes the guided modes in smoothly-irregular waveguide structures (for details see Section 2 of Ref.  [15]). In this study without loss of generality, a four-layered structure will be considered.

The AWM model makes use of the asymptotic method  [16], in which electromagnetic fields are presented in the form  [15]:

$$\begin{aligned} \vec {E}\left( x,y,z,t \right) =\sum \limits _{s=0}^{\infty }{\frac{{{{\vec {E}}}^{s}}\left( x;y,z \right) }{{{\left( -i\omega \right) }^{\gamma +s}}}}\exp \left\{ i\omega t-i{{k}_{0}}\varphi \left( y,z \right) \right\} , \end{aligned}$$
(1)
$$\begin{aligned} \vec {H}\left( x,y,z,t \right) =\sum \limits _{s=0}^{\infty }{\frac{{{{\vec {H}}}^{s}}\left( x;y,z \right) }{{{\left( -i\omega \right) }^{\gamma +s}}}}\exp \left\{ i\omega t-i{{k}_{0}}\varphi \left( y,z \right) \right\} , \end{aligned}$$
(2)

where \({{k}_{0}}\) is the wavenumber, \(\varphi \left( y,z \right) \) is the phase, and \({{\vec {E}}^{s}}\left( x;y,z \right) \), \({{\vec {H}}^{s}}\left( x;y,z \right) \) determine the amplitude of the s-th order. In the notation of \({{\vec {E}}^{s}}\left( x;y,z \right) \), \({{\vec {H}}^{s}}\left( x;y,z \right) \) the separation of x by a semicolon means the following assumption: \(\partial {{\vec {E}}^{s}}/\partial y\), \(\partial {{\vec {E}}^{s}}/\partial z\), \(\partial {{\vec {H}}^{s}}/\partial y\), \(\partial {{\vec {H}}^{s}}/\partial z\) are small quantities.

In other words, the following expressions for the derivatives are valid:

$$\begin{aligned} \frac{\partial \vec {E}}{\partial y}=-i{{k}_{0}}{{\varphi }_{y}}\vec {E}, \end{aligned}$$
$$\begin{aligned} \frac{\partial \vec {E}}{\partial z}=-i{{k}_{0}}{{\varphi }_{z}}\vec {E}, \end{aligned}$$

and the analogous expressions:

$$\begin{aligned} \frac{\partial \vec {H}}{\partial y}=-i{{k}_{0}}{{\varphi }_{y}}\vec {H}, \end{aligned}$$
$$\begin{aligned} \frac{\partial \vec {H}}{\partial z}=-i{{k}_{0}}{{\varphi }_{z}}\vec {H}, \end{aligned}$$

in which \({{\varphi }_{y}}\) and \({{\varphi }_{z}}\) are partial derivatives of \(\varphi \left( y,z \right) \) in y and z, respectively.

2.2 AWM Model. Reduction of Maxwell Equations

The Maxwell equations in the zero order (\(s=0\)) of the asymptotic expansion reduce to a system of ordinary differential equations of the first order  [15]:

$$\begin{aligned} \frac{\partial \vec {u}}{\partial x}+A\left( x,y,z \right) \vec {u}=\vec {0}, \end{aligned}$$
(3)

and two additional relations

$$\begin{aligned} E_{x}^{0}={\frac{1}{\varepsilon }}\left( {{\varphi }_{z}}H_{y}^{0}-{{\varphi }_{y}}H_{z}^{0} \right) , \end{aligned}$$
(4)
$$\begin{aligned} H_{x}^{0}=-{\frac{1}{\mu }}\left( {{\varphi }_{z}}E_{y}^{0}-{{\varphi }_{y}}E_{z}^{0} \right) , \end{aligned}$$
(5)

where the desired vector function \(\vec {u}\left( x;y,z \right) \) consists of the variables

$$\vec {u}\left( x;y,z \right) ={{\left( \begin{matrix} E_{y}^{0} &{} H_{z}^{0} &{} H_{y}^{0} &{} E_{z}^{0} \\ \end{matrix} \right) }^{T}}$$

that describe the distribution of the appropriate field components along the x-axis at each point \(\left( y,z \right) \). Matrix A is defined as follows  [15]

$$\begin{aligned} A\left( x,y,z \right) =\left( \begin{matrix} 0 &{} -\frac{i{{k}_{0}}\varphi _{y}^{2}}{\varepsilon }+i{{k}_{0}}\mu &{} \frac{i{{k}_{0}}{{\varphi }_{y}}{{\varphi }_{z}}}{\varepsilon } &{} 0 \\ -\frac{i{{k}_{0}}\varphi _{z}^{2}}{\mu }+i{{k}_{0}}\varepsilon &{} 0 &{} 0 &{} \frac{i{{k}_{0}}{{\varphi }_{y}}{{\varphi }_{z}}}{\mu } \\ -\frac{i{{k}_{0}}{{\varphi }_{y}}{{\varphi }_{z}}}{\mu } &{} 0 &{} 0 &{} \frac{i{{k}_{0}}\varphi _{y}^{2}}{\mu }-i{{k}_{0}}\varepsilon \\ 0 &{} -\frac{i{{k}_{0}}{{\varphi }_{y}}{{\varphi }_{z}}}{\varepsilon } &{} \frac{i{{k}_{0}}\varphi _{z}^{2}}{\varepsilon }-i{{k}_{0}}\mu &{} 0 \\ \end{matrix} \right) \end{aligned}$$
(6)

where \(\varepsilon =\varepsilon \left( x,y,z \right) \) and \(\mu =\mu \left( x,y,z \right) \) are the piecewise constant permittivity and permeability, respectively.

2.3 AWM Model. Reduction of Boundary Conditions for Maxwell Equations

At the discontinuity surfaces of \(\varepsilon =\varepsilon \left( x,y,z \right) \) and \(\mu =\mu \left( x,y,z \right) \) the matching conditions must be satisfied that follow from the boundary conditions for Maxwell equations. For planar boundaries \(x=c\,\,\left( c=const \right) \) the tangential components \(E_{y}^{0},H_{z}^{0},H_{y}^{0},E_{z}^{0}\) must be continuous, i.e., in vector notation  [15],

$$\begin{aligned} {{\left. \left[ {\vec {u}} \right] \right| }_{x=c}}=\vec {0}, \end{aligned}$$
(7)

where \({{\left. \left[ {\vec {u}} \right] \right| }_{x=c}}={{\left. {\vec {u}} \right| }_{x=c-0}}-{{\left. {\vec {u}} \right| }_{x=c+0}}\) is the jump of vector function \(\vec {u}\) at the point \(x=c\). For curved boundaries \(x=h\left( y,z \right) \) the continuity conditions  [15]

$$\begin{aligned} {{\left. \left[ \vec {u}+V\vec {u} \right] \right| }_{x=h\left( y,z \right) }}=\vec {0}, \end{aligned}$$
(8)

must be fulfilled, where matrix V has the following form:

$$\begin{aligned} V=\left( \begin{matrix} 0 &{} \frac{{h}_{y}{\varphi }_{y}}{\varepsilon } &{} -\frac{{h}_{y}{\varphi }_{z}}{\varepsilon } &{} 0 \\ -\frac{{h}_{z}{\varphi }_{z}}{\mu } &{} 0 &{} 0 &{} \frac{{h}_{z}{\varphi }_{y}}{\mu } \\ \frac{{h}_{y}{\varphi }_{z}}{\mu } &{} 0 &{} 0 &{} -\frac{{h}_{y}{\varphi }_{y}}{\mu } \\ 0 &{} -\frac{{h}_{z}{\varphi }_{y}}{\varepsilon } &{} \frac{{h}_{z}{\varphi }_{z}}{\varepsilon } &{} 0 \\ \end{matrix} \right) , \end{aligned}$$
(9)

where \({{h}_{y}}\) and \({{h}_{z}}\) are partial derivatives of \(h\left( y,z \right) \) in y and z, respectively.

Guided modes correspond to electromagnetic fields that satisfy the asymptotic conditions  [17]

$$\begin{aligned} \left\| {\vec {u}} \right\| \xrightarrow [x\rightarrow \pm \infty ]{}0. \end{aligned}$$
(10)

2.4 AWM Model. The Approximation of “Horizontal” Boundary Conditions

At first let us restrict ourselves to the approximation of “horizontal” boundary conditions (7), which will play the role of zero-order approximation to the boundary conditions (8) with respect to the small parameter \(\nu \) at

$$\begin{aligned} \nu =\left\| V \right\| \ll 1, \end{aligned}$$
(11)

where \(\left\| V \right\| = \underset{i,j}{\mathop {\max }}\,\left\{ \left| {{v}_{i,j}} \right| \right\} \).

Remark

Relation (11) is valid if any of the quantities \({{h}_{y}}{{\varphi }_{y}}\), \({{h}_{y}}{{\varphi }_{z}}\), \({{h}_{z}}{{\varphi }_{y}}\) and \({{h}_{z}}{{\varphi }_{z}}\) is small in absolute value. In the AWM model the smoothly irregular structures are considered, for which \({{h}_{y}}\), \({{h}_{z}}\) are small. Hence, \(\nu \) is not small only when the quantities \({{\varphi }_{y}}\) and \({{\varphi }_{z}}\) (or at least one of them) are much greater than unity. Therefore, the principal aspect of the considered approximation is the estimation of smallness of \(\nu \), which will be performed a posteriori in the course of numerical calculations.

2.5 AWM Model. Setting of the Problem for the Current Study

In Ref.  [15], system (3) is solved in the symbolic form for constant \(\varepsilon ,\mu \), which offers a possibility of solving the system (3) for piecewise constant \(\varepsilon ,\mu \). Given the general solution of the system (3) in each domain of constant \(\varepsilon ,\mu \) and the matching conditions (7) for the boundaries between these domains, using the conditions (10) for unlimited domains of constant \(\varepsilon ,\mu \), we derive a homogeneous system of equations. The unknowns in this system are coefficients at the functions of the fundamental system of solutions in each domain of constant \(\varepsilon ,\mu \). The determinant of this system should be zero to ensure the existence of a nontrivial solution.

In the layer number \(\alpha \) with constant permittivity and permeability \(\varepsilon ={{\varepsilon }_{\alpha }}\), \(\mu ={{\mu }_{\alpha }}\) the solution of the system of differential Eq. (3) has the form  [15]

$$\begin{aligned} \begin{aligned} {{{\vec {u}}}_{\alpha }}\left( x;y,z \right)&={{A}_{\alpha }}\left( \begin{matrix} {{q}_{\alpha }} \\ -i{{\varepsilon }_{\alpha }}{{\eta }_{\alpha }} \\ 0 \\ {{\varphi }_{y}}{{\varphi }_{z}} \\ \end{matrix} \right) {{e}^{{{\gamma }_{\alpha }}x}}+{{B}_{\alpha }}\left( \begin{matrix} -i{{\mu }_{\alpha }}{{\eta }_{\alpha }} \\ {{p}_{\alpha }} \\ {{\varphi }_{y}}{{\varphi }_{z}} \\ 0 \\ \end{matrix} \right) {{e}^{{{\gamma }_{\alpha }}x}}+ \\&+{{C}_{\alpha }}\left( \begin{matrix} {{q}_{\alpha }} \\ i{{\varepsilon }_{\alpha }}{{\eta }_{\alpha }} \\ 0 \\ {{\varphi }_{y}}{{\varphi }_{z}} \\ \end{matrix} \right) {{e}^{-{{\gamma }_{\alpha }}x}}+{{D}_{\alpha }}\left( \begin{matrix} i{{\mu }_{\alpha }}{{\eta }_{\alpha }} \\ {{p}_{\alpha }} \\ {{\varphi }_{y}}{{\varphi }_{z}} \\ 0 \\ \end{matrix} \right) {{e}^{-{{\gamma }_{\alpha }}x}}, \\ \end{aligned} \end{aligned}$$
(12)

where \({{q}_{\alpha }}=\varphi _{y}^{2}-{{\varepsilon }_{\alpha }}{{\mu }_{\alpha }}\), \({{p}_{\alpha }}=\varphi _{z}^{2}-{{\varepsilon }_{\alpha }}{{\mu }_{\alpha }}\), \({{\eta }_{\alpha }}=\sqrt{\varphi _{y}^{2}+\varphi _{z}^{2}-{{\varepsilon }_{\alpha }}{{\mu }_{\alpha }}}\), \({{\gamma }_{\alpha }}={{k}_{0}}{{\eta }_{\alpha }}\), and \({{A}_{\alpha }},{{B}_{\alpha }},{{C}_{\alpha }},{{D}_{\alpha }}\) are indefinite constants at each point \(\left( y,z \right) \).

In this study, using the computer algebra system, we formulate an approximate problem of computing the coefficient of phase deceleration in a general case of a smoothly irregular four-layer structure by an example of the Luneburg waveguide lens.

To present the problem in symbolic form, we consider a four-layer waveguide structure with one layer of variable thickness, which is characterized by the following permittivity and permeability:

$$\begin{aligned} \varepsilon =\left\{ \begin{array}{l l} {{\varepsilon }_{c}},\,\,\, &{} x>{{h}_{2}}\left( y,z \right) \\ {{\varepsilon }_{l}},\,\,\, &{} {{h}_{1}}<x<{{h}_{2}}\left( y,z \right) \\ {{\varepsilon }_{f}}, \,\,\, &{} 0<x<{{h}_{1}} \\ {{\varepsilon }_{s}},\,\,\, &{} x<0 \\ \end{array} \right. ,\,\,\,\,\,\,\,\,\mu =\left\{ \begin{array}{l l} {{\mu }_{c}},\,\,\, &{} x>{{h}_{2}}\left( y,z \right) \\ {{\mu }_{l}},\,\,\, &{} {{h}_{1}}<x<{{h}_{2}}\left( y,z \right) \\ {{\mu }_{f}},\,\,\, &{} 0<x<{{h}_{1}} \\ {{\mu }_{s}},\,\,\, &{} x<0 \\ \end{array} \right. \end{aligned}$$
(13)

The symbolic representation of the solution \({{\vec {u}}_{\alpha }}\left( x;y,z \right) \) in each layer \(\alpha =s,f,l,c\) is known (see (12)). This allows writing down a symbolic representation of the characteristic matrix of boundary conditions in the zero-order approximation with respect to \(\nu \), i.e., the conditions (7) at the boundaries \(x=0,x={{h}_{1}}\) and \(x={{h}_{2}}\left( y,z \right) \). Using standard Maple  [18] commands subs, expand and simplify, we derive a system of boundary equations based on the solutions \({{\vec {u}}_{\alpha }}\left( x;y,z \right) \) and the boundary conditions. In each of the four layers, the solution comprises four indefinite constants (see (12)), while the boundary conditions at three boundaries \(x=0,x={{h}_{1}}\) and \(x={{h}_{2}}\left( y,z \right) \) yield only 12 equations. The other 4 equations follow from asymptotic conditions (10).

The resulting system of equations at any fixed \(\left( y,z \right) \) is a system of linear algebraic homogeneous equations having the form

$$\begin{aligned} {{M}^{*}}\left( y,z,{{\varphi }_{y}},{{\varphi }_{z}} \right) \vec {C}=\vec {0}, \end{aligned}$$
(14)

where \({{M}^{*}}\) is the matrix of coefficients generally dependent on both y, z and partial derivatives of the sought function \({{\varphi }_{y}},{{\varphi }_{z}}\); \(\vec {C}\) is a vector composed of the indefinite coefficients \({{A}_{\alpha }},{{B}_{\alpha }},{{C}_{\alpha }}\) and \({{D}_{\alpha }}\) looked for. System (14) has a nontrivial solution if and only if

$$\begin{aligned} \det {{M}^{*}}\left( y,z,{{\varphi }_{y}},{{\varphi }_{z}} \right) =0. \end{aligned}$$
(15)

Equation (15) is a nonlinear partial differential equation of the first order. It is convenient to solve this equation using the method of characteristics, which reduces the initial nonlinear partial differential equation to a system of ordinary differential equations for the characteristics  [19].

Thus, the sought phase of the adiabatic waveguide mode \(\varphi \left( y,z \right) \) must satisfy the nonlinear Eq. (15), which can be explicitly written only after calculating the determinant in a symbolic form.

Remark

Symbolic calculation of a \(12\times 12\) determinant is possible only using the libraries of symbolic transformations. The authors make use of Maple system for this purpose.

Before calculating the determinant (15), we performed symbolic transformations to simplify the elements of matrix \({{M}^{*}}\) specified symbolically. As a result of symbolic simplifications, problem (15) reduces to two problems:

  1. 1.

    Finding zeros of the determinant of the reduced matrix for the considered domain of \(\left( y,z \right) \), or, in other words, solving the non-linear equation

    \(\det M\left( y,z, {{\beta }^{2}}\left( y,z \right) \right) =0\) (where \({{\beta }^{2}}\left( y,z \right) =\varphi _{y}^{2}+\varphi _{z}^{2}\)) and finding desired \({{\beta }^{2}} \left( y,z \right) \) for each \(\left( y,z \right) \) from the considered domain;

  2. 2.

    Subsequent solution of the reduced nonlinear differential equation with the right-hand side calculated at Step 1: \(\varphi _{y}^{2}+\varphi _{z}^{2}={{\beta }^{2}}\left( y,z \right) \).

Problem 1 was solved using the function Determinant of the Maple package LinearAlgebra. The zeros of determinant were approximately found using the classical bisection method  [20].

Remark

A specific feature of waveguide problems is that the localizing a zero of the determinant within an interval of \({{10}^{-15}}\) one has to deal with the values of the determinant itself of the order of \({{10}^{30}}\). Therefore, in the numerical calculations we used the numbers with enlarged mantissa by setting Digits := 30.

Problem 2 was solved by the method of characteristics  [19] using the command charstrip from the library PDETools  [18], which allows getting a system of ordinary differential equations for characteristics from a nonlinear first-order partial differential equation. This system complemented with the initial conditions was solved numerically using a Fehlberg fourth-fifth-order Runge-Kutta method with degree four interpolant – rkf45 – with the parameter, determining the relative error relerr = \({{10}^{-12}}\)  [18]. The method is implemented in Maple in a symbolic-numerical form.

2.6 Numerical Experiment. Verification

To verify the implemented method we consider the waveguide Lunenburg lens of the radius R, designed to focus the waveguide mode \(T{{E}_{0}}\) at the distance \(F=2R\). Within the frameworks of the AWM in the zero-order approximation with respect to \(\nu \ll 1\) (approximation of “horizontal” boundary conditions) the problem of finding the phase for different lens radii (from \({{10}^{2}}\) to \({{10}^{4}}\) wavelengths) was solved. Besides, we estimated a posteriori the order of \(\nu \) for the same lens radii to determine the range of validity of the approximation of “horizontal” boundary conditions.

As the initial data we took the parameters of the Luneburg lens designed by Konstantin Lovetskiy  [21] using the method of cross sections, the initial data for which were provided by the solution of the Morgan equation  [22].

3 Results

3.1 Results Obtained in Symbolic Form

We consider the four-layer waveguide structure, formed by a three-layered waveguide on which the fourth layer of variable thickness is deposited, sufficiently extended in the plane yOz to ensure the conditions \(\left| \partial {{h}_{2}}/\partial y \right| \ll 1,\,\,\,\,\left| \partial {{h}_{2}}/\partial z \right| \ll 1\).

Fig. 1.
figure 1

Structure of the irregular four-layer waveguide (additional waveguide layer has variable thickness \(d={{h}_{2}}\left( y,z \right) -{{h}_{1}}\))

Full size image

Using the Maple toolkit, we write the boundary equations of the AWM model in the zero-order approximation with respect to \(\nu \ll 1\) in a symbolic form.

The Main Result. In the zero-order approximation with respect to \(\nu \ll 1\) (the approximation of “horizontal” boundary conditions) the phase \(\varphi \left( y,z \right) \) in the AWM model satisfies the eikonal equation

$$\begin{aligned} \varphi _{y}^{2}+\varphi _{z}^{2}={{\beta }^{2}}\left( y,z \right) , \end{aligned}$$
(16)

where \({{\beta }^{2}}\left( y,z \right) \) is the square of the phase deceleration coefficient.

Appendix. The quantity \({{\beta }^{2}}\left( y,z \right) \) is determined as a root of the equation

$$\begin{aligned} \det M\left( y,z, {{\beta }^{2}}\left( y,z \right) \right) =0, \end{aligned}$$
(17)

where the \(8\times 8\) matrix M is defined as

$$\begin{aligned} M=\left( \begin{matrix} {{M}_{11}} &{} {{M}_{12}} \\ {{M}_{21}} &{} {{M}_{22}} \\ \end{matrix} \right) , \end{aligned}$$
(18)

where

$$\begin{aligned} {{M}_{11}}=\left( \begin{matrix} {{\theta }_{s}} &{} i{{\eta }_{f}}{{\mu }_{f}}-i{{\eta }_{s}}{{\mu }_{s}} &{} {{\theta }_{s}} &{} -i{{\eta }_{f}}{{\mu }_{f}}-i{{\eta }_{s}}{{\mu }_{s}} \\ i{{\eta }_{f}}{{\varepsilon }_{f}}-i{{\eta }_{s}}{{\varepsilon }_{s}} &{} {{\theta }_{s}} &{} -i{{\eta }_{f}}{{\varepsilon }_{f}}-i{{\eta }_{s}}{{\varepsilon }_{s}} &{} {{\theta }_{s}} \\ {{\theta }_{f}}{{e}^{{{\gamma }_{f}}{{h}_{1}}}} &{} -i{{e}^{{{\gamma }_{f}}{{h}_{1}}}}{{\eta }_{f}}{{\mu }_{f}} &{} {{\theta }_{f}}{{e}^{-{{\gamma }_{f}}{{h}_{1}}}} &{} i{{e}^{-{{\gamma }_{f}}{{h}_{1}}}}{{\eta }_{f}}{{\mu }_{f}} \\ -i{{e}^{{{\gamma }_{f}}{{h}_{1}}}}{{\eta }_{f}}{{\varepsilon }_{f}} &{} {{\theta }_{f}}{{e}^{{{\gamma }_{f}}{{h}_{1}}}} &{} i{{e}^{-{{\gamma }_{f}}{{h}_{1}}}}{{\eta }_{f}}{{\varepsilon }_{f}} &{} {{\theta }_{f}}{{e}^{-{{\gamma }_{f}}{{h}_{1}}}} \\ \end{matrix} \right) , \end{aligned}$$
(19)
$$\begin{aligned} {{M}_{12}}=\left( \begin{matrix} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} i{{e}^{-{{\gamma }_{l}}d}}{{\eta }_{l}}{{\mu }_{l}} &{} 0 &{} -i{{e}^{{{\gamma }_{l}}d}}{{\eta }_{l}}{{\mu }_{l}} \\ i{{e}^{-{{\gamma }_{l}}d}}{{\eta }_{l}}{{\varepsilon }_{l}} &{} 0 &{} -i{{e}^{{{\gamma }_{l}}d}}{{\eta }_{l}}{{\varepsilon }_{l}} &{} 0 \\ \end{matrix} \right) , \end{aligned}$$
(20)
$$\begin{aligned} {{M}_{21}}=\left( \begin{matrix} {{e}^{{{\gamma }_{f}}{{h}_{1}}}} &{} 0 &{} {{e}^{-{{\gamma }_{f}}{{h}_{1}}}} &{} 0 \\ 0 &{} {{e}^{{{\gamma }_{f}}{{h}_{1}}}} &{} 0 &{} {{e}^{-{{\gamma }_{f}}{{h}_{1}}}} \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{matrix} \right) , \end{aligned}$$
(21)
$$\begin{aligned} {{M}_{22}}=\left( \begin{matrix} -{{e}^{-{{\gamma }_{l}}d}} &{} 0 &{} -{{e}^{{{\gamma }_{l}}d}} &{} 0 \\ 0 &{} -{{e}^{-{{\gamma }_{l}}d}} &{} 0 &{} -{{e}^{{{\gamma }_{l}}d}} \\ {{\theta }_{c}} &{} i{{\eta }_{c}}{{\mu }_{c}}+i{{\eta }_{l}}{{\mu }_{l}} &{} {{\theta }_{c}} &{} i{{\eta }_{c}}{{\mu }_{c}}-i{{\eta }_{l}}{{\mu }_{l}} \\ i{{\eta }_{c}}{{\varepsilon }_{c}}+i{{\eta }_{l}}{{\varepsilon }_{l}} &{} {{\theta }_{c}} &{} i{{\eta }_{c}}{{\varepsilon }_{c}}-i{{\eta }_{l}}{{\varepsilon }_{l}} &{} {{\theta }_{c}} \\ \end{matrix} \right) \end{aligned}$$
(22)

and \({{\eta }_{\alpha }}=\sqrt{{{\beta }^{2}}\left( y,z \right) -{{\varepsilon }_{\alpha }}{{\mu }_{\alpha }}}\), \(d={{h}_{2}}\left( y,z \right) -{{h}_{1}}\), \({{\theta }_{c}}={{\varepsilon }_{l}}{{\mu }_{l}}-{{\varepsilon }_{c}}{{\mu }_{c}}\), \({{\theta }_{f}}={{\varepsilon }_{l}}{{\mu }_{l}}-{{\varepsilon }_{f}}{{\mu }_{f}}\), \({{\theta }_{s}}={{\varepsilon }_{f}}{{\mu }_{f}}-{{\varepsilon }_{s}}{{\mu }_{s}}\).

3.2 Results Obtained Numerically

To verify the result obtained we consider the Luneburg waveguide lens designed to focus the waveguide mode \(T{{E}_{0}}\) at length \(F=2R\), where R is the waveguide lens radius.

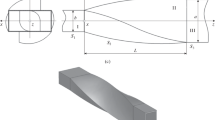
We consider the guided mode \(T{{E}_{0}}\), propagating in a three-layer waveguide from \(z=-\infty \) (see Fig. 1) in the positive direction of the z-axis with the phase \({{\varphi }_{0}}\left( z \right) ={{\beta }_{0}}\left( z+R \right) \), where \({{\beta }_{0}}\) is the coefficient of phase deceleration. At \(z=-R\) the mode enters the waveguide lens. The phase in this domain satisfies the eikonal Eq. (16), which is to be solved.

Initial Data: The wavelength \(\lambda =0.55\left[ \text { }\!\!\mu \!\!\text { m} \right] \); the wavenumber \({{k}_{0}}=2\pi /\lambda \left[ \text { }\!\!\mu \!\!\text { }{{\text {m}}^{-1}} \right] \); the waveguide lens radius \(R={{10}^{3}}\lambda \); the thickness of the main waveguide layer \({{h}_{1}}=2\lambda \); the coating and the substrate in the model are semi-infinite; the variable thickness of the additional waveguide layer is defined as \(d\left( y,z \right) ={{h}_{2}}\left( y,z \right) -{{h}_{1}}\). Due to the cylindrical symmetry of the lens, \({{h}_{2}}\left( y,z \right) ={{\left. h\left( r \right) \right| }_{r=\sqrt{{{y}^{2}}+{{z}^{2}}}/R}}\), the plot of \(h\left( r \right) \) is shown in Fig. 2; the permittivities of the materials are \({{\varepsilon }_{c}}=1\), \({{\varepsilon }_{f}}=2.449225,\,\,{{\varepsilon }_{l}}=3.61,\,\,{{\varepsilon }_{s}}=2.1609\), and their permeabilities are \({{\mu }_{c}}={{\mu }_{f}}={{\mu }_{l}}={{\mu }_{s}}=1\); the coefficient of phase deceleration of the mode \(T{{E}_{0}}\) of the three-layer waveguide is \({{\beta }_{0}}\approx {1.55149273806929012586}\).

Fig. 2.
figure 2

The upper boundary of the additional waveguide layer

Full size image

Numerical Results. The variable thickness \(d\left( y,z \right) \) of the additional waveguide layer corresponds to the function \({{\beta }^{2}}\left( y,z \right) \) that determines the square of the phase deceleration coefficient at the point \(\left( y,z \right) \), presented in Fig. 3.

Fig. 3.
figure 3

Plot of \({{\beta }^{2}}\left( y,z \right) \)

Full size image

The characteristics of the eikonal equation with the right-hand side \({{\beta }^{2}}\left( y,z \right) \) (shown in Fig. 3) are presented in Fig. 4 by the projections of the characteristics on the plane yOz, which we will refer to as rays, and in Fig. 5 by the integral surface \(\varphi \left( y,z \right) \) of the eikonal Eq. (16), composed of the family of integral curves.

Fig. 4.
figure 4

Projections of characteristics on the yOz plane for the Luneburg lens with \(R={{10}^{3}}\lambda \), \(F=2R\)

Full size image
Fig. 5.
figure 5

Integral surface of the phase, composed of the family of integral curves for the Luneburg lens with \(R={{10}^{3}}\lambda \), \(F=2R\)

Full size image

Remark

The calculations for lenses with radii \(R={{10}^{2}}\lambda ,\,\,{{10}^{3}}\lambda ,\,\,{{10}^{4}}\lambda \) yield seemingly similar results (like in Fig. 4, 5) differing only in the scale of the considered domain.

The crossing points of all calculated rays passed through the lens are localized in the interval \({{I}_{F}}=\left[ {{z}_{\min }}\,\,;\,\,\,{{{z}}_{\max }} \right] \). In Table 1 for \(R={{10}^{2}}\lambda ,\,\,{{10}^{3}}\lambda ,\,\,{{10}^{4}}\lambda \) we present the calculated interval lengths \(\left| {{I}_{F}} \right| ={{{z}}_{\max }}-{{z}_{\min }}\), as well as \(\left| {{I}_{F}} \right| /F\), where \(F=2R\). For each \(R={{10}^{2}}\lambda ,\,\,{{10}^{3}}\lambda ,\,\,{{10}^{4}}\lambda \) we also present the limit value of A/R in percent, where the rays, coming from the points \(-A\le z\le A\) cross among themselves, while the rays coming from the points \(z>A\) and \(z<-A\) are parallel to the z-axis.

Table 1. Lengths of the localization interval of the ray crossing point and apertures for different lens radii
Full size table

We also calculate the discrepancy of the eikonal equation

$$\begin{aligned} {{\delta }_{abs}}=\max \left| \varphi _{y}^{2}+\varphi _{z}^{2}-{{\beta }^{2}}\left( y,z \right) \right| , \end{aligned}$$
$$\begin{aligned} {{\delta }_{rel}}=\max \left\{ \left| \varphi _{y}^{2}+\varphi _{z}^{2}-{{\beta }^{2}}\left( y,z \right) \right| /\left| {{\beta }^{2}}\left( y,z \right) \right| \right\} \end{aligned}$$

along the rays, where \({{\varphi }_{y}}\) and \({{\varphi }_{z}}\) are found approximately using the method of characteristics (Table 2).

Table 2. Discrepancy of the eikonal equation
Full size table

The calculated values of \(\max \left| {{\varphi }_{y}}{{h}_{y}} \right| ,\max \left| {{\varphi }_{z}}{{h}_{y}} \right| ,\max \left| {{\varphi }_{y}}{{h}_{z}} \right| \) and \(\max \left| {{\varphi }_{z}}{{h}_{z}} \right| \) are summarized in Table 3.

Table 3. Calculated values of \(\max \left| {{\varphi }_{y}}{{h}_{y}} \right| ,\max \left| {{\varphi }_{z}}{{h}_{y}} \right| ,\max \left| {{\varphi }_{y}}{{h}_{z}} \right| \) and \(\max \left| {{\varphi }_{z}}{{h}_{z}} \right| \)
Full size table

4 Discussion

4.1 Symbolic Results

In this paper, we investigate the AWM model  [14, 15] in the zeroth order of the asymptotic method using the approximation of “horizontal” boundary conditions. The latter is important from a physical point of view, since it allows comparing the AWM model calculations with the results of the cross-sectional method  [21, 23, 24], which also makes use of “horizontal” boundary conditions.

In waveguide problems, the system of boundary equations plays an important role, because its solution determines the phase of the guided modes and the constants for their further numerical construction.

A symbolic-calculation study of the system of boundary equations (in the zeroth approximation with respect to the parameter \(\nu \)) allowed simplifying the form of the system at the symbolic level and reducing the problem in a form convenient for numerical solution.

Instead of solving equation \(\det {{M}^{*}}\left( y,z,{{\varphi }_{y}},{{\varphi }_{z}} \right) =0\), which is extremely difficult to analyze in the symbolic form (the matrix dimension in the general case is \(12\times 12\)) we obtain symbolically the eikonal equation \(\varphi _{y}^{2}+\varphi _{z}^{2}={{\beta }^{2}}\left( y,z \right) \), where only the right-hand side is specified numerically. The quantity \({{\beta }^{2}}\left( y,z \right) \) is specified numerically because it is a solution of the equation \(\det M\left( y,z, {{\beta }^{2}}\left( y,z \right) \right) =0\), where due to symbolic manipulations the initial system of boundary equations with the \(12\times 12\) matrix \({{M}^{*}}\) is reduced to an equivalent system with the \(8\times 8\) matrix M (see. (18)–(22)). Moreover, the computer algebra tools allow determination of \({{\beta }^{2}}\left( y,z \right) \) with enhanced accuracy, using the values with extended number of decimal digits.

The eikonal equation links geometric optics to wave optics, and in the present work its explicit derivation in the AWM model for the particular case of small \(\nu \) is important for geometric interpretation of the guided propagation of adiabatic modes.

Moreover, numerical experiments answer the question about the applicability of the approximation of “horizontal” boundary conditions within the frameworks of the AWM model.

4.2 Numerical Results

In numerical experiments we consider the waveguide Luneburg lens designed to focus the radiation at the distance \(F=2R\), where R is the waveguide lens radius. The calculated rays, passing through the lens, with sufficient accuracy intersect in the focus point (see Fig. 4). The relative error is of the order of \({{10}^{-5}}\) (see Table 1, column 3) for the radii of the lens \({{10}^{2}}\lambda -{{10}^{4}}\lambda \).

In fact, the rays calculated using the AWM model with high accuracy cross in the lens focus at any considered radii of the lens. It is important that the calculations demonstrate that the greater the lens radius (see Table 1, column 4), the greater is the lens aperture within the given accuracy. Thus, for the lens radius \({{10}^{4}}\lambda \) the aperture amounts to \(98.8\%\).

In other words, the greater the radius of the waveguide lens, the more exactly the behavior of the rays close to the lens edges is described by the AWM model in the approximation of “horizontal” boundary conditions.

The applicability of “horizontal” boundary conditions is largely determined by the smallness of the parameter \(\nu \). Commonly \(\nu \) is considered small if it is by two orders of magnitude smaller than unity, i.e., if \(\nu \sim {{10}^{-2}}\). By definition, \(\nu =\left\| V \right\| =\max \left\{ \max \left| {{\varphi }_{y}}{{h}_{y}} \right| ,\max \left| {{\varphi }_{z}}{{h}_{y}} \right| ,\max \left| {{\varphi }_{y}}{{h}_{z}} \right| ,\max \left| {{\varphi }_{z}}{{h}_{z}} \right| \right\} \). Table 3 presents the values of \(\max \left| {{\varphi }_{y}}{{h}_{y}} \right| ,\max \left| {{\varphi }_{z}}{{h}_{y}} \right| ,\max \left| {{\varphi }_{y}}{{h}_{z}} \right| \) and \(\max \left| {{\varphi }_{z}}{{h}_{z}} \right| \) calculated along the rays. Only for the lens with the radius \({{10}^{4}}\lambda \) the parameter \(\nu \) is of the order of \({{10}^{-2}}\) and can be considered small.

From Table 3 it is also seen that the larger the radius of the waveguide lens, the smaller the parameter \(\nu \). Therefore, for extended Luneburg lenses with \(R>{{10}^{4}}\lambda \) the approximation of “horizontal” boundary conditions is likely to be valid.

The AWM model is formulated for smoothly irregular waveguide structures, so that the approximation of “horizontal” boundary conditions is a natural first step. However, this approximation does not describe the complete variety of physical effects, e.g., the effect of mode hybridization. Note, that the AWM model as such can describe vector fields without using the approximation of “horizontal” boundary conditions. In this case it is necessary to solve the problem \(\det {{M}^{*}}\left( y,z,{{\varphi }_{y}},{{\varphi }_{z}} \right) =0\), to which the method of characteristics can be also applied. An additional difficulty will consist in the necessity to calculate partial derivatives of the determinant. This problem is also expected to be solved using the computer algebra system that allows symbolic differentiation of cumbersome expressions like a determinant.

In the present work, we solved only the problem of approximate determination of the phase. We did not set the problems of describing the field in the waveguide lens completely and, what is of primary importance, of constructing the field near the focal point, which is much more difficult.

The present study is focused at developing symbolic-numerical techniques for phase determination. A necessary condition is the use of symbolic manipulations with symbolic expressions, which allows the formulation of the main result.

The Maple option of numerical calculations using extended number of decimal digits appears to be extremely important for solving ill-conditioned problems.

All Maple programs created within the framework of the current study are publicly available at the following link https://bitbucket.org/DmitriyDivakov/waveguide-luneburg-lens/downloads/.

5 Conclusion

In this work, the eikonal equation is symbolically derived, governing the phase of the adiabatic waveguide mode in the approximation of “horizontal” boundary conditions. Based on numerical calculations, it was found that the approximation of “horizontal” boundary conditions is valid for Luneburg waveguide lenses with a radius of more than \(10^4 \lambda \).

Potential applicability of the model of adiabatic waveguide modes to describing the electromagnetic field behavior in focusing problems is demonstrated, which is of importance for modeling and design of waveguide lenses.

As the next step, it is planned to consider the same Luneburg waveguide lens without using the approximation of “horizontal” boundary conditions in the frameworks of the AWM model.