Vehicle Routing Problem with Reverse Cross-Docking: An Adaptive Large Neighborhood Search Algorithm

Abstract

Cross-docking is a logistics strategy that aims at less transportation costs and fast customer deliveries. Incorporating an efficient vehicle routing could increase the benefits of the cross-docking. In this paper, the vehicle routing problem with reverse cross-docking (VRP-RCD) is studied. Reverse logistics has attracted more attention due to its ability to gain more profit and maintain the competitiveness of a company. VRP-RCD includes a four-level supply chain network: suppliers, cross-dock, customers, and outlets, with the objective of minimizing vehicle operational and transportation costs. A two-phase heuristic that employs an adaptive large neighborhood search (ALNS) with various destroy and repair operators is proposed to solve benchmark instances. The simulated annealing framework is embedded to discover a vast search space during the search process. Experimental results show that our proposed ALNS obtains optimal solutions for 24 out of 30 problems of the first set of benchmark instances while getting better results for all instances in the second set of benchmark instances compared to optimization software.

1 Introduction

In a supply chain network, suppliers deliver their products to customers in two different ways, either through a direct shipment or a transhipment process. This supply chain is a vital function since customers want to receive products in quick and easy ways. In a direct shipment, each supplier may dispatch one or more vehicles in order to fulfil all customer demands, resulting in long origin-to-destination paths and a large number of vehicles dispatched [15]. On the other hand, adopting an intermediate facility for a transshipment process can improve supply chain performance as a whole and provide better delivery performance to customers. Products from suppliers are first sent to a cross-dock, sorted and consolidated according to customer demands, and then delivered to customers afterwards. It can provide enhanced customer service and it can speed up customer deliveries. Advantages of cross-docking will be enhanced by an efficient vehicle routing [6]. It is important for a distribution network because it reduces or eliminates the storage activities that belong to the warehousing system. Products are not allowed to be stored inside the cross-dock. [14] compared the performance between adopting the cross-docking strategy and direct shipments. The experiments conclude that cross-docking is capable to achieve cost savings compared to the direct-shipping under certain conditions.

The VRP plays an essential role in the field of supply chain management and logistics. It is associated with important role in distribution management and logistics, as well as the costs associated with operating vehicles with the objective of finding optimal delivery from a warehouse to a set of customers with respect to limited constraints. Customers are served by some identical vehicles with a limited capacity from suppliers. This combined VRP and cross-docking model is addressed as a vehicle routing problem with cross-docking (VRPCD) that has been widely studied [4, 11, 19]. Many industries or companies have started to pay more attention in reverse logistics as this concept has been recognized as a source of profitability and competitiveness for their businesses [1, 8, 10]. Apple, H&M, and Dasani are some examples of companies that implement reverse logistics. In reverse logistics, the returned products from customers are collected and sent back to the suppliers [9] for further processes such as break down or re-manufacture process. Due to the advantages of adopting cross-docking in the forward flow, [20] studied the VRPCD in reverse logistics flow, the so-called VRP with reverse cross-docking (VRP-RCD). We then re-visit this VRP-RCD which is suitable for companies with seasonal demand patterns, such as fashion, books, and electronics, and which commercialize the returned (unsold) products through secondary channels (e.g. outlet stores). The practice of introducing cross-docking as a viable strategy for handling returned products in the European apparel industry is highlighted by [22]. The main difference with the problem discussed in [9] is that VRP-RCD [20] happens in a four-level supply chain network consisting of suppliers, customers, outlets, and a cross-dock, while [9] only considers a three-level supply chain network: suppliers, customers, and a cross-dock. Furthermore, VRP-RCD [20] considers a multiple product scenario and a situation where some of the supplied products can be defective.

In this paper, we introduce a two-phase heuristic that employs an adaptive large neighborhood search (ALNS) to solve the VRP-RCD [20]. ALNS was firstly introduced by [16] as the extension of LNS [18]. It has been widely adopted to solve many variants of VRP such as the pollution-routing problem (PRP) [2], the two echelon VRP (2E-VRP) [7], the VRP with drones [17] and the VRPCD [4]. ALNS has also been implemented to perform the column generation process in a matheuristic approach to solve the VRPCD with time windows [3] and the VRPCD [5]. Due to the superiority of ALNS to solve various combinatorial optimization problems, we adopted the ALNS used in [4] to solve the VRP-RCD. However it should be noted that the algorithm needs several modifications due to different assumptions in both problems, such as: 1) VRPCD assumes all nodes are visited, while in VRP-RCD some nodes might not be visited, 2) VRPCD only involves customer and supplier nodes, while VRP-RCD involves customer, supplier, and outlet nodes, and 3) VRPCD considers an individual pickup (delivery) process in supplier (customer) nodes, while VRP-RCD also considers the simultaneous pickup and delivery processes in outlet nodes. In general, ALNS employs destroy and repair operators to repetitively remove some nodes from a solution and to re-insert these back to a more profitable position. We also employ simulated annealing (SA) acceptance criteria that gives us a chance to accept a worse solution rather than always reject it, so as in order not to get stuck in local optima. The proposed ALNS performs well in solving the available benchmark VRP-RCD instances. For the first set of instances, it is able to obtain optimal solutions for 24 out of 30 instances. For the second set of instances which is a larger set, it outperforms optimization software, CPLEX, by obtaining 38.81% better results on average, with significantly faster computational times.

The rest of the paper is organized as follows. In the next section, we provide the problem description of the VRP-RCD. Section 3 presents the proposed ALNS algorithm. The computational results are presented in Sect. 4. Finally, Sect. 5 concludes the paper with our findings and directions of future research.

2 Problem Description

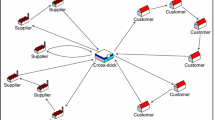
The VRP-RCD network (as shown in Fig. 1) involves |C| customers, |O| outlets, |S| suppliers, and a cross-dock facility to handle the reverse logistics process. In this problem, customers can be shops or wholesalers that are trying to sell products, but may not be able to sell all. Since those products may almost reach their end of life (EOL) period to be sold on the customers site, they are then passed to the outlets for the second round of selling process with lower prices. However, those products may not be sold in outlets and have to be replaced with newer products, therefore they will be returned to the supplier who supplied those products, for further processing (e.g. re-manufacture or break down).

Each connected arc between customer and cross-dock nodes has a travel distance of $e_{ij}^{'}$ and a travel time of $t_{ij}^{'}$. For outlet and cross-dock nodes, each connected arc has a travel distance of $e_{ij}^{''}$ and a travel time of $t_{ij}^{''}$. Finally, between supplier and cross-dock nodes, we represent a travel distance of $e_{ij}^{'''}$ and a travel time of $t_{ij}^{'''}$ for each connected arc. Let c represent the transportation cost per unit distance.

Fig. 1.

VRP-RCD network

A set of homogeneous vehicles $V={1,2,\ldots ,|V|}$ with the same vehicle capacity q and operational cost H is available at the cross-dock to perform any one of three processes involved in VRP-RCD: 1) customer pickup process, 2) outlet delivery and pickup process, and 3) supplier delivery process. Let $r_{ik}^{'}$ be defined as the amount of returned products k from customer i and $r_{ik}^{''}$ as the amount of returned products k from outlet i.

In the first process, a vehicle starts from the cross-dock, visits one or more customers to pick up any returned products $r_{ik}^{'}$, and back to the cross-dock at the end of its trip. Among the returned products type k, $p_k$ percent is considered as defective products, which hence, only $(100-p_k)$ percent of the returned products type k can be distributed to any outlet nodes for the reselling process. Therefore, outlet i with demand of product type k as much as $d_{ik}^{''}$ may not be able to receive all of its demand. If the non-defective unsold products k from all customers are able to fulfil all outlets demand of product k, then, all outlets with demands of product k will be visited. Otherwise, only several outlets will be visited, which depends on the number of non-defective unsold products k. The second process is thus implemented to cover this delivery process to outlet nodes, as well as to pick up their returned products $r_{ik}^{''}$. Finally, all returned and defective products are sent back to each supplier that supplied that product in the third process. It is assumed that one supplier supplies one type of product. The VRP-RCD then aims to decide the number of vehicles used as well as to construct the route sequence of the used vehicles such that all processes are done within the $T_{max}$ time horizon, while minimizing the total costs in the process (vehicle transportation and fixed operational costs). The VRP-RCD assumes a synchronous arrival scenario where the second process can only be performed after the first process is finished, and subsequently the third process can only be performed after the second process is done. This assumption is adopted from the original VRPCD [11, 12, 21].

The VRP-RCD addressed here is slightly different compared to the one of [20] in terms of defining the amount of returned products from customers and outlets. The VRP-RCD [20] considers the amount of customer returned products as a fraction of their demand in the previous cycle, while the amount of outlet returned products was defined as a fraction of the amount of products they received during the delivery process in the previous cycle. However, it might be hard to find the relationship between those two values in practice. Therefore, the VRP-RCD in this paper models the amount of returned products as known parameters $r_{ik}^{'}$ and $r_{ik}^{''}$ when the routing is planned, as how it is addressed in the literature [9].

3 Proposed Algorithm

Our proposed algorithm is divided into two phases. The first phase aims to decide the selected nodes and the second phase aims to construct the routing sequence given the selected nodes from the first phase, such that the total transportation and operational costs is minimized. The selected nodes from the first phase will be treated as the input and will not be modified during the second phase. Therefore, we carefully derive some rules to determine which nodes to be visited in Sect. 3.1. The second phase, described in Sect. 3.2, employs an adaptive large neighborhood search (ALNS) to find a set of routes sequence given the selected nodes from the first phase.

3.1 Phase 1: Node Selection

Since not all nodes are mandatory to be visited in this problem, we need to select which nodes to be visited. We define $m_i^{'}$ equals to 1 if node i must be visited during the customer pickup process; 0 otherwise $(i \in C)$, $m_i^{''}$ equals to 1 if node i must be visited during the outlet delivery and pickup process; 0 otherwise $(i \in O)$, and $m_i^{'''}$ equals to 1 if node i must be visited during the supplier delivery process; 0 otherwise $(i \in S)$. The decision of $m_i^{'}$ is done in a very straightforward rule, where customer i is visited $(m_i^{'} = 1)$ if there is any returned products from customer i, and $m_i^{'} = 0$ otherwise.

For deciding the value of $m_i^{''}$, we need to calculate the amount of delivered product k to node i in advance, denoted as $\vartheta _{ik}^{''}$. If the amount of non-defective returned product k from all customers are more than outlets demand of product k, we set $\vartheta _{ik}^{''} = d_{ik}^{''} \;\; \forall i \in O, \forall k \in S$. Otherwise, we apply a sorting criteria on the outlets and then iteratively assign $\vartheta _{ik}^{''}$ according to this sorting until the amount of available units is reached. One of the following sorting criteria is randomly selected to decide the amount of $\vartheta _{ik}^{''}$:

• outlet with the highest demand of product k

• outlets that have demand of product k by splitting the same amount of non-defective returned product k from all customers to those outlets.

• outlet with demand of product k that is located nearest to the cross-dock and any other outlets

• outlet with the highest product types demand

• outlet with the highest cumulative demand of all product types

• outlet with the lowest unique returned product types

• outlet with the lowest cumulative returned products of all product types

Hence, outlet i will only be visited $(m_i^{''} = 1)$ if there is any delivered and/or returned products from outlet i, and $m_i^{''} = 0$ otherwise. Finally, supplier k is visited $(m_k^{'''} = 1)$ if there is any returned products to supplier k, as formulated in Eq. (1).

$$\begin{aligned} m_k^{'''} = {\left\{ \begin{array}{ll} 1, &{} \text {if } \sum _{i \in C} r_{ik}^{'} - \sum _{i \in O} \vartheta _{ik}^{''} + \sum _{i \in O} r_{ik}^{''} > 0\\ 0, &{} \text {if } \sum _{i \in C} r_{ik}^{'} - \sum _{i \in O} \vartheta _{ik}^{''} + \sum _{i \in O} r_{ik}^{''} = 0\\ \end{array}\right. } \;\; \forall k \in S \end{aligned}$$

(1)

3.2 Phase 2: Adaptive Large Neighborhood Search (ALNS)

A two-dimensional solution representation with each row v representing the route sequence performed by a particular vehicle, $v \in |V|$ is designed. Hence, a solution has a fixed number of |V| rows and a different number of columns in each row v, which depends on the number of visited nodes by vehicle v. This solution representation is illustrated in Fig. 2. For example, starting from the cross-dock (node 0), vehicle 1 visits suppliers 3, 2, 1, and 4 respectively, and returns back to node 0. The amount of non-defective returned products from customers can only fulfil demands of outlets 2 and 4, therefore only outlets 2 and 4 are visited by vehicle 2. Due to the vehicle capacity and time horizon constraints, one vehicle alone is unable to visit all customers. Vehicle 3 visits customers 3, 1, and 4, while vehicle 4 visits customers 2, 6, and 5. In this example, in total four vehicles are required to complete the entire process.

Fig. 2.

Example of solution representation with $|S|=4, |O|=5, |C|=6, |V|=5$

3.2.1 Initial Solution

Based on the selected nodes from the first phase (Sect. 3.1), we perform the following five steps to construct an initial solution:

STEP 1: Node allocation. We allocate nodes to vehicles by solving the following mathematical model.

• $a_i^{'v}$ is a binary decision variable with value 1 indicating node i is visited by vehicle v in the customer pickup process; 0 otherwise $(i \in C, v \in V)$

• $a_i^{''v}$ is a binary decision variable with value 1 indicating node i is visited by vehicle v in the outlet delivery and pickup process; 0 otherwise $(i \in O, v \in V)$

• $a_i^{'''v}$ is a binary decision variable with value 1 indicating node i is visited by vehicle v in the supplier delivery process; 0 otherwise $(i \in S, v \in V)$

• $x^{'v}$ is a binary decision variable with value 1 indicating vehicle v in used in customer pickup process; 0 otherwise $(v \in V)$

• $x^{''v}$ is a binary decision variable with value 1 indicating vehicle v in used in outlet delivery and pickup process; 0 otherwise $(v \in V)$

• $x^{'''v}$ is a binary decision variable with value 1 indicating vehicle v in used in supplier delivery process; 0 otherwise $(v \in V)$

The objective function (2) minimizes the number of vehicles used.

$$\begin{aligned} Min \;\; \sum _{v \in V} x^{'v} + x^{''v} + x^{'''v} \end{aligned}$$

(2)

All mandatory visited nodes are visited by exactly one vehicle, as addressed in constraints (3) to (5).

$$\begin{aligned} \sum _{v \in V} a_i^{'v} = m_i^{'} \;\; \forall i \in C \end{aligned}$$

(3)

$$\begin{aligned} \sum _{v \in V} a_i^{''v} = m_i^{''} \;\; \forall i \in O \end{aligned}$$

(4)

$$\begin{aligned} \sum _{v \in V} a_i^{'''v} = m_i^{'''} \;\; \forall i \in S \end{aligned}$$

(5)

The vehicle capacity constraints are presented by constraints (6) to (8). Constraint (6) ensures that the amount of picked-up products from any customers assigned to vehicle v does not exceed the vehicle capacity. Constraint (7) ensures that the amount of max(picked-up, delivered) products from/to any outlets assigned to vehicle v does not exceed the vehicle capacity. Constraint (8) ensures that the amount of delivered products to any suppliers assigned to vehicle v does not exceed the vehicle capacity. The amount of delivered products equals the sum of (the difference between customers returned products and amount of products delivered to outlets) and (outlets returned products).

$$\begin{aligned} \sum _{i \in C} \sum _{k \in S} a_i^{'v} r_{ik}^{'} \le q \;\; \forall v \in V \end{aligned}$$

(6)

$$\begin{aligned} \sum _{i \in O} a_i^{''v} \times \text {max}\left( \sum _{k \in S}\vartheta _{ik}^{''},\sum _{k \in S}r_{ik}^{''}\right) \le q \;\; \forall v \in V \end{aligned}$$

(7)

$$\begin{aligned} \sum _{k \in S} a_k^{'''v} \left( \sum _{i \in C} r_{ik}^{'} - \sum _{i \in O} \vartheta _{ik}^{''} + \sum _{i \in O} r_{ik}^{''}\right) \le q \;\; \forall v \in V \end{aligned}$$

(8)

Constraints (9) to (11) keep track of the used vehicle in each process and constraint (12) ensures that each vehicle is being used in at most one of the three processes.

$$\begin{aligned} |C| x^{'v} \ge \sum _{i \in C} a_i^{'v} \;\; \forall v \in V \end{aligned}$$

(9)

$$\begin{aligned} |O| x^{''v} \ge \sum _{i \in O} a_i^{''v} \;\; \forall v \in V \end{aligned}$$

(10)

$$\begin{aligned} |S| x^{'''v} \ge \sum _{i \in S} a_i^{'''v} \;\; \forall v \in V \end{aligned}$$

(11)

$$\begin{aligned} x^{'v} + x^{''v} + x^{'''v} \le 1 \;\; \forall v \in V \end{aligned}$$

(12)

STEP 2: Route sequence construction. We implemented a nearest neighbor heuristic to construct a route sequence in each vehicle.

STEP 3: Time feasibility checking. It is done by recording the maximum transportation time in each process, denoted as $Tcp_{max}$, $Todp_{max}$, and $Tsd_{max}$. If the total of $Tcp_{max}$, $Todp_{max}$, and $Tsd_{max}$ does not exceed time horizon, we continue to STEP 5. Otherwise, go to STEP 4.

STEP 4: Repair time infeasibility. We remove a node from a vehicle that has the highest total transportation time, and relocate this node to another vehicle as long as it does not violate the vehicle capacity and time horizon constraints. Otherwise, this node will be relocated to a new vehicle. This step is repeated until time horizon constraint is satisfied.

STEP 5: Objective function value calculation. The objective function is calculated by adding up the total of transportation and operational costs.

3.2.2 Algorithm

ALNS employs destroy and repair operators that aims to remove $\pi$ nodes from a solution and then to reinsert them back in a more profitable position, such that a new solution is observed. The performance of each operator is then evaluated and is given a higher score if it generates a better solution. This score later becomes the base for calculating its weight, which adjusts its probability to be selected in the following iterations. When a combination of destroy-repair operators is able to generate a better solution, its score is increased and also its weight and probability. Additionally, in order to escape from local optima, we incorporate simulated annealing (SA) acceptance criteria by giving chance to accept worse solution during the search process.

Let us define $R = \{R_r | r = 1, 2, \ldots , |R|\}$ and $I = \{I_i | i = 1, 2, \ldots , |I|\}$ as the set of destroy and repair operators respectively (see Sect. 3.2.3). Every time destroy and repair operators generate a new solution, we adjust its score using Eq. (13), where $\delta _1> \delta _2 > \delta _3$ [13]. In our implementation, we use $\delta _1=0.5, \delta _2=0.33, \delta _3=0.17$.

$$\begin{aligned} s_j = {\left\{ \begin{array}{ll} s_j + \delta _1, &{} \text {if } j \text { is selected and the new solution is} \\ &{} \text {the best found solution so far} \\ s_j + \delta _2, &{} \text {if }j \text { is selected and the new solution} \\ &{} \text {improves the current solution} \\ s_j + \delta _3, &{} \text {if }j \text { is selected and the new solution} \\ &{} \text {does not improve the current solution,} \\ &{} \text {but it is accepted} \\ \end{array}\right. } \;\; \forall j \in R \cup I \end{aligned}$$

(13)

After $\eta _{ALNS}$ iterations, we calculate each operators weight by following Eq. (14). Subsequently, operators probability are adjusted by following Eq. (15).

$$\begin{aligned} w_j = {\left\{ \begin{array}{ll} (1-\gamma )w_j + \gamma \frac{s_j}{\chi _j}, &{} \text {if } \chi _j > 0 \\ (1-\gamma )w_j, &{} \text {if } \chi _j = 0 \\ \end{array}\right. } \;\; \forall j \in R \cup I \end{aligned}$$

(14)

$$\begin{aligned} p_j = {\left\{ \begin{array}{ll} \frac{w_j}{\sum _{k \in R} w_k} \;\; \forall j \in R\\ \frac{w_j}{\sum _{k \in I} w_k} \;\; \forall j \in I\\ \end{array}\right. } \end{aligned}$$

(15)

The pseudocode is presented in Algorithm 1. ALNS starts by setting the current solution $(Sol_0)$, the best solution so far $(Sol^*)$, and the starting solution in each iteration $(Sol')$ equals to InitialSolution, which is constructed based on Sect. 3.2.1 (line 1). The current temperature Temp is set as initial temperature $(T_0)$ (line 2) which will be reduced by $\alpha$ after $\eta _{SA}$ (line 32). FoundBestSol is set as False in the beginning (line 4) and every $\eta _{SA}$ iterations (line 31). Its value will only be True if a new better than $Sol^*$ solution is found (lines 17–19). Subsequently, when it is True, then NoImpr is reset as 0 (lines 28–30), otherwise it is increased by one (lines 25–27). At the beginning, all operators are initialized by the same score, weight, and probability (line 5).

In every iteration, $\pi$ nodes are removed from $Sol_0$ (lines 8–11) by a Destroy operator. Those $\pi$ nodes are then reinserted to $Sol_0$ by a Repair operator (lines 12–15). A new solution is directly accepted if improves $Sol^*$ or $Sol'$. Otherwise, it will only be accepted by a $e^{\frac{-(TC(Sol_0)-TC(Sol'))}{Temp}}$ chance (line 16), where TC(x) represents the total cost of solution x. Subsequently, we update operators score, weight, and probability. The ALNS terminates when there is no solution improvements after $\theta$ successive temperature reductions.

3.2.3 Operators

We list down the operators used in the proposed algorithm:

Random removal ($R_1$): randomly remove a node from $Sol_0$.

Worst removal ($R_2$): remove a node that has the $x^{th}$ highest removal gain (i.e. the difference in objective function values between including and excluding this node). x is decided by following Eq. (16), where $y_1 \sim U(0,1)$, $p = 3$, and $\xi$ is the number of candidate nodes which is formally formulated in Eq. (17), case 1.

$$\begin{aligned} x = \lceil y_1^p \times \xi \rceil \end{aligned}$$

(16)

$$\begin{aligned} \xi = {\left\{ \begin{array}{ll} |C|+|S|-\textsc {RemovedNodes}, &{} \text {for }R_2 \\ |C|+|S|-\textsc {RemovedNodes}-2, &{} \text {for }R_4, R_5\\ \textsc {RemovedNodes}, &{} \text {for }I_9 \\ \end{array}\right. } \end{aligned}$$

(17)

Route removal ($R_3$): randomly select a vehicle and remove z visited nodes. $z=\text {min}(\pi ,\beta )$, where $\beta$ is the number of nodes visited by that vehicle.

Node pair removal ($R_4$): remove a pair of nodes that has the $x^{th}$ highest transportation cost. x is determined by Eq. (16) while $\xi$ follows Eq. (17) case 2. The idea is to remove two adjacent nodes with a high transportation cost from the $Sol_0$, such that when repair reinserts them back to $Sol_0$, they can be located in better, probably separated, positions.

Worst pair removal ($R_5$): similar to $R_2$, but $R_5$ chooses a pair of nodes instead of only one node. The underlying difference between $R_4$ and $R_5$ is that $R_4$ only focuses in the transportation cost between two nodes, while $R_5$ considers the overall costs. x is determined by Eq. (16) while $\xi$ is determined by Eq. (17) case 2.

Shaw removal ($R_6$): remove a node that is highly related with other removed nodes in a predefined way, so as it is easier to replace the positions of one another during the repair process. Let us define node i as the last removed node and node j as the next candidate to be removed. The relatedness value of node j $(\varphi _j)$ to node i is calculated by Eq. (18), where $\phi _1$ to $\phi _3$ are weights given to each of the related components in terms of travel distance, travel time, and node position ($l_{ij} = -1$ if nodes i and j are in the same vehicle; 1 otherwise). This means that the lower the $\varphi _j$ is, the more related node j to i is. Therefore, node j with lowest $\varphi _j$ is then selected and removed from $Sol_0$. We implement $\phi _1 = \phi _2 = \phi _3 = \frac{1}{3}$.

$$\begin{aligned} \varphi _j = {\left\{ \begin{array}{ll} \phi _1 e_{ij}^{'} + \phi _2 t_{ij}^{'} + \phi _3 l_{ij}, &{} \text {if } i \in C\\ \phi _1 e_{ij}^{''} + \phi _2 t_{ij}^{''} + \phi _3 l_{ij}, &{} \text {if } i \in O \\ \phi _1 e_{ij}^{'''} + \phi _2 t_{ij}^{'''} + \phi _3 l_{ij}, &{} \text {if } i \in S \\ \end{array}\right. } \end{aligned}$$

(18)

Greedy insertion ($I_1$): insert a node to a position with the lowest insertion cost (i.e. the difference in objective function values between after and before inserting a node to a particular position).

k-regret insertion ($I_2$ , $I_3$ , $I_4$): a regret value is defined as the difference in objective function values when node j is inserted in the best position (denoted as $TC_1(j)$) and in the k-best position (denoted as $TC_k(j)$). A node with the largest regret value (see Eq. (19)) is then inserted in its best position.

$$\begin{aligned} \mathop {\mathrm {argmax}}\limits _{j \in \textsc {RemovedNodes}} \left\{ \sum ^{k}_{i=2} (TC_i(j) - TC_1(j)) \right\} \end{aligned}$$

(19)

Greedy insertion with noise function ($I_5$): an extension of $I_1$ by introducing a noise function to the objective function value (20) when selecting the best position of a node, where $\overline{\mathrm{e}}$ is the maximum transportation cost between nodes (problem-dependent), $\mu$ is a noise parameter (set to 0.1 in our case), and $y_2 \sim U(-1,1)$.

$$\begin{aligned} TC_{new} = TC + \overline{\mathrm{e}} \times \mu \times y_2 \end{aligned}$$

(20)

k-regret insertion with noise function ($I_6$ , $I_7$ , $I_8$): an extension of $I_2$, $I_3$, and $I_4$ by applying a noise function to the objective function value (20) when calculating the regret value.

GRASP insertion ($I_9$): similar to $I_1$, but instead of choosing a node with the lowest insertion cost, $I_9$ chooses a node that has the $x^{th}$ lowest insertion cost. x is determined by Eq. (16) while $\xi$ is determined by Eq. (17) case 3.

4 Computational Results

Our proposed ALNS is tested on the available benchmark VRP-RCD instances introduced in [20]. The instances are available in https://www.mech.kuleuven.be/en/cib/op/opmainpage#section-50. The benchmark VRP-RCD instances consists of two sets, the first set of instances with 15 nodes and the second set of instances with 40 nodes, each having 30 problems. Parameter values of these instances are summarized in Table 1. OFAT (One-factor-at-a-time) method is used to tune parameters by solving randomly selected instances. The best values for parameters are summarized in Table 2. The following experiments are then conducted based on this setting.

Table 1. VRP-RCD parameter values

Table 2. ALNS parameter values

The proposed ALNS is coded in C++ and run on a computer with Intel Core i7-8700 CPU @ 3.20 GHz processor, 32.0 GB RAM. We perform 5 replications for each instance and the best total cost (TC) obtained is recorded. Subsequently, the average and total computational time of 5 replications are also presented. Tables 3 and 4 summarize results on Sets 1 and 2 instances, respectively. Since no state-of-the-art algorithms have been introduced to solve this problem, we compare our TC results against those obtained by CPLEX by calculating Gap (%) using the following Eq. (21). We also remark the lowest TC in each problem instance by bold.

$$\begin{aligned} Gap~(\%) = \frac{(TC_{ALNS} - TC_{CPLEX})}{TC_{CPLEX}} \times 100 \end{aligned}$$

(21)

Table 3. Results on Set 1 instances

Table 4. Results on Set 2 instances

Results on the first set of instances show that our proposed ALNS is able to get the optimal solutions for 24 out of 30 problems with significantly shorter computational times compared to CPLEX (around 0.1% of CPLEX computational time). For the second set of instances, ALNS provides better solutions than CPLEX for all instances, with an average gap of 38.81% within again, only 0.1% of CPLEX’s computational times. From the practical perspective, ALNS outperforms CPLEX since it only needs a few seconds. For larger instances, ALNS is expected to solve them within reasonable computational times. However, it may be possible that ALNS could not solve all larger instances to optimality.

5 Conclusion

This paper studies the reverse flow of the vehicle routing problem and cross-docking, namely vehicle routing problem with reverse cross-docking (VRP-RCD). The VRP-RCD considers a four level supply chain network involving suppliers, cross-dock, customers, and outlets. There are three processes that must be conveyed in the VRP-RCD, which are the customer pickup process, outlet delivery and pickup process, and supplier delivery process. We designed a two-phase heuristic that employs an adaptive large neighborhood search (ALNS) to solve the VRP-RCD. ALNS uses various destroy and repair operators to generate neighborhood solutions. Furthermore, a simulated annealing (SA) framework is embedded to discover a vast search space during the search process.

We tested our proposed ALNS by solving the available benchmark VRP-RCD instances. Experimental results on the first set of instances show that our proposed ALNS is able to obtain optimal solutions for 24 out of 30 problem instances with significantly shorter computational time. When solving the second set of instances, ALNS is able to obtain better solution for all problem instances with an average improvement of 38.81% and only need 0.1% of CPLEX’s computational times. Generating and solving larger instances, e.g. with 100 or 200 nodes, would be interesting for future research. It is noted that selecting which outlets to visit is fixed and it is not a part of the routing problem in our problem. However, this could be integrated in the future, but then the problem becomes much more complicated if selecting the outlets is considered as part of the routing problem. Other possible extensions, such as introducing exact algorithms, imposing penalties for unvisited nodes and partial deliveries, considering a mixture of direct-shipping and cross-docking, asynchronous arrival scenario, multi-period settings, can be further studied. Introducing new and larger instances can be explored as well in order to represent real-sized problems faced by industries.