Higgs Boson Data Analysis

Roskes, Jeffrey

doi:10.1007/978-3-030-58011-7_5

Jeffrey Roskes²

Part of the book series: Springer Theses ((Springer Theses))

187 Accesses

Abstract

This chapter presents a series of analyses, increasing in complexity and precision, to measure anomalous couplings of the Higgs boson. The later measurements in the sequence use the Higgs boson’s decay to four leptons onshell and offshell, its production in association with jets or top quarks, to measure its interactions with vector bosons and fermions. Advanced statistical methods are employed to measure multiple anomalous couplings simultaneously, taking into account the complicated contributions of quantum mechanical interference.

Access provided by Autonomous University of Puebla. Download chapter PDF

Keywords

With the data processed and recorded and the theoretical basis for the calculations understood, we can analyze the data to measure the Higgs boson’s properties. Figs. 5.1 and 5.2 shows the mass distribution of the four-lepton events from the Run 2 dataset, with the Higgs boson peak at 125 shown in red. Most of the analyses shown here use some or all of these events.

5.1 Run 1 Results

Measuring the spin and parity of the Higgs boson was one of the first experimental priorities after its discovery. The earliest papers from Run 1 of the LHC confirmed that the newly discovered particle primarily interacts as a spin-zero particle with J ^CP = 0⁺⁺, with results from both CMS [5,6,7] and ATLAS [8, 9]. The spin analyses used the Higgs boson’s decay to H →ZZ → 4ℓ, H →WW → 2ℓ2ν, and γγ, while the parity analyses, which need more degrees of freedom than a two-body decay can provide, used H →ZZ → 4ℓ and H →WW → 2ℓ2ν.

As a validation of the spin analysis, it is also interesting to measure the spin of the Z boson, which is well known to be a spin-1 particle, using identical methods. This serves as a validation of the matrix element procedure as well as of the background modeling. The Z boson can decay to 4 leptons through the diagram shown in Fig. 5.3, which forms the peak at 91.2 in Fig. 5.2. This is distinguished from the alternate hypothesis of a new H boson at 91.2 that decays to 4 leptons via H →ZZ → 4ℓ. It is also possible that the Z boson exists and behaves as expected, but a tiny fraction of the peak f _H is made by a new Higgs boson. Using methods similar to the ones that will be described below, the fractional contribution of a spin 0 particle to the Z peak is measured to be less than 0.8 % at 95 % confidence level, as shown in Fig. 5.4.

After hypotheses such as a pure a ₃ contribution were excluded, it still remains interesting to search for a small anomalous contribution to the Higgs boson’s interactions. The first comprehensive paper, searching for a wide variety of alternate spin and coupling hypotheses, was [7], which used H →ZZ → 4ℓ, H →WW → 2ℓ2ν, and H → γγ data. These early analyses form the starting point for the more complicated analyses in Run 2, to be discussed further.

The simplest analyses assumed that a maximum of one anomalous term is nonzero and that the anomalous couplings are real, so that the amplitude and probability for the Higgs boson’s decay to four fermions, as a function of the SM coupling a ₁, an anomalous coupling a _i, and the lepton kinematics $\vec {\Omega }$ is

$$\displaystyle \begin{aligned} \mathcal{A}(a_1,a_i,\vec{\Omega})&=a_1\mathcal{A}_1(\vec{\Omega})+a_i\mathcal{A}_i(\vec{\Omega}) \end{aligned} $$

(5.1)

$$\displaystyle \begin{aligned} \mathcal{P}(a_1,a_i,\vec{\Omega})={\left\lvert \mathcal{A} \right\rvert}^2&=a_1^2\mathcal{P}_1(\vec{\Omega})+a_i^2\mathcal{P}_i(\vec{\Omega})+a_1a_i\mathcal{P}_{\text{int}}(\vec{\Omega}) {} \end{aligned} $$

(5.2)

The analysis proceeds by constructing templates, n-dimensional histograms that parameterize the probability as a function of Ω, for $\mathcal {P}_1$, $\mathcal {P}_i$, and $\mathcal {P}_{\text{int}}$, as well as for the background contributions. The signal templates are all constructed from gluon fusion Monte Carlo produced by POWHEG [10,11,12,13,14] with the H →ZZ → 4ℓ decay provided by JHUGEN [15,16,17,18,19]. The irreducible backgrounds for this analysis are qq → 4ℓ, also estimated through Monte Carlo simulated by POWHEG, and gg → 4ℓ, estimated through MCFM [20] simulation. Additionally, the Z + X background, which comes primarily from jets that are misinterpreted as leptons in the detector, is estimated using a control region in the data.

In principle, the ideal way to go would be to construct templates using the full probability distribution as a function of the angles and masses that define $\vec {\Omega }$, as shown in Fig. 4.8. This was done in some simplified cases in that paper, but does not scale well. Instead, we project $\vec {\Omega }$ onto the most relevant degrees of freedom using the MELA discriminants described in Sect. 4.6.2 and bin the distribution in 3D histograms. For an analysis that searches for just one anomalous coupling, it is possible to choose three observables that lose no information: $\mathcal {D}_{\text{bkg}}$, which separates signal from background; a $\mathcal {D}_{ai}$ discriminant to separate the SM coupling from the chosen BSM coupling a _i; and a $\mathcal {D}_{\text{int}}$ discriminant to separate the interference contribution. $\mathcal {D}_{\text{bkg}}$ is calculated from the reconstructed Higgs boson’s invariant mass m _4ℓ as well as the kinematics from the decay, the angles and dilepton invariant masses in Fig. 4.8. The other discriminants rely only on the decay kinematics. Figure 5.5 shows the distributions of some of these discriminants in the Monte Carlo simulation and data.

The interference discriminant shown in Fig. 5.5c is special in the sense that it represents interference between a CP-even and a CP-odd process. The distribution of this discriminant for any purely CP-even (such as a pure SM Higgs boson or any background process) or CP-odd process (such as a pure a ₃ Higgs boson) will be symmetric around 0, as shown in the figure. Although this analysis and other similar ones described below search for nonzero f _a3, any statistically significant asymmetry in $\mathcal {D}_{CP}$ would be a sign of CP violation, even if it does not match a particular hypothesis. Another interference discriminant is used in the analysis measuring a ₂, which detects the interference between a ₁ and a ₂, but that discriminant shows no special symmetry because the interference is between two CP-even terms.

In this simplest example, the only contributions to the probability are background, SM signal, pure BSM signal, and interference. For this reason, three discriminants are sufficient to contain all the information from the kinematics, as described in Sect. 4.6.2. A small amount of information is lost due to finite binning of those discriminants, but enough bins were used that the loss is small.

Once the templates are constructed, we perform an unbinned extended maximum likelihood fit [21], where the probability density is normalized to the total event yield in each process j and category k. In the analyses here, the events were divided into categories depending on the final state lepton flavor: H → 2e2μ, 4e, or 4μ, and the signal processes are all included together, but the notation is general to accommodate later, more complicated analyses. The overall probability density function is given by

$$\displaystyle \begin{aligned} \mathcal{P}_{jk}(\vec{\Omega};\mu_j,\vec{f}_j) = \mu_j \mathcal{P}_{jk}^{\text{sig}} \left( \vec{\Omega};\vec{f} \right) + \mathcal{P}_{jk}^{\text{bkg}} \left( \vec{\Omega}\right), {} \end{aligned} $$

(5.3)

$\mathcal {P}^{\text{sig}}$ is defined by Eq. (5.2) for these analyses and similar expressions for the more complicated ones described later. It is a function of the kinematics $\vec {\Omega }$, the anomalous couplings $\vec {f}$, and the overall scaling μ. As described in Sect. 4.4, we reparameterize the SM coupling a ₁ and n anomalous couplings $\vec {a}_i$ into n f _ai’s (Eq. (4.2)), one for each anomalous coupling, and the signal strength μ. In this way, we decorrelate the shape of the event distributions, which is our primary interest in these analyses, from the number of events. In more complicated analyses, different signal processes will have separate μ _j’s.

The result of the analysis is a likelihood scan that gives the log likelihood for each value of f _ai. At each point in the scan, μ as well as various systematic uncertainties are profiled, so that the result is independent of the signal yield. Any value of f _ai where the log likelihood is above the lower dotted line is excluded at 68 % confidence level, and any point above the upper dotted line is excluded at 95 % confidence level. Some of the scans from Run 1 are shown in Fig. 5.6.

The same paper also included fits for two simultaneous anomalous couplings, with an amplitude and probability distribution given by

$$\displaystyle \begin{aligned} &\mathcal{A}(a_1,a_i,a_j,\vec{\Omega})=a_1\mathcal{A}_1(\vec{\Omega})+a_i\mathcal{A}_i(\vec{\Omega})+a_j\mathcal{A}_j(\vec{\Omega}) \end{aligned} $$

(5.4)

$$\displaystyle \begin{aligned} &\begin{array}{rl} \mathcal{P}(a_1,a_i,a_j,\vec{\Omega})={\left\lvert \mathcal{A} \right\rvert}^2=&a_1^2\mathcal{P}_1(\vec{\Omega})+a_i^2\mathcal{P}_i(\vec{\Omega})+a_j^2\mathcal{P}_j(\vec{\Omega})\\ &+a_1a_i\mathcal{P}_{\text{int}}^{1i}(\vec{\Omega})+a_1a_j\mathcal{P}_{\text{int}}^{1j}(\vec{\Omega})+a_ia_j\mathcal{P}_{\text{int}}^{ij}(\vec{\Omega}) \end{array} {} \end{aligned} $$

(5.5)

Note that the number of signal terms has increased from 3 to 6, and there is no longer a way to provide optimal separation between all the terms with only 3 discriminants. These results are not shown here, but this equation shows how the number of terms grows with more couplings, which will be revisited later. Additionally, some analyses allowed the couplings to be complex, which requires a second interference term for each pair of couplings.

Later analyses used Run 1 data to search for anomalous couplings in production: VH in the case of CMS [22] and VBF in the case of ATLAS [23]. As mentioned in Sect. 4.4, production is sensitive to small anomalous couplings; however, due to the low statistics available from Run 1 data, the results were at a low confidence level.

In addition, CMS [24] and ATLAS [25] searched for offshell Higgs boson production and put constraints on its width. The CMS analysis searched for the Λ_Q coupling from Eq. (4.1), and these results are currently the only constraints on this coupling.

5.2 First Run 2 Results

The first CMS H →ZZ → 4ℓ analysis in Run 2 [1] used the data taken in 2015. Using the first year of 13 data, CMS observed the Higgs boson peak in Fig. 5.1a at a confidence level of 2.5σ. The analysis also searched for events produced in vector boson fusion.

With the increased luminosity in 2016, the data, shown in Fig. 5.1b, were sufficient to conduct more detailed analyses of the Higgs boson’s properties [2], including the first anomalous coupling measurements in production (the Higgs boson’s “context”) and decay (its “end”) at the same time [26], using kinematics of VBF and VH production, where the associated vector boson in VH production decays to quarks. The results shown here are from the next iteration of this analysis [27], which used the same strategies applied to the data from 2016 and 2017.

In order to isolate VBF and VH, a MELA discriminant $\mathcal {D}_{\text{2jet}}$ is used to separate VBF and VH production from gluon fusion produced in association with two jets. This discriminant is defined by Eq. (4.19), with VBF or VH production in the numerator and gluon fusion in the denominator. For VBF or VH production, each analysis uses the maximum of the probability under the SM and the probability under the pure anomalous hypothesis considered in that analysis. In this way, the categorization efficiently selects both SM and BSM events, for greater sensitivity. Other requirements on the number of jets and leptons in the event are also applied in order to suppress the $\mathrm {t}\bar {\mathrm {t}}\mathrm {H}$ contribution.

The VBF-tagged category requires exactly four leptons, either two or three jets of which at most one is b-quark flavor-tagged, or more if none are b-tagged jets, and $\mathcal {D}_{\text{2jet}}^{\text{VBF}}>0.5$ using either the SM or the BSM signal hypotheses for the VBF production.
The VH-tagged category requires exactly four leptons, either two or three jets, or more if none are b-tagged jets, and $\mathcal {D}_{\text{2jet}}^{{\mathrm {V}\mathrm {H}}}=\max \left ( \mathcal {D}_{\text{2jet}}^{{\mathrm {W}\mathrm {H}}},\mathcal {D}_{\text{2jet}}^{{\mathrm {Z}\mathrm {H}}} \right )>0.5$ using either the SM or the BSM signal hypothesis for the VH production.
The untagged category contains the remaining events.

Plots of the MELA discriminants used for categorization are shown in Fig. 5.7, using the f _a3 analysis as an example.

For VBF or VH production of a Higgs boson that subsequently decays H →ZZ → 4ℓ, the HVV vertex appears twice: once on the production side and once on the decay side. Equation (5.2) is modified to:

$$\displaystyle \begin{aligned} \mathcal{A}(a_1,a_i,\vec{\Omega})&=\left(a_1\mathcal{A}_1^{\mathrm{prod}}(\vec{\Omega})+a_i\mathcal{A}_i^{\text{prod}}(\vec{\Omega})\right)\left(a_1\mathcal{A}_1^{\text{dec}}(\vec{\Omega})+a_i\mathcal{A}_i^{\text{dec}}(\vec{\Omega})\right) \end{aligned} $$

(5.6)

$$\displaystyle \begin{aligned} \mathcal{P}(a_1,a_i,\vec{\Omega})={\left\lvert \mathcal{A} \right\rvert}^2&=a_1^4\mathcal{P}_0(\vec{\Omega})+a_1^3a_i\mathcal{P}_1(\vec{\Omega})+a_1^2a_i^2\mathcal{P}_2(\vec{\Omega})+a_1a_i^3\mathcal{P}_3(\vec{\Omega})+a_i^4\mathcal{P}_4(\vec{\Omega}) {} \end{aligned} $$

(5.7)

There are now five terms in the probability, each represented by a template, which is constructed using Monte Carlo simulation from JHUGEN. The gluon fusion contribution to the probability is unchanged and still follows Eq. (5.2), with templates modeled through POWHEG+ JHUGEN simulations.

In each category, discriminants are chosen to best utilize the information provided by the production mode targeted by that category. In the untagged category, which does not target any specific production mode and is dominated by gluon fusion, the same setup as in Run 1 is used. In the VBF and VH categories, in principle, we would need four discriminants to separate between the five terms in Eq. (5.7), plus another one to separate signal from background. Using so many discriminants is impractical, so we choose the ones that separate the most useful degrees of freedom: $\mathcal {D}_{\text{bkg}}^{\text{VBF}/{\mathrm {V}\mathrm {H}}+\text{dec}}$, which separates signal from background using the product of the production and decay probabilities; $\mathcal {D}_{\text{alt}}^{\text{VBF}/{\mathrm {V}\mathrm {H}}+\text{dec}}$, which separates SM signal from pure BSM signal, again using both the production and decay probabilities; and $\mathcal {D}_{\text{int}}^{\text{VBF}/{\mathrm {V}\mathrm {H}}}$, which separates the interference component for production. In the VBF-tagged category, VBF information is used, while in the VH category, VH information is used. Distributions of these discriminants, again using the f _a3 analysis as an example, are shown in Fig. 5.8. Production information combined with decay information provides significantly more separation between hypotheses than decay information alone.

In this analysis, the HZZ and HWW couplings are assumed to be equal. This is relevant for VBF production, which can proceed through either ZZ or WW fusion, and for VH production. The overall scaling for VBF and VH signal strength, μ _V, is floated separately from the scaling μ _F for the other production modes, ggH, $\mathrm {t}\bar {\mathrm {t}}\mathrm {H}$, and bbH. In this way, μ _V absorbs the common normalization of a ₁ and the anomalous coupling a _i, while μ _F allows the fermion coupling κ to float as well. The discriminants used in this analysis are insensitive to anomalous fermion couplings.

The results for this analysis are shown in Fig. 5.9 for four anomalous couplings: a ₃, a ₂, Λ₁, and $\Lambda _1^{\mathrm {Z}\gamma }$. The last one is included because, as described in Sect. 4.4.1.1, it is the only coupling involving photons that does not have stringent limits from onshell photon production. In addition, the results also include data from Run 1 and the small dataset collected in 2015, which were not categorized due to the small expected number of VBF and VH events in those datasets.

The most striking new feature of these results, as compared to the ones in Fig. 5.6, is a narrow but shallow minimum around f _ai = 0. This is a result of the discussion in Sect. 4.4.1. Because the anomalous couplings are proportional to q ² of the vector bosons, and because the vector bosons in VBF and VH production have a higher q ², VBF and VH are sensitive to smaller anomalous couplings than decay is. Conversely, when the anomalous couplings are large (f _a3 ≳ 0.005, with slightly different numerical values for the other anomalous couplings), the SM contribution to VBF and VH is much smaller than the anomalous contribution, and further increases in f _a3 do not affect the VBF shape. The minimum is shallow because its depth is limited by the relatively small number of events in the VBF- and VH-tagged categories, which can be seen by counting events in Fig. 5.8.

5.3 Offshell Higgs Boson Properties

The same paper [27] also includes measurements of anomalous couplings in the offshell region above 200 . Similar to VBF and VH production, the offshell region is sensitive to smaller anomalous couplings than the onshell region, because both Z bosons from the decay are onshell, with a mass of around 91.2 . By contrast, in the onshell region the lighter Z boson often has an invariant mass around 30 , as shown in Fig. 4.4a. In this way, the offshell region can provide additional sensitivity to anomalous couplings. The left plot of Fig. 4.6 shows this effect: anomalous couplings result in an increased number of events in the offshell region.

Another interesting parameter, which is correlated with anomalous couplings, is the Higgs boson’s width. As described in Sect. 4.3, the cross section to produce an offshell Higgs boson is proportional to its width. Seeing a higher-than-expected number of events in the offshell region can be a result of either a larger width or anomalous couplings. To distinguish between them, we use the same kinds of MELA discriminants as in the onshell region. Afterwards, we scan the anomalous couplings and float the width, and separately scan the width and float anomalous couplings. In this way, the measurement uses as few assumptions as possible.

The offshell measurement is more complicated because of interference between signal and background. (In the onshell case, this interference is essentially zero because of the narrow peak at 125 , and we neglect it in all onshell analyses.) Each process in the offshell region interferes with background processes with the same initial and final states and similar topology. Gluon fusion interferes with gg →ZZ; VBF interferes with vector boson scattering, which is the same Feynman diagram as VBF but involving vertices of three or four Z or W bosons and no Higgs boson; and VH interferes with VVV production. The result is that the signal probability density function for gluon fusion (5.2) becomes

$$\displaystyle \begin{aligned} &\mathcal{A}(a_1,a_i,\vec{\Omega})=a_1\mathcal{A}_1(\vec{\Omega})+a_i\mathcal{A}_i(\vec{\Omega})+\mathcal{A}_{\text{bkg}}(\vec{\Omega}) \end{aligned} $$

(5.8)

$$\displaystyle \begin{aligned} &\begin{array}{rl} \mathcal{P}(a_1,a_i,\vec{\Omega})={\left\lvert \mathcal{A} \right\rvert}^2=&a_1^2\mathcal{P}_1(\vec{\Omega})+a_i^2\mathcal{P}_i(\vec{\Omega})+a_1a_i\mathcal{P}_{\text{int}}^{1i}(\vec{\Omega})\\+&a_1\mathcal{P}_{\text{bkgint}}^1(\vec{\Omega})+a_i\mathcal{P}_{\text{bkgint}}^i(\vec{\Omega})\\+&\mathcal{P}_{\text{bkg}}(\vec{\Omega}) \end{array} {} \end{aligned} $$

(5.9)

The first and last lines of Eq. (5.9) were already included in Eqs. (5.2) and (5.3), while the middle line is new. Similarly, the VBF and VH probability Eq. (5.7) becomes

$$\displaystyle \begin{aligned} &\begin{array}{rl} \mathcal{A}(a_1,a_i,\vec{\Omega})=&\left(a_1\mathcal{A}_1^{\text{prod}}(\vec{\Omega})+a_i\mathcal{A}_i^{\text{prod}}(\vec{\Omega})\right)\left(a_1\mathcal{A}_1^{\text{dec}}(\vec{\Omega})+a_i\mathcal{A}_i^{\text{dec}}(\vec{\Omega})\right)\\ +&\mathcal{A}_{\text{bkg}}(\vec{\Omega}) \end{array} \end{aligned} $$

(5.10)

$$\displaystyle \begin{aligned} &\begin{array}{rl} \mathcal{P}(a_1,a_i,\vec{\Omega})={\left\lvert \mathcal{A} \right\rvert}^2=&a_1^4\mathcal{P}_0(\vec{\Omega})+a_1^3a_i\mathcal{P}_1(\vec{\Omega})+a_1^2a_i^2\mathcal{P}_2(\vec{\Omega})+a_1a_i^3\mathcal{P}_3(\vec{\Omega})+a_i^4\mathcal{P}_4(\vec{\Omega})\\ +&a_1^2\mathcal{P}_{\text{bkgint}}^0(\vec{\Omega})+a_1a_i\mathcal{P}_{\text{bkgint}}^1(\vec{\Omega})+a_i^2\mathcal{P}_{\text{bkgint}}^2(\vec{\Omega})\\ +&\mathcal{P}_{\text{bkg}}(\vec{\Omega}) \end{array} {} \end{aligned} $$

(5.11)

Some background processes, such as QCD-induced qq →ZZ, do not interfere with signal and are included separately in Eq. (5.3) as before.

The offshell events are divided into categories using the same criteria as in the previous section, and similar discriminants are used. In the onshell region, $\mathcal {D}_{\text{bkg}}$ combined the four lepton invariant mass with the other kinematic information, because signal events are expected to have an invariant mass of . In the offshell region, the invariant mass is nowhere near 125 , and the shape of the mass spectrum can provide additional information to measure the width and anomalous couplings. Therefore, the mass is used as a separate observable, and the other kinematic information to separate signal from background is separated into another observable $\mathcal {D}_{\text{bkg}}^{\text{kin}}$, which includes decay information in all categories and VBF or VH information in the respective categories. Additionally, a pure discriminant, such as $\mathcal {D}_{0-}$ in the case of the f _a3 measurement, separates the SM from the anomalous contribution.

The discriminants used in the three categories, again using the example of the f _a3 analysis, are shown in Fig. 5.10.

The offshell anomalous coupling results are shown in Fig. 5.11. The improvement brought by the offshell region is primarily illustrated by the difference between the green curves, which use only onshell events, and the red ones, which use offshell events as well while allowing the width to float.

Figure 5.12 shows the likelihood scan for the Higgs boson width. To make a more model-independent measurement, various configurations are used for the fit, each one floating a different anomalous coupling. No matter which coupling is floated, the results are the same: the zero width hypothesis for the Higgs boson width is excluded at 95 % confidence level, as is a width 2.2 times larger than the SM width.

5.4 High Mass Search

Using similar methods to the offshell analysis, it is possible to search for a new resonance in the high mass region [28]. This resonance could have a significant width, which would mean that it interferes with background and with the offshell tail of the Higgs boson, as described in Sect. 4.5.2. Additionally, it could be produced through any combination of gluon fusion and VBF. The high mass search uses both the 4ℓ, 2ℓ2q, and 2ℓ2ν final states. In the 4ℓ channel, 3 categories are used: untagged, VBF-tagged, and RSE. The RSE category, which stands for “reduced selection electrons”, includes events with electrons that fail some of the normal selection criteria, which can be bypassed in the high mass region due to lower background. The categorization schemes are different for the other final states, but all cases include a category targeting VBF events and a category targeting gluon fusion events (Fig. 5.13).

The results of the analysis are shown in Fig. 5.14. No new resonance is found.

5.5 Anomalous Couplings in the H → ττ Channel

Searches for anomalous HVV couplings using decay information are limited to the H →ZZ and H →WW decays. However, searches for anomalous couplings in production can happen in any decay channel. This section will discuss results from CMS’s anomalous couplings analysis in H → ττ, using data from 2016 [29].

Detecting the ττ final state and separating it from background requires different analysis methods than the ZZ → 4ℓ final state used in the rest of the analyses here. This analysis closely follows the methods used for the discovery of the H → ττ decay by CMS [30]. The events are divided into categories based on how the τ leptons decay, in categories called τ _h τ _h, eτ _h, μ _h τ _h, and eμ. The τ _h decays include all hadronic decays, typically including various pions and kaons. All τ _h decays include a neutrino, and leptonic decays include two, so the reconstruction is complicated by the fact that neutrinos can only be reconstructed through MET. The other possible final states, ee and μμ, are not included due to the overwhelming background in those channels. The algorithm used to identify hadronic τ decays is described in [31, 32].

Because there is no HVV vertex on the decay side, the gluon fusion process is unchanged for any anomalous couplings. The VBF and VH processes have a single HVV vertex, and their shape as a function of anomalous couplings is described by Eq. (5.2), just like a H →ZZ → 4ℓ decay produced in gluon fusion.

The events are divided into three categories:

The 0-jet category contains events with no jets that have .
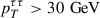The VBF category contains events with two jets that satisfy various requirements to isolate the VBF topology. These cuts vary by category in order to suppress category-specific backgrounds, but typically require a large dijet invariant mass m _JJ, a large η separation between the jets, and/or a high $p_T^{\tau \tau }$ invariant mass.
The boosted category includes all events that do not fall into the other two categories. It is called “boosted” because the events have at least one jet, giving the H boson a nonzero p _T.

The backgrounds for this analysis are complicated enough that there is no simple way to construct a $\mathcal {D}_{\text{bkg}}$ observable. Instead, we use the mass of the visible τ decay products m _vis and an estimate of the actual ττ mass m _ττ, obtained using the SVFIT algorithm [33]. In the boosted category, $p_T^{\tau \tau }$ is used, and this observable provides extra sensitivity to anomalous couplings. In the VBF category, MELA discriminants are constructed to separate between the SM and anomalous hypotheses, using information from VBF kinematics.

Some of the distributions are shown in Fig. 5.15. Because of limited statistics in control regions in data, the number of bins is reduced with respect to the analyses described earlier. However, we use the fact that the distribution of $\mathcal {D}_{CP}$ is symmetric for any CP-conserving process, which includes all backgrounds. In this way, a 2-bin distribution of $\mathcal {D}_{CP}$ can be constructed for free, without losing any statistics: it is flat for everything except the CP-violating interference components, as shown in Fig. 5.15e.

The boosted category does not have 2 VBF-like jets, and so there is not enough information to construct a MELA discriminant. However, because anomalous couplings are enhanced at higher q ², they also result in a harder p _T spectrum. The boosted category significantly enhances the sensitivity to anomalous couplings, even when it is missing some jet information, as shown in Fig. 5.15f.

The results of this analysis are also combined with the ones from the H →VV → 4ℓ analysis, described in Sect. 5.2. In doing this combination, the κ _τ coupling is allowed to float as a free parameter, so that there are three independent parameters describing the signal strengths of different processes. The four possible μ’s are related by

$$\displaystyle \begin{aligned} \frac{\mu_V^{\mathrm{H}\mathrm{Z}\mathrm{Z}}}{\mu_F^{\mathrm{H}\mathrm{Z}\mathrm{Z}}}= \frac{\mu_V^{\mathrm{H}\tau\tau}}{\mu_F^{\mathrm{H}\tau\tau}}. \end{aligned}$$

This constraint adds additional sensitivity to the result.

The are shown in Fig. 5.16, separately and also combined with the ones from H →VV → 4ℓ. The red curves here are equivalent to the ones in Fig. 5.9. Because the ττ process has no decay information, it contains only the narrow, shallow minimum i6n the center, but levels off after that. Sensitivity to small anomalous couplings comes from both final states, while additional sensitivity for large anomalous couplings is contributed by the H →VV → 4ℓ decay.

5.6 Multiple Anomalous Couplings

As a natural extension of the search for anomalous couplings, we search for more than one at a time [34], reducing the model dependence of our measurement. Measuring more anomalous couplings also makes it possible to translate between the amplitude parameterization in Eq. (4.1) and other parameterizations. Because Eq. (4.1) contains all Lorentz-invariant terms up to $\mathcal {O}\left (q^2\right )$, any other parameterization to the same order can only differ by including a linear combination of our couplings. Therefore, a fit for all couplings at the same time can be translated into any other parameterization with no loss of information.

In this analysis, the categorization is modified from the one in Sect. 5.2. Because we search for all couplings at once, the VBF and VH categories use MELA discriminants for the SM and all anomalous couplings instead of just one at a time. A boosted category is adopted, similar to the one in Sect. 5.5, and two other categories sensitive to the VBF and VH yield are added. This increases the sensitivity by adding additional constraints that prevent the fit from sending μ _V to 0 when anomalous couplings are large. The categorization is defined as follows:

The VBF-2jet-tagged category requires exactly four leptons, either two or three jets of which at most one is b-quark flavor-tagged, or more if none are b-tagged jets, and $\mathcal {D}_{\text{2jet}}^{\text{VBF}}>0.5$ using either the SM or any of the four BSM signal hypotheses for the VBF production.
The VH-hadronic-tagged category requires exactly four leptons, either two or three jets, or more if none are b-tagged jets, and $\mathcal {D}_{\text{2jet}}^{{\mathrm {V}\mathrm {H}}}=\max \left ( \mathcal {D}_{\text{2jet}}^{{\mathrm {W}\mathrm {H}}},\mathcal {D}_{\text{2jet}}^{{\mathrm {Z}\mathrm {H}}} \right )>0.5$ using either the SM or any of the four BSM signal hypotheses for the VH production.
The VH-leptonic-tagged category requires no more than three jets and no b-tagged jets and exactly one additional lepton or pair of opposite-sign-same-flavor leptons. In addition, events with no jets and at least one additional lepton are included in this category.
The VBF-1jet-tagged category requires exactly 4 leptons, exactly 1 jet, and $\mathcal {D}_{\text{1jet}}^{\text{VBF}}>0.7$. This discriminant is calculated using the SM hypothesis for the VBF production.
The Boosted category requires exactly 4 leptons, three or fewer jets, or more if none are b-tagged jets, and the transverse momentum of the four-lepton system
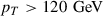
The Untagged category consists of the remaining events.

The category discriminants, defined as the maximum of the individual discriminants for the SM and anomalous hypotheses, are shown in Fig. 5.17.

Fitting for more than one anomalous coupling at the same time essentially involves the same procedure as fitting for only one. Three additional complications arise:

1.
To distinguish between several different hypotheses, more discriminants (Sect. 4.6.2) are needed.
2.
As the number of couplings grows, the number of interference terms grows even faster.
3.
The multidimensional fit naturally grows more complicated when there are more dimensions, especially when there are correlations between the different parameters of the fit.

In the most general case, there can be 13 parameters: a ₁, a ₂, a ₃, and Λ₁ for ZZ and WW; a ₂, a ₃, and Λ₁ for Zγ; and a ₂ and a ₃ for γγ. For this analysis, in addition to the Standard Model coupling a ₁, we search for four anomalous couplings at the same time: a ₂, a ₃, Λ₁, and $\Lambda _1^{Z\gamma }$. As in the fits previously described, we assume that $a_i^{ZZ}=a_i^{WW}\equiv a_i$. The difficulties listed above prove to be surmountable for this fit. This procedure could be extended to search for even more couplings at a time, but the difficulties grow quickly with the number of couplings, and I will give examples for the most general case where they are relevant.

5.6.1 Multiparameter Discriminant

To distinguish between background, Standard Model signal, and four anomalous tensor structures, we use seven discriminants: $\mathcal {D}_{\text{bkg}}$, $\mathcal {D}_{0-}$, $\mathcal {D}_{0h+}$, $\mathcal {D}_{\Lambda 1}$, $\mathcal {D}_{\Lambda 1}^{Z\gamma }$, $\mathcal {D}_{CP}$, and $\mathcal {D}_{\text{int}}$. For each of the untagged, VBF tagged, and VH tagged categories, the first five discriminants are calculated for decay, VBF + decay, and VH + decay, respectively, and the last two are calculated for decay, VBF, and VH respectively, exactly as in the earlier analyses. We use three bins for each of the first five discriminants and two bins for the last two.

There is a high degree of correlation between these discriminants. The most extreme case is in the untagged category, where the discriminants are calculated using decay information only. As described in Sect. 4.6.2, the last six discriminants are calculated based on only five parameters: θ ₁, θ ₂, Φ, m ₁, and m ₂. ($\mathcal {D}_{\text{bkg}}$ also contains information from m _4ℓ, θ ^∗, and Φ₁.) In the limit of an infinite number of bins, one of these discriminants is redundant. With a finite number of bins, and especially with only two or three bins as we use, each discriminant provides some information, but the correlations mean that many bins are empty. The same is true in the VBF and VH tagged categories, even though more observables go into those discriminants.

Because this analysis uses only two bins for $\mathcal {D}_{CP}$, these bins can be populated with no loss of statistics, as mentioned in Sect. 5.5. $\mathcal {D}_{\text{bkg}}$ uses more observables and is also less correlated with the other discriminants. We therefore first look at the distribution of the remaining five discriminants. This five-dimensional distribution contains 3⁴ × 2 = 162 bins. For each category, around half of these bins contain almost no events for any signal or background process. To avoid statistical fluctuations while keeping all events as part of the measurement, all of those bins are merged into a single bin. The unrolled five-dimensional distribution contains about 80 bins taken from the original five-dimensional distribution, plus one bin that covers all of the remaining original bins.

Once the bins to be merged are identified, the final distribution to be used in the analysis contains three dimensions: $\mathcal {D}_{\text{bkg}}$ in three bins, $\mathcal {D}_{CP}$ in two bins, and the distribution described in the previous paragraph. It contains around 480 bins; however, as in Sect. 5.5, only half of that number are statistically independent due to the symmetry of $\mathcal {D}_{CP}$.

In the three new categories, boosted, VBF-1jet-tagged, and VH-leptonic-tagged, we use p _T and D _bkg, similar to the boosted category in Sect. 5.5.

Figures 5.18, 5.19, 5.20, and 5.21 shows distributions of the discriminants used for the analysis.

5.6.2 Template Parameterization

The primary difficulty of the multiparameter analysis is the number of templates, or histograms, needed to parameterize the probability distribution grows quickly with number of couplings. For processes with a single HVV vertex, such as gg →H →ZZ, the probability distribution is

$$\displaystyle \begin{aligned} P(a_i,\vec{\Omega})\sim{\left\lvert \sum_{i=1}^{N}a_iA_i\left(\vec{\Omega}\right) \right\rvert}^2, {} \end{aligned} $$

(5.12)

where $\vec {\Omega }$ is the observables, A _i is the amplitude corresponding to the coupling a _i and N is the number of couplings in the fit, including the Standard Model coupling a ₁. When multiplied out, assuming the couplings are real, the probability distribution contains $\binom {N+2-1}{2}$ terms that look like $a_ia_jT_{ij}\left (\vec {\Omega }\right )$, where $T_{ij}\left (\vec {\Omega }\right )$ is a product of amplitudes and is parameterized by a template. In the four-anomalous-coupling fit described here, this number is 15. In the most general case with 13 parameters, we have $\binom {9+2-1}{2}=45$ terms, because the WW couplings do not contribute to the 4ℓ decay.

The number of templates grows significantly faster when we consider a process with two HVV vertices, such as VH or VBF production. In this case, the probability distribution is

$$\displaystyle \begin{aligned} P(a_i,\vec{\Omega})\sim{\left\lvert \sum_{i=1}^{N}\left[a_iA_i^{\text{VBF}}\left(\vec{\Omega}\right)\right]\sum_{i=1}^{N}\left[a_iA_i^{\text{decay}}\left(\vec{\Omega}\right)\right] \right\rvert}^2, {} \end{aligned} $$

(5.13)

which multiplies out to $\binom {5+4-1}{4}=70$ terms in our four-anomalous-coupling fit. Each term looks like $a_ia_ja_ka_lT_{ijkl}\left (\vec {\Omega }\right )$ and is again represented by a template. The fully general fit with 13 parameters contains 1605 terms for VBF. This number comes from a sum of binomial coefficients to address the fact that VBF production includes WW couplings and 4ℓ decay does not.

The number of templates is increased further because a separate parameterization is needed for each of the categories and lepton flavor combinations. All told, several thousand templates are needed for the four-parameter fit, and an order of magnitude more would be needed for the fully general case.

5.6.2.1 Avoiding Statistical Fluctuations

An important consideration is avoiding statistical fluctuations in the templates. Most people find it impossible to visualize a seven-dimensional distribution, and it is even more impossible to visualize thousands of seven-dimensional distributions, so visual sanity checks are not feasible. One simple check is to change the binning—for example, remove both the background contribution and $\mathcal {D}_{\text{bkg}}$. This does not appreciably change the expected limits, indicating that statistical fluctuations are small enough that they do not impact the results.

However, one type of statistical fluctuation is particularly dangerous. If an interference term fluctuates up in a particular bin and a pure term fluctuates down, it is possible that, for a particular combination of the parameters, the total probability parameterization is negative. This is physical and mathematical nonsense, and it causes the fit to fail. A safeguard is needed to avoid this behavior.

To populate the templates, we use the following algorithm, separately for each bin: for each template a, we obtain an estimate of the bin’s content by reweighting, as described in Sect. 4.6.1, from each of the generated samples b: x _ab ± δx _ab. To simplify the computation, we need to approximate the weighted Poisson distribution as a Gaussian distribution, where the error is the square root of the sum of weights squared.

Errors on a Poisson count are notoriously difficult to estimate when few statistics are available, as is the case in several of the bins. However, in our case we have a way of determining when an error estimate is too small and correcting for it: if sample b has zero or few events in a particular bin, we look at the better- or similarly-populated samples b ^′ and inflate δx _ab to ${\delta x}_{ab^\prime }$.

Finally, we estimate the final bin content y _a. For reasons that will be made clear below, we do this at the same time for all a by parameterizing the likelihood of a particular set of bin contents $\vec {y}$. In principle, this is a multidimensional Poisson distributions, including the correlations among these dimensions because the same samples are used to produce those events. However, to simplify the math and computation time, we approximate it as an uncorrelated Gaussian distribution:

$$\displaystyle \begin{aligned} -2\ln{L\left(\vec{y}\right)}=\sum_{a,b}\left(\frac{y_{a}-x_{ab}}{{\delta x}_{ab}}\right)^2 {} \end{aligned} $$

(5.14)

In this form, maximizing the likelihood, or minimizing Eq. (5.14), is simple, as it is just a sum of quadratics. This gives us the first estimate of $\vec {y}$.

The next step is to check whether this estimate is feasible, i.e., that the probability for an event to fall in the bin remains positive for all possible values of the couplings.

Determining whether the probability parameterization can ever go negative for a particular $\vec {y}$ is a complicated undertaking and requires a section of its own.

5.6.2.2 Detecting Negative Probability

In this section, it is necessary to make the relationship between the templates explicit instead of just enumerating them. Therefore, I will expand the index a of the previous section into ij or ijkl from Eqs. (5.12) and (5.13). I will first describe the simplest case, gluon fusion with a single anomalous coupling, and progress to the most complicated, VBF with multiple anomalous couplings.

For gluon fusion with a single parameter, there are only three templates, with bin contents y ₁₁, y ₁₂, and y ₂₂. Equation (5.12) expands into

$$\displaystyle \begin{aligned} P(a_i,\vec{\Omega})\sim a_1^2y_{11} + a_1a_2y_{12} + a_2^2y_{22}, {} \end{aligned} $$

(5.15)

which is always positive as long as

$$\displaystyle \begin{aligned} y_{11}&>0 \\ y_{12}&>0 \\ {\left\lvert y_{12}\left(\vec{\Omega}\right) \right\rvert}&\le2\sqrt{y_{11}y_{12}} {} \end{aligned} $$

(5.16)

With multiple parameters, the criteria for the gluon fusion probability density to always be positive are similarly

$$\displaystyle \begin{aligned} y_{ii}&>0 \\ {\left\lvert y_{ij}\left(\vec{\Omega}\right) \right\rvert}&\le2\sqrt{y_{ii}y_{jj}} {} \end{aligned} $$

(5.17)

for all i ≠ j.

The VBF probability density is more complicated. With a single parameter, Eq. (5.13) expands into

$$\displaystyle \begin{aligned} P(a_i,\vec{\Omega})\sim a_1^4y_{1111} + a_1^3a_2y_{1112} + a_1^2a_2^2y_{1122} + a_1a_2^3y_{1222} + a_2^4y_{2222}. {} \end{aligned} $$

(5.18)

To ensure that this is always positive, we first ensure that y ₁₁₁₁ and y ₂₂₂₂ are positive. Then, we set a ₁ = 1 (or, equivalently, divide through by $a_1^4$) to obtain a quartic polynomial f(a ₂). We differentiate, obtaining a cubic polynomial f ^′(a ₂), and find its 1, 2, or 3 real zeros z _i using the cubic formula. We then plug those zeros into the original quartic polynomial and find the smallest f(z _i). This is the minimum of the quartic polynomial. The criteria for $\vec {y}$ to be reasonable are

$$\displaystyle \begin{aligned} y_{1111}&>0 \\ y_{2222}&>0 \\ \min_i\left(f\left(z_i\right)\right)&\ge0 \end{aligned} $$

(5.19)

The most complicated case is VBF with multiple parameters. Unlike in gluon fusion, there are terms with up to four different couplings, which means that there is no way to decouple the interference terms between different couplings, as we did in the case of gluon fusion. We end up with a multivariate quartic polynomial, ∑_i,j,k,l y _ijkl a _i a _j a _k a _l, which is similar to Eq. (5.18) but with more terms (70, where there are four anomalous couplings). In theory, the strategy for minimizing this is the same as in the one-parameter case: set a ₁ = 1 to obtain a quartic polynomial $f\left (a_2, \ldots \right )$, find the gradient $\vec {\nabla }f$ by differentiating with respect to each of the rest of the parameters, solve $\vec {\nabla }f=0$, find the value of f(a ₂, …) at each of the real solutions, and take the smallest.

Practically, the difficult part of this is solving the system of cubic equations $\vec {\nabla }f=0$. Solving simultaneous polynomial equations in general is a complicated task.

Extensive discussion of algebraic approaches to this problem can be found in [35]. One approach is to find what is known as a Gröbner basis by means of Buchberger’s algorithm [36]. In practical terms, a Gröbner basis is a set of polynomials that have the same solutions as the original ones, but with particular mathematical properties, with the result that they can be more easily solved. Gröbner bases in general are unstable with respect to small changes in the coefficients and are therefore only practical when working with integer or small rational coefficients. The algorithm in [37] produces modified Gröbner bases that are stable for floating point numbers, with control over the size of the deviation from the real Gröbner basis for the system. Unfortunately, the efficiency of running this algorithm is highly sensitive to the chosen order of terms in the polynomial; when a “bad” order is chosen, it runs for many minutes and produces several gigabytes of output before converging. In our case, we need to solve hundreds of systems of cubic polynomials. Determining the best order by trial and error is too slow, and there is no obvious structure to the coefficients that would help to determine an order. This approach is therefore not feasible for our application.

Another method for solving polynomial equations is known as homotopy continuation, described in [38]. This method is analytical rather than algebraic. It starts with a similar system of polynomials with known solutions, such as $x_i^3-1=0$ for however many i’s are needed. It then continuously transforms the system, tracking the solutions in the complex space, until it reaches the one we want to solve. We use the Hom4PS program [39, 40] for this. The efficiency of running homotopy continuation is simplified by the fact that because our polynomials have random coefficients, they are unlikely to have degenerate roots or solutions where one of the variables is zero, cases which require special treatment. Hom4PS takes about half a second to solve the system of four cubic polynomials needed for the four-parameter fit.

5.6.2.2.1 At Infinity

The multidimensional case has a further complication: the polynomial can be negative at infinity. For the single parameter case in Eq. (5.22), bad behavior at infinity can be avoided by just requiring that the pure terms y ₁₁₁₁ and y ₂₂₂₂ are positive. For the multidimensional case, instead of two points, we have a sphere at infinity and have to avoid negative behavior anywhere around this sphere.

Written explicitly in an example with two anomalous couplings, the polynomial under consideration looks like

$$\displaystyle \begin{aligned} f(a_2, a_3) = &y_{1111} + y_{1112}a_2 + y_{1113}a_3 + y_{1122}a_2^2 + y_{1123}a_2a_3 \\ + &y_{1133}a_3^2 + y_{1222}a_2^3 + y_{1223}a_2^2a_3 + y_{1233}a_2a_3^2 + y_{1333}a_3^3 \\ + &y_{2222} a_2^4 + y_{2223} a_2^3a_3 + y_{2233} a_2^2a_3^2 + y_{2333}a_2a_3^3 + y_{3333}a_3^4 \end{aligned} $$

(5.20)

On the sphere at infinity, the terms with degree 3 dominate, giving

$$\displaystyle \begin{aligned} f(a_2, a_3)\approx y_{2222} a_2^4 + y_{2223} a_2^3a_3 + y_{2233} a_2^2a_3^2 + y_{2333}a_2a_3^3 + y_{3333}a_3^4 \end{aligned} $$

(5.21)

We can then apply the same strategy as before: let a ₂ = 1 and minimize this polynomial. If it is ever negative, at a ₂ = 1, a ₃ = α, then the original polynomial is also negative at a ₂ = c, a ₃ = cα when c is large enough. We also have to look at the infinite points of this smaller polynomial. In this case, that just means ensuring that y ₃₃₃₃ > 0; with more couplings, it is necessary to recursively find and minimize a boundary polynomial.

5.6.2.3 Avoiding Negative Probability

Now that we have a procedure to detect when negative probability can occur, we can construct the templates in a way that avoids it. This is accomplished by minimizing Eq. (5.14) subject to the constraint that the probability is always positive. This constraint involves all elements of $\vec {y}$, and so it is necessary to do a multidimensional minimization for all a at the same time.

To do this minimization, we use the cutting planes method for convex minimization [41] . This method relies on the fact that both the equation to be minimized and the region over which it is minimized are convex. Equation (5.14) is convex simply because it is a sum of independent, one-dimensional quadratics, each of which is convex in its own dimension. The fact that the constraint region is convex is less obvious. Written explicitly for the four-parameter VBF fit, the set of allowed $\vec {y}$ is:

$$\displaystyle \begin{aligned} \left\{\vec{y}\in\mathbb{R}^{70}\middle|\forall\vec{a}\in\mathbb{R}^4: \sum_{i,j,k,l}y_{ijkl}a_ia_ja_ka_l>0\right\} {} \end{aligned} $$

(5.22)

A set is convex if, given two points $\vec {y}_1$ and $\vec {y}_2$ inside it, any point on the line between them also lies inside the set. Equation (5.22) can be viewed as an infinite set of individual constraints, each of which, despite being a complicated function of $\vec {a}$, is linear in $\vec {y}$. Each of these linear constraints is convex, and therefore, so is their intersection. Intuitively, because the quartic polynomials defined by $\vec {y}_{1,2}$ are always positive, as the polynomial moves linearly from one to the other, it remains always positive.

The cutting planes method works in iterations. First, we minimize Eq. (5.14) unconstrained, which is easy to do because it is a sum of independent quadratics, obtaining a solution $\vec {y}_1$. If this solution satisfies the constraint, there is nothing more to do. If not, we find a particular set of couplings $\vec {a}$ where the polynomial is negative, and choose the linear constraint defined by those couplings from Eq. (5.22). Then we minimize Eq. (5.14) again, using this linear constraint. The process continues, with more and more linear constraints, until eventually the minimization converges to a point that satisfies Eq. (5.22).

This procedure works because minimizing a sum of quadratics subject to a set of linear constraints is significantly easier than minimizing it subject to an arbitrary constraint. We use the CVXPY package [42, 43] interfaced to Gurobi [44] in each iteration.

5.6.2.3.1 Numerical Stability

Several mathematical tricks are used to make the minimization work better.

5.6.2.3.1.1 Scaling the Couplings

For effective numerical minimization, it is important that the relevant scales not diverge over too many orders of magnitude; instead, all numbers involved should be as close as possible to 1. A simple approach would be to scale each term of Eq. (5.14) by a factor $k_{a}^2$, which would be set so that the coefficient of each quadratic term is 1 and then divide the resulting y _a by k _a to get the final bin content. This would work perfectly well in the first iteration of the minimization. However, because these k _a do not relate to the structure of the polynomial in Eq. (5.22), we would also have to use y _a∕k _a in finding the minimum of this polynomial, and the linear constraints defined by this minimum would still have large numbers. This procedure only moves the large numbers from one place to another in the fit without solving the underlying problem.

Instead, we compute k _a = k _ijkl in a correlated way across all coefficients in a way that leaves the constraint unchanged. We accomplish this by noting that Eq. (5.22) can be rewritten, for any positive $\vec {\kappa }$, as

$$\displaystyle \begin{aligned} &\left\{\vec{y}\in\mathbb{R}^{70}\middle|\forall\vec{a}\in\mathbb{R}^4: \sum_{i,j,k,l}(y_{ijkl}\kappa_i\kappa_j\kappa_k\kappa_l)\frac{a_i}{\kappa_i}\frac{a_j}{\kappa_j}\frac{a_k}{\kappa_k}\frac{a_l}{\kappa_l}>0\right\} \end{aligned} $$

(5.23)

$$\displaystyle \begin{aligned} =&\left\{\vec{y}\in\mathbb{R}^{70}\middle|\forall\vec{a}\in\mathbb{R}^4: \sum_{i,j,k,l}(y_{ijkl}\kappa_i\kappa_j\kappa_k\kappa_l)a_ia_ja_ka_l>0\right\}. {} \end{aligned} $$

(5.24)

In other words, we can pick any five κ’s, one for each coupling, and set k _ijkl = κ _i κ _j κ _k κ _l. We find the optimal κ’s to use by minimizing $\sum _{ijkl}\log ^2{(\kappa _i\kappa _j\kappa _k\kappa _ly_{ijkl})}$ for the known coefficients y _ijkl. By this procedure, the final coefficients that go into the fit are typically in the 10⁻²–10² range, which Gurobi is able to handle without a problem.

5.6.2.3.1.2 Finding “Divergent” Minima

When Hom4PS tracks the solutions of a multidimensional polynomial, sometimes one of the solutions moves away to infinity. In that case, Hom4PS calls the solution “divergent.” Divergent solutions usually result from some kind of special structure in the coefficients. In our case, the coefficients are random, and so there is almost never any such structure.

However, one possibility occasionally does give rise to a divergent solution. In later iterations of the cutting plane procedure, the successive linear constraints try to eliminate negative probability by pushing the coefficients in a particular direction. Sometimes, the result is that a negative minimum of the original polynomial gets pushed away towards infinity. If it actually reaches infinity, then it will be detected when minimizing the boundary polynomial, as described above. However, if it reaches large but finite values of the variables, Hom4PS may give up and report the solution as divergent anyway.

Empirically, this happens occasionally and is much more likely than unlucky values of the coefficients giving a divergent complex solution or a divergent real solution that corresponds to a maximum of the probability. Therefore, when Hom4PS reports a divergent solution, we have to take this warning seriously and identify it.

When a false divergent solution is present, it can be made finite by “inverting” the system of polynomials. First, we introduce a variable α and homogenize the cubic polynomials by multiplying each term by a power of α so that it has degree 3. The system is now underconstrained: it has one more variable than it does equations. We then choose numbers $\vec {\beta }$ and add a linear equation

$$\displaystyle \begin{aligned}\beta_0+\sum_{i}\beta_ia_i+\beta_\alpha\alpha=0\end{aligned}$$

to the system and solve with Hom4PS. Each solution $(\alpha , \vec {a})$ of the new system of polynomials corresponds to a solution $\vec {a}/\alpha $ of the original system.

A false divergent solution corresponds to large values of $\vec {a}/\alpha $: large enough that Hom4PS gave up on tracking these values. The trick here is to choose $\vec {\beta }$ in such a way that $\vec {a}$ is not that large, meaning that α will be very small. In general, choosing the correct $\vec {\beta }$ is difficult. In our case, we have a handle on the correct values. As already noted, the divergent solution most likely (1) is real and (2) corresponds to a minimum. That being the case, if it had made it all the way to infinity, it would correspond to a minimum of the boundary polynomial. Even though the false minimum apparently did not go all the way to infinity, we expect it to be near a minimum of the boundary polynomial. Therefore, we can look at those minima and choose $\vec {\beta }$ such that ∑_i β _i a _i = 0 at one of them. (β ₀ is arbitrary because it corresponds to a common rescaling of $\vec {a}$ and α; β _α is arbitrary because it corresponds to a rescaling of α.)

We can note here that α is essentially taking the place of a ₁, which we set to 1 earlier in the process. An actual divergent minimum would indicate that our probability goes negative when a ₁ = 0 for some values of the other couplings. A false divergent minimum means that the probability goes negative at some point with small a ₁. By introducing α, we reintroduce a ₁. The linear equation gives us an estimate of the values of the couplings at the target minimum.

5.6.2.3.1.3 Permuting the Order of Variables

As mentioned earlier, the first step in finding whether the original homogeneous polynomial (Eq. (5.18) in the one-dimensional case) goes negative was to set a ₁ = 1. This was an arbitrary choice; we could instead have set a ₂ = 1. This choice of which variable to remove does not affect whether the resulting polynomial ever goes negative, but it does affect the numerical value of the constraints. For a simple example, we can take the polynomial $f(\vec {a})=a_1^4-a_2^4$. If we instead set a ₂ = 1, this has a minimum of f(0) = −1. If we instead set a ₁ = 1, it has no minimum, but $\lim _{a_2\to \pm \infty }=-\infty $. These are both illustrated in Fig. 5.22.

In the one parameter case, this difference is negligible. When there are multiple parameters, some choices of which variable to remove result in large numbers in the cutting plane constraint, causing the fit to fail. The multiparameter case is also more complicated because, when looking at the behavior around the sphere at infinity, we set more variables to 1. The order in which we apply this procedure affects the numerical stability of the fit.

As long as the default procedure performs well, we ignore the potential numerical problems. If Hom4PS finds “failed paths”, meaning that it loses track of one of the minima during the transformation process, we try different orders of variables until one succeeds. Similarly, when Gurobi fails for numerical reasons, we restart the cutting plane procedure. This time, when we search for negative probability in each iteration of the cutting plane method, we try every possible order of variables to remove, skipping variable orders that give divergent or failed results in Hom4PS. We choose the linear constraint that has the smallest spread in numerical values of the coefficients. In addition, we optimally look for linear constraints that involve as many as possible of the coefficients, because in our application constraints involving only a few coefficients tend to cause the cutting plane algorithm to converge slowly. This procedure is only used when necessary because each iteration is much slower than in the default procedure; however, in practice it is only needed for a few bins, so it does not significantly slow down the overall process.

5.6.3 Results

The results of the multiparameter HVV anomalous couplings analysis are shown in Fig. 5.23.

The blue scans in Fig. 5.23 are similar to the ones in Fig. 5.9. There are two major differences:

The amount of data collected is increased. The previous scans used data from 2016 and 2017, and these add the data collected in 2018.
This analysis uses additional categories, improving the sensitivity to anomalous couplings in VBF and VH production in particular.

Due to these improvements, we expect to exclude small anomalous couplings at 95 % CL.

The red scans float the other anomalous couplings. The differences between red and blue are primarily at large values of the anomalous couplings, indicating that while the anomalous coupling parameters are correlated—in some cases highly correlated—in decay, VBF and VH production do not show these correlations, and the exclusion is about the same whether or not we float the other anomalous couplings. This is due to the fact that, as described in Sect. 4.4 and shown in Fig. 4.10, the SM is an extreme point in the parameter space with many events at low $q_V^2$. The anomalous couplings all show an enhancement at high $q_V^2$, and no correlation or interference effect will remove this enhancement. If the true minimum was at nonzero $\vec {f}_{ai}$, we would expect to see a larger difference between the blue and red curves, because $f_{a2}^{\text{VBF}}=0.1$ and $f_{a3}^{\text{VBF}}=0.1$, for example, look similar in their q ² spectrum. Discrimination would still be available from the angles, but would be less sensitive.

The two curves meet at f _ai = ±1, by definition: if f _ai = 1, then all other f _aj must be 0.

When we look at the observed results from data, the blue curves look similar to the expectation. However, when all four anomalous couplings are allowed to float independently, the best fit values are $(f_{a3} , f_{a2}, f_{\Lambda 1}, f_{\Lambda 1}^{\mathrm {Z}\gamma })=(\pm 0.01, -0.29, 0.13, -0.06)$, where the two minima at positive and negative values of f _a3 are degenerate. These global minima are driven by the decay information from H →ZZ → 4ℓ and is only slightly preferred to the local minimum at (0, 0, 0, 0), with a difference in $-2\ln \left ({\mathcal {L}}\right )$ of 0.1 between the SM value and the global minima. The local minimum at (0, 0, 0, 0) is still evident in the four-dimensional distribution and its projections on each parameter, and is driven by the production information, as discussed above for the fits with one parameter. Due to this statistical fluctuation in the observed data when the $-2\ln \left ({\mathcal {L}}\right )$ minima obtained from the decay and from the production kinematics differ, the observed constraints appear weaker than expected. The results are still statistically consistent with the SM and with the expected constraints in the SM.

Figure 5.24 shows the two-dimensional likelihood scans from this analysis.

5.6.3.1 EFT Relations with SU(2) × U(1) Symmetry

These studies repeated using the SU(2)×U(1) symmetry in Eqs. (4.9) to (4.13) . In this case, the $f_{\Lambda 1}^{\mathrm {Z}\gamma }$ parameter is not independent and can be derived following Eq. (4.13). Therefore, constraints on the three parameters f _a3, f _a2, f _Λ1, and the signal strength are obtained in this scenario following the same approach as above. These constraints are shown in Fig. 5.25.

Since the relationship of the HWW and HZZ couplings does not affect the measurement of the f _a3 parameter in the H → 4ℓ decay, the constraints from the decay information in the wider range of f _a3 in Approach 2 are unaffected compared to Approach 1, when other couplings are fixed to zero. However, with one less parameter to float, the constraints are modified somewhat when all other couplings are left unconstrained. The modified relationship between the HWW and HZZ couplings also leads to some modification of constraints using production information in the narrow range of f _a3. On the other hand, the f _a2 and f _Λ1 parameters are modified substantially because the $f_{\Lambda 1}^{\mathrm {Z}\gamma }$ information gets absorbed into these measurements.

The measurement of the signal strength μ _V and the f _a3, f _a2, and f _Λ1 parameters can be re-interpreted in terms of the δc _z, c _zz, , and $\tilde c_{zz}$ coupling strength parameters. Observed one- and two-dimensional constraints from a simultaneous fit of EFT parameters are shown in Figs. 5.26 and 5.27. The c _gg and $\tilde c_{gg}$ couplings are left unconstrained.

5.7 Hff Anomalous Couplings

This section will describe the first search for anomalous couplings in Hff. As described in Sect. 4.4.2, there is only one anomalous Hff coupling, $\tilde {\kappa }$, and it can be measured either through gluon fusion with 2 associated jets or through $\mathrm {t}\bar {\mathrm {t}}\mathrm {H}$ production. This analysis uses both.

Events are divided into seven categories, similar to the ones in Sect. 5.6:

The VBF-2jet-tagged category requires exactly four leptons, either two or three jets of which at most one is b-quark flavor-tagged, or more if none are b-tagged jets, and $\mathcal {D}_{\text{2jet}}^{\text{VBF}}>0.5$ using the SM hypothesis.
The VH-hadronic-tagged category requires exactly four leptons, either two or three jets, or more if none are b-tagged jets, and $\mathcal {D}_{\text{2jet}}^{{\mathrm {V}\mathrm {H}}}=\max \left ( \mathcal {D}_{\text{2jet}}^{{\mathrm {W}\mathrm {H}}},\mathcal {D}_{\text{2jet}}^{{\mathrm {Z}\mathrm {H}}} \right )>0.5$ using the SM hypothesis for the VH production.
The VH-leptonic-tagged category requires no more than three jets and no b-tagged jets and exactly one additional lepton or pair of opposite-sign-same-flavor leptons. In addition, events with no jets and at least one additional lepton are included in this category.
The $\mathrm {t}\bar {\mathrm {t}}\mathrm {H}$-hadronic-tagged category requires at least 4 jets of which at least 1 is b-tagged and no additional leptons;
The $\mathrm {t}\bar {\mathrm {t}}\mathrm {H}$-leptonic-tagged category requires at least 1 additional lepton in the event;
The VBF-1jet-tagged category requires exactly 4 leptons, exactly 1 jet, and $\mathcal {D}_{\text{1jet}}^{\text{VBF}}>0.7$. This discriminant is calculated using the SM hypothesis for the VBF production.
The Untagged category consists of the remaining events.

The categories directly used for anomalous couplings are the two categories that target $\mathrm {t}\bar {\mathrm {t}}\mathrm {H}$ production and the VBF-2jet-tagged category. Although the primary focus is gluon fusion rather than VBF, the gluon fusion events most sensitive to anomalous couplings are the ones that look like VBF events with gluons instead of Z or W bosons. Those are the ones most likely to be in the VBF-2jet-tagged category. The other categories are used to control yields of VBF, VH, and gluon fusion production, and the only observable used in those categories is $\mathcal {D}_{\text{bkg}}$.

In the VBF-2jet-tagged category, the observables used are $\mathcal {D}_{\text{bkg}}$ to separate signal from background; $\mathcal {D}_{\text{2jet}}^{\text{VBF}}$, which separates gluon fusion from VBF (using only the region from 0.5 to 1, since smaller values of $\mathcal {D}_{\text{2jet}}^{\text{VBF}}$ are excluded from this category); $\mathcal {D}_{0-}^{{\mathrm {g}\mathrm {g}\mathrm {H}}}$; and $\mathcal {D}_{CP}^{{\mathrm {g}\mathrm {g}\mathrm {H}}}$. The probabilities for the $\mathcal {D}_{0-}^{{\mathrm {g}\mathrm {g}\mathrm {H}}}$ discriminant are calculated assuming that the initial state particles are quarks, not gluons, because this initial state is most likely to produce the VBF-like topology sensitive to anomalous couplings.

In the $\mathrm {t}\bar {\mathrm {t}}\mathrm {H}$ category, because of the neutrinos present in leptonic decays and large number of jets, with possible permutations, present in hadronic decays, direct use of matrix elements is difficult. We therefore use machine learning, as described in Sect. 4.6.2.2, to construct a $\mathcal {D}_{0-}$ discriminant. It is possible to construct a $\mathcal {D}_{CP}$ discriminant as well using the techniques described there, but this discriminant loses its sensitivity for $\mathrm {t}\bar {\mathrm {t}}\mathrm {H}$ when, as in our case, we do not have a way to know the jet flavors and signs.

The discriminants used for this analysis are shown in Fig. 5.28.

5.7.1 ggH Results

The results for the ggH analysis are shown in Fig. 5.29. The observed constraint in the $f_{a3}^{\mathrm {g}\mathrm {g}\mathrm {H}}$ measurement appears to prefer close to the maximum mixture of the CP-odd and CP-even amplitudes with the negative relative sign, with the best fit value at $f_{a3}^{\mathrm {g}\mathrm {g}\mathrm {H}}=-0.68$. The $\mathcal {D}_{\text{CP}}^{{\mathrm {g}\mathrm {g}\mathrm {H}}}$ and $\mathcal {D}_{\text{0-}}^{{\mathrm {g}\mathrm {g}\mathrm {H}}}$ distributions in Fig. 5.28 both indicate a preference for about equal contribution of CP-odd and CP-even amplitudes, but are still consistent with the SM expectation of the pure CP-even contribution. This result is statistically consistent with $f_{a3}^{\mathrm {g}\mathrm {g}\mathrm {H}}=0$, as expected in the SM, at 1.3 σ. The significance of separation of the maximal mixture with the positive relative sign ($f_{a3}^{\mathrm {g}\mathrm {g}\mathrm {H}}\sim +0.5$) is larger because this scenario would lead to the opposite forward-backward asymmetry in the $\mathcal {D}_{\text{CP}}^{{\mathrm {g}\mathrm {g}\mathrm {H}}}$ discriminant distribution shown in Fig. 5.28 for $f_{a3}^{\mathrm {g}\mathrm {g}\mathrm {H}}\sim -0.5$.

These two parameters $f_{a3}^{\mathrm {g}\mathrm {g}\mathrm {H}}$ and μ _ggH are equivalent to the measurement of the CP-even and CP-odd couplings on the production side, while the HVV couplings on the decay side are constrained from the simultaneous measurement of the VBF and VH processes with f _a3 and μ _V profiled. The c _gg and ${\tilde c}_{gg}$ couplings, introduced in Eq. (4.8), can be extracted from the above measurements. We follow the parameterization of the cross section and the total width from [19]. In the total width parameterization, we assume that there are no unobserved or undetected H boson decays. We also assume that fermion couplings Hff are not affected by possible new physics. We allow variation of the HVV and effective Hgg couplings. The former are scaled with the μ _V parameter, and the latter are parameterized with c _gg and ${\tilde c}_{gg}$, which describe both SM and BSM contributions to the gluon fusion loop. The small contribution of the H → γγ and Zγ decays to the total width is assumed to be SM-like. The resulting constraints are shown in Fig. 5.29. The pure signal strength measurement μ _ggH, available even without the fit for $f_{a3}^{\mathrm {g}\mathrm {g}\mathrm {H}}$, provides constraint on $(c_{gg}^2+{\tilde c}_{gg}^2)$, which is a ring on a two-parameter plane in Fig. 5.29. The measurement of $f_{a3}^{\mathrm {g}\mathrm {g}\mathrm {H}}$ resolves the area within this ring. The H boson width dependence on c _gg and ${\tilde c}_{gg}$ is relatively weak and does not alter this logic considerably. The results are consistent with the SM expectation of $(c_{gg},{\tilde c}_{gg})=(0.0084,0)$ at 1.1 σ. The correlation between the two parameters is + 0.980. There is a degeneracy in the measurement between any two points $(c_{gg},{\tilde c}_{gg})$ and $(-c_{gg},{\tilde c}_{gg})$, as there is no observable information to resolve this ambiguity.

5.7.2 $\mathrm {t}\bar {\mathrm {t}}\mathrm {H}$ Results

Figure 5.30 presents the measurement of anomalous couplings of the H boson to top quarks First, the measurements of $f_{CP}^{\mathrm {H}\mathrm {t}\mathrm {t}}$ from the ${\mathrm {t}\bar {\mathrm {t}}\mathrm {H}}$ process only are reported. The signal strength $\mu _{\mathrm {t}\bar {\mathrm {t}}\mathrm {H}}$, which is the ratio of the measured cross section of the $\mathrm {t}\bar {\mathrm {t}}\mathrm {H}$ process to that expected in the SM, is profiled when the $f_{CP}^{\mathrm {H}\mathrm {t}\mathrm {t}}$ results are reported. The measured value of $\mu _{\mathrm {t}\bar {\mathrm {t}}\mathrm {H}}=0.22^{+0.86}_{-0.22} $ is consistent with that reported in [4] without the fit for CP structure of interactions. The correlation between the two parameters is − 0.029. The signal strength of the VBF and VH processes μ _V, ggH process μ _ggH, and their CP properties f _a3 and $f_{a3}^{\mathrm {g}\mathrm {g}\mathrm {H}}$ are also profiled when this measurement is performed. This ${\mathrm {t}\bar {\mathrm {t}}\mathrm {H}}$ analysis is not sensitive to the sign of $f_{CP}^{\mathrm {H}\mathrm {t}\mathrm {t}}$. However, for later combination with the ggH measurement, presented above, under the assumption of the top quark dominance in the gluon fusion loop, symmetric constraints on $f_{CP}^{\mathrm {H}\mathrm {t}\mathrm {t}}$ are reported.

With just about two signal $\mathrm {t}\bar {\mathrm {t}}\mathrm {H}$ events expected to appear in the fit in the H → 4ℓ channel under the assumption of the SM cross section, the expected confidence levels of the $f_{CP}^{\mathrm {H}\mathrm {t}\mathrm {t}}$ constraints are low. Nonetheless, the very clean signature in the H → 4ℓ channel makes any observed event candidate count. The observed best-fit value corresponds to the pure CP-odd Yukawa coupling. This is consistent with the negative value of the $\mathcal {D}_{\text{0-}}^{\mathrm {t}\bar {\mathrm {t}}\mathrm {H}}$ discriminant for the one observed signal-like event in Fig. 5.28. However, this result is statistically consistent with the pure CP-even Yukawa coupling expected in the SM at 1.5 σ.

CMS recently reported the measurement of the $f_{CP}^{\mathrm {H}\mathrm {t}\mathrm {t}}$ parameter in the $\mathrm {t}\bar {\mathrm {t}}\mathrm {H}$ production process with the decay H → γγ [45]. In that measurement, the signal strength $\mu _{\mathrm {t}\bar {\mathrm {t}}\mathrm {H}}^{\gamma \gamma }$ parameter is profiled, while the signal strengths in other production processes are fixed to the SM expectation. However, there is a very weak correlation of the measurement in the $\mathrm {t}\bar {\mathrm {t}}\mathrm {H}$ process with parameters in the other production mechanisms. We therefore proceed with a combination of the $f_{CP}^{\mathrm {H}\mathrm {t}\mathrm {t}}$ measurements in the H → 4ℓ and γγ channels, where we correlate their common systematic uncertainties, but not the signal strengths of the processes. In particular, we do not relate the $\mu _{\mathrm {t}\bar {\mathrm {t}}\mathrm {H}}$ and $\mu _{\mathrm {t}\bar {\mathrm {t}}\mathrm {H}}^{\gamma \gamma }$ signal strengths because they could be affected differently by the particles appearing in the loops responsible for the H → γγ decay. The results of this combination are presented in Fig. 5.30. Since the two H boson decay channels have the opposite best-fit values, the combined result has a somewhat smaller confidence level compared to the H → γγ channel alone, excluding the pure pseudoscalar hypothesis at 3.1 σ. However, the expected exclusion at 2.6 σ has a higher confidence level than individual channels. Below we also present an interpretation of these results where the signal strengths in the two H boson decay channels are related.

In the above measurements, the $f_{CP}^{\mathrm {H}\mathrm {t}\mathrm {t}}$ parameter has the same meaning in both the H → 4ℓ and γγ channels. However, the signal strength may have different interpretation due to potentially unknown BSM contributions to the loop in the H → γγ decay. In order to make an EFT coupling interpretation of results, we have to make a further assumption that no BSM particles contribute to the loop in the H → γγ decay. Without this or a similar assumption, the signal strength in the H → γγ decay cannot be interpreted without ambiguity. We further re-parameterize the cross section following Ref. [19] with the couplings κ _t and $\tilde \kappa _{\mathrm {t}}$, and fix κ _b = 1 and $\tilde \kappa _{\mathrm {b}}=0$. The bottom quark coupling has a very small contribution to the loop in the H → γγ decay, but it has large contribution to the total decay width, where we assume that there are no unobserved or undetected H boson decays. In order to simplify the fit, we do not allow anomalous HVV couplings, and the measurement of the signal strength _muV constrains the contribution of the a ₁ coupling in the loop. The $f_{a3}^{\mathrm {g}\mathrm {g}\mathrm {H}}$ and μ _ggH parameters are profiled in this fit. The observed confidence level intervals on the κ _t and $\tilde \kappa _{\mathrm {t}}$ couplings from the combined fit of the H → 4ℓ and γγ channels are shown in Fig. 5.30.

5.7.3 Combined Results

The measurement of anomalous couplings of the H boson to top quarks in the ggH process, assuming top quark dominance in the gluon fusion loop, is presented in Fig. 5.31. Similarly to the case of the H → γγ loop discussed above, the cross section of the ggH process, normalized to the SM expectation, is parameterized following Ref. [19] to account for CP-odd Yukawa couplings as follows

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle \frac{\sigma(\mathrm{g}\mathrm{g}\mathrm{H})}{\sigma_{\mathrm{SM}}} = \kappa_{\mathrm{f}}^2 + 2.38 \tilde\kappa_{\mathrm{f}}^2 \,, {} \end{array} \end{aligned} $$

(5.25)

where we set κ _f = κ _t = κ _b and $\tilde \kappa _{\mathrm {f}}= \tilde \kappa _{\mathrm {t}}=\tilde \kappa _{\mathrm {b}}$. Equation (5.25) sets the relationship between the $f_{CP}^{\mathrm {H}\mathrm {t}\mathrm {t}}$ and $f_{a3}^{\mathrm {g}\mathrm {g}\mathrm {H}}$, reported in Fig. 5.29, according to Eq. (4.6).

Constraints on $f_{CP}^{\mathrm {H}\mathrm {t}\mathrm {t}}$ are also shown with combination of the ggH and $\mathrm {t}\bar {\mathrm {t}}\mathrm {H}$ processes with H → 4ℓ only and with H → γγ included in the combination, see Fig. 5.31. The gain in this combination of the ggH and $\mathrm {t}\bar {\mathrm {t}}\mathrm {H}$ processes is beyond the simple addition of the two constraints. While in the ggH and $\mathrm {t}\bar {\mathrm {t}}\mathrm {H}$ analyses the signal strength of the two processes is independent, these could be related under the assumption of top quark dominance in the loop using Eq. (5.25). As discussed in Sect. 4.4.2, the CP-odd coupling predicts rather different cross sections in the two processes: $\sigma (\tilde \kappa _f=1)/ \sigma (\kappa _f=1)$ is 2.38 in the gluon fusion process dominated by the top quark loop and 0.391 in the $\mathrm {t}\bar {\mathrm {t}}\mathrm {H}$ process. This means that the ratio differs by a factor of 6.09 for $f_{CP}^{\mathrm {H}\mathrm {t}\mathrm {t}}=1$ when compared to SM ($f_{CP}^{\mathrm {H}\mathrm {t}\mathrm {t}}=0$). This correlation enhances the sensitivity in the $f_{CP}^{\mathrm {H}\mathrm {t}\mathrm {t}}$ measurement.

The combination of the H → 4ℓ and γγ channels in combination of the ggH and $\mathrm {t}\bar {\mathrm {t}}\mathrm {H}$ processes proceed in a manner similar. In particular, we do not allow anomalous HVV couplings, and the measurement of the signal strength μ _V constrains the contribution of the a ₁ coupling in the H → γγ loop. The full combination of the $f_{CP}^{\mathrm {H}\mathrm {t}\mathrm {t}}$ results is also shown in Fig. 5.31.

Finally, the re-interpretation of the $f_{CP}^{\mathrm {H}\mathrm {t}\mathrm {t}}$ and signal strength measurements in terms of constraints on κ _f and $\tilde \kappa _{\mathrm {f}}$ shown in Fig. 5.31. In this fit, it is assumed that κ _f = κ _t = κ _b = κ _c = κ _μ and $\tilde \kappa _{\mathrm {f}}=\tilde \kappa _{\mathrm {t}}=\tilde \kappa _{\mathrm {b}}=\tilde \kappa _{\mathrm {c}}=\tilde \kappa _\mu $ in the fermion coupling contribution to the production processes and in the decay width parameterization [19]. The measurement of the signal strength μ _V constrains the contributions of the a ₁ coupling and anomalous HVV couplings are not allowed. It is assumed that there are no unobserved or undetected H boson decays.

References

CMS Collaboration, Studies of Higgs boson production in the four-lepton final state at $\sqrt {s} = 13$ TeV. CERN, Geneva, Tech. Rep. CMS-PAS-HIG-15-004, 2016. https://cds.cern.ch/record/2139978
A.M. Sirunyan et al., Measurements of properties of the Higgs boson decaying into the four-lepton final state in pp collisions at $\sqrt {s} = 13$ TeV. J. High Energy Phys. 11, 047 (2017). https://doi.org/10.1007/JHEP11(2017)047. arXiv: 1706.09936 [hep-ex]
CMS Collaboration, Measurements of properties of the Higgs boson in the four-lepton final state at $\sqrt {s} = 13$ TeV. CERN, Geneva, Tech. Rep. CMS-PAS-HIG-18-001, 2018. https://cds.cern.ch/record/2621419
CMS Collaboration, Measurements of properties of the Higgs boson in the four-lepton final state in proton-proton collisions at $\sqrt {s} = 13$ TeV. CERN, Geneva, Tech. Rep. CMS-PAS-HIG-19-001, 2019. https://cds.cern.ch/record/2668684
S. Chatrchyan et al., On the mass and spin-parity of the Higgs boson candidate via its decays to Z boson pairs. Phys. Rev. Lett. 110, 081803 (2013) . https://doi.org/10.1103/PhysRevLett.110.081803. arXiv: 1212.6639 [hep-ex]
S. Chatrchyan et al., Measurement of the properties of a Higgs boson in the four-lepton final state. Phys. Rev. D 89, 092007 (2014). https://doi.org/10.1103/PhysRevD.89.092007. arXiv: 1312.5353 [hep-ex]
V. Khachatryan et al., Constraints on the spin-parity and anomalous HVV couplings of the Higgs boson in proton collisions at 7 and 8 TeV. Phys. Rev. D 92, 012004 (2015). https://doi.org/10.1103/PhysRevD.92.012004. arXiv: 1411.3441 [hep-ex]
G. Aad et al., Evidence for the spin-0 nature of the Higgs boson using ATLAS data. Phys. Lett. B 726, 120 (2013). https://doi.org/10.1016/j.physletb.2013.08.026. arXiv: 1307.1432 [hep-ex]
G. Aad et al., Study of the spin and parity of the Higgs boson in diboson decays with the ATLAS detector. Eur. Phys. J. C 75, 476 (2015). https://doi.org/10.1140/epjc/s10052-015-3685-1. arXiv: 1506.05669 [hep-ex]
S. Frixione, P. Nason, C. Oleari, Matching NLO QCD computations with parton shower simulations: the POWHEG method. J. High Energy Phys. 11, 070 (2007). https://doi.org/10.1088/1126-6708/2007/11/070. arXiv: 0709.2092 [hep-ph]
E. Bagnaschi, G. Degrassi, P. Slavich, A. Vicini, Higgs production via gluon fusion in the POWHEG approach in the SM and in the MSSM. J. High Energy Phys. 2, 088 (2012). https://doi.org/10.1007/JHEP02(2012)088. arXiv: 1111.2854 [hep-ph]
P. Nason, C. Oleari, NLO Higgs boson production via vector-boson fusion matched with shower in POWHEG. J. High Energy Phys. 2, 037 (2010). https://doi.org/10.1007/JHEP02(2010)037. arXiv: 0911.5299 [hep-ph]
G. Luisoni, P. Nason, C. Oleari, F. Tramontano, HW^±∕HZ + 0 and 1 jet at NLO with the POWHEG BOX interfaced to GoSam and their merging within MiNLO. J. High Energy Phys. 10, 083 (2013). https://doi.org/10.1007/JHEP10(2013)083. arXiv: 1306.2542 [hep-ph]
H.B. Hartanto, B. Jager, L. Reina, D.Wackeroth, Higgs boson production in association with top quarks in the POWHEG BOX. Phys. Rev. D 91, 094003 (2015). https://doi.org/10.1103/PhysRevD.91.094003. arXiv: 1501.04498 [hep-ph]
Y. Gao, A.V. Gritsan, Z. Guo, K. Melnikov, M. Schulze, N.V. Tran, Spin determination of single-produced resonances at hadron colliders. Phys. Rev. D 81, 075022 (2010). https://doi.org/10.1103/PhysRevD.81.075022. arXiv: 1001.3396 [hep-ph]
S. Bolognesi, Y. Gao, A.V. Gritsan, K. Melnikov, M. Schulze, N.V. Tran, A. Whitbeck, Spin and parity of a single-produced resonance at the LHC. Phys. Rev. D 86, 095031 (2012). https://doi.org/10.1103/PhysRevD.86.095031. arXiv: 1208.4018 [hep-ph]
I. Anderson, S. Bolognesi, F. Caola, Y. Gao, A.V. Gritsan, C.B. Martin, K. Melnikov, M. Schulze, N.V. Tran, A. Whitbeck, Y. Zhou, Constraining anomalous HVV interactions at proton and lepton colliders. Phys. Rev. D 89, 035007 (2014). https://doi.org/10.1103/PhysRevD.89.035007. arXiv: 1309.4819 [hep-ph]
A.V. Gritsan, R. Röntsch, M. Schulze, M. Xiao, Constraining anomalous Higgs boson couplings to the heavy flavor fermions using matrix element techniques. Phys. Rev. D 94, 055023 (2016). https://doi.org/10.1103/PhysRevD.94.055023. arXiv: 1606.03107 [hep-ph]
A. V. Gritsan, J. Roskes, U. Sarica, M. Schulze, M. Xiao, and Y. Zhou, “New features in the JHU generator framework: constraining Higgs boson properties from on-shell and off-shell production,” Phys. Rev. D, vol. 102, no. 5, p. 056022, 2020. https://doi.org/10.1103/PhysRevD.102.056022.arXiv:2002.09888 [hep-ph]
J.M. Campbell, R.K. Ellis, MCFM for the Tevatron and the LHC. Nucl. Phys. Proc. Suppl. 205–206, 10 (2010). https://doi.org/10.1016/j.nuclphysbps.2010.08.011. arXiv: 1007.3492 [hep-ph]
R.J. Barlow, Extended maximum likelihood. Nucl. Instrum. Meth. A 297, 496 (1990). https://doi.org/10.1016/0168-9002(90)91334-8
Article ADS Google Scholar
V. Khachatryan et al., Combined search for anomalous pseudoscalar HVV couplings in VH($\mathrm {H} \rightarrow \mathrm {b}\bar {\mathrm {b}}$) production and H →VV decay. Phys. Lett. B 759, 672 (2016). https://doi.org/10.1016/j.physletb.2016.06.004. arXiv: 1602.04305 [hep-ex]
G. Aad et al., Test of CP invariance in vector-boson fusion production of the Higgs boson using the optimal observable method in the ditau decay channel with the ATLAS detector. Eur. Phys. J. C 76, 658 (2016). https://doi.org/10.1140/epjc/s10052-016-4499-5. arXiv: 1602.04516 [hep-ex]
V. Khachatryan et al., Limits on the Higgs boson lifetime and width from its decay to four charged leptons. Phys. Rev. D 92, 072010 (2015). https://doi.org/10.1103/PhysRevD.92.072010. arXiv: 1507.06656 [hep-ex]
G. Aad et al., Constraints on the off-shell Higgs boson signal strength in the high-mass ZZ and WW final states with the ATLAS detector. Eur. Phys. J. C 75, 335 (2015). https://doi.org/10.1140/epjc/s10052-015-3542-2. arXiv: 1503.01060 [hep-ex]
A.M. Sirunyan et al., Constraints on anomalous Higgs boson couplings using production and decay information in the four-lepton final state. Phys. Lett. B 775, 1 (2017). https://doi.org/10.1016/j.physletb.2017.10.021. arXiv: 1707.00541 [hep-ex]
A.M. Sirunyan et al., Measurements of the Higgs boson width and anomalous HVV couplings from on-shell and off-shell production in the four-lepton final state. Phys. Rev. D vol. 99(11), 112003 (2019). https://doi.org/10.1103/PhysRevD.99.112003. arXiv: 1901.00174 [hep-ex]
A.M. Sirunyan et al., Search for a new scalar resonance decaying to a pair of Z bosons in proton-proton collisions at $\sqrt {s}\ =\ 13$ TeV. J. High Energy Phys. 6, 127 (2018). [Erratum: JHEP 3, 128 (2019)]. https://doi.org/10.1007/JHEP06(2018)127. arXiv: 1804.01939 [hep-ex]
A.M. Sirunyan et al., Constraints on anomalous HVV couplings from the production of Higgs bosons decaying to τ lepton pairs. Phys. Rev. D 100(11), 112002 (2019). https://doi.org/10.1103/PhysRevD.100.112002. arXiv: 1903.06973 [hep-ex]
A.M. Sirunyan et al., Observation of the Higgs boson decay to a pair of τ leptons with the CMS detector. Phys. Lett. B779, 283–316 (2018). https://doi.org/10.1016/j.physletb.2018.02.004. arXiv: 1708.00373 [hep-ex]
V. Khachatryan et al., Reconstruction and identification of τ lepton decays to hadrons and ν _τ at CMS. JINST 11, P01019 (2016). https://doi.org/10.1088/1748-0221/11/01/P01019. arXiv: 1510.07488 [physics.ins-det]
A.M. Sirunyan et al., Performance of reconstruction and identification of τ leptons decaying to hadrons and ν _τ in pp collisions at $\sqrt {s}\ =\ 13$ TeV. JINST 13, P10005 (2018). https://doi.org/10.1088/1748-0221/13/10/P10005. arXiv: 1809.02816 [hep-ex]
L. Bianchini, J. Conway, E.K. Friis, C. Veelken, Reconstruction of the Higgs mass in H → ττ events by dynamical likelihood techniques. J. Phys. Conf. Ser. 513, 022035 (2014). https://doi.org/10.1088/1742-6596/513/2/022035.
Article Google Scholar
CMS collaboration, Constraints on anomalous Higgs boson couplings to vector bosons and fermions in production and decay H → 4lchannel. Report No.: CMS-PAS-HIG-19-009, to be submitted to Phys. Rev. D. http://cds.cern.ch/record/2725543
H. Stetter, Numerical Polynomial Algebra (Society for Industrial and Applied Mathematics, 2004). https://doi.org/10.1137/1.9780898717976
B. Buchberger, A theoretical basis for the reduction of polynomials to canonical forms. SIGSAM Bull. 10(3), 19–29 (1976). ISSN: 0163-5824. https://doi.org/10.1145/1088216.1088219
Article MathSciNet Google Scholar
A. Kondratyev, H.J. Stetter, F. Winkler, Numerical Computation of Gröbner Bases (Citeseer, 2004), pp. 295–306
Google Scholar
T. Chen, T.-Y. Li, Homotopy continuation method for solving systems of nonlinear and polynomial equations. Commun. Inf. Syst. 15(2), 119–307 (2015). ISSN: 15267555, 21634548. https://doi.org/10.4310/CIS.2015.v15.n2.a1
T. Chen, T.-L. Lee, T.-Y. Li, Hom4PS-3: A parallel numerical solver for systems of polynomial equations based on polyhedral homotopy continuation methods, in Mathematical Software—ICMS 2014, ed. by H. Hong, C. Yap, Lecture Notes in Computer Science, vol. 8592 (Springer, Berlin, 2014), pp. 183–190. ISBN: 978-3-662-44199-2. https://doi.org/10.1007/978-3-662-44199-2_30
T. Chen, T.-L. Lee, and T.-Y. Li, Mixed cell computation in Hom4PS-3. J. Symb. Comput. 79(Part 3), 516–534 (2017), ISSN: 0747-7171. https://doi.org/10.1016/j.jsc.2016.07.017
A.S. Nemirovsky, D.B. Yudin, Problem Complexity and Method Efficiency in Optimization (Wiley, London, 1983)
Google Scholar
S. Diamond, S. Boyd, CVXPY: A Python-embedded modeling language for convex optimization. J. Mach. Learn. Res. 17(83), 1–5 (2016)
MathSciNet MATH Google Scholar
A. Agrawal, R. Verschueren, S. Diamond, S. Boyd, A rewriting system for convex optimization problems. J. Control Decis. 5(1), 42–60 (2018)
Article MathSciNet Google Scholar
Gurobi Optimization, LLC, Gurobi Optimizer Reference Manual (2018). http://www.gurobi.com
A.M. Sirunyan et al., Measurements of tt̄H production and the CP structure of the Yukawa interaction between the Higgs boson and top quark in the diphoton decay channel (2020). arXiv: 2003.10866 [hep-ex]
Google Scholar

Download references

Author information

Authors and Affiliations

Bloomberg Center for Physics & Astronomy, Johns Hopkins University, Baltimore, MD, USA
Jeffrey Roskes

Authors

Jeffrey Roskes
View author publications
You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

Copyright information

About this chapter

Cite this chapter

Roskes, J. (2020). Higgs Boson Data Analysis. In: A Boson Learned from its Context, and a Boson Learned from its End. Springer Theses. Springer, Cham. https://doi.org/10.1007/978-3-030-58011-7_5

Download citation

DOI: https://doi.org/10.1007/978-3-030-58011-7_5
Published: 20 November 2020
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-58010-0
Online ISBN: 978-3-030-58011-7
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)

Publish with us

Policies and ethics