Keywords

1 Introduction

It is widely believed that kinetic theory of granular gases [1, 2] is the correct framework to model dilute granular flows, but fails in dealing with dense situations. This belief rests on the assumptions that, in dense granular flows, the particle interactions are no longer uncorrelated, binary and nearly instantaneous, the particle surface friction plays a dominant role and the particle velocity fluctuations—measured by the granular temperature [3], one-third of the mean square of the fluctuation velocity of the particles, a key ingredient of kinetic theory—are no longer meaningful.

Over the last 15 years, a phenomenological approach to dense granular flows [4] acquired vast popularity. It is based on an empirical, local relation (the so-called μ-I rheology) between the particle shear stress, pressure and shear rate which depends upon dimensional arguments and ignores the role of velocity fluctuations. It has been shown to work in many flow configurations (e.g., simple shearing [5], inclined heap flows [6]), although, more recently, it has become apparent that it fails in situations dominated by the boundaries (thin flows over rigid beds [7]) and in regions where the ratio of the particle shear stress to the particle pressure is less than a yield [8] (granular beds). To repair this, Kamrin and coworkers [9] have proposed the introduction of a new state variable, the granular fluidity, and an evolution equation for it that contains a diffusive-like term, which permits nonlocal effects to be treated. A recently revealed relation between the fluidity and the velocity fluctuations [10] suggests that Kamrin’s nonlocal rheology and the kinetic theory of granular gases can be reconciled.

Kinetic theory of granular gases has been extended in significant ways over the last 20 years to make it applicable to dense granular flows. A length scale has been introduced in the constitutive relation for the rate at which fluctuation kinetic energy is dissipated in collisions [11,12,13]; this accounts for the velocity correlation that develops at solid volume fraction larger than the freezing point [14,15,16]. The transformation of translational kinetic energy into rotational kinetic energy associated with particle surface friction has been modelled by introducing an effective coefficient of collisional restitution [17, 18]. Moreover, the role of friction in determining the maximum volume fraction at which a random assembly of rigid spheres can be sheared is now understood [19]. Finally, the possibility of non-instantaneous collisions and the development of rate-independent components of the stresses associated with finite particle stiffness have been incorporated in the theory [20].

Experiments [21] and numerical simulations [8, 22] have shown that velocity decays exponentially inside granular beds at the bottom of shearing flows. In the search for boundary conditions for the differential equations of kinetic theory that govern granular shearing, Jenkins and Askari [23] have suggested that in the bed, the working of the shear stress can be ignored; so that in steady, fully developed flows, the diffusion of fluctuation energy of the particles exactly balances its rate of collisional dissipation. This balance results in exponentially decaying profiles of the granular temperature.

Recently, we have employed an extended kinetic theory for dense granular gases to determine profiles of average velocity, solid volume fraction and temperature for granular flows in a Couette cell [20, 24]. In that case, the granular material was sheared by the motion of a bumpy, rigid boundary in the absence of gravity. We assumed that a granular bed was present at a distance from the moving boundary, and showed how the exponential decay of the granular temperature predicted by Jenkins and Askari [23] determined the exponential decay of the average particle velocity.

Here, we use extended kinetic theory to determine features of the inhomogeneous flow of identical spheres sheared between two parallel, bumpy planes, one moving at constant velocity and one at rest, when gravity acts perpendicular to the planes. We first determine the influence of the velocity of the moving plane and gravity on the flow and show that our results are in agreement with experiments [25] in which a slider was pulled at constant velocity on the top of a granular layer composed of glass spheres. We then apply the theory to the annular shearing between two coaxial cylinders in the absence of gravity, with the inner cylinder rotating at constant angular velocity, while the outer cylinder is at rest. In this case, it is the centrifugal force which breaks the symmetry of the problem and induces inhomogeneity. We show that our predictions are in qualitative agreement with numerical simulations on disks [8].

2 Planar Granular Shearing with Gravity

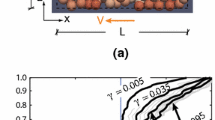
Identical spheres of mass density ρ p and diameter d are sheared between two parallel planes, with the upper plane moving at constant velocity, in the presence of gravity. The two planes are made bumpy by gluing a layer of spheres, identical to those of the flow, in a regular, hexagonal fashion. The bumpiness ψ of the planes is determined by the mean interparticle distance between the glued grains [26]. We take x and y to be the directions parallel and perpendicular to the planes, respectively, with the y-axis pointing upward. The only non-zero component of the average particle velocity is the x-component, u; while ν is the solid volume fraction. The distance, h, between the planes, the velocity, V , of the upper plane and the gravity, g, are the control variables of the system. The flow configuration is depicted in Fig. 1.

Fig. 1
figure 1

Sketch of the planar shearing in the presence of gravity with the frame of reference

Full size image

We focus on dense situations, in which the dependence of the solid volume fraction on the y-coordinate can be neglected and the y-momentum balance integrated to provide the following distribution of particle pressure:

$$\displaystyle \begin{aligned} p = P+0.6\rho_pg(h-y), \end{aligned} $$
(1)

where P is the pressure at the moving plane and 0.6 is, roughly, the depth-averaged solid volume fraction. When the pressure gradient along the x-direction is negligible, the x-momentum balance indicates that the particle shear stress s is uniform and equal to its value, S, at the moving plane. As observed in the simulations, the flow domain can, in general, be divided into two sub-regions: a region of fast flow, adjacent to the moving boundary of thickness δ and a region of slow flow, of thickness h − δ (Fig. 1). Koval et al. [8] distinguished between the two regions by whether the local value of the stress ratio s∕p was greater or less than its minimum (yield) value in simple shearing. Here, we identify the fast and slow flows as those in which the solid volume fractions are, respectively, less than and greater than the largest value, ν E, for which the aggregate can be sheared without expanding.

2.1 Fast Flow

In the fast flow, we use the constitutive relations for the pressure and the shear stress of kinetic theory [2] in the dense limit [19],

$$\displaystyle \begin{aligned} p = \rho_p2(1+e)\nu^2g_0T; \end{aligned} $$
(2)

and

$$\displaystyle \begin{aligned} S = \rho_pd \frac{8J\nu^2g_0}{5\pi^{1/2}} T^{1/2}u', \end{aligned} $$
(3)

where e is the coefficient of normal restitution (the negative of the ratio of pre- to post-collisional relative velocity along the line of centres of two colliding grains); g 0 is the radial distribution function at contact, here taken to be the dense limit of a fit to the results of numerical simulations of simple shearing [19], \(g_0=2/\left (\nu _c-\nu \right )\), for e less than 0.95, where ν c is critical volume fraction whose value depends on particle friction [27]; T is the granular temperature; and J = (1 + e)∕2 + π(1 + e)2(3e − 1)∕[96 − 24(1 − e)2 − 20(1 − e 2)]. Here, and in what follows, a prime indicates a derivative with respect to y.

The fluctuation energy balance is

$$\displaystyle \begin{aligned} Q' = su'-\varGamma, \end{aligned} $$
(4)

where Q is the flux of fluctuation energy:

$$\displaystyle \begin{aligned} Q = -\rho_pd \frac{4M\nu^2g_0}{\pi^{1/2}} T^{1/2}T', \end{aligned} $$
(5)

with M = (1 + e)∕2 + 9π(1 + e)2(2e − 1)∕[128 − 56(1 − e)]; and Γ is the collisional rate of dissipation:

$$\displaystyle \begin{aligned} \varGamma = \rho_p \frac{12\left(1-\epsilon^2\right)\nu^2g_0}{\pi^{1/2}L} T^{3/2}, \end{aligned} $$
(6)

where 𝜖 is an effective coefficient of restitution that incorporates rolling and sliding [18]. The quantity L in (6) is the correlation length of extended kinetic theory [12, 28] that accounts for the failure of molecular chaos at volume fractions larger than 0.49. Here, as in [13], we employ

$$\displaystyle \begin{aligned} L = \left[\frac{4J}{15\left(1-\epsilon^2\right)}\right]^{1/2}\left[1+\frac{26\left(1-\epsilon\right)}{15}\frac{\nu-0.49}{0.64-\nu}\right]^{3/2}\frac{d^2u'}{T^{1/2}}. \end{aligned} $$
(7)

We now make lengths dimensionless by d, velocities by \(\left (P/\rho _p\right )^{1/2}\), stresses by P, and energy flux by \(\left (P^3/\rho _p\right )^{1/2}\). Then, the dimensionless forms of the upper plate velocity and gravity are \(V\rho _p^{1/2}/P^{1/2}\) and gρ pd∕P, respectively. For simplicity, in what follows, we employ the same notation, even if we refer to dimensionless quantities.

We take the derivative of (2) with respect to y, and use (1) and (5) to obtain a differential equation for the solid volume fraction [28]:

$$\displaystyle \begin{aligned} \nu' =\frac{\pi^{1/2}Q}{4M\left(\nu^2g_0\right)_\nu T^{3/2}}-\frac{0.6g}{2(1+e)\left(\nu^2g_0\right)_\nu T}; \end{aligned} $$
(8)

where the subscript indicates the derivative with respect to ν and, from (1) and (2), \(T=\left [1+0.6g(h-y)\right ]\left [2(1+e)\nu ^2g_0\right ]^{-1}\). A differential equation for the particle velocity is obtained by inverting (3),

$$\displaystyle \begin{aligned} u' =\frac{5\pi^{1/2}S}{8J\nu^2g_0T^{1/2}}. \end{aligned} $$
(9)

Finally, the differential equation for the energy flux is, from (4) with (6) and (9),

$$\displaystyle \begin{aligned} Q' =\frac{5\pi^{1/2}S^2}{8J\nu^2g_0T^{1/2}}-\frac{12\left(1-\epsilon^2\right)\nu^2g_0T^{3/2}}{\pi^{1/2}L}, \end{aligned} $$
(10)

where L is calculated from (7) and (9). The system of three differential equations (8) through (10) permits the determination of the distribution of ν, u and Q in the fast flow, once appropriate boundary conditions are provided.

At y = h, we use the boundary conditions derived by Richman [26] for the flows of spheres over bumpy planes: a slip velocity given by

$$\displaystyle \begin{aligned} u_B =\left(\frac{\pi}{2}\right)^{1/2} S \left\{\frac{1-5(1+e)(1+B)\sin^2\psi/\left(2^{5/2}J\right)}{(2/3)\csc^2\psi(1-\cos\psi)-\cos\psi} +\frac{5(1+e)}{2^{3/2}J}\right\}T_h^{1/2}, \end{aligned} $$
(11)

where B = 12π∕21∕2 and an energy flux given as

$$\displaystyle \begin{aligned} Q_B = Su_B-\frac{2^{3/2}(1-\cos\psi)\csc^2\psi(1-\epsilon)}{\pi^{1/2}L_h}T_h^{1/2}. \end{aligned} $$
(12)

In (11) and (12), T h and L h are the granular temperature and correlation length evaluated at y = h.

At y = h − δ, the interface between the fast and the slow flows, we employ the boundary condition for the energy flux at an erodible boundary [23], modified by the introduction of the correlation length,

$$\displaystyle \begin{aligned} Q_E = -2(1+0.6g\delta)\left[\frac{3M(1-\epsilon)}{\pi L_{h-\delta}}\right]^{1/2}T_{h-\delta}^{1/2}, \end{aligned} $$
(13)

where T h−δ and L h−δ are the granular temperature and correlation length evaluated at y = h − δ. We also fix the solid volume fraction there to be equal to ν E. Finally, we require the value u E of the particle velocity at y = h − δ to be continuous with that in the bed, determined analytically in the next section.

The five boundary conditions u(y = h) = V − u B, u(y = h − δ) = u E, ν(y = h − δ) = ν E, Q(y = h) = −Q B and Q(y = h − δ) = Q E permit the solution of the system of differential equations (8) through (10) using the Matlab® routine ‘bvp4c’, with the thickness δ and the value of the uniform shear stress S determined as part of the solution.

2.2 Slow Flow

In the slow flow, for y ≤ h − δ in which the solid volume fraction exceeds the greatest for which shearing takes place without expansion, the stresses are likely generated by physical mechanisms besides momentum exchange in random collisions. In simple shearing, for instance, if the spheres are sufficiently compliant, there is an additional, elastic component of the stresses [20]. On the other hand, recent numerical simulations [10] showed that the constitutive relations for compliant spheres [20] do not always apply, especially in the case of wall-bounded, inhomogeneous flows. Another physical mechanism, such as the development of spatial anisotropy in the network of contacts is likely to be involved. In shearing flows, it is probable that such a mechanism affects the particle shear stress and pressure in a similar way, so that their ratio remains equal to the ratio of (3) to (2). This assumption seems corroborated by a preliminary analysis of the numerical measurements [10] on inhomogeneous flows, and it permits the reproduction of the results of numerical simulations of simple shearing [20]. With this

$$\displaystyle \begin{aligned} \frac{S}{p} = \frac{4J}{5\pi^{1/2}(1+e)}\frac{u'}{T^{1/2}}. \end{aligned} $$
(14)

We also assume, as elsewhere [20, 24], that the fluctuation energy balance in this slow flow region reduces to a balance between the diffusion and the collisional dissipation of energy—that is, the rate of energy production due to the working of the shear stress is negligible. As shown in [23], this results in a differential equation for the granular temperature of the form:

$$\displaystyle \begin{aligned} T'' = \frac{T}{\lambda^2}, \end{aligned} $$
(15)

where \(\lambda ^2=LM/\left [3\left (1-\epsilon \right )\right ]\), differing from that of [23] because of the introduction of the correlation length. For simplicity, we take L to be equal to its value in simple shearing [20],

$$\displaystyle \begin{aligned} L = 1+\frac{26\left(1-\epsilon\right)}{15}\frac{\nu_c-0.49}{0.64-\nu_c}. \end{aligned} $$
(16)

The analytical solution of (15) is

$$\displaystyle \begin{aligned} T = T_{h-\delta}\exp\left(-\frac{h-\delta-y}{\lambda}\right). \end{aligned} $$
(17)

Using (17) in (14), with (1), and integrating, with the boundary condition u = 0 when y = 0, gives

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} u &\displaystyle = &\displaystyle \frac{5\pi^{1/2}(1+e)}{4J}\frac{ST_{h-\delta}^{1/2}}{0.6g}\exp\left(\frac{1+0.6g\delta}{1.2g\lambda}\right)\\ &\displaystyle &\displaystyle \times\left[-\mbox{Ei}\left(-\frac{1+0.6g(h-y)}{1.2g\lambda}\right)+\mbox{Ei}\left(-\frac{1+0.6gh}{1.2g\lambda}\right) \right], \end{array} \end{aligned} $$
(18)

where \(\mbox{Ei}(x)=\int _{-\infty }^x\exp (t)/t\mbox{d}t\) is the exponential integral. When y = h − δ, (18) provides the value of the velocity u E to be used as the boundary condition in the numerical solution of the fast flow of the previous section:

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} u_E &\displaystyle = &\displaystyle \frac{5\pi^{1/2}(1+e)}{4J}\frac{ST_{h-\delta}^{1/2}}{0.6g}\exp\left(\frac{1+0.6g\delta}{1.2g\lambda}\right)\\ &\displaystyle &\displaystyle \times\left[-\mbox{Ei}\left(-\frac{1+0.6g\delta}{1.2g\lambda}\right)+\mbox{Ei}\left(-\frac{1+0.6gh}{1.2g\lambda}\right) \right]. \end{array} \end{aligned} $$
(19)

From (18) and (19), we obtain the expression of the scaled velocity profile in the slow flow:

$$\displaystyle \begin{aligned} \frac{u}{u_E}=\frac{-\mbox{Ei}\left(-\frac{1+0.6g(h-y)}{1.2g\lambda}\right)+\mbox{Ei}\left(-\frac{1+0.6gh}{1.2g\lambda}\right) }{-\mbox{Ei}\left(-\frac{1+0.6g\delta}{1.2g\lambda}\right)+\mbox{Ei}\left(-\frac{1+0.6gh}{1.2g\lambda}\right) }. \end{aligned} $$
(20)

2.3 Results

We now indicate the results of the present theory for a representative set of parameters. We take e = 0.9 and ν c = 0.587, appropriate for particles of surface friction μ = 0.5 [27], with 𝜖 = 0.7 [18]; ν E = 0.58 (the solid volume fraction at the interface between the fast flow and the bed in numerical simulations of laterally confined, inclined flows of frictional spheres [22]) and ψ = π∕6. We take h = 70 and use different values of dimensionless velocity V  and dimensionless gravity g to determine the influence of these parameters on the results.

Figure 2 shows the dimensionless average particle velocity as a function of the distance from the moving plane. In a semi-log plot, it is possible to appreciate the exponential behaviour of (18) in the slow flow. The thickness of the fast flow, marked by the knee in the velocity profiles of Fig. 2, increases with increasing dimensionless V  and decreasing dimensionless g. This is more evident in Figs. 3 and 4 where δ is plotted as a function of V  and g, respectively. For g = 0.05, the fast flow disappears when V  is less than 0.25 (Fig. 3). For a given velocity of the moving plane, the fast flow shrinks when dimensionless gravity increases (Fig. 4).

Fig. 2
figure 2

Dimensionless velocity profiles for h = 70 and V = 2 and g = 0.05 (solid line); V = 2 and g = 0.5 (dashed line); and V = 1 and g = 0.05 (dot-dashed line)

Full size image
Fig. 3
figure 3

Thickness of the fast flow as a function of the dimensionless velocity of the moving plane for h = 70 and g = 0.05

Full size image
Fig. 4
figure 4

Thickness of the fast flow as a function of dimensionless gravity for h = 70 and V = 2

Full size image

Unlike the thickness of the fast flow, the particle shear stress always increases with both increase in V  and g (Figs. 5 and 6). In other words, pulling a plane over a granular assembly is increasingly more difficult if we increase the velocity of the plane and/or the gravity, relative to the applied pressure, as expected.

Fig. 5
figure 5

Shear stress as a function of the dimensionless velocity of the moving plane for h = 70 and g = 0.05

Full size image
Fig. 6
figure 6

Shear stress as a function of dimensionless gravity for h = 70 and V = 2

Full size image

Experimental profiles of the velocity of glass spheres in a layer sheared by a slider pulled at constant velocity have been measured in Siavoshi et al. [25]. In dimensionless terms, those experiments were performed with V = 0.0015 and g = 0.24 by changing the total thickness h. Based on Figs. 3 and 4, we do not expect a fast flow to be present. The velocity profile is, therefore, analytical and given by (20). Figure 7 shows that our predictions are in good agreement with the experiments.

Fig. 7
figure 7

Experimental (symbols, after Siavoshi et al. [25]) and predicted (lines, (20)) scaled velocity in the slow flow when V = 0.0015, g = 0.24 and h = 4 (dot-dashed line and squares); h = 7 (dashed line and triangles); h = 10 (solid line and circles)

Full size image

3 Annular Shearing

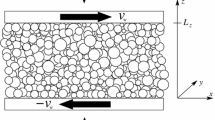
We now assume that the identical spheres are sheared between two coaxial cylinders in the absence of gravity, with the inner cylinder moving at constant angular velocity. As for the case of planar shearing with gravity, the surfaces of the cylinders are made bumpy by gluing a layer of spheres, identical to those of the flow, in a regular, hexagonal array. We take x and y to be the directions locally tangential and perpendicular to the cylinders, respectively (the inner and the outer cylinders are at y = h and y = 0). The tangential component of the velocity, the only one present, is u. The distance, h, between the inner and the outer cylinder and the tangential velocity, V , of the inner cylinder are the control variables of the system (as in Koval et al. [8], we assume that the radius of the inner cylinder is equal to h). The flow configuration is depicted in Fig. 8.

Fig. 8
figure 8

Sketch of the annular shearing with the frame of reference

Full size image

As measured in numerical simulations [8], we take the particle pressure to be uniform and equal to P and the particle shear stress to be

$$\displaystyle \begin{aligned} s = S\left(\frac{h}{2h-y}\right)^2, \end{aligned} $$
(21)

where S is the particle shear stress at the inner cylinder. Also in this case, we focus on dense situations. The flow domain can still be divided into two sub-regions: a fast flow adjacent to the moving boundary of thickness δ and a slow flow of thickness h − δ (Fig. 8). We use the criterion based on the largest solid volume fraction for which the granular material can be sheared without expanding, ν E, to distinguish the two regions.

3.1 Fast Flow

In the fast flow, Eqs. (2) through (7) are still valid. As in the previous case, we make lengths dimensionless by d, velocities by \(\left (P/\rho _p\right )^{1/2}\), stresses by P, and energy flux by \(\left (P^3/\rho _p\right )^{1/2}\). Then, the dimensionless forms of the inner cylinder tangential velocity and the gap between the cylinders are \(V\rho _p^{1/2}/P^{1/2}\) and h∕d, respectively. For simplicity, in what follows, we employ the same notation, even if we refer to dimensionless quantities.

In the annular shearing, the derivative of the pressure (2) with respect to y vanishes. Then, with (1) and (5), we obtain a differential equation for the solid volume fraction [28]:

$$\displaystyle \begin{aligned} \nu' =\frac{\pi^{1/2}Q}{4M\left(\nu^2g_0\right)_\nu T^{3/2}}, \end{aligned} $$
(22)

where, from (1) and the uniform distribution of pressure, \(T=\left [2(1+e)\nu ^2g_0\right ]^{-1}\). The differential equation for the particle velocity is obtained by inverting (3),

$$\displaystyle \begin{aligned} u' =\frac{5\pi^{1/2}s}{8J\nu^2g_0T^{1/2}}. \end{aligned} $$
(23)

Finally, the differential equation for the energy flux is, from (4) with (6) and (23),

$$\displaystyle \begin{aligned} Q' =\frac{5\pi^{1/2}s^2}{8J\nu^2g_0T^{1/2}}-\frac{12\left(1-\epsilon^2\right)\nu^2g_0T^{3/2}}{\pi^{1/2}L}, \end{aligned} $$
(24)

where L is calculated from (7) and (23). The system of three differential equations, (22) though (24), permits the determination of the distribution of ν, u and Q in the fast flow, with the boundary conditions: u(y = h) = V − u B, with u B given in (11); u(y = h − δ) = u E (velocity at the interface with the slow flow determined in the next section); ν(y = h − δ) = ν E; Q(y = h) = −Q B, with Q B given in (12); and Q(y = h − δ) = Q E, with

$$\displaystyle \begin{aligned} Q_E = -2\left[\frac{3M(1-\epsilon)}{\pi L_{h-\delta}}\right]^{1/2}T_{h-\delta}^{1/2}, \end{aligned} $$
(25)

different from (13), because of the uniform distribution of particle pressure.

3.2 Slow Flow

In the slow flow region, the distribution of granular temperature is still given by (17). We still assume that the stress ratio is equal to

$$\displaystyle \begin{aligned} \frac{s}{p} = \frac{4J}{5\pi^{1/2}(1+e)}\frac{u'}{T^{1/2}}. \end{aligned} $$
(26)

We can then invert (26) and obtain the equation that governs the distribution of the shear rate in the slow flow, using the distributions of the stresses in the annular shearing:

$$\displaystyle \begin{aligned} u'=\frac{5\pi^{1/2}(1+e)}{4J}Sh^2T_{h-\delta}^{1/2}\frac{1}{(2h-y)^2} \exp\left(-\frac{h-\delta-y}{2\lambda}\right).\end{aligned} $$
(27)

Integrating, with the boundary condition u = 0 at y = 0, gives

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} u &\displaystyle =&\displaystyle \frac{5\pi^{1/2}(1+e)}{4J}Sh^2T_{h-\delta}^{1/2}\\ &\displaystyle &\displaystyle \times\Bigg[ \frac{1}{2\lambda}\exp\left(\frac{h+\delta}{2\lambda}\right)\mbox{Ei}\left(-\frac{2h-y}{2\lambda}\right)+\frac{1}{2h-y}\exp\left(-\frac{h-\delta-y}{2\lambda}\right) \\ &\displaystyle &\displaystyle -\frac{1}{2\lambda}\exp\left(\frac{h+\delta}{2\lambda}\right)\mbox{Ei}\left(-\frac{h}{\lambda}\right)-\frac{1}{2h}\exp\left(-\frac{h-\delta}{2\lambda}\right)\Bigg]. \end{array} \end{aligned} $$
(28)

When y = h − δ, (28) provides the value of the velocity u E to be used as the boundary condition in the numerical solution of the fast flow of the previous section:

$$\displaystyle \begin{aligned} \begin{array}{rcl}{} u_E &\displaystyle =&\displaystyle \frac{5\pi^{1/2}(1+e)}{4J}Sh^2T_{h-\delta}^{1/2}\\ &\displaystyle &\displaystyle \times\Bigg[ \frac{1}{2\lambda}\exp\left(\frac{h+\delta}{2\lambda}\right)\mbox{Ei}\left(-\frac{h+\delta}{2\lambda}\right)+\frac{1}{h+\delta} \\ &\displaystyle &\displaystyle -\frac{1}{2\lambda}\exp\left(\frac{h+\delta}{2\lambda}\right)\mbox{Ei}\left(-\frac{h}{\lambda}\right)-\frac{1}{2h}\exp\left(-\frac{h-\delta}{2\lambda}\right)\Bigg]. \end{array} \end{aligned} $$
(29)

3.3 Results

We now make qualitative comparisons between the results of the present theory for annular shearing and the numerical simulations on disks in an annular shear cell [8]. We take e = 0.7 and ν c = 0.587, appropriate for particles of surface friction μ = 0.5 [27], with 𝜖 = 0.5 [18]; ν E = 0.58 and ψ = π∕6. We then vary h and V  to check their influence on the results.

Figure 9 shows the particle velocity, scaled with the tangential velocity of the inner cylinder, as a function of the distance from the inner cylinder. As seen by Koval et al. [8], there is a slip velocity at y = h, an exponential behaviour in the slow flow; and when h = 50 and V = 2.5, there is a change in the concavity of the velocity profile in the fast flow. The thickness of the fast flow, marked by the knee in the velocity profiles of Fig. 9, apparently increases with increasing h and V .

Fig. 9
figure 9

Scaled velocity profiles for: h = 50 and V = 2.5 (solid line); h = 100 and V = 2.5 (dashed line); h = 200 and V = 2.5 (dot-dashed line); and h = 50 and V = 1 (dotted line)

Full size image

The behaviour of δ with V  is non-monotonic, as shown in Fig. 10 for the case h = 50. The thickness δ is zero when V  is less than 0.1, and has a maximum when V  is near 2.5; for large values of V , it decreases slightly and seems to saturate for even larger values. This is qualitatively similar to the relation between the shear stress at y = h and the tangential velocity of the inner cylinder depicted in Fig. 11, although in that case the decrease after the peak is much more pronounced. Koval et al. [8] measured monotone increase of δ and S with V . However, they did not perform simulations for V  larger than 2.5, and their Figs. 9a and 3b seem to confirm that the measurements are approaching a maximum at that value. However, it may be possible that the solutions showing a decrease of δ and S with V  are actually unstable.

Fig. 10
figure 10

Thickness of the fast flow as a function of the dimensionless tangential velocity of the inner cylinder for h = 50

Full size image
Fig. 11
figure 11

Shear stress as a function of the dimensionless tangential velocity of the inner cylinder for h = 50

Full size image

4 Conclusions

We have made use of recent extensions of kinetic theory for dense, dissipative shearing flows to phrase and solve boundary-value problems for steady, inhomogeneous flows of a relatively dense aggregate of identical frictional spheres. We have considered two configurations: planar granular shearing in a gravitational field between horizontal, rigid, bumpy boundaries due to the motion of the upper boundary; and annular shearing between coaxial, bumpy cylinders, with the inner cylinder in motion at constant angular velocity. In both cases, the flow consisted of a region of rapid, collisional shearing and a denser region of slower shearing in which more enduring particle contacts played a role. In the denser region, or bed, we assumed that the collisional production of energy is negligible and the anisotropy of the contact forces influences the shear stress and the pressure in the same way. The resulting profiles of average velocity show an exponential decay into the bed, in qualitative and quantitative accordance with numerical simulations and physical experiments. We have also shown that the thickness of the fast flow and the shear stress increase as the boundary velocity is increased at fixed pressure or as the pressure is decreased at fixed velocity. Although the results of the present theory are in good qualitative agreement with 2D discrete numerical simulations and in quantitative agreement with some physical experiments, 3D discrete numerical simulations are required to fully test the capability of the theory to reproduce dense granular flows in inhomogeneous configurations. We hope that the predictions included above will inspire such simulations to test them.

In our view, the analyses that we have performed indicate the relationship between applications of the extended kinetic theory to dense, steady, inhomogeneous flows and the nonlocal extensions of the μ-I rheology developed by Kamrin and collaborators [7, 9, 10]. We hope to explore this relationship further in other contexts.