Hypotheses Tests Using Non-asymptotic Fuzzy Estimators and Fuzzy Critical Values

Abstract

In fuzzy hypothesis testing we use fuzzy test statistics produced by fuzzy estimators and fuzzy critical values. In this paper we use the non-asymptotic fuzzy estimators in fuzzy hypothesis testing. These are triangular shaped fuzzy numbers that generalize the fuzzy estimators based on confidence intervals in such a way that eliminates discontinuities and ensures compact support. Our approach is particularly useful in critical situations, where subtle fuzzy comparisons between almost equal statistical quantities have to be made. In such cases the hypotheses tests that use non-asymptotic fuzzy estimators give better results than the previous approaches, since they give us the possibility of partial rejection or not of $H_0$.

1 Introduction

The use of fuzzy hypothesis tests is necessary: 1) in cases of samples of crisp data for which the value of the test statistic is very close to critical value, the crisp test is unstable, since small changes in few observations drive from rejection to no rejection or vice-versa, 2) in cases in which the available observations are fuzzy.

In a fuzzy test of a null hypothesis of the form $H_0:\, U=U_0$ with alternative $H_1:\, U\ne U_0$ for a parameter u we use a fuzzy test statistic, which is constructed using a fuzzy estimator. Since the test statistic is fuzzy, the critical region will be determined by fuzzy critical values $CV_i,\;i=1,2$. The $a-$cuts of $CV_i$ are found in each case as described in [5] and presented in Sects. 2 and 3. So, $H_0$ is rejected or not rejected in a certain significance level with the help of a fuzzy statistic U which is constructed using a fuzzy estimator and fuzzy inequalities between U and the fuzzy critical values, like $U<CV$, $U>CV$ or $U\approx CV$.

In our new approach, from the various types of existing fuzzy estimators we use the non-asymptotic fuzzy estimators [11], which are more convenient since they are triangular shaped fuzzy numbers with compact support without discontinuities.

We apply this concept in Sects. 2 and 3 testing hypotheses for: 1) the mean and 2) the variance of a normal distribution and compare results with these of the respective tests with fuzzy statistics constructed with the estimators of Buckley [5].

1.1 Ordering Fuzzy Numbers

The fuzzy hypotheses tests are based on ordering fuzzy numbers, for which we will use one of the several procedures used [7], according to which the degree $v(A\le B)$ of the inequality $A\le B$ that counts the degree to which the fuzzy number A is less or equal than the fuzzy number B is

$$\begin{aligned} v(A\le B) =\max \left\{ \min (A(x),B(y)) \;\;\; x\le y\right\} \end{aligned}$$

(1)

Fig. 1.

Ordering triangular shaped fuzzy numbers

If $v(A\le B) =1$ we define the truth-value (degree of confidence) d of $A<B$ as

$$\begin{aligned} v(A<B)=d \Leftrightarrow v(A\le B) =1\;\; \text{ and } \;\; v(B\le A) =1-d \end{aligned}$$

(2)

If $v(B\le A) =1$ the truth-value d of $B<A$ is

$$\begin{aligned} v(B<A)=d \Leftrightarrow v(B\le A) =1\; \text{ and } \; v(A\le B) =1-d \end{aligned}$$

(3)

So, the truth-value $\eta$ of $A\approx B$ is defined as

$$v(A\approx B)= \eta \Leftrightarrow v(A\le B)= 1\; \text{ and } \; v(B\le A)=\eta $$

$$\begin{aligned} \text{ or } \; v(B\le A)=1\; \text{ and } \; v(A\le B) =\eta \end{aligned}$$

(4)

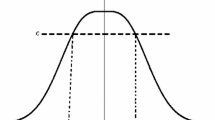
In the case of the triangular shaped fuzzy numbers of Fig. 1, which appears often in fuzzy hypotheses tests, we can see that:

$v(A\le B) =1$, according to (1) since the core of A lies to the left of the core of B,

$v(B\le A) =y_0$, according to (1), where $y_0$ the truth level of the point of intersection of the right part of A and the left part of B.

Thus according to Eq. (2) and (4),

$$v(A<B)=1-y_0\;\; \text{ and } \;\;v(A\approx B)= y_0$$

2 Hypothesis Test for the Mean of a Normal Distribution with Known Variance

We test in significance level $\gamma$ the null hypothesis that the mean value $\mu$ of a random variable X that follows normal distribution with known variance $\sigma$ is equal to $\mu _0$

$$\begin{aligned} H_0:\; \mu =\mu _0 \end{aligned}$$

with alternative the (two sided test)

$$\begin{aligned} H_1:\; \mu \ne \mu _0 \end{aligned}$$

using a random sample of observations of X of size n. In the crisp case we test $H_0$ using the statistic

Fig. 2.

The fuzzy statistic Z and the fuzzy critical values for the test of $H_0:\; \mu =5$ from a sample with $\overline{x}_1 =5.4$

$$\begin{aligned} Z ={\overline{x}-\mu _0 \over {\sigma \over \sqrt{n}} } \end{aligned}$$

(5)

where $\overline{x}$ is the sample mean value.

$H_0$ is rejected if $z<-z_c$ or $z>z_c$ where $z_c$ the critical value of the test

$$\begin{aligned} z_c=z_{\gamma /2}=\varPhi ^{-1}\left( 1-{\gamma \over 2}\right) \end{aligned}$$

(6)

and $\varPhi ^{-1}$ the inverse distribution function of the standard normal distribution. While, if $-z_c<z<z_c$, then $H_0$ is not rejected.

In the fuzzy case for the test of $H_0$ we use the fuzzy statistic of Buckley [5]

$$\begin{aligned} \overline{Z} ={\widehat{\mu }-\mu _0 \over {\sigma \over \sqrt{n}}} \end{aligned}$$

(7)

that is generated by (5) using a fuzzy estimator $\widehat{\mu }$ of the mean value.

We use the non-asymptotic fuzzy estimator $\widehat{\mu }$ the $\alpha -$cuts of which are [11]

Fig. 3.

The fuzzy statistic Z and the fuzzy critical values for the test of $H_0:\; \mu =5$ from a sample with $\overline{x}_1 =5.45$

$$\begin{aligned} \widehat{\mu } [\alpha ]=\left[ \overline{x}-z_{h(\alpha )}{\sigma \over \sqrt{n}},\;\overline{x}+z_{h(\alpha )}{\sigma \over \sqrt{n}}\right] ,\;\;\;\;\;\;\alpha \in (0,1] \end{aligned}$$

(8)

where

$$\begin{aligned} h:(0,1]\rightarrow \left[ {\gamma \over 2} , {1\over 2}\right] \;\;\;\;\;\; h(\alpha )=\left( {1\over 2}-{\gamma \over 2}\right) \alpha +{\gamma \over 2} \end{aligned}$$

(9)

and

$$\begin{aligned} z_{h(\alpha )}=\varPhi ^{-1} (1-h(\alpha ) )\end{aligned}$$

(10)

where $\varPhi ^{-1}$ the inverse distribution function of the standard normal distribution.

From (7) and (8) follows that the $\alpha -$cuts of the fuzzy statistic $\overline{Z}$ are

$$\begin{aligned} \overline{Z}[\alpha ]=\left[ z_0-z_{h(\alpha )},\;z_0+z_{ h(\alpha )}\right] ,\;\;\;\;\;\;\alpha \in (0,1] \end{aligned}$$

(11)

where

$$\begin{aligned} z_0= {\overline{x}-\mu _0 \over {\sigma \over \sqrt{n}} }\end{aligned}$$

(12)

Since the test statistic is fuzzy, the critical values as described in [5] are the fuzzy numbers $\overline{CV}_2$ and $\overline{CV}_1=-CV_2$, the $\alpha -$cuts of which are

$$\begin{aligned} \overline{CV}_1[\alpha ]= & {} \left[ z_{\gamma /2}-z_{ \alpha /2},\;z_{\gamma /2}+z_{ \alpha /2}\right] \end{aligned}$$

(13)

$$\begin{aligned} \overline{CV}_2[\alpha ]= & {} \left[ -z_{\gamma /2}-z_{ \alpha /2},\;-z_{\gamma /2}+z_{ \alpha /2}\right] \;\;\;\;\;\;\alpha \in (0,1] \end{aligned}$$

(14)

Having the fuzzy test statistic $\overline{Z}$ and the fuzzy critical values $\overline{CV}_i$, our decision for rejecting $H_0$ or not in significance level $\gamma$, depends on the comparison of the fuzzy numbers $\overline{Z}$ and $\overline{CV}_i$, as given in Sect. 1.1. So:

• if $\max \left( v(\overline{Z}>\overline{CV}_2),v(\overline{Z}< \overline{CV}_1\right) =d$, then $H_0$ is rejected with a degree of confidence less or equal to d,

• if $\min \left( \overline{Z}>\overline{CV}_1),v( \overline{Z}<\overline{CV}_2)\right) =d$, then $H_0$ is not rejected with a degree of confidence less or equal to d,

• if $\max \left( v(\overline{Z}\approx \overline{CV}_2), v(\overline{Z}\approx \overline{CV}_1\right) =1-d$, then we cannot make a decision on rejecting or not $H_0$ with degree of confidence greater or equal to d.

Example 1

Comparison of fuzzy and crisp hypothesis test. In the crisp test in significance level $\gamma =0.05$ of the null hypothesis

$$\begin{aligned} H_0:\; \mu =5 \end{aligned}$$

with alternative the (two sided test)

$$\begin{aligned} H_1:\; \mu \ne 5 \end{aligned}$$

for the mean value $\mu$ of a random variable X that follows normal distribution with standard deviation $s=2$ using a sample of 80 observations with sample mean $\overline{x}_1 =5.4$, we evaluate the value of the statistic (5)

$$\begin{aligned} z_0 ={5.4-5 \over {2\over \sqrt{80}} }=1.799 \end{aligned}$$

Since

$$\begin{aligned} z_0 = 1.799 <z_{0.05/2}=z_{0.025 }=1.96 \end{aligned}$$

$H_0$ is not rejected.

For a second sample with sample mean $\overline{x}_2 =5.45$ the value of the statistic Eq. (5) is

$$\begin{aligned} z_0 ={5.45-5 \over {2\over \sqrt{80}} }=2.012 \end{aligned}$$

So, since

$$\begin{aligned} z_0 = 2.012 >z_{0.05/2}=z_{0.025 }=1.96 \end{aligned}$$

$H_0$ is rejected.

Fig. 4.

Fuzzy statistic $\overline{Z}$ and fuzzy critical values $\overline{CV}_i$ for the test of $H_0:\; \mu =1$ using non-asymptotic fuzzy estimator

Applying the above described fuzzy test of $H_0$ for the first sample ($\overline{x} =5.4$) we get Fig. 2, where the point of intersection of the fuzzy numbers $\overline{Z}$ and $\overline{CV}_2$ is $y_0=0.93$. So according to Eq. (2), $v(\overline{Z}<\overline{CV}_2)=1-0.93=0.07$. Therefore, from this sample we cannot make a decision on rejecting or not $H_0$ with degree of confidence $d\ge 0.07$.

For the second sample ($\overline{x} =5.45$) we plot $\overline{Z}$ and $\overline{CV}_2$ in Fig. 3, where we can see that the point of intersection of the fuzzy numbers $\overline{Z}$ and $\overline{CV}_2$ is $y_0=1$. So according to Eq. (4), $v(\overline{Z}\approx \overline{CV}_2)=1$. Therefore, from this sample we cannot make a decision on rejecting $H_0$ or not with any degree of confidence d.

Example 2

We test in significance level 0.1 the hypothesis

$$\begin{aligned} H_0:\; \mu =1 \end{aligned}$$

with alternative the

$$\begin{aligned} H_1:\; \mu \ne 1 \end{aligned}$$

for the mean value $\mu$ of a random variable X that follows normal distribution with standard deviation $s=2$ using a sample of 100 observations with sample mean value $\overline{x}_1 =1.24$.

Fig. 5.

Fuzzy statistic $\overline{Z}$ and fuzzy critical values $\overline{CV}_i$ for the test of $H_0:\; \mu =1$ using fuzzy estimator of Buckley [5]

Applying the fuzzy test of $H_0$ (using the non-asymptotic fuzzy estimator of mean value) we get Fig. 4, where the point of intersection of the fuzzy statistics Z and $CV_2$ is below 0.8. So, the truth-value of $Z< CV_2$ is greater than $1-0.8=0.2$. Therefore, $H_0$ is not rejected in degree of confidence $d=0.2$. While, applying the fuzzy test of $H_0$ using the fuzzy estimator of mean value of Buckley [5] we get Fig.  5, in which the point of intersection of the fuzzy test statistics $\overline{Z}$ and $\overline{CV}_2$ is above 0.8. So, $v(\overline{Z}< \overline{CV}_2)<0.2$. Therefore, according to this test, we cannot make a decision on the rejection or not of $H_0$ with degree of confidence $d= 0.2$.

3 Hypothesis Test for the Variance of a Normal Distribution

We test in significance level $\gamma$ the null hypothesis that the variance $\sigma ^2$ of a random variable X that follows normal distribution is equal to $\sigma ^2_0$

$$\begin{aligned} H_0:\; \sigma ^2 =\sigma ^2_0 \end{aligned}$$

with alternative the (two sided test)

$$\begin{aligned} H_1:\; \sigma ^2 \ne \sigma ^2_0 \end{aligned}$$

using a random sample of observations of X of size n.

In the crisp case we test $H_0$ using the test statistic

$$\begin{aligned} \chi ^2_0 ={(n-1)s^2 \over \sigma ^2_0}\end{aligned}$$

(15)

where $s^2$ is the sample variance.

$H_0$ is rejected if $\chi ^2_0< \chi ^2_{L;\gamma /2}$ or $\chi ^2_0> \chi ^2_{R;\gamma /2}$ where $\chi ^2_{L;\gamma /2}$ and $\chi ^2_{R;\gamma /2}$ the critical values of the test,

$$\begin{aligned} \chi ^2_{L;\gamma /2}= F^{-1}\left( {\gamma \over 2}\right) \;\;\; \text{ and } \;\;\; \chi ^2_{R;\gamma /2}= F^{-1}\left( 1-{\gamma \over 2}\right) \end{aligned}$$

(16)

where $F^{-1}$ the inverse distribution function of the $\chi ^2_{n-1}$ distribution with n degrees of freedom. While, if $\chi ^2_{L;\gamma /2}<\chi ^2<\chi ^2_{R;\gamma /2}$, then $H_0$ is not rejected.

In the fuzzy case for the test of $H_0$ we use the unbiased fuzzy statistic $\overline{\chi }^2$ [5] with the non-asymptotic fuzzy estimator [11] the $\alpha -$cuts of which are

$$\begin{aligned} \overline{\chi }^2[a]=\left[ {(n-1)\chi ^2_0 \over (1-h(a))\chi ^2_{R;\gamma /2}+(n-1)h(a) }, \;\;{(n-1)\chi ^2_0 \over (1-h(a))\chi ^2_{L;\gamma /2}+(n-1)h(a) }\right] \end{aligned}$$

(17)

where

$$\begin{aligned} h:(0,1]\rightarrow [ \gamma , 1 ] \;\;\;\;\;\; h(\alpha )= (1- \gamma )\alpha + \gamma ,\;\;\;\;\;\;\alpha \in (0,1] \end{aligned}$$

(18)

The fuzzy critical values of the test, as described in Buckley [5], (using the non-asymptotic fuzzy estimator [11]) are the fuzzy numbers $\overline{CV}_1$ and $\overline{CV}_2$, the $\alpha -$cuts of which are

$$\begin{aligned} \overline{CV}_1[a]= & {} \left[ {(n-1)\chi ^2_{L;\gamma /2} \over (1-h(a))\chi ^2_{R;\gamma /2}+(n-1)h(a) }, \;\;{(n-1)\chi ^2_{L;\gamma /2}\over (1-h(a))\chi ^2_{L;\gamma /2}+(n-1)h(a) }\right] \\[5mm] \overline{CV}_2[a]= & {} \left[ {(n-1)\chi ^2_{R;\gamma /2} \over (1-h(a))\chi ^2_{R;\gamma /2}+(n-1)h(a) }, \;\;{(n-1)\chi ^2_{R;\gamma /2}\over (1-h(a))\chi ^2_{L;\gamma /2}+(n-1)h(a) }\right] \end{aligned}$$

Fig. 6.

The fuzzy statistic $\overline{Z}$ and the fuzzy critical values for the test of $H_0:\; \sigma ^2 =2$ from a sample with variance $s^2=2.73$

Example 3

We test in significance level 0.1 the hypothesis

$$\begin{aligned} H_0:\; \sigma ^2 =2 \end{aligned}$$

with alternative the (two sided test)

$$\begin{aligned} H_1:\; \sigma ^2 \ne 2 \end{aligned}$$

using a random sample of 100 observations with sample variance $s^2 =2.73$.

Applying the above described fuzzy test of $H_0$ we get the result of Fig. 6, where the point of intersection of the fuzzy numbers $\overline{Z}$ and $\overline{CV}_2$ is $y_0=0.79$. So, according to Sect. 1.1 $v(\overline{Z}> \overline{CV}_2)=1-0.79=0.21$. Therefore, $H_0$ is rejected in degree of confidence $d\le 0.21$.

4 Conclusions

If the value of the test statistic of a hypothesis is close to the critical values of the test, then the crisp hypothesis test is unstable, since a small change in the sample mean value (addition or removal or a change of one observation) may lead from rejection to no rejection of $H_0$ or vice-versa. While, the fuzzy hypothesis testing in such cases gives a very low degree of confidence of the rejection or not of the null hypothesis, as shown in Example 1.

Comparing with a computer program (in Matlab) the results of the fuzzy test with non-asymptotic fuzzy estimator with the respective fuzzy test with fuzzy estimator of Buckley [5] we see a slight difference, which in some cases leads to a different decision, as shown in the Example 2.

Our approach that uses non-asymptotic fuzzy estimators for the construction of the fuzzy statistics and a degree of confidence for the rejection or not of a hypothesis gives better results than the existing ones, since it gives us the possibility to make a decision on a partial rejection of it in a certain degree of confidence.