Dealing with Imperfect Elicitation Results

Abstract

The trial-and-roulette method is a popular method to extract experts’ beliefs about a statistical parameter. However, most studies examining the validity of this method only use ‘perfect’ elicitation results. In practice, it is sometimes hard to obtain such neat elicitation results. In our project about predicting fraud and questionable research practices among Ph.D. candidates, we ran into issues with imperfect elicitation results. The goal of the current chapter is to provide an overview of the solutions we used for dealing with these imperfect results, so that others can benefit from our experience. We present information about the nature of our project, the reasons for the imperfect results and how we resolved these supported by annotated R-syntax.

1 Introduction

The trial-and-roulette method, also called the chips and bins method or the histogram method, is a popular method to extract experts’ beliefs about a statistical parameter (Clemen et al. 2000; Goldstein et al. 2008; Goldstein and Rothschild 2014; Gore 1987; Haran et al. 2010; Haran and Moore 2014). During the elicitation procedure experts are provided with a number of ‘chips’ to allocate probability to specific values of the parameter space. The number of chips placed over a certain value reflects the expert’s view on the probability of that value. The method has been used in different fields (e.g. Johnson et al. 2010), but hardly in the social and behavioural sciences. One exception is the study by Zondervan-Zwijnenburg et al. (2017), who made a case for using the method as developed by Johnson et al. (2010) in the social and behavioural sciences. They tested the method with behavioural practitioners who provided their judgements with respect to the correlation between cognitive potential and academic performance for two separate populations enrolled at a special education school for youth with severe behavioural problems: youth with Autism Spectrum Disorder (ASD), and youth with diagnoses other than ASD. They also investigated face validity, feasibility, convergent validity, coherence and intra-rater reliability and concluded that the method can also be used in the social and behavioural sciences. Veen et al. (2017b) adjusted the method by adding a step to the procedure, providing the experts with visual feedback during the elicitation process.

However, these studies by Johnson et al. (2010), Veen et al. (2017b) and Zondervan-Zwijnenburg et al. (2017) use only ‘perfect’ elicitation results. That is, in an ideal situation the expert places the stickers neatly on top of and equally spaced next to each other within the allowed parameter space, see Fig. 18.1a. Subsequently, the best fitting probability distribution is computed with software like SHELF (Sheffield Elicitation Framework; Oakley and O’Hagan 2010). The accompanying hyperparameter values, see Fig. 18.1b, can then be used for other purposes, like Bayesian updating with data (see, e.g. Zondervan-Zwijnenburg et al. 2017) or computing prior-data conflicts (Veen et al. 2017a). In practice, however, such neat elicitation results are hard to obtain and the results will look more like the ones in Fig. 18.2.

Fig. 18.1

The result of a ‘perfect’ elicited distribution using the trial roulette method and b the probability distribution obtained with the SHELF software resulting in a Beta distribution with hyperparameters 21.40 and 80.67

Fig. 18.2

Examples of imperfect elicitation results for seven different situations, the statistical distribution obtained via our solutions, and the results from SHELF. Results for all experts can be found on the OSF

In a project about predicting fraud among Ph.D. candidates, we ran into issues with such imperfect elicitation results. The goal of the current chapter is to provide an overview of the solutions we used to deal with these imperfect results, so that others can benefit from our work. In what follows, we first present more information about our project and the reasons for the imperfect results, followed by a discussion of how we dealt with this. We will present our solutions with annotated R-syntax. All elicitation results, the R-code to apply our solutions, the SHELF input, all resulting parametric distributions, etc., can be found on the Open Science Framework (https://osf.io/bq28j/).

2 Case Study: Predicting Fraud Among Ph.D. Candidates

Academic integrity has attracted increasingly more attention over the past years (Steneck 2006; John et al. 2012). Studies quantifying the prevalence of questionable research practices and fraud reveal that a substantial number of scientists does not behave according to academic integrity standards (Fanelli 2009; Martinson et al. 2005; Tijdink et al. 2014). Yet, obtaining grants or getting a job is still highly dependent on (the number of) publications (Sonneveld et al. 2010; Van de Schoot et al. 2012). According to Hofmann et al. (2013) there is a tendency amongst young scholars to respect and learn from the scientific norms and practices of other scholars. With the increasing time pressure and publication pressure and the growing number of scholars and the interdisciplinary and international studies being conducted, academic norms have become too diverse and complicated; we cannot and should not simply copy them from one another.

However, young scholars and especially Ph.D. candidates rely heavily on their supervisors and will mimic their behaviour (Van de Schoot et al. 2013). They are in a dependent relation with one or more senior faculty member which makes them prone to senior pressure. In other words, the senior faculty member has a great influence on the Ph.D. candidate and his or her behaviour may thus also influence the Ph.D. candidate’s scientific behaviour. Our project is about investigating the ways in which behaviour of senior scholars influences the behaviour of Ph.D. candidates with respect to questionable research practices. Note that the entire study was approved by the Ethics Committee of the faculty of Social and Behavioural Sciences at Utrecht University (FETC15-108), and that the questionnaires were co-developed and pilot-tested by two university-wide organization of Ph.D. candidates as well as the Dutch National organization of Ph.D. candidates.

We developed several scenarios based on different types of questionable research practices/fraud, ranging from objectively fraudulent behaviour (data fabrication), via serious forms of misconduct (deleting outliers to get significant results), to arguably milder forms of questionable research practices (salami-slicing); see the text we used in the Box 18.1.

Box 18.1 Text used for the three Scenarios

Suppose you have been working on this research project with the project leader and senior team member for a few months. The following situation occurs. Together with the project leader and the senior team member you are developing an article. You are in charge of the data analysis.

Scenario 1—data fabrication:

When you are working on the analysis, you discover that something is wrong with the data: you have good reasons to assume the data has been made up, most likely by the senior team member, who was responsible for data collection. You discuss this point of concern with the senior team member, but you have not discussed this with the project leader. The senior team member advises you to use the data anyway because it leads to very interesting conclusions. You figure that publishing the results based on these data might result in a very good article which will be crucial in allowing you to finish your thesis in time.

Scenario 2—deleting outliers to get significant results:

You checked the data and there appears to be no problem with it. However, your most important hypotheses are not supported by the data. You discuss this point of concern with the senior team member, but you have not discussed this with the project leader. The senior team member proposes to reanalyse the data together. Before doing this he removes some outliers/interview quotes that, according to the senior member, disturb the data. He provides no further information. The new analysis shows support for your hypotheses. The senior team member advises you to use this data because it leads to very interesting conclusions. You figure that publishing the results based on this data might result in a very good article which will be crucial in allowing you to finish your thesis in time.

Scenario 3—salami-slicing:

You checked the data and there appears to be no problem with it. Your analysis shows support for your main hypotheses. However, with the current analysis it seems as if you will be able to publish just one article based on this research project. You discuss this point of concern with the senior team member, but you have not discussed this with the project leader. The senior team member asks you to analyze the data in such a way that the group can publish three similar articles instead of one, based on the same dataset. The three proposed articles will differ from each other marginally. You figure that publishing three articles instead of one will be crucial in allowing you to finish your thesis in time.

Question: would you try to publish the results of this study?

The project involved asking 36 senior scholars working at 10 different faculties of Social and Behavioural Sciences or Psychology in The Netherlands—such as deans, vice deans, heads of department, research directors and confidentiality persons—what they know about the behaviour of Ph.D. candidates regarding questionable research practises. We asked them to indicate the percentage of Ph.D. candidates who would answer ‘yes’ to the question at the end of the vignette in Box 18.1: would you try to publish the results of this study?

In a face-to-face interview with the first author (RvdS), the participants were asked to place twenty stickers, each representing five percent of a distribution, on an axis where the left indicates that 0% of the Ph.D. candidates in their faculty would say ‘yes’ to the scenario, and the right indicates 100%. The placement of the first sticker on a certain position on the axis indicated perceived likeliness by the expert for that value. The other stickers represented other plausible values. If all stickers are placed exactly on top of each other, this indicates the expert was 100% certain the observed percentage would be that particular value. Stickers placed next to each other resemble uncertainty about the estimate.

Ideally, the elicitation procedure resulted in a neat stickered distribution like the one in Fig. 18.1a which could easily be transformed into a probability distribution using the software SHELF. However, most of the results were not this ‘perfect’: see Fig. 18.2. This was due to lack of time or stickers being too small for large hands (really!). The challenge was to translate the intended distribution of the expert into meaningful input to be fed to the software SHELF in order to obtain logical statistical distributions. The goal of the current chapter is to describe our procedure.

3 The Perfect Situation

To transform the stickered distribution into a parametric distribution, we applied the following steps:

• 1. The x-axis was divided into 1.000 sections. The density of each section depended on the height of the stickers, each sticker representing 5% of the density mass. The 5% was divided across the sections where the sticker was placed, using the following rule: 5/[number of sections on x-axis] = [density per section]. With a triangle ruler, for each stack, lines were drawn from both sides of the lowest sticker, perpendicular to the x-axis. The distance from the left edge of the x-axis (0%) to the left and the right line was then measured and rounded to a tenth of a cm. This distance was then used to compute the proportion of the x-axis (rounded to 1 decimal) that the sticker-stack occupies, using the following formula: [position on x-axis in cm]/[length x-axis (here 25.8 cm)] * 100%. This delivered a left and right edge of the interval and the proportion corresponds to a number of sections on the x-axis (each section = 0.1%). We used this information to create a vector of numbers in R using the following formula: [number of stickers] * [percent per sticker (here 5%)]/[number of sections this stack of stickers covers]. If there were no stickers for a certain interval, we repeated the values 0 for those sections.

For the distribution in Fig. 18.1a, the following procedure was applied. In the sections from 0 to 17.5% on the x-axis, no stickers are pasted, represented in a vector with rep(0,175). The first stack containing three stickers (so 3*5% of the total density mass) covers 31 sections on the x-axis and is therefore represented as rep(3*5/31,31). After an empty space of 8 sections [rep(0,8)], the procedure repeats itself ending at the empty interval at the right of the distribution [rep(0,634)]. Finally, a vector that shows the density at each section of the x-axis is acquired using the following R-syntax:

• 2. The resulting vector with section densities was used as input for the elicitation programme SHELF using the following syntax:

After the final line of code, a window opens in which the density of each section is filled in by hand. The software then computes the best fitting beta distribution, and the hyperparameters of this distribution can be requested using the following command: elicited.group.data

The hyperparameters can be used to create a plot of the distribution using the following syntax (Fig. 18.1b): curve(dbeta(x, 21.40791, 80.6748))

• 3. The parametric distribution plot (Fig. 18.1b) was then compared to the sticker distribution (Fig. 18.1a) by the authors (RvdS, EG) to assess the face validity of the elicitation. In the case of Fig. 18.1, the parametric distribution nicely represents the stickered distribution.

4 Seven Elicitation Issues with Seven Solutions

The following section describes how the ideal method was adjusted to fit the ‘problematic’ sticker distributions. We refer to Fig. 18.2 for example distributions. We developed seven solutions for seven issues.

4.1 Issue 1: The Expert Includes Numbers/Percentages with Their Distribution

The numbers experts include on the x-axis often do not correspond to the actual interval at that point of the x-axis. In these cases, the numbers included by the expert are leading. This means that the part of the x-axis that the expert used for their distribution needs to be rescaled. Some examples are

• 1. A start and end percentage is included. The distance between these two points is then equal to the difference in percentages that are noted by the expert. This distance is used to compute the intervals.

• 2. There is only a percentage/number at the centre of the stickered distribution. The distance between the 0% point and this number is then equal to the percentage at the centre (this could be any percentage, not necessarily 50%). The rest of the x-axis is rescaled according to this distance and percentage.

• 3. There is a start, end and centre percentage of the stickered distribution (Fig. 18.2—scenario 1). There are now two intervals (left to centre, and centre to right). Both have to be rescaled separately based on the distance between the two points. The R-script to reproduce these results is shown below. The first nonzero density is present after ten percent of the x-axis, which is clearly supported by the zero density for the first 100 sections . The right edge of the distribution is set at 40%, which is shown by the zero density of the final 600 sections of the x-axis , resulting in:

4.2 Issue 2: Stickers Are Pasted in Neat Vertical Stacks with Different Vertical Distancing

For the situation that stacks are not neatly placed next to each other, we relied on the perpendicular distance between the x-axis and the top of the stack. To compute the proportion of x-axis taken up by the stack, we first used the percentages for the left and right edges. If the stickers also overlap horizontally, we use the highest sticker of the stack to measure the proportion of the stack on the x-axis. After computing all these proportions on the x-axis, and their corresponding heights of the stack, we can compute the total area of the distribution using $\sum \left( {x_{2} - x_{1} } \right)y_{1}$, where $x_{1}$ and $x_{2}$ represent the percentages (one decimal) for the left and right edges and $y_{1}$ represents the height of the stack in cm (one decimal). For each interval, we computed the percentages of total area, using

$$ \frac{{100\left( {x_{2} - x_{1} } \right)y_{1} }}{{\sum \left( {x_{2} - x_{1} } \right)y_{1} }}, $$

where $\left( {x_{2} - x_{1} } \right)y_{1}$ is the area of the specific interval which is divided by the sum in the demominator (the total surface area). To decide the percentage of total area per 1/1.000th part of the x-axis (the info we need for SHELF), we used

$$ \frac{{100\left( {x_{2} - x_{1} } \right)y_{1} }}{{\sum \left( {x_{2} - x_{1} } \right)y_{1} }} \times \frac{1}{{10\left( {x_{2} - x_{1} } \right)}} = \frac{{10y_{1} }}{{\sum \left( {x_{2} - x_{1} } \right)y_{1} }} $$

where the 10 in the denominator was added to the second fraction to convert from percentages to 1/1.000th parts. After computing these numbers for every interval (stack of stickers), we created another series of numbers for SHELF. For example, the array represents a stack with height , a total area of sections.

4.3 Issue 3: Stickers Are not Stacked Exactly on Top of Each Other

If the stickers were pasted in a disorderly fashion, more like a cloud than neat stacks (see Fig. 18.2—Issue 3), we used the highest sticker at each point of the x-axis to compute the input for SHELF. So, instead of basing the stacks edged on the x-axis on the lowest sticker, you use the highest sticker to find $x_{1}$ and $x_{2}$ for each interval and apply the same approach as used in Issue 2.

4.4 Issue 4: The Distribution Lacks Stickers in a Specific Part of the Parameter Space

When the expert sketches a distribution he or she occasionally fails to fill it all up with stickers, see Fig. 18.2—Issue 4. If we had applied our default strategy, the distribution would have been bumpy. To solve this, we relied on linear interpolation and we added the minimum number of points needed to fill out the distribution. Any newly added point was added in the centre of its two surrounding points (sticker stacks), both with regard to the x- and y-axis. Each point simulates a sticker and is thus of the same width and height. Each point is thus equal to 3.1% of the x-axis. To find the location of this new point or stack, we added 1.55% to the left and right of the point and noted the location on the x-axis. For example in Fig. 18.2 two stickers were added between the stacks with height y of . First, 8.85 is the midpoint of . The inserted y of is the midpoint of and 8.85; the inserted y of is the midpoint of and 8.85.

4.5 Issue 5: All Stickers at One Point

This is a special case since the expert indicated to be 100% certain that the number of Ph.D. candidates answering ‘yes’ to the question was a specific value, typically zero. During the elicitation process, it was explained to these experts what the consequences were if they still decided to go for this particular answer. It appeared some experts truly believed that 0% of the Ph.D. candidates would never ever agree with publishing the results if they did not trust the data. If this was truly their answer we had to apply a trick because SHELF does not allow to add only one value. So, we used two intervals instead and put 99% of the density mass from 0.0 to 0.1%, and only 1% to the 0.1–0.2 interval:

4.6 Issue 6: Stickers Fall (Partially) Outside of the X-Axis

Pasting stickers outside the limits of the x-axis can take on two forms:

• 1. There is a stack at the limit, and some of these stickers go beyond the limit of the x-axis. If the expert was clear in saying that this stack should represent 0 or 100%, we put all stickers in the stack in the first (0.0–0.1) or last (99.9–100.0) interval of the x-axis. If they were not clear, then the interval was decided by the edge of the sticker that is just inside the parameter space (0 or 100%), and is the entire density added to the first or last interval.

• 2. There is only one sticker, or a small part of the stickered distribution indicated by the stickers outside the limit of the x-axis. In this situation, we decided to lengthen the x-axis to fit this sticker. This meant that any computations using the length of the x-axis need to be adjusted to a new length (instead of 25.8 cm).

4.7 Issue 7: One Sticker Is an Outlier

In some cases, experts added some ‘outlier’ stickers to their distribution that SHELF cannot handle. In this case, we made the interval on the x-axis wider, while at the same time making these ‘outlier’ stickers ‘flatter’, so that the total percentage of the distribution accounted for by these stickers did not change. That is, the density of stickers is reduced to and redistributed over steps. This leads to the following R-code:

5 Results

5.1 Perfect and Imperfect Elicitation Results

First, we applied the seven strategies to the results of the 36 (experts) * 3 (scenarios) = 108 stickered distributions. One expert misunderstood the instructions about how to interpret the x-axis (as only appeared after the interview was done) and none of the three stickered distributions could be used, see for example Fig. 18.3a. For one other stickered distribution it was completely unclear what the intended distribution should look like, see Fig. 18.3b. And for another distribution, see Fig. 18.3c, a beta distribution could not be applied because of the bi-modal shape. So, for 103 stickered distributions the seven solutions could be applied. For one expert, see Fig. 18.4, we decided that the obtained distribution did not fit the stickered distribution and this result was therefore also omitted from future analyses, resulting in a total of 102 distributions.

Fig. 18.3

Examples of stickered distributions we omitted: a the expert misunderstood the x-axis (n = 3) and (b and c) the expert placed the stickers in a non-identifiable distribution

Fig. 18.4

For one expert we decided the parametric distribution (b) did not resemble the stickered distribution (a)

Out of the 102 stickered distributions, only 23 (22.5%) could be entered in the software SHELF without any adjustments. This implies that most of the elicitation results suffered from one or more of the issues described above and would have been useless without adjustments. Table 18.1 provides an overview of the prevalence of each of the seven issues.

Table 18.1 Overview of the prevalence of the perfect results, the seven issues and possible combinations for each of the three scenarios with a total of 79 problematic distributions with 109 issues and 23 perfect distributions

5.2 Mixture Distributions

As a second step, to summarize the parametric distributions, we merged the individual distributions of all experts into three clusters:

• 1. Experts who indicated to be certain that zero percent of the Ph.D. candidates would publish the results (almost all density put on zero percentage; blue line);

• 2. Experts who believed the percentage to be low, but not exactly zero (zero had to be in the 95% density mass; orange line);

• 3. Experts who believed the percentage to be clearly higher than zero (zero fell outside the 95% density mass; yellow line).

To do so, we applied the following procedure for scenario 1 and the group of experts who expected exactly zero percent. We first constructed a data frame:

Then, we assigned an equal weight-value to all expert priors [1/total number of experts]:

Next, we created a new density distribution (Y1g1) and looped over all the experts:

This procedure was repeated for all other expert-groups and for each scenario separately. The complete syntax is available on the OSF (https://osf.io/bq28j/).

5.2.1 Mixture Results—Scenario 1

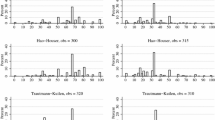
Eight seniors indicated to be hundred percent sure not one single Ph.D. candidate would agree to publishing the results in the situation as described in Scenario 1 (i.e. data fabrication), see Fig. 18.5a. In addition, 20 seniors indicated the percentage of Ph.D. candidates to be close to zero, but not exactly zero. The majority of these second groups’ combined probability mass is well below 20%. Combining these two groups, this shows that 82% of the seniors believed the percentage of Ph.D. candidates willing to publish a paper, even if they did not trust the data because of potential data fabrication, to be zero or close to zero. A third group of six seniors (18%) believed the percentage to be higher than zero, but they vary widely in their beliefs between, roughly, between 5 and 75%.

Fig. 18.5

Combined results of all parametric distributions split into three categories: (1) Experts who indicated to be certain zero percent of the Ph.D. candidates would publish the results (blue); (2) Experts who believed the percentage to be low, but not exactly zero (orange); (3) Experts who believed the percentage to be clearly higher than zero (yellow)

5.2.2 Mixture Results—Scenario 2

There are only two seniors who were very sure zero percent of the Ph.D. candidates would publish the results in the second scenario (i.e. deleting outliers to obtain a significant effect) and another 12 seniors believing the percentage to be very close to zero. These two groups represent a total of 40% of the seniors, a much lower percentage compared to the first scenario; see also Fig. 18.5b. The remaining 22 seniors (60%), who believed the percentage to be larger than zero, disagreed even more than on the first scenario and provided distributions covering the entire range up until, roughly, 95%.

5.2.3 Mixture Results—Scenario 3

Only one senior indicated the percentage of Ph.D. candidates willing to publish a paper in scenario 3 (i.e. splitting results from one study across multiple publications) to be exactly zero, see also Fig. 18.5c. Another five indicated their belief to be close to zero, but with much more variability (i.e. larger variance of the combined distribution) than in the previous two scenarios. Most of the seniors (n = 27; 82%) believed the percentage to be much higher, and some even close to 100%.

6 Conclusion—Empirical Data

In general, the seniors believed the Ph.D. candidates are very likely to ‘salami-slice’ their papers (82%) or to delete outliers (60%) and some even believe they are likely to go ahead with fabricated data (18%). Based on these distributions the senior administrators seem to believe that the acceptance of serious misconduct is relatively low amongst Ph.D. candidates when compared to questionable research practices such as deleting outliers without a proper reason and, especially, salami tactics, which are believed to be quite common. Even so, some seniors believe that Ph.D. candidates, if feeling sufficiently pressured, would go ahead and publish even with fake data.

7 Conclusion—Elicitation Procedure

Ideally, an elicitation procedure should be properly prepared by allowing for enough time to train the experts, provide them with feedback, etc. (see, e.g. Johnson et al. 2010; Zondervan-Zwijnenburg et al. 2017). However, usually time constraints make it difficult or sometimes even impossible to obtain ‘perfect’ elicitation results which can directly be entered in elicitation software like SHELF (Oakley and O’Hagan 2010). It would be a pity if results from such an elicitation procedure had to be discarded. Moreover, the experts, at least in our empirical example, had a clear idea of how the distribution should have looked like, but simply lacked the time or skills for the correct placement of the stickers. In our chapter, we provided seven different issues with ‘imperfect’ elicitation results, and we provided solutions for translating these results into empirical distributions reflecting the original stickered distributions.

Another way of obtaining ‘perfect’ results when time for the elicitation process is extremely limited, is to use digital procedures for the trial-and-roulette methods. Veen et al. (2017b) developed a five-step method for the trial-and-roulette method which can be used on a mobile device. Lek and Van De Schoot (2018) developed another app for mobile devices in the context of educational testing for the elicitation of a beta distribution for primary school teachers. In both procedures, a direct feedback step is included in which the expert can approve the translation of their stickered distribution into an empirical distribution. Such new developments are to be preferred when compared with the solutions we presented in our chapter. On the other hand, many experts indicated the placing of stickers was fun and inspiring. Filling out the online apps would ‘just’ be another task at a computer, of which they already have too many.