Oxygen in the Tumor Microenvironment: Mathematical and Numerical Modeling

Abstract

There are many reasons to try to achieve a good grasp of the distribution of oxygen in the tumor microenvironment. The lack of oxygen – hypoxia – is a main actor in the evolution of tumors and in their growth and appears to be just as important in tumor invasion and metastasis. Mathematical models of the distribution of oxygen in tumors which are based on reaction-diffusion equations provide partial but qualitatively significant descriptions of the measured oxygen concentrations in the tumor microenvironment, especially when they incorporate important elements of the blood vessel network such as the blood vessel size and spatial distribution and the pulsation of local pressure due to blood circulation. Here, we review our mathematical and numerical approaches to the distribution of oxygen that yield insights both on the role of the distribution of blood vessel density and size and on the fluctuations of blood pressure.

4.1 Introduction

One cannot underestimate the role of oxygen in the tumor microenvironment, as it regulates both the life and death of tumor cells in many ways. Oxygen in tumors also determines the efficacy of many therapies. For instance, radiotherapy depends in a crucial way on the oxygen effect [1], and one of the basic aims of fractionated radiotherapy is just providing enough oxygen after each fraction to help killing tumor cells in the next fraction.

In spite of its importance for tumor biology and the clinical course of the disease, however, the current understanding of the quantitative aspects of oxygen diffusion in tumors is not complete, and there is no doubt that this is at least partly due to the biological and biochemical complexity of the tumor microenvironment.

It is known that in addition to tumor cells, the tumor microenvironment comprises nonmalignant cells of different origin, such as stromal and immune cells. These nonmalignant cells play an active role in tumor progression by exchanging a number of molecular signals with tumor cells [2]. The mixture of different cells is mechanically supported by an extracellular matrix of polysaccharides and fibrous proteins, and all this complex tissue structure is fed by an irregular network of blood vessels [2, 3]. The network of blood vessels in tumors differs substantially from that of normal tissue. Tumor blood vessels are in general more tortuous, irregular, and leaky [4], and, importantly, the intervascular distances are larger. This means that the blood flow is irregular and that the cells that are far apart from feeding vessels receive low amounts of oxygen. Many tumors show in fact hypoxic or even anoxic inner areas [3,4,5,6,7]. In turn, hypoxia induces significant genomic and proteomic changes in tumor cells, and it has been shown to induce also genomic instability by increasing the mutation frequency of cells [4, 5]. The highly selective tumor microenvironment can then promote the growth of more aggressive tumor phenotypes [4,5,6].

In their search for nutrients, living cells wrap around blood vessels to form cords of living cells. They consume oxygen, nutrients, and eventually drugs, and since their spatial distribution in the tumor is not homogeneous, the concentration field of such molecules in the tumor microenvironment is not homogeneous as well. For example, hypoxia shows up differently in different tumors and even in different parts of individual tumors, where it is heterogeneous both in space and in time [7, 8]. Therefore the spatial distribution of cells alters the environment bringing about a complex feedback loop.

From this very short introduction to the biophysics of oxygen in the tumor microenvironment, it is clear that it displays all the complexities of biological systems. The environmental details span several hierarchical levels, from individual molecules to fully formed tumors; there is a large number of interacting elements, starting again from the individual molecules belonging to many chemical species to cells of many different types – both normal and tumor. There are structures that belong to normal tissues and their deformed counterparts in the tumor mass. Finally, all these elements are closely interacting, and the interactions are usually nonlinear. This means that mathematical and numerical approaches can only scratch the surface of this all-embracing complexity and that we must be confident in our ability of correctly separating the hierarchical levels and finding good phenomenological approximations to compensate for the shortcomings of calculations.

While here we concentrate on one single chemical species, O₂, it cannot be considered in isolation, and the equations that describe its diffusion in the microenvironment must be complemented by reaction terms that specify its interaction with the other parts of the microenvironment. This problem of the reaction-diffusion of oxygen in tissues in general and in tumors in particular has already been considered in some of its aspects by other workers in this field (see, e.g., [9, 10] and references cited therein). In the following sections, we review the two approaches that we have followed in our work: an analytical one, which brings out rather nicely the time-dependent features of oxygen diffusion in the tumor microenvironment, and a numerical approach which starts from the simulation of individual cells and capillary vessels and that recreates the hypoxic recesses with large chemical gradients that drive the Darwinian evolution of different tumor genotypes.

4.2 The Fourier Problem

Before dealing with the analytical model of oxygen in the tumor microenvironment, it is useful to introduce the methods used later on with a seemingly unrelated problem, which was considered long ago by Jean-Baptiste Joseph Fourier, that of the diffusion of the sun’s heat into the ground [11].

The soil temperature is still an outstanding problem in agriculture, as it influences the growth of plants, but nowadays this is commonly monitored by measurements with temperature probes. However, for Fourier it was different, it was not just a matter of measurements, and it was something that he wanted to understand in depth, and to this end, he started from the newly discovered diffusion equation for temperature in one dimension¹:

$$\displaystyle \begin{aligned} \frac{\partial T}{\partial t} = D \frac{\partial^2 T}{\partial z^2}, \end{aligned} $$

(4.1)

where T = T(t, z) is the temperature, a function of both time t and of space coordinate z. The equation says that the rate of change of temperature at a given position in space depends on the values of the temperature all around that given position, i.e., on the flow of heat to and from the neighborhood of that position. In the problem considered by Fourier, there is just one spatial dimension, z, because he was interested in the approximation where the ground is a uniform plane and z represents the depth.

It is important to note that the diffusion equation (4.1) is linear. This means that if we find two different solutions T ₁(t, z) and T ₂(t, z), then any linear combination T(t, z) = a × T ₁(t, z) + b × T ₁(t, z), where a and b are real numbers, is again a solution of the equation. In the jargon of physics, this means that the principle of superposition holds.²

Obviously, when dealing with the Earth’s ground, the source of heat is the sun, a source which is doubly modulated, daily and yearly. This double modulation can be roughly described as the sum of two sinusoidal terms

$$\displaystyle \begin{aligned} T(t,0) = A_d \cos{}(\omega_d t + \phi_d) + A_y \cos{}(\omega_y t + \phi_y) \end{aligned} $$

(4.2)

with ω _d = 2π∕T _d, ω _y = 2π∕T _y, where T _d = 86, 400 s is the duration of one day, and T _y ≈ 3.1558 × 10⁷ s is the duration of the astronomical year. A _d and A _y are the amplitudes of the sinusoidal terms and depend on the latitude (for instance, on the equator daylight always lasts 12h, there is only a weak dependence on the day of the year, and A _y ≈ 0). The constants ϕ _d and ϕ _y are two phases that depend on the choice of the origin of the time axis and are irrelevant in the present calculation.

Thanks to the principle of superposition, we can find the solution of the diffusion equation (4.1) for each single sinusoidal term and combine them thereafter. Before proceeding further, it is also helpful to go one step further with the superposition principle. We note that a cosine is itself a weighted sum of two complex exponential functions, and therefore we can apply the superposition principle “backward.” Since a given cosine function is a solution of the diffusion equation, then the two complex exponentials are themselves solutions of the same equation. This means that we can go through the whole process of solving the diffusion equation with exponential functions, use their decomposition $\mathrm{e} ^{\mathrm{i} x} = \cos x + \mathrm{i} \sin x$, and use again one final time the superposition principle to just discard the “unphysical” imaginary part. This choice of the complex exponentials greatly simplifies all the calculations, and on the boundary plane (the ground), we can take the “complex” temperature $\hat {T}(t,0) = \hat {A} \mathrm{e} ^{\mathrm{i} \omega t}$, where the hat denotes complex variables, and $\hat {A} = A \mathrm{e} ^{\mathrm{i} \phi }$.

Because of the linear character of the diffusion equation, we know that the time dependence remains the same at all depths; however, we still have to determine the space dependence of temperature. Therefore, we write $\hat {T}(t,z) = \hat {A}(z) \mathrm{e} ^{\mathrm{i} \omega t}$, we substitute in Eq. (4.1), and we find

$$\displaystyle \begin{aligned} \mathrm{i}\omega\hat{A}(z) = D \frac{\mathrm{d}^2 \hat{A}}{\mathrm{d} z^2}. \end{aligned} $$

(4.3)

Equation (4.3) is the same equation one has to solve for a harmonic oscillator, albeit with complex coefficients, and it is well-known that its solution is just a linear combination of exponential terms (again). Therefore, we can repeat the steps that we have already taken with the time-dependent part and write the space-dependent part $\hat {A}(z)$ as a linear combination of complex exponentials e^αz that depend on the depth z. We can determine the constant α by substitution into Eq. (4.3), and we find the algebraic equation

$$\displaystyle \begin{aligned} \mathrm{i}\omega = D \alpha^2, \end{aligned} $$

(4.4)

which has the solutions $\alpha = \pm \mathrm{e} ^{\mathrm{i} \pi /4}\sqrt {\omega /D}=\pm (1+\mathrm{i} )\sqrt {\omega /2D}$. Mathematically, this determines two spatial solutions

$$\displaystyle \begin{aligned} \hat{A}(z) = A_\pm \exp\left( \pm (1+\mathrm{i})\sqrt{\frac{\omega}{2D}} z \right), \end{aligned}$$

but only the solution with the minus sign is acceptable, because the other one is unphysical, with its amplitude which increases exponentially in time.

Assembling the factors together, and equating its value at the boundary (the ground) with the known modulation $A\cos {}(\omega t + \phi )$, we find the complete solution

$$\displaystyle \begin{aligned}T(t,z) &= A \exp\left( - \sqrt{\frac{\omega}{2D}} z \right) \cos\left( \sqrt{\frac{\omega}{2D}} z \right) \cos{}(\omega t + \phi) \end{aligned} $$

(4.5)

$$\displaystyle \begin{aligned} &= \frac{A}{2} \exp\left( - \sqrt{\frac{\omega}{2D}} z \right) \left[ \cos\left( \omega t + \phi + \sqrt{\frac{\omega}{2D}} z \right) + \cos\left( \omega t + \phi - \sqrt{\frac{\omega}{2D}} z \right) \right] \end{aligned} $$

(4.6)

Equation (4.6) shows that while at any given depth the oscillation has the same frequency as on the ground, it decomposes into two components with different depth-dependent and frequency-dependent phases. Moreover the amplitude itself decreases exponentially with a characteristic length λ which is again frequency dependent, $\lambda = \sqrt {2D/\omega }$, and decreases steadily for increasing frequency.

Applying the principle of superposition to each modulation, diurnal and annual, we find the solution of the original Fourier problem:

$$\displaystyle \begin{aligned} T(t,z) = A_d \exp\left( - \sqrt{\frac{\omega_d}{2D}} z \right) \cos\left( \sqrt{\frac{\omega_d}{2D}} z \right) \cos{}(\omega_d t + \phi_d) \\ + A_y \exp\left( - \sqrt{\frac{\omega_y}{2D}} z \right) \cos\left( \sqrt{\frac{\omega_y}{2D}} z \right) \cos{}(\omega_y t + \phi_y). \end{aligned} $$

(4.7)

This ingenious solution was the beginning of the Fourier series, as Fourier understood that it could be extended to any number of sinusoidal components. It also displays from the very start one of the strengths of the Fourier series, namely, that they can be used as a tool to solve any kind of linear differential equation – be it an ordinary differential equation or a partial differential equation – thanks to the principle of superposition.

As we shall see in the next sections, all the basic features of the solution (4.7) are carried over to the case of oxygen diffusion in the tumor microenvironment.

4.3 Linear Model of Oxygen Diffusion and Consumption

When we consider the complex tumor microenvironment, we find that the concentration of any chemical follows the same basic rules as the temperature of Fourier’s problem. There is a molecular current from regions of higher concentration to regions of lower concentration which follows Fick’s law J = −D∇ Φ, where Φ is the concentration, and there is relation which is an extension of the conservation of energy in the previous section

$$\displaystyle \begin{aligned} \frac{\partial \Phi}{\partial t} = - \nabla\cdot\boldsymbol{J} - f\left( \Phi(\boldsymbol{r},t),\boldsymbol{r},t) \right) \end{aligned}$$

This means that the rate of change of the concentration in a given region of space around position r depends both on the outflow of molecules from that region – described by the current term – and from the disappearance of those molecules because of the reaction with other chemicals – described by the reaction term $f\left ( \Phi (\boldsymbol {r},t),\boldsymbol {r},t) \right )$.

Combining these equations together, we find the complete reaction-diffusion equation

$$\displaystyle \begin{aligned} \frac{\partial \Phi}{\partial t} = \nabla \cdot \left( D \nabla \Phi \right) - f\left( \Phi(\boldsymbol{r},t),\boldsymbol{r},t) \right). \end{aligned} $$

(4.8)

Equation (4.8) is very general: the diffusion coefficient D which parameterizes the speed of diffusion of molecules in the environment can be position- and time-dependent, D = D(r, t), and the reaction term is in general a combination of one or more Michaelis-Menten (or Hill) terms.³

Here, we concentrate our attention on a very small spatial region, and we assume that D does not depend on r. We also assume that the reaction term can be linearized in a simple way, $f\left ( \Phi (\boldsymbol {r},t),\boldsymbol {r},t) \right ) \approx \gamma \Phi (\boldsymbol {r},t)$, which is consistent with the low-concentration approximation of a Michaelis-Menten reaction term. Then, Eq. (4.8) becomes

$$\displaystyle \begin{aligned} \frac{\partial \Phi}{\partial t} = D\nabla^2 \Phi -\gamma\Phi.\end{aligned} $$

(4.9)

In this case we are going to use this formalism to understand how the fluctuations of oxygen concentration in the blood vessels influence the concentration of oxygen in the microenvironment, and it is instructive to start with Eq. (4.9) in the one-dimensional case

$$\displaystyle \begin{aligned} \frac{\partial \Phi}{\partial t} = D\frac{\partial^2 \Phi}{\partial z^2} -\gamma\Phi,\end{aligned} $$

(4.10)

which we solve with the same methods used in Sect. 4.2. We let again $\hat {\Phi }(t,0) = \hat {A} \mathrm{e} ^{\mathrm{i} \omega t}$, and we obtain the ordinary differential equation

$$\displaystyle \begin{aligned} (\mathrm{i}\omega+\gamma) \hat{\Phi} = D\frac{\mathrm{d}^2 \hat{\Phi}}{\mathrm{d} z^2},\end{aligned} $$

(4.11)

which is nearly the same as Eq. (4.3). The solution is again an exponential function e^αz, where α solves the algebraic equation

$$\displaystyle \begin{aligned} \mathrm{i}\omega+\gamma = D\alpha^2. \end{aligned}$$

With a little complex algebra, it can be shown that

$$\displaystyle \begin{aligned} \hat{\Phi}(z,t) = A \exp\left[ \mathrm{i}\left(\omega t + \varphi(z)\right) \right] \mathrm{e}^{-z/\ell}, \end{aligned}$$

where the position-dependent phase is

$$\displaystyle \begin{aligned} \varphi(z) = \left( \frac{\omega^2+\gamma^2}{D^2}\right)^{1/4} \sin\left( \frac{1}{2}\arctan\frac{\omega}{\gamma} \right) z, \end{aligned}$$

and the decay length is

$$\displaystyle \begin{gathered} \ell(\omega,\gamma) = \sqrt{\frac{2D}{\gamma+\sqrt{\omega^2+\gamma^2}}} = \ell_0(\omega) \sqrt{\frac{2}{1+\sqrt{1+\omega^2/\gamma^2}}}, \end{gathered} $$

with

$$\displaystyle \begin{aligned} \ell_0(\omega) = \ell(\omega,0) = \sqrt{D/\omega} \end{aligned}$$

Except for a factor $\sqrt {2}$ – which comes from our preferred definition of the ratio ℓ∕ℓ ₀ – the decay length ℓ ₀ is the same as in the Fourier problem in Sect. 4.2 where there is no absorption term, and here we see that the introduction of the consumption/absorption coefficient γ modifies the decay length making it somewhat smaller. It also shows that usual formulations of the reaction-diffusion problem which take into account the consumption/absorption term but ignore modulation do not properly estimate the decay length as they tend to overestimate it and therefore also the penetration of oxygen into the microenvironment. On the whole, we find that the concentration of oxygen in the tumor microenvironment must be influenced by the frequency of the fluctuations of oxygen concentration in its blood vessels.

Another interesting feature of the reaction-diffusion solution is that while the decay length ℓ ₀(ω) diverges for ω → 0, the presence of the consumption/absorption term limits the decay length to

$$\displaystyle \begin{aligned} \ell(\omega,\gamma) \le \ell(0,\gamma) = \sqrt{{D}/{\gamma}}. \end{aligned}$$

The complete behavior of the ℓ∕ℓ ₀ ratio is shown in Fig. 4.1.

Fig. 4.1

Log-log plot of the decay length of the solution of the one-dimensional diffusion problem. Solid line: the curve is nearly flat for ω < γ, and its value is close to 1. Dashed line: if ω ≫ γ, the ratio of decay lengths approaches the behavior of the decay length without consumption/absorption, i.e., the simple power law ℓ∕ℓ ₀ ∼ ω ^−1∕2. The transition between the two regimes occurs at ω ≈ γ

To conclude this section, we recall that in the solution of the Fourier problem, there were two Fourier components of the ground temperature that fluctuated about an average value of zero. When considering temperature in Celsius degrees, this may be adequate, but negative swings are certainly forbidden with chemical concentrations. It is easy to cure this problem by adding a constant component (a zero-frequency component) that restores the non-negativity of the concentration, as in Fig. 4.2.

Fig. 4.2

Periodic fluctuations of the concentration about an average value (concentration normalized to the peak value vs. time in arbitrary units). In this elementary example, the relative concentration c(t) is described by just two Fourier components: $c(t) = 0.8 + 0.2 \cos {}(2\pi t + 0.7) = \Re (0.8 + 0.2 \mathrm{e} ^{(2\pi t + 0.7)\mathrm{i} })$, where $\Re (x)$ is the real part of the complex number x. The solid line represents the sum of the two terms, while the dashed line represents the constant term which is essential for the consistency of the mathematical description

4.4 The Near-Cylindrical Geometry of Blood Vessels

The discussion of the previous section cannot be considered complete without a proper appraisal of the role of blood vessel geometry. In this section we briefly consider the role of the cylindrical geometry which locally approximates the geometry of blood vessels. We remark that the validity of the approach is limited to blood vessels with a diameter much smaller than their length. In an environment crowded with blood vessels, the approach is useful in the linear limit of Eq. (4.9), as the overall oxygen concentration can be computed – from the principle of superposition – from the sum of the concentrations due to the individual blood vessels (see also [13]), and this holds for a fluctuating oxygen concentration as well.

We use cylindrical coordinates (r, θ, z) and take the z-axis along the axis of a blood vessel (locally approximated by a cylinder with radius R), then we find the reaction-diffusion equation

$$\displaystyle \begin{aligned} \frac{\partial \Phi}{\partial t} = D \frac{1}{r} \frac{\partial}{\partial r}\left( r \frac{\partial \Phi}{\partial r} \right) - \gamma\Phi. \end{aligned} $$

(4.12)

where r is the distance from the axis of the blood vessel. When we take again $\hat {\Phi }(t,0) = \hat {A} \mathrm{e} ^{\mathrm{i} \omega t}$, Eq. (4.12) becomes

$$\displaystyle \begin{aligned} r \frac{\partial}{\partial r}\left( r \frac{\partial \hat{\Phi}}{\partial r} \right) - \frac{i\omega+\gamma}{D} r^2 \hat{\Phi} = 0, \end{aligned} $$

(4.13)

which is a modified Bessel equation. The solution of Eq. (4.13) with a boundary condition which is set by the oxygen concentration on the surface of the blood vessel $\hat {\Phi }(R,t) = \hat \Phi _0 \mathrm{e} ^{\mathrm{i} \omega t}$ is qualitatively similar to the simpler one-dimensional case with a plane boundary that has been considered above, though with some added mathematical complexities which are described in detail in reference [14]. The main difference with respect to the one-dimensional case is that the Bessel function that solves equation (4.13) – a modified Bessel function of the second kind with complex argument, $K_0\left ( \sqrt {(\gamma +i\omega )/Dr} \right )$ – decays faster than exponentially, as shown in Fig. 4.3, where several other details are illustrated.

Fig. 4.3

Plots of $K_0 \left ( \sqrt {\gamma /Dr} \right )/K_0 \left ( \sqrt {\gamma /DR} \right )$ (solid line) and of the exponential function $e^{-r/\ell _0}$ (dashed line) vs. r∕ℓ ₀ for 2R = 0.01ℓ ₀. This shows the contribution of the constant Fourier component of the fluctuating oxygen concentration to the concentration in the surrounding environment, in the case of a blood vessel with a diameter which is 1% of the decay length ℓ ₀. Since ℓ ₀ is about 0.96 mm with physiological parameters (D = 2000 μm²/s; γ ≈ 2.16 × 10⁻³ s⁻¹, see Sect. 4.5 for further discussion about the parameters), this corresponds to a blood vessel with diameter 2R ≈ 20 μm. The smallest diameter is one order of magnitude lower. Upper panel: this plot has a linear vertical scale and shows the dramatic effect of the cylindrical geometry, which leads to decay of the concentration which is much faster than in the one-dimensional, planar case (the dashed exponential). Lower panel: same plot, but with a logarithmic vertical scale, where we note that for large radius, the solution behaves again almost exponentially, but with a drops more than one order of magnitude below the one-dimensional planar case. These plots display quite starkly the effect of the cylindrical geometry of the individual blood vessels. Finally, it is important to note that the difference between the cylindrical and the plane geometry depends on the radius of the blood vessels: it is reduced for large radii, while it is enhanced for small radii

4.5 Dealing with Dead Cells: Tumor Cords

The solution discussed in the previous section is characterized by an extremely fast decrease of the oxygen concentration when the blood vessels are surrounded by a uniform population of live cells. In normal tissues this fast decrease is compensated by a high density of blood vessels, that are never too far apart, so that the superposition of the concentrations is always in a physiological range and cells live. However, this is not the case in the majority of tumor tissues, where blood vessels are often far apart and have a chaotic distribution and shape that lower the efficiency of oxygen transport. Hypoxic regions appear where the harsh conditions cause the death of many cells, and the resulting environment develops gradients of the concentration of live cells. Eventually, live cells are mostly concentrated around blood vessels – making up the so-called tumor cords [15] – with extended necrotic regions in between the blood vessels.

The uneven distribution of live cells means that the consumption/absorption coefficient γ is position-dependent. Here we consider a general exponential model of (radial) space dependence, motivated by our previous numerical work [16, 17]

$$\displaystyle \begin{aligned} \gamma(r)= \gamma_0 + \gamma_c\exp(-r/\lambda_c), \end{aligned} $$

(4.14)

where γ ₀ corresponds to the binding of oxygen to some environmental chemical (and we assume this to vanish in most tissues) and γ _c is the oxygen consumption associated with a population of live cells. Model (4.14) leads to the following Fourier coefficients (i.e., amplitudes of the time-dependent terms, see [14] for more details):

$$\displaystyle \begin{gathered} {}\ln \phi(r,\omega) = \ln \phi(R,\omega) + \int_R^{r} \sqrt{\frac{\mathrm{i}\omega+\gamma(r')}{D}} \frac{K_0^\prime\left(\sqrt{\mathrm{i}\omega+\gamma(r')/D}\; r'\right)}{K_0\left(\sqrt{\mathrm{i}\omega+\gamma(r')/D}\; r'\right)} dr' \end{gathered} $$

(4.15)

Equation (4.15) is noteworthy because it represents a decently realistic model of the oxygen concentration in a small fraction of the tumor microenvironment where the blood vessels are far apart. However, a comparison with actual data requires properly chosen parameter values. All the parameters used in the numerical evaluations that follow are extrapolated from experimental data and apply to solid tumors. We take the estimates in [16, 17] for the decay length in the definition (4.14): λ _c = 120 μm. The diffusion constant of oxygen as measured both in blood and tissues D = 2 × 10⁻⁹ m²∕s is taken from [18, 19]. The rates of oxygen consumption in different areas of in vivo tumors have been precisely measured and shown to vary in the range 1.66 10⁻⁴ – 5 10⁻³ s⁻¹ (mean value 2.16 10⁻³ s⁻¹) [20,21,22]. Finally, we note that measurements on melanomas [23] indicate that the average microvessel diameter is about 5 μm, i.e., R = 2.5 μm, just enough to let one erythrocyte through.

The reduced consumption/absorption coefficient at larger depth means that when tumor cords form, the decay of the oxygen concentration is not as fast as in the straightforward cylindrical case. This is illustrated in Fig. 4.4 which compares the concentration decay for tumor cords with the previously examined cases (the simple exponential decay found in the one-dimensional case and the enhanced decay found in the case with cylindrical symmetry).

Fig. 4.4

Relative concentration in the case of tumor cords (solid line) vs. radial distance r. Similarly to Fig. 4.3, other curves show the corresponding decays in the one-dimensional case (dotted line) and in the case with cylindrical symmetry (dashed line). The parameter values used here are D = 2 × 10⁻⁹ m²∕s, γ ₀ = 0, γ _c = 2.16 × 10⁻³s⁻¹, and λ _c = 120 μm. Notice that, once again, this is the plot for the Fourier component with ω = 0, and we know that the Fourier components with ω > 0 decrease faster than shown here

To conclude this section, we note that the time dependence of the boundary conditions has a very important effect on the concentration also in the case of the tumor cords. Figure 4.5 shows the concentration vs. the radial distance r for several Fourier amplitudes ϕ(ω, r) computed using average parameter values for solid tumors and a blood vessel diameter close to the minimum (6 μm), and we see that fluctuations that correspond to a normal heartbeat (60 beats/minute = 1 Hz) have a very short penetration depth into the tumor tissue.

Fig. 4.5

Plots of |ϕ(ω, r)∕ϕ ₍ω, R)| vs. r (μm) in the case of a tumor cords, Eq. (4.15), for different frequencies ν = ω∕2π. All curves have been calculated with 2R = 6 μm, D = 2000 μm²/s, γ ₀ = 0, γ _c = 2.16 10⁻³ s⁻¹, and λ _c = 120 μm. The black line is the stationary solution (ν = 0); the other line shows the relative concentration for frequencies ranging from ν = 0.001 Hz to ν = 1 Hz

4.6 Comparison with Experimental Data

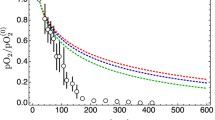
Experimental data are very hard to come by, but some high-quality data have been produced by Helmlinger et al. [24] (see Fig. 4.6), and they show a very fast decrease of the partial oxygen pressure at increasing distance from blood vessels in a colon adenocarcinoma xenograft. This is in line with the qualitative indications in the previous sections, but can we make this correspondence more robust?

Fig. 4.6

Experimental data taken in measurements on colon adenocarcinoma xenografts, redrawn from Fig. 3 in Ref. [24]. The figure shows values of partial oxygen pressure (pO₂) in the tumor interstitium as a function of the distance from blood vessels (circles; bars represents the s.e.m. calculated from 15 samples). In this figure pO₂ has been normalized with respect to the central value in the nearest blood vessel (pO$_2^{(0)}$). The observed median radius of the blood vessels in [24] is R = 22.5 μm

Figure 4.7 shows the same data as Fig. 4.6 and some additional curves. In particular, it shows that the data can be bracketed by two curves calculated for tumor cords and that correspond to Fourier components with frequencies 10 and 100 mHz (0.6 cycles/minute and 6 cycles/minute). These frequencies define the interval of the observed frequencies with the highest amplitude for oxygen oscillations in the tumor microcirculation as observed by Braun et al. [25]. This indicates that low-frequency fluctuations in the tumor tissue may explain the observed decrease of the partial oxygen pressure. However, there are still too many parameter values that have been fixed to produce Fig. 4.7, and this may leave the impression that the agreement is somewhat ad hoc.

Fig. 4.7

Comparison of the observed relative oxygen pressure redrawn from [24] as in Fig. 3 vs. the distance r from axis of the nearest blood vessel. The solid line shows the decay of the relative oxygen pressure in the case of a tumor cord, while the dashed line shows the straightforward case with cylindrical symmetry, in both cases for ν = 0. The grayed band delimits the region between ν = 0.01 Hz to ν = 0.1 Hz. All curves are calculated with the values D = 2000 μm²/s, γ ₀ = 0, γ _c = 2.16 10⁻³ s⁻¹, and λ _c = 120 μm and with the median blood vessel radius R = 22.5 μm

This can be remedied with a better exploration of the parameter space, which can be provided, e.g., by a Monte Carlo simulation. Consider Fig. 4.7, which has been drawn taking the median blood vessel radius R = 22.5 μm: what happens if we let this fluctuate within a reasonable range? The answer is shown in Fig. 4.8, where both the frequency (range: ν = 0.01 Hz – ν = 0.1 Hz) and the radius of the blood vessel (range: 3 μm – 160 μm) are uniformly distributed in the respective ranges. We see that the distribution of radius does not significantly alter the band of Fig. 4.7. We can push the method further and introduce a fluctuation of the diffusion coefficient and of the consumption/absorption coefficient in addition to the fluctuation of the blood vessel diameter. The results are shown in Figs. 4.9 and 4.10, and we see once again that the resulting bands fit rather well the actual data. There are other factors that might influence these results, such as the shape of the probability density function of the blood vessel radius; a test carried out with an exponential distribution of the radius (with mean value 22.5 μm, not shown) displays very little variation with respect to Figs. 4.8, 4.9, and 4.10.

Fig. 4.8

Monte Carlo simulation of the model predictions that takes into account the fluctuation of the frequencies and of the blood vessel radii. The parameters used for the Monte Carlo are the same as those of Fig. 4.7, except that here both the radius and the frequency are allowed to fluctuate following uniform distributions in the range (0.01 and 0.1 Hz) (frequency) and (3 and 160 μm) (radius)

Fig. 4.9

Monte Carlo simulation of the model predictions that takes into account the fluctuation of the diffusion coefficient as well as that of the frequencies and of the blood vessel radii. The parameters used for the Monte Carlo are the same as those of Fig. 4.8, except that here the diffusion coefficient fluctuates as well, following a uniform distribution in the range (1000 and 3000 μm²/s)

Fig. 4.10

Monte Carlo simulation of the model predictions that takes into account the fluctuation of the consumption/absorption coefficient as well as that of the frequencies and of the blood vessel radii. The parameters used for the Monte Carlo are the same as those of Fig. 4.8, except that here the consumption/absorption coefficient fluctuates as well, following a uniform distribution in the range (0.5 × 2.16 10⁻³ s⁻¹, 2 × 2.16 10⁻³ s⁻¹)

The conclusion that we can draw from this study is that the frequency of the fluctuations is the single most important factor in determining the penetration of oxygen in the microenvironment in the case of isolated blood vessels. In the next sections, we move on to consider blood vessel geometry, the importance of its remodeling in cancer tissues, and more.

4.7 Into the Future: Numerical Simulations of Vascularized Tumors

While the considerations in the preceding sections are very useful to understand the general behavior of oxygen, they are not sufficient to describe the spatial complexity of the tumor microenvironment. A detailed calculation of the oxygen concentration due to the blood vessels in a tumor and in the surrounding healthy tissue defies the analytical methods, and we must turn instead to numerical tools. These tools are important both to gauge the importance of nonlinear effects and to unveil those aspects of the complexity that escape a simple description as the one given in the previous sections. In particular, we note that

• We neglected that the tumor microenvironment comprises both healthy and cancerous vessels/cells at the same time.

• In Sect. 4.3, we noted that the Michaelis-Menten and the Hill equations are biologically reasonable models of the reaction terms in the reaction-diffusion equation. However, the linearization of these nonlinear model works only for low concentrations, and the linear hypothesis may not be adequate in many circumstances (for instance, it may lead to an overestimate of the oxygen consumption in well-oxygenated regions).

• Finally, the most severe simplification is the small system size comprising a single blood vessel only. Realistic tissues feature a vasculature consisting of many blood vessels of different radii and surface characteristics. Since blood vessels are the source of the oxygen inside tissue, the exact form of the oxygen field depends on the strength of the sources and on the arrangement of the sources in space, i.e., the oxygen concentration field depends crucially on vascular morphology. During the growth progression of solid tumors, both the source strength and the arrangement of the vessels are altered. The vasculature becomes irregular, tortuous, and leaky with corresponding consequences for the oxygen transport.

All of these limitations can be overcome by computer simulations, which are a comprehensive tool to study tumor growth and the tumor microenvironment in a much more realistic way, although at the non-negligible cost of a large coding and computational effort [26].

4.7.1 The Oxygen Concentration Field of Simulated Vascularized Tumors Embedded in Normal Tissue

To address the problem of vessel geometry, we explicitly model each blood vessel as a cylinder with length l, radius r, and thickness w. The problem of creating realistic arteriovenous blood vessel networks in 3D was solved in [27]. Upon the construction of the initial vasculature, tumor growth starts to remodel the vasculature by vessel dilation and collapse, wall degeneration, and angiogenesis. While the first three processes require the modification of existing blood vessels, sprouting angiogenesis refers to the establishment of new connections. Blood vessels are surrounded by a layer of endothelial cells, and tumor cells secrete numerous chemicals. One family of chemical messengers, the vascular endothelial growth factor (VEGF), triggers the proliferation of endothelial cells and their migration toward the formation of new vessels. In our simulation program (Tumorcode), angiogenesis is turned on when the concentration of VEGF exceeds a specific threshold. Once this happens, angiogenesis proceeds as a two-step random process: first, a sprout is initialized, and second, a present sprout may be extended.

Tumor vasculature cannot be considered in isolation because it feeds the tumor. And just as the tumor grows and changes, so does its vasculature, and these two entities influence each other in a complex feedback loop that involves oxygen, nutrients, and messenger molecules. This means that the computational model of the vasculature must be coupled with a properly chosen model of tumor tissue.

In our approach we have adopted two different models of tumor tissue: one of them is a continuum description, which is computationally efficient and is well suited for the description of tumors of clinical interest but lacks the ability to describe processes at the individual cell level, such as the evolutionary processes that produce the heterogeneity of the tumor microenvironment. The other one is based on a model of individual cells, and excels in the description of the single-cell events, but is much more computationally demanding.

4.7.2 Continuum Description of Tumor Tissue

A description of tumor development and growth based on continuum mechanics must deal with the fact that cells proliferate and die, in addition to the conditions of mass and momentum conservation that must normally be met. Just like the equation that expresses the conservation of thermal energy in Sect. 4.2, we can express the conservation of the number of cells (which corresponds to the conservation of mass) by means of the equation

$$\displaystyle \begin{aligned} -\frac{\partial \Phi}{\partial t} = \nabla\cdot (\Phi \boldsymbol{u}) \end{aligned} $$

(4.16)

where the tumor cell density Φ(x, t) depends on the space and time coordinates x and t, u is the local velocity field, and Φu is the current of cells that enter and leave a small volume centered at position x, at time t.

Since the number of cells is not actually conserved because cells proliferate and die, we must add a term f that modifies the time derivative as follows

$$\displaystyle \begin{aligned} -\frac{\partial \Phi}{\partial t} = \nabla \cdot (\Phi \boldsymbol{u}) - f \end{aligned} $$

(4.17)

Using the identities

$$\displaystyle \begin{aligned} \nabla(\Phi \boldsymbol{u}) =\Phi \nabla\cdot \boldsymbol{u} + \boldsymbol{u} \cdot \nabla\Phi \end{aligned}$$

and

$$\displaystyle \begin{aligned}\frac{\mathrm{d} \Phi}{\mathrm{d} t}=\frac{\partial \Phi}{\partial t} + \boldsymbol{u}\cdot \nabla \Phi\end{aligned}$$

we can rearrange equation (4.17) in the form

$$\displaystyle \begin{aligned} \frac{\mathrm{d} \Phi}{\mathrm{d} t} = -\Phi \nabla\cdot \boldsymbol{u} + f \end{aligned} $$

(4.18)

which is the standard way in which this equation is usually presented.

In turn, cell death and proliferation cause shape changes that produce mechanical forces. To model this aspect, it is necessary to turn to the theory of plastic solids and introduce an equation that corresponds to the conservation of momentum. The general form of the equation of motion is

$$\displaystyle \begin{aligned} \frac{\mathrm{d} (\Phi \boldsymbol{u})}{\mathrm{d} t} = \nabla \cdot \sigma + \boldsymbol{F} \end{aligned} $$

(4.19)

where σ is the Cauchy stress tensor and F is the total body force accounting for gravity and other external forces (see, e.g., [28] for a general derivation of the equation).

There are several other details that can be taken into account and in the bulk-tissue simulation of Tumorcode, and we follow the continuum-based model described in [29]. This is a state-of-the-art multiphase or mixture model [30]. In such models, the mass, the momentum, and the stress are given by summation over the contributions from all constituents. We take into account solid-like contributions from tumor cells ( Φ_T), normal cells ( Φ_N), necrotic cells ( Φ_D), and fluid-like contributions from interstitial fluid (l). For each constituent, the velocity field, the mass conservation equation, and the momentum balance are explicitly formulated in [31]. The cells (solid-like contributions) are modeled as viscous liquid (including an isotropic pressure, friction, and adhesion) neglecting inertial force because tissue growth and cell migration happen at very low Reynolds numbers (Re ≪ 1). The liquid (fluid-like contribution) is modeled as a liquid within a porous medium resulting in a variant of Darcy’s law. In our model, the liquid part of the blood (plasma) is allowed to extravasate from the vessels into the interstitium. Therefore we consider additional source terms for the liquid proportional to the local volume vessel density. Finally we solve an elliptic equation for the pressure of the liquid.

To mimic a tumor mass, we impose that tumor cells and normal cells are immiscibly separated by an interface. This is defined via an auxiliary function in the context of the level set method [32,33,34]. This method allows to perform numerical computations involving surfaces without parameterization; therefore it is suitable for fast modeling of time-varying objects that include shape changes such as solid tumors.

We solved this coupled set of continuum equations numerically with the method of finite differences (FD). The FD methods applied to the elliptic equations of our model result in sparse matrix systems. Since sparse matrices are a specialized field within mathematical numerical research, a lot of tools are available to solve systems with sparse matrices (direct factorization, fast Fourier transform, multigrid and iterative preconditioned Krylov subspace methods). Because of the high portability, we decided to use the implementation of the numerical library Trilinos [35].

To facilitate computations and enable tumor sizes of clinical relevance, we have simplified the bulk-tissue tumor model [29]. In our “fake tumor simulation,” the tumor is described as a growing sphere with constant radial expansion speed v _tum. Moreover, even though the tissue and liquid dynamics are neglected, the growing tumor is still a source of VEGF, and the remodeling of the vasculature takes place accordingly.

In our comprehensive numerical approach, we compute the oxygen saturation within tissue for arteriovenous blood vessel networks both before and after they are subject to the modifications of solid tumors [36]. Because oxygen diffusion happens much faster than vascular remodeling, it is not necessary to consider diffusion as an out-of-equilibrium process; rather it is sufficient to stop the vascular remodeling, calculate the oxygen distribution for a fixed vessel network configuration, and continue the vascular remodeling. Since the oxygen diffuses across the blood-tissue interface, the net oxygen flux depends not only on tissue microenvironment but also on the blood pressure inside the vessel [37]. Therefore the local blood pressure is an important input for the calculation of the oxygen field. Moreover, intravascular oxygen transport takes place by free diffusion, and since oxygen is bound to red blood cells (RBCs) in blood vessels, the consideration of RBCs is also crucial for a realistic calculation of the oxygen source strength.

We refer the reader to the original papers for all model details. Here we focus briefly on the part of model that deals with the oxygen calculation. The calculation of intravascular pO2 is a demanding task [38]. Since our focus is on the oxygen field in the tissue, we treat the vessels as one-dimensional line segments neglecting intravascular pO2 variations in radial direction. The net transvascular oxygen flux per blood-tissue interface surface area j _tv is proportional to the oxygen pressure gradient from inside the vessel (P) to the outside in the tissue (P _t)

$$\displaystyle \begin{aligned} j_{\mathrm{tv}} = \gamma \left( P - P_t \right). {} \end{aligned} $$

(4.20)

Equation 4.20 is a phenomenological assumption with an effective (tissue dependent) proportionality factor γ that comprises information about the vessel wall and the tissue/tumor microenvironment (see the supplemental material “S1Appendix.PDF” of [36] for details on the determination of γ). Together with Michaelis-Menten-like uptake of oxygen by the tissue/tumor

$$\displaystyle \begin{aligned} M(P) = M_0 \frac{P}{P+P_{50}} {}\end{aligned} $$

(4.21)

Eqs. (4.20) and (4.21) build the reaction part used in our implementation of the oxygen transport. To obtain the partial oxygen pressure inside the tissue, we solve numerically the following equation:

$$\displaystyle \begin{aligned} 0=\alpha_t D \nabla^2 P_t - M(P_t) + J_{tv} {}\end{aligned} $$

(4.22)

with the solubility of oxygen in tissue α _t and diffusion constant of oxygen in tissue D. Note that unlike the previous sections, Eq. (4.22) considers the stationary equilibrium case only.

As an additional complication, in the physiological coupling of intravascular and extravascular oxygen transport, we must also match different discretization grids. To solve Eq. (4.22), the tissue domain is discretized on a regular cubic grid, but the vessel network is not defined on the same grid. To interpolate P from an arbitrary point along the one-dimensional vessel line to the tissue grid point (where P _t is defined), we follow standard finite elements methods (FEM) using three-dimensional piecewise trilinear functions.

In summary, the oxygen transport across the vessel wall and inside the microenvironment of the solid tumors is complicated because of many reasons. Numerical simulations are not able to solve all problems, but at least in this approach, we can overcome the simplifications mentioned at the beginning of this section and in particular:

• (a) we find realistic values for the source strength of oxygen by fitting the transvascular oxygen mass transfer coefficient γ to available literature values;

• (b) we use the full nonlinearity of the Michaelis-Menten and Hill equations in the reaction part;

• (c) we do take into account the chaotic and inhomogeneous architecture of blood vessel networks in tumors for the calculation of the oxygen field.

Figure 4.11 shows the result of one of our continuum-based simulations, as reported in [36]: it is interesting to observe the strong correlation between the pO2 in the local microenvironment and the blood vessel distribution. For further details, we refer the interested reader to reference [39].

Fig. 4.11

Oxygen in a growing solid tumor. This simulation assumes a spherical expanding tumor mass including the full vessel remodeling dynamics of Tumorcode (“fake tumor”). The simulation setup is identical to the one described in [36] and comprises a volume of 8 mm³ containing about 340k vessel segments. Both panels show a slice through the center of the simulation domain at simulation time t = 600 h. The vessels shown are in a 200 μm thick slice above the central plane. Upper panel: tissue pO2 in a central slice overlain with vessels (color-coded by their pO2 value). The color bar is in mmHg. Lower panel: vessels color-coded by oxygen saturation level

4.7.3 Simulation of Individual Tumor Cells

A computational description based on individual cells provides an even finer view of the microenvironmental pO2: in our case it is based on another piece of software (VBL, Virtual Biophysics Lab) that has been used in the past to simulate small avascular solid tumors [16, 40, 41].

The VBL computational model is based on a lattice-free representation where cells are free to move and to exert both attractive and repulsive biomechanical forces on neighboring cells. The resulting motions of individual cells in the disordered tumor tissue can be followed in time, while the overall tumor structure takes its shape. On the whole the growth dynamics of the simulated avascular tumors is determined by this collective behavior of cells. At the same time, cells live, proliferate, and die, thanks to an embedded model of the cell cycle. The cycle is set in motion by a phenomenological model of the biochemical networks that describes nutrient uptake and utilization by cells. Nutrients can either be directly converted to ATP or energy-storing molecules in cells. The modeled pathways also include metabolites and waste products. The waste products are secreted into the surrounding environment, while both ATP and metabolites are used to build up proteins, DNA, and cellular structures. The model features a limited description of protein synthesis, with some specific named proteins such as cyclins and kinases that regulate the timing and the fate of the cell cycle [42, 43].

The pathways included in the model have been studied independently to fix model parameters and to reduce their known complexity to a few basic simplified reaction schemes. In this way we have reduced the computational cost of the model and, at the same time, preserved its quantitative predictability. All the pathways have been connected together to obtain a basic metabolic model of tumor cells [41,42,43]. When needed, the overall biochemical description can be modified in an incremental way to include additional pathways to address specific aspects of tumor biology.

In VBL, cells are complex objects, while the basic actors are nutrient and waste molecules which interact in the intertwined biochemical pathways that regulate a cell’s life. The model assumes that tumor cells are never quiescent so that cells always grow and proliferate (or die). On an individual basis, the cell volume increases, while the cell’s components – such as proteins, DNA, and organelles – are built, and the growth process proceeds in parallel with the phases of the cell cycle up to mitosis. Just as in real cells, mitosis is uneven, and the mother cell material is subdivided randomly between the two daughter cells [41,42,43]. The individual variability in cell division propagates to the cell population, and it is one of the random factors that determine the chaotic movements of cells in the simulated tumor.

The computer code contains a mixture of deterministic steps – those related to the numerical solution of the reaction diffusion equations, and the mechanical movements – and random steps, such as the division of the cell’s materials at mitosis or the protein synthesis, which is related to the availability of nutrients in a chaotic environment. The deterministic steps describe the dynamics of structures that span at least 3 orders of magnitude in space (from the few μm of cell radius up to a few mm of diameter of an avascular tumor) and 12 orders of magnitude in time (from a few tens of μs that are typical diffusion times of the molecular species up to ∼ 10⁷ s for the full development of an avascular tumor) [44]. Thus, our computer code is a true multiscale model of small avascular tumors, and it requires the use of appropriate algorithms to manage the stiff set of differential equations for reaction-diffusion and mechanical movements [45].

On the whole, the behavior of each individual cell is controlled by ∼100 parameters, and this lends great flexibility to the computer code, which can mix in the same simulation several kinds of tumor cells. Comparisons of the results of simulation runs with experimental data have shown that our simulation program is a reliable model of the growth of avascular tumors [41, 43]. Usually we assume that cells are nonpolar and spherical and that they are immersed in a uniform environment with which they exchange oxygen, nutrients, and metabolites: in such conditions we obtain cell clusters that are invariably nearly spherical and that reproduce in good detail the structure and the chemical gradients found in tumor spheroids [46].

The computer code can also handle more complex situations, like the growth of cells around a single blood vessel that acts as the only source of oxygen and nutrients, with a surrounding environment that is oxygen- and nutrient-poor and filled with metabolites such as lactic acid that make it acidic. This case is illustrated in Fig. 4.12, which shows two different views of the same object, a simulated tumor cord about 480 μm long. The first view shows the O₂ concentration. The second view shows the distribution of cell phases, which displays the fine-grained level of detail that is reached in the simulation. Given the conditions of the simulation, the O₂ concentration is highest close to the blood vessel, and it decreases sharply further away from the vessel. Correspondingly, cells are distributed in various phases in the vicinity of the blood vessel, while they are mostly dead further away from it.

Fig. 4.12

Longitudinal section of a simulated tumor cord about 480 μm long (the blood vessel runs along the axis of the cord and is not shown). Top panel: O₂ concentration; the highest value in the color scale corresponds to O₂ in equilibrium with atmospheric oxygen. Bottom panel: cell phases. The cell phases are labeled with the numbers 1–5 (1 = early G1 phase; 2 = late G1 phase; 3 = S phase; 4 = G2 phase; 5 = M phase), while 6 indicates the dead cells

4.7.4 Oxygen in a Fine-Grained Simulation of the Tumor Microenvironment

As noted above, the continuum model is computationally efficient and capable of simulating tumors of clinical relevance. On the other hand, the less efficient cell-based simulation is extremely fine-grained and offers a different view of the tumor, one that has the potential to give a glimpse of the transformative, evolutionary events that produce the heterogeneity that is observed in real tumors. We have recently taken steps in this direction, and we have obtained the very first computational snapshots of the tumor microenvironment at the cellular level [47]. While our simulation is not yet sufficiently detailed to actually deliver the promised results on tumor heterogeneity – they still lack the plurality of cell types that populate a real tumor – they already display such basic features of the microenvironment as the large gradients that lead to the formation of ecological niches and ultimately drive the Darwinian evolution of tumor cells [48]. Obviously, one of these important gradients is associated with the local oxygen concentration.

In the combined simulation of Tumorcode and VBL [47], we improved two mean field assumptions of the standalone version of Tumorcode – the VEGF field and the oxygen uptake field – thanks to the availability of the detailed representation of individual cells. The VEGF field was previously extracted from the bulk-tissue tumor or was assumed to be spherically symmetric in the case of the fake tumor. In the combined program, we assume that each cell is a point source for the VEGF and constructs the VEGF field as a superposition of single-cell contributions. The tumor models already integrated in Tumorcode comprise three kinds of tissue: normal, tumor, and necrotic tissue, and each of them has its own oxygen consumption parameters in the Michaelis-Menten equation for the oxygen uptake. In contrast, VBL calculates the oxygen uptake for each cell, and we use this fine-grained information to interpolate a continuous oxygen uptake field which is a more realistic input for the oxygen computation in Tumorcode.

Recently, we used the combined program to study the tumor microenvironment at the angiogenic switch. The angiogenic switch is an important step toward malignancy, since it marks the onset of tumor vascularization [49]. After the angiogenic switch, malignant tumors can invade vessels, spread throughout the body via the blood stream, and metastasize at different locations. This step of the progression is particularly important in the development of cancer and therefore of special interest for the prognosis and therapy of the disease. We performed two experiments: one in analogy with the experimental setup used by Helminger et al. [24] and one that nearly matches the maximum problem size on our current hardware.

Helminger et al. measured the pO2 and pH in human tumor xenografts, utilizing phosphorescence quenching for pO2 and fluorescence ratio imaging for pH. The measurements were done for different blood vessel arrangements. We focused on the topology used for panels c and d of Fig. 2 in [24], which is the measurement along a straight line between the bifurcation of two blood vessels, as illustrated in Fig. 4.13. To recreate this setup in our simulation, we used Tumorcode to build an arteriovenous blood vessel network, searched for a similar bifurcation, seeded the VBL spheroid in between the bifurcation, and started the simulation run. The resulting pO2 gradients along the line between the blood vessels are quantitatively quite similar to the measured gradients of Helminger et al. (see Fig. 4.14 and compare with the corresponding figures in [24]).

Fig. 4.13

Geometry of the measurements of Helminger et al. [24]. The measurements were carried out along an ideal line connecting two points on different branches of a bifurcation. The pO2 was reported as a function of the distance traveled along this line from A to B

Fig. 4.14

pO2 and pH vs. distance traveled along a segment joining two branches of a bifurcation, as in reference [24], at simulated time t = 350 h

In the second experiment, we followed the tumor growth dynamics up to a wall time⁴ of about 1 month, resulting in simulated time of 580 h past the initial seeding of the tumor. Because oxygen and other nutrients are released by blood vessels, the distance of a cell to its nearest vessel is certainly an interesting quantity to look at. Experimentally it would be impossible (or at least very tedious) to quantify the distance of each cell in a tumor to its nearest blood vessel. For computer simulations, this can be made automatic, and it provides us with some intriguing data.

We histogrammed the pO2 for every cell according to the distance to the nearest blood vessel, thus producing a set of empirical probability distributions of pO2 for a set selected distances to the nearest blood vessel. For early time points (380 h past the initial seeding), we find that the median of these distributions decays exponentially vs. distance (see Fig. 4.15), as expected for a spheroid embedded in a homogenous tissue. However, for increasing simulation time (480 h and 580 h past the initial seeding), the medians change, up to a point where they start to increase again with distance. This happens because of the modifications of the blood vessel network and because of the death of many cells which leads to a reduction of the oxygen consumption. In the vascularized tumor mass, we observe cells that are more than 100 μm away from the nearest blood vessel and still are sufficiently oxygenated.

Fig. 4.15

Combined representation of the pO2 values of cells at given distances from nearest blood vessels, for three different time points past the angiogenic switch: blue 380 h, green 480 h, and orange 580 h. For the two earlier timepoints (380 and 480 h), the blue bullets and the green triangles show the median value. For the last time point, the median is shown by an orange line inside a box that marks the positions of the 25th and 75th percentiles. The whiskers represent the 10th and 90th percentiles. It is interesting to note the large widths of the distance distributions

In [47], we have shown that such computer simulations of vascularized multicellular tumor spheroids are in good qualitative agreement with measurements of human tumor xenograft, and we showed that in our particular in silico model, the transport of vascular oxygen results in a continually changing and rugged microenvironment. This means that the niche diversity is large and consequently that the evolutionary pressure is high and leads to a very effective selection of different tumor clones even in small tumors.

4.8 Conclusions

As we have already noted, the numerical simulations do not take everything into account, and yet, it is interesting to observe that on average, they are in quite good agreement with the measurements in [24]. The simulations are driven by model parameters that have been taken from the literature and which have been obtained with different experimental systems and tumor cell types. Whenever experimental measurements were missing, we estimated parameter values from independent biophysical modeling of available data, once again collected in experiments with different tumor systems [44]. Therefore, model parameters have not been tuned to describe the behavior of any specific tumor, and yet we obtain a good agreement of the oxygen concentration with the actual measurements. But shouldn’t there be a measurable specificity of tumor cells and tissue that shows up in the simulations? How can we explain the observed agreement?

One simple answer may be that for all their differences, tumor cells are similar in their average metabolic behavior, as we noted in our derivation of the metabolic law in reference [17] (see Fig. 4.2 in that paper). There, we found that the mean values of metabolic consumption are very effective descriptors of an average metabolic consumption, even though the figure summarizes the behavior of different tumor types. Incidentally, this would also mean that a model of metabolism of cells is all we need to describe the oxygen concentration.

This answer highlights that the agreement between our simulations and observations has been established for the average behavior of the simulations (we have compared the median values to the observations), but a careful observation of Fig. 4.15 shows that the empirical distributions of the distance to the closest vessel are quite wide. These spatial fluctuations are extremely important, actually they are one of the main results of our simulation effort. Indeed, they produce a large niche diversity even in small vascularized solid tumors. This means that already at the early stages of tumor progression, i.e., close to the angiogenic switch, the microenvironment can exert a high evolutionary pressure that drives the Darwinian selection of different clones. Here we stress that while the molecular mechanisms that promote genotypic changes in tumor clones are well-known and characterized, genotypic variation is but one ingredient of tumor evolution, the other important feature being the variability of the environment that supervenes the genome and sets the stage for the evolutionary process. With our computational tool, we can start to explore this Darwinian dynamics in tumors and grasp the role of evolutionary forces in the establishment of more or less aggressive tumor phenotypes.

In the first part of this chapter, we also examined the importance of time fluctuations, whose existence is supported by several experiments; see [8, 25, 50, 51]. Together with the oxygen consumption by cells, they conspire to further limit the penetration of oxygen in the tumor tissue. This may have an important clinical impact, because tumor hypoxia is known to negatively affect radiotherapy [1, 52, 53]. Our model predicts that by blocking the pathophysiological oscillations of oxygen observed in the tumor microcirculation, the oxygen concentrations in the tumor tissue should increase. It is known that the low-frequency rhythms of arterial circulation can be strongly attenuated, or even abolished, after alpha-adrenoreceptor blockade [54, 55]. Alpha blockers are well-tolerated drugs, and they are already used in the clinical setting to treat a variety of disorders such as anxiety, panic, and post-traumatic stress disorders [56,57,58]. Thus, this class of drugs could be used in combination with radiotherapy to transiently improve the oxygenation of the tumor microenvironment and increase the efficacy of radiation treatments.

Such considerations prove that mathematical and numerical approaches to the distribution of oxygen in the tumor microenvironment are more than mere mathematical exercises; they yield new and useful insights on the role of the distribution of blood vessel density and size and on the fluctuations of blood oxygenation and pressure, with implications on both tumor biology and radiotherapy. More generally, these models are not affected by the practical limitations that hamper the experimental collection of quantitative data at appropriate spatial and temporal resolution. For example, with current technologies it is almost impossible to follow the evolution kinetics of individual clones in solid tumors and carry out experiments to explore the space of parameters. Analytic and numerical models can illuminate the basic features of complex biological systems and can uncover novel ones.