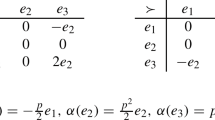On n-ary Generalization of BiHom-Lie Algebras and BiHom-Associative Algebras

Abstract

The aim of this paper is to introduce n-ary BiHom-algebras, generalizing BiHom-algebras. We introduce an alternative concept of BiHom-Lie algebra called BiHom-Lie-Leibniz algebra and study various type of n-ary BiHom-Lie algebras and BiHom-associative algebras. We show that n-ary BiHom-Lie-Leibniz algebra can be represented by BiHom-Lie-Leibniz algebra through fundamental objects. Moreover, we provide some key constructions and study n-ary BiHom-Lie algebras induced by $(n-1)$-ary BiHom-Lie algebra.

5.1 Introduction

The investigations of various q-deformations (quantum deformations) of Lie algebras began a period of rapid expansion in 1980’s stimulated by introduction of quantum groups motivated by applications to the quantum Yang-Baxter equation, quantum inverse scattering methods and constructions of the quantum deformations of universal enveloping algebras of semi-simple Lie algebras. In [2, 10,11,12,13,14,15,16, 21, 22, 31,32,33] various versions of q-deformed Lie algebras appeared in physical contexts such as string theory, vertex models in conformal field theory, quantum mechanics and quantum field theory in the context of q-deformations of infinite-dimensional algebras, primarily the q-deformed Heisenberg algebras, q-deformed oscillator algebras and q-deformed Witt and q-deformed Virasoro algebras, and some interesting q-deformations of the Jacobi identity for Lie algebras in these q-deformed algebras were observed.

Hom-Lie algebras and more general Quasi-Hom-Lie algebras where introduced first by Larsson, Hartwig and Silvestrov in [20], where the general quasi-deformations and discretizations of Lie algebras of vector fields using more general $\sigma$-derivations (twisted derivations) and a general method for construction of deformations of Witt and Virasoro type algebras based on twisted derivations have been developed, initially motivated by the q-deformed Jacobi identities observed for the q-deformed algebras in physics, along with q-deformed versions of homological algebra and discrete modifications of differential calculi. The general abstract quasi-Lie algebras and the subclasses of quasi-Hom-Lie algebras and Hom-Lie algebras as well as their general colored (graded) counterparts have been introduced [20, 27,28,29, 39]. Subsequently, various classes of Hom-Lie admissible algebras have been considered in [34]. In particular, in [34], the Hom-associative algebras have been introduced and shown to be Hom-Lie admissible, that is leading to Hom-Lie algebras using commutator map as new product, and in this sense constituting a natural generalization of associative algebras, as Lie admissible algebras leading to Lie algebras via commutator map as new product. In [34], moreover several other interesting classes of Hom-Lie admissible algebras generalising some classes of non-associative algebras, as well as examples of finite-dimensional Hom-Lie algebras have been described. Since these pioneering works [20, 27,28,29,30, 34], Hom-algebra structures have developed in a popular broad area with increasing number of publications in various directions.

Ternary algebras and more generally n-ary Lie algebras first appeared in Nambu’s generalization of Hamiltonian mechanics, using a ternary generalization of Poisson algebras. The mathematical algebraic foundations of Nambu mechanics have been developed by Takhtajan and Daletskii in [17, 40, 41]. Filippov, in [18] introduced n-Lie algebras, and then Kasymov [23] investigated their properties. This approach uses the interpretation of Jacobi identity expressing the fact that the adjoint map is a derivation. There is also another type of n-ary Lie algebras, in which the n-ary Jacobi identity is the sum over $S_{2n-1}$ instead of $S_3$ in the binary case. One reason for studying such algebras was that n-Lie algebras introduced by Filippov were mostly rigid, and these algebras offered more possibilities to this regard.

Hom-type generalization of n-ary algebras, such as n-Hom-Lie algebras and other n-ary Hom algebras of Lie type and associative type, were introduced in [7], by twisting the identities defining them using a set of linear maps, together with the particular case where all these maps are equal and are algebra morphisms. A way to generate examples of such algebras from non Hom-algebras of the same type is introduced. Further properties, construction methods and examples of n-ary Hom-algebras have been considered in [4,5,6, 24, 25, 42, 45].

In [9], authors looked at Hom-algebras from a category theoretical point of view, constructing a category on which algebras would be Hom-algebras. A generalization of this approach led to the discovery of BiHom-algebras in [19], called BiHom-algebras because the defining identities are twisted by two morphisms instead of only one for Hom-algebras.

The aim of this work is to introduce n-ary generalizations of BiHom-algebras and study their basic properties. Namely, we introduce two types of n-BiHom-Lie algebras, each one of them conserving a part of the properties of n-Lie algebras. We also define totally BiHom-associative and partially BiHom-associative algebras. In Sect. 5.2, we present BiHom-Lie algebras as in [19] and add an alternative definition which is not equivalent but reduces to the same definition in the case of Hom-Lie algebras. We also define two types of n-BiHom-Lie algebras and present their properties. In Sect. 5.3, we introduce n-ary totally BiHom-associative and partially BiHom-associative algebras and generalize to these cases the Yau twisting. In Sect. 5.4, we extend the construction of $(n+1)$-Lie algebras induced by n-Lie algebras (see [1, 4,5,6, 24, 25]) to the case of n-ary BiHom-Lie algebras. Then we look at the conditions under which this construction is possible, in terms of image and kernel of the generalized trace map and the twisting maps.

5.2 BiHom-Lie Algebras and n-BiHom-Lie Algebras

BiHom-algebras are a generalization of Hom-algebras regarding their construction using categories, which was introduced by Caenepeel and Goyvaerts in [9]. All the considered vector spaces are over a field of characteristic 0. Everywhere hereafter, the notation $\widehat{x_i}$ in the arguments of an n-linear map means that $x_i$ is excluded, for example, we write $f\left( {x_1,\ldots ,\widehat{x_i},\ldots ,x_n}\right)$ for $f\left( {x_1,\ldots ,x_{i-1},x_{i+1},\ldots ,x_n}\right)$.

Definition 5.1

([19]) A BiHom-Lie algebra is a vector space A together with a bilinear map $\left[ { \cdot ,\cdot }\right] : A^2 \rightarrow A$ and two linear maps $\alpha ,\beta : A \rightarrow A$ satisfying the following conditions:

• 1. $\alpha \circ \beta = \beta \circ \alpha$.

• 2. $\forall x,y \in A, \alpha \left( {\left[ {x,y}\right] }\right) = \left[ {\alpha (x),\alpha (y)}\right]$ and $\beta \left( {\left[ {x,y}\right] }\right) = \left[ {\beta (x),\beta (y)}\right]$.

• 3. BiHom-skewsymmetry: 

  $$\begin{aligned} \forall x,y \in A, \left[ {\beta (x),\alpha (y)}\right] = - \left[ {\beta (y),\alpha (x)}\right] . \end{aligned}$$

• 4. BiHom-Jacobi identity: 

  $$\begin{aligned} \forall x,y,z \in A, \underset{x,y,z}{\circlearrowleft }\left[ {\beta ^2(x),\left[ {\beta (y),\alpha (z)}\right] }\right] = 0. \end{aligned}$$

One can also define a BiHom-Lie algebra using a generalization of the Jacobi identity under the form stating that the adjoint maps are derivations, we consider the following definition:

Definition 5.2

An BiHom-Lie-Leibniz algebra is a vector space A together with a bilinear map $\left[ { \cdot ,\cdot }\right] : A^2 \rightarrow A$ and two linear maps $\alpha ,\beta : A \rightarrow A$ satisfying the following conditions:

• 1. $\alpha \circ \beta = \beta \circ \alpha$.

• 2. $\forall x,y \in A, \alpha \left( {\left[ {x,y}\right] }\right) = \left[ {\alpha (x),\alpha (y)}\right]$ and $\beta \left( {\left[ {x,y}\right] }\right) = \left[ {\beta (x),\beta (y)}\right]$.

• 3. BiHom-skewsymmetry

  $$\begin{aligned} \forall x,y \in A, \left[ {\beta (x),\alpha (y)}\right] = - \left[ {\beta (y),\alpha (x)}\right] . \end{aligned}$$

• 4. BiHom-Leibniz identity:

  $$\begin{aligned} \forall x,y,z \in A, \left[ {\beta ^2(x),\left[ {\beta (y),\alpha (z)}\right] }\right] = \left[ {\left[ {\beta (x),\alpha (y)}\right] ,\beta ^2(z)}\right] + \left[ {\beta ^2(y),\left[ {\beta (x),\alpha (z)}\right] }\right] . \end{aligned}$$

We also define a generalization of Leibniz algebras, which are a non-skewsymmetric version of Lie algebras, or in other words, algebras in which left multiplication satisfies the Leibniz rule.

Definition 5.3

A BiHom-Leibniz algebra is a vector space A together with a bilinear map $\left[ { \cdot ,\cdot }\right] : A^2 \rightarrow A$ and two linear maps $\alpha ,\beta : A \rightarrow A$ satisfying the following conditions:

• 1. $\alpha \circ \beta = \beta \circ \alpha$.

• 2. $\forall x,y \in A, \alpha \left( {\left[ {x,y}\right] }\right) = \left[ {\alpha (x),\alpha (y)}\right]$ and $\beta \left( {\left[ {x,y}\right] }\right) = \left[ {\beta (x),\beta (y)}\right]$.

• 3. BiHom-Leibniz identity:

  $$\begin{aligned} \forall x,y,z \in A, \left[ {\beta ^2(x),\left[ {\beta (y),\alpha (z)}\right] }\right] = \left[ {\left[ {\beta (x),\alpha (y)}\right] ,\beta ^2(z)}\right] + \left[ {\beta ^2(y),\left[ {\beta (x),\alpha (z)}\right] }\right] . \end{aligned}$$

Example 5.1

We present here some examples of BiHom-Lie-Leibniz algebras. These examples were generated using a computer algebra software. Let A be a 3-dimensional vector space with basis $(e_1,e_2,e_3)$, the following brackets and matrices, defining linear maps in the considered basis, define on A a BiHom-Lie-Leibniz algebra structure:

• 1. $[\alpha ]=\begin{pmatrix}0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0\\ 0 &{} 0 &{} a\end{pmatrix}$ ; $[\beta ]= \begin{pmatrix}b &{} 0 &{} 0 \\ 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 1\end{pmatrix}$ ; $[e_2,e_2]=c_1 e_2$ ; $[e_3,e_1]=c_2 e_1$ ; $[e_i,e_j]=0$ if $(i,j)\ne (2,2),(3,1)$, where $a,b,c_1,c_2 \in \mathbb {K}$.

• 2. $[\alpha ]=\begin{pmatrix}0 &{} 0 &{} 0 \\ 0 &{} a &{} 0\\ 0 &{} 0 &{} a^2\end{pmatrix}$ ; $[\beta ]= \begin{pmatrix}b &{} 0 &{} 0 \\ 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0\end{pmatrix}$ ; $[e_2,e_2]=c e_3$ ; $[e_i,e_j]=0$ if $(i,j)\ne (2,2)$, where $a,b,c \in \mathbb {K}$.

• 3. $[\alpha ]=\begin{pmatrix}0 &{} 0 &{} 0 \\ 0 &{} a &{} 0\\ 0 &{} 0 &{} 1\end{pmatrix}$ ; $[\beta ]= \begin{pmatrix}0 &{} 0 &{} 0 \\ 0 &{} b &{} 0\\ 0 &{} 0 &{} 1\end{pmatrix}$ ; $[e_1,e_1]=c_1 e_1$ ; $[e_1,e_2]=c_2 e_1$ ; $[e_1,e_3]=c_3 e_1$; $[e_2,e_1]=c_4 e_1$; $[e_3,e_1]=c_5 e_1$ ; $[e_i,e_j]=0$ for the remaining pairs (i, j), where $a,b,c_k \in \mathbb {K} ; (1 \le k \le 5)$.

Remark 5.1

The preceding definitions are not equivalent, and give two different classes of algebras. Unlike Lie algebras, such algebras are not skewsymmetric, and thus BiHom-Jacobi and BiHom-Leibniz identities are not equivalent. However, both of them reduce to Lie algebras when the considered morphisms $\alpha$ and $\beta$ are equal to the identity map. Also, if $\alpha$ and $\beta$ are equal and surjective, algebras given by both definitions are multiplicative Hom-Lie algebras.

Remark 5.2

BiHom-Jacobi and BiHom-Leibniz identities are equivalent if one assumes that the bracket is in addition skewsymmetric in the usual sense. Notice that BiHom-skewsymmetry is equivalent in this case to $[\beta (x),\alpha (y)]=[\alpha (x),\beta (y)]$.

Generalizing n-Lie algebras following the same process gives a class of algebra which does not reduce to BiHom-Lie algebras for $n=2$. We use instead a different form for the fundamental identity to construct our generalization, namely:

Definition 5.4

An n-BiHom-Lie algebra is a vector space A, equipped with an n-linear operation $\left[ {\cdot ,\ldots ,\cdot }\right]$ and two linear maps $\alpha$ and $\beta$ satisfying the following conditions:

• 1. $\alpha \circ \beta = \beta \circ \alpha$.

• 2. $\forall x_1,\ldots ,x_n \in A$,

  $$\begin{aligned} \alpha \left( {\left[ {x_1,\ldots ,x_n}\right] }\right) = \left[ {\alpha (x_1),\ldots ,\alpha (x_n)}\right] \text { and } \beta \left( {\left[ {x_1,\ldots ,x_n}\right] }\right) = \left[ {\beta (x_1),\ldots ,\beta (x_n)}\right] . \end{aligned}$$

• 3. BiHom-skewsymmetry: $\forall x_1,\ldots ,x_n \in A,\forall \sigma \in S_n,$

  $$ \left[ {\beta (x_1),\ldots ,\beta (x_{n-1}),\alpha (x_n)}\right] = Sgn(\sigma ) \left[ {\beta (x_{\sigma (1)}),\ldots ,\beta (x_{\sigma (n-1)}),\alpha (x_{\sigma (n)})}\right] . $$

• 4. n-BiHom-Jacobi identity:  $\forall x_1,\ldots ,x_{n-1},y_1,\ldots ,y_n \in A$,

  $$\begin{aligned}&\left[ {\beta ^2(x_1),\ldots ,\beta ^2(x_{n-1}),\left[ {\beta (y_1),\ldots ,\beta (y_{n-1}),\alpha (y_n)}\right] }\right] \\&=\sum _{k=1}^n (-1)^{n-k} \left[ {\beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_k)},\ldots ,\beta ^2(y_n),\left[ {\beta (x_1),\ldots ,\beta (x_{n-1}),\alpha (y_k)}\right] }\right] . \end{aligned}$$

The straightforward generalization of n-Lie algebras leads to a class of n-ary algebras which reduces to BiHom-Lie-Leibniz algebras for $n=2$, we will call them n-BiHom-Lie-Leibniz algebras, and define them by:

Definition 5.5

An n-BiHom-Lie-Leibniz algebra is a vector space A, equipped with an n-linear operation $\left[ {\cdot ,\ldots ,\cdot }\right]$ and two linear maps $\alpha$ and $\beta$ satisfying the following conditions:

• 1. $\alpha \circ \beta = \beta \circ \alpha$.

• 2. $\forall x_1,\ldots ,x_n \in A$,

  $$\begin{aligned} \alpha \left( {\left[ {x_1,\ldots ,x_n}\right] }\right) = \left[ {\alpha (x_1),\ldots ,\alpha (x_n)}\right] \text { and } \beta \left( {\left[ {x_1,\ldots ,x_n}\right] }\right) = \left[ {\beta (x_1),\ldots ,\beta (x_n)}\right] . \end{aligned}$$

• 3. BiHom-skewsymmetry: $\forall x_1,\ldots ,x_n \in A,\forall \sigma \in S_n,$

  $$ \left[ {\beta (x_1),\ldots ,\beta (x_{n-1}),\alpha (x_n)}\right] = Sgn(\sigma ) \left[ {\beta (x_{\sigma (1)}),\ldots ,\beta (x_{\sigma (n-1)}),\alpha (x_{\sigma (n)})}\right] . $$

• 4. BiHom-Nambu identity: $\forall x_1,\ldots ,x_{n-1},y_1,\ldots ,y_n \in A,$

  $$\begin{aligned}&\left[ {\beta ^2(x_1),\ldots ,\beta ^2(x_{n-1}),\left[ {\beta (y_1),\ldots ,\beta (y_{n-1}),\alpha (y_n)}\right] }\right] \\&=\sum _{k=1}^n \left[ {\beta ^2(y_1),\ldots ,\left[ {\beta (x_1),\ldots ,\beta (x_{n-1}),\alpha (y_k)}\right] ,\ldots ,\beta ^2(y_n)}\right] . \end{aligned}$$

Now, we introduce the notions of morphisms, subalgebras and ideals of such algebras. After that we will extend some properties of n-Lie algebras and n-Hom-Lie algebras to this case, some of these properties hold only for one of the classes of algebras defined above.

Let $(A,\left[ {\cdot ,\ldots ,\cdot }\right] ,\alpha ,\beta )$ and $(A,\left[ {\cdot ,\ldots ,\cdot }\right] ,\alpha ',\beta ')$ be n-BiHom-Lie algebras (resp. Leibniz)

Definition 5.6

A linear map $f: A \rightarrow B$ is said to be an n-BiHom-Lie algebra morphism if it satisfies the following properties:

• $\alpha '\circ f = f \circ \alpha$ and $\beta ' \circ f = f \circ \beta$,

• $\forall x_1,\ldots ,x_n \in A, f\left( {\left[ {x_1,\ldots ,x_n}\right] }\right) = \left[ {f(x_1),\ldots ,f(x_n)}\right]$.

Definition 5.7

A subset $S \subseteq A$ is a subalgebra if

$$\begin{aligned} \alpha (S)\subseteq S, \beta (S)\subseteq S\text { and }\forall x_1,\ldots ,x_n \in S, \left[ {x_1,\ldots ,x_n}\right] \in S. \end{aligned}$$

It is said to be an ideal if

$$\begin{aligned} \alpha (S)\subseteq S,\beta (S)\subseteq S \text { and } \forall x_1,\ldots ,x_{n-1} \in A, s \in S, \left[ {x_1,\ldots ,x_{n-1},s}\right] \in S. \end{aligned}$$

5.2.1 Fundamental Objects and Basic Algebra

In n-Lie algebras, the adjoint maps, and more generally actions and representations of an n-Lie algebra are defined by giving $n-1$ elements of the algebra. This leads to the notion of fundamental objects and basic Leibniz algebra [17]. We generalize these constructions to an n-BiHom-Lie-Leibniz algebra, under some conditions on the linear maps $\alpha$ and $\beta$ of this algebra.

Let $\left( {A,\left[ {\cdot ,\ldots ,\cdot }\right] ,\alpha ,\beta }\right)$ be an n-BiHom-Lie-Leibniz algebra such that $\alpha$ is bijective and $\beta$ is surjective. Notice that under these conditions, the algebra’s bracket becomes skewsymmetric in its $(n-1)$ first arguments.

Definition 5.8

Fundamental object of the BiHom-algebra $\left( {A,\left[ {\cdot ,\ldots ,\cdot }\right] ,\alpha ,\beta }\right)$ are elements of the $(n-1)$-th exterior power of A, that is $\wedge ^{n-1}A$.

We also define, for all $X = x_1\wedge ... \wedge x_{n-1}$, $Y = y_1\wedge ... \wedge y_{n-1}$ in $\wedge ^{n-1}A$ and $z\in A$ the following operations:

• The action of fundamental objects on A:

$$\begin{aligned} X \cdot z = ad_X(z) = \left[ {x_1,\ldots ,x_{n-1},z}\right] . \end{aligned}$$

• The multiplication of fundamental objects:

$$\begin{aligned} X \cdot Y =\left[ {X,Y}\right] = \sum _{i=1}^{n-1} \beta ^2\circ \alpha ^{-1}(y_1)\wedge ... \wedge \left[ {x_1,\ldots ,x_{n-1},y_i }\right] \wedge ...\wedge \beta ^2\circ \alpha ^{-1}(y_{n-1}). \end{aligned}$$

• The linear maps $\bar{\alpha },\bar{\beta } : \wedge ^{n-1}A \rightarrow \wedge ^{n-1}A$:

$$\begin{aligned} \bar{\alpha }(X) = \alpha (x_1)\wedge ...\wedge \alpha (x_{n-1}) \text { and } \bar{\beta }(X) = \beta (x_1)\wedge ...\wedge \beta (x_{n-1}). \end{aligned}$$

We extend the preceding definitions to the whole set of fundamental objects by linearity.

The definition above of the multiplication of fundamental objects may seem unnatural, the motivation behind it is that using this definition, one can write the BiHom-Nambu identity in the following form:

$$\begin{aligned} \bar{\beta }^2(X)\cdot \left( {\bar{\beta }(Y) \cdot \alpha (z)}\right) = \left( {\bar{\beta }(X)\cdot \bar{\alpha }(Y)}\right) \cdot \beta ^2(z) + \bar{\beta }^2(Y) \cdot \left( {\bar{\beta }(X) \cdot \alpha (z)}\right) , \end{aligned}$$

for all $X, Y \in \wedge ^{n-1}A$, and for all $z \in A$. The multiplication of fundamental objects satisfies the following property, generalizing a similar property in n-Lie algebras case:

Theorem 5.1

Let $\left( {A,\left[ {\cdot ,\ldots ,\cdot }\right] ,\alpha ,\beta }\right)$ be a n-BiHom-Lie-Leibniz algebra such that $\alpha$ is bijective and $\beta$ is surjective. The set of fundamental objects, which we denote by L(A), equipped with the multiplication of fundamental objects and the maps $\bar{\alpha }$ and $\bar{\beta }$ defined above, is a BiHom-Leibniz algebra.

Proof

Let $X=x_1\wedge ... \wedge x_{n-1}$ and $Y=y_1\wedge ...\wedge y_{n-1}$, then we have:

$$\begin{aligned} \bar{\alpha }\circ \bar{\beta }(X)&= \bar{\alpha }\left( {\beta (x_1)\wedge ... \wedge \beta (x_{n-1})}\right) \\&= \alpha \circ \beta (x_1)\wedge ...\wedge \alpha \circ \beta (x_{n-1})\\&= \beta \circ \alpha (x_1)\wedge ...\wedge \beta \circ \alpha (x_{n-1})\\&= \bar{\beta }\left( {\alpha (x_1)\wedge ...\wedge \alpha (x_{n-1})}\right) =\bar{\beta }\circ \bar{\alpha }(X), \end{aligned}$$

$$\begin{aligned} \bar{\alpha }\left( {\left[ {X,Y}\right] }\right)&=\sum _{i=1}^{n-1}\bar{\alpha }\left( {\beta ^2\circ \alpha ^{-1}(y_1)\wedge ... \wedge X \cdot y_i \wedge ... \wedge \beta ^2\circ \alpha ^{-1}(y_{n-1})}\right) \\&= \sum _{i=1}^{n-1}\left( {\alpha \circ \beta ^2\circ \alpha ^{-1}(y_1)\wedge ... \wedge \alpha (X \cdot y_i) \wedge ... \wedge \alpha \circ \beta ^2\circ \alpha ^{-1}(y_{n-1})}\right) \\&= \sum _{i=1}^{n-1}\left( \beta ^2\circ \alpha ^{-1}(\alpha (y_1))\wedge ... \wedge \left[ {\alpha (x_1),\ldots ,\alpha (x_{n-1}),\alpha (y_i)}\right] \wedge ... \wedge \right. \\&\qquad \left. \wedge \beta ^2\circ \alpha ^{-1}(\alpha (y_{n-1})) \right) = \left[ {\bar{\alpha }(X),\bar{\alpha }(Y)}\right] , \end{aligned}$$

that is $\bar{\alpha }$ is an algebra morphism. One can show, in the same way, that $\bar{\beta }$ is a morphism. For all $X=x_1\wedge ... \wedge x_{n-1}$, $Y=y_1\wedge ... \wedge y_{n-1}$ and $Z=z_1\wedge ... \wedge z_{n-1}$, we have

$$\begin{aligned}&\left[ {\bar{\beta }^2(X),\left[ {\bar{\beta }(Y),\bar{\alpha }(Z)}\right] }\right] \\&= \sum _{i=1}^{n-1} \left[ {\bar{\beta }^2(X), \left( {\beta ^2(z_1)\wedge ...\wedge \left[ {\beta (y_1),\ldots ,\beta (y_{n-1}),\alpha (z_i)}\right] \wedge ...\wedge \beta ^2(z_{n-1}) }\right) }\right] \\&= \sum _{i=1}^{n-1} \sum _{j=1}^{i-1} \big (\beta ^2\circ \alpha ^{-1}\circ \beta ^2(z_1)\wedge ...\wedge \beta ^2(X\cdot z_j\big )\wedge \\&\qquad \wedge ...\wedge \beta ^2\circ \alpha ^{-1}\left( {\left[ {\beta (y_1),\ldots ,\beta (y_{n-1}),\alpha (z_i)}\right] }\right) \wedge ...\wedge \beta ^2\circ \alpha ^{-1}\circ \beta ^2(z_{n-1}) \big ) \\&+ \sum _{i=1}^{n-1} \sum _{j=i+1}^{n-1} \big ( \beta ^2\circ \alpha ^{-1}\circ \beta ^2(z_1)\wedge ...\wedge \beta ^2\circ \alpha ^{-1}\left( {\left[ {\beta (y_1),\ldots ,\beta (y_{n-1}),\alpha (z_i)}\right] }\right) \\&\qquad \wedge ...\wedge \beta ^2(X\cdot z_j)\wedge ...\wedge \beta ^2\circ \alpha ^{-1}\circ \beta ^2(z_{n-1}) \big )\\&+ \sum _{i=1}^{n-1} \big ( \beta ^2\circ \alpha ^{-1}\circ \beta ^2(z_1)\wedge ...\wedge \bar{\beta }^2\left( {X}\right) \cdot \left[ {\beta (y_1),\ldots ,\beta (y_{n-1}),\alpha (z_i)}\right] \wedge \\&\qquad \wedge ...\wedge \beta ^2\circ \alpha ^{-1}\circ \beta ^2(z_{n-1}) \big ) \\&= \sum _{i=1}^{n-1} \sum _{j=1}^{i-1} \big ( \beta ^2\circ \alpha ^{-1}\circ \beta ^2(z_1)\wedge ...\wedge \beta ^2(X\cdot z_j)\wedge ...\wedge \\&\qquad \wedge \beta ^2\circ \alpha ^{-1}\left( {\left[ {\beta (y_1),\ldots ,\beta (y_{n-1}),\alpha (z_i)}\right] }\right) \wedge ...\wedge \beta ^2\circ \alpha ^{-1}\circ \beta ^2(z_{n-1}) \big ) \\&- \sum _{i=1}^{n-1} \sum _{j=1}^{i-1} \big ( \beta ^2\circ \alpha ^{-1}\circ \beta ^2(z_1)\wedge ...\wedge \beta ^2(X\cdot z_j)\wedge ...\wedge \\&\qquad \wedge \beta ^2\circ \alpha ^{-1}\left( {\left[ {\beta (y_1),\ldots ,\beta (y_{n-1}),\alpha (z_i)}\right] }\right) \wedge ...\wedge \beta ^2\circ \alpha ^{-1}\circ \beta ^2(z_{n-1}) \big ) \\&+\sum _{i=1}^{n-1} \left( {\beta ^2\circ \alpha ^{-1}\circ \beta ^2(z_1)\wedge ...\wedge \bar{\beta }^2\left( {X}\right) \cdot \left( {\bar{\beta }(Y) \cdot \alpha (z_i)}\right) \wedge ...\wedge \beta ^2\circ \alpha ^{-1}\circ \beta ^2(z_{n-1}) }\right) \\&= \sum _{i=1}^{n-1} \left( {\beta ^2\circ \alpha ^{-1}\circ \beta ^2(z_1)\wedge ...\wedge \bar{\beta }^2\left( {X}\right) \cdot \left( {\bar{\beta }(Y) \cdot \alpha (z_i)}\right) \wedge ...\wedge \beta ^2\circ \alpha ^{-1}\circ \beta ^2(z_{n-1}) }\right) \\&= \sum _{i=1}^{n-1} \left( {\beta ^2\circ \alpha ^{-1}\circ \beta ^2(z_1)\wedge ...\wedge \left( {\bar{\beta }(X) \cdot \bar{\alpha }(Y)}\right) \cdot \beta ^2\left( {z_i}\right) \wedge ...\wedge \beta ^2\circ \alpha ^{-1}\circ \beta ^2(z_{n-1}) }\right) \\&+ \sum _{i=1}^{n-1} \left( {\beta ^2\circ \alpha ^{-1}\circ \beta ^2(z_1)\wedge ...\wedge \bar{\beta }^2\left( {Y}\right) \cdot \left( {\bar{\beta }(X) \cdot \alpha (z_i)}\right) \wedge ...\beta ^2\circ \alpha ^{-1}\circ \wedge \beta ^2(z_{n-1}) }\right) \\&= \left[ {\left[ {\bar{\beta }(X),\bar{\alpha }(Y)}\right] ,\bar{\beta }^2(Z)}\right] + \left[ {\bar{\beta }^2(Y),\left[ {\bar{\beta }(X),\bar{\alpha }(Z)}\right] }\right] . \end{aligned}$$

   $\square$

Although the multiplication of fundamental objects needs not to be skewsymmetric, it yields a BiHom-Leibniz-Lie algebra structure on the set of $ad_X$. Namely:

Proposition 5.1

Suppose that both $\alpha$ and $\beta$ are bijective. The image of $ad : L(A) \rightarrow End(A)$, that is $F(A)=\{ ad_X, X\in L(A) \}$, together with the bracket

$$\begin{aligned} \left[ {ad_X,ad_Y}\right] =(\beta ad_X \alpha ^{-1} ad_Y \alpha \beta ^{-1} - \beta ^2 \alpha ^{-1} ad_Y \beta ^{-2} \alpha ad_X) \alpha \beta ^{-2}, \end{aligned}$$

and the structure maps:

$$\begin{aligned} \tilde{\alpha }(ad_X)=\alpha ad_X \alpha ^{-1}, \quad \tilde{\beta }(ad_X)=\beta ad_X \beta ^{-1}, \end{aligned}$$

is a BiHom-Leibniz-Lie algebra.

Proof

Since ad is linear, F(A) is a vector subspace of End(A), moreover, it is sufficient to prove our statement for $X=x_1\wedge ... \wedge x_{n-1}$, $Y=y_1\wedge .... \wedge y_{n-1}$ and extend by linearity. for all $z \in A$, we have:

$$\begin{aligned} ad_{\bar{\alpha }(X)}(z)&= \left[ {\alpha (x_1),\ldots ,\alpha (x_{n-1}),z}\right] \\&=\left[ {\alpha (x_1),\ldots ,\alpha (x_{n-1}),\alpha (\alpha ^{-1}(z))}\right] \\&= \alpha \left( {\left[ {x_1,\ldots ,x_{n-1},\alpha ^{-1}(z)}\right] }\right) \\&=\alpha (ad_X(\alpha ^{-1}(z)))\\&= \alpha ad_X \alpha ^{-1} (z). \end{aligned}$$

The same goes for $ad_{\bar{\beta }(X)}$. We also have:

$$\begin{aligned} ad_{X\cdot Y}(z)&= (X\cdot Y) \cdot z\\&=(\bar{\beta }(\bar{\beta }^{-1}(X))\cdot \bar{\alpha }(\bar{\alpha }^{-1}(Y))) \cdot \beta ^2(\beta ^{-2}(z)) \\&= \bar{\beta }^2(\bar{\beta }^{-1}(X) ) \cdot (\bar{\beta }(\bar{\alpha }^{-1}(Y))\cdot \alpha (\beta ^{-2}(z)))\\&\quad - \bar{\beta }^2(\bar{\alpha }^{-1}(Y)) \cdot (\bar{\beta }(\bar{\beta }^{-1}(X)) \cdot \alpha (\beta ^{-2}(z)) )\\&= \bar{\beta }(X) \cdot (\bar{\beta }(\bar{\alpha }^{-1}(Y))\cdot \alpha (\beta ^{-2}(z))) - \bar{\beta }^2(\bar{\alpha }^{-1}(Y)) \cdot (X \cdot \alpha (\beta ^{-2}(z)) )\\&= ad_{\bar{\beta }(X)} \big ( ad_{\bar{\beta }(\bar{\alpha }^{-1}(Y))}(\alpha (\beta ^{-2}(z))) \big ) - ad_{\bar{\beta }^2(\bar{\alpha }^{-1}(Y))} \big ( ad_X (\alpha (\beta ^{-2}(z))) \big )\\&=\left( {ad_{\bar{\beta }(X)} \circ ad_{\bar{\beta }\circ \bar{\alpha }^{-1}(Y)}\circ \alpha \circ \beta ^{-2} - ad_{\bar{\beta }^2\circ \bar{\alpha }^{-1}(Y)} \circ ad_X \circ \alpha \circ \beta ^{-2}}\right) (z). \end{aligned}$$

Using the formulas for $ad_{\bar{\alpha }(X)}$ and $ad_{\bar{\beta }(X)}$, we get:

$$\begin{aligned} ad_{X\cdot Y}&=ad_{\bar{\beta }(X)} \circ ad_{\bar{\beta }\circ \bar{\alpha }^{-1}(Y)}\circ \alpha \circ \beta ^{-2} - ad_{\bar{\beta }^2\circ \bar{\alpha }^{-1}(Y)} \circ ad_X \circ \alpha \circ \beta ^{-2}\\&= \beta \circ ad_{X}\circ \beta ^{-1} \circ \beta \circ \alpha ^{-1} ad_{Y}\circ \alpha \circ \beta ^{-1} \alpha \circ \beta ^{-2} \\&\quad - \beta ^2 \circ \alpha ^{-1} \circ ad_{Y} \circ \beta ^{-2} \circ \alpha \circ ad_X \circ \alpha \circ \beta ^{-2} \\&= \left( {\beta \circ ad_{X}\circ \alpha ^{-1} ad_{Y}\circ \alpha \circ \beta ^{-1} - \beta ^2 \circ \alpha ^{-1} \circ ad_{Y} \circ \beta ^{-2} \circ \alpha \circ ad_X}\right) \circ \alpha \circ \beta ^{-2}\\&= \left[ {ad_X , ad_Y}\right] . \end{aligned}$$

That is, ad is an algebra morphism from L(A) on F(A). We only have BiHom-skewsymmetry left to show:

$$\begin{aligned} \left[ \tilde{\beta }(ad_X)\right.&\!\left. ,\tilde{\alpha }(ad_Y)\right] = \beta \circ \beta \circ ad_{X}\circ \beta ^{-1} \circ \alpha ^{-1}\circ \alpha \circ ad_{Y}\circ \alpha ^{-1}\circ \alpha \circ \beta ^{-1}\circ \alpha \circ \beta ^{-2}\\&\quad - \beta ^2 \circ \alpha ^{-1} \circ \alpha \circ ad_{Y}\circ \alpha ^{-1} \circ \beta ^{-2} \circ \alpha \circ \beta ad_X \circ \beta ^{-1}\circ \alpha \circ \beta ^{-2}\\&= \left( {\beta ^2 \circ ad_{X}\circ \beta ^{-1} \circ ad_{Y}\circ \beta ^{-1} - \beta ^2 \circ ad_{Y} \circ \beta ^{-1} ad_X \circ \beta ^{-1}}\right) \circ \alpha \circ \beta ^{-2}. \end{aligned}$$

On the other hand, we have:

$$\begin{aligned} \left[ {\tilde{\beta }(ad_Y),\tilde{\alpha }(ad_X)}\right]&= \beta \circ \beta \circ ad_{Y}\circ \beta ^{-1}\circ \alpha ^{-1} \circ \alpha \circ ad_{X}\circ \alpha ^{-1}\circ \alpha \circ \beta ^{-1} \circ \alpha \circ \beta ^{-2}\\&\quad - \beta ^2 \circ \alpha ^{-1} \circ \alpha \circ ad_{X}\circ \alpha ^{-1} \circ \alpha \circ \beta ^{-2} \circ \beta \circ ad_Y\circ \beta ^{-1} \circ \alpha \circ \beta ^{-2}\\&= \left( {\beta ^2 \circ ad_{Y}\circ \beta ^{-1}\circ ad_{X}\circ \beta ^{-1} - \beta ^2 \circ ad_{X}\circ \beta ^{-1}\circ ad_Y\circ \beta ^{-1}}\right) \circ \\&\qquad \circ \alpha \circ \beta ^{-2}\\&=- \left( {\beta ^2 \circ ad_{X}\circ \beta ^{-1} \circ ad_{Y}\circ \beta ^{-1} - \beta ^2 \circ ad_{Y} \circ \beta ^{-1} ad_X \circ \beta ^{-1}}\right) \circ \\&\qquad \circ \alpha \circ \beta ^{-2}\\&= - \left[ {\tilde{\beta }(ad_X),\tilde{\alpha }(ad_Y)}\right] , \end{aligned}$$

which completes the proof.    $\square$

5.2.2 Algebra Twisting

The following result gives a method to construct BiHom-Lie algebras, and more generally n-BiHom-Lie algebras, starting from a Lie or n-Lie algebra and two commuting algebra endomorphisms. It generalizes results from [7, 44] for Hom-algebras.

Theorem 5.2

Let $(A,\left[ {\cdot ,\ldots ,\cdot }\right] )$ be an n-Lie algebra, and let $\alpha ,\beta : A \rightarrow A$ be algebra morphisms such that $\alpha \circ \beta = \beta \circ \alpha$. The algebra $(A, \left[ {\cdot ,\ldots ,\cdot }\right] _{\alpha \beta },\alpha ,\beta )$, where $\left[ {\cdot ,\ldots ,\cdot }\right] _{\alpha \beta }$ is defined by

$$\begin{aligned} \left[ {x_1,\ldots ,x_n}\right] _{\alpha \beta } = \left[ {\alpha (x_1),\ldots ,\alpha (x_{n-1}),\beta (x_n)}\right] , \end{aligned}$$

is an n-BiHom-Lie algebra.

Proof

The maps $\alpha$ and $\beta$ commute, by hypothesis, we show that they are algebra morphisms, for all $x_1,\ldots ,x_n \in A$, we have:

$$\begin{aligned} \alpha \left( {\left[ {x_1,\ldots ,x_n}\right] _{\alpha \beta }}\right)&= \alpha \left( {\left[ {\alpha (x_1),\ldots ,\alpha (x_{n-1}),\beta (x_n)}\right] }\right) \\&= \left[ {\alpha ^2(x_1),\ldots ,\alpha ^2(x_{n-1}),\alpha \circ \beta (x_n)}\right] \\&=\left[ {\alpha ^2(x_1),\ldots ,\alpha ^2(x_{n-1}),\beta \circ \alpha (x_n)}\right] \\&=\left[ {\alpha (x_1),\ldots ,\alpha (x_n)}\right] _{\alpha \beta }. \end{aligned}$$

One can prove, in a very similar way, that $\beta$ is also a morphism. We have also:

$$\begin{aligned}&\left[ {\beta (x_{\sigma (1)}),\ldots ,\beta (x_{\sigma (n-1)}),\alpha (x_{\sigma (n)})}\right] _{\alpha \beta }\\&\qquad \qquad = \left[ {\alpha \circ \beta (x_{\sigma (1)}),\ldots ,\alpha \circ \beta (x_{\sigma (n-1)}),\beta \circ \alpha (x_{\sigma (n)})}\right] \\&\qquad \qquad = \alpha \circ \beta \left( {\left[ {x_{\sigma (1)},\ldots ,x_{\sigma (n)}}\right] }\right) \\&\qquad \qquad = Sgn(\sigma ) \alpha \circ \beta \left( {\left[ {x_1,\ldots ,x_n}\right] }\right) \\&\qquad \qquad = Sgn(\sigma ) \left[ {\alpha \circ \beta (x_{1}),\ldots ,\alpha \circ \beta (x_{n-1}),\beta \circ \alpha (x_{n})}\right] \\&\qquad \qquad =Sgn(\sigma ) \left[ {\beta (x_1),\ldots ,\beta (x_{n-1}),\alpha (x_n)}\right] _{\alpha \beta }. \end{aligned}$$

For all $x_1,\ldots ,x_{n-1},y_1,\ldots ,y_n \in A$, we have:

$$\begin{aligned}&\left[ {\beta ^2(x_1),\ldots ,\beta ^2(x_{n-1}),\left[ {\beta (y_1),\ldots ,\beta (y_{n-1}),\alpha (y_n)}\right] _{\alpha \beta }}\right] _{\alpha \beta }\\ =&\left[ {\alpha \circ \beta ^2(x_1),\ldots ,\alpha \circ \beta ^2(x_{n-1}),\beta \left( {\left[ {\alpha \circ \beta (y_1),\ldots ,\alpha \circ \beta (y_{n-1}),\beta \circ \alpha (y_n)}\right] }\right) }\right] \\ =\,&\alpha \circ \beta ^2\left( {\left[ {x_1,\ldots ,x_{n-1},\left[ {y_1,\ldots ,y_n}\right] }\right] }\right) \\ =&\sum _{k=1}^n \alpha \circ \beta ^2\left( {\left[ {y_1,\ldots ,\left[ {x_1,\ldots ,x_{n-1},y_k}\right] ,\ldots ,y_n}\right] }\right) \\ =&\sum _{k=1}^n (-1)^{n-k} \alpha \circ \beta ^2\left( {\left[ {y_1,\ldots ,\widehat{y_k},\ldots ,y_n,\left[ {x_1,\ldots ,x_{n-1},y_k}\right] }\right] }\right) \\ =&\sum _{k=1}^n (-1)^{n-k} \left[ {\alpha \circ \beta ^2(y_1),\ldots ,\widehat{\alpha \circ \beta ^2(y_k)},\ldots ,\alpha \circ \beta ^2(y_n),\alpha \circ \beta ^2\left( {\left[ {x_1,\ldots ,x_{n-1},y_k}\right] }\right) }\right] \\ =&\sum _{k=1}^n (-1)^{n-k} \left[ \alpha \circ \beta ^2(y_1),\ldots ,\widehat{\alpha \circ \beta ^2(y_k)},\ldots ,\alpha \circ \beta ^2(y_n), \right. \\&\qquad \beta \left( {\left[ {\alpha \circ \beta (x_1),\ldots ,\alpha \circ \beta (x_{n-1}),\beta \circ \alpha (y_k)}\right] }\right) \Big ] \\ =&\sum _{k=1}^n (-1)^{n-k} \left[ {\beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_k)},\ldots ,\beta ^2(y_n),\left[ {\beta (x_1),\ldots ,\beta (x_{n-1}),\alpha (y_k)}\right] _{\alpha \beta }}\right] _{\alpha \beta }, \end{aligned}$$

which completes the proof.    $\square$

Example 5.2

We consider the 4-dimensional 3-Lie algebra defined with respect to a basis $(e_1,e_2,e_3,e_4)$, by:

$$\begin{aligned}{}[e_1,e_2,e_3]=e_4 ; [e_1,e_2,e_4]=e_3 ; [e_1,e_3,e_4]=e_2 ; [e_2,e_3,e_4]=e_1. \end{aligned}$$

We have two morphisms $\alpha$, $\beta$ of this algebra defined, with respect to the same basis, by:

$$ [\alpha ]=\begin{pmatrix}-1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} -1 \end{pmatrix} ; [\beta ]= \begin{pmatrix} 0 &{} 0 &{} 0 &{} -1 \\ 0 &{} 0 &{} -1 &{} 0 \\ 0 &{} -1 &{} 0 &{} 0 \\ 1 &{} 0 &{} 0 &{} 0 \end{pmatrix}. $$

One can easily check that $\alpha$ and $\beta$ commute, then one may to construct a n-BiHom-Lie algebra using Theorem 5.2, we get the following bracket:

$$\begin{aligned}{}[e_1,e_2,e_1]&= - e_3 ; [e_1,e_2,e_2]=e_4 ; [e_1,e_3,e_1]=-e_2 ; [e_1,e_3,e_3]=-e_4 ; \\ [e_1,e_4,e_2]&=e_2 ; [e_1,e_4,e_3]=e_3; [e_2,e_1,e_1]=e_3; [e_2,e_1,e_2]=-e_4 ; \\ [e_2,e_3,e_1]&=e_1 ; [e_2,e_3,e_4]=-e_4 ; [e_2,e_4,e_2]=-e_1 ; [e_2,e_4,e_4]=e_3 ; \\ [e_3,e_1,e_1]&=e_2 ; [e_3,e_1,e_3]=e_4 ; [e_3,e_2,e_1]=-e_1 ; [e_3,e_2,e_4]=e_4 ; \\ [e_3,e_4,e_3]&=e_1 ; [e_3,e_4,e_4]=e_2 ; [e_4,e_1,e_2]=-e_2 ; [e_4,e_1,e_3]=-e_3 ; \\ [e_4,e_2,e_2]&=e_1 ; [e_4,e_2,e_4]=-e_3 ; [e_4,e_3,e_3]=-e_1 ; [e_4,e_3,e_4]=-e_2 ; \end{aligned}$$

5.3 Associative Type n-ary BiHom-Algebras

In this section, we present generalizations of n-ary algebras of associative type, namely totally BiHom-associative and partially BiHom-associative algebras, we also give a generalization of the Yau twist corresponding to these structures. These algebras also generalize the n-ary Hom-algebra of associative type introduced in [7].

Definition 5.9

An n-ary totally BiHom-associative algebra is a vector space A together with an n-linear map $m: A^n \rightarrow A$ and two linear maps $\alpha$, $\beta$ satisfying the following conditions:

• $\alpha \circ \beta = \beta \circ \alpha$.

• $\alpha \left( {m\left( {x_1,\ldots ,x_n}\right) }\right) = m\left( {\alpha \left( {x_1}\right) ,\ldots ,\alpha \left( {x_n}\right) }\right) , \forall x_1,\ldots ,x_n \in A$.

• $\beta \left( {m\left( {x_1,\ldots ,x_n}\right) }\right) = m\left( {\beta \left( {x_1}\right) ,\ldots ,\beta \left( {x_n}\right) }\right) , \forall x_1,\ldots ,x_n \in A$.

• Total BiHom-associativity: $\forall x_1,\ldots ,x_{2n-1}\in A, \forall i,j: 1\le i,j \le n$

  $$\begin{aligned} m&\left( {\alpha (x_1),\ldots ,\alpha (x_{i-1}),m(x_i,\ldots ,x_{n+i-1}),\beta (x_{n+i}),\ldots ,\beta (x_{2n-1})}\right) \\&= m\left( {\alpha (x_1),\ldots ,\alpha (x_{j-1}),m(x_j,\ldots ,x_{n+j-1}),\beta (x_{n+j}),\ldots ,\beta (x_{2n-1})}\right) . \end{aligned}$$

Definition 5.10

An n-ary partially BiHom-associative algebra is a vector space A together with an n-linear map $m: A^n \rightarrow A$ and two linear maps $\alpha$, $\beta$ satisfying the following conditions:

• $\alpha \circ \beta = \beta \circ \alpha$.

• $\alpha \left( {m\left( {x_1,\ldots ,x_n}\right) }\right) = m\left( {\alpha \left( {x_1}\right) ,\ldots ,\alpha \left( {x_n}\right) }\right) , \forall x_1,\ldots ,x_n \in A$.

• $\beta \left( {m\left( {x_1,\ldots ,x_n}\right) }\right) = m\left( {\beta \left( {x_1}\right) ,\ldots ,\beta \left( {x_n}\right) }\right) , \forall x_1,\ldots ,x_n \in A$.

• Partial BiHom-associativity: $\forall x_1,\ldots ,x_{2n-1}\in A,$

  $$\begin{aligned} \sum _{i=1}^n m\left( {\alpha (x_1),\ldots ,\alpha (x_{i-1}),m(x_i,\ldots ,x_{n+i-1}),\beta (x_{n+i}),\ldots ,\beta (x_{2n-1})}\right) =0. \end{aligned}$$

Remark 5.3

In the definitions above, the particular case where $\alpha =\beta$ leads us to the definitions of n-ary totally Hom-associative (resp. partially Hom-associative) algebras. Choosing $\alpha =\beta =Id_A$ gives the definitions of n-ary totally associative (resp. partially associative) algebras.

Now, we introduce as for n-Lie algebras, a generalization of the Yau twist, allowing us to construct n-ary BiHom-algebra of associative type given an n-ary algebra of associative type and two linear maps satisfying some conditions.

Proposition 5.2

Let (A, m) be an n-ary totally associative (resp. partially associative) algebra, and let $\alpha$, $\beta$ be two algebra endomorphisms of A satisfying $\alpha \circ \beta = \beta \circ \alpha$. We define $m_{\alpha ,\beta }:A^n \rightarrow A$ by:

$$\begin{aligned} m_{\alpha ,\beta }\left( {x_1,\ldots ,x_n}\right) =m\left( {\alpha ^{n-1}(x_1),\alpha ^{n-2}\circ \beta (x_2),\ldots ,\alpha \circ \beta ^{n-2}(x_{n-1}),\beta ^{n-1}(x_n)}\right) . \end{aligned}$$

Then $(A,m_{\alpha ,\beta },\alpha ^{n-1},\beta ^{n-1})$, which we will denote by $A_{\alpha ,\beta }$, is an n-ary totally (resp. partially) BiHom-associative algebra.

Proof

The first three conditions come down from $\alpha$ and $\beta$ being commuting algebra morphisms, we only have to show the total (resp. partial) BiHom-associativity. Let $x_1,\ldots ,x_{2n-1} \in A$, we have, for $i : 1\le i \le n$:

$$\begin{aligned} m_{\alpha ,\beta }&\left( {\alpha ^{n-1}(x_1),\ldots ,\alpha ^{n-1}(x_{i-1}),m_{\alpha ,\beta }(x_i,\ldots ,x_{i+n-1}),\beta ^{n-1}(x_{n+i}),\ldots ,\beta ^{n-1}(x_{2n-1}) }\right) \\&=m\left( \alpha ^{n-1}\circ \alpha ^{n-1}(x_1),\ldots ,\alpha ^{n-i+1}\circ \beta ^{i-2}\circ \alpha ^{n-1}(x_{i-1}),\alpha ^{n-i}\circ \beta ^{i-1}\circ \right. \\&\quad \circ m\left( \alpha ^{n-1}(x_i),\ldots ,\beta ^{n-1}(x_{i+n-1}) \right) ,\alpha ^{n-i-1}\circ \beta ^{i}\circ \beta ^{n-1}(x_{n+i}),\ldots ,\times \\&\qquad \times \beta ^{n-1}\circ \beta ^{n-1}(x_{2n-1}) \big )\\&= m( \alpha ^{2n-2}(x_1),\ldots ,\alpha ^{2n-i}\circ \beta ^{i-2}(x_{i-1}),m(\alpha ^{2n-i-1}\circ \beta ^{i-1}(x_i),\ldots ,\times \\&\qquad \times \alpha ^{n-i}\circ \beta ^{n+i-2}(x_{n+i-1}) ), \alpha ^{n-i-1}\circ \beta ^{n+i-1}(x_{n+i}),\ldots ,\beta ^{2n-2}(x_{2n-1}) ). \end{aligned}$$

For $j\ne i$, we get, following the same process:

$$\begin{aligned} m_{\alpha ,\beta }&\left( \alpha ^{n-1}(x_1),\ldots ,\alpha ^{n-1}(x_i),\ldots ,\alpha ^{n-1}(x_{i-1}),m_{\alpha ,\beta }(x_i,\ldots ,x_{i+n-1}),\times \right. \\&\quad \left. \times \beta ^{n-1}(x_{n+i}),\ldots ,\beta ^{n-1}(x_{2n-1}) \right) \\&= m( \alpha ^{2n-2}(x_1),\ldots ,\alpha ^{2n-j-1}\circ \beta ^{j-1}(x_j),\ldots ,\alpha ^{2n-j}\circ \beta ^{j-2}(x_{j-1}),\times \\&\quad \times m(\alpha ^{2n-j-1}\circ \beta ^{j-1}(x_j),\ldots ,\alpha ^{n-j}\circ \beta ^{n+j-2}(x_{n+j-1}) ),\times \\&\quad \times \alpha ^{n-j-1}\circ \beta ^{n+j-1}(x_{n+j}) ,\ldots ,\beta ^{2n-2}(x_{2n-1}) ). \end{aligned}$$

Using total associativity of m, we get:

$$\begin{aligned} m&\left( \alpha ^{2n-2}(x_1),\ldots ,\alpha ^{2n-j-1}\circ \beta ^{j-1}(x_j),\ldots ,\alpha ^{2n-j}\circ \beta ^{j-2}(x_{j-1}),\right. \times \\&\times \left. m\left( \alpha ^{2n-j-1}\circ \beta ^{j-1}(x_j),\ldots ,\alpha ^{n-j}\circ \beta ^{n+j-2}(x_{n+j-1}) \right) , \alpha ^{n-j-1}\circ \beta ^{n+j-1}(x_{n+j})\times \right. \\&\left. \times ,\ldots ,\beta ^{2n-2}(x_{2n-1}) \right) = \\&m( \alpha ^{2n-2}(x_1),\ldots ,\alpha ^{2n-i}\circ \beta ^{i-2}(x_{i-1}),m(\alpha ^{2n-i-1}\circ \beta ^{i-1}(x_i),\ldots ,\times \\&\times \alpha ^{n-i}\circ \beta ^{n+i-2}(x_{n+i-1}) ), \alpha ^{n-i-1}\circ \beta ^{n+i-1}(x_{n+i}),\ldots ,\beta ^{2n-2}(x_{2n-1}) ) = \\&m_{\alpha ,\beta }\left( {\alpha ^{n-1}(x_1),\ldots ,\alpha ^{n-1}(x_{i-1}),m_{\alpha ,\beta }(x_i,\ldots ,x_{i+n-1}),\beta ^{n-1}(x_{n+i}),\ldots ,\beta ^{n-1}(x_{2n-1}) }\right) . \end{aligned}$$

Let us show the partial associativity condition for the relevant case. For $x_1,\ldots ,x_{2n-1} \in A$, we have:

$$\begin{aligned} \sum _{i=1}^n m_{\alpha ,\beta }&\left( {\alpha ^{n-1}(x_1),\ldots ,\alpha ^{n-1}(x_{i-1}),m_{\alpha ,\beta }(x_i,\ldots ,x_{i+n-1}),\beta ^{n-1}(x_{n+i}),\ldots ,\beta ^{n-1}(x_{2n-1}) }\right) \\&=\sum _{i=1}^n m( \alpha ^{n-1}\circ \alpha ^{n-1}(x_1),\ldots ,\alpha ^{n-i+1}\circ \beta ^{i-2}\circ \alpha ^{n-1}(x_{i-1}),\alpha ^{n-i}\circ \beta ^{i-1}\circ \\&\quad \circ m(\alpha ^{n-1}(x_i),\ldots ,\beta ^{n-1}(x_{i+n-1}) ),\alpha ^{n-i-1}\circ \beta ^{i}\circ \beta ^{n-1}(x_{n+i}),\ldots ,\times \\&\quad \times \beta ^{n-1}\circ \beta ^{n-1}(x_{2n-1}) )\\&= \sum _{i=1}^n m( \alpha ^{2n-2}(x_1),\ldots ,\alpha ^{2n-i}\circ \beta ^{i-2}(x_{i-1}),m(\alpha ^{2n-i-1}\circ \beta ^{i-1}(x_i),\ldots ,\times \\&\times \alpha ^{n-i}\circ \beta ^{n+i-2}(x_{n+i-1}) ), \alpha ^{n-i-1}\circ \beta ^{n+i-1}(x_{n+i}),\ldots ,\beta ^{2n-2}(x_{2n-1}) ) =0, \end{aligned}$$

which completes the proof    $\square$

The definitions and result above can be extended to some variants of n-ary algebras of associative type. Namely n-ary weak totally associative algebras, where the total associativity holds only for $i=1$, $j=n$ in the definition above, and n-ary alternate partially associative algebras, where the the terms in the sum defining partial associativity are multiplied by $(-1)^i$.

5.4 $(n+1)$-BiHom-Lie Algebras Induced by n-BiHom-Lie Algebras

The aim of this section is to extend, to n-BiHom-Lie algebras, the construction of $(n+1)$-Hom-Lie algebras from n-Hom-Lie algebras introduced in [6], and to see under which conditions such a generalization is possible. First, we give some definitions and lemmas allowing to reach our goal.

Definition 5.11

([5, 6]) Let A be a vector space, $\phi : A^n \rightarrow A$ be an n-linear map and $\tau$ be a linear form. We define the $(n+1)$-linear map $\phi _\tau$ by:

$$\begin{aligned} \forall x_1,\ldots ,x_{n+1} \in A, \phi _\tau \left( {x_1,\ldots ,x_{n+1}}\right) = \sum _{i=1}^{n+1} (-1)^{i-1} \tau (x_i)\phi \left( {x_1,\ldots ,\widehat{x_i},\ldots ,x_{n+1}}\right) . \end{aligned}$$

As in the case of n-Lie or n-Hom-Lie algebras, we focus on linear forms $\tau$ satisfying a generalization of the properties of the trace of matrices, namely, we consider the following definition:

Definition 5.12

Let A be a vector space, $\phi : A^n \rightarrow A$ be an n-linear map, let $\tau$ be a linear form and $\alpha ,\beta : A \rightarrow A$ be linear maps. The map $\tau$ is said to be an $(\alpha ,\beta )$-twisted $\phi$-trace if if satisfies the following condition:

$$\begin{aligned} \forall x_1,\ldots ,x_n \in A, \tau \left( {\phi \left( {\beta (x_1),\ldots ,\beta (x_{n-1}),\alpha (x_n)}\right) }\right) = 0. \end{aligned}$$

If the maps $\phi$, $\alpha$ and $\beta$ above are clear from the context, we will simply refer to such linear forms by twisted traces.

Lemma 5.1

Let A be a vector space, $\phi : A^n \rightarrow A$ be an n-linear map, $\tau$ be a linear form and $\alpha ,\beta : A \rightarrow A$ be linear maps. If $\tau$ is an $(\alpha ,\beta )$-twisted $\phi$-trace satisfying the condition $\tau (\alpha (x))\beta (y) = \tau (\beta (x))\alpha (y)$, $\forall x,y \in A$, then $\tau$ is an $(\alpha ,\beta )$-twisted $\phi _\tau$-trace.

Proof

For $x_1,\ldots ,x_{n+1} \in A$, we have:

$$\begin{aligned}&\tau \left( {\phi _\tau \left( {\beta (x_1),\ldots ,\beta (x_n),\alpha (x_{n+1})}\right) }\right) \\&\qquad \quad = \sum _{i=1}^n (-1)^{i-1} \tau \left( { \tau (\beta (x_i)) \phi \left( {\beta (x_1),\ldots ,\widehat{x_i},\ldots ,\beta (x_n),\alpha (x_{n+1})}\right) }\right) \\&\qquad \qquad \quad \,\,\,+ (-1)^n \tau \left( {\tau (\alpha (x_{n+1}))\phi \left( {\beta (x_1),\ldots ,\beta (x_n)}\right) }\right) \\&\qquad \qquad \quad \,\,\,= (-1)^n \tau \left( {\phi \left( {\beta (x_1),\ldots ,\tau (\alpha (x_{n+1}))\beta (x_n)}\right) }\right) \\&\qquad \qquad \qquad \qquad \quad = (-1)^n \tau \left( {\tau (\beta (x_{n+1}))\phi \left( {\beta (x_1),\ldots ,\alpha (x_n)}\right) }\right) = 0, \end{aligned}$$

which completes the proof.    $\square$

Lemma 5.2

Let A (resp. B) be a vector space, $\phi$ (resp. $\psi$) be an n-linear map on A (resp. B) and $\tau$ (resp. $\sigma$) be a linear form on A (resp. B). Let $f : A \rightarrow B$ be a linear map satisfying:

$$\begin{aligned} \forall x_1,\ldots ,x_n \in A, f\left( {\phi \left( {x_1,\ldots ,x_n}\right) }\right) = \psi \left( {f(x_1),\ldots ,f(x_n)}\right) , \end{aligned}$$

and $\tau = \sigma \circ f$, then f satisfies:

$$\begin{aligned} \forall x_1,\ldots ,x_{n+1} \in A, f\left( {\phi _\tau \left( {x_1,\ldots ,x_{n+1}}\right) }\right) = \psi _\tau \left( {f(x_1),\ldots ,f(x_{n+1})}\right) . \end{aligned}$$

Proof

For all $x_1,\ldots ,x_{n+1} \in A$, we have

$$\begin{aligned}&f\left( {\phi _\tau \left( {x_1,\ldots ,x_{n+1}}\right) }\right) = \sum _{i=1}^{n+1} (-1)^{i-1} \tau (x_i)f\left( {\phi \left( {x_1,\ldots ,x_{i-1},x_{i+1},\ldots ,x_{n+1}}\right) }\right) \\&\qquad \quad \, = \sum _{i=1}^{n+1} (-1)^{i-1} \tau (x_i)\psi \left( {f(x_1),\ldots ,f(x_{i-1}),f(x_{i+1}),\ldots ,f(x_{n+1})}\right) \\&\qquad = \sum _{i=1}^{n+1} (-1)^{i-1} \sigma (f(x_i))\psi \left( {f(x_1),\ldots ,f(x_{i-1}),f(x_{i+1}),\ldots ,f(x_{n+1})}\right) \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad = \psi _\sigma \left( {f(x_1),\ldots ,f(x_{n+1})}\right) , \end{aligned}$$

which completes the proof.    $\square$

Now, using the definitions and lemmas above, one can, under some conditions, construct an $(n+1)$-BiHom-Lie algebra using an n-BiHom-Lie algebra and a twisted trace, this construction is given by the following theorem:

Theorem 5.3

Let $(A,\left[ {\cdot ,\ldots ,\cdot }\right] ,\alpha ,\beta )$ be an n-BiHom-Lie algebra (resp. and n-BiHom-Lie-Leibniz algebra), and let $\tau$ be an $(\alpha ,\beta )$-twisted $\left[ {\cdot ,\ldots ,\cdot }\right]$-trace. If the conditions:

$$\begin{aligned} \forall x,y \in A, \tau (\alpha (x))\beta (y) = \tau (\beta (x))\alpha (y), \end{aligned}$$

$$\begin{aligned} \tau \circ \alpha = \tau \text { and } \tau \circ \beta = \tau , \end{aligned}$$

are satisfied then $(A,\left[ {\cdot ,\ldots ,\cdot }\right] _\tau ,\alpha ,\beta )$, where $\left[ {\cdot ,\ldots ,\cdot }\right] _\tau$ is given by Definition 5.11, is an $(n+1)$-BiHom-Lie algebra (resp. and n-BiHom-Lie-Leibniz algebra). We say that this algebra is induced by $(A,\left[ {\cdot ,\ldots ,\cdot }\right] ,\alpha ,\beta )$.

Proof

The fact that $\alpha$ and $\beta$ commute comes from the given algebra. Lemma 5.2 provides that $\alpha$ and $\beta$ are morphisms for the bracket $\left[ {\cdot ,\ldots ,\cdot }\right] _\tau$. We show that this bracket satisfies the BiHom-skewsymmetry and the $(n+1)$-BiHom-Jacobi (resp. BiHom Nambu) identity.

$$\begin{aligned} \begin{array}{c} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\left[ {\beta (x_1),\ldots ,\beta (x_{j+1}),\beta (x_j),\ldots ,\beta (x_n),\alpha (x_{n+1})}\right] _\tau \\ \quad = \sum \limits _{i=1}^{j-1} (-1)^{i+1}\tau (\beta (x_i)) \left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_{j+1}),\beta (x_j),\ldots ,\beta (x_n),\alpha (x_{n+1})}\right] \\ + (-1)^{j-1} \tau (\beta (x_{j+1})) \left[ {\beta (x_1),\ldots ,\beta (x_{j-1}),\beta (x_j),\beta (x_{j+2}),\ldots ,\beta (x_n),\alpha (x_{n+1})}\right] \\ + (-1)^{j} \tau (\beta (x_{j})) \left[ {\beta (x_1),\ldots ,\beta (x_{j-1}),\beta (x_{j+1}),\beta (x_{j+2}),\ldots ,\beta (x_n),\alpha (x_{n+1})}\right] \\ + \sum \limits _{i=j+2}^{n} (-1)^{i+1}\tau (\beta (x_i)) \left[ {\beta (x_1),\ldots ,\beta (x_{j+1}),\beta \left( {x_j}\right) ,\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_n),\alpha (x_{n+1})}\right] \\ + (-1)^n \tau (\alpha (x_{n+1})) \left[ {\beta (x_1),\ldots ,\beta (x_{j+1}),\beta (x_j),\ldots ,\beta (x_n)}\right] \\ = - \sum \limits _{i=1}^{j-1} (-1)^{i+1}\tau (\beta (x_i)) \left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_j),\beta (x_{j+1}),\ldots ,\beta (x_n),\alpha (x_{n+1})}\right] \\ - (-1)^{j-1} \tau (\beta (x_{j})) \left[ {\beta (x_1),\ldots ,\beta (x_{j-1}),\beta (x_{j+1}),\beta (x_{j+2}),\ldots ,\beta (x_n),\alpha (x_{n+1})}\right] \\ - (-1)^{j} \tau (\beta (x_{j+1})) \left[ {\beta (x_1),\ldots ,\beta (x_{j-1}),\beta (x_j),\beta (x_{j+2}),\ldots ,\beta (x_n),\alpha (x_{n+1})}\right] \\ - \sum \limits _{i=j+2}^{n} (-1)^{i+1}\tau (\beta (x_i)) \left[ {\beta (x_1),\ldots ,\beta (x_j),\beta (x_{j+1}),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_n),\alpha (x_{n+1})}\right] \\ + (-1)^n \tau (\beta (x_{n+1})) \left[ {\beta (x_1),\ldots ,\beta (x_{j+1}),\beta (x_j),\ldots ,\alpha (x_n)}\right] \\ = - \sum _{i=1}^n (-1)^{i-1} \tau (\beta (x_i)) \left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_n),\alpha (x_{n+1})}\right] \\ - (-1)^n \tau (\beta (x_{n+1})) \left[ {\beta (x_1),\ldots ,,\beta (x_{n-1})\alpha (x_n)}\right] \\ = - \sum _{i=1}^n (-1)^{i-1} \tau (\beta (x_i)) \left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_n),\alpha (x_{n+1})}\right] \\ - (-1)^n \tau (\alpha (x_{n+1})) \left[ {\beta (x_1),\ldots ,,\beta (x_{n-1})\beta (x_n)}\right] \\ \qquad \qquad \qquad \qquad \qquad \qquad = -\left[ {\beta (x_1),\ldots ,\beta (x_n),\alpha (x_{n+1})}\right] _\tau . \end{array} \end{aligned}$$

$$\begin{aligned}&\left[ {\beta (x_1),\ldots ,\beta (x_{n+1}),\alpha (x_{n})}\right] _\tau \\&\qquad \qquad =\sum _{i=1}^{n-1}(-1)^{i-1}\tau (\beta (x_i)) \left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_{n+1}),\alpha (x_n)}\right] \\&\qquad \qquad \quad + (-1)^{n-1} \tau (\beta (x_{n+1})) \left[ {\beta (x_1),\ldots ,\beta (x_{n-1}),\alpha (x_n)}\right] \\&\qquad \qquad \qquad + (-1)^n \tau (\alpha (x_n)) \left[ {\beta (x_1),\ldots ,\beta (x_{n-1}),\beta (x_{n+1})}\right] \\&\qquad \qquad = - \sum _{i=1}^{n-1}(-1)^{i-1}\tau (\beta (x_i)) \left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_{n}),\alpha (x_{n+1})}\right] \\&\qquad \qquad \qquad - (-1)^{n} \tau (\beta (x_{n+1})) \left[ {\beta (x_1),\ldots ,\beta (x_{n-1}),\alpha (x_n)}\right] \\&\qquad \qquad \quad - (-1)^{n-1} \tau (\alpha (x_n)) \left[ {\beta (x_1),\ldots ,\beta (x_{n-1}),\beta (x_{n+1})}\right] \\&\qquad \qquad = - \sum _{i=1}^{n-1}(-1)^{i-1}\tau (\beta (x_i)) \left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_{n}),\alpha (x_{n+1})}\right] \\&\qquad \qquad \qquad - (-1)^{n} \tau (\alpha (x_{n+1}) \left[ {\beta (x_1),\ldots ,\beta (x_{n-1}),\beta (x_n)}\right] \\&\qquad \qquad \quad - (-1)^{n-1} \tau (\beta (x_n)) \left[ {\beta (x_1),\ldots ,\beta (x_{n-1}),\alpha (x_{n+1})}\right] \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad = - \left[ {\beta (x_1),\ldots ,\beta (x_n),\alpha (x_{n+1})}\right] _\tau . \end{aligned}$$

We denote by $L_1$ and $R_1$ respectively the left and the right hand sides of the $(n+1)$-BiHom-Jacobi identity. Then, for all $x_1,\ldots ,x_n,y_1,\ldots ,y_{n+1} \in A$,

$$\begin{aligned}&L_1= \left[ {\beta ^2(x_1),\ldots ,\beta ^2(x_n),\left[ {\beta (y_1),\ldots ,\beta (y_n),\alpha (y_{n+1})}\right] _\tau }\right] _\tau \\&= \sum _{i=1}^n (-1)^{i-1}\tau (\beta ^2(x_i))\left[ {\beta ^2(x_1),\ldots ,\widehat{\beta ^2(x_i)},\ldots ,\beta ^2(x_n),\left[ {\beta (y_1),\ldots ,\beta (y_n),\alpha (y_{n+1})}\right] _\tau }\right] \\&+ (-1)^n \tau \left( {\left[ {\beta (y_1),\ldots ,\beta (y_n),\alpha (y_{n+1})}\right] _\tau }\right) \left[ {\beta ^2(x_1),\ldots ,\beta ^2(x_n)}\right] \\&= \sum _{i=1}^n\sum _{j=1}^n (-1)^{i+j}\tau (\beta ^2(x_i))\tau (\beta (y_j)) \times \\&\qquad \times \left[ {\beta ^2(x_1),\ldots ,\widehat{\beta ^2(x_i)},\ldots ,\beta ^2(x_n),\left[ {\beta (y_1),\ldots ,\widehat{\beta (y_j)},\ldots ,\beta (y_n),\alpha (y_{n+1})}\right] }\right] \\&+ \sum _{i=1}^n (-1)^{i+n-1}\tau (\beta ^2(x_i))\tau (\alpha (y_{n+1})) \times \\&\qquad \times \left[ {\beta ^2(x_1),\ldots ,\widehat{\beta ^2(x_i)},\ldots ,\beta ^2(x_n),\left[ {\beta (y_1),\ldots ,\beta (y_n)}\right] }\right] \\&= \sum _{i=1}^n\sum _{j=1}^n (-1)^{i+j}\tau (\beta ^2(x_i))\tau (\beta (y_j)) \times \\&\qquad \times \left[ {\beta ^2(x_1),\ldots ,\widehat{\beta ^2(x_i)},\ldots ,\beta ^2(x_n),\left[ {\beta (y_1),\ldots ,\widehat{\beta (y_j)},\ldots ,\beta (y_n),\alpha (y_{n+1})}\right] }\right] \\&+ \sum _{i=1}^n (-1)^{i+n-1}\tau (\beta ^2(x_i))\tau (\beta (y_{n+1})) \times \\&\qquad \times \left[ {\beta ^2(x_1),\ldots ,\widehat{\beta ^2(x_i)},\ldots ,\beta ^2(x_n),\left[ {\beta (y_1),\ldots ,\beta (y{n-1}),\alpha (y_n)}\right] }\right] \\&= \sum _{i=1}^n\sum _{j=1}^n (-1)^{i+j}\tau (\beta ^2(x_i))\tau (\beta (y_j)) \sum _{k=1}^{j-1} (-1)^{n-k} \times \\&\qquad \times \Big [ \beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_k)},\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\beta ^2(y_{n+1}),\times \\&\qquad \quad \times \left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_n),\alpha (y_{k})}\right] \Big ] \\&+ \sum _{i=1}^n\sum _{j=1}^n (-1)^{i+j}\tau (\beta ^2(x_i))\tau (\beta (y_j)) \sum _{k=j+1}^{n+1} (-1)^{n-k-1}\times \\&\qquad \times \Big [ \beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_k)},\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\beta ^2(y_{n+1}),\times \\&\qquad \quad \times \left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_n),\alpha (y_{k})}\right] \Big ] \\&+ \sum _{i=1}^n (-1)^{i+n-1}\tau (\beta ^2(x_i))\tau (\beta (y_{n+1})) \times \\&\qquad \times \sum _{k=1}^n (-1)^{n-k} \Big [ \beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_k)},\ldots ,\beta ^2(y_n),\times \\&\qquad \quad \times \left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_n), \alpha (y_k)}\right] \Big ] \\&= \sum _{i=1}^n\sum _{j=1}^{n+1} \sum _{k=1}^{j-1}(-1)^{i+j}(-1)^{n-k}\tau (\beta ^2(x_i))\tau (\beta (y_j))\times \\&\qquad \times \Big [ \beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_k)},\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\beta ^2(y_{n+1}),\times \\&\qquad \quad \times \left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_n),\alpha (y_{k})}\right] \Big ] \\&+ \sum _{i=1}^n\sum _{j=1}^{n+1} \sum _{k=j+1}^{n+1} (-1)^{i+j}(-1)^{n-k-1} \tau (\beta ^2(x_i))\tau (\beta (y_j))\times \\&\qquad \times \Big [\beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_k)},\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\beta ^2(y_{n+1}),\times \\&\qquad \quad \times \left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_n),\alpha (y_{k})}\right] \Big ] \end{aligned}$$

For the right hand side, we have:

$$\begin{aligned}&R_1= \sum _{k=1}^{n+1} (-1)^{n+1-k} \left[ {\beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_k)},\ldots ,\beta ^2(y_{n+1}),\left[ {\beta (x_1),\ldots ,\beta (x_n),\alpha (y_k)}\right] _\tau }\right] _\tau \\&= \sum _{k=1}^{n+1} (-1)^{n+1-k} \sum _{j=1}^{k-1} (-1)^{j-1} \tau (\beta ^2(y_j))\times \\&\qquad \times \left[ {\beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\widehat{\beta ^2(y_k)},\ldots ,\beta ^2(y_{n+1}),\left[ {\beta (x_1),\ldots ,\beta (x_n),\alpha (y_k)}\right] _\tau }\right] \\&+ \sum _{k=1}^{n+1} (-1)^{n+1-k} \sum _{j=k+1}^{n+1} (-1)^{j} \tau (\beta ^2(y_j))\times \\&\qquad \times \left[ {\beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_k)},\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\beta ^2(y_{n+1}),\left[ {\beta (x_1),\ldots ,\beta (x_n),\alpha (y_k)}\right] _\tau }\right] \\&+ \sum _{k=1}^{n+1} (-1)^{n+1-k} (-1)^{n} \tau (\left[ {\beta (x_1),\ldots ,\beta (x_n),\alpha (y_k)}\right] _\tau )\times \\&\qquad \times \left[ {\beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_k)},\ldots ,,\ldots ,\beta ^2(y_{n+1})}\right] \\&= \sum _{k=1}^{n+1} (-1)^{n+1-k} \sum _{j=1}^{k-1} \sum _{i=1}^n (-1)^{i-1} (-1)^{j-1} \tau (\beta ^2(y_j)) \tau (\beta (x_i)) \times \\&\qquad \times \Big [ \beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\widehat{\beta ^2(y_k)},\ldots ,\beta ^2(y_{n+1}),\times \\&\qquad \quad \times \left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_n),\alpha (y_k)}\right] \Big ]\\&+ \sum _{k=1}^{n+1} (-1)^{n+1-k} \sum _{j=k+1}^{n+1} \sum _{i=1}^n (-1)^{i-1} (-1)^{j} \tau (\beta ^2(y_j)) \tau (\beta (x_i)) \times \\&\qquad \times \Big [ \beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_k)},\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\beta ^2(y_{n+1}),\times \\&\qquad \quad \times \left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_n),\alpha (y_k)}\right] \Big ]\\&+\sum _{k=1}^{n+1} (-1)^{n+1-k} \sum _{j=1}^{k-1} (-1)^{j-1} (-1)^n \tau (\alpha (y_k)) \tau (\beta ^2(y_j))\times \\&\qquad \times \left[ {\beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\widehat{\beta ^2(y_k)},\ldots ,\beta ^2(y_{n+1}),\left[ {\beta (x_1),\ldots ,\beta (x_n)}\right] }\right] \\&+ \sum _{k=1}^{n+1} (-1)^{n+1-k} \sum _{j=k+1}^{n+1} (-1)^{j} (-1)^n \tau (\alpha (y_k)) \tau (\beta ^2(y_j))\times \\&\qquad \times \left[ {\beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_k)},\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\beta ^2(y_{n+1}),\left[ {\beta (x_1),\ldots ,\beta (x_n)}\right] }\right] \\&=\sum _{i=1}^n \sum _{k=1}^{n+1}\sum _{j=1}^{k-1} (-1)^{n+1-k} (-1)^{i-1} (-1)^{j-1} \tau (\beta ^2(y_j)) \tau (\beta (x_i)) \times \\&\qquad \times \Big [ \beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\widehat{\beta ^2(y_k)},\ldots ,\beta ^2(y_{n+1}),\times \\&\qquad \quad \times \left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_n),\alpha (y_k)}\right] \Big ]\\&+ \sum _{i=1}^n \sum _{k=1}^{n+1} \sum _{j=k+1}^{n+1} (-1)^{n+1-k} (-1)^{i-1} (-1)^{j} \tau (\beta ^2(y_j)) \tau (\beta (x_i)) \times \\&\qquad \times \Big [ \beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_k)},\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\beta ^2(y_{n+1}),\times \\&\qquad \quad \times \left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_n),\alpha (y_k)}\right] \Big ]\\&+\sum _{k=1}^{n+1} \sum _{j=1}^{k-1} (-1)^{n+1-k}(-1)^{j-1} (-1)^n \tau (\alpha (y_k)) \tau (\beta ^2(y_j))\times \\&\qquad \times \left[ {\beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\widehat{\beta ^2(y_k)},\ldots ,\beta ^2(y_{n+1}),\left[ {\beta (x_1),\ldots ,\beta (x_n)}\right] }\right] \\&+ \sum _{j=1}^{n+1} \sum _{k=1}^{j-1} (-1)^{n+1-k} (-1)^{j} (-1)^n \tau (\alpha (y_k)) \tau (\beta ^2(y_j))\times \\&\qquad \times \left[ {\beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_k)},\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\beta ^2(y_{n+1}),\left[ {\beta (x_1),\ldots ,\beta (x_n)}\right] }\right] \\&=\sum _{i=1}^n \sum _{j=1}^{n+1}\sum _{k=j+1}^{n+1} (-1)^{n+1-k} (-1)^{i-1} (-1)^{j-1} \tau (\beta ^2(y_j)) \tau (\beta (x_i)) \times \\&\qquad \times \Big [\beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\widehat{\beta ^2(y_k)},\ldots ,\beta ^2(y_{n+1}),\times \\&\qquad \quad \times \left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_n),\alpha (y_k)}\right] \Big ] \\&+ \sum _{i=1}^n \sum _{j=1}^{n+1} \sum _{k=1}^{j-1} (-1)^{n+1-k} (-1)^{i-1} (-1)^{j} \tau (\beta ^2(y_j)) \tau (\beta (x_i)) \times \\&\qquad \times \Big [ \beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_k)},\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\beta ^2(y_{n+1}),\times \\&\qquad \quad \times \left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_n),\alpha (y_k)}\right] \Big ] = L_1. \end{aligned}$$

For the BiHom-Nambu identity, we have for all $x_1,\ldots ,x_n\in A$, $y_1,\ldots ,y_{n+1} \in A$:

$$\begin{aligned}&L_2= \left[ {\beta ^2(x_1),\ldots ,\beta ^2(x_n),\left[ {\beta (y_1),\ldots ,\beta (y_n),\alpha (y_{n+1})}\right] _\tau }\right] _\tau \\&= \sum _{i=1}^n (-1)^{i-1}\tau (\beta ^2(x_i))\left[ {\beta ^2(x_1),\ldots ,\widehat{\beta ^2(x_i)},\ldots ,\beta ^2(x_n),\left[ {\beta (y_1),\ldots ,\beta (y_n),\alpha (y_{n+1})}\right] _\tau }\right] \\&+ (-1)^n \tau \left( {\left[ {\beta (y_1),\ldots ,\beta (y_n),\alpha (y_{n+1})}\right] _\tau }\right) \left[ {\beta ^2(x_1),\ldots ,\beta ^2(x_n)}\right] \\&= \sum _{i=1}^n\sum _{j=1}^n (-1)^{i+j}\tau (\beta ^2(x_i))\tau (\beta (y_j) \times \\&\qquad \times \left[ {\beta ^2(x_1),\ldots ,\widehat{\beta ^2(x_i)},\ldots ,\beta ^2(x_n),\left[ {\beta (y_1),\ldots ,\widehat{\beta (y_j)},\ldots ,\beta (y_n),\alpha (y_{n+1})}\right] }\right] \\&+ \sum _{i=1}^n (-1)^{i+n-1}\tau (\beta ^2(x_i))\tau (\alpha (y_{n+1}))\times \\&\qquad \times \left[ {\beta ^2(x_1),\ldots ,\widehat{\beta ^2(x_i)},\ldots ,\beta ^2(x_n),\left[ {\beta (y_1),\ldots ,\beta (y_n)} \right] }\right] \\&= \sum _{i=1}^n\sum _{j=1}^n (-1)^{i+j}\tau (\beta ^2(x_i))\tau (\beta (y_j))\times \\&\qquad \times \left[ {\beta ^2(x_1),\ldots ,\widehat{\beta ^2(x_i)},\ldots ,\beta ^2(x_n),\left[ {\beta (y_1),\ldots ,\widehat{\beta (y_j)},\ldots ,\beta (y_n),\alpha (y_{n+1})}\right] }\right] \\&+ \sum _{i=1}^n (-1)^{i+n-1}\tau (\beta ^2(x_i))\tau (\beta (y_{n+1}))\times \\&\qquad \times \left[ {\beta ^2(x_1),\ldots ,\widehat{\beta ^2(x_i)},\ldots ,\beta ^2(x_n),\left[ {\beta (y_1),\ldots ,\beta (y{n-1}),\alpha (y_n)}\right] }\right] \\&= \sum _{i=1}^n \sum _{j=1}^n (-1)^{i+j}\tau (\beta ^2(x_i))\tau (\beta (y_j))\sum _{k=1;k\ne j}^{n+1}\times \\&\qquad \times \left[ {\beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_n),\alpha (y_k)}\right] ,\ldots ,\beta ^2(y_{n+1}) }\right] \\&+ \sum _{i=1}^n (-1)^{i+n-1}\tau (\beta ^2(x_i))\tau (\beta (y_{n+1}))\sum _{k=1}^n\times \\&\qquad \times \left[ {\beta ^2(y_1),\ldots ,\left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_{n}),\alpha (y_k)}\right] ,\ldots ,\beta ^2(y_n) }\right] \\&= \sum _{i=1}^n \sum _{j=1}^{n+1} (-1)^{i+j}\tau (\beta ^2(x_i))\tau (\beta (y_j))\sum _{k=1;k\ne j}^{n+1}\times \\&\qquad \times \left[ {\beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_n),\alpha (y_k)}\right] ,\ldots ,\beta ^2(y_{n+1}) }\right] , \end{aligned}$$

$$\begin{aligned}&R_2= \sum _{k=1}^{n+1} \left[ {\beta ^2(y_1),\ldots ,\left[ {\beta (x_1),\ldots ,\beta (x_n),\alpha (y_k)}\right] _\tau ,\ldots ,\beta ^2(y_{n+1}) }\right] _\tau \\&= \sum _{k=1}^{n+1} \sum _{j=1;j\ne k}^{n+1} (-1)^{j-1} \tau \left( {\beta ^2(y_j)}\right) \times \\&\times \left[ {\beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\left[ {\beta (x_1),\ldots ,\beta (x_n),\alpha (y_k)}\right] _\tau ,\ldots ,\beta ^2(y_{n+1}) }\right] \\&= \sum _{k=1}^{n+1} \sum _{j=1;j\ne k}^{n+1} (-1)^{j-1} \tau \left( {\beta ^2(y_j)}\right) \sum _{i=1}^n (-1)^{i-1}\tau \left( {\beta (x_i)}\right) \times \\&\times \left[ {\beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_n),\alpha (y_k)}\right] ,\ldots ,\beta ^2(y_{n+1}) }\right] \\&+ \sum _{k=1}^{n+1} \sum _{j=1;j\ne k}^{n+1} (-1)^{j+n-1} \tau \left( {\beta ^2(y_j)}\right) \tau (\alpha (y_k))\times \\&\times \left[ {\beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\beta ^2(y_{k-1}),\left[ {\beta (x_1),\ldots ,\beta (x_n)}\right] ,\ldots ,\beta ^2(y_{n+1}) }\right] \\&=\sum _{i=1}^n \sum _{j=1}^{n+1}\sum _{k=1;k\ne j}^{n+1} (-1)^{i+j} \tau \left( {\beta (x_i)}\right) \tau \left( {\beta ^2(y_j)}\right) \times \\&\times \left[ {\beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\left[ {\beta (x_1),\ldots ,\widehat{\beta (x_i)},\ldots ,\beta (x_n),\alpha (y_k)}\right] ,\ldots ,\beta ^2(y_{n+1}) }\right] \\&+ \sum _{k=1}^{n+1} \sum _{j=1;j\ne k}^{n+1} (-1)^{j+n-1} \tau \left( {\beta ^2(y_j)}\right) \tau (\beta (y_k))\times \\&\times \left[ {\beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\beta ^2(y_{k-1}),\left[ {\beta (x_1),\ldots ,\beta (x_n)}\right] ,\ldots ,\alpha \circ \beta (y_{n+1}) }\right] = \\&L_2 + \sum _{k=1}^{n+1} \sum _{j=1}^{k-1} (-1)^{j+n-1}\tau \left( {\beta ^2(y_j)}\right) \tau (\beta (y_k))\times \\&\times \left[ {\beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\beta ^2(y_{k-1}),\left[ {\beta (x_1),\ldots ,\beta (x_n)}\right] ,\ldots ,\alpha \circ \beta (y_{n+1}) }\right] \\&+ \sum _{k=1}^{n+1} \sum _{j=k+1}^{n+1} (-1)^{j+n-1} \tau \left( {\beta ^2(y_j)}\right) \tau (\beta (y_k)) \times \\&\times \left[ {\beta ^2(y_1),\ldots ,\beta ^2(y_{k-1}),\left[ {\beta (x_1),\ldots ,\beta (x_n)}\right] ,\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\alpha \circ \beta (y_{n+1}) }\right] = \\&L_2 + \sum _{k=1}^{n+1} \sum _{j=1}^{k-1} (-1)^{j+n-1} \tau \left( {\beta ^2(y_j)}\right) \tau (\beta (y_k)) \times \\&\times \left[ {\beta ^2(y_1),\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\beta ^2(y_{k-1}),\left[ {\beta (x_1),\ldots ,\beta (x_n)}\right] ,\ldots ,\alpha \circ \beta (y_{n+1}) }\right] \\&+ \sum _{k=1}^{n+1} \sum _{j=k+1}^{n+1} (-1)^{j+n-1} \tau \left( {\beta ^2(y_j)}\right) \tau (\beta (y_k)) \times \\&\times \left[ {\beta ^2(y_1),\ldots ,\beta ^2(y_{k-1}),\left[ {\beta (x_1),\ldots ,\beta (x_n)}\right] ,\ldots ,\widehat{\beta ^2(y_j)},\ldots ,\alpha \circ \beta (y_{n+1}) }\right] , \end{aligned}$$

which completes the proof.    $\square$

Remark 5.4

If one considers a weaker version of n-BiHom-Lie algebras, namely considering the maps $\alpha$ and $\beta$ to be any linear maps instead of being algebra morphisms, then one can replace the conditions $\tau \circ \alpha = \tau \text { and } \tau \circ \beta = \tau$ by the condition $\tau (\beta (x))\tau (\beta ^2(y)) = \tau (\beta ^2(x))\tau (\beta (y)).$

We study now the conditions on $\alpha$ and $\beta$ in the Theorem 5.3, to see how restrictive they are for the choice of an n-BiHom-Lie algebra to use for the construction.

We consider an n-BiHom-Lie algebra $\left( {A,\left[ {\cdot ,\ldots ,\cdot }\right] ,\alpha ,\beta }\right)$ and $\tau : A \rightarrow \mathbb {K}$ a twisted trace such that none of $\left[ {\cdot ,\ldots ,\cdot }\right]$, $\tau$, $\alpha$ and $\beta$ is identically zero. Suppose that they satisfy the conditions of Theorem 5.3, then we get the following:

$$\begin{aligned} \alpha (\ker (\tau )) \subseteq \ker (\tau ) \text { and } \beta (\ker (\tau )) \subseteq \ker (\tau ). \end{aligned}$$

The two conditions of Theorem 5.3 put together also lead to the following:

Let $x\in A$ such that $\tau (x)\ne 0$, for all $y\in A$, we have:

$$\begin{aligned} \tau (\alpha (x))\beta (y) = \tau (\beta (x))\alpha (y)&\implies \tau (x)\beta (y) = \tau (x)\alpha (y) \\&\implies \beta (y) = \alpha (y). \qquad \text { (since }\tau (x)\ne 0) \end{aligned}$$

If one drops some conditions as explained in Remark 5.4, it is possible to get a less restrictive situation.

Example 5.3

Let A be a vector space, $\dim A = n=3$ with basis $(e_i)_{1\le i \le n}$ and the linear maps $\left[ {\cdot ,\cdot }\right] : A \otimes A \rightarrow A$ and $\alpha ,\beta : A \rightarrow A$ given by:

$$\begin{aligned} \left[ {e_i,e_j}\right] =\sum _{k=1}^n c_{ij}^k e_k, \forall i,j : 1\le i,j \le n, \end{aligned}$$

and $[\alpha ]=(a_{i,j})_{1\le i,j \le n} ; [\beta ]=(b_{i,j})_{1\le i,j \le n}.$ We suppose $[\alpha ]$ and $[\beta ]$ to be diagonal, which implies $\alpha \circ \beta = \beta \circ \alpha$. The remaining conditions for $(A,\left[ {\cdot ,\cdot }\right] ,\alpha ,\beta )$ to be a BiHom-Lie-Leibniz algebra are given, under the assumptions above, by:

• $\alpha ,\beta$-skewsymmetry:

$$\begin{aligned} \sum _{k=1}^n \sum _{l=1}^n (a_{ki}b_{lj}+a_{kj}b_{li})c_{lk}^p = 0, \forall i,j,p : 1\le i,j,p \le n. \end{aligned}$$

• Multiplicativity

$$\begin{aligned} \sum _{k=1}^n c_{ij}^k a_{kq} - \sum _{k=1}^n \sum _{l=1}^n a_{ki}a_{lj}c_{kl}^q = 0, \forall i,j,q : 1 \le i,j,q \le n. \end{aligned}$$

• BiHom-Leibniz identity:

$$\begin{aligned} \sum _{l=1}^n \sum _{p=1}^n \sum _{q=1}^n \sum _{r=1}^n \sum _{s=1}^n (b_{pl}b_{li}b_{qj}a_{rk} c_{qr}^s c_{ps}^t - b_{pl}b_{lk}b_{qi}a_{rj} c_{qr}^s c_{sp}^t - b_{pl}b_{lj}b_{qi}a_{rk} c_{qr}^s c_{ps}^t)=0,&\\ \forall i,j,k,t : 1 \le i,j,k,t \le n.&\end{aligned}$$

We solve these equations, starting with $\alpha ,\beta$-skewsymmetry, then BiHom-Leibniz identity and multiplicativity, while choosing at each step solutions where none of $\left[ {\cdot ,\cdot }\right]$, $\alpha$ and $\beta$ are zero. This way, we can find examples of BiHom-Lie-Leibniz algebras.

We consider now a linear map $\tau : A \rightarrow \mathbb {K}$, given by:

$$\begin{aligned} \tau (e_i)=t_i, \forall i : 1\le i \le n. \end{aligned}$$

The conditions of Theorem 5.3 become:

$$\begin{aligned} \sum _{k=1}^n \sum _{l=1}^n \sum _{o=1}^n b_{ki} a_{lj} c_{cl}^o t_o = 0, \forall i,j : 1\le i,j \le 3. \end{aligned}$$

$$\begin{aligned} t_i-\sum _{k=1}^n a_{ki}t_k = 0, \forall i : 1\le i \le n. \end{aligned}$$

$$\begin{aligned} \sum _{k=1}^n (a_{ki}b_{lj}t_k - b_{ki}a_{lj}t_k)=0, \forall i,j,l : 1\le i,j,l \le n. \end{aligned}$$

Solving these equations gives conditions on $\tau$, $\alpha$, $\beta$ (and sometimes on $\left[ {\cdot ,\cdot }\right]$) such that one can construct the induced Leibniz 3-BiHom-Lie algebra. We give now some examples obtained using this procedure:

• 1. The bracket and the structure maps are given by:

$$\begin{aligned}{}[e_1, e_3]=c_1 e_3 ; [e_2,e_3]=c_2 e_3 ; [e_3,e_1]=c_3 e_3 ; [e_3,e_2]=c_4 e_3 ; [e_3,e_3]=c_5 e_3. \end{aligned}$$

$$\begin{aligned}{}[\alpha ]=\begin{pmatrix} a_1 &{} 0 &{} 0\\ 0 &{} a_2 &{} 0 \\ 0 &{} 0 &{} 0 \end{pmatrix} ; \quad [\beta ]=\begin{pmatrix} b_1 &{} 0 &{} 0\\ 0 &{} b_2 &{} 0 \\ 0 &{} 0 &{} 0 \end{pmatrix}. \end{aligned}$$

One solution to have the conditions of Theorem 5.3 is given by:

$$\begin{aligned} t_2=t_3=0 ; a_1=b_1=1 ; a_2=b_2. \end{aligned}$$

We get a Leibniz 3-BiHom-Lie algebra defined by:

$$\begin{aligned}{}[e_1,e_2,e_3]&=t_1 c_2 e_3 ;\ [e_1,e_3,e_1]=(t_1 c_1+t_1c_3) e_3 ;\ [e_1,e_3,e_2]=t_1 c_4 e_3 ;\\ [e_1,e_3,e_3]&=t_1 c_5 e_3 ;\\ [e_2,e_1,e_3]&=-t_1 c_2 e_3 ;\ [e_2,e_3,e_1]=t_1 c_2 e_3 ;\ [e_3,e_1,e_2]=-t_1 c_4 e_3 ;\\ [e_3,e_1,e_3]&=-t_1 c_5 e_3 ;\\ [e_3,e_2,e_1]&=t_1 c_4 e_3 ;\ [e_3,e_3,e_3]=t_1 c_5 e_3. \end{aligned}$$

$$\begin{aligned}{}[\alpha ]=\begin{pmatrix} 1 &{} 0 &{} 0\\ 0 &{} a_2 &{} 0 \\ 0 &{} 0 &{} 0 \end{pmatrix} ; \quad [\beta ]=\begin{pmatrix} 1 &{} 0 &{} 0\\ 0 &{} a_2 &{} 0 \\ 0 &{} 0 &{} 0 \end{pmatrix}. \end{aligned}$$

• 2. The bracket and the structure maps are given by:

$$\begin{aligned}{}[e_1, e_2]=c_1 e_2+c_2 e_3 ; [e_1,e_3]=c_3 e_3 ; [e_2,e_2]=c_4 e_2+c_5 e_3 ; [e_3,e_2]=c_6 e_3. \end{aligned}$$

$$\begin{aligned}{}[\alpha ]=\begin{pmatrix} a_1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \end{pmatrix} ; \quad [\beta ]=\begin{pmatrix} 1 &{} 0 &{} 0\\ 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 1 \end{pmatrix}. \end{aligned}$$

In this case, there is no (nonzero) $\tau$ satisfying the conditions of Theorem 5.3.

• 3. The bracket and the structure maps are given by:

$$\begin{aligned}{}[e_1, e_3]=c_1 e_3 ; [e_3,e_1]=-c_1 e_3. \end{aligned}$$

$$\begin{aligned}{}[\alpha ]=\begin{pmatrix} 1 &{} 0 &{} 0\\ 0 &{} a_1 &{} 0 \\ 0 &{} 0 &{} a_2 \end{pmatrix} ; \quad [\beta ]=\begin{pmatrix} 1 &{} 0 &{} 0\\ 0 &{} b_1 &{} 0 \\ 0 &{} 0 &{} a_2 \end{pmatrix}. \end{aligned}$$

In this case, when solving equations for $\tau$, $\alpha$ and $\beta$ to satisfy the conditions of Theorem 5.3, we get either $\tau =0$ or $\alpha =\beta$. In the second case, the chosen algebra becomes a Hom-Lie algebra (see [19]) if $a_1,a_2$ are non-zero. Namely, all possible solutions (where $\tau \ne 0$) are:

$$\begin{aligned} a_1 = 1 ; b_1 = 1 ; t_3 = 0. \end{aligned}$$

$$\begin{aligned} b_1=a_1 ; t_2=0 ; t_3=0. \end{aligned}$$

The second solution leads to the induced algebra’s bracket being zero. Let us look at the first one. The structure maps, under these conditions become:

$$\begin{aligned}{}[\alpha ]=\begin{pmatrix} 1 &{} 0 &{} 0\\ 0 &{} a_1 &{} 0 \\ 0 &{} 0 &{} a_2 \end{pmatrix} ; \quad [\beta ]=\begin{pmatrix} 1 &{} 0 &{} 0\\ 0 &{} b_1 &{} 0 \\ 0 &{} 0 &{} a_2 \end{pmatrix}, \end{aligned}$$

and the bracket of the induced algebra is skewsymmetric and is given by:

$$\begin{aligned}{}[e_1,e_2,e_3]=t_2 c_1 e_3. \end{aligned}$$

Example 5.4

Now let us look at a case where we drop the condition that $\alpha$ and $\beta$ need to be morphisms of the induced algebra, as in Remark 5.4. The equations $\tau \circ \alpha = \tau$ and $\tau \circ \beta = \tau$ will be replaced by the following:

$$\begin{aligned} \forall x,y \in A, \tau (\beta ^2(x))\tau (\beta (y))=\tau (\beta (x))\tau (\beta ^2(y)). \end{aligned}$$

In terms of structure constants, it takes the following form:

$$\begin{aligned} \sum _{k=1}^{n}\sum _{o=1}^{n}\sum _{l=1}^{n}\left( \left( b_{kl}b_{li}b_{oj}-b_{ki}b_{ol}b_{lj}\right) t_{k}t_{o}\right) =0. \end{aligned}$$

We consider the BiHom-Lie-Leibniz algebra, generated in the same way as above:

$$\begin{aligned}{}[e_2, e_1]=c_1 e_2 ; [e_2,e_2]=c_2 e_2 ; [e_2,e_3]=c_3 e_2. \end{aligned}$$

$$\begin{aligned}{}[\alpha ]=\begin{pmatrix} a_1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} a_2 \end{pmatrix} ; \quad [\beta ]=\begin{pmatrix} b_1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} b_2 \end{pmatrix}. \end{aligned}$$

One solution to have the conditions of Theorem 5.3 and Remark 5.4 is given by:

$$\begin{aligned} t_1=t_3=0. \end{aligned}$$

And we get the following induced 3-BiHom-Lie-Leibniz algebra (without the multiplicativity property for $\alpha$ and $\beta$) defined by the bracket is given by:

$$\begin{aligned}{}[e_2,e_1,e_2]=t_2 c_1 e_2; [e_2,e_2,e_2]=t_2 c_2 e_2; [e_2,e_3,e_2]=t_2 c_3 e_2, \end{aligned}$$

together with the same linear maps $\alpha$ and $\beta$.