1 Introduction

In this paper we consider a type of singularly perturbed parabolic initial and boundary value problem given by

$$\displaystyle \begin{aligned} \left \{ \begin{array}{l} L_{\boldsymbol{\varepsilon}} \mathbf{u} \equiv \displaystyle\frac{\partial \mathbf{u}}{\partial t}(x,t) + \mathscr{L}_{x,\boldsymbol{\varepsilon}} \mathbf{u}(x,t){+\mathbf{A}(x,t,\mathbf{u}) }= \mathbf{0}, \ (x,t) \in Q \equiv \varOmega \times (0,T], \\ \mathbf{u}(0,t) ={\mathbf{g_0}(t), \ \mathbf{u}(1,t) = \mathbf{g_1}(t),} \ \forall \ t \in [0,T], \ \mathbf{u}(x,0) = \mathbf{\boldsymbol{\varphi}}(x), \ \forall \ x \in \bar{\varOmega}, \end{array} \right. \end{aligned} $$
(1)

where Ω = (0, 1), the spatial differential operator \(\mathscr {L}_{x,\boldsymbol {\varepsilon }}\) is defined by

$$\displaystyle \begin{aligned} \mathscr{L}_{x,\boldsymbol{\varepsilon}} \equiv - {\mathscr D}_{\boldsymbol{\varepsilon}} \displaystyle \frac{\partial^2 }{\partial x^2}, \end{aligned} $$
(2)

\(\mathbf {u}\,{=}\,(u_1, u_2)^T, \mathbf {\boldsymbol {\varphi }}\,{=}\,(\boldsymbol {\varphi }_1,\boldsymbol {\varphi }_2)^T, \mathbf {g_0}\,{=}\,(g_{1,0}, g_{2,0})^T, \mathbf {g_1}\,{=}\,(g_{1,1}, g_{2,1})^T, \ {\mathscr D}_{\boldsymbol {\varepsilon }}\,{=}\,\mbox{ diag } (\varepsilon _1, \varepsilon _2)\), and the reaction term is given by A(x, t, u) = (a 1(x, t, u), a 2(x, t, u))T. We assume that the vector diffusion parameter ε = (ε 1, ε 2)T satisfies 0 < ε 1 ≤ ε 2  ≤ 1, and that both ε i, i = 1, 2 can be very small and they can have different orders of magnitude; we also assume that the components a i(x, t, u), i = 1, 2 of the reaction matrix are sufficiently smooth functions and that sufficient compatibility conditions among all of these data hold, in order that the exact solution \(\mathbf {u} \in C^{4,2}(\overline {Q})\), (see [11, 12] for a detailed discussion); more details are given posteriorly in (3).

In many previous works, see [2, 6, 8, 10, 13] and references therein, the linear case of problem (1) is analyzed; in this case the differential equation is given by

$$\displaystyle \begin{aligned} \displaystyle{\frac{\partial \mathbf{u}}{\partial t}(x,t) + \left(- {\mathscr D}_{\boldsymbol{\varepsilon}} \frac{\partial^2}{\partial x^2} + {\mathscr A}\right) \mathbf{u}(x,t) = \mathbf{f}(x,t),} \end{aligned}$$

where \({\mathscr A} = (a_{ij}(x,t)), \ i,j=1,2\) and f(x, t) = (f 1(x, t), f 2(x, t))T. In those works, the combination of classical schemes to discretize in space and time variables, together with the use of a priori or equidistributed special meshes in space, gave numerical methods which are uniformly convergent with respect to the diffusion parameter ε. Nevertheless, in general, the computational cost of the numerical methods used to solve singularly coupled systems is high due to the coupling of the components of the discrete solution. To reduce this computational cost, in [2, 3] additive schemes were used to solve parabolic linear systems of reaction-diffusion type for one and two dimensional linear problems respectively, and in [4] a decomposition technique, named splitting by components, was used for parabolic one dimensional linear systems. Both techniques allow the decoupling of the components of the system to calculate the discrete solution.

Extending the main ideas of [4], in this paper we design a numerical algorithm to solve the semilinear problem (1) which is also uniformly convergent with respect to the diffusion parameters and its computational cost is similar to the proposed one in [4] for the linear case. Note that for nonlinear problems, the computational cost increases if an iterative method is used to solve them. Then, we construct our method by combining the idea of the splitting by components combined with a local linearization of the nonlinear reaction term; in this way, the numerical solution is obtained by solving only tridiagonal linear systems, without requiring the use of any iterative method. In this work we present some mathematical details only for the case of systems with two equations; nevertheless, the technique can be applied to systems with an arbitrary number of equations. Moreover, our proposal becomes more and more advantageous as long as the number of equations which compose the system increases. Up to our knowledge, paper [1] is the first one where problem (1) is considered; in that work, a nonlinear finite difference scheme is defined and a monotone iterative method, which constructs sequences of ordered upper and lower solutions, is used to construct a numerical solution; moreover, the method is uniformly convergent and it has first order in time and almost first order in space.

The paper is structured as follows. In Sect. 2, we describe the asymptotic behavior of the exact solution with respect to the diffusion parameters and we give appropriate estimates for its derivatives. In Sect. 3, we construct the spatial semidiscretization for (1) and we prove that if the discretization is defined on a piecewise uniform mesh of Shishkin type then it is uniformly convergent of almost second order. In Sect. 4, we give our proposal for the numerical integration in time; the algorithm combines the fractional implicit Euler method, a splitting by components of the discrete diffusion-reaction operator and a local linearization of the reaction term. We prove that this discretization is uniformly and unconditionally convergent of first order in time. Moreover, we prove that the fully discrete method, which follows of the combination of the time and space discretizations, is uniformly convergent of almost second order in space and of first order in time. Finally, in Sect. 5, we show the numerical results obtained for a test problem, which corroborates the uniform convergence of the algorithm.

Henceforth, ∥⋅∥ denotes the infinity norm in R 2, C denotes a generic positive constant independent of the diffusion parameters ε 1, ε 2, and also of the discretization parameters N and M and \(\Vert \mathbf {f} \Vert _G\equiv \max \{\Vert f_1 \Vert _G, \Vert f_2 \Vert _G\}\), where ∥f∥G is the maximum norm of f on the closed set G.

2 Asymptotic Behavior of the Exact Solution

In this section we show the asymptotic behavior of the solution u of (1) with respect to the diffusion parameters ε, and we give some estimates for its derivatives, which are useful below for the analysis of the uniform convergence of the numerical method. To do that, we assume that the coefficients of the reaction matrix satisfy

$$\displaystyle \begin{aligned} \begin{array}{l} \displaystyle{\frac{\partial a_i}{\partial u_i}(x,t,\mathbf{v}) \ge \beta > 0, \ \frac{\partial a_i}{\partial u_{i'}} (x,t,\mathbf{v}) \le 0, \ i \ne i', \ i, i' = 1,2,} \\ {} \displaystyle{\min_{\mathbf{v}\in {\mathbf{R}}^2}\left(\frac{\partial a_i}{\partial u_1}(x,t,\mathbf{v}) + \frac{\partial a_i}{\partial u_2}(x,t,\mathbf{v})\right) \ge \alpha > 0, \ i =1,2.} \end{array} \end{aligned} $$
(3)

Under assumptions (3), problem (1) has a unique solution (see Theorem 3.1, Chap. 8 in [12]). Moreover, following [1], by using the mean-value theorem, we have

$$\displaystyle \begin{aligned} \displaystyle{a_i(x,y,\mathbf{u}) = a_i(x,t,\mathbf{0}) + \frac{\partial a_i}{\partial u_1}(x,t,\mathbf{v}) u_1 + \frac{\partial a_i}{\partial u_2}(x,t,\mathbf{v}) u_2, \ i = 1,2,} \end{aligned} $$
(4)

and therefore the solution of problem (1) can be studied as the solution of a linear variant of it. Using the same argument, the following inverse positivity result can be deduced.

Theorem 1

If −A(x, t, 0), g 0(t), g 1(t), φ(x) have only non-negative components, then u(x, t) has only non-negative components.

Proof

See [5].

Using a similar reasoning as in [9] we obtain the following estimates for the time derivatives.

Lemma 1

The solution of problem (1) satisfies

$$\displaystyle \begin{aligned} \left\Vert \frac{\partial^k \mathbf{u}{(x,t)}}{\partial t^k} \right\Vert \le C, \ \ {(x,t)\in \bar{Q}}, \ k=0,1,2. \end{aligned} $$
(5)

On the other hand, in [1] the estimates

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} &\displaystyle &\displaystyle \left\vert \displaystyle\frac{\partial u_1 (x,t)}{\partial x} \right\vert \le C \left(1 + \varepsilon_1^{-1/2} B_{\varepsilon_1}(x) + \varepsilon_2^{-1/2} B_{\varepsilon_2}(x)\right), \\ &\displaystyle &\displaystyle \left\vert \displaystyle\frac{\partial u_2 (x,t)}{\partial x} \right\vert \le C \left(1 + \varepsilon_2^{-1/2} B_{\varepsilon_2}(x)\right), \end{array} \end{aligned} $$
(6)

were proven for first derivatives respect to spatial variable x; following [1], using (4) and the technique of [9] we deduce

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} &\displaystyle &\displaystyle \left\vert \displaystyle\frac{\partial^2 u_1(x,t)}{\partial x^2} \right\vert\le C\left(1 + \varepsilon_1^{-1}B_{\varepsilon_1}(x) + \varepsilon_2^{-1} B_{\varepsilon_2}(x)\right),\ \left\vert \displaystyle\frac{\partial^2 u_2(x,t)}{\partial x^2} \right\vert \le C\left(1 + \varepsilon_2^{-1} B_{\varepsilon_2}(x)\right), \\ &\displaystyle &\displaystyle \left\vert \displaystyle\frac{\partial^k u_1(x,t)}{\partial x^k} \right\vert \le C\left(1 + \varepsilon_1^{-k/2}B_{\varepsilon_1}(x) + \varepsilon_2^{-k/2} B_{\varepsilon_2}(x)\right), \ \ k = 3,4, \\ &\displaystyle &\displaystyle \left\vert \displaystyle\frac{\partial^k u_2(x,t)}{\partial x^k} \right\vert \le C\left(1 + \varepsilon_2^{-1}(\varepsilon_1^{(2-k)/2}B_{\varepsilon_1}(x) + \varepsilon_2^{(2-k)/2} B_{\varepsilon_2}(x))\right), \ \ k = 3,4, \end{array} \end{aligned} $$

for any \((x,t)\in \bar {Q}\), with

$$\displaystyle \begin{aligned} \displaystyle{B_\gamma(x) = e^{-x\sqrt{\alpha/\gamma}}+e^{-(1-x)\sqrt{\alpha /\gamma}}},\end{aligned} $$
(7)

where γ is a generic positive constant and α is the parameter defined in (3).

3 Spatial Semidiscretization

To construct our fully discrete scheme, which will solve numerically the continuous problem (1), firstly we discretize such problem only with respect to the spatial variable x. From the asymptotic behavior of the exact solution, described in previous section, it follows that, in general, two overlapping parabolic boundary layers can appear at both end points of the spatial domain. Then, we construct piecewise uniform meshes of Shishkin type, which concentrate the grid points in the boundary layer regions. To do that, taking multiple of 8 positive integers denoted N, we define the transition parameters

$$\displaystyle \begin{aligned} \sigma_{\varepsilon_2} = \min{\left \{1/4,2 \sqrt{\varepsilon_2}\ln {N} \right \}}, \quad \sigma_{\varepsilon_1} = \min{\left \{\sigma_{\varepsilon_2}/2,2 \sqrt{\varepsilon_1}\ln {N} \right\}}. \end{aligned}$$

Then, the grid points of the mesh, \(\overline {\varOmega }_N \equiv \{0 = x_0 < x_1 < \ldots < x_N = 1\}\), are given by

$$\displaystyle \begin{aligned} x_j = \left\{ \begin{array}{ll} jh_{\varepsilon_1}, & j = 0,\ldots, N/8, \\ x_{N/8} + (j-N/8)h_{\varepsilon_2}, & j = N/8+1,\ldots,N/4, \\ x_{N/4} + (j-N/4)H, & j = N/4+1,\ldots,3N/4, \\ x_{3N/4} + (j-3N/4)h_{\varepsilon_2}, & j = 3N/4+1,\ldots,7N/8, \\ x_{7N/8} + (j-7N/8)h_{\varepsilon_1}, & j = 7N/8+1, \ldots, N, \end{array} \right. \end{aligned} $$
(8)

where \(h_{\varepsilon _1} = 8\sigma _{\varepsilon _1}/N,\ h_{\varepsilon _2} = 8(\sigma _{\varepsilon _2}-\sigma _{\varepsilon _1})/N, \ H = 2(1-2\sigma _{\varepsilon _2})/N \). Below, we denote by h i = x i − x i−1, i = 1, …, N, and \(\overline {h}_i = (h_i + h_{i+1})/2, \ \ i = 1, \ldots , N-1\).

On these special piecewise uniform meshes, we approximate the exact solution at the grid points, u(x i, t) ≡ (u 1(x i, t), u 2(x i, t))T, with \(x_i\in \overline {\varOmega }_N\) and t ∈ [0, T], by the semidiscrete functions \({\mathbf {U}}_{N,i}(t)=({U_{N,i,1}(t), U_{N,i,2}(t)})^T\in \mathbf {\mathscr {R}}^2, \ i=0, 1, \ldots , N\). These functions are the solutions of the following family of initial value problems

$$\displaystyle \begin{aligned} \left \{ \begin{array}{@{}l} \displaystyle{{(L_{\boldsymbol{\varepsilon},N} {\mathbf{U}}_{N}(t))_i} {\,\equiv\,} \frac {d }{dt}{\mathbf{U}}_{N,i}(t) {\,+\,} (\mathscr{L}_{N,\boldsymbol{\varepsilon}}{\mathbf{U}}_{N}(t))_i+{\mathbf{A}(x_i,t,{\mathbf{U}}_{N,i}(t))} {\,=\,} \mathbf{0}, \ i {\,=\,} 1,\ldots, N{\,-\,}1,}\\ {} {\mathbf{U}}_{N,0}(t) {\,=\,} {\mathbf{g}}_{0}(t), \ {\mathbf{U}}_{N,N}(t) {\,=\,} {\mathbf{g}}_{1}(t),\\ {} {\mathbf{U}}_{N}(0) {\,=\,} (\boldsymbol{\varphi}(x_0),\ldots,\boldsymbol{\varphi}(x_N)), \end{array} \right.\end{aligned} $$
(9)

being

$$\displaystyle \begin{aligned} {\mathbf{U}}_N(t)\equiv ({\mathbf{U}}_{N,0}(t), {\mathbf{U}}_{N,1}(t), \ldots, {\mathbf{U}}_{N,N}(t)),\end{aligned}$$
$$\displaystyle \begin{aligned}{\mathscr{L}_{N,\boldsymbol{\varepsilon}}{\mathbf{U}}_{N}(t) \equiv ({ \mathscr{L}_{N,\boldsymbol{\varepsilon},1}}{\mathbf{U}}_{N}(t),{\mathscr{L}_{N,\boldsymbol{\varepsilon},2}}{\mathbf{U}}_{N}(t))^T},\end{aligned}$$

with

$$\displaystyle \begin{aligned} \begin{array}{ll} \displaystyle(\mathscr{L}_{N,\boldsymbol{\varepsilon},1} {\mathbf{U}}_N (t))_i &\equiv - \frac{\varepsilon_1}{\overline{h}_i}\left(\frac{U_{N,i+1,1} - U_{N,i,1}}{h_{i+1}} - \frac{U_{N,i,1} - U_{N,i-1,1}}{h_{i}}\right),\\ &\quad i = 1,\ldots N-1, \end{array}\end{aligned} $$

and

$$\displaystyle \begin{aligned} \begin{array}{ll} \displaystyle(\mathscr{L}_{N,\boldsymbol{\varepsilon},2} {\mathbf{U}}_{N} (t))_i &\equiv - \frac{\varepsilon_2}{\overline{h}_i}\left(\frac{U_{N,i+1,2} - U_{N,i,2}}{h_{i+1}} - \frac{U_{N,i,2} - U_{N,i-1,2}}{h_{i}}\right),\\ &\quad i = 1,\ldots N-1. \end{array}\end{aligned} $$

Similar to [4], for this spatial discretization we obtain the following result, which is the discrete analogue of Theorem 1.

Theorem 2

Assuming that all of the data (−A(x i, t, 0), g 0(t), g 1(t), φ(x i)), i = 0, …, N, of problem (9) have only non-negative values in their components, its solution U N(t) has only non-negative components.

Using Theorem 2 and suitable discrete barrier functions on a linearized rewriting of (9), it follows that its solution satisfies

$$\displaystyle \begin{aligned} \begin{array}{l} \|{\mathbf{U}}_{N} (t)\|{}_{ \overline{\varOmega}_N} \le \\ \displaystyle \max\{\|\mathbf{g_0}(t)\|{}_{[0,T]},\|\mathbf{g_1}(t)\|{}_{[0,T]}, \|[\boldsymbol{\varphi}(x)]_N\|{}_{ \overline{\varOmega}_N}, \, \frac {\|[-\mathbf{A}(x,t,\mathbf{0})]_N \|{}_{ \overline{\varOmega}_N \times[0,T]}}{\alpha}\}, \forall \ t \ {\in\,} [0,T], \end{array}\end{aligned} $$
(10)

where [.]N denotes the restriction of a function defined on \(\overline {\varOmega }\) to \( \overline {\varOmega }_N\). Therefore, problem (9) is well-posed independently of ε and N. Also, the result (10) can be viewed as a uniform stability property of the semidiscretization process.

The local error at any time t ∈ [0, T], at the grid point \(x_i \in \overline {\varOmega }_N, \ i = 1,\ldots N-1\), is given by

$$\displaystyle \begin{aligned} \upsilon_{i,N}(t) \equiv L_{\boldsymbol{\varepsilon}} \mathbf{u}(x_i,t) - {(L_{\boldsymbol{\varepsilon},N} [\mathbf{u}(x,t)]_N)_i}.\end{aligned} $$
(11)

Taking into account that the contribution of the time derivatives to the local error is zero, using appropriate Taylor expansions and the estimates (7) and the same technique as in [9] we prove that

$$\displaystyle \begin{aligned} \Vert \upsilon_N \Vert_{\overline{\varOmega}_N} \le C (N^{-1} \ln N)^2.\end{aligned} $$
(12)

Combining this result of uniform consistency and the uniform stability, the following uniform convergence result for the spatial semidiscretization is deduced.

Theorem 3

The global error associated to the spatial discretization (9) on the Shishkin mesh (8) satisfies

$$\displaystyle \begin{aligned} \|[\mathbf{u}(x,t)]_{N}-{\mathbf{U}}_{N} (t)\|{}_{\overline{\varOmega}_N}\le C (N^{-1} \ln N)^2, \quad \forall \ t \in [0,T].\end{aligned} $$
(13)

Proof

See [5].

4 The Fully Discrete Scheme: Uniform Convergence

The second step to construct our numerical algorithm consists of integrating in time, numerically, the family of initial value problems (9) introduced in previous section. For simplicity, we consider a uniform mesh \(\overline {w}_M = \{t_m = m \tau , \ m = 0, 1, \ldots , M\}\) , with τ = T∕M. Let us denote by \({\mathbf {U}}^m = (U_{1}^{m}, U_{2}^{m})^T\) the approximations to u(t m) = (u 1(t m), u 2(t m))T on the grid points of \(\overline {\varOmega }_N\) at each time level t m, m = 0, 1, …, M. In order to get an efficient integration process we have chosen a linearized variant of the fractional implicit Euler method. Then, the fully discrete scheme can be written as

$$\displaystyle \begin{aligned} \left\{\!\!\begin{array}{l} {\mathbf{U}}_N^0 = {\mathbf{U}}_N(0) ,\\ {} \mbox{ For }m = 0, 1, \ldots, M -1,\\ {} \mbox{ First half step}\\ \begin{array}{l} \left \{\begin{array}{l} U_{N,0,1}^{m+1/2} = g_{1,0}(t_{m+1}),\\ \displaystyle{\frac {U_{N,i,1}^{m+1/2}-U_{N,i.1}^{m}}{\tau} }+(\mathscr{L}_{N,\boldsymbol{\varepsilon},1} {\mathbf{U}}_N^{m+1/2} )_i + a_1\left(x_i,t_{m+1},{\mathbf{U}}_{N,i}^{m}\right) +\\ \qquad \qquad \qquad \qquad \displaystyle{\frac{\partial a_1}{\partial u_1} \left(x_i,t_{m+1},{\mathbf{U}}_{N,i}^{m}\right)\left(U_{N,i,1}^{m+1/2} - U_{N,i,1}^{m}\right)}= 0, \ i = 1,\ldots, N-1,\\ {} \ U_{N,N,1}^{m+1/2} = g_{2,0}(t_{m+1}), \end{array} \right.\\ {} U_{N,i,2}^{m+1/2} = U_{N,i,2}^{m}, \ i = 0,\ldots, N, \\ {} \end{array} \\ {} \mbox{ Second half step}\\ \begin{array}{l} U_{N,i,1}^{m+1} =U_{N,i,1}^{m+1/2} , \ i = 0,\ldots, N, \\ {} \end{array} \\ \left \{\begin{array}{l}U_{N,0,2}^{m+1} = g_{1,1}(t_{m+1}),\\ \displaystyle{\frac {U_{N,i,2}^{m+1}-U_{N,i,2}^{m+1/2}}{\tau} } +(\mathscr{L}_{N,\boldsymbol{\varepsilon},2} {\mathbf{U}}_N^{m+1} )_i + a_2\left(x_i, t_{m+1},{\mathbf{U}}_{N,i}^{m+1/2}\right) +\\ \qquad \qquad \qquad \displaystyle{\frac{\partial a_2}{\partial u_2} \left(x_i,t_{m+1},{\mathbf{U}}_{N,i}^{m+1/2}\right)\left(U_{N,i,2}^{m+1} - U_{N,i,2}^{m+1/2}\right)}= 0, \ i = 1,\ldots, N-1,\\ {} \ U_{N,N,2}^{m+1} = g_{2,1}(t_{m+1}). \end{array} \right. \end{array}\right.\end{aligned} $$
(14)

Note that this algorithm has many advantages from a numerical point of view. The first one is that the linearization which we have carried out avoids having to solve nonlinear systems at each time level; on the other hand, the splitting by components decouples the approximation of both components, and therefore only one tridiagonal linear system must be solved at each half step. The combination of these facts makes that the computational cost of the algorithm is considerably smaller than the associated one to classical implicit schemes.

Next, we state the main theoretical results which permit to prove that this method is unconditionally and uniformly convergent of first order in time.

Theorem 4

The resolution of the half steps defined in (14) involves systems of the form

$$\displaystyle \begin{aligned} A_{N,j} U_{N}^{m+j/2}=b_{N,j},\ j=1,2, \end{aligned}$$

whose matrices are tridiagonal, inverse positive and satisfy

$$\displaystyle \begin{aligned}\|(A_{N,j})^{-1}\|{}_{\infty}\le \frac{1}{1+\beta\tau}, \ j=1,2.\end{aligned} $$
(15)

This result plays a main role to obtain the uniform and unconditional stability, as well as the uniform and unconditional consistency of first order for method given by (14). Such properties are stated in the following two theorems.

Theorem 5 (Uniform Stability)

Assuming the following Lipschitz type restrictions on the reaction terms

$$\displaystyle \begin{aligned}\begin{array}{c} \displaystyle c_1\ge\frac {\partial a_{i}}{\partial u_i}(x,t,\mathbf{u}), \ i=1,2,\\ {} \displaystyle \|\mathbf{A} (x,t,\mathbf{u})- \mathbf{A} (x,t,\tilde{\mathbf{u}})\|\le c_2 \|\mathbf{u}-\tilde{\mathbf{u}}\|,\\ {} \displaystyle \left|\frac {\partial a_{i}}{\partial u_i}(x,t,\mathbf{u}) u_i- \frac {\partial a_{i}}{\partial u_i}(x,t,\tilde{\mathbf{u}})\tilde{u}_i \right| \le c_3 | u_i-\tilde{u}_i |,\ i=1,2,\\ \end{array}\end{aligned} $$
(16)

two solutions of (14), obtained with different initial conditions \({\mathbf {U}}_N^0\) and \(\widetilde {\mathbf {U}}_N^0\), satisfy

$$\displaystyle \begin{aligned}\|{\mathbf{U}}^{m+1}_N-\widetilde{\mathbf{U}}^{m+1}_N\|{}_{\varOmega_N}\le \frac{1+c\tau} {1+\beta\tau} \|{\mathbf{U}}^{m}_N-\widetilde{\mathbf{U}}^{m}_N\|{}_{\varOmega_N}, \end{aligned} $$
(17)

where c depends only of c 1, c 2 and c 3.

To study the consistency of the discretization, we introduce in a standard way the concept of the local error at time t m, denoted by \(e_N^m\), as the difference \({\mathbf {U}}_{N}(t_m) - \widehat {\mathbf {U}}_{N}^m\), being \(\widehat {\mathbf {U}}_{N}^m \) the solution of

$$\displaystyle \begin{aligned} \begin{array}{l} \begin{array}{l} \left \{\begin{array}{l} \widehat{U}_{N,0,1}^{m-1/2} = g_{1,0}(t_{m}),\\ \displaystyle{\frac {\widehat{U}_{N,i,1}^{m-1/2}-U_{N,i.1}(t_{m-1})}{\tau} }+(\mathscr{L}_{N,\boldsymbol{\varepsilon},1} \widehat{\mathbf{U}}_N^{m-1/2} )_i + a_1\left(x_i,t_{m},{\mathbf{U}}_{N,i}(t_{m-1})\right) +\\ \qquad \qquad \qquad \qquad \displaystyle{\frac{\partial a_1}{\partial u_1} \left(x_i,t_{m},{\mathbf{U}}_{N,i}({t_{m-1}})\right)\left(\widehat{U}_{N,i,1}^{m-1/2} - U_{N,i,1}(t_{m-1})\right)}= 0,\\ \qquad \qquad \qquad \qquad i = 1,\ldots, N-1,\\ {} \ \widehat{U}_{N,N,1}^{m-1/2} = g_{2,0}(t_{m}), \end{array} \right.\\ {} \widehat{U}_{N,i,2}^{m-1/2} = U_{N,i,2}({t_m}), \ i = 0,\ldots, N, \\ {} \end{array} \\ {} \begin{array}{l} \widehat{U}_{N,i,1}^{m} =\widehat{U}_{N,i,1}^{m-1/2} , \ i = 0,\ldots, N, \\ {} \end{array} \\ \left \{\begin{array}{l}\widehat{U}_{N,0,2}^{m} = g_{1,1}(t_{m}),\\ \displaystyle{\frac {\widehat{U}_{N,i,2}^{m}-\widehat{U}_{N,i,2}^{m-1/2}}{\tau} } +(\mathscr{L}_{N,\boldsymbol{\varepsilon},2} \widehat{\mathbf{U}}_N^{m} )_i + a_2\left(x_i, t_{m},\widehat{\mathbf{U}}_{N,i}^{m-1/2}\right) +\\ \qquad \qquad \qquad \displaystyle{\frac{\partial a_2}{\partial u_2} \left(x_i,t_{m},\widehat{\mathbf{U}}_{N,i}^{m-1/2}\right)\left(\widehat{U}_{N,i,2}^{m} - \widehat{U}_{N,i,2}^{m-1/2}\right)}= 0,\\ \qquad \qquad \qquad i = 1,\ldots, N-1,\\ {} \ \widehat{U}_{N,N,2}^{m} = g_{2,1}(t_{m}). \end{array} \right.\end{array} \end{aligned} $$
(18)

Then, the following consistency result follows.

Theorem 6

Under the previous assumptions for the data of (1), it holds

$$\displaystyle \begin{aligned}\|e_N^m\|{}_{\varOmega_N}\le C M^{-2},\quad \forall \tau \ \in (0,\tau_0], \ m = 1, 2, \ldots, M. \end{aligned} $$
(19)

Proof

It is analogue to the proof of Theorem 7 in [5].

To conclude the analysis of the time integration process we introduce the global error in time, at time t m as

$$\displaystyle \begin{aligned}E_N^m\equiv{\mathbf{U}}_{N}(t_{m})-{\mathbf{U}}_{N}^m\end{aligned}$$

and combining the last two results the following uniform and unconditional first order convergence result is deduced.

Theorem 7

Under the previous assumptions for the data of (1), the global error of the time discretization holds

$$\displaystyle \begin{aligned} \| E_N^m\|{}_{\varOmega_N}\le C M^{-1}. \ m=1,\ \ldots M. \end{aligned} $$
(20)

Finally, combining the results (3) and (20) we are ready to state the main result for our numerical algorithm.

Theorem 8

Under the previous assumptions for (1), the global errors for (14), satisfy that

$$\displaystyle \begin{aligned} \max_{0\le m \le M, \ 0\le i \le N} \|{\mathbf{U}}_{N,i}^m - \mathbf{u}(x_i,t_m)\| \le C \left((N^{-1} \ln N)^2+ M^{-1}\right), \end{aligned} $$
(21)

where, as we mentioned before, C is a positive constant independent of the diffusion parameters ε 1, ε 2 and the discretization parameters N and M. Then, the fully discrete scheme is a uniformly and unconditionally convergent method of first order in time and of almost second order in space.

5 Numerical Results

In this section we show the numerical results obtained with the algorithm proposed here to solve a test problem of type (1). The data of the example are given by

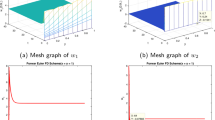
$$\displaystyle \begin{aligned}\begin{array}{l} \displaystyle a_{1}(x,t,\mathbf{u}) = 2 u_1 + t (u_1 -\sin{}(u_1)) - u_2 - t e^{3t}\sin{}(\pi x) ,\\ {} \displaystyle a_{2}(x,t,\mathbf{u}) = - u_1 + 2 u_2 + (1-e^{-t}) \displaystyle\frac{u_2}{1+u_2^2},\\ {} \mathbf{g_0}(t) = \mathbf{g_1}(t) =(8t+e^{-8t},16t+e^{-16t})^T, \ \mathbf{\boldsymbol{\varphi}}(x) = (1,1)^T. \end{array}\end{aligned} $$
(22)

Figure 1 displays the numerical approximation for both components, for specific small values of ε 1 and ε 2, showing the boundary layers at x = 0 and x = 1.

Fig. 1
figure 1

Components 1 (left) and 2 (right) of problem (22) for ε 1 = 10−6, ε 2 = 10−4 with N = M = 32

Full size image

As the exact solution is unknown, to approximate the norm of errors

$$\displaystyle \begin{aligned}\|{\mathbf{U}}^m_{N,i}-\mathbf{u}(x_i,t_m) \|, \ i = 0, 1, \ldots, N, \ m = 0, 1, \ldots, M,\end{aligned}$$

we use a variant of the double-mesh principle (see [7] for instance), i.e, we calculate

$$\displaystyle \begin{aligned} { d}^{N,M}_{\boldsymbol{\varepsilon},j} = \max_{0\le m \le M } \max_{0\le i \le N}\| U^m_{N,i,j }- \widehat{U}^{2m}_{2N,2i,j}\|, \ {d}^{N,M}_j = \max_\varepsilon {d}^{N,M}_{\boldsymbol{\varepsilon},j}, \quad j=1,2, \end{aligned} $$
(23)

where \(\{\widehat {\mathbf {U}}^m_{2N}\}\) is the numerical solution on a finer mesh \(\{(\hat x_i,\hat {t}_m)\}\) that is composed of the mesh points of the coarse mesh joint to their midpoints, i.e.,

$$\displaystyle \begin{aligned} \begin{array}{c} \hat{x}_{2i} = x_i, \ \ i = 0,\ldots, N, \quad \hat{x}_{2i+1} = (x_i+x_{i+1})/2, \ \ i = 0,\ldots,N-1, \\ \hat{t}_{2m} = t_m, \ \ m = 0,\ldots, M, \quad \hat{t}_{2m+1} = (t_m+t_{m+1})/2, \ \ m = 0,\ldots,M-1. \end{array} \end{aligned} $$
(24)

From the double-mesh differences computed in (23), we obtain the corresponding orders of convergence by

$$\displaystyle \begin{aligned} { p^{N,M}_{\boldsymbol{\varepsilon},j}}=\displaystyle\log ({ d}^{N,M}_{\boldsymbol{\varepsilon},j}/{ d}^{2N,2M}_{\boldsymbol{\varepsilon},j})/\log 2, \ { p}^{uni}_j=\log ({ d}^{N,M}_j/{ d}^{2N,2M}_j)/\log 2, \quad j=1,2. \end{aligned} $$
(25)

Table 1 shows maximum errors and their corresponding orders of convergence for some values of ε 2 when ε 1 is in the set R = {ε 1;ε 1 = ε 2, 2−2ε 2, …, 2−32}, and some values of the discretization parameter N and M = N∕4. Concretely, each cell of this table has four numbers which, from above to below, correspond to \({ d}^{N,M}_{\boldsymbol {\varepsilon },1},p^{N,M}_{\boldsymbol {\varepsilon },1} , { d}^{N,M}_{\boldsymbol {\varepsilon },2} \) and \(p^{N,M}_{\boldsymbol {\varepsilon },2} \). From them, the uniformly convergent behavior of the method can be observed; concretely, for large values of ε 2 clearly we see first order of convergence for both components; for smaller values of ε 2, for the first component we again observe first order and for the second component almost second appears.

Table 1 Maximum errors and orders of convergence for problem (22)
Full size table

To highlight the uniformly convergent behavior in space, we have made a second table (see Table 2), where we diminish the influence of the errors in time by taking M = 4N. From it, we observe more clearly the almost second order of uniform convergence in space of the algorithm, according to the theoretical results.

Table 2 Maximum errors and orders of convergence for problem (22)
Full size table

6 Conclusions

In this work we design, analyze and test a new numerical method for solving semilinear, time dependent, singularly perturbed diffusion reaction systems. The method is the result of combining a standard central difference scheme on a special mesh of Shishkin type, to discretize in space, and a linearized version of the fractional implicit Euler method which permits to split by components the linear systems involved in the time integration process. It is shown that the method is uniformly convergent of almost second order in space and of first order in time; besides, the computational cost of this numerical algorithm is very low because only two small tridiagonal systems per time step must be solved to advance in time.