Multi-Fidelity for MDO Using Gaussian Processes

Abstract

The challenges of handling uncertainties within an MDO process have been discussed in Chapters 6 and 7. Related concepts to multi-fidelity are introduced in this chapter. Indeed, high-fidelity models are used to represent the behavior of a system with an acceptable accuracy. However, these models are computationally intensive and they cannot be repeatedly evaluated, as required in MDO. Low-fidelity models are more suited to the early design phases as they are cheaper to evaluate. But they are often less accurate because of simplifications such as linearization, restrictive physical assumptions, dimensionality reduction, etc. Multi-fidelity models aim at combining models of different fidelities to achieve the desired accuracy at a lower computational cost. In Section 8.2, the connection between MDO, multi-fidelity, and cokriging is made through a review of past works and system representations of code architectures.

1 Introduction

The challenges of handling uncertainties within an MDO process have been discussed in Chapters 6 and 7. Related concepts to multi-fidelity are introduced in this chapter. Indeed, high-fidelity models are used to represent the behavior of a system with an acceptable accuracy. However, these models are computationally intensive and they cannot be repeatedly evaluated, as required in MDO. Low-fidelity models are more suited to the early design phases as they are cheaper to evaluate. But they are often less accurate because of simplifications such as linearization, restrictive physical assumptions, dimensionality reduction, etc. Multi-fidelity models aim at combining models of different fidelities to achieve the desired accuracy at a lower computational cost. In Section 8.2, the connection between MDO, multi-fidelity, and cokriging is made through a review of past works and system representations of code architectures.

Then, the rest of this chapter is divided into two main parts. First, in Section 8.3, a general model for cokriging is described that is based on the linear combination of independent (latent) processes. It is shown how, through its covariance structure, this model can represent all types of couplings between codes, whether they are serial (Markovian), fully coupled, or parallel. Second, in Section 8.4, optimization approaches that use multiple outputs cokriging model are presented. They can work with any type of correlated outputs, including multi-fidelity outputs. They are generalizations of the EGO algorithm (Jones et al. 1998) where not only the next set of inputs but also the fidelity level changes at each iteration. The main method is called SoS for Step or Stop. The benefits brought by SoS are illustrated with a series of analytical test cases that mimic three typical types of multi-fidelity: mesh size variation in finite element like codes, number of samples in Monte Carlo simulations, and time steps in dynamical systems.

2 MDO and Multi-Fidelity: Past Works

2.1 A Brief Overview of Multi-Fidelity for MDO

2.1.1 Multi-Fidelity for Design Within a Single Discipline

The topic of multi-fidelity for design is already profuse in contributions. Two surveys of multi-fidelity methods have been performed by Fernández-Godino et al. (2016) and Peherstorfer et al. (2018). The analysis of complex systems such as uncertainty propagation, sensitivity analysis, or optimization requires repeated model evaluations at different locations in the design space which typically cannot be afforded with high-fidelity models. Multi-fidelity techniques aim to speed up these analyses by capitalizing on models of various accuracies. Multi-fidelity methodologies perform model management that is to say, they balance the fidelity levels to mitigate cost and ensure the accuracy in analysis. In the review of Peherstorfer et al., the authors classified the multi-fidelity techniques in three categories: adaptation, fusion, and filtering. The adaptation category encompasses the methods that enhance the low-fidelity models with results from the high-fidelity ones while the computation proceeds. An example is given by the model correction approach (Kennedy and O’Hagan 2000) where an autoregressive process is used to reflect the hierarchy between the accuracy of the various outputs. The fusion techniques aim to build models by combining low and high-fidelity model outputs. Two examples of fusion techniques are the cokriging (Myers 1982; Perdikaris et al. 2015) and the multilevel stochastic collocation (Teckentrup et al. 2015). Finally, the filtering consists in calling low-fidelity models to decide when to use high-fidelity models (e.g., multi-stage sampling).

The early multi-fidelity optimization techniques were developed to alternate between the computationally inexpensive simplified models (typically metamodels, also known as surrogates) and the more accurate and costly ones: although it would be preferred to optimize the simulator with high accuracy, low-fidelity experiments can help ruling out some uninteresting regions of the input space (or on the contrary help finding interesting ones) while preserving the computational budget. A popular example of such alternation between low and high-fidelity models can be found in Jones et al. (1998). The use of metamodels allows to decide both which input parameters and which model fidelity should be chosen within the remaining computational budget (Huang et al. 2006).

Then, another philosophy emerged. Instead of replacing high-fidelity models by low-fidelity models in sequential phases, new techniques have been proposed to synthesize all information of various fidelities by weighting them. Bayesian statistics and in particular cokriging are approaches to merge models. Multi-fidelity Bayesian optimization methods have been explored in several articles (Forrester et al. 2007; Keane 2012; Sacher 2018), and an original contribution will be detailed in Section 8.4.

2.1.2 Multi-Fidelity and MDO

Until now, contributions in multi-fidelity optimization that, by default, tackle single discipline optimization problem have been mentioned. For multidisciplinary problems, because of the numerous subsystems that are interacting, multi-fidelity is still principally used at the subsystem level and the above references apply.

In addition, there is a body of works that studies the implementation of multi-fidelity optimization specifically in MDO problems. To further combine multi-fidelity optimization approaches with MDO formulations (see Chapter 1 for more details on deterministic MDO formulations), it is necessary to consider the organization of the disciplines and the surrogate modeling interactions. Several works have combined surrogate models of the computationally intensive disciplines with MDO formulations.

Sellar et al. (1996) presented a response surface-based CSSO (Concurent SubSpace Optimization) to reduce the computation cost, while (Simpson et al. 2001) explored the combination of Kriging and MDF (MultiDisciplinary Feasible—MDF) architecture. Sobieski and Kroo (2000) described a collaborative optimization formulation which utilizes the Response Surface Method (RSM). Paiva et al. compared polynomial response surfaces, Gaussian Processes, and neural networks for a MDF process (Paiva et al. 2010). Even if these MDO studies replace high-fidelity models by surrogate models, they do not manage model fidelities. Only a limited number of studies, cited hereafter, focus on the adaptation of multi-fidelity to multidisciplinary problems.

Allaire et al. (2010) proposed a Bayesian approach to multi-fidelity MDO. The method focuses on the probabilistic quantification of the model inadequacy, which is related to model fidelity. The model fidelity is managed using a belief that a model is true given that the true model is in the set of the considered models. The approach consists in solving a deterministic MDO problem with a fixed modeling level for the different disciplines. Then, based on the estimated optimal design, an evaluation of the performance and constraint variances is carried out. If the variances are too important, a second problem is solved to identify which discipline modeling uncertainties are the most influential (using Sobol measures). The level of fidelity of these disciplines is increased and the approach is repeated. Allaire et al. outlined that this approach does not guarantee the determination of a global optimum but it alleviates the challenge of managing several disciplines and modeling levels in a single MDO problem. This approach has been extended by Christensen (2012) to appropriately account for interdisciplinary couplings in a Bayesian approach to multi-fidelity MDO. The proposed process breaks the coupling loop into a series of disciplinary feedforward evaluations which may be computed sequentially. The method is a first attempt to account for coupled subsystems and multi-fidelity, and it facilitates the estimation of the objectives and constraints. But it only provides an approximation of the coupling variable uncertainties as the feedback-feedforward problem is decomposed and the multidisciplinary consistency is not ensured.

Zadeh and Toropov (2002) described a Collaborative Optimization (CO) formulation that solves MDO problems with high and low-fidelity models. At the discipline level optimization, a corrected low-fidelity simulation model is used. It combines high and low-fidelity simulations with model building (based on design of experiments and mathematical approximation). The mathematical aggregation of the simulations is carried out with polynomials and least squares for the determination of the polynomial hyperparameters. However, the construction of the multi-fidelity models used in CO is done off-line, without any model update.

March and Willcox (2012) proposed two methods to parallelize MDO. The first strategy decomposes the MDO process into multiple subsystem optimizations that are solved in parallel. The second technique defines a set of designs to be evaluated with computationally expensive simulations, runs these evaluations in parallel, and then solves a surrogate-based MDO problem. Both methods are examples of multi-fidelity optimization in MDO.

Wang et al. (2018) developed a multi-fidelity MDO framework with a switching mechanism between the different fidelity levels. First, an initial MDO formulation and a fidelity level are selected to start the search process. During the MDO iterations, if the switching criterion is met, the optimization process stops, increments the model fidelity, and updates the MDO architecture (if necessary, changes the MDO formulation). The authors employed the Adaptive Model Switching (AMS) (Mehmani et al. 2015). This criterion estimates if the uncertainty associated with the current level of fidelity for the model output dominates the latest improvement in normalized objective function.

2.2 From Code Interaction to Cokriging

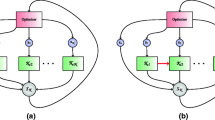
Simulation codes, as soon as they reach a minimal level of complexity, are made of separate subprograms that interact with each other. This is one of the working assumptions behind MDO. Such nested codes are composed of modules that are connected as sketched in Figure 8.1 where z are the inputs to the codes and y _i the associated scalar output of code i: fully coupled models, on the left of Figure 8.1, are the central topic of multidisciplinary optimization (cf. the disciplinary loops described in Chapter 1). When some of the feedback links are removed, the structure can become serial or parallel. Any nested code is a composition of pairs of programs connected in a fully coupled, serial, and parallel manner.

Fig. 8.1

Nesting possibilities for two codes. From left to right: fully coupled, series, and parallel

A multi-fidelity simulation is a special type of nested code where each output corresponds to an approximation of the same quantity, but with different levels of accuracy and computational costs. For example, in aerodynamics, y ₁ and y ₂ could both describe the drag of an airfoil but y ₁ would result from the Euler equations that neglect fluid viscosity, while y ₂ would stem from the complete Navier–Stokes equations. In general, multi-fidelity codes can have any of the fully coupled, series, or parallel structure. In the previous aerodynamics example, a serial code structure would have y ₁ as an input to y ₂ in order to accelerate the non-linear iterations; vice versa, in a parallel implementation, y ₂ could stand alone and the Navier–Stokes equations would be solved from another initial guess.

Describing uncertainties is an essential part of many codes in the fields of neutronics, reliability analysis, etc., and is usually done through Crude Monte Carlo (CMC) simulations. CMC simulations make an important class of multi-fidelity models where a code with stochastic output is run independently several times before averaging all outputs. The fidelity grows with the number of samples of the CMC simulation, and the result of a code can always be made more accurate by adding more samples, but this comes with an increase of the cost.

The most general approach to multi-fidelity is the addition to the high-fidelity code structure of statistical models (i.e., metamodels). The latter are built from a set of simulation inputs-outputs, and they provide a computationally efficient approximation to the code (or part of the code) output that can mitigate the computational burden. Kriging (or Gaussian Process Regression) has proven to be a powerful method to approximate computer codes (Santner et al. 2003). In the current chapter, we will focus on kriging and its relation to the code architecture, with an emphasis on kriging for multiple outputs.

The idea behind multi-output models is that the (loose) dependence between the different outputs can be exploited to get more accurate models: since y ₁ carries some information about y ₂, it is interesting to build a joint model on (y ₁, y ₂) even if we are only interested in predicting y ₂. We use in this chapter the name cokriging to refer to GP models for multivariate outputs. This term has been coined in the geostatistic literature (Cressie 1992), but other communities can refer to the same model as multi-output or dependent GP models (Boyle and Frean 2005; Fricker et al. 2013).

Cokriging models exploit the linear dependence (i.e., the correlation) between the different outputs to improve both the predictions and the uncertainty measures of the statistical models. Early contributions to cokriging can be found in the geostatistic literature in the late 1970s and early 1980s (Journel and Huijbregts 1978; Myers 1982). The main challenge when it comes to modeling multi-output codes is to define a valid covariance structure over the joint distribution of all outputs. Although a large number of covariances have been proposed in the literature (see Section 8.3.3 and Alvarez et al. (2012) for a detailed review), a very common approach for building these multivariate covariances is the linear model of coregionalization (Goovaerts et al. (1997) and Section 8.3.1).

3 Cokriging for Multi-Fidelity Analysis

3.1 Cokriging by Linear Model of Coregionalization

3.1.1 General Presentation of the Model

Standard kriging models (that have been introduced in Chapter 3) can be extended to multiple outputs that are learned together. One would like to learn together the function y ₁(⋅), …, y _m(⋅) from observations made at the sets of points Z ₁, …, Z _m, respectively. Generalizing kriging, the statistical model we rely on is a set of dependent Gaussian processes (Y ₁(⋅), …, Y _m(⋅)). This is called cokriging. Cokriging models can be seen as regular kriging models with a special ordering of the observations. For compatibility with the multi-fidelity context, we shall assume that the outputs have constant execution times that are ranked in increasing order, t ₁ ≤… ≤ t _m. For example, in a 2 levels multi-fidelity case, one could partition the vector of observations as the vector of observations of level 1 first followed by the observations of level 2, y(Z) = [y ₁(Z ₁), y ₂(Z ₂)], N = Card(Z ₁) + Card(Z ₂), and resort to the model of Kriging as presented in Chapter 3 (for the mean prediction and the covariance equation). There is no constraint on the relationship between y ₁(⋅) and y ₂(⋅) which can represent different physical quantities. For example, cokriging could be an approach to the handling of qualitative variables, with y ₂(⋅) representing the qualitative variable. Thus, cokriging can represent the multi-fidelity problems where all y _i(⋅)’s describe the same quantity, but it is more general.

The difficulty associated to cokriging is to generalize the covariance function to multiple outputs k _(ij)(z, z′) = Cov(Y _i(z), Y _j(z′)). In a few particular cases, the multi-output covariance function is directly defined by algebraic operations on the usual (single output) kriging kernels. For example, kriging with derivatives involves deriving the kriging kernel, see (Laurent et al. 2019). But in general, there are many ways in which multi-output kernels can be created. They just have to guarantee that the kernels are positive semi-definite, i.e., they must yield positive semi-definite covariance matrices for any design of experiments $\mathcal {Z}$. In addition, kernels have to strike a compromise between tunability, so that they can adapt to the data at hand, and sparsity in the number of internal parameters in order to be easy to learn and to avoid overfitting. Sparsity is a challenge with m outputs as there are m(m + 1)∕2 kernels to define for all (Y _i(⋅), Y _j(⋅)) pairs.

This chapter focuses on the simple yet versatile Linear Model of Coregionalization (LMC) (Fricker et al. 2013) which provides a systematic way to build cokriging models. LMC cokriging models are simply generated as linear combinations of a set of GPs, T _i(⋅),

$$\displaystyle \begin{aligned} Y(\mathbf{z}) = \begin{pmatrix} Y_1(\mathbf{z}) \\ Y_2(\mathbf{z}) \\ \ldots \\ Y_m(\mathbf{z}) \end{pmatrix} = Q \begin{pmatrix} T_1(\mathbf{z}) \\ T_2(\mathbf{z}) \\ \ldots \\ T_m(\mathbf{z}) \end{pmatrix} = Q T(\mathbf{z}) ~. \end{aligned} $$

(8.1)

Here, the T _i(⋅)’s are independent, non-observed, latent GPs supposed to underly what is specific to each output i. The T _i(⋅)’s have unit variance and spatial covariances (i.e., correlations)

$$\displaystyle \begin{aligned} \begin{aligned} & r_i(\mathbf{z},\mathbf{z}') \mathrel{\mathop:}= \text{Cov}(T_i(\mathbf{z}),T_i(\mathbf{z}')) \\ & \text{Cov}(T_i(\mathbf{z}),T_j(\mathbf{z}')) = 0 \quad , \quad \forall i \ne j ~. \end{aligned} \end{aligned} $$

(8.2)

There must be at least m latent GPs and Q must be full rank for the final kriging covariance matrix, K, to be invertible. In the LMC, the latent processes T _i(⋅) describe the covariances in the Z space, while the Q matrix determines the covariances between outputs y _i(⋅), i = 1, …, m. A generalization of the local GP variance σ ² to multivariate outputs GPs is the m × m inter-group covariance,

$$\displaystyle \begin{aligned} {\Sigma_2} = \text{Cov}(Y(\mathbf{z}),Y(\mathbf{z})) = Q \text{Cov}(T(\mathbf{z}),T(\mathbf{z})) Q^\top = Q Q^\top. \end{aligned} $$

(8.3)

With stationary GPs, the inter-group covariance matrix does not account for space and should not be mistaken with the much larger ($\sum _i^m N_i \times \sum _i^m N_i$) covariance matrix of the kriging equations,

$$\displaystyle \begin{aligned} K &=& \text{Cov}\left( \begin{pmatrix} Y_1({\mathbf{Z}}_1) \\ Y_2({\mathbf{Z}}_2) \\ \ldots \\ Y_m({\mathbf{Z}}_m) \end{pmatrix}, \begin{pmatrix} Y_1({\mathbf{Z}}_1) \\ Y_2({\mathbf{Z}}_2) \\ \ldots \\ Y_m({\mathbf{Z}}_m) \end{pmatrix} \right) \\ &=&\begin{bmatrix} \text{Cov}(Y_1({\mathbf{Z}}_1),Y_1({\mathbf{Z}}_1)) & \ldots & \text{Cov}(Y_1({\mathbf{Z}}_1),Y_m({\mathbf{Z}}_m)) \\ \vdots & \ddots & \vdots\\ \text{Cov}(Y_m({\mathbf{Z}}_m),Y_1({\mathbf{Z}}_1)) & \ldots & \text{Cov}(Y_m({\mathbf{Z}}_m),Y_m({\mathbf{Z}}_m)) \\ \end{bmatrix} \end{aligned} $$

(8.4)

where each Cov(Y _i(Z _i), Y _j(Z _j)) is a N _i × N _j submatrix of generic term Cov(Y _i(z ^k), Y _j(z ^l)), z ^k ∈ Z _i, z ^l ∈ Z _j. In LMCs, the kernel is generalized to multiple outputs and becomes the following m × m matrix,

$$\displaystyle \begin{aligned} k(\mathbf{z},\mathbf{z}') &\mathrel{\mathop:}= \text{Cov}(Y(\mathbf{z}),Y(\mathbf{z}')) = Q \,\text{diag}(r_i(\mathbf{z},\mathbf{z}'))\, Q^\top = \sum_{i=1}^m r_i(\mathbf{z},\mathbf{z}') Q^i {Q^i}^\top \\ &\mathrel{\mathop:}= \sum_{i=1}^m r_i(\mathbf{z},\mathbf{z}') {\mathbf{V}}^i ~, \end{aligned} $$

(8.5)

where V ⁱ are the coregionalization matrices, which clarifies the name Linear Model of Coregionalization.

Given an inter-group covariance matrix Σ₂, there are many ways to define Q because the factorization of Equation (8.3) is not unique (e.g., Cholesky and eigen-decomposition). Each factorization yields a different kernel k(⋅, ⋅) in Equation (8.5), hence different K and other covariance terms in the kriging equations. As it will be further explained, changing Q fundamentally changes the statistical model even if Σ₂ is fixed.

There is a need for a systematic way to choose the matrix Q. It is proposed to derive Q from the code architecture, or hypotheses about the code architecture.

The basic model, which is sketched in Figure 8.2, says that the code i takes as input z and the outputs of codes j ∈ E, and outputs a GP of the form:

$$\displaystyle \begin{aligned} \frac{Y_i(\cdot)}{\sigma_i} = \sum_{j \in E}b_{i,j} \frac{Y_{j}(\cdot)}{\sigma_{j}} + T_i(\cdot) ~. \end{aligned} $$

(8.6)

Fig. 8.2

Building block of the cokriging statistical model (Equation (8.6))

The σ _i’s are positive scaling factors and b _i,j is a scalar (the correlation between Y _i(⋅) and Y _j(⋅) if E contains only j). Such a structure should be read as: the output to code i is linearly linked to the outputs of its predecessors j ∈ E plus an independent latent process T _i(⋅). Note that $\frac {Y_i(\cdot )}{\sigma _i}$ does not necessarily have unit variance as σ _i is a scaling factor, not a variance (Equation (8.9) below will quantify the variance of Y _i(⋅)). Denoting as B the matrix of the b _i,j’s where b _i,i = 0, Q and B are related by

$$\displaystyle \begin{aligned} Q = D (I - B)^{-1}~. \end{aligned} $$

(8.7)

This is proved by writing Equation (8.6) as

$$\displaystyle \begin{aligned} D^{-1} Y(\cdot) = B D^{-1} Y(\cdot) + I\, T(\cdot) \end{aligned}$$

and solving for Y (⋅).

It will be easier to slightly change notations and write Q as a product of process scaling terms and interactions

$$\displaystyle \begin{aligned} Q = D P \mathrel{\mathop:}= \text{diag}(\sigma_i) P ~. {} \end{aligned} $$

(8.8)

The matrix of interactions between latent processes, P, is made of the terms ρ _i,j. P and B are linked by

$$\displaystyle \begin{aligned} P = (I - B)^{-1}~. \end{aligned}$$

A generic term of the cokriging kernel of Equation (8.5) can be rewritten with the scalings and interactions:

$$\displaystyle \begin{aligned} k^{(ij)}(\mathbf{z},\mathbf{z}') &= \text{Cov}(Y_i(\mathbf{z}),Y_j(\mathbf{z}')) = \text{Cov}(Q_{i.} T(\mathbf{z}),Q_{j.} T(\mathbf{z}')) \\ & = Q_{i.} \text{Cov}(T(\mathbf{z}),T(\mathbf{z}')) Q_{j.}^\top = Q_{i.} \text{diag}(r_k(\mathbf{z},\mathbf{z}')) Q_{j.}^\top \\ & \overset{(\text{8.8})}{=} \sum_{k=1}^m \sigma_i \sigma_j \rho_{i,k} \rho_{j,k} r_k(\mathbf{z},\mathbf{z}') {} \end{aligned} $$

(8.9)

Building a cokriging LMC boils down to choosing values for the σ _i’s and the ρ _i,j’s, choosing a particular ordering of the observations at the different levels (typically y(Z) = [y ₁(Z ₁), …, y _m(Z _m)], and calling in the usual kriging equations for the prediction and the covariance or their counterpart with trends). Because there may be a large number (m ²) of ρ _i,j’s, it will be useful to further impose structure on the model and make it sparser. In the following, we will see how the building block of Equation (8.6) can be composed to yield different Q’s. Two fundamental LMC will be explained, first the symmetrical and next the Markovian cokriging. Finally, the construction of such LMC based on the knowledge of the code structure is discussed.

3.1.2 Symmetrical Cokriging

A simple example of two codes that mutually depend on each other is firstly used like in the fully coupled relation of Figure 8.1. In this situation it is natural to assume that the cokriging model is made of two connected building blocks such as represented in Figure 8.3. The dependency between the processes,

$$\displaystyle \begin{aligned} \frac{Y_1(\cdot)}{\sigma_1} &= b_{1,2}\frac{Y_2(\cdot)}{\sigma_2} + T_1(\cdot) \\ \frac{Y_2(\cdot)}{\sigma_2} &= b_{2,1}\frac{Y_1(\cdot)}{\sigma_1} + T_2(\cdot) \end{aligned} $$

Fig. 8.3

A cokriging LMC model with 2 fully coupled outputs

is rewritten

$$\displaystyle \begin{aligned} \begin{pmatrix} Y_1(\cdot)/\sigma_1 \\ Y_2(\cdot)/\sigma_2 \end{pmatrix} ~=~ \frac{1}{1-b_{1,2}b_{2,1}} \begin{bmatrix} 1 & b_{1,2} \\ b_{2,1} & 1 \end{bmatrix} \begin{pmatrix} T_1(\cdot) \\ T_2(\cdot) \end{pmatrix} \end{aligned}$$

which is the instantiation when m = 2 of the previous general LMC, D ⁻¹Y (⋅) = (I − B)⁻¹T(⋅) = PT(⋅). The symmetrical LMC model for cokriging further simplifies P by assuming it is symmetrical. With this, the number of parameters in D and P falls from m + m ² to m + m(m − 1)∕2 = m(m + 1)∕2. The general expression for the kernel, k(z ⁱ, z′ ^j) = Cov(Y _i(z), Y _j(z′)), is the same as that in Equation (8.9) with ρ _i,j = ρ _j,i.

Note that if the symmetrical LMC model is adapted to fully coupled codes, it can be applied to any correlated codes like the parallel ones in Figure 8.1.

3.1.3 Markovian Cokriging

Let us now consider statistical models made of building blocks in series. They are called Markovian because each part only depends on the output of the previous part and z. In the literature, they are also known as autoregressive kriging (Kennedy and O’Hagan 2000) or LMC model with Cholesky decomposition (Fricker et al. 2013).

Such a relationship matches multi-fidelity codes where the output of a code can serve as input to a higher fidelity code. In this situation, one can consider that higher fidelity codes have more latent variables, i.e., there is a hierarchy of models. A common example is given by CMC simulations that are divided into groups, or by a Euler CFD simulation providing an initial state to a Navier–Stokes code. Figure 8.4 shows 3 blocks in series that are related through the relations,

$$\displaystyle \begin{aligned} \frac{Y_1(\cdot)}{\sigma_1} &= T_1(\cdot) \\ \frac{Y_2(\cdot)}{\sigma_2} &= b_{2,1} \frac{Y_1(\cdot)}{\sigma_1} + T_2(\cdot) \\ \frac{Y_3(\cdot)}{\sigma_3} &= b_{3,2} \frac{Y_2(\cdot)}{\sigma_2} + T_3(\cdot) \end{aligned} $$

or, by separating the Y ’s and the T’s and writing the result in matrix form,

$$\displaystyle \begin{aligned} D^{-1} Y(\cdot) = \begin{bmatrix} 1 & 0 & 0 \\ b_{2,1} & 1 & 0 \\ b_{3,2} b_{2,1} & b_{3,2} & 1\end{bmatrix} T(\cdot) = P T(\cdot) \end{aligned}$$

Fig. 8.4

A Markovian LMC cokriging model with 3 outputs in series

Notice how in the above equation the P matrix is lower triangular. This is a general feature of the Markovian cokriging model where

$$\displaystyle \begin{aligned} \frac{Y_i(\cdot)}{\sigma_i} &= b_{i,i-1} \frac{Y_{i-1}(\cdot)}{\sigma_{i-1}} + T_i(\cdot) \\ ~ &= b_{i,i-1} b_{i-1,i-2} \frac{Y_{i-2}(\cdot)}{\sigma_{i-2}} + b_{i,i-1} T_{i-1}(\cdot) + T_i(\cdot) = \ldots \\ ~ & = \sum_{j=1}^{i-1} \left( \prod_{k=j}^{i-1} b_{k+1,k}\right) T_j(\cdot) + T_i(\cdot). {} \end{aligned} $$

(8.10)

Equation (8.10) means that the P matrix is made of the coefficients

$$\displaystyle \begin{aligned} \begin{aligned} \rho_{i,j} & = \prod_{k=j}^{i-1} b_{k+1,k} \qquad \text{ if } j<i~,\\ ~ & = 1 \qquad \text{ if } j=i~,\\ ~ & = 0 \qquad \text{ if } j>i~. \end{aligned} {} \end{aligned} $$

(8.11)

The kernel of the Markovian cokriging model is then directly obtained by substituting the value of ρ _i,j into the expression for k(z ⁱ, z ^′j) in Equation (8.9) (the sum can be limited to the first min(i, j) < m terms).

The Markovian cokriging model has a reduced number of parameters making its covariance: besides the m σ _i’s, there are only m − 1 b _i+1,i’s to set from data (e.g., through likelihood maximization). m + (m − 1) = 2m − 1 parameters make the Markovian cokriging sparser than the symmetric model of section “Symmetrical Cokriging” which has m(m + 1)∕2 covariance parameters as soon as m ≥ 3.

3.1.4 LMC for General Nested Code Structures

Even though it is not necessary, matching the cokriging covariance and the code interaction structures allows to simplify the statistical model while keeping it interpretable. For example, when there is a hierarchy in the outputs, the Markovian statistical model is the simplest multi-output GP where the latent variables can be interpreted as a specific calculation performed by each module. It is always possible to fit any multi-output code with any statistical model. Putting a Markovian structure on a code that does not match this assumption means creating a hierarchy within the latent variables that does not exist. Using a symmetrical model for a code that is serial generates a computational complexity which could have been avoided. And of course, one can fall back on using independent GPs for each output, but this cancels any effort to share information between the GPs.

A good practice is thus to base the structure of the cokriging covariance on the dependencies of the code modules. This parameterization of the covariance can be inferred from the mix of series and parallel building blocks. As an example, let us consider the modules of code drawn in Figure 8.5. A direct translation of the interactions in terms of our statistical model is written as follows:

$$\displaystyle \begin{aligned} \frac{Y_1(\cdot)}{\sigma_1} &= T_1(\cdot)\\ \frac{Y_2(\cdot)}{\sigma_2} &= b_{2,1} \frac{Y_1(\cdot)}{\sigma_1} + b_{2,3} \frac{Y_3(\cdot)}{\sigma_3} + T_2(\cdot)\\ \frac{Y_3(\cdot)}{\sigma_3} &= b_{3,1} \frac{Y_1(\cdot)}{\sigma_1} + b_{3,2} \frac{Y_2(\cdot)}{\sigma_2} + T_3(\cdot)\\ \frac{Y_4(\cdot)}{\sigma_4} &= b_{4,2} \frac{Y_2(\cdot)}{\sigma_2} + b_{4,3} \frac{Y_3(\cdot)}{\sigma_3} + T_4(\cdot). \end{aligned} $$

Fig. 8.5

Example of a code mixing 4 modules in parallel and series

Solving for the Y ’s in terms of the T’s yields P, the matrix of interactions between the latent processes introduced in Equation (8.8). In addition, if we add the symmetries b _2,3 = b _3,2, b _2,1 = b _3,1, and b _4,2 = b _4,3, P becomes

$$\displaystyle \begin{aligned} P ~=~ \begin{bmatrix} 1 & 0 & 0 & 0 \\ \frac{b_{2,1}}{1-b_{2,3}} & \frac{1}{1-b_{2,3}^2} & \frac{b_{2,3}}{1-b_{2,3}^2} & 0 \\ \frac{b_{2,1}}{1-b_{2,3}} & \frac{b_{2,3}}{1-b_{2,3}^2} & \frac{1}{1-b_{2,3}^2} & 0 \\ \frac{2 b_{2,1} b_{4,2}}{1-b_{2,3}} & \frac{b_{4,2}}{1-b_{2,3}} & \frac{b_{4,2}}{1-b_{2,3}} & 1 \end{bmatrix}. \end{aligned}$$

One recognizes parallel and the series features in this interaction matrix: the mainly Markovian structure of the model makes P lower triangular apart from the 2 × 2 central submatrix which corresponds to the parallel blocks number 2 and 3. Up to a normalization constant, P ₄₁ is equal to the product b _2,1 × (b _4,2 + b _4,3), which is typical of Markovian models.

3.2 Illustrations

3.2.1 Presentation of the Test Cases

In order to qualify the efficiency of the previous cokriging models, a standard objective function is considered, modified for the purpose of studying multi-fidelity. A slight modification to the Branin function will be the basis of our tests:

$$\displaystyle \begin{aligned} \begin{aligned} \overline{z_1} &= 15 z_1 -5 , \quad \overline{z_2} = 15 z_2 \\ y(\mathbf{z}) & = \left( \overline{z_2} - \frac{5 {\overline{z_1}}^2}{4 \pi^2} + \frac{5 \overline{z_1}}{\pi} -6 \right)^2 + 10 \left(1 - \frac{1}{8\pi}\right) \cos{}(\overline{z_1}) +11 \\ & \quad - \exp\left(-\frac{(\overline{z_1}-0.5)^2}{15}\right). \end{aligned} \end{aligned} $$

(8.12)

The function is plotted in Figure 8.6. The modification aims at having only one global optimum at (0.543, 0.150) and two local optima. The modified Branin function will soon be further transformed with different perturbations to emulate mesh-based, Monte Carlo, and time-step simulators, which correspond to three different convergence behaviors.

Fig. 8.6

The modified Branin function of formula (8.12) which serves as the simulation of highest fidelity. The filled bullet is the global optimum, the empty bullets are the local optima

Mesh-based simulations (like finite-elements solvers) are mainly converging smoothly with the mesh size. They yield objectives that evolve continuously with the level of details and tend to an asymptotic objective function. Of course, this characterization of mesh-based simulations neglects possible numerical instabilities that occur with changes in discretization. The smooth convergence is emulated as a ponderation between the asymptotic objective function and a continuous perturbation (a quadratic polynomial). The weighting is a logarithm of the number of nodes (see Figure 8.7).

Fig. 8.7

Emulation of mesh-based multi-fidelity simulations by continuous perturbations of the Branin function

Monte Carlo based simulations are converging with an added white noise which decreases with the size of the random sample used. This noise, standing for the simulation error, follows the central limit theorem and its variance decreases in 1/(number of samples). Moreover, the white noise has no correlation in the space of the parameters (z ₁, z ₂). The effect of such fidelity levels is illustrated in Figure 8.8.

Fig. 8.8

Emulation of Monte Carlo based multi-fidelity simulations by added white noise perturbations of the Branin function

In the two previous examples, the simulation fidelity describes the degree of convergence of a simulation. Cokriging is also useful for discrete iterative simulations where the results of one step give the boundary conditions of the next one. Time or space iterated solvers are typical cases. Such time dependent simulations (like a discrete-time iterative MDO solver) are not converging toward an asymptotic solution, in the sense that the ending “time” (which may also be another dimension) is not approximated by previous times with an “error” that decreases with steps. Nevertheless, the intrinsic Markovian behavior of such a simulation is well suited to cokriging models. A third analytical test case is made of 4 steps of an autoregressive process (AR1) whose last iteration is the “high-fidelity” Branin objective function (see Figure 8.9).

Fig. 8.9

Illustration of the 4 AR time steps that make the third analytical test case

3.2.2 Test Cases Results

The kriging and cokriging models of the Mesh-based simulations displayed in Figure 8.7 are compared. The kriging model is adjusted over a 14 points design (10 points in Latin Hypercube Sampling (LHS) and four in the corners) evaluated on the mesh function with 10⁸ nodes (considered as the real function). For comparative purpose, two cokriging models, a symmetrical and a Markovian one (as described in Section 8.3.1), are adjusted with the same design plus 64 LHS points at the lower level (the one with 10⁴ nodes) considered as much cheaper to evaluate (Figure 8.10).

Fig. 8.10

Experimental design used to adjust kriging and cokriging models, mesh function

Using the prediction mean given by the kriging model, we compute a Mean Square Error (MSE) of 313.07. The Markovian model greatly improves this prediction and its MSE goes down to 0.98. From the way our two precision levels are built, one may think the Markovian model is not the most appropriate. Indeed, the symmetrical model leads to a MSE of 0.04.

Comparing MSE may not be enough. Since we have stochastic models, we can wonder if the actual errors match the predicted errors. To answer this, the standardized residuals can be computed, taking into account the correlations between the test points. If the cokriging mean and covariance ideally correspond to the observed data, the standardized residuals should be distributed as a normal distribution.

In Figure 8.11, it can be seen that the predicted errors are overestimated (which translates in the Figure in a smaller spread of the standardized actual errors than the standard Gaussian). In this example, the real function is smoother than what the model estimates. In other terms, the predictions are more accurate than expected or the cokriging models are conservative. Overestimated predicted errors are better than underestimated ones since it prevents an overconfidence in the predictions, which could be prejudicial during algorithm operations. Since the models estimate their own errors bigger than the actual errors, we can say they are conservative. In this example, kriging and cokriging models show a similar behavior for their predicted uncertainty.

Fig. 8.11

Densities of the standardized residuals

3.3 Alternative Multi-Output Gaussian Models

The LMC introduced above is a general construction that encompasses several constructions that have been proposed in the literature. For example, cokriging with a separable covariance Cov(Y _i(z), Y _j(z′)) = k(z, z′) Σ_i,j (Conti and O’Hagan 2010) can be seen as LMC where Q is the Cholesky factor of Σ (Fricker et al. 2013). Similarly, the models introduced in Seeger et al. (2005) and Micchelli and Pontil (2005) are also particular cases of the LMC that have been developed in the machine learning community, from either a Bayesian or a functional analysis point of view.

There are however several alternative constructions of cokriging that cannot be interpreted as LMC. The most popular one is probably based on the convolution of a random process (such as white noise) with different smoothing kernels G _i (Alvarez and Lawrence 2011; Fricker et al. 2013):

$$\displaystyle \begin{aligned} Y_i(\mathbf{z}) = \int G_i (\mathbf{z} - \mathbf{s}) T(\mathbf{s}) d\mathbf{s}. \end{aligned} $$

(8.13)

One advantage of this approach is that it allows to obtain correlated outputs, even if their length-scale or regularity is different. As opposed to the LMC, the parameters controlling the spatial correlation are more intuitive (one usually picks a smoothing kernel that leads to a known covariance function for Y _i), but the parameters controlling the between-output covariance are less intuitive. One drawback however is that the convolution is not analytical for all smoothing kernels. For a detailed review on the above methods, we refer the reader to Alvarez et al. (2012). Finally, several extensions to cokriging have been proposed to relax the assumption that the output distribution is Gaussian. One example of such a construction can be found in Marque-Pucheu et al. (2017) where nested emulators Y ₂(Y ₁(z), z) are studied, or in Le Gratiet (2013) where a similar structure is investigated in detail.

4 Multi-Level Cokriging for Optimization

4.1 Bayesian Black-Box Optimization

Bayesian black-box optimization designates a family of algorithms that minimize an objective function y(⋅) known at a finite set of points $\left ({\mathbf {z}}^{(1)},\ldots ,{\mathbf {z}}^{(N)}\right )$ by, iteratively, deducting a new desirable point to be calculated from a statistical model of the function, calculating the true function at that point, and updating the statistical model. The standard Efficient Global Optimization (EGO) algorithm is presented in Chapter 5.

An illustration of the working of the EGO algorithm on the Branin function is shown in Figures 8.12 and 8.13. After an initial random sample (Latin Hypercube Sampling − LHS + corners) of 10 points and 9 iterations of EGO, the design space is sampled as shown in Figure 8.12. Note how the EGO points (black bullets) tend to gather around the local optima of the Branin function.

Fig. 8.12

Illustration of EGO: contour lines of the Branin function, initial DoE (empty bullets) and 9 points generated by EGO (filled and numbered bullets)

Fig. 8.13

Contour lines of EI after the optimization shown in Figure 8.12. Note how EI peaks in the basins of attraction of the Branin function

The Expected Improvement (EI) function after these 10 + 9 evaluations of the objective function is plotted in Figure 8.13. The EI maximizer yields the next iterate, which in this example is: (0.12,0.83).

4.2 Bayesian Optimization with Cokriging

Cokriging brings new opportunities to save evaluation time during optimizations thanks to, both, a statistical model of better accuracy and thanks to the opportunity to use lower fidelity models. The point of view that is taken in this chapter is the most general one, where only the highest level m is the quantity of interest that is minimized, i.e., we want to solve

$$\displaystyle \begin{aligned} \min_{\mathbf{z} \in D} y^{(m)}(\mathbf{z}) ~. \end{aligned}$$

This assumption goes beyond multi-fidelity and leaves the possibility for the other levels to be any correlated quantity. In other terms, y ⁽ⁱ⁾(⋅) , i≠m, may be of a nature different from y ^(m)(⋅), for example, in the case of a negative correlation minimizing y ^(m)(⋅) can be related to maximizing y ⁽ⁱ⁾(⋅) , i≠m. The execution time t _i of each output y ⁽ⁱ⁾(⋅) is a factor that is accounted for when optimizing using cokriging.

In the particular situation of strict independent multi-fidelity where y ⁽ⁱ⁾(⋅) , i = 1, …, m, represent the same quantity computed at different fidelity levels and the evaluations of output levels are independent of one another, each optimization iteration must not only define the next point z ^(N+1) but also the level of fidelity at which it should be evaluated. In Sacher (2018), this question is answered by maximizing the expected improvement per unit of time over both z and the fidelity level l,

$$\displaystyle \begin{aligned} \left({\mathbf{z}}^{(N+1)},l^{(N+1)}\right) ~=~ \arg \max_{(\mathbf{z},l) \in D \times \{1,\ldots,m\}} \frac{EI^{(l)}(\mathbf{z})}{t^l}, \end{aligned}$$

where

$$\displaystyle \begin{aligned} EI^{(l)}(\mathbf{z}) &= \mathbb E_{Y^{(l)}} \left(\max \left(0,Y^{(l)}(\mathbf{z})-y^{(l)}_{\text{min}} \right)\right) \text{ , } \\ \quad y^l_{\text{min}}&=\min \left(y^{(l)}\left({\mathbf{z}}^{(1)}\right),\ldots,y^{(l)}\left(z^{(N)}\right)\right)~. {} \end{aligned} $$

(8.14)

The algorithms proposed here differ from this work as it is assumed that the outputs 1 to i − 1 must be calculated before output i. This assumption is relevant, for example, in the case of chained simulators like Monte Carlo calculations. Furthermore, it is often reasonable to impose that all low cost outputs at z be evaluated before the output of highest cost.

4.2.1 Simple EGO with Cokriging

It has been seen in section “Test Cases Results” that cokriging is appealing for the sheer sake of accuracy. The cokriging model can then simply replace a single level kriging model in a Bayesian optimization algorithm. At each iteration, all the outputs are evaluated at the new point and the search benefits, in comparison to a single output situation, from the knowledge of all the outputs. Such a strategy is legitimate when the cost of the low rank models is smaller than the cost of the quantity of interest, $\sum _{i=1}^{m-1} t_i < t_m$.

Simple EGO with cokriging is similar to the EGO algorithm described in Section 8.4.1, with two changes: First, EI(z) is replaced by EI ^(l)(z) (cf. Equation (8.14)). The level m GP Y ^(m)(⋅) which intervenes in EI ^(m)(⋅) is obtained by replacing the covariance vector $k(\mathbf {z},\mathcal {Z})$ in the kriging equations of the mean prediction and the covariance (see Chapter 3) by the vector $k^{(m\cdot )}(\mathbf {z},\mathcal {Z}) = \text{Cov}(Y^{(m)}(\mathbf {z}),[Y^{(1)}({\mathbf {Z}}_1),\ldots ,Y^{(m)}({\mathbf {Z}}_m)])$ where the general expression for this covariance is given in Equation (8.9). Second, at each iteration, the outputs are evaluated at all levels so that Z ₁ = ⋯ = Z _m. In short, EGO with cokriging is similar to standard EGO but ${\mathbf {z}}^{(N+1)} = \arg \max _{\mathbf {z} \in D} EI^{(m)}(\mathbf {z})$ and at each iteration $y^{(1)}\left ({\mathbf {z}}^{(N+1)}\right ) , \ldots , y^{(m-1)}\left ({\mathbf {z}}^{(N+1)}\right )$ and y ^(m)(z ^(N+1)) are added to the DoE. An example of points generated by EGO with a cokriging model can be found in Figure 8.14. The cokriging model is a Markovian LMC which means that P is lower triangular (see section “Markovian Cokriging”). It is not possible to compare the performance of EGO with kriging and cokriging through a single run. This will be the goal of Section 8.4.3. Nonetheless, we can observe in Figure 8.14 that EGO with cokriging, like EGO with kriging, creates iterates biased towards global and local minima of the modified Branin function.

Fig. 8.14

Illustration of cokriging and EGO: contour lines of the Branin function, initial DoE (empty bullets) and 9 points generated by cokriging EGO (filled and numbered bullets)

4.2.2 The Step or Stop (SoS) Algorithm

As above with EGO and cokriging, the Step or Stop (SoS) algorithm encompasses multi-fidelity but is more general in the sense that the different outputs do not have to represent the same quantities. Furthermore, the SoS algorithm always evaluates the outputs in increasing order, first y ⁽ⁱ⁻¹⁾(z) and then, if necessary, y ⁽ⁱ⁾(z). Again, it is usually a sensible hypothesis since we have ordered the models such that t _i−1 ≤ t _i. At each iteration, the SoS asks the question: should we make a step to a new z where no y ⁽ⁱ⁾(z) has ever been calculated or should we stop at a point z ⁱ calculated up to level l − 1 and calculate the next output level there, y ^(l)(z ⁽ⁱ⁾)? The acquisition function used to answer this question is the expected improvement at the highest level m (the only level that has to describe the objective function) divided by the remaining time to complete all output levels and hence have an objective function value,

$$\displaystyle \begin{aligned} \begin{aligned} \text{EI}^{\text{SoS}}(\mathbf{z}) &= \frac{EI^{(m)}(\mathbf{z})}{\sum_{k=1}^m t_k} \quad \text{ if } \mathbf{z} \notin {\mathbf{Z}}_1, \\ &= \frac{EI^{(m)}(\mathbf{z})}{\sum_{k=l(z)}^m t_k} \quad \text{ if } \mathbf{z} \in {\mathbf{Z}}_1, \end{aligned} \end{aligned} $$

(8.15)

where l(z) is the level at which the point z should next be evaluated. For example, a point z that has never been evaluated has l(z) = 1, and a point z for which y ⁽¹⁾(z), …, y ⁽ⁱ⁾(z) have been evaluated has l(z) = i + 1. The EI^SoS refers to Z ₁, the set of points that have already been calculated for at least the first level y ₁(z). The SoS procedure is described in Algorithm 1. The initial DoE is made of the same points, gathered in Z ₁, evaluated at all levels. In our implementation, the GP is a LMC cokriging model that is either symmetrical or Markovian (cf. Section 8.3.1). Because of the definition of EI^SoS, the maximization in line 2 is composed of a discrete maximization at the points that have already been evaluated (those in Z ₁) and a continuous maximization in D. The discrete maximization is a plain enumeration and the continuous optimization is carried out with a multi-start BFGS algorithm.

Algorithm 1: SoS Bayesian optimization algorithm for multiple outputs

Figure 8.15 shows an example of how SoS behaves with the mesh-based test case at three levels (number of nodes = 100, 10³, 10⁸). The contour lines of the functions at the three levels are drawn. Notice that the minima at level 1 and 2 do not coincide with the minima at the level of interest (the third). The costs of each level are 0.01, 0.1 and 0.89. The initial DoE is made of a 10 points LHS evaluated at all three levels. The run is stopped after 10 points have been added to the third level, i.e., t ^max = 10.

Fig. 8.15

Illustration of SoS working on the 3 levels mesh test case. The empty and filled bullets are the initial DoE and the points added, respectively. The contour lines are the functions at different levels

In the run plotted in the Figure, the region of interest is hit at the point 0.5312, 0.1586 for the highest level after a cost of 1.27$. Notice that the iterates at the first and second levels are not necessarily close to the minima for these levels, because these minima are far from those of the third, relevant, level.

4.3 Optimization Test Cases Results

We now investigate the efficiency of the SoS optimization algorithm by comparing it to the classical EGO algorithm through 50 repeated independent optimizations. The problems considered are the benchmarks described in Section 8.3.2: the mesh-based test case that mimics the effect of refining a spatial mesh in partial differential equations solvers, the Monte Carlo test case that represents the effect of adding samples in a CMC estimation, and the time-step test case that imitates four time steps of a simulator. In all cases, only two outputs are taken, the one with highest fidelity (fourth level) and the second level. They all have as highest fidelity the modified Branin function (see Figure 8.6). By convention, 1 iteration “costs 1 $” ($\sum _{i=1}^m t_i = 1$). A standard EGO implementation serves as baseline optimization algorithm. When applied to the modified Branin function (equivalent to all highest fidelity levels for the different test cases), it converges as shown in Figure 8.16a.

Fig. 8.16

Convergence of EGO (a) and SoS (b, c, and d): log of minimum function value versus number of iterations, 50 independent runs. (a) EGO algorithm on the modified Branin function. (b) SoS algorithm for the 2 levels mesh-based problem. (c) SoS algorithm for the 2 levels Monte Carlo problem. (d) SoS algorithm for the 2 levels time-step problem

We now compare the EGO convergence to that of the SoS algorithm which uses an intermediate output level to speed up the optimization process. By default, our version of the SoS algorithm relies on a Markovian LMC cokriging model as it has the fewest parameters. The three benchmarks are tested in turn. Results for the mesh, the Monte Carlo, and the time step test cases are reported in Figure 8.16b–d, respectively. Note that, in the time-step problem of Figure 8.16d, a symmetrical cokriging model is used because in this specific test case it performs better than the Markovian model.

By comparing the convergence curves of Figure 8.16b, c, and d to those of EGO in Figure 8.16a, it is clearly seen that SoS decreases the objective function value (y ⁽⁴⁾(⋅)) faster and more consistently than EGO in all the tested test cases. This is due to the ability of the cokriging to exploit the second level outputs that cost here a hundredth of the cost of the true objective function.

5 Concluding Remarks

This chapter has presented the cokriging Linear Model of Coregionalization for making statistical models of functions with multiple outputs. multi-fidelity is an important application of such models, although not the only one. Care was taken to interpret the LMC model as a linear combination of codes outputs (including disciplines) and latent Gaussian processes specific to each code or discipline. This model accommodates the effects of couplings between disciplines. The interpretation and the decomposition of the matrix of interactions between the latent processes (P) are a first original contribution of this work. The LMC cokriging model should be further studied in order to understand the meaning and use of the posterior latent processes that likely act as a signature for each code. It is also necessary to better characterize the link between the statistical model structure and the code interactions.

The availability of several signals correlated to the costly objective function is a feature of most optimization problems that cannot be overlooked. In a second part, this chapter has shown how cokriging can serve to take advantage of these auxiliary information. The SoS (Step or Stop) method has been proposed. It is a new generalization of the EGO algorithm to multiple output problems. It can be directly applied to multi-fidelity and multidisciplinary optimization problems by taking any low-fidelity or disciplinary information as complementary output. In the future, it will be appropriate to lift the SoS constraint about the order of evaluation of the outputs. This will allow the approach to truly decide which code or discipline should be called next. Another perspective is to consider an infinite number of fidelity levels such as the mesh size or the number of CMC samples.