Uncertainty Characterization and Modeling

Abstract

The design process of complex systems such as aerospace vehicles involves physics-based and mathematical models. A model is a representation of the reality through a set of simulations and/or experimentations under appropriate assumptions. Due to simplification hypotheses, lack of knowledge, and inherent stochastic quantities, models represent reality with uncertainties. These uncertainties are quite large at the early phases of the design process. The term uncertainty has various definitions and taxonomies depending on the research communities. The concept of uncertainty is related to alternative concepts such as imperfection, ignorance, ambiguity, imprecision, vagueness, incompleteness, etc.

1 Introduction

1.1 Taxonomy of Uncertainty

The design process of complex systems such as aerospace vehicles involves physics-based and mathematical models. A model is a representation of the reality through a set of simulations and/or experimentations under appropriate assumptions (Der Kiureghian and Ditlevsen 2009). Due to simplification hypotheses, lack of knowledge and inherent stochastic quantities, models represent reality with uncertainties. These uncertainties are quite large at the early phases of the design process. The term uncertainty has various definitions and taxonomies depending on the research communities. The concept of uncertainty is related to alternative concepts such as imperfection, ignorance, ambiguity, imprecision, vagueness, incompleteness, etc.

Two different meanings are generally distinguished for uncertainty (Jousselme et al. 2003):

• Uncertainty as a state of mind,

• Uncertainty as a physical property of information.

The first meaning describes the lack of knowledge and information of an agent to make a decision. The second meaning refers to a physical property, representing the limitation of the perception systems (for instance measurement uncertainty). Different taxonomies and classifications of uncertainty have been proposed in the literature such as the Bronner’s sociological point of view (Bronner 2015), the taxonomy of ignorance by Smithson (2012), the uncertainty classification proposed by Krause and Clark (2012), the uncertainty model developed by Bouchon-Meunier and Nguyen (1996), the different types of uncertainty presented by Klir and Wierman (2013), etc. To deal with uncertainty, a framework must be defined in which knowledge, information and uncertainty can be represented, combined, managed, reduced, updated, etc.

In the aerospace design field, a consensus has been established on two main categories of uncertainty: aleatory and epistemic, reflecting the two possible meanings of uncertainty (Table 2.1), (Thunnissen 2005). Aleatory uncertainty is an inherent physical property of information and cannot be reduced by collecting more data or information. Epistemic uncertainty results from a lack of knowledge and can be reduced by increasing our knowledge or collecting more information. Table 2.1 provides definition for these two types of uncertainty with some examples.

Table 2.1 Aleatory and epistemic uncertainty

The distinction between the two types of uncertainty is important because the use of an appropriate mathematical framework for uncertainty modeling depends on the type, the knowledge, and data available to characterize such uncertainties. Uncertainty can be classified in general into two categories, however, the sources of uncertainty in the modeling of a system are multiples and are briefly detailed in next section. The objective of this chapter is to present the different frameworks that may be adopted to deal with uncertainty in the analysis and design of aerospace systems. The rest of the chapter is organized as follows. In Section 2.1.2, the various sources of uncertainty are discussed with a focus on the engineering field. Then, in Section 2.2 various mathematical formalisms used to describe uncertainty are presented. Two key mathematical concepts are firstly introduced: the sets and the measures. Then, the main existing uncertainty theories are briefly overviewed including Imprecise probability theory, Evidence theory, Possibility theory, Probability boxes theory, Interval formalism, and Probability theory. A particular focus on the probability theory tools and associated methods is carried out in Section 2.2.6. A final discussion to compare these formalisms and their applicability to engineering problems is discussed in Section 2.3.

1.2 Sources of Uncertainty

Thunnissen (2005) distinguished four sources of uncertainty for engineering design problems: input, model-parameter, measurement and operational/environmental. Input uncertainty describes the imprecision and ambiguity that might exist in the definition of the requirements. Model-parameter uncertainty refers to the uncertainty introduced by a representation of the reality through a set of mathematical and physics-based models. Measurement uncertainty describes lack of precision and errors that could arise from experiment measurements and results. Eventually, operational/environmental uncertainty is present because of unknown, uncontrollable external perturbations.

Several sources of uncertainty can be distinguished. Let us consider a parameterized model representing a real physical system (Figure 2.1). The model involves a set of input variables represented by a set of uncertain variables u = (u ₁, …, u _d). Moreover, the model outputs are given by the mapping: y = c(u, p), with p parameters of the physical model. In this chapter, we do not consider any multidisciplinary aspect. Thus, y is just a generic output of the model without consideration of any coupling as described in Chapter 1. For the same reasons, the design variables z are not considered in this chapter for the sake of simplicity.

Fig. 2.1

Generic model

In this context, we can identify the following nonexhaustive sources of uncertainty (Der Kiureghian and Ditlevsen 2009):

• Uncertainty due to the inherent randomness of the input variables u (e.g., on-board propellant mass at launch vehicle take-off due to constant boiling evaporation of cryogenic propellants for the rocket tanks in the launch pad, material properties such that Young modulus coefficient, Poisson coefficient),

• Uncertainty due to the choice of the uncertainty modeling of the input variables u, used to describe the available information to the designer (e.g., probability, evidence theory, possibility theory),

• Uncertainty due to the choice of modeling of the physical phenomena represented by c(u, p) (e.g., Ideal gas or Van der Waals gas modeling, Euler or Navier–Stokes flow modeling),

• Uncertainty due to the model parameters p (e.g., convergence parameters in a model, internal algorithm initialization),

• Uncertainty in the computation of y, due to the numerical approximations, errors (e.g., precision of numerical integration, ordinary differential equation tolerances),

• Uncertainty due to the non-modeling of interactions between different disciplines involved in the considered system, etc.

The interaction uncertainty (Thunnissen 2005) is particular for multidisciplinary systems and consequently is interesting in the context of MDO. It refers to the unknown and non-modeled interactions between the disciplines involved in the design of the complex systems. For instance, considering an aerospace vehicle, it can be assumed that the drag coefficient is not function of velocity and angle of attack and therefore an interdisciplinary coupling between the trajectory and the aerodynamics disciplines is not modeled. This introduces uncertainty on the drag coefficient estimated with this model. In a MDO framework, the identification of the sources of uncertainty has to be driven with experts of each discipline and with experts of aerospace vehicle design to identify all the potential sources of uncertainty. More discussions on MDO and uncertainty are presented in Chapters 6 and 7.

Optimization techniques are engineering tools that are often used in design problems in order to find the optimal design under some specifications and constraints with respect to some design variables. In terms of design optimization problem, these sources of uncertainty may be classified according to three categories:

• Uncertainty due to the inherent random nature of the input variables u (Figure 2.2). One might prefer to find a minimum that is less perturbed by uncertainties in the inputs, it is linked to the concept of robust optimization (see Chapter 5 for more details).

  Fig. 2.2

  

  Uncertainty due to the input variables

• Uncertainty due to the model parameters p that are not perfectly known (Figure 2.3). When possible, increasing the knowledge on the model parameters p by collecting more data could help to reduce the impact of such parameters on the design optimization problem.

  Fig. 2.3

  

  Uncertainty due to the parameters

• Uncertainty due to the choice of modeling, e.g. simplifying assumptions, numerical approximations, etc. (Figure 2.4). The uncertainty in the models has to be taken into account in the early design phases to avoid designs that are not possible if a refinement with higher fidelity models is performed in the latter design phases. This issue is linked to multi-fidelity design and is discussed more in-depth in Chapter 8.

  Fig. 2.4

  

  Uncertainty in the model

2 Overview of Existing Mathematical Formalisms to Describe Uncertainty

2.1 Fundamentals

Uncertainty analysis relies on two key mathematical concepts: the sets and the measures. A brief overview of these concepts is presented in the next section. Then, an introduction on the existing mathematical formalisms to model uncertainty is proposed.

2.1.1 Some Vocabulary and Prerequisites

The uncertainty mathematical formalisms are strongly grounded in the probability theory and Hilbert spaces (but not only as illustrated in this chapter) and therefore a prerequisite is to be familiar with the measure and the probability theory but also the functional analysis. A brief recall of these essential elements is carried out in this chapter. Some vocabulary is first introduced:

• A measurable space is a pair $(\mathcal {X},\mathcal {A})$ with $\mathcal {X}$ a set called the sample space and $\mathcal {A}$ a σ −algebra on $\mathcal {X}$, meaning a collection of subsets of $\mathcal {X}$ containing the empty set ∅ and closed under countable applications of the classical operations of intersection, union, complementation. The elements of $\mathcal {A}$ are referred to as measurable sets or events.

• On any set $\mathcal {X}$ it is possible to define the power set σ −algebra $\mathcal {P}_{\mathcal {X}}$ in which every subset of $\mathcal {X}$ is measurable. It corresponds to the set of all subsets of $\mathcal {X}$.

• If $\mathcal {X}$ is a metric or normed space, it is classical to consider $\mathcal {A}$ to be the Borel σ −algebra $\mathcal {B}(\mathcal {X})$ which is the smallest σ −algebra on $\mathcal {X}$ so that every open set is measurable.

For more details on these vocabulary elements please refer for instance to Tijms (2012). In the probability theory (as explained in Section 2.2.6) the sample space of a probability space is often referred to as Ω.

2.1.2 Crisp and Fuzzy Sets

Uncertainty analysis is based on the concept of a set. Any collection of distinct elements is called a set. A set can be defined as a collection of elements from a universe of interest. For instance, considering a six-sided die, the sample set Ω is equal to Ω = {1, 2, 3, 4, 5, 6}. For more complex systems, the sample set can be infinite. A random event corresponds to a set of outcomes of a random experiment (experiment that leads to different results depending on the randomness). A classical set (also referred to as crisp set) is defined as a set in which it is possible to determine uniquely whether any given individual is or is not a member of the set (left side of Figure 2.5).

Fig. 2.5

Illustration of crisp set and fuzzy set

A characteristic function μ may be defined for a given crisp set A such that:

$$\displaystyle \begin{aligned} \mu: \Omega \rightarrow \{0,1\} \end{aligned} $$

(2.1)

which assigns to any element of the universe set Ω a characteristic:

$$\displaystyle \begin{aligned}\mu(x)=\begin{cases} 1 & \forall x \in A \\ 0 & \forall x \notin A. \end{cases}\end{aligned}$$

In engineering problems, the notion of crisp set is essential for instance in reliability analysis. In a first approximation, a system is often considered in two possible modes: a safe state or a failure state. Therefore, the system status either belongs to one mode or another. However, it is sometimes required to have a finer description of the states in cases where the transition from a safe state to a failure state is gradual rather than abrupt. In the fuzzy sets, the notion of membership to a set is modified compared to the crisp sets (Zadeh et al. 1965). For the fuzzy sets, the boundary is not precise and there exists a degree of membership for an element to a given set. Therefore, the change from membership to non-membership for a fuzzy set is gradual rather than abrupt as with classical sets. This progressive change is characterized by a membership function defined such that:

$$\displaystyle \begin{aligned} \mu: \; \Omega \rightarrow [0,1] \end{aligned} $$

(2.2)

leading to an interval rather than a set of two alternative options. Let consider A a label of the fuzzy set defined by this function, for a given x ∈ Ω. The value taken by μ(x) indicates the degree of membership in the fuzzy set A, meaning the grade of compatibility of x with the concept represented by the fuzzy set A. Instead of taking only two possible values {0, 1}, with fuzzy sets, the membership function takes all the values in the interval [0, 1]. The larger the value, the higher the degree of membership to the fuzzy set (meaning the higher the evidence that x belongs to A).

Considering a fuzzy set A defined on the universe Ω and a number a ∈ [0, 1] in the unit interval of membership, it is possible to define the a-cut of A, denoted ^aA which is the crisp set that consists of all elements of A with membership degrees greater than or equal to a (Figure 2.5, right side):

$$\displaystyle \begin{aligned}^{a}{A} = \{x | \mu(x) \geq a \}. \end{aligned} $$

(2.3)

This crisp set is a set of x values such that the membership value μ(x) is greater than or equal to a. The core set of a fuzzy set A is defined by a a-cut set such that a = 1 (Figure 2.5, right side).

2.1.3 Monotone Additive and Non-additive Measures

A measure is a function that affects a value to quantify a notion of a metric representing a subset of a given set. Classically, a measure corresponds to a mapping of each element of a set A to a real axis (Figure 2.6). It generalizes the concept of length, area, or volume in the Euclidean geometry.

Fig. 2.6

Measure illustration

A regular monotone measure is defined as a mapping μ from a family of subsets A of a universe Ω to an interval [0, 1]. Usually, A is the power set of Ω (the set of all the subsets of Ω, denoted $\mathcal {P}_\Omega$). This function may be expressed as: μ : A → [0, 1] and in addition to continuity, it follows some properties:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \text{Boundary conditions:} &\displaystyle \;&\displaystyle \; \mu(\emptyset)= 0 \; \text{and} \; \mu(\Omega) = 1 \end{array} \end{aligned} $$

(2.4)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \text{Monotonicity:} &\displaystyle \;&\displaystyle \; \forall C_i \; \text{and} \; C_j {\in} A \; \text{if} \; C_i \subseteq C_j \; \text{then} \; \mu(C_i) {\leq} \mu(C_j) \end{array} \end{aligned} $$

(2.5)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \text{Continuity from above:} &\displaystyle \;&\displaystyle \; \text{for} \; C_1 \supseteq C_2 \supseteq \cdots \supseteq C_n \; \text{sets in A} \end{array} \end{aligned} $$

(2.6)

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle \;&\displaystyle \; \text{if } \bigcap_{\text{all i}}C_i \in A, \; \text{then} \; \lim_{i\rightarrow \infty} \mu(C_i) = \mu\left( \bigcap_{\text{all i}}C_i \right) \end{array} \end{aligned} $$

(2.7)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \text{Continuity from below:} &\displaystyle \;&\displaystyle \; \text{for} \; C_1 \subseteq C_2 \subseteq \cdots \subseteq C_n \; \text{sets in A} \end{array} \end{aligned} $$

(2.8)

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle \;&\displaystyle \; \text{if } \bigcup_{\text{all i}}C_i \in A, \; \text{then} \; \lim_{i\rightarrow \infty} \mu(C_i) = \mu\left( \bigcup_{\text{all i}}C_i \right).~~~~ {} \end{array} \end{aligned} $$

(2.9)

For two sets C ₁ and C ₂ ∈ A such that C ₁ ∩ C ₂ = ∅, a monotone measure is able to represent the following cases:

• superadditivity: μ(C ₁ ∪ C ₂) > μ(C ₁) + μ(C ₂)

• additivity: μ(C ₁ ∪ C ₂) = μ(C ₁) + μ(C ₂)

• subadditivity: μ(C ₁ ∪ C ₂) < μ(C ₁) + μ(C ₂)

The generalization of the set theory (Zadeh et al. 1965) and the measure theory (Halmos 1950; Choquet 1954) enables to diversify the uncertainty mathematical formalisms through various theories representing different approaches for the uncertainty modeling (Figure 2.7 and Table 2.2). The modern probability theory was the first advanced mathematical theory dealing with uncertainty formalized by Kolmogorov in 1933 (see Kolmogorov 1950 for the translation of the original paper of Kolmogorov). It is based on the classical monotone additive measure and on crisp set. Choquet (1954) generalized the classical measure theory to the theory of monotone measures under the name of “theory of capacities.” Negoita et al. (1978) and Zadeh (1999) generalized the set theory by developing the concept of fuzzy sets. By combining alternative definitions of sets (based on fuzzy sets) and measures (non-additive measures) it is possible to define alternative uncertain formalisms. All the theories listed in the Table 2.2 do not have the same degree of maturity and development for practical use by engineers and scientists in design problems. Consequently, only the mature and fully developed ones are briefly discussed in following sections of this chapter.

Fig. 2.7

Extensions of the concepts of set and measure to create alternative uncertainty modeling theories

Table 2.2 Classification of uncertainty theories (Ayyub and Klir 2006)

2.2 Imprecise Probability Theory

The imprecise probability theory, developed by Walley (1991), is a generalization of the existing uncertainty theories to cover all the mathematical models which measure the uncertainty without sharp numerical probabilities. Let ( Ω,  Υ) a measurable space, with Υ an algebra of measurable subsets of Ω and Π a set of monotone measures on the measurable space. It is possible to define two measures such that:

• upper probability: $\overline {P}(A)= \underset {P \in \Pi }{\text{sup}}[P(A)]; \; \forall A \subseteq \Omega$

• lower probability: $\underline {P}(A)= \underset {P \in \Pi }{\text{inf}}[P(A)]; \; \forall A \subseteq \Omega$

Lower and upper probabilities are characterized by the following rules (Walley 2000):

• $\underline {P}(A)=1-\overline {P}(A^c)$

• $\underline {P}(\emptyset )=\overline {P}(\emptyset )=0$

• $0 \leq \underline {P}(A) \leq \overline {P}(A) \leq 1$

• $\underline {P}(A)+ \underline {P}(B) \leq \underline {P}(A \cup B) \leq \underline {P}(A) + \overline {P}(B) \leq \overline {P}(A \cup B) \leq \overline {P}(A) +\overline {P}(B)$

where A and B are disjoint sets, and A ^c is the complementary set of A.

$\underline {P}$ and $\overline {P}$ define two measures that are, respectively, the inferior and the superior bounds over all the monotone measures that could be defined on the measurable space (Baudrit and Dubois 2006) (Figure 2.8). $\overline {P}$ is a superadditive measure and $\underline {P}$ is a subadditive measure. The lower probability may be understood as the maximal price one would be willing to pay for the gamble A which pays 1 unit if the event A occurs. It is the maximal betting rate at which one would be disposed to bet on A. The upper probability may be interpreted as the minimal selling price for the gamble A, or one minus the maximal rate at which an agent would bet against A. The two measures encode a family of measures. The introduction of these two measures enables to quantify the confidence in the uncertainty modeling, and the difference between the two measures reflects the incomplete nature of the knowledge (Baudrit and Dubois 2006). Indeed, the available information about the uncertainty in the performance of a future complex systems is often partial (DeLaurentis and Mavris 2000) and the uncertainty in the available knowledge needs to be quantified. Nevertheless, reasoning on a family of measures can be very complex. Further details on imprecise theory can be found in Walley (1991). In the following sections, four uncertainty formalisms are briefly reviewed. They represent special expressions of lower and upper measures which allow practical engineering applications: Evidence theory (Dempster 1967; Shafer 1976), Probability theory (Kolmogorov 1950), Possibility theory (Negoita et al. 1978) and Probability boxes (Ferson et al. 1996).

Fig. 2.8

Example of upper and lower probability measures

Relations exist between these uncertainty theories. As represented on Figure 2.9, Imprecise probability theory is a generalization of uncertainty theories and Evidence theory, Possibility theory, Probability theory, Probability boxes are a particular construction of the upper and lower bounds $\underline {P}$ and $\overline {P}$ depending on the available knowledge and data concerning the uncertainty and its treatment and combination.

Fig. 2.9

Relations between the different uncertainty theories

2.3 Evidence Theory

Dempster–Shafer Theory (DST), also referred to as theory of evidence was developed by Dempster (1967) and Shafer (1976). This theory is based on two monotonic non-additive measures: the belief (Bel) and the plausibility (Pl). In comparison, the probability theory uses just one measure, the probability of an event (see Section 2.2.6). The probability theory and the possibility theory may be seen as special cases of the evidence theory. The belief and plausibility measures are determined based on the known evidence about a proposition without requiring to distribute the evidence to subsets of the proposition. An ensemble of evidences represented by a family of sets may be characterized by a basic mass assignment $m:\mathcal {P}_\Omega \rightarrow [0,1]$ (with $\mathcal {P}_\Omega$ the power set of Ω) constructed to ease the data and information synthesis. A basic assignment assesses the likelihood of each set in a family of sets. Considering an event E which is a subset of the universe Ω, m(E) refers to the basic mass assignment corresponding to the event E and it expresses the degree of support of the evidential claim that the true realization is in the set E, but no information are provided about a potential distribution among the subsets of E. The mass assignment may be obtained from a wide range of sources such as theoretical evidence, experimental data, opinion of experts concerning the belief of occurrence of an event or value of a parameter.

The basis of evidence theory is the impossible discernment of the mass distribution inside this element. A basic assignment has to satisfy the following two conditions:

• m(∅) = 0

• $\sum _{\text{all } E \in \mathcal {P}_\Omega } m(E) = 1$

If m(E) > 0, E is called a focal element. The mass assignment function can encode a family of measures as: $\Pi (m)=\{P| \forall E \in \mathcal {P}_\Omega , \; Bel_m(E) \leq P(E) \leq Pl_m(E)\}$ (Shafer 1976). The upper and lower imprecise probability measures are defined such that:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \underline{P}(E) &\displaystyle =&\displaystyle Bel(E) = \sum_{\text{all } A_i \subseteq E} m(A_i) \end{array} \end{aligned} $$

(2.10)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \overline{P}(E) &\displaystyle =&\displaystyle Pl(E) = \sum_{\text{all } A_i \cap E \neq \emptyset} m(A_i). \end{array} \end{aligned} $$

(2.11)

The mappings Bel(⋅), Pl(⋅), and m(⋅) can be understood as alternative representations of the same information. These functions describe the likelihood that an element e belongs to each E as a belief measure (strongest), plausibility measure (weakest) and a basic mass assignment (collected evidences). Once one of these mappings is defined, the two others may be uniquely determined. The belief of an event is calculated by summing the mass assignment of the propositions that totally agree with the event E, whereas the plausibility of an event is calculated by summing the mass assignment of propositions that agree totally and only partially with the event E. Bel(⋅) and Pl(⋅) give, respectively, the lower and upper bounds of the measure on the event.

Considering the example of Figure 2.10 with the universal set Ω, a set A and six elements E _i, i = 1, …, 6 with their associated mass assignments m(E _i), i = 1, …, 6. In this case, the Belief and Plausibility functions are given by

$$\displaystyle \begin{aligned} \begin{array}{rcl} Bel(A) &\displaystyle =&\displaystyle m(E_2) + m(E_4) \end{array} \end{aligned} $$

(2.12)

$$\displaystyle \begin{aligned} \begin{array}{rcl} Pl(A) &\displaystyle =&\displaystyle m(E_2) + m(E_3) +m(E_4)+ m(E_6). \end{array} \end{aligned} $$

(2.13)

Fig. 2.10

Example of evidence mass assignments, belief and plausibility measures for a given set A

The Belief function only accounts for the mass of the elements E ₂ and E ₄ as they are fully included in the set A. The Plausibility function, in addition to account for E ₂ and E ₄, takes the contributions of E ₃ and E ₆ that overlap the set A.

Figure 2.11 presents another example of Bel(⋅) and Pl(⋅) measure constructions based on 10 evidences (E ₁, …, E ₁₀) with the same mass assignment m(E _i) = 0.1 ∀i ∈ [1, 10]. The cumulative Belief function is a lower bound of the possible measures and the cumulative Plausibility function is an upper bound.

Fig. 2.11

Example of evidence mass assignment, belief, and plausibility cumulative distribution in the case m(E _i) = 0.1 ∀i ∈ [1, 10]

The Evidence theory allows the combination of the evidences from different sources and experts through different rules of combination of evidence (Dempster’s rule, Yager’s rule, etc.) (Yager 1987; Inagaki 1991).

The interval formalism for uncertainty modeling, referred to as interval analysis (see Section 2.2.5), models an uncertain variable as an interval with a minimum and a maximum values that the uncertain variable might take. The interval analysis can be seen as a special case of the evidence theory in which only one focal element exists for the uncertain variable with a mass assignment of one.

The evidence theory has the advantages to enable the handling of both epistemic and aleatory uncertainties and facilitates the combination of expert opinions from different sources. Moreover, by relying on two measures, the evidence theory provides a level of confidence on the uncertainty modeling. However, compared to the probability theory, in an engineering design context, it might be difficult to interpret the uncertainty modeling and to obtain evidences for the different elements from non-evidence theory experts.

2.4 Possibility Theory

Different perspectives exist to present the possibility theory (Negoita et al. 1978; Dubois and Prade 2012) (Figure 2.12). The possibility theory may be interpreted as a subcase of the evidence theory. It can be applied only when there is no conflict in the provided body of evidence. In this case, the focal elements are nested (e.g., E ₁ ⊂ E ₂ ⊂⋯ ⊂ E _n), and the associated belief and plausibility measures are called consonant. In this case, the belief and plausibility measures are characterized by the following relations:

$$\displaystyle \begin{aligned} \begin{array}{rcl} Bel(B \cap C) &\displaystyle =&\displaystyle \text{min}[Bel(B),Bel(C)] \text{ for all } B,C \in \mathcal{P}^2_\Omega \end{array} \end{aligned} $$

(2.14)

$$\displaystyle \begin{aligned} \begin{array}{rcl} Pl(B \cup C) &\displaystyle =&\displaystyle \text{max}[Pl(B),Pl(C)] \text{ for all } B,C \in \mathcal{P}^2_\Omega. \end{array} \end{aligned} $$

(2.15)

Fig. 2.12

Different interpretations for possibility theory

In the possibility theory, special counterparts of belief and plausibility measures are called Necessity (Nec) and Possibility (Pos) measures (Dubois and Prade 1998). Every possibility measures Pos(⋅) on $\mathcal {P}_\Omega$ may be uniquely defined by a possibility distribution function r(⋅):

$$\displaystyle \begin{aligned} r:\varOmega \rightarrow [0,1] \end{aligned} $$

(2.16)

with the following relation: $Pos(A) = \underset {x\in A}{\text{max }} r(x)$ for each $A \in \mathcal {P}_\Omega$. The Necessity and Possibility are dual measures related by: $Nec(A) = 1 -Pos\left (\overline {A}\right )$. Like the Belief and Plausibility, the Necessity and Possibility measures are non-additive measures and satisfy the following relations:

$$\displaystyle \begin{aligned} \begin{array}{rcl} Nec(A) &\displaystyle \leq &\displaystyle Pos(A) \end{array} \end{aligned} $$

(2.17)

$$\displaystyle \begin{aligned} \begin{array}{rcl} Pos(A) &\displaystyle +&\displaystyle Pos(\overline{A}) \geq 1 \end{array} \end{aligned} $$

(2.18)

$$\displaystyle \begin{aligned} \begin{array}{rcl} Nec(A) &\displaystyle +&\displaystyle Nec(\overline{A}) \leq 1 \end{array} \end{aligned} $$

(2.19)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \text{max}\left[Pos(A) \right. &\displaystyle ,&\displaystyle \left. Pos \left(\overline{A}\right)\right] =1 \end{array} \end{aligned} $$

(2.20)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \text{min}\left[Nec(A)\right. &\displaystyle ,&\displaystyle \left. Nec\left(\overline{A}\right)\right] =0. \end{array} \end{aligned} $$

(2.21)

The possibility theory may also be seen as an extension of the fuzzy sets and the fuzzy logic theory adapted to the presence of sparse information about the uncertainty as introduced by Zadeh (1999). In the fuzzy set approach to possibility theory, the focal elements are represented by a −cuts of the associated fuzzy set. The possibility theory enables to define various confidence intervals (a −cut) around the true probability based on the fuzzy set (see section “Crisp and Fuzzy Sets”). As with the probability measures, which are characterized by probability distribution functions, the possibility measures can be represented by the possibility distribution function r :  Ω → [0, 1] such that:

$$\displaystyle \begin{aligned} Pos(A) = \underset{x \in A}{\text{max }} r(x). \end{aligned} $$

(2.22)

The possibility measures are equivalent to the fuzzy sets. The membership grade of an element x corresponds to the plausibility of the singleton {x}. Indeed, as presented in section “Crisp and Fuzzy Sets,” a fuzzy set A of the universal set Ω is characterized by a membership function μ _A(⋅). Zadeh (1999) defined a possibility distribution function r(⋅) associated with A as r(x) = μ _A(x), ∀x ∈ Ω. Then, the possibility measure Pos(⋅) may be defined as:

$$\displaystyle \begin{aligned} Pos(A) = \underset{x\in A}{\text{sup }} r(x) \; \text{for each } A\in \mathcal{P}_\Omega. \end{aligned} $$

(2.23)

Therefore, if the possibility distribution function is known for a response Y , it is then possible to define an interval for the true (unknown in general) probability $\mathbb {P}$: $Nec(Y) \leq \mathbb {P}(Y) \leq Pos(Y)$.

For instance, assuming that the following information are collected using expert opinions:

• I am sure that X ∈ [0, 10],

• I am sure at 80% that X ∈ [2, 10],

• I am sure at 60% that X ∈ [4, 8],

• I am sure at 25% that X ∈ [4.5, 6.5].

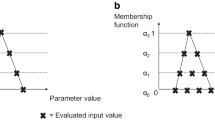
Then, it is possible to define the Possibility and Necessity measures that characterize these information (Figures 2.13 and 2.14).

Fig. 2.13

Possibility and necessity measures

Fig. 2.14

Cumulative possibility and necessity functions

The cumulative possibility and necessity functions bracket the true unknown cumulative probability function, giving intervals of confidence. The possibility theory presents the same advantages of evidence theory in its ability to describe both aleatory and epistemic events and to combine them inside a single formalism. Moreover, the possibility theory also relies on two measures to account for lack of knowledge in the uncertainty modeling. However, for the design of aerospace systems, these possibility information might not be easy to interpret in terms of performance under uncertainty. For more details on the possibility theory, one can refer to Dubois and Prade (1998) and Zadeh (1999).

2.5 Interval Analysis

Interval data are commonly encountered in practical engineering problems. Ferson et al. (2007) and Du et al. (2005) discussed such situations where interval data are present. For instance, in the early design phase, the experts often cannot provide a complete Probability Density Function (PDF, see Section 2.2.6) of the uncertain variables U and the only available information is in the form of an expert opinion expressed through interval data which specifies a range of possible values for the variable. Moreover, it appears that a uniform distribution might not be adapted in some cases because it requires to know that the samples are distributed with an iso-probability inside the interval to be appropriately used (Klir 2005; Ferson et al. 2007).

A closed interval for a real-valued continuous uncertain variable u is a set defined as:

$$\displaystyle \begin{aligned} \Upsilon=\{u\in \mathbb{R} | u_{\text{min}} \leq u \leq u_{\text{max}} \} \end{aligned} $$

(2.24)

with u _min and u _max, respectively, the lower and upper bounds of the interval. An interval is denoted by its bounds [u _min, u _max]. For a d-dimensional uncertain variable $\mathbf {u}=\left [u^{(1)},\ldots ,u^{(d)}\right ]$, its representation by an interval is given by

$$\displaystyle \begin{aligned} \boldsymbol{\Upsilon}=\{\mathbf{u}\in \mathbb{R}^d | u^{(i)} \in \left[u_{\text{min}}^{(i)} , u_{\text{min}}^{(i)}\right], \; \forall i \in \{ 1, \ldots, d \} \}. \end{aligned} $$

(2.25)

As intervals are sets, the same arithmetical operations are possible such as intersection, unions, sums, etc. For more details on interval formalism, one can refer to Moore et al. (2009).

2.6 Probability Theory

Fundamental definitions of the probability theory have been proposed by Kolmogorov (1950). The purpose of this section is to review the main elements of this theory; for more complete information on that topic, see (Tijms 2012) for instance.

Uncertainty may be seen as a collection of states that occur randomly. A random experiment leads to different results depending on the randomness. The result of the experiment is called an outcome or a realization and is generally denoted by ω. In that case, the basic tool to model that situation with the probability theory is the probability space defined by the triple $\left (\Omega ,A, \mathbb {P} \right )$ where :

• the universal set Ω is assumed to be non-empty. It corresponds to the set of all the possible outcomes ω.

• the σ-algebra A is a family of subsets of Ω (called events), such that:

  • Ω ∈ A,

  • if B ∈ A, then B ^c ∈ A,

  • if B ₁, B ₂, … B _n belong to A, then B ₁ ∪ B ₂ ∪⋯ ∪ B _n ∈ A.

  A common σ-algebra is the Borel algebra. A Borel algebra on Ω is the smallest σ-algebra containing all the open sets. If $\Omega = \mathbb {R}$, the Borel algebra $\mathcal {B}(\mathbb {R})$ is the smallest σ-algebra on $\mathbb {R}$ which contains all the intervals. Another example of σ −algebra is the power set of Ω, noted $\mathcal {P}_\Omega$.

• the probability measure $\mathbb {P}$ is a countable additive measure, $\mathbb {P}: A\rightarrow [0,1]$ such that

  • $\mathbb {P}(\Omega )=1$ and $\mathbb {P}( \emptyset )=0$,

  • let (B ₁, B ₂, …, B _n) be a countable collection of disjoint events in A, then $\mathbb {P}\left (\displaystyle \bigcup _{i=1}^{n} B_i\right ) = \displaystyle \sum _{i=1}^{n} \mathbb {P}(B_i)$.

According to the theory of measure, the couple ( Ω, A) is a measurable space. The probability measure $\mathbb {P}$ gives the probability of any event of A. These definitions lead to the following properties if one considers B and C, two subsets of A:

• $\mathbb {P}(B^c) = 1 - \mathbb {P}(B)$

• $\mathbb {P}(C\cup B) = \mathbb {P}(C) + \mathbb {P}(B) - \mathbb {P}(C\cap B)$,

• All the properties of a generic measure μ apply here (see Equations 2.5–2.9) with $\mu =\mathbb {P}$.

A real-valued random variable U is a measurable function from the probability space $(\Omega , A, \mathbb {P})$ into the real numbers $\mathbb {R}$. U(ω) is a realization of the random variable. The set $\left \{\omega \in \Omega , U(\omega )\leq c\right \}$ must belong to A for all $c\in \mathbb {R}$. If $A=\mathcal {B}(\mathbb {R})$, this previous assertion is valid by definition. The probability that U takes a value in $\left \{\omega \in \Omega , U(\omega )\leq c\right \}$ is $\mathbb {P}\left (\omega \in \Omega , U(\omega )\leq c\right )=\mathbb {P}(U\leq c)$. The set of probabilities $\mathbb {P}(U\in [a,b]),~\forall a,~b \in \mathbb {R}, a\leq b$ is the probability distribution or probability law of U. The probability distribution of U is uniquely characterized by the Cumulative Distribution Function (CDF) F(⋅) of U :

$$\displaystyle \begin{aligned}F(u)=\mathbb{P}(U \leq u),~ \text{for}~u\in\mathbb{R}.\end{aligned}$$

For continuous random variables, the Probability Density Function (PDF) ϕ(⋅) of U is defined by

$$\displaystyle \begin{aligned}\forall u \in \mathbb{R}, \; F(u)=\int_{-\infty}^u \phi(t) dt. \end{aligned}$$

An example of Gaussian CDF and PDF for a standard Gaussian distribution is illustrated in Figure 2.15.

Fig. 2.15

Example of normal CDF (left) and PDF (right) for a standard Gaussian distribution (mean=0. and variance=1.)

The different properties (limits, positiveness, etc.) of F(⋅) and ϕ(⋅) are not detailed in this book for the sake of conciseness. Assuming that U is a continuous random variable with a PDF ϕ(⋅), if the integral convergence is defined, then it is possible to define some statistical moments of the random variable U:

• Expected value (first-order statistical moment): (the scalar expected value is often noted μ),

• The variance (centered second-order statistical moment): $\mathbb {V}(U)=$

• The standard deviation defined by: $\sigma = \sqrt {\mathbb {V}(U)}$

• The p-order centered moment

The notion of random variable can be extended to random vectors. A real-valued random vector $\mathbf {U}=\left (U^{(1)},U^{(2)},\ldots ,U^{(d)} \right )$ of dimension d is a measurable function from the probability space $(\Omega , A, \mathbb {P})$ into $\mathbb {R}^d$. The joint CDF of U is defined by

$$\displaystyle \begin{aligned} \begin{array}{rcl} F(\mathbf{u})&\displaystyle =&\displaystyle F\left(u^{(1)},u^{(2)},\ldots,u^{(d)}\right)= \mathbb{P}\left(U^{(1)} \leq u^{(1)},U^{(2)} \leq u^{(2)},\ldots,U^{(d)} \leq u^{(d)} \right) \\ &\displaystyle &\displaystyle \text{for } \mathbf{u}=\left(u^{(1)},u^{(2)},\ldots,u^{(d)}\right)\in \mathbb{R}^d. \end{array} \end{aligned} $$

(2.26)

If U is a continuous random variable, the associated joint PDF ϕ is given by

$$\displaystyle \begin{aligned}\phi(\mathbf{u})=\left.\frac{\partial^d F(\mathbf{u})}{\partial u^{(1)}\partial u^{(2)}\partial u^{(d)}}\right|{}_{\mathbf{u}}.\end{aligned}$$

It is also possible to define the covariance between to jointly distributed random variables X and Y  (assuming that the finite second moments are defined for the two variables), then the covariance between X and Y  is given by

$$\displaystyle \begin{aligned} \text{cov}(X,Y) = \mathbb{E}\left[\left(X-\mathbb{E}\left[ X\right] \right) \left( Y - \mathbb{E}\left[ Y \right] \right) \right]. \end{aligned} $$

(2.27)

In practice, the distribution of the uncertain random variable U has to be determined. In some applications, this distribution may be assumed with expert knowledge or with some physical considerations of modeled phenomenon. In other cases, this distribution has to be learned from samples (for instance collected through experimentation) that can be seen as realizations of U. We assume in the next sections that a set of M independent and identically distributed samples U ₍₁₎(ω), U ₍₂₎(ω), …, U _(M)(ω) of the random variable U is available and U is a continuous random variable. The ω dependencies is no more recalled in the following sections and for the sake of conciseness, we use the notation u _(i) = U _(i)(ω). We will review in the following paragraphs the main estimation techniques of a probability distribution (Silverman 1986).

2.6.1 Empirical Distribution

From the samples u ₍₁₎, u ₍₂₎, … u _(M), it is possible to evaluate their empirical CDF defined by

with an indicator function equal to 1 if u _(i) ≤ u and 0 otherwise. F ^emp is the distribution of a discrete random variable, and thus, the notion of PDF is not defined. Figure 2.16 represents an empirical CDF obtained with 100 samples generated according to a distribution. Both the empirical distribution and the exact distribution at the origin of the samples are represented for comparison. The empirical distribution is close to the exact one however not enough data are available to represent accurately the exact CDF. It is possible to sample from this distribution with a uniform sampling with replacement among the samples u _(i). It corresponds to the principle of bootstrap (Efron and Tibshirani 1994) in that case and it is particularly interesting for the estimation of some statistical moments of U and their associated confidence interval. Nevertheless, this approach will never propose samples that have not been observed in the data which may be seen as restrictive notably if the sample size M is limited.

Fig. 2.16

Example of exact and empirical CDFs obtained from a set of samples

2.6.2 Entropy and Divergence Measures

In order to choose an appropriate probability law depending on the available data, one can use the maximum of entropy theorem. The entropy of a continuous random variable is defined by

(2.28)

where $\mathbb {U}=\{u\in \mathbb {R} | \phi (u)>0 \}$ is the support of ϕ(⋅). The entropy quantifies the amount of information that a random variable produces and it is linked to the information theory (Shannon 1948). Another measure derived from entropy called Kullback-Leibler divergence (Joyce 2011) (also referred as relative entropy) is a measure of how a probability distribution differs from a second one. For two continuous probability distributions p(⋅) and q(⋅), the Kullback-Leibler divergence is defined by

(2.29)

The divergence is always non-negative, it is not symmetric and it tends to zero when p(⋅) converge to q(⋅).

2.6.3 Parametric Approaches

There exists a set of common probability distributions (e.g., Gaussian, Uniform, Gamma, Weibull) that allows to generate random samples but also to model existing collected data. A brief overview of these distributions is given in the following paragraphs.

Uniform Distribution

The PDF of the uniform distribution $\mathcal {U}_{(a,b)}$ over an interval [a, b] is given by

(2.30)

with an indicator function equal to 1 if u ∈ [a, b] and 0 otherwise. The mathematical expectation of a random variable U following a uniform distribution over the interval [a, b] is given by: $\mathbb {E}(U)=\frac {a+b}{2}$ and the variance is given by: $\mathbb {V}(U)=\frac {(b-a)^2}{12}$. The uniform distribution is often selected to model a random variable with probability formalism when only the bounds on the variable are known but no information of its distribution over the interval is available. This choice may be explained by the maximum entropy theorem as the uniform distribution is the one that maximizes the entropy with only an information on the bounds.

Gaussian Distribution

The PDF of the univariate Gaussian distribution $\mathcal {N}\left (\mu ,\sigma ^2 \right )$ is given by

$$\displaystyle \begin{aligned} \phi(u)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp{-\left(\frac{u-\mu}{\sqrt{2\sigma}}\right)^2}, \;\;\; \text{for } u \in \mathbb{R} \end{aligned} $$

(2.31)

μ and σ ² are the mathematical expectation and the variance of the Gaussian distribution (also named as Normal distribution). The Gaussian distribution is one of the most employed distributions to model random variables and to characterize a set of collected data. The Gaussian distribution is the law that maximizes the entropy among all real-valued distributions if a mathematical expectation and a variance are provided. Moreover, the Central Limit Theorem (CLT) (Laplace 1810) also justifies the use of Normal distribution in a lot of applications. CLT establishes that, under some hypotheses, when independent random variables are summed, their normalized sum tends toward a normal distribution even if the original variables are not normally distributed. This distribution will be particularly used for illustrative purposes in this book. The standard Gaussian distribution is given by $\mathcal {N}\left (0,1 \right )$ (see Figure 2.15).

Gamma Distribution

The PDF of the Gamma law Γ(λ, α), with λ > 0 and α > 0 is given by

$$\displaystyle \begin{aligned} \phi(u)=\frac{1}{\Gamma(\alpha)}\lambda^\alpha u^{\alpha-1}\exp{(\lambda u)}, \;\;\; \text{for } u \in \mathbb{R}^*_{+}, \end{aligned} $$

(2.32)

where . The expectation and the variance are given by: $\mathbb {E}(U)=\frac {\alpha }{\lambda }$ and $\mathbb {V}(U)=\frac {\alpha }{\lambda ^2}$. The Gamma distribution is often used in applications such as financial services or queuing problems.

An illustration of classical PDFs is presented in Figure 2.17. For more details on common probability distributions see Tijms (2012).

Fig. 2.17

Example of classical PDFs

Fit of Parametric Distribution

Suppose that a given statistical model is available or assumed. It corresponds in fact to a PDF family ϕ(⋅|θ) (for instance one of the distributions presented in the previous paragraphs) indexed by a parameter θ ∈  Θ that may be multidimensional. ϕ(⋅) is often chosen among usual distributions such as Gaussian distribution (θ is then its mean and/or its variance), etc. Different considerations can be taken into account for this choice such as the shape proximity between the CDF of ϕ(⋅|θ) and F ^emp, the required complexity of the model or some expert knowledge. The problem of distribution estimation now consists in estimating θ with $\hat {\boldsymbol {\theta }}$ from the samples u ₍₁₎, …, u _(M). A large number of methods (Sahu et al. 2015) has been proposed for that purpose such as the Maximum Likelihood Estimation (MLE) or the generalized method of moments. We will not detail all these methods and only give a brief focus on MLE.

The likelihood of the samples is the function $\mathcal {L}\left (\theta |u_{(1)},u_{(2)},\dots ,u_{(M)}\right )$. For continuous random variables and if the samples u ₍₁₎, …, u _(M) are independent and identically distributed, then $\mathcal {L}\left (\theta |(u_{(1)},u_{(2)},\dots ,u_{(M)}\right )$ is given by

$$\displaystyle \begin{aligned}\mathcal{L}\left(\theta|u_{(1)},u_{(2)},\dots,u_{(M)}\right)=\prod_{i=1}^M \phi(u_{(i)}|\theta).\end{aligned}$$

The estimate $\hat {\theta }_{ML}$ with maximum likelihood estimation is then computed in the following way:

$$\displaystyle \begin{aligned}\hat{\theta}_{ML}=\underset{{{\theta}} \in \boldsymbol{\Theta}}{\operatorname{argmax}}\left\{ \mathcal{L}\left(\theta|(u_{(1)},u_{(2)},\dots,u_{(M)}\right) \right\},\end{aligned}$$

if this maximum exists. In many cases, it is not necessary to perform the optimization, as an analytical expression of $\hat {\theta }_{ML}$ is available. $\hat {\theta }_{ML}$ has also some interesting theoretical properties such as consistency and efficiency.

At the end of the parametric estimation, the density of U is estimated with $\hat {\phi }=\phi (\cdot |\hat {\theta })$.

An example of Maximum Likelihood Estimation for different parametric distributions for a set of samples is presented in Figure 2.18. The set of samples have been generated according to a Gamma distribution and different MLE estimations of the hyperparameters are performed for a Normal, a Student, a Log-normal, and a Gamma distributions. Moreover, it is compared to a nonparametric approach detailed in the next section. The different MLE fit with more or less precision the exact distribution and the corresponding histogram representing the existing data. The Gamma fit is the closest to the histogram distribution which is coherent with the existing data.

Fig. 2.18

Example of maximum likelihood estimation for different parametric distributions and a KDE (see next section) for a set of samples. The bottom sticks represent the samples also illustrated with the associated histogram

2.6.4 Nonparametric Approaches

When no parametric classic density fits with an acceptable accuracy the samples, nonparametric approaches may be an efficient alternative (Izenman 1991). The most well-known nonparametric density estimate is Kernel Density Estimator (KDE). It enables to approximate the PDF of U in the following way:

$$\displaystyle \begin{aligned}\phi({u})=\frac{1}{M h}\sum_{i=1}^{M}K\left(\frac{{u}-{u}_{(i)}}{h}\right),\end{aligned}$$

where K is a kernel (a non-negative symmetric function that integrates to one) and h is a positive scalar called bandwidth. There is a large number of potentially efficient kernels, but in practice the most used kernel is the Gaussian kernel, defined by

$$\displaystyle \begin{aligned}K(u)=\frac{1}{\sqrt{2\pi}}e^{\frac{-u^2}{2}}.\end{aligned}$$

The choice of the kernel also depends on the assumptions one makes on the PDF of the samples u _(i) as their distribution tail, etc. The bandwidth values correspond to a trade-off between the bias and the variance of ϕ(⋅). In general, a small bandwidth in a given dimension implies a small bias but a large variance. Different approaches propose an estimate of the optimal bandwidth for a given criterion. In most cases, one may choose an adapted bandwidth h _opt that minimizes the mean integrated square error (MISE) (Heidenreich et al. 2013). The application of KDE to random vectors is possible but suffers from the curse of dimensionality.

From a set of samples generated according to a Gaussian distribution, Figure 2.19 illustrates a KDE estimation. Moreover, the influence of the bandwidth is represented on the right of Figure 2.19. Figure 2.20 represents the associated kernels to each data of the collected samples that is used in the kernel density estimator. Figure 2.21 illustrates a two-dimensional KDE estimation of a set of data.

Fig. 2.19

Example of KDE estimation for a set of data (left) and different bandwidth assumptions (right)

Fig. 2.20

Gaussian kernel around each data to be used in KDE

Fig. 2.21

Example of KDE estimation for a set of data in two dimensions

2.6.5 Semi Parametric Approaches

Semi-parametric approaches combine parametric and nonparametric elements. A popular semi-parametric density estimation approach is the expectation maximization algorithm (Moon 1996). It uses Gaussian mixture model and MLE to estimate PDF for a given data set.

A quite different semi-parametric approach is the maximum entropy principle, introduced by Jaynes (1957), that estimates the PDF ϕ(⋅) of U by the PDF that somehow bears the largest uncertainty given available information on U. The measure of uncertainty of U is defined by the differential entropy of the PDF ϕ(⋅) (see Equation 2.28). In addition, the information available on the sought density is of the form $\mathbb {E}\left [g(U)\right ] = \mathbf {b} \in \mathbb {R}^m$, where g(⋅) is a given mapping from $\mathbb {R}$ to $\mathbb {R}^m$ with m the number of constraints. For instance, one may know the first two moments μ ₁ and μ ₂ and the support S of U, corresponding to and b = (μ ₁, μ ₂, 1). Then, the maximum entropy estimate $\hat {\phi }(\cdot )$ of ϕ(⋅) is defined as a solution of the following optimization problem:

$$\displaystyle \begin{aligned} \left\{ \begin{array}{l l} \hat{\phi} = \arg \max \ H(\phi) \\ \text{s.t.}\ \int g(u)\phi(u)du = \mathbf{b} \ \text{and} \ \phi \in L^1(S,\mathbb{R}^+). \end{array} \right. \end{aligned} $$

(2.33)

Equation (2.33) is a convex optimization problem that may be reformulated by using Lagrange multipliers, see for instance (Boyd and Vandenberghe 2004). The moments $\mathbb {E}\left [g(U)\right ]$ may be unknown in practice and be estimated with the samples u ₍₁₎, …, u _(M). Considering fractional moments provide better estimates than integer moments for the constraint choice (Zhang and Pandey 2013). Maximum entropy density can be extended to random vectors but suffers however from the curse of dimensionality.

2.6.6 Statistical and Qualitative Tests

At the end of the distribution learning process, it may be useful to verify that the estimated PDF $\hat {\phi }(\cdot )$ (and its associated CDF $\hat {F}(\cdot )$) fits well the observed samples u ₍₁₎, …, u _(M) with a statistical test. Various goodness of fit tests may be applied such as Kuiper’s test, Kolmogorov–Smirnov test, Cramér–von Mises criterion, Pearson’s chi-squared test, Anderson–Darling test, etc. (D’Agostino 1986). These tests measure how well do the observed data correspond to the fitted distribution model. For instance, the Kolmogorov–Smirnov test evaluates the distance between F ^emp(⋅) and $\hat {F}(\cdot )$. The Kolmogorov–Smirnov statistics D _k is given by

$$\displaystyle \begin{aligned}D_k=\underset{{{u}} }{\operatorname{sup}}|F^{emp}(u)-\hat{F}(u)|.\end{aligned}$$

D _k is in [0, 1]. If D _k is near 0, the model fits well the observed samples and conversely.

In addition to the statistical tests, qualitative tests may be used in order to validate the choice of a suited distribution to represent the considered data. For instance, the QQ-plot (quantile-quantile plots) aims to determine graphically whether two sets of samples come from the same probability distribution or not. The QQ-plot relies on the notion of quantile. An α-quantile q _U(α) of a set of data U is defined by

$$\displaystyle \begin{aligned} \mathbb{P}(U \leq q_U(\alpha)) = \alpha. \end{aligned} $$

(2.34)

For two set of samples U and U′ corresponding to the same probability distribution, the α-quantile value should be closed. Thus, graphically, the data set defined by: $\{\hat {q}_U(\alpha ),\hat {q}_{U'}(\alpha ), \alpha =\frac {i-1}{M}, 1 \leq i \leq M \}$ should be closed to the diagonal if U and U′ are corresponding to the same PDF.

In Figure 2.22 an example of two QQ-plots for a set of data are illustrated. Two hypotheses for the distribution of the data are made: a Normal (right side) or a Gumbel (left side) distributions. The hyperparameters of the parametric distributions are determined by MLE. The QQ-plot of the Gumbel hypothesis is more close to the diagonal than the Normal distribution hypothesis (and the set of data have been generated according to a Gumbel distribution which is compliant with the QQ-plot result).

Fig. 2.22

QQplot for two MLE fits for a one-dimensional set of data (generated with a Gumbel distribution)

2.6.7 Identification of Dependency Between the Variables

The different density estimation methods described in the previous sections can be applied on random vectors with some adaptations. Nevertheless, when the dimension d increases, parametric and nonparametric may present some computational drawbacks. An alternative approach is to characterize the dependency between the components of a random vector. The density ϕ(⋅) of a random vector U = (U ⁽¹⁾, U ⁽²⁾, …, U ^(d)) may be decomposed uniquely as Nelsen (2007)

$$\displaystyle \begin{aligned} \phi\left(u^{(1)},u^{(2)},\ldots,u^{(d)}\right)&=\phi_{U^{(1)}}\left(u^{(1)}\right)\times \phi_{U^{(2)}}\left(u^{(2)}\right)\times \cdots\times \phi_{U^{(d)}}\left(u^{(d)}\right) \\ &\quad \times c\!\left(F_{U^{(1)}}\left(u^{(1)}\right),F_{U^{(2)}}\left(u^{(2)}\right),\ldots,F_{U^{(d)}}\left(u^{(d)}\right)\!\right), \end{aligned} $$

(2.35)

where $\phi _{U^{(i)}}(\cdot )$ and $F_{U^{(i)}}(\cdot )$ are, respectively, the PDF and CDF of U ⁽ⁱ⁾. They are the marginal distributions along the dimension i. c(⋅) is a multivariate density whose support is the hypercube [0, 1]^d and its marginal distribution are uniform laws. The density c(⋅) is known as the copula density. The copula framework allows to separate for a joint probability distribution the contribution of the marginals and the contribution of the dependence structure between each component of the considered random vector.

The marginal distribution U ⁽ⁱ⁾ is then estimated with one-dimensional parametric or nonparametric approaches as detailed in the previous sections. The copula may be estimated notably in a parametric way from a given copula family (Nelsen 2007), in a nonparametric way (Chen and Huang 2007) or in a semi-parametric framework with vine copulas (Joe et al. 2010).

Unlike the marginals, the structure of dependence between different random variables is generally difficult to grasp. Parametric copula (e.g., Gaussian, Clayton, Gumbel) may be fit in order to reflect at best the structure of dependence. An illustration of different parametric copula fit for a set of data is presented in Figure 2.23.

Fig. 2.23

Comparison of different copula fit for a set of data (generated with a Gumbel copula)

2.7 Theory of Probability Boxes

The probability boxes (Pboxes in short), also referred to as probability bounds may be interpreted as a combination of the probability theory and the interval analysis (Ferson et al. 1996; Beer et al. 2013). Similarly to an interval bound for an uncertain real variable, a probability−box bounds an uncertain CDF. It enables the modeling of epistemic uncertainty about the shape of a probability distribution, the distribution of uncertain parameters, etc.

Consider U as a random variable defined on the probability space $(\Omega ,A,\mathbb {P})$ and a pair $( \underline {F}, \overline {F})$ of non-intersecting cumulative distributions. The Pbox $[ \underline {F}, \overline {F}]$ encodes a class of probability measures whose CDFs F are bounded by the pair of CDFs $\underline {F}$ and $\overline {F}$ such that: $\underline {F}(u) \leq F(u) \leq \overline {F}(u) \text{;}\; \forall u \in \Omega$ (Beer et al. 2013).

To ease the Pbox construction and calculations, these probability bounds of the CDF of a random variable can be represented as step functions. Moreover, in practice, a restriction is added to ensure that the steps for both left and right functions occur at the same CDF values.

For two variables X and Y , assuming an independence between them, operations on these variables, such as X + Y , require first to partition the uncertain spaces of X and Y with suited intervals. Then, interval arithmetic on all the combinations of the Cartesian space of X and Y is carried out, and finally, the resulting Pboxes are estimated by computing the corresponding probabilities of the output intervals as the product of the respective pairs. Williamson and Downs (1990) developed algorithms to compute bounds on the result of addition, subtraction, multiplication, and division of random variables when only bounds on their input distributions are given.

Pbox incorporates both the imprecision on the available knowledge and the probabilistic characterization. It is possible to distinguish two types of Pboxes, the parameterized Pboxes and the general Pboxes (Figure 2.24). In the case of parameterized Pboxes, the distribution is known but the parameters characterizing the distribution are unknown, only intervals can be identified. General Pboxes are distribution-free representation methods using only statistical or experimental data. It exists different rules to construct Pboxes based on the available information (Beer et al. 2013; Ferson et al. 2015). For parameterized Pboxes, assume that, based on expert opinion, it is supposed that a distribution is Gaussian, but the precise values of the distribution hyperparameters (mean and standard deviation) are known only in an interval. Bounds on the possible distributions may be obtained in the form of a Pbox by computing the envelop of all Gaussian distributions that have their hyperparameters within the specified intervals. Considering the set of hyperparameters Θ = {(μ, σ)|μ ∈ [μ _min, μ _max], σ ∈ [σ _min, σ _max]}, the upper and lower bounds on the possible CDF are defined by

$$\displaystyle \begin{aligned} \begin{array}{rcl} \underline{F}(u) &\displaystyle =&\displaystyle \underset{\boldsymbol{\theta} \in \boldsymbol{\Theta}}{\text{min }} F_\theta(u) \end{array} \end{aligned} $$

(2.36)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \overline{F}(u) &\displaystyle =&\displaystyle \underset{\boldsymbol{\theta} \in \boldsymbol{\Theta}}{\text{max }} F_\theta(u). \end{array} \end{aligned} $$

(2.37)

Fig. 2.24

Example of general and parameterized probability boxes

Parametric Pboxes enable for a clear distinction between aleatory and epistemic uncertainties: aleatory uncertainty is represented by the distribution function family, whereas epistemic uncertainty is modeled by the intervals in the distribution hyperparameters. However, the parametric Pboxes are more restrictive than the general Pboxes because the knowledge about the distribution family is required.

The Pboxes may also be derived in case the distribution family is unknown resulting in general Pboxes. For these latter, the true CDF can have any arbitrary shape, it only has to follow the characteristics of a generic CDF and lie within the bounds of the Pbox. In case additional information are available such as the mean of the exact CDF, it enables to constrain the Pbox to a smaller region by defining more accurate bounds.

Relations between the Pboxes and the Dempster–Shaffer Structures (DSS) exist (Ferson et al. 2015). In DSS, unless a singleton is considered, a focal element represents usually a set of possible values for the variable U that existing evidence or measurement is not able to distinguish. However, the mass assigned to any particular focal element is a precise number. In DSS, the uncertainty lies in the u-value and certainty about the p-value. In contrast, the Pboxes express epistemic uncertainty about the mass assignment but a kind of certainty about the event U (its interval of definition). There is a duality between the two perspectives, and each approach may be converted to the other. However, there exists different Dempster–Shafer structures corresponding to a single Pbox, therefore there is not a one-to-one correspondence.

Moreover, connection between Pboxes and possibility measures have been established in different works such as Troffaes et al. (2013). In this work, the authors proved that almost every possibility measure may be interpreted as a Pbox, by reordering the elements according to increasing possibility. Therefore the Pboxes generalize the possibility measures.

3 Summary and Comparison of Uncertainty Modeling Formalisms

Based on the brief presentation of the existing mature uncertainty modeling formalisms suited for engineering design, some conclusions on advantages and drawbacks may be learned (Table 2.3).

Table 2.3 Comparison of uncertainty modeling formalisms

The probability theory is the most used formalism to model uncertainty by engineers and researchers in the field of complex system design. The probability theory is particularly suited to represent the aleatory uncertainty, and the methods and tools (sampling techniques, sensitivity analysis, reliability analysis, etc.) developed with the probability are adapted for the design in the presence of uncertainty. Compared to the alternative uncertainty formalisms, the uncertainty propagation is easier especially for complex models (see Chapter 3). Classical approaches such as Crude Monte Carlo are easy to implement and commonly used for the uncertainty propagation. One drawback of the probability formalism is the need to obtain information on each singleton of a subset through the probability distribution. Sometimes, information on the uncertainty distribution within a subset is unknown and only bounds are available. Although, uniform distribution is the distribution that maximizes the entropy when only the bounds of an uncertain variables are unknown, assuming a uniform distribution without additional information might be problematic. Indeed, considering two uncertain variables U ₁ and U ₂ for which only the bounds are known: U ₁, U ₂ ∈ [0, 1]². Let consider the uncertain variable Y  defined such as Y = U ₁ + U ₂. If uniform distribution between 0 and 1 are assumed for U ₁ and U ₂, by summing these variables, the obtained distribution for Y  is a triangular distribution between 0 and 2 with a maximum at 1, which is different from a uniform between 0 and 2. If interval formalism is used in such cases, the resulting bounds for Y  is [0, 2]. By assuming uniform distribution for the variables, it leads to an a-priori on Y  without any reason because of the absence of information on the distribution of U ₁, U ₂ (Figure 2.25).

Fig. 2.25

Example of the sum of two variables with two different formalisms

An advantage for the alternative uncertainty modeling techniques (evidence theory, possibility theory, imprecise probability and Pboxes) compared to the probability theory is the ability to measure the confidence in the uncertainty modeling information. Indeed, as the alternative techniques are based on non-additive measures, it enables to define two measures that provide an interval of confidence in the available uncertainty information that bracket the probability measure that would be obtained with the same information. Therefore, it naturally allows to account for epistemic uncertainty that often exists in the available data collected in the field and the aggregation of different expert opinions. The probability theory may be viewed as a special case of the alternative uncertainty formalisms which offer an easier aggregation of different types of uncertainty information. One important drawback of these formalisms is the difficulty to interpret the results in complex system design and especially with respect to all the existing regulations, design rules and constraints that are expressed with the probability theory. Moreover, the access to information from experts (in terms of the possibility distribution or the evidence) might be complicated with non-initiated experts. Finally, in terms of complex system design, the complexity and the computational cost associated to the uncertainty propagation for these alternative formalims is usually more important than with probability theory.

One major lesson learnt with this brief introduction of the different uncertainty modeling formalisms is that it is important to choose a formalism based on the available information (data, expert opinions, etc.) than trying to fit the existing information to a formalism chosen by default.