Structural Analysis and Modular Control Law for Modular Multilevel Converter (MMC)

Abstract

This paper proposes an in-depth analysis from the control point of view of dynamic models of a modular multilevel converter (MMC) for high-voltage direct current (HV-DC) application. Firstly, a generic method of analysis is presented for a natural arm-level state-space model. Its structural analysis highlights the decoupled nature of the MMC. Secondly, the well-known sum and difference of the upper and lower arm state and control variables is considered to obtain a (Σ∕Δ) model. This transformation leads to a coupling between state and control variables and to an increase of the system complexity. Using the analysis results of the natural model and the (Σ∕Δ) model, an original arm-modular control is finally proposed. The simulation results show the effectiveness of the proposed control, which is simpler to design compared to a conventional (Σ∕Δ) control.

1 Introduction

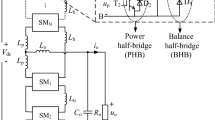
With the constant development of renewable energy and interconnections between countries, the high-voltage direct current (HVDC) transmission technology is in expansion, thanks to its lower footprint and greater controllability. The reference conversion structure today is the modular multilevel converter (MMC), which solves most of the problems of the former technologies, providing a good efficiency and an easy voltage scalability. MMC [1] has been invented and patented by Rainer Marquardt in 2001, and published for the first time in 2003. Even if different configurations of submodules are available, the most used today is the “half-bridge”, shown in Fig. 1. The SM configuration has little or no influence on the normal operation, and is essentially important for the fault condition, especially when the DC link is shorted.

Fig. 1

Half-Bridge MMC schematic

Many works have been made for the MMC modelling, such as switching models, arm averaged models, non-linear state-space models or linearized small-signal state-space models [2, 3]. Averaged type modelling is generally used for control design. After examining the prior art in modelling analysis and control design of MMC, it was found that on the one hand, not most models were enough exploited from the control point of view, and on the other hand, most controls were based on (Σ∕Δ) transformation [4, 5] by using the sum and difference of the upper and lower arm state and control variables. Compared to the previous published work on MMC model analysis, the first contribution of this paper is to propose a generic analysis method, which demonstrates the decoupled nature of the averaged model in natural coordinates contrary to the (Σ∕Δ) model where the state and control variables are coupled between arms leading to a complex control system. This approach comes with inherent benefits, like the use of the output variables as state variables or the partial separation of AC and DC quantities, allowing the use of very classical control means (e.g., Park transform for AC-grid-side and PI control for DC grid side). However, additional conditions are necessary to make the (Σ∕Δ) model decoupled for its control design. When these assumptions are not verified, the control quality can be degraded, hence leading to an interest of arm-based control. Thus, the second contribution of this paper is to propose a new MMC control based on the averaged model in natural coordinate.

The paper is organized as follows: in Sect. 2, the description of average equivalent schematic of the MMC is given. Based on a unified formulation, a global non-linear state-space model is proposed both for natural coordinate system and for (Σ∕Δ) transformation. In Sect. 3, a structural analysis is performed for both models. A new control is developed and validated in simulation in Sect. 4.

2 MMC Modelling

For MMC modelling, the “average” approach [3] is often used. Relying on the assumption that every capacitor in a given stack has the same voltage level thanks to a lower level control [6], it reduces strongly the model dimension. Each stack is simply replaced by a DC transformer with a controllable ratio, feeding an equivalent capacitor. This controllable ratio is called the modulation index of the stack. For an half-bridge stack, it has the range $m\in \left [0,+1 \right ]$ , and it becomes $m\in \left [-1,+1 \right ]$ for a full-bridge stack. The resulting schematic is shown in Fig. 2.

Fig. 2

MMC—equivalent average schematic

The modelling will be made under the following assumptions:

• All switching elements are considered to be ideal

• Each element of the equivalent schematic is linear

• Each storage element is associated with a dissipative term,¹ as shown in Fig. 2

• The saturation of control variables is not modelled

The three-phase MMC has 12 state variables, 6 arm currents (noted $I^{u,l}_{abc}$) and 6 equivalent capacitor voltages (noted $U^{u,l}_{abc}$). It also has six control variables, the modulation indexes of the six stacks, noted $m^{u,l}_{abc}$. The state vector is expressed in (1), and the control vector in (2). The arm inductor is defined by its inductance L ₁ and its series resistance R ₁, whereas the stack capacitor is defined by its capacitance C ₂ and its parallel resistance R ₂. The DC voltage E and the AC voltages V _g,abc appear as exogenous disturbances on the model.

$$\displaystyle \begin{aligned} \begin{aligned} x &= \left[ I^u_a , U^u_a , I^l_a , U^l_a , I^u_b , U^u_b , I^l_b , U^l_b , I^u_c , U^u_c , I^l_c , U^l_c \right] ^T \\ &:= \left[ x_{1a} , x_{2a} , x_{3a} , x_{4a} , x_{1b} , x_{2b} , x_{3b} , x_{4b} , x_{1c} , x_{2c} , x_{3c} , x_{4c} \right] ^T \end{aligned} \end{aligned} $$

(1)

$$\displaystyle \begin{aligned} \begin{aligned} u &= \left[ m^u_a , m^l_a , m^u_b , m^l_b , m^u_c , m^l_c \right] ^T \\ &:= \left[ u_{1a} , u_{2a} , u_{1b} , u_{2b} , u_{1c} , u_{2c} \right] ^T \end{aligned} \end{aligned} $$

(2)

A non-linear average state-space model of the MMC, under the form $\dot {x} = f(x,u)$, is presented in (3), and the state and control space over which it is defined is shown in (4). Note that the absence of _abc and/or ^u,^l indexes indicates that the result is relevant whatever the considered phase or arm.

$$\displaystyle \begin{aligned} f(x,u) = \begin{bmatrix} 1/L_1 \cdot \left( E/2 - V_{ga} - R_1 \cdot x_{1a} - x_{2a} \cdot u_{1a} \right) \\ 1/C_2 \cdot \left( x_{1a} \cdot u_{1a} - x_{2a}/R_2 \right) \\ 1/L_1 \cdot \left( E/2 + V_{ga} - R_1 \cdot x_{3a} - x_{4a} \cdot u_{2a} \right) \\ 1/C_2 \cdot \left( x_{3a} \cdot u_{2a} - x_{4a}/R_2 \right) \\ 1/L_1 \cdot \left( E/2 - V_{gb} - R_1 \cdot x_{1b} - x_{2b} \cdot u_{1b} \right) \\ 1/C_2 \cdot \left( x_{1b} \cdot u_{1b} - x_{2b}/R_2 \right) \\ 1/L_1 \cdot \left( E/2 + V_{gb} - R_1 \cdot x_{3b} - x_{4b} \cdot u_{2b} \right) \\ 1/C_2 \cdot \left( x_{3b} \cdot u_{2b} - x_{4b}/R_2 \right) \\ 1/L_1 \cdot \left( E/2 - V_{gc} - R_1 \cdot x_{1c} - x_{2c} \cdot u_{1c} \right) \\ 1/C_2 \cdot \left( x_{1c} \cdot u_{1c} - x_{2c}/R_2 \right) \\ 1/L_1 \cdot \left( E/2 + V_{gc} - R_1 \cdot x_{3c} - x_{4c} \cdot u_{2c} \right) \\ 1/C_2 \cdot \left( x_{3c} \cdot u_{2c} - x_{4c}/R_2 \right) \\ \end{bmatrix} \end{aligned} $$

(3)

$$\displaystyle \begin{aligned} x_{1,3} \in \mathbb{R} ~,~ x_{2,4} \in \mathbb{R^+} ~,~ u_{1,2} \in \left[ 0 , +1 \right] \end{aligned} $$

(4)

As shown in [4, 5, 7, 8], the most common method for MMC analysis and control is based on both a state and a control change of coordinates, using sums and differences of top/bottom state and control variables in a given leg.

This corresponds to state and control variable transformations defined in (5).

$$\displaystyle \begin{aligned} \begin{aligned} \begin{bmatrix}z_1,& z_2,&z_3 ,& z_4 \end{bmatrix} ^T &= \begin{bmatrix} x_1+x_3 ,& x_2+x_4 ,& x_1-x_3 ,& x_2-x_4 \end{bmatrix} ^T \\ \begin{bmatrix}v_1,& v_2 \end{bmatrix} ^T &= \begin{bmatrix} u_1+u_2 ,& u_1-u_2 \end{bmatrix} ^T \end{aligned} \end{aligned} $$

(5)

The transformed model becomes $\dot {z} = \bar {f}(z,v)$, whose components are detailed in (6).

$$\displaystyle \begin{aligned} \begin{aligned} \bar{f}(z,v) = \begin{bmatrix} 1/L_1 \cdot \left( E - R_1 \cdot z_{1a} - v_{1a} \cdot z_{2a} /2 - v_{2a} \cdot z_{4a} /2 \right) \\ 1/C_2 \cdot \left( v_{1a} \cdot z_{1a} /2 - z_{2a}/R_2 + v_{2a} \cdot z_{3a} /2 \right) \\ 1/L_1 \cdot \left( -2 V_{ga} + R_1 \cdot z_{3a} - v_{2a} \cdot z_{2a} /2 - v_{1a} \cdot z_{4a} /2 \right) \\ 1/C_2 \cdot \left( v_{2a} \cdot z_{1a} /2 - z_{4a} / R_2 + v_{1a} \cdot z_{3a} /2 \right) \\ 1/L_1 \cdot \left( E - R_1 \cdot z_{1b} - v_{1b} \cdot z_{2b} /2 - v_{2b} \cdot z_{4b} /2 \right) \\ 1/C_2 \cdot \left( v_{1b} \cdot z_{1b} /2 - z_{2b}/R_2 + v_{2b} \cdot z_{3b} /2 \right) \\ 1/L_1 \cdot \left( -2 V_{gb} + R_1 \cdot z_{3b} - v_{2b} \cdot z_{2b} /2 - v_{1b} \cdot z_{4b} /2 \right) \\ 1/C_2 \cdot \left( v_{2b} \cdot z_{1b} /2 - z_{4b} / R_2 + v_{1b} \cdot z_{3b} /2 \right) \\ 1/L_1 \cdot \left( E - R_1 \cdot z_{1c} - v_{1c} \cdot z_{2c} /2 - v_{2c} \cdot z_{4c} /2 \right) \\ 1/C_2 \cdot \left( v_{1c} \cdot z_{1c} /2 - z_{2c}/R_2 + v_{2c} \cdot z_{3c} /2 \right) \\ 1/L_1 \cdot \left( -2 V_{gc} + R_1 \cdot z_{3c} - v_{2c} \cdot z_{2c} /2 - v_{1c} \cdot z_{4c} /2 \right) \\ 1/C_2 \cdot \left( v_{2c} \cdot z_{1c} /2 - z_{4c} / R_2 + v_{1c} \cdot z_{3c} /2 \right) \\ \end{bmatrix} \end{aligned} \end{aligned} $$

(6)

3 Structural Analysis

The underlying idea of the proposed analysis method is to obtain simple and if possible non-parametric conclusions from the non-linear models presented above. These conclusions play a role into the comprehension of the behaviour of MMC, thus making the control law development easier. The difference between structural and parametric properties will be highlighted.

3.1 Natural Model Analysis

3.1.1 Local Differentiation (Jacobian Analysis)

Formally, the Jacobian matrix $\mathcal {J}_{f}$ of the vector field f(⋅) is defined over the entire argument vector, $\alpha := \left [ x | u \right ]$. We introduce the partial Jacobian matrix $\mathcal {J}_{f,x}$ and $\mathcal {J}_{f,u}$ such that $\mathcal {J}_{f,\alpha } = \left [ \mathcal {J}_{f,x} | \mathcal {J}_{f,u} \right ]$

These matrix are presented, respectively, in (7) and (8).

(7)

$$\displaystyle \begin{aligned} \mathcal{J}_{f,u} = \begin{bmatrix} -\frac{x_{2a}}{L_1} & 0 & 0 & 0 & 0 & 0 \\ \frac{x_{1a}}{C_2} & 0 & 0 & 0 & 0 & 0 \\ 0 & -\frac{x_{4a}}{L_1} & 0 & 0 & 0 & 0 \\ 0 & \frac{x_{3a}}{C_2} & 0 & 0 & 0 & 0 \\ 0 & 0 & -\frac{x_{2b}}{L_1} & 0 & 0 & 0 \\ 0 & 0 & \frac{x_{1b}}{C_2} & 0 & 0 & 0 \\ 0 & 0 & 0 & -\frac{x_{4b}}{L_1} & 0 & 0 \\ 0 & 0 & 0 & \frac{x_{3b}}{C_2} & 0 & 0 \\ 0 & 0 & 0 & 0 & -\frac{x_{2c}}{L_1} & 0 \\ 0 & 0 & 0 & 0 & \frac{x_{1c}}{C_2} & 0 \\ 0 & 0 & 0 & 0 & 0 & -\frac{x_{4c}}{L_1} \\ 0 & 0 & 0 & 0 & 0 & \frac{x_{3c}}{C_2} \\ \end{bmatrix} \end{aligned} $$

(8)

3.1.2 Coupling Analysis

In the proposed analysis method, both input-state and state-state coupling will be studied. Whereas the former describes the access of energy inside the system, the latter corresponds to its propagation inside it. To study the behaviour of the global converter, both are significant. For the first point, it is clear from the block structure of $\mathcal {J}_{f,u}$ that the arms are decoupled from their inputs, because each modulation index only affects its own arm. On the other hand, the analysis of $\mathcal {J}_{f,x}$ shows that it is purely block-diagonal. Consequently, there is no coupling paths between the phases of the converter, neither between the upper and lower arms in each phase. The natural representation of the MMC is consequently purely decoupled.

The analysis performed above shows that the converter can effectively be decomposed in three phases and each phase in two arms, and that its whole behaviour can be described by one latter only. By definition, this arm will be defined as the irreducible element of the converter. After linearization and by defining $x_i := X_i+\tilde {x}_i$ (resp. $u_i := U_i+\tilde {u}_i$), the small variations $\tilde {x}_i$ dynamics around X _i (resp. U _i) are described in (9).

$$\displaystyle \begin{aligned} \begin{bmatrix} \dot{\tilde{x_1}} \\ \dot{\tilde{x_2}} \end{bmatrix} = \begin{bmatrix} -\frac{R_1}{L_1} & -\frac{U}{L_1} \\ \frac{U}{C_2} & -\frac{1}{R_2 \cdot C_2} \end{bmatrix} \cdot \begin{bmatrix} \tilde{x_1} \\ \tilde{x_2} \end{bmatrix} + \begin{bmatrix} -\frac{X_2}{L_1} \\ +\frac{X_1}{C_2} \end{bmatrix} \cdot \tilde{u}\end{aligned} $$

(9)

It plays a very significant role in the converter analysis, since all the important properties (like stability, observability and controllability) can be studied directly on this element, whose size is much reduced compared to the full-order model.

3.2 Transformed (Σ∕Δ) Model Analysis

3.2.1 Local Differentiation (Jacobian Analysis)

Using the same formalism, the two partial Jacobian matrix of the transformed system are shown in (10) and (11).

(10)

$$\displaystyle \begin{aligned} \mathcal{J}_{\bar{f},v} = \begin{bmatrix} -\frac{z_{2a}}{2 L_1} & -\frac{z_{4a}}{2 L_1} & 0&0&0&0 \\ \frac{z_{1a}}{2 C_2} & \frac{z_{3a}}{2 C_2} & 0&0&0&0 \\ -\frac{z_{4a}}{2 L_1} & -\frac{z_{2a}}{2 L_1} & 0&0&0&0 \\ \frac{z_{3a}}{2 C_2} & \frac{z_{1a}}{2 C_2} & 0&0&0&0 \\ 0&0& -\frac{z_{2b}}{2 L_1} & -\frac{z_{4b}}{2 L_1} & 0&0 \\ 0&0& \frac{z_{1b}}{2 C_2} & \frac{z_{3b}}{2 C_2} & 0&0 \\ 0&0& -\frac{z_{4b}}{2 L_1} & -\frac{z_{2b}}{2 L_1} & 0&0 \\ 0&0& \frac{z_{3b}}{2 C_2} & \frac{z_{1b}}{2 C_2} & 0&0 \\ 0&0&0&0& -\frac{z_{2c}}{2 L_1} & -\frac{z_{4c}}{2 L_1} \\ 0&0&0&0& \frac{z_{1c}}{2 C_2} & \frac{z_{3c}}{2 C_2} \\ 0&0&0&0& -\frac{z_{4c}}{2 L_1} & -\frac{z_{2c}}{2 L_1} \\ 0&0&0&0& \frac{z_{3c}}{2 C_2} & \frac{z_{1c}}{2 C_2} \\ \end{bmatrix} \end{aligned} $$

(11)

3.2.2 Coupling Analysis

In the (Σ∕Δ) coordinates, the system is no longer decoupled. Whereas the three phases remain independent, a structural coupling appears between the two arms of each one through the “difference” quantities, in this case the equilibrium points of v ₂, z ₃ and z ₄, as shown in (10) and (11). To illustrate these phenomena, it is possible to consider an identical current flowing through both arms in the presence of two different modulation indexes (v ₂ ≠ 0). As this current will charge differently both capacitors, it contributes to the apparition of a differential voltage: the sum current z ₁ contributes to the differential voltage z ₄ through the differential modulation index v ₂.

From the coupling analysis presented before, it is obvious that the irreducible element is now a whole phase. The small-signal model of one phase around an arbitrary [V, Z] operating point is shown in (12).

$$\displaystyle \begin{aligned} \begin{aligned} \begin{bmatrix} \dot{\tilde{z_1}} \\ \dot{\tilde{z_2}} \\ \dot{\tilde{z_3}} \\ \dot{\tilde{z_4}} \end{bmatrix} &= \begin{bmatrix} -\frac{R_1}{L_1} & -\frac{V_{1}}{2 L_1} & 0 & -\frac{V_{2}}{2 L_1} \\ \frac{V_{1}}{2 C_2} & -\frac{1}{R_2 C_2} & \frac{V_{2}}{2 C_2} & 0 \\ 0 & -\frac{V_{2}}{2 L_1} & -\frac{R_1}{L_1} & -\frac{V_{1}}{2 L_1} \\ \frac{V_{2}}{2 C_2} & 0 & \frac{V_{1}}{2 C_2} & -\frac{1}{R_2 C_2} \\ \end{bmatrix} \cdot \begin{bmatrix} \tilde{z_1} \\ \tilde{z_2} \\ \tilde{z_3} \\ \tilde{z_4} \end{bmatrix} \\ &\quad + \begin{bmatrix} -\frac{Z_{2}}{2 L_1} & -\frac{Z_{4}}{2 L_1} \\ \frac{Z_{1}}{2 C_2} & \frac{Z_{3}}{2 C_2} \\ -\frac{Z_{4}}{2 L_1} & -\frac{Z_{2}}{2 L_1} \\ \frac{Z_{3}}{2 C_2} & \frac{Z_{1}}{2 C_2} \\ \end{bmatrix} \cdot \begin{bmatrix} \tilde{v_1} \\ \tilde{v_2} \end{bmatrix} \end{aligned} \end{aligned} $$

(12)

3.2.3 Parametric Condition for Decoupling

To obtain a decoupling configuration comparable with the initial one, the conditions V ₂ = Z ₃ = Z ₄ = 0 should be respected. In steady-state, v ₂, z ₃ and z ₄ are essentially sinusoidal, corresponding indeed to the AC component of the manipulated quantities. Even if the former assumptions are relevant from the control point of view (if $v_2(t)=\sin {}(\omega t)$ then $V_2=< \sin {}(\omega t) >=0$), they are questionable because the so-called sine waves inside m ^u, m ^l, I ^u and I ^l are comparable in magnitude to their DC components. In other words, the Σ∕Δ transformation changes a structural arm-arm decoupling into a questionable parametric arm-arm decoupling.

4 Proposed Control and Simulation Results

Making use of the arm-decoupled behaviour of the MMC, the proposed controller contains six control systems, almost identical except the feedforward/modulating terms. Its structure is shown in Fig. 3. Each control system includes two standard single-input, single-output dynamic controllers (arm current controller and stack voltage controller), making each state variable controlled explicitly one time. The proposed scheme allows both active, reactive and circulating current control.

Fig. 3

Block diagram of the proposed control law

The DC-grid power is explicitly controlled through the DC arm current, which is equal between top and bottom arms. To maintain the DC stack voltage, the associated controller generates an individual AC power set point, converted into an instantaneous active current reference. By adding the latter, the former DC component, a reactive current reference and possibly a 2f circulating current reference (not shown in Fig. 3), the global arm current reference is obtained. It is then fed to the dedicated controller with generates the corresponding arm voltage.

As explained in the colour legend, all the white blocks have a diagonal behaviour, meaning that a given output does only depend on the input(s) which share the same index. For instance, the arm current controller first² output V _fb[1] depends freely on I[1] and I ^#[1], but not on I[2] or I ^#[2]. For the stack voltage controller, the same principle applies excepted that the reference is common to all the six arms.

The non-diagonal (grey) blocks behaviour is detailed in (13) and (14). The Q-to-I block is obtained by replacing $\cos {}(\cdot )$ by $\sin {}(\cdot )$ in (14).

$$\displaystyle \begin{aligned} \begin{aligned} V_{ff} =\begin{bmatrix} \frac{E}{2} - V_{ga} ,& \frac{E}{2} + V_{ga} ,& \frac{E}{2} - V_{gb} ,& \frac{E}{2} + V_{gb} ,& \frac{E}{2} - V_{gc} ,& \frac{E}{2} + V_{gc} \end{bmatrix} ^T \end{aligned} \end{aligned} $$

(13)

$$\displaystyle \begin{aligned} I_{arm,act}^\# = \frac{2}{\hat{V_g}} \times \begin{bmatrix} + P_{ac,arm}[1] \times \cos ( \theta_{PLL} - 0\pi/3 ) \\ - P_{ac,arm}[2] \times \cos ( \theta_{PLL} - 0\pi/3 ) \\ + P_{ac,arm}[3] \times \cos ( \theta_{PLL} - 2\pi/3 ) \\ - P_{ac,arm}[4] \times \cos ( \theta_{PLL} - 2\pi/3 ) \\ + P_{ac,arm}[5] \times \cos ( \theta_{PLL} - 4\pi/3 ) \\ - P_{ac,arm}[6] \times \cos ( \theta_{PLL} - 4\pi/3 ) \\ \end{bmatrix} \end{aligned} $$

(14)

To validate the proposed control law, simulations based on a three-phase MMC average model have been made with Matlab/Simulink. Its parameters, corresponding to Fig. 2, are summarized in Table 1

Table 1 Simulation parameters

The power references have a rise time of 100 ms,³ and an amplitude of ±700 MW and ±300 MVAR. Both controllers of each control system are polynomial, linear controllers. The global simulation results are shown in Fig. 4, with a zoom on a steady-state condition (P = 700 MW, Q = 0 MVAR) in Fig. 5. In general two slow active and reactive power controllers are used for HVDC-VSC control, but they are not shown here since they would hide the proposed, inner control dynamics. These results exhibit both good transient and steady-state performance, with good dynamics, little or no overshoot and low harmonic distortion.

Fig. 4

Simulation results: global overview

Fig. 5

Simulation results: steady-state operation

5 Conclusion

The control of the MMC is known as a challenging task, leading to an important work of both academic and industrial actors. While most of the contributions in this field involve a common formalism, using sums and differences of the normal state variables, it has been shown that this practice was indeed increasing the system complexity, introducing coupling between state and control variables, leading to hard to interpret phenomena. After the computation of the non-linear model of the MMC, it has been analysed and the independence of arms has been proved. Based on this concept, a purely independent control based on arm-modularity with few parameters and straightforward tuning was proposed, and its validity was shown in simulation. Moreover, this control law lends itself well to distributed control, and to MMC-type converters with an arbitrary number of phases, for example, for HVDC DC/DC [9] applications.

The study of the consequence of the HVDC link configuration (monopolar/bipolar) and the station transformer coupling is considered as a perspective, such as the design of different controllers for increased performance.