Learning from Field Measurements Through Heuristic Back Analysis

Abstract

Back-analysis involves the determination of input parameters required in computational models using field monitored data, and is particularly suited to underground constructions, where more information about ground conditions and response become available as the construction progresses. A crucial component of back-analysis is an algorithm to find a set of input parameters that will minimize the difference between predicted and measured performance (e.g., in terms of deformations, stresses or tunnel support loads). Methods of back-analysis can be broadly classified as direct and gradient-based optimization techniques. An alternative methodology to carry out the required nonlinear optimization in back-analyses is the use of heuristic techniques. Heuristic methods refer to experience-based techniques for problem solving, learning, and discovery that find a solution which is not guaranteed to be optimal, but is good enough for a given set of goals. Two heuristic methods are presented and discussed, namely, Simulated Annealing (SA) and Differential Evolution Genetic Algorithm (DEGA). SA replicates the metallurgical processing of metals annealing, which involves a gradual and sufficiently slow cooling of a metal from the heated phase, which leads to a final material with a minimum imperfections and internal dislocations. DEGA emulates the Darwinian evolution theory of the survival of the fittest. Descriptions of SA and DEGA, their implementations in the computer code Fast Lagrangean Analysis of Continua (FLAC), and uses in the back-analysis of the response of idealized tunnelling problems, and a real case of a twin tunnel in China are presented.

1 Introduction

Computational models for geotechnical applications have undergone major improvements in the past several decades. They can be used in performance-based engineering design and evaluation of geotechnical structures by providing detailed evaluation of response and estimated consequences. However, determination of model input parameters remains to be the ‘Achilles’ heel’ of computational modelling [1]. This is particularly true due to significant uncertainties in material properties and loads encountered in geotechnical engineering. Geological, geophysical, in situ and laboratory investigations needed in analysis and design are time consuming and expensive and are carried out extensively only for very important projects. Even in these important projects are data inevitably incomplete. Estimates of initial model parameters are usually established from laboratory tests on limited number of core samples. However, laboratory scale measurements from a few small core samples are inadequate in characterizing properties because of their inability to capture heterogeneities at large scales, and of unavoidable sample disturbance.

An alternative procedure to determining input to computational models is by monitoring field response. Direct measurements of field response can provide fast and economical means of determining or validating model parameters and for improving the reliability of model predictions. Predicted response from computer simulation using an initial set of model parameters can be compared with observations. If predicted and observed response deviate, input data are iteratively revised, often by manual trial-and-error procedure. The process of adjusting model parameters so that the model matches observed response during some historical period can be accomplished by inverse modelling or back-analysis. Iterative procedures are often used since direct inversion is only possible for very simple analytical models. Back analysis is essentially an optimization problem where the objective is to minimize, in a least squares sense, the differences between predicted and monitored response. Back-analysis is particularly suited for underground constructions such as tunneling where more information on the ground characteristics and response become available as the construction progresses. Using data from monitoring, models can be calibrated, and the design can be modified as the structure is being built. However, back-analysis is time consuming and requires much effort, and thus is not widely adopted in routine engineering practice.

Back-analysis requires an algorithm to handle the minimization of the differences between predicted and measured response, to find an improved set of input parameters. The present paper focuses on the application of so-called heuristics-based global search algorithms in the back-analysis of tunnel behavior from field measurements using a commercially available code. A description of heuristic algorithm, particularly Simulate Annealing (SA) and Differential Evolution Genetic Algorithm (DEGA), and their implementations in the commercial computer code Fast Lagrangean Analysis of Continua (FLAC) developed by Itasca [2] are presented. The uses of SA and DEGA in back-analysis of tunnel response are analyzed in terms of the uniqueness of the solution, the stability and efficiency of the code under highly non-linear circumstances, the sensitivity of the solution to the initial trial assumption and the sensitivity of the solution to the monitoring data. The application of the proposed back-analysis procedures is demonstrated in the combined back- and forward-modelling of the Heshang Highway Tunnel project in China.

2 Back-Analysis Procedures

Back-analysis methods can be broadly classified as local and global. Local back-analysis methods can be further classified as direct and gradient-based. Generally, direct optimization methods are easier to implement since they do not require formulation and calculation of gradients of the error function. These methods can be employed for well-posed geotechnical problems, for example problems involving elastic analysis with one to three parameters to be back-analyzed. Gradient-based methods are those that require derivatives of the objective function that is being minimized. Examples are the Steepest Descent, the Conjugate Gradient, the Newton and the Quasi-Newton methods. The main advantage of gradient methods is the property of quadratic convergence which accelerates the solution progress. When constraints are required for the parameters, then either a penalty procedure must be superimposed on the optimization process, or a more appropriate method needs to be used. Of the latter methods, a modified version of the Simplex, the Complex method, a constrained version of the Simplex, has shown good results in the literature [3]. Gradient-based methods are powerful algorithms but present some challenges. The need to evaluate derivatives makes the use of gradient methods difficult in iterative non-linear numerical analysis, for example by using the finite element method. This could be dealt with when there are only a two to three unknowns, however, when the number of unknowns increases then the process becomes not only computationally expensive but sometimes impossible.

Many direct and gradient methods have been applied successfully in back-analysis of ground deformations for various simplified geotechnical problems. Cividini et al. [4, 5] provide an excellent outline of back analysis principles and describe the successful application of the Simplex method, for back-analysis of a geotechnical problem with two and four unknown variables. Application of back-analysis to geotechnical problems requires careful consideration of the type, and nature of available monitoring data. Other important factors in the back-analysis using monitoring data are the uncertainties and errors associated with both the monitoring program and the instruments. An excellent review of the various field monitoring equipment including their sensitivities and potential sources of error is found in Dunnicliff [6], and Xiang et al. [3]. Gioda and Sakurai [7], Londe [8], Sakurai [9], Sakurai et al. [10], and Hrubesova and Mohyla [11] discuss the applications of back-analysis in tunneling.

2.1 Heuristic Methods of Back-Analysis

Heuristic methods refer to problem-solving techniques that employ practical methodologies not guaranteed to be truly optimal or perfect, but adequate to produce a sufficiently satisfactory solution that approximates the exact solution for a problem at hand in a reasonable time. Heuristic methods can find optimal solutions by using search trees, however, instead of generating all possible solution branches, a heuristic method selects branches more likely to produce outcomes than other branches. They follow iterative procedures where the search learns what paths to follow and which ones to avoid by assessing how close the current iteration is to the solution. Heuristic methods are sometimes the most viable techniques for difficult optimization of non-linear problems where the best approach is to exploit randomness in the system to get an approximate answer. Heuristic algorithms mostly fall into four broad categories: Neural Networks (NN), Simulated Annealing (SA), Genetic Algorithm (GA) and Evolutionary Algorithm (EA). Genetic and evolutionary algorithms are generally similar techniques but follow different implementations.

2.2 Simulated Annealing

Simulated Annealing (SA) was first introduced by Kirkpatrick et al. [13] and belongs to a general class of combinatorial optimization techniques. SA was initially introduced for discrete optimization problems, but it has recently gained attention for its ability to solve large-scale continuous optimization problems where highly irregular objective functions with multiple local optima may exist. SA got its name from the metallurgical annealing of metals such as steel, by which a gradual and sufficiently slow cooling of a metal from the heated phase, leads to a final material with theoretically perfect crystalline structure having a minimum number of imperfections and internal dislocations. During cooling, nature follows its own optimization path for the given circumstances. This is what the SA back-analysis procedure tries to emulate.

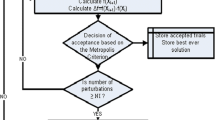
SA applied to back-analysis works by replacing a trial solution to an optimization problem by a random nearby solution. The new nearby solution is chosen with a probability that depends on a global parameter T called the “temperature” of the system. The probabilities are chosen so that the system ultimately tends to move to states of lower energy following the Boltzmann probability distribution. The steps are repeated, and when enough time is made available for cooling, the higher is the probability of attaining a minimum energy state at the end. If the solution is controlled in such a way that the algorithm scans over progressively smaller solution spaces, then there is good chance to converge to a global optimum.

Consider the objective function $f({\mathbf{X}})$ related to the least-squares error between prediction and measurement, where ${\mathbf{X}}$ is the n-dimensional solution vector. An example of $f({\mathbf{X}})$ is the relative error between measured and predicted values:

$$ f({\mathbf{X}}) = \left| {\frac{{{\mathbf{X}}_{{\mathbf{m}}} - {\mathbf{X}}_{{\mathbf{p}}} }}{{{\mathbf{X}}_{{\mathbf{p}}} }}} \right| $$

(1)

where ${\mathbf{X}}_{{\mathbf{m}}}$ and ${\mathbf{X}}_{{\mathbf{p}}}$ are the vectors of measured and predicted quantities, respectively. The goal of the optimization is to seek $Min\left[ {f({\mathbf{X}})} \right]$ subject to the constraints $x_{i}^{L} \le x_{i} \le x_{i}^{U} ,i = 1, \ldots ,n$, where $x_{i} \in {\mathbf{X}}$, and $x_{i}^{L} \;{\text{and}}\;x_{i}^{U}$ are the expected lower and upper bound values of x_i. The solution starts from an initial trial solution vector X₁. An arbitrary initial starting “temperature” $T_{o}$ corresponding to X₁ is also assumed. A dedicated cooling schedule is required to perform the SA, which determines how the temperature is decreased from an initial value T_o during the annealing. An example annealing schedule often encountered in the literature is an exponential cooling

At each temperature stage T_k, several iterations NI are performed using different, sequentially and randomly generated combinations (or permutations) of the solution vector around the present trial ${\mathbf{X}}_{i + 1} = {\mathbf{X}}_{i} + {\mathbf{\Delta X}}$. The vector change ΔX must yield a new vector relatively close to the previous solution. If a new vector X_i+1 from the random perturbation does not satisfy Eq. (1), then the random generation of ΔX is repeated until a valid trial vector is found. The new vector X_i+1 is used as input in the numerical analysis and a new objective function value $f({\mathbf{X}}_{i + 1} )$ is obtained. The new trial is accepted if it leads to a decrease of the objective function value, i.e. $\Delta f = f\left( {{\mathbf{X}}_{i + 1} } \right) - f\left( {{\mathbf{X}}_{i} } \right) < 0$. On the other hand, if $\Delta f > 0$, then the Metropolis et al. (1953) criterion is used to control the acceptance or not of the present trial. The probability of the objective value change is calculated and compared to a random number $r \in [0,1]$. Thus, by setting E = Δf as a measure of the energy of the system and the Boltzmann’s constant k = 1.0, the probability yields:

$$ P(\Delta f) = \exp \left( {\frac{ - \Delta f}{T}} \right) $$

(2)

If this probability is greater than a randomly generated number r, the new solution is accepted and becomes the starting solution for the next iteration. Otherwise, if the probability is less than r, the new solution is rejected, and the present solution remains the same from the previous step. The randomly generated vector ΔX of perturbations around a present solution vector also needs some consideration. In [14], a discussion is made regarding the importance and efficiency of various methods of calculating the ΔX vector. The present implementation involves a simple scheme in which the present solution value is randomly perturbed by a small value.

2.3 Differential Evolution Genetic Algorithm

Differential Evolution Genetic Algorithm (DEGA) combines the concepts of Differential Evolution and Genetic Algorithms to handle optimization of non-binary valued nonlinear functions. DEGA uses two arrays to store a population of NP, D-dimensional vectors of parameters that are being back-calculated (D = n = number of parameters). The parameter vector may consist of heterogeneous data from different types of monitoring (e.g., displacements, strain, loads on structures, pore pressures, etc.) The first array contains the primary values of the present vector population, and the secondary array stores sequentially the products or “offspring” for the next generation. The algorithm starts by filling the primary array with NP vectors with randomly generated parameter values. The initial random generation should satisfy the constraints on the parameters. The primary array is also called as the “trial vector” since it contains NP vectors that will later be tried for fitness. Each of these individual randomly-generated vectors X_i is considered sequentially for genetic operations. For each of the chosen vectors, three other vectors X_A, X_B, X_C are randomly chosen from the remaining vectors of the primary array. The following mutation is then performed to generate a new trial vector:

$$ {\mathbf{X}}_{1}^{m} = {\mathbf{X}}_{A} + F({\mathbf{X}}_{B} - {\mathbf{X}}_{C} ) $$

(3)

where ${\mathbf{X}}_{1}^{m}$ is the new mutant vector and F is a mutation factor in the range $0 < F \le 1.2$ with an optimum value in the range 0.4 to 1 [14].

At this stage, the crossover takes place. A randint(i) = random integer number in the range [1, n], and for each parameter j = 1, …, n, randnum(j) = random number in the range [0, 1] are generated. Then a new vector is created from the original X_i parent and the mutant vector using the crossover criterion:

$$ x_{i,j}^{\prime } = \left\{ {\begin{array}{*{20}l} {x_{i,j}^{m} \;\;if\;\;randnum \le XR\;\;or\;\;randint(i) = j} \hfill \\ {x_{i,j} \;\;if\;\;randnum > XR\;\;and\;\;randint(i) \ne j} \hfill \\ \end{array} } \right. $$

(4)

where XR is a crossover rate in the range [0, 1]. The crossover scheme essentially means that if randnum > XR, the new i^th trial vector will receive the j parameter from the parent vector, otherwise the parameter will be obtained from the mutant vector ${\mathbf{X}}_{1}^{m}$. In this way if XR = 1, then every trial vector will be obtained from the mutant vector, or if XR = 0, then all except for one parameter will be called from the parent trial vector. The new vector ${\mathbf{X}}_{i,j}^{\prime }$ is tested against X_i for fitness.

For minimization problems, the vector corresponding to the lower value (fittest candidate) is entered in the secondary array. The same procedure is followed until all vectors of the original primary array are processed and an equal size secondary array has been formed. At this stage the secondary array values are transferred and update the primary array while the secondary array is purged. This marks the end of one generation. Obviously, many generations are required for convergence. The above steps are repeated until a maximum number of generations is reached. When the algorithm converges to the global optimum based on the criterion, then all vectors of the primary array theoretically become equal.

3 Application to Back-Analysis of Tunnel Response

To illustrate their applicability to real problems, the SA and DEGA back-analysis procedure was implemented in the widely-used finite difference code FLAC [2], using its built-in programming language FISH. In the interest of avoiding a very lengthy paper, and since the results and conclusions from the two methods are very similar, only the results from the SA back-analysis are presented below. The implemented procedure is then applied to the analysis of the response during construction of the Heshang Highway Tunnel located in the Fujian province of South East China and is a part of the transportation system between the local airport and Fuzhou city. It is a twin tunnel project and approximately 450 m long. Each of the two tunnels is approximately 11.5 m high and 15 m wide. The tunnel passes through highly weathered volcanic material. Due to the poor quality of the rock mass and the lateral proximity of the two tunnels, a wide array of instrumentation methods was employed.

During construction, three sections of the tunnel were fully instrumented consisting of: (1) multipoint extensometer measurements, (2) surface subsidence, (3) tunnel convergence, (4) crown subsidence by surveying, (5) anchor tensioning, and (6) lining axial and radial pressure. The back-analysis was performed using only the extensometer data and surface subsidence. The details and locations of the field sensors used in the back-analysis are shown in Figs. 1 and 2.

Fig. 1.

Locations and details of extensometer measurements at Station K6+300 of Heshang Tunnel.

Fig. 2.

Locations and details of surface subsidence measurements at Station K6+300 of Heshang Tunnel.

The sequential excavation of the Heshang tunnel was designed in accordance with anticipated ground conditions, with different excavation sequences used for the left and right tunnels. The left tunnel was excavated with two side drifts, a top and a bottom core (Stages 1, 2, 3 and 5). The right tunnel was excavated by a top heading, two bench sections and followed by an invert (Stages 4, 6, 7 and 8). The back-analysis is performed using monitoring data obtained from the Stages 1 and 2 in the excavation of the left tunnel. These include extensometer displacements measured at K01 and K02, and surface displacements measured at P2 to P8. Model parameters obtained from the back-analysis of the left tunnel (Stages 1 and 2) are then used in the prediction (or forward modelling) of the response of both the left and right tunnels during subsequent stages (Stages 3 to 8) of construction. The combined back- and forward-modelling was performed for Station K6+300. It is noted that there are no lateral differences in rock types encountered in the left and right tunnels at Station K6+300.

The ground is modelled by a Mohr-Coulomb failure criterion. Two-dimensional plane strain conditions are assumed, and three-dimensional loading effects due to deformation before the tunnel face are approximated using the Convergence-Confinement method [15]. The forepoling umbrella is simulated using finite difference zones with equivalent continuum properties instead of using structural elements using a simple homogenization scheme suggested by [12]. The unknown rock mass properties that were back-analyzed are the rock elastic Young’s modulus E, Poisson’s ratio ν, the cohesion c and friction angle ϕ, and the average unit weight of the rock γ.

The finite difference grid used to discretize the entire cross-section of the tunnel is shown Fig. 3 together with a close-up of the left tunnel showing the sequence of excavations and the locations of the instrumentation. A refined discretization is used close to the tunnel to better simulate a possible plastic zone. Roller boundaries are used for the left, bottom and right boundaries of the model. Initial stresses due to self-weight of the materials are applied, and then the staged excavation sequence is closely simulated in the model. Estimates of the ranges of values for the model parameters involved in the back-analysis were based on preliminary geotechnical studies of the predominant rock types encountered at the tunnel site. Initial values or guesses corresponded to estimated average values of the different parameters.

Fig. 3.

Finite difference discretization of Heshang Tunnel: (a) full cross-section at Station K6+300; (b) region around the left tunnel.

Figure 4 shows comparisons of the extensometer displacements from locations K01 and K02 from monitoring and the complete iterative back-analysis. The comparisons are shown for the end of Stages 1 and 2 of the construction. Figure 5 shows the comparisons of surface subsidence in locations P2 to P8 at the end of construction Stages 1 and 2 from monitoring and back-analysis. Good agreement between measured and back-analyzed results were obtained for both the extensometer and surface displacement measurements, and for both construction stages. The back-analyzed parameters were then used to predict the response of the left and right tunnels during subsequent excavation Stages 3 to 8 using forward modelling.

Fig. 4.

Comparisons of extensometer displacements at Station K6+300 from monitoring and back-analysis: (TOP) end of Stage 1 and (BOTTOM) end of Stage 2.

Fig. 5.

Comparisons of surface subsidence at the end of construction Stages 1 and 2 at Station K6+300 from measurements and back-analysis.

The predicted results from the forward modelling of the tunnel response at the completion of tunnel construction (after construction Stages 3 to 8) are shown in Figs. 6 and 7. Figure 6 shows a comparison of the predicted and measured tunnel response from the extensometer displacements obtained from all extensometer locations K01 to K06. Due to excavation of the right tunnel, all extensometers are now registering detectable displacements. A similar comparison is shown in Fig. 7 in terms of the surface subsidence measurements from points P1 to P8. As can be seen, there is very good agreement between predicted and measured response. The differences between predicted and measured response are less than 1 cm in most cases. The good agreement between predicted and monitored response indicates the validity of the model parameters obtained from the back-analysis of the tunnel response at the earlier stages of construction.

Fig. 6.

Comparison of measured and predicted (from combined back- and forward-analysis) extensometer measurements at Station K6+300 of Heshang Tunnel.

Fig. 7.

Comparisons of measured and predicted (from forward analysis) extensometer displacements at end of tunnel construction at Station K6+300.

Table 1 lists the estimated range of values for the model parameters involved in the back-analysis, the step sizes, the initial values or guesses used at the start of the back-analysis, and the final back-analyzed values obtained from the back-analysis. The estimated range of parameters values is based on preliminary geotechnical studies of the predominant rock types encountered at the tunnel site.

Table 1. Range, initial and back-calculated values of model parameters for Section K6+300 of Heshang Tunnel.

4 Conclusions

The paper proposed the use of heuristics-based methods, which are experience-based techniques for problem solving, in the back-analysis of geotechnical problems particularly tunnel constructions. Using heuristic methods, solutions, which are found by using search trees, are not guaranteed to be optimal, but good enough for a given set of goals. Instead of generating all possible solution branches, branches more likely to produce outcomes are selected. Iterative search procedures are employed that learn what paths to follow and avoid by assessing how close the current iteration is to the solution. Heuristic methods can be the most viable techniques for difficult optimization of non-linear problems where the best approach is to exploit randomness in the system to get suitable answers.

Two methods namely, Simulated Annealing (SA) and Differential Evolution Genetic Algorithm (DEGA), were described and implemented in the widely available computer code FLAC. Both methods systematically search for the best set of model parameters that will minimize the objective function which is the least-squares normalized difference between model predictions and monitored results. The searches of the vectors of potential parameter values follow natural processes of metal annealing in the case of SA, and genetic evolution in the case of DEGA. Application in the case of the Heshang Tunnel in China showed the power of the proposed methods to converge towards optimal model parameter values from different initial values or guesses of the model parameters. Using monitoring data from the first two of the eight tunnel excavation stages, model parameters were back-analyzed using the proposed systems. These model parameters were then used in forward modelling to predict the response of the twin tunnels during subsequent excavation stages. Good agreement was obtained between predicted and measured response in all stages of construction indicating the validity of the proposed system.

The following are the main advantages of heuristic methods of back-analysis including SA and DEGA: (1) Not “greedy” and uphill movements are frequently allowed during optimization so solution does not get stuck in local optima; (2) Independent of the initial parameter assumptions; (3) Suitable for non-continuous, non-differentiable functions; (4) Independent of convexity status; (5) Can be used with heterogeneous monitoring data; (6) Can be used with relative values of monitoring data; (7) The solution history usually provides information regarding strong local optima (possible solution candidates); and (8) Parameter constraints can be easily applied.