The Extended High Order Sandwich Panel Theory for the Static and Dynamic Analysis of Sandwich Structures

Abstract

The Extended High Order Sandwich Panel Theory (EHSAPT) is a structural theory that includes the transverse shear and the in-plane rigidity of the core as well as the compressibility of the core in the transverse direction. It was introduced several years ago and was proven to be the most accurate sandwich structural theory by comparing its predictions to the ones from corresponding elasticity solutions. It is especially noteworthy that this theory is very accurate not only for the softer cores but also for the cases of stiffer cores, for which cases the other available sandwich structural theories cannot predict correctly the stress fields involved. Thus, this theory can be used with any combinations of core and face sheets and not only the very soft cores that the other theories demand. The theory is derived so that all core/face displacement continuity conditions are fulfilled. In this review article the basic premises of the theory are outlined in both its nonlinear static and dynamic versions for a one-dimensional (beam or wide plate) configuration and its accuracy is validated by considering the cases of static distributed loading, dynamic blast loading and wrinkling behavior. These results are compared with the corresponding ones from the elasticity solution. Furthermore, the results using the classical sandwich model without shear, the first order shear and the earlier High-Order sandwich panel theory (HSAPT) are also presented for completeness. Finally, it should be noted that the theory is formulated for sandwich panels with a generally asymmetric geometric layout.

1 Introduction

Sandwich construction is a structural concept that results in a very stiff but lightweight structure. In addition, these structures normally possess a high-energy absorption capability. These attributes are achieved due to the existence of a relatively soft and lightweight core, typically made out of polymeric or metallic foam or honeycomb. The core is between two stiff metallic or composite thin face sheets, which provide the stiffness. As a result, sandwich structures have found applications in aerospace vehicles, including satellites, helicopter and fixed-wing aircraft components, as well as naval vehicles, wind turbines and civil infrastructure. The initial studies on sandwich panels were done by neglecting the transverse deformation of the core (see the textbooks [1,2,3]). The core of a sandwich structure was considered as infinitely rigid in the thickness direction and only its shear stresses could be taken into account while the in-plane stresses were neglected as a result of its low rigidity in this direction relative to that of the face sheets. Plantema [1] and Allen [2] well summarized the work done in the 1960s. The earliest models are called the classical (no transverse shear of the core) or first order shear deformation (FOSD) theory (transverse shear of the core included). These models are based on the Euler-Bernoulli (classical) or Timoshenko beam (first order shear) theories. These assumptions could potentially be quite inaccurate esp. for dynamic loading; in particular, sudden loading experiments conducted by Wang et al. [4] showed large amounts of core compression. Consideration of the core compressibility implies that the displacements of the upper and lower face sheets may not be identical.

The first theory to consider the core compressibility is the High Order Sandwich Panel Theory (HSAPT) formulated by Frostig et al. [5] in the 1990s; in this theory, the resulting shear strain in the core is constant and the resulting transverse normal strain in the core is linear in the transverse coordinate, as a result of the assumption that the in-plane rigidity of the core is negligible. In the 2000s Hohe et al. [6] proposed a model for sandwich plates by assuming the transverse normal strain to be constant along the transverse coordinate, while the shearing strains were assumed to be linear in the transverse coordinate.

The accuracy of any of these models can be readily assessed if corresponding elasticity solutions exists. To this extent, for a three dimensional sandwich plate consisting of orthotropic material, static elasticity solutions were developed by Vlasov [7] for isotropic plates and by Pagano [8] for a restricted case of material sandwich combination. And these solutions were extended to cover all possible orthotropic face sheet and core combinations of a sandwich beam/wide plate by Kardomateas and Phan [9] and for a plate of arbitrary aspect ratio by Kardomateas [10]. Regarding the blast loading case, a sandwich beam/wide plate elasto-dynamic solution was developed by Kardomateas et al. [11]. The latter work was extended to the three-dimensional elasticity sandwich plate of arbitrary aspect ratio case by Kardomateas et al. [12]. Besides flat panels, an elasticity solution was developed by Kardomateas et al. [13] for the geometry of curved sandwich beams/panels. Regarding buckling, an elasticity solution for the global buckling of a sandwich beam/wide plate was presented by Kardomateas [14] and for the case of wrinkling of a sandwich beam/wide, a corresponding elasticity solution was presented by Kardomateas in [15].

The Extended High Order Sandwich Panel theory (EHSAPT) was introduced in 2012 by Phan et al. [16], and is a theory that allows for the transverse shear distribution in the core to acquire the proper distribution as the core stiffness increases as a result of non-negligible in-plane stresses in the core; thus it is valid for weak or stiff cores. This theory is an extension of the high-order sandwich panel theory [5]; its novelty is that it allows for three generalized coordinates in the core (the axial and transverse displacements at the centroid of the core, and the rotation at the centroid of the core) instead of just one (mid-point transverse displacement) commonly adopted in other available theories. The theory was formulated for a sandwich panel with a general layout. The major assumptions of the theory are as follows: (1) the face sheets satisfy the Euler-Bernoulli assumptions, and their thicknesses are small compared with the overall thickness of the sandwich section; they can be made of different materials and can have different thicknesses; they undergo large displacements with moderate rotations; (2) the core is compressible in the transverse and axial directions (transverse displacement is 2nd order in the transverse coordinate (z) and axial displacement is 3rd order in z); it has in-plane, transverse and shear rigidities; and it undergoes large displacements but with kinematic relations of small deformations due to its low in-plane rigidity as compared with that of the face sheets; and (3) the face sheets and core are perfectly bonded at their interfaces. Subsequently, the dynamic version of the Extended High-Order Sandwich Panel Theory was formulated in its full nonlinear version [17]. A simply supported sandwich beam subjected to a sinusoidal distributed blast load on the top face was studied and the results were compared to the dynamic elasticity solution in [11]; it was shown that the EHSAPT is very accurate and can capture the complex dynamic phenomena observed during the initial, transient phase of blast loading.

The EHSAPT was applied to the problem of global buckling of a sandwich wide plate/beam in [18]. Three different solution approaches were presented to investigate the effect of simplifying the loading case: (a) axial load applied exclusively to the face sheets and the geometric nonlinearities in the core are neglected (linear core); (b) uniform axial strain applied through the entire thickness and, again, linear core; and (c) uniform axial strain applied through the entire thickness but now the geometric nonlinearities in the core are included (non-linear core). The results were also compared with these from a benchmark elasticity solution [14] and, furthermore, from the simple sandwich buckling formula of Allen (thick faces version) [2] and the High Order Sandwich Panel Theory [5]. It was found that all three theories are close to the elasticity solution for “soft” cores with core over face modulus ratio less than 0.001. However, for the more “moderate” cores, i.e. with core over face modulus above 0.001, the theories diverge from each other, with the EHSAPT being the most accurate, i.e. the closest to elasticity.

A similar study was conducted on the wrinkling problem [19] and the results were, again, compared to the ones from a benchmark elasticity solution [15]. In addition, edgewise compression experiments were conducted on Glass Face/Nomex Honeycomb Core specimens and the ensuing wrinkling point was compared with the theoretical predictions. A comparison was also made with earlier edgewise compression experiments on Aluminum face/Granulated-cork core reported in literature. Other wrinkling formulas that were included in the comparison are: the Hoff-Mautner [20], and the High-Order Sandwich Panel Theory (HSAPT) [5]. In all cases the EHSAPT was the closest to both the Elasticity predictions and the experimental data. The HSAPT was in significant error for the relatively thinner faces. The large discrepancy between HSPAT and EHSAPT for very low ratios of face over total thickness (when the beam is most susceptible to wrinkling), and the associated smaller discrepancy for higher such ratios (when the beam tends to buckle globally), indicates that including the axial rigidity of the core (as in EHSAPT) is very important for wrinkling.

Recently, a linear finite element was formulated based on the EHSAPT [21]. It was proven that the finite element version of the EHSAPT constitutes a very powerful analytical tool for sandwich panels. Furthermore, the effects of geometric non-linearities were studied in detail in [22]. A critical assessment of including the various nonlinear terms in the faces and the core was conducted. The nonlinear buckling response of sandwich panels was subsequently studied [23]. It was shown that the axial rigidity of the core has a pronounced effect on both the critical load and the buckling mode. The corresponding non-linear post-buckling response was studied in [24]. It was found that due to the interaction between faces and core, localized effects may be easily initiated by imperfections after the sandwich structure has buckled globally. Furthermore, this could destabilize the post-buckling response. It was also found that the axial rigidity of the core, although it is very small compared to that of the faces, has a significant effect on the post-buckling response. This underscores the need to include it, as is done in the formulation of the EHSAPT.

Finally, the EHSAPT was also extended recently to the geometry of a curved panel [25]. Two distinct core displacement fields were proposed and investigated. One is a logarithmic (it includes terms that are linear, inverse, and logarithmic functions of the radial coordinate). The other is a polynomial (it consists of second and third order polynomials of the radial coordinate) and it is an extension of the corresponding field for the flat panel. The relative merits of these two approaches were assessed by comparing the results to an elasticity solution [13]. It was shown that the logarithmic formulation is more accurate than the polynomial especially for the stiffer cores and for curved panels of smaller radius.

In this review article, we present the basic premises, the formulation, and a series of accuracy studies for the Extended High Order Sandwich Panel Theory (EHSAPT).

2 Formulation of the Extended High Order Sandwich Panel Theory

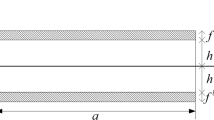
Let us consider a sandwich panel of length a with a core of thickness 2c and top and bottom face sheet thicknesses f_t and f_b, respectively (Fig. 1). A Cartesian coordinate system (x,y,z) is defined at one end of the beam and its origin is placed at the middle of the core. Only loading in the x-z plane is considered to act on the beam which solely causes displacements in the x and z directions designated by u and w, respectively. The superscripts t, b, and c shall refer to the top face sheet, bottom face sheet, and core, respectively. We should also note that in our formulation the rigidities and all applied loadings are per unit width.

Fig. 1

Definition of the geometry and the loading

The displacement field of the top and bottom face sheets are assumed to satisfy the Euler-Bernoulli assumptions: Therefore, the displacement field for the top face, c ≤ z ≤ c + f_t, is:

$$ {w}^t\left(x,z\right)={w}_0^t(x);\kern1.32em {u}^t\left(x,z\right)={u}_0^t(x)-\left(z-c-\frac{f_t}{2}\right){w}_{0,x}^t(x), $$

(1a)

and for the bottom face, −(c + f_b) ≤ z ≤ −c:

$$ {w}^b\left(x,z\right)={w}_0^b(x);\kern1.32em {u}^b\left(x,z\right)={u}_0^b(x)-\left(z+c+\frac{f_b}{2}\right){w}_{0,x}^b(x), $$

(1b)

In these relations, the sub script 0 refers to the centroid (middle surface).

The only nonzero strain in the faces is the axial strain, which in the general nonlinear case (necessary, for example, for buckling) is:

$$ {\varepsilon}_{xx}^{t,b}\left(x,z\right)={u}_{,x}^{t,b}\left(x,z\right)+\frac{1}{2}{\left[{w}_{0,x}^{t,b}(x)\right]}^2, $$

(1c)

If a linear analysis is pursued, the second (squared) term in (1c) is neglected.

While the face sheets can change their length only longitudinally, the core can change its height and length. The displacement fields considered for the core are of the form:

$$ {w}^c\left(x,z\right)={w}_0^c(x)+{zw}_1^c(x)+{z}^2{w}_2^c(x), $$

(2a)

$$ {u}^c\left(x,z\right)={u}_0^c(x)+z{\phi}_0^c(x)+{z}^2{u}_2^c(x)+{z}^3{u}_3^c(x), $$

(2b)

where w₀^c and u₀^c are the transverse and in-plane displacements, respectively, ϕ₀^c is the slope at the centroid of the core, while w₁^c, w₂^c, and u₂^c, u₃^c, are transverse and in-plane unknown functions to be determined by the transverse and the in-plane compatibility conditions applied at the upper, z = c, and lower, z = −c, face-core interfaces:

$$ {w}^c\left(x,c\right)={w}_0^t(x);\kern1.32em {u}^c\left(x,c\right)={u}_0^t(x)-\frac{f_t}{2}{w}_{0,x}^t(x), $$

(2c)

$$ {w}^c\left(x,-c\right)={w}_0^b(x);\kern1.32em {u}^b\left(x,-c\right)={u}_0^b(x)+\frac{f_b}{2}{w}_{0,x}^b(x), $$

(2d)

Hence, using the first Eqs. in (2c, d) and Eqs. (1a) and (2a) yields the following distribution of the transverse displacement in the core:

$$ {w}^c\left(x,z\right)=\left(-\frac{z}{2c}+\frac{z^2}{2{c}^2}\right){w}_0^b(x)+\left(1-\frac{z^2}{c^2}\right){w}_0^c(x)+\left(\frac{z}{2c}+\frac{z^2}{2{c}^2}\right){w}_0^t(x). $$

(3a)

The axial displacement of the core, u^c(x,z), is determined through the fulfillment of the continuity conditions in the in-plane direction [see second Eqs. in (2c,d)]. Hence, after some algebraic manipulation:

$$ {\displaystyle \begin{array}{l}{u}^c\left(x,z\right)=\kern2pt z\left(1-\frac{z^2}{c^2}\right){\phi}_0^c(x)+\frac{z^2}{2{c}^2}\left(1-\frac{z}{c}\right){u}_0^b(x)+\left(1-\frac{z^2}{c^2}\right){u}_0^c(x)\\ {}+\frac{z^2}{2{c}^2}\left(1+\frac{z}{c}\right){u}_0^t(x)+\frac{f_b{z}^2}{4{c}^2}\left(-1+\frac{z}{c}\right){w}_{0,x}^b+\frac{f_t{z}^2}{4{c}^2}\left(1+\frac{z}{c}\right){w}_{0,x}^t\kern0.36em .\end{array}} $$

(3b)

Therefore, this theory is in terms of seven generalized coordinates (unknown functions of x): two for the top face sheet, w₀^t, u₀^t, two for the bottom face sheet, w₀^b, u₀^b, and three for the core, w₀^c, u₀^c, and ϕ₀^c.

The strains can be obtained from the displacements using the linear strain-displacement relations. For the core, the transverse normal strain is:

$$ {\varepsilon}_{zz}^c\left(x,z\right)=\frac{\partial {w}^c}{\partial z}=\left(\frac{z}{c^2}-\frac{1}{2c}\right){w}_0^b(x)-\frac{2z}{c^2}{w}_0^c(x)+\left(\frac{z}{c^2}+\frac{1}{2c}\right){w}_0^t(x), $$

(4a)

and the shear strain

$$ {\displaystyle \begin{array}{l}{\gamma}_{xz}^c\left(x,z\right)=\frac{\partial {u}^c}{\partial z}+\frac{\partial {w}^c}{\partial x}=\left(1-\frac{3{z}^2}{c^2}\right){\phi}_0^c(x)+\left(\frac{z}{c^2}-\frac{3{z}^2}{2{c}^3}\right){u}_0^b(x)-\frac{2z}{c^2}{u}_0^c(x)\\ {}+\left(\frac{z}{c^2}+\frac{3{z}^2}{2{c}^3}\right){u}_0^t(x)+\left[-\frac{\left(c+{f}_b\right)}{2{c}^2}z+\frac{\left(2c+3{f}_b\right)}{4{c}^3}{z}^2\right]\;{w}_{0,x}^b\\ {}+\left(1-\frac{z^2}{c^2}\right){w}_{0,x}^c+\left[\frac{\left(c+{f}_t\right)}{2{c}^2}z+\frac{\left(2c+3{f}_t\right)}{4{c}^3}{z}^2\right]\;{w}_{0,x}^t\kern0.36em .\end{array}} $$

(4b)

There is also a nonzero linear axial strain in the core ε_xx^c = ∂u^c/∂x, which has the same structure as Eq. (3b), but with the generalized function coordinates replaced by one order higher derivative with respect to x.

In the following we use the notation 1 ≡ x, 3 ≡ z, and 55 ≡ xz. We assume orthotropic face sheets, thus the non-zero stresses for the faces are:

$$ {\sigma}_{xx}^{t,b}={C}_{11}^{t,b}{\varepsilon}_{xx}^{t,b};\kern0.84em {\sigma}_{zz}^{t,b}={C}_{13}^{t,b}{\varepsilon}_{xx}^{t,b}, $$

(5a)

where, in terms of the extensional (Young’s) modulus, E₁^t,b, and the Poisson’s ratio ν₃₁^t,b, the stiffness constants for a beam are: C₁₁^t,b = E₁^t,b and C₁₃^t,b = ν₃₁^t,b E₁^t,b. Notice that the σ_zz^t,b does not ultimately enter into the variational equation because the corresponding strain ε_zz^t,b is assumed to be zero.

We also assume an orthotropic core with stress-strain relations:

$$ \left[\begin{array}{c}{\sigma}_{xx}^c\\ {}{\sigma}_{zz}^c\\ {}{\tau}_{xz}^c\end{array}\right]=\left[\begin{array}{ccc}{C}_{11}^c& {C}_{13}^c& 0\\ {}{C}_{13}^c& {C}_{33}^c& 0\\ {}0& 0& {C}_{55}^c\end{array}\right]\;\left[\begin{array}{c}{\varepsilon}_{xx}^c\\ {}{\varepsilon}_{zz}^c\\ {}{\gamma}_{xz}^c\end{array}\right], $$

(5b)

where C_ij^c are the stiffness constants for the core. These constants are determined from the inverse of the compliance matrix. In particular, they are [26]

$$ {C}_{11}^c={E}_1^c\frac{\left(1-{\nu}_{23}^c{\nu}_{32}^c\right)}{C_0};\kern0.5em {C}_{13}^c={E}_3^c\frac{\left({\nu}_{13}^c-{\nu}_{12}^c{\nu}_{23}^c\right)}{C_0};\kern0.5em {C}_{33}^c={E}_3^c\frac{\left(1-{\nu}_{12}^c{\nu}_{21}^c\right)}{C_0}, $$

(5c)

$$ {C}_0=1-\left({\nu}_{12}^c{\nu}_{21}^c+{\nu}_{23}^c{\nu}_{32}^c+{\nu}_{13}^c{\nu}_{31}^c\right)-\left({\nu}_{12}^c{\nu}_{23}^c{\nu}_{31}^c+{\nu}_{21}^c{\nu}_{13}^c{\nu}_{32}^c\right), $$

(5d)

$$ {C}_{55}^c={G}_{31}^c. $$

(5e)

In the following we’ll formulate the problem for the general case of dynamic loading. If the problem is static, the time terms in the equations just need be neglected. The governing equations and boundary conditions are derived from Hamilton’s principle:

$$ \underset{t_1}{\overset{t_2}{\int }}\delta \left(U+V-T\right) dt=0, $$

(6a)

where U is the strain energy of the sandwich beam, V is the potential due to the applied loading, and T is the kinetic energy. The first variation of the strain energy per unit width of the sandwich beam is:

$$ \delta U=\underset{0}{\overset{a}{\int }}\left[\underset{-c-{f}_b}{\overset{-c}{\int }}{\sigma}_{xx}^b{\delta \varepsilon}_{xx}^b dz+\underset{-c}{\overset{c}{\int }}\left({\sigma}_{xx}^c{\delta \varepsilon}_{xx}^c+{\sigma}_{zz}^c{\delta \varepsilon}_{zz}^c+{\tau}_{xz}^c{\delta \gamma}_{xz}^c\right) dz+\underset{c}{\overset{c+{f}_t}{\int }}{\sigma}_{xx}^t{\delta \varepsilon}_{xx}^t dz\right]\kern0.24em dx, $$

(6b)

and the first variation of the external potential per unit width is:

$$ {\displaystyle \begin{array}{l}\delta V=-\underset{0}{\overset{a}{\int }}\left({q}^t\delta {w}_0^t+{q}^b\delta {w}_0^b+{p}^t\delta {u}_0^t+{p}^b\delta {u}_0^b+{m}^t\delta {w}_{0,x}^t+{m}^b\delta {w}_{0,x}^b\right)\\ {}-{\left[\underset{-c}{\overset{c}{\int }}\left({n}^c\delta {u}^c+{s}^c\delta {w}^c\right) dz\right]}_{x=0}^a-{\left[{N}^t\delta {u}_0^t\;\right]}_{x=0}^a-{\left[{N}^b\delta {u}_0^b\;\right]}_{x=0}^a-{\left[{V}^t\delta {w}_0^t\;\right]}_{x=0}^a\\ {}-{\left[{V}^b\delta {w}_0^b\;\right]}_{x=0}^a-{\left[{M}^t\delta {w}_{0,x}^t\;\right]}_{x=0}^a-{\left[{M}^b\delta {w}_{0,x}^b\;\right]}_{x=0}^a,\end{array}} $$

(6c)

where, by reference to Fig. 1, q^t,b is the distributed transverse (along z) force per unit width, p^t,b is the distributed in-plane (along x) force per unit width and m^t,b is the distributed moment per unit width on the top and bottom faces. Moreover N^t,b is the end axial force per unit width, V^t,b is the end shear force per unit width and M^{t, b} is the end moment per unit width at the top and bottom face sheets, at the ends x = 0, a. In addition, n^c is the end axial force per unit width and s^c is the end shear force per unit width at the core, at the ends x = 0, a.

In the following, we assume that n^c and s^c are constant. In this case,

$$ \underset{-c}{\overset{c}{\int }}{n}^c\delta {u}^c dz={n}^cc\;\left[\frac{1}{3}\left(\delta {u}_0^b+\delta {u}_0^t\right)+\frac{4}{3}\delta {u}_0^c-\frac{f_b}{6}\delta {w}_{0,x}^b+\frac{f_t}{6}\delta {w}_{0,x}^t\right], $$

(6d)

$$ \underset{-c}{\overset{c}{\int }}{s}^c\delta {w}^c dz={s}^cc\;\left[\frac{1}{3}\left(\delta {w}_0^b+\delta {w}_0^t\right)+\frac{4}{3}\delta {w}_0^c\right]. $$

(6e)

Of course, the theory can admit any variation of n^c and s^c along z; for example, a bending moment on the core would correspond to a linear variation of n^c with respect to z. However, for most practical purposes, loads are applied to the skins and not the core.

The kinetic energy term is:

$$ {\displaystyle \begin{array}{c}\delta T=\underset{0}{\overset{a}{\int }}\left[\underset{\left(c+{f}_b\right)}{\overset{-c}{\int }}{\rho}^b\left({\dot{u}}^b\delta {\dot{u}}^b+{\dot{w}}^b\delta {\dot{w}}^b\right) dz+\underset{-c}{\overset{c}{\int }}{\rho}^c\left({\dot{u}}^c\delta {\dot{u}}^c+{\dot{w}}^c\delta {\dot{w}}^c\right) dz\right.\\ {}\left.+\underset{c}{\overset{c+{f}_t}{\int }}{\rho}^t\left({\dot{u}}^t\delta {\dot{u}}^t+{\dot{w}}^t\delta {\dot{w}}^t\right) dz\right] dx.\end{array}} $$

(6f)

For the sandwich plates made out of orthotropic materials, we can substitute the stresses in terms of the strains from the constitutive relations, Eqs. (5a), and then the strains in terms of the displacements and the displacement profiles, Eqs. (1–4), and finally apply the variational principle, Eqs. (6a); thus we can write a set of non-linear governing differential Eqs. (D.Es) in terms of the seven unknown generalized coordinates as follows:

Top face sheet D.Es (two nonlinear):

$$ {\displaystyle \begin{array}{l}\kern0.24em \delta {u}_0^t:\kern1.2em -\left(\frac{4}{5}{C}_{55}^c+\frac{2{c}^2}{35}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right){\phi}_0^c-\left(\frac{7}{30c}{C}_{55}^c+\frac{c}{35}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right){u}_0^b\\ {}-\left(\frac{4}{3c}{C}_{55}^c+\frac{2c}{15}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right){u}_0^c+\left[\frac{47}{30c}{C}_{55}^c-{\alpha}_1^t\frac{\partial^2}{\partial {x}^2}\right]{u}_0^t\\ {}-\left({\alpha}_2^b\frac{\partial }{\partial x}-\frac{cf_b}{70}{C}_{11}^c\frac{\partial^3}{\partial {x}^3}\right){w}_0^b+\left({\beta}_1\frac{\partial }{\partial x}\right){w}_0^c+\left({\alpha}_3^t\frac{\partial }{\partial x}-\frac{3{cf}_t}{35}{C}_{11}^c\frac{\partial^3}{\partial {x}^3}\right){w}_0^t\\ {}+{D}_u^t={p}^t+{F}_u^t,\end{array}} $$

(7a)

where F_u^t is the nonlinear term:

$$ \kern0.24em {F}_u^t={C}_{11}^t{f}_t\;{w}_{0,x}^t\;{w}_{0, xx}^t, $$

(7b)

and D_u^t is the dynamic term:

$$ {\displaystyle \begin{array}{l}\kern0.24em {D}_u^t={\rho}^c\frac{2{c}^2}{35}\frac{\partial^2{\phi}_0^c}{\partial {t}^2}+{\rho}^c\frac{c}{35}\frac{\partial^2{u}_0^b}{\partial {t}^2}+{\rho}^c\frac{2c}{15}\frac{\partial^2{u}_0^c}{\partial {t}^2}+\left({\rho}^c\frac{6c}{35}+{\rho}^t{f}_t\right)\frac{\partial^2{u}_0^t}{\partial {t}^2}\\ {}\kern2.44em -{\rho}^c\frac{cf_b}{70}\frac{\partial^3{w}_0^b}{\partial x\partial {t}^2}+{\rho}^c\frac{3{cf}_t}{35}\frac{\partial^3{w}_0^t}{\partial x\partial {t}^2}.\end{array}} $$

(7c)

and

$$ {\displaystyle \begin{array}{l}\;\delta {w}_0^t:\kern1.2em \left({\alpha}_4^t\frac{\partial }{\partial x}+\frac{c^2{f}_t}{35}{C}_{11}^c\frac{\partial^3}{\partial {x}^3}\right){\phi}_0^c+\left({\alpha}_5^t\frac{\partial }{\partial x}+\frac{cf_t}{70}{C}_{11}^c\frac{\partial^3}{\partial {x}^3}\right){u}_0^b\\ {}+\left({\alpha}_6^t\frac{\partial }{\partial x}+\frac{cf_t}{15}{C}_{11}^c\frac{\partial^3}{\partial {x}^3}\right){u}_0^c+\left(-{\alpha}_3^t\frac{\partial }{\partial x}+\frac{3{cf}_t}{35}{C}_{11}^c\frac{\partial^3}{\partial {x}^3}\right){u}_0^t\\ {}+\left(\frac{1}{6c}{C}_{33}^c+{\beta}_2\frac{\partial^2}{\partial {x}^2}-\frac{cf_b{f}_t}{140}{C}_{11}^c\frac{\partial^4}{\partial {x}^4}\right){w}_0^b+\left(-\frac{4}{3c}{C}_{33}^c+{\alpha}_7^t\frac{\partial^2}{\partial {x}^2}\right){w}_0^c\\ {}+\left(\frac{7}{6c}{C}_{33}^c+{\alpha}_8^t\frac{\partial^2}{\partial {x}^2}+{\alpha}_9^t\frac{\partial^4}{\partial {x}^4}\right){w}_0^t+{D}_w^t={q}^t-{m}_{,x}^t+{F}_w^t,\end{array}} $$

(8a)

where F_w^t is the nonlinear term:

$$ \kern0.24em {F}_w^t={C}_{11}^t{f}_t\;\left[{w}_{0,x}^t\;{u}_{0, xx}^t+{u}_{0,x}^t\;{w}_{0, xx}^t+\frac{3}{2}{\left({w}_{0,x}^t\right)}^2{w}_{0, xx}^t\right], $$

(8b)

and D_w^t is the dynamic term:

$$ {\displaystyle \begin{array}{l}\;{D}_w^t=-{\rho}^c\frac{f_t{c}^2}{35}\frac{\partial^3{\phi}_0^c}{\partial x\partial {t}^2}-{\rho}^c\frac{f_tc}{70}\frac{\partial^3{u}_0^b}{\partial x\partial {t}^2}-{\rho}^c\frac{f_tc}{15}\frac{\partial^3{u}_0^c}{\partial x\partial {t}^2}-{\rho}^c\frac{3{f}_tc}{35}\frac{\partial^3{u}_0^t\;}{\partial x\partial {t}^2}\\ {}+\left(-{\rho}^c\frac{c}{15}\frac{\partial^2}{\partial {t}^2}+{\rho}^c\frac{cf_b{f}_t}{140}\frac{\partial^4}{\partial {x}^2\partial {t}^2}\right){w}_0^b+{\rho}^c\frac{2c}{15}\frac{\partial^2{w}_0^c}{\partial {t}^2}\\ {}+\left[\left({\rho}^c\frac{4c}{15}+{\rho}^t{f}_t\right)\frac{\partial^2}{\partial {t}^2}-\left({\rho}^c\frac{3{cf}_t^2}{70}+{\rho}^t\frac{f_t^3}{12}\right)\frac{\partial^4}{\partial {x}^2\partial {t}^2}\right]{w}_0^t.\end{array}} $$

(8c)

Core D.Es (three linear):

$$ {\displaystyle \begin{array}{l}\kern0.24em \delta {u}_0^c:\kern1.2em -\left(\frac{4}{3c}{C}_{55}^c+\frac{2c}{15}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right){u}_0^b+\left(\frac{8}{3c}{C}_{55}^c-\frac{16c}{15}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right){u}_0^c\\ {}-\left(\frac{4}{3c}{C}_{55}^c+\frac{2c}{15}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right){u}_0^t+\left({\alpha}_6^b\frac{\partial }{\partial x}+\frac{cf_b}{15}{C}_{11}^c\frac{\partial^3}{\partial {x}^3}\right){w}_0^b\\ {}-\left({\alpha}_6^t\frac{\partial }{\partial x}+\frac{cf_t}{15}{C}_{11}^c\frac{\partial^3}{\partial {x}^3}\right){w}_0^t+{D}_u^c=0,\end{array}} $$

(9a)

where D_u^c is the dynamic term:

$$ \kern0.24em {D}_u^c={\rho}^c\left[\frac{2c}{15}\frac{\partial^2{u}_0^b}{\partial {t}^2}+\frac{16c}{15}\frac{\partial^2{u}_0^c}{\partial {t}^2}+\frac{2c}{15}\frac{\partial^2{u}_0^t}{\partial {t}^2}-\frac{cf_b}{15}\frac{\partial^3{w}_0^b}{\partial x\partial {t}^2}+\frac{cf_t}{15}\frac{\partial^3{w}_0^t}{\partial x\partial {t}^2}\kern0.24em \right]. $$

(9b)

$$ {\displaystyle \begin{array}{l}\kern0.24em {\delta \phi}_0^c:\kern1.2em \left(\frac{8c}{5}{C}_{55}^c-\frac{16{c}^3}{105}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right){\phi}_0^c+\left(\frac{4}{5}{C}_{55}^c+\frac{2{c}^2}{35}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right){u}_0^b\\ {}-\left(\frac{4}{5}{C}_{55}^c+\frac{2{c}^2}{35}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right){u}_0^t-\left({\alpha}_4^b\frac{\partial }{\partial x}+\frac{c^2{f}_b}{35}{C}_{11}^c\frac{\partial^3}{\partial {x}^3}\right){w}_0^b+\left({\beta}_3\frac{\partial }{\partial x}\right){w}_0^c\\ {}-\left({\alpha}_4^t\frac{\partial }{\partial x}+\frac{c^2{f}_t}{35}{C}_{11}^c\frac{\partial^3}{\partial {x}^3}\right){w}_0^t+{D}_{\phi}^c=0,\end{array}} $$

(10a)

where D_ϕ^c is the dynamic term:

$$ \kern0.24em {D}_{\phi}^c={\rho}^c\left[\frac{16{c}^3}{105}\frac{\partial^2{\phi}_0^c}{\partial {t}^2}-\frac{2{c}^2}{35}\frac{\partial^2{u}_0^b}{\partial {t}^2}+\frac{2{c}^2}{35}\frac{\partial^2{u}_0^t}{\partial {t}^2}+\frac{f_b{c}^2}{35}\frac{\partial^3{w}_0^b}{\partial x\partial {t}^2}+\frac{f_t{c}^2}{35}\frac{\partial^3{w}_0^t}{\partial x\partial {t}^2}\kern0.24em \right], $$

(10b)

and

$$ {\displaystyle \begin{array}{l}\kern0.24em \delta {w}_0^c:\kern1.2em -\left({\beta}_3\frac{\partial }{\partial x}\right){\phi}_0^c+\left({\beta}_1\frac{\partial }{\partial x}\right){u}_0^b-\left({\beta}_1\frac{\partial }{\partial x}\right){u}_0^t+\left(-\frac{4}{3c}{C}_{33}^c+{\alpha}_7^b\frac{\partial^2}{\partial {x}^2}\right){w}_0^b\\ {}+\left(\frac{8}{3c}{C}_{33}^c-\frac{16c}{15}{C}_{55}^c\frac{\partial^2}{\partial {x}^2}\right){w}_0^c\kern0.36em +\left(-\frac{4}{3c}{C}_{33}^c+{\alpha}_7^t\frac{\partial^2}{\partial {x}^2}\right){w}_0^t+{D}_w^c=0,\end{array}} $$

(11a)

where D_w^c is the dynamic term:

$$ \kern0.24em {D}_w^c={\rho}^c\left[\frac{2c}{15}\frac{\partial^2{w}_0^b}{\partial {t}^2}+\frac{16c}{15}\frac{\partial^2{w}_0^c}{\partial {t}^2}+\frac{2c}{15}\frac{\partial^2{w}_0^t}{\partial {t}^2}\right]. $$

(11b)

Bottom face sheet D.Es (two nonlinear):

$$ {\displaystyle \begin{array}{l}\kern0.24em \delta {u}_0^b:\kern.7em \left(\frac{4}{5}{C}_{55}^c+\frac{2{c}^2}{35}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right){\phi}_0^c+\left[\frac{47}{30c}{C}_{55}^c-{\alpha}_1^b\frac{\partial^2}{\partial {x}^2}\right]{u}_0^b\\ {}-\left(\frac{4}{3c}{C}_{55}^c+\frac{2c}{15}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right){u}_0^c-\left(\frac{7}{30c}{C}_{55}^c+\frac{c}{35}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right){u}_0^t\\ {}+\left(-{\alpha}_3^b\frac{\partial }{\partial x}+\frac{3{cf}_b}{35}{C}_{11}^c\frac{\partial^3}{\partial {x}^3}\right){w}_0^b-\left({\beta}_1\frac{\partial }{\partial x}\right){w}_0^c+\left({\alpha}_2^t\frac{\partial }{\partial x}-\frac{cf_t}{70}{C}_{11}^c\frac{\partial^3}{\partial {x}^3}\right){w}_0^t\\ {}+{D}_u^b={p}^b+{F}_u^b,\end{array}} $$

(12a)

where F_u^b is the nonlinear term:

$$ \kern0.24em {F}_u^b={C}_{11}^b{f}_b\;{w}_{0,x}^b\;{w}_{0, xx}^b, $$

(12b)

and D_u^b is the dynamic term:

$$ {\displaystyle \begin{array}{l}\kern0.24em {D}_u^b=-{\rho}^c\frac{2{c}^2}{35}\frac{\partial^2{\phi}_0^c}{\partial {t}^2}+\left({\rho}^c\frac{6c}{35}+{\rho}^b{f}_b\right)\frac{\partial^2{u}_0^b}{\partial {t}^2}+{\rho}^c\frac{2c}{15}\frac{\partial^2{u}_0^c\;}{\partial {t}^2}+{\rho}^c\frac{c}{35}\frac{\partial^2{u}_0^t\;}{\partial {t}^2}\\ {}\kern2.7em -{\rho}^c\frac{3{f}_bc}{35}\frac{\partial^3{w}_0^b}{\partial x\partial {t}^2}+{\rho}^c\frac{f_tc}{70}\frac{\partial^3{w}_0^t}{\partial x\partial {t}^2},\end{array}} $$

(12c)

and

$$ {\displaystyle \begin{array}{l}\kern0.24em \delta {w}_0^b:\kern1.2em \left({\alpha}_4^b\frac{\partial }{\partial x}+\frac{c^2{f}_b}{35}{C}_{11}^c\frac{\partial^3}{\partial {x}^3}\right){\phi}_0^c+\left({\alpha}_3^b\frac{\partial }{\partial x}-\frac{3{cf}_b}{35}{C}_{11}^c\frac{\partial^3}{\partial {x}^3}\right){u}_0^b\\ {}-\left({\alpha}_6^b\frac{\partial }{\partial x}+\frac{cf_b}{15}{C}_{11}^c\frac{\partial^3}{\partial {x}^3}\right){u}_0^c-\left({\alpha}_5^b\frac{\partial }{\partial x}+\frac{cf_b}{70}{C}_{11}^c\frac{\partial^3}{\partial {x}^3}\right){u}_0^t\\ {}+\left(\frac{7}{6c}{C}_{33}^c+{\alpha}_8^b\frac{\partial^2}{\partial {x}^2}+{\alpha}_9^b\frac{\partial^4}{\partial {x}^4}\right){w}_0^b+\left(-\frac{4}{3c}{C}_{33}^c+{\alpha}_7^b\frac{\partial^2}{\partial {x}^2}\right){w}_0^c\\ {}+\left(\frac{1}{6c}{C}_{33}^c+{\beta}_2\frac{\partial^2}{\partial {x}^2}-\frac{cf_b{f}_t}{140}{C}_{11}^c\frac{\partial^4}{\partial {x}^4}\right){w}_0^t+{D}_w^b={q}^b-{m}_{,x}^b+{F}_w^b,\end{array}} $$

(13a)

where F_w^b is the nonlinear term:

$$ \kern0.24em {F}_w^b={C}_{11}^b{f}_b\;\left[{w}_{0,x}^b\;{u}_{0, xx}^b+{u}_{0,x}^b\;{w}_{0, xx}^b+\frac{3}{2}{\left({w}_{0,x}^b\right)}^2{w}_{0, xx}^b\right],\kern0.36em $$

(13b)

and D_w^b is the dynamic term:

$$ {\displaystyle \begin{array}{l}\kern0.24em {D}_w^b=-{\rho}^c\frac{f_b{c}^2}{35}\frac{\partial^3{\phi}_0^c}{\partial x\partial {t}^2}+{\rho}^c\frac{3{f}_b{c}^2}{35}\frac{\partial^3{u}_0^b}{\partial x\partial {t}^2}+{\rho}^c\frac{f_bc}{15}\frac{\partial^3{u}_0^c}{\partial x\partial {t}^2}+{\rho}^c\frac{f_b}{70}\frac{\partial^3{u}_0^t}{\partial x\partial {t}^2}\\ {}\kern2.88em +\left[\left({\rho}^c\frac{4c}{15}+{\rho}^b{f}_b\right)\frac{\partial^2}{\partial {t}^2}-\left({\rho}^c\frac{3{f}_b^2c}{70}+{\rho}^b\frac{f_b^3}{12}\right)\frac{\partial^4}{\partial {x}^2\partial {t}^2}\right]{w}_0^b\\ {}\kern2.88em +{\rho}^c\frac{2c}{15}\frac{\partial^2{w}_0^c}{\partial {t}^2}+{\rho}^c\left(-\frac{c}{15}\frac{\partial^2}{\partial {t}^2}+\frac{cf_b{f}_t}{140}\frac{\partial^4}{\partial {x}^2\partial {t}^2}\right){w}_0^t.\end{array}} $$

(13c)

In the above expressions, the following constants are defined:

$$ \kern0.24em {\alpha}_1^i=\frac{6c}{35}\;{C}_{11}^c+{f}_i{C}_{11}^i;\kern1.2em {\alpha}_2^i=\frac{1}{30}\;{C}_{13}^c+\left(\frac{1}{30}-\frac{7{f}_i}{60c}\right)\;{C}_{55}^c, $$

(14a)

$$ {\alpha}_3^i=-\frac{11}{30}\;{C}_{13}^c+\left(\frac{19}{30}+\frac{47{f}_i}{60c}\right){C}_{55}^c;\kern0.96em {\alpha}_4^i=\frac{4c}{15}\;{C}_{13}^c+\left(\frac{4c}{15}+\frac{2{f}_i}{5}\right)\;{C}_{55}^c, $$

(14b)

$$ {\alpha}_5^i=-{\alpha}_2^i;\kern0.96em {\alpha}_6^i=\frac{2}{3}\;{C}_{13}^c+\left(\frac{2}{3}+\frac{2{f}_i}{3c}\right)\;{C}_{55}^c;\kern0.48em {\alpha}_7^i=-\frac{f_i}{5}\;{C}_{13}^c-\left(\frac{2c}{15}+\frac{f_i}{5}\right){C}_{55}^c; $$

(14c)

$$ \kern0.6em {\alpha}_8^i=\frac{11{f}_i}{30}\;{C}_{13}^c-\left(\frac{4c}{15}+\frac{19{f}_i}{30}+\frac{47{f}_i^2}{120c}\right)\;{C}_{55}^c;\kern0.96em {\alpha}_9^i=\frac{f_i^3}{12}\;{C}_{11}^i+\frac{3{cf}_i^2}{70}{C}_{11}^c, $$

(14d)

and

$$ {\beta}_1=\frac{2}{5}\;\left({C}_{13}^c+{C}_{55}^c\right);\kern1.56em {\beta}_3=\frac{8c}{15}\;\left({C}_{13}^c+{C}_{55}^c\right), $$

(14e)

$$ {\beta}_2=\frac{f_b+{f}_t}{60}{C}_{13}^c+\left(\frac{c}{15}+\frac{f_b+{f}_t}{60}-\frac{7{f}_b{f}_t}{120c}\right){C}_{55}^c. $$

(14f)

The corresponding boundary conditions (B.Cs) at x = 0,a, read as follows (at each end there are nine boundary conditions, three for each face sheet and three for the core):

Top face sheet B.Cs (three):

• (i) Either δu₀^t = 0 or,

$$ {\displaystyle \begin{array}{l}\;\left(\frac{2{c}^2}{35}{C}_{11}^c\frac{\partial }{\partial x}\right){\phi}_0^c+\left(\frac{c}{35}{C}_{11}^c\frac{\partial }{\partial x}\right){u}_0^b+\left(\frac{2c}{15}{C}_{11}^c\frac{\partial }{\partial x}\right){u}_0^c+\left({\alpha}_1^t\frac{\partial }{\partial x}\right){u}_0^t-\left(\frac{2}{5}{C}_{13}^c\right){w}_0^c\\ {}+\left(\frac{1}{30}{C}_{13}^c-\frac{cf_b}{70}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right){w}_0^b+\left(\frac{11}{30}{C}_{13}^c+\frac{3{cf}_t}{35}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right){w}_0^t={N}^t+\frac{n^cc}{3}+{B}_u^t,\end{array}} $$

(15a)

where N^t is the end axial force per unit width at the top face and n^c is the (uniformly distributed) end axial force per unit width at the core (at the end x = 0 or x = a) and B_u^t is the nonlinear term

$$ {B}_u^t=-\frac{f_t}{2}{C}_{11}^t{\left({w}_{0,x}^t\right)}^2. $$

(15b)

• (ii) Either δw₀^t = 0 or,

$$ {\displaystyle \begin{array}{l}-\left[\frac{2\left(2c+3{f}_t\right)}{15}{C}_{55}^c+\frac{c^2{f}_t}{35}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right]{\phi}_0^c+\left[\frac{\left(2c-7{f}_t\right)}{60c}{C}_{55}^c-\frac{cf_t}{70}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right]{u}_0^b\\ {}-\left[\frac{2\left(c+{f}_t\right)}{3c}{C}_{55}^c+\frac{cf_t}{15}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right]{u}_0^c+\left[\frac{\left(38c+47{f}_t\right)}{60c}{C}_{55}^c-\frac{3{cf}_t}{35}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right]{u}_0^t\\ {}+\left[\left(\frac{f_b}{60}{C}_{13}^c-{\beta}_2\right)\frac{\partial }{\partial x}+\frac{cf_b{f}_t}{140}{C}_{11}^c\frac{\partial^3}{\partial {x}^4}\right]{w}_0^b-\left({\alpha}_7^t\frac{\partial }{\partial x}\right){w}_0^c\\ {}+\left[\left(\frac{11{f}_t}{60}{C}_{13}^c-{\alpha}_8^t\right)\frac{\partial }{\partial x}-{\alpha}_9^t\frac{\partial^3}{\partial {x}^3}\right]{w}_0^t={V}^t+{m}^t+\frac{s^cc}{3}+{B}_w^t+{L}_w^t,\\ {}\kern0em \end{array}} $$

(16a)

where V^t is the end shear force per unit width at the top face and s^c is the (assumed constant) end shear force per unit width at the core (at the end x = 0 or x = a) and B_w^t is the nonlinear term:

$$ \kern0.24em {B}_w^t=-\frac{f_t}{2}{C}_{11}^t{w}_{0,x}^t\;\left[\;2{u}_{0,x}^t+{\left({w}_{0,x}^t\right)}^2\right], $$

(16b)

and L_w^t is the dynamic term:

$$ {\displaystyle \begin{array}{l}\;{L}_w^t=\frac{f_t}{420}\left[\begin{array}{l}{\rho}^c12{c}^2\frac{\partial^2{\phi}_0^c}{\partial {t}^2}+{\rho}^c6c\frac{\partial^2{u}_0^b}{\partial {t}^2}+{\rho}^c28c\frac{\partial^2{u}_0^c}{\partial {t}^2}+{\rho}^c36c\frac{\partial^2{u}_0^t}{\partial {t}^2}\\ {}\kern1.8em -{\rho}^c3{cf}_b\frac{\partial^3{w}_0^b}{\partial x\partial {t}^2}+\left({\rho}^c18{cf}_t+{\rho}^t35{f}_t^2\right)\frac{\partial^3{w}_0^t}{\partial x\partial {t}^2}\;\end{array}\right].\\ {}\kern0em \end{array}} $$

(16c)

• (iii) Either δw_0,x^t = 0 or,

$$ {\displaystyle \begin{array}{l}\;\left(\frac{c^2{f}_t}{35}{C}_{11}^c\frac{\partial }{\partial x}\right){\phi}_0^c+\left(\frac{cf_t}{70}{C}_{11}^c\frac{\partial }{\partial x}\right){u}_0^b+\left(\frac{cf_t}{15}{C}_{11}^c\frac{\partial }{\partial x}\right){u}_0^c+\left(\frac{3{cf}_t}{35}{C}_{11}^c\frac{\partial }{\partial x}\right){u}_0^t\\ {}+\left(\frac{f_t}{60}{C}_{13}^c-\frac{cf_b{f}_t}{140}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right){w}_0^b-\left(\frac{f_t}{5}{C}_{13}^c\right){w}_0^c+\left(\frac{11{f}_t}{60}{C}_{13}^c+{\alpha}_9^t\frac{\partial^2}{\partial {x}^2}\right){w}_0^t\\ {}={M}^t+\frac{n^c{cf}_t}{6},\end{array}} $$

(17)

where M^t is the end moment per unit width at the top face (at the end x = 0 or x = a).

Core B.Cs (three):

• (i) Either δu₀^c = 0 or,

$$ {\displaystyle \begin{array}{l}\;\left(\frac{2c}{15}{C}_{11}^c\frac{\partial }{\partial x}\right){u}_0^b+\left(\frac{16c}{15}{C}_{11}^c\frac{\partial }{\partial x}\right){u}_0^c\kern0.36em +\left(\frac{2c}{15}{C}_{11}^c\frac{\partial }{\partial x}\right){u}_0^t\\ {}-\left(\frac{2}{3}{C}_{13}^c+\frac{cf_b}{15}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right){w}_0^b+\left(\frac{2}{3}{C}_{13}^c+\frac{cf_t}{15}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right){w}_0^t=\frac{4{n}^cc}{3}.\end{array}} $$

(18)

• (ii) Either δϕ ₀ ^c  = 0 or,

$$ {\displaystyle \begin{array}{l}\kern0.24em \left(\frac{16{c}^3}{105}{C}_{11}^c\frac{\partial }{\partial x}\right){\phi}_0^c-\left(\frac{2{c}^2}{35}{C}_{11}^c\frac{\partial }{\partial x}\right){u}_0^b\kern0.36em +\left(\frac{2{c}^2}{35}{C}_{11}^c\frac{\partial }{\partial x}\right){u}_0^t\\ {}+\left(\frac{4c}{15}{C}_{13}^c+\frac{c^2{f}_b}{35}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right){w}_0^b-\left(\frac{8c}{15}{C}_{13}^c\right){w}_0^c+\left(\frac{4c}{15}{C}_{13}^c+\frac{c^2{f}_t}{35}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right){w}_0^t=0.\end{array}} $$

(19)

• (iii) Either δw ₀ ^c  = 0 or,

$$ {C}_{55}^c\left[\frac{8c}{15}{\phi}_0^c-\frac{2}{5}{u}_0^b+\frac{2}{5}{u}_0^t+\frac{\left(2c+3{f}_b\right)}{15}{w}_{0,x}^b+\frac{16c}{15}{w}_{0,x}^c+\frac{\left(2c+3{f}_t\right)}{15}{w}_{0,x}^t\right]=\frac{4}{3}\;{s}^cc. $$

(20)

Bottom face sheet B.Cs (three):

• (i) Either δu₀^b = 0 or,

$$ {\displaystyle \begin{array}{l}-\left(\frac{2{c}^2}{35}{C}_{11}^c\frac{\partial }{\partial x}\right){\phi}_0^c+\left({\alpha}_1^b\frac{\partial }{\partial x}\right){u}_0^b+\left(\frac{2c}{15}{C}_{11}^c\frac{\partial }{\partial x}\right){u}_0^c+\left(\frac{c}{35}{C}_{11}^c\frac{\partial }{\partial x}\right){u}_0^t\\ {}+\left(\frac{2}{3}{C}_{13}^c\right){w}_0^c-\left(\frac{11}{30}{C}_{13}^c+\frac{3{cf}_b}{35}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right){w}_0^b\\ {}+\left(-\frac{1}{30}{C}_{13}^c+\frac{cf_t}{70}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right){w}_0^t={N}^b+\frac{n^cc}{3}+{B}_u^b,\end{array}} $$

(21a)

where N^b is the end axial force per unit width at the bottom face and B_u^b is the nonlinear term,

$$ {B}_u^b=-\frac{f_b}{2}{C}_{11}^b{\left({w}_{0,x}^b\right)}^2. $$

(21b)

• (ii) Either δw₀^b = 0 or,

$$ {\displaystyle \begin{array}{l}-\left[\frac{2\left(2c+3{f}_b\right)}{15}{C}_{55}^c+\frac{c^2{f}_b}{35}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right]{\phi}_0^c+\left[-\frac{\left(38c-47{f}_b\right)}{60c}{C}_{55}^c+\frac{3{cf}_b}{35}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right]{u}_0^b\\ {}+\left[\frac{2\left(c+{f}_b\right)}{3c}{C}_{55}^c+\frac{cf_b}{15}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right]{u}_0^c+\left[\frac{\left(-2c+7{f}_b\right)}{60c}{C}_{55}^c+\frac{cf_b}{70}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right]{u}_0^t\\ {}-\left({\alpha}_7^b\frac{\partial }{\partial x}\right){w}_0^c+\left[\left(\frac{11{f}_b}{60}{C}_{13}^c-{\alpha}_8^b\right)\frac{\partial }{\partial x}-{\alpha}_9^b\frac{\partial^3}{\partial {x}^3}\right]{w}_0^b\\ {}+\left[\left(\frac{f_t}{60}{C}_{13}^c-{\beta}_2\right)\frac{\partial }{\partial x}+\frac{cf_b{f}_t}{140}{C}_{11}^c\frac{\partial^3}{\partial {x}^3}\right]{w}_0^t+{L}_w^b\\ {}={V}_0^b+{m}^b+\frac{s^cc}{3}+{B}_w^b,\end{array}} $$

(22a)

where V^b is the end shear force per unit width at bottom face and B_w^b is the nonlinear term:

$$ \kern0.24em {B}_w^b=-\frac{f_b}{2}{C}_{11}^b{w}_{0,x}^b\;\left[\;2{u}_{0,x}^b+{\left({w}_{0,x}^b\right)}^2\right], $$

(22b)

and L_w^b is the dynamic term:

$$ {\displaystyle \begin{array}{l}\kern0.24em {L}_w^b=\frac{f_b}{420}\left[\begin{array}{l}{\rho}^c12{c}^2\frac{\partial^2{\phi}_0^c}{\partial {t}^2}-{\rho}^c36c\frac{\partial^2{u}_0^b}{\partial {t}^2}-{\rho}^c28c\frac{\partial^2{u}_0^c}{\partial {t}^2}-{\rho}^c6c\frac{\partial^2{u}_0^t}{\partial {t}^2}\\ {}\kern2.04em +\left({\rho}^c18{cf}_b+{\rho}^b35{f}_b^2\right)\frac{\partial^3{w}_0^b}{\partial x\partial {t}^2}-{\rho}^c3{cf}_t\frac{\partial^3{w}_0^t}{\partial x\partial {t}^2}\kern0.24em \end{array}\right]\kern0.36em .\\ {}\kern0em \end{array}} $$

(22c)

• (iii) Either δw_0,x^b = 0 or,

$$ {\displaystyle \begin{array}{l}\;\left(\frac{c^2{f}_b}{35}{C}_{11}^c\frac{\partial }{\partial x}\right){\phi}_0^c-\left(\frac{3{cf}_b}{70}{C}_{11}^c\frac{\partial }{\partial x}\right){u}_0^b-\left(\frac{cf_b}{15}{C}_{11}^c\frac{\partial }{\partial x}\right){u}_0^c-\left(\frac{cf_b}{70}{C}_{11}^c\frac{\partial }{\partial x}\right){u}_0^t\\ {}\kern.6em -\left(\frac{f_b}{5}{C}_{13}^c\right){w}_0^c+\left(\frac{11{f}_b}{60}{C}_{13}^c+{\alpha}_9^b\frac{\partial^2}{\partial {x}^2}\right){w}_0^b+\left(\frac{f_b}{60}{C}_{13}^c-\frac{cf_b{f}_t}{140}{C}_{11}^c\frac{\partial^2}{\partial {x}^2}\right){w}_0^t\\ {}\kern.6em ={M}^b-\frac{n^c{cf}_b}{6},\end{array}} $$

(23)

where M^b is the end moment per unit width at the bottom face.

Hamilton’s principle results in 7 coupled partial differential equations, Eqs. (7a) to (13a), four of which are nonlinear due to the consideration of nonlinear axial strains in the face sheets. The order of the equations of motion is 18. Therefore, there are 18 boundary conditions, 9 at each end at x = 0 and x = a, given by Eqs. (15a) to (23). Notice that since the rotations of the face sheets are assumed to be the derivative of the transverse displacement with respect to x, there exist inertial terms L_w^t and L_w^b in the boundary conditions in equations, (16a) and (22a). The 7 unknowns of EHSAPT are: u₀^t(x,t), u₀^c(x,t), u₀^b(x,t), ϕ₀^c(x,t), w₀^t(x,t), w₀^c(x,t) and w₀^b(x,t).

3 Accuracy Study I: A Statically Loaded Simply Supported Sandwich Panel

In this section we shall study the linear response of a simply supported sandwich panel under transversely applied loading of the form:

$$ \kern0.24em {q}^t(x)={q}_0\sin \frac{\pi x}{a}. $$

(24a)

In this case, the boundary conditions for x = 0, a (Fig. 1) are the three kinematic conditions

$$ \kern0.24em {w}_0^t={w}_0^b={w}_0^c=0. $$

(24b)

and the 6 natural boundary conditions in (15), (17), (18), (19), (21) and (23).

All these are satisfied by displacements in the form:

$$ \kern0.24em {u}_0^{t,b,c}={U}_0^{t,b,c}\cos \frac{\pi x}{a};\kern1.68em {w}_0^{t,b,c}={W}_0^{t,b,c}\sin \frac{\pi x}{a}\kern0.36em ;\kern1.68em {\phi}_0^c={\Phi}_0^c\cos \frac{\pi x}{a}. $$

(24c)

We consider the linear problem, which means that the nonlinear terms F_u,w^t,b in the governing differential Eqs and the nonlinear terms B_w^t,b in the boundary conditions are neglected.

Substituting Eq. (25a) into Eq. (10–14) results in a system of seven linear equations for the seven unknown constants U₀^t, U₀^c, U₀^b, Φ₀^c, W₀^t, W₀^c, and W₀^b.

We shall consider sandwich configurations where the two face sheets are assumed identical with thickness f_t = f_b = f = 2 mm. The core thickness is 2c = 16 mm. The total thickness of the beam/plate is defined as h_tot = 2f + 2c and the length of the beam is a = 20h_tot.

Regarding materials, the faces are made out of graphite-epoxy with moduli (GPa): E₁^f = 181.0; E₂^f = E₃^f = 10.3; G₂₃^f = 5.96; G₃₁^f = G₁₂^f = 7.17 and Poisson’s ratios: ν₃₂^f = 0.40; ν₃₁^f = 0.016; ν₁₂^f = 0.277.

The core is made out of glass-phenolic honeycomb with moduli (GPa): E₁^c = E₂^c = 0.032; E₃^f = 0.300; G₂₃^c = G₃₁^c = 0.048; G₁₂^c = 0.013 and Poisson’s ratios: ν₃₂^c = ν₃₁^c = ν₁₂^c = 0.25.

In the following results, the displacements are normalized with w_norm = 3q₀a⁴/(2π⁴f³E₁^f) and the stresses with q₀.

Plotted in Fig. 2 is the normalized displacement at the top face sheet as a function of x. In this figure, we also show the predictions of the simple Classical beam theory, which does not include transverse shear, as well as the First Order Shear theories; for the latter, there are two versions: one that is based only on the core shear stiffness and one that includes the face sheet stifnesses. In addition, we show the predictions of the High Order sandwich panel theory [5]. This theory, which is based on an assumption that the in-plane rigidity of the core is neglected and yields a constant shear stress and zero axial stress in the core. Finally, we also show the predictions from a finite element method (FEM) study [21].

Fig. 2

Transverse displacement, w, at the top

From Fig. 2, we can see that both the Classical and First Order Shear (both versions) seem to be inadequate. The Classical theory is too non-conservative and the First Order Shear theory with face sheets included can hardly make a difference. On the other hand, the First Order Shear theory where shear is assumed to be carried exclusively by the core is too conservative; this clearly demonstrates the need for higher order theories in dealing with sandwich structures. In this regard, both the Frostig et al. [5] and the Extended High Order theories give a displacement profile which is essentially identical to the Elasticity solution. In Fig. 2 we can also readily observe the large effect of transverse shear, which is an important feature of sandwich structures.

The distribution of the axial stress in the core, σ_xx, as a function of z at the midspan location, x = a/2 (where the bending moment is maximum), is plotted in Fig. 3. The Extended High Order theory predicts a stress profile practically identical to the Elasticity. Note that the HSAPT [5] neglects the in-plane rigidity of the core, yielding a zero axial stress. The Classical and First Order Shear theories give practically identical predictions but they are in appreciable error by comparison to the Elasticity, the error increasing towards the lower end of the core (z = −c). All curves are linear. Notice also that for the Elasticity and the Extended High Order theory there is not a symmetry with regard to the mid line (z = 0) unlike the Classical and First Order Shear theories.

Fig. 3

Through-thickness distribution in the core of the axial stress, σ_xx, at midspan

The through-thickness distribution of the transverse normal stress in the core, σ_zz, at the midspan location, x = a/2, is shown in Fig. 4. Note that the First Order Shear theory and the Classical theory consider the core incompressible. Both high order theories are practically coinciding with the Elasticity curve and all are nearly linear.

Fig. 4

Through-thickness distribution in the core of the transverse normal stress, σ_zz, at midspan

The transverse shear profile, τ_xz, is investigated in detail by considering a sandwich construction in which both the face sheets and the core are isotropic. By varying the moduli ratio, we can accordingly increase the shear stress range in the core. Thus, we assume that the face sheets are made out of isotropic Aluminum Alloy with E_f = 100 GPa and the core is made out of isotropic material having a modulus E_c such that the ratio E_f/E_c assumes the values of: 50, 5 and 2. The Poisson’s ratios are assumed ν_f = ν_c = 0.30. Fig. 5 shows the shear stress distribution through the thickness near the support wher the shear force is large, x = a/10. For the moduli ratio of 2 the range is very large, with the maximum over minimum shear stress ratio being about 2. On the contrary, for the moduli ratio of 50, the shear stress range is very small, with the corresponding maximum over minimum shear stress ratio being only about 1.04. The Extended High Order theory is capable of capturing the shear stress profile in all cases, even the most demanding case of E_f/E_c = 2, and in all cases is very close to the Elasticity. On the contrary, a constant shear stress assumption as is [5] would be applicable only for the large ratios of E_f/E_c.

Fig. 5

Through-thickness distribution in the core of the transverse shear stress, τ_xz, at x = a/10 for the case of isotropic aluminum alloy faces and a wide range of isotropic cores

4 Accuracy Study II: Wrinkling of a Sandwich Panel

The EHSAPT formulation for predicting the critical wrinkling load for a simply supported sandwich was done in [19]. The simplest way to apply the compressive loading is for concentrated compressive loads to be applied on the top and bottom faces such that they sum up to the total applied compressive load with the pre-buckling axial strains being equal on the top and bottom faces. The core is considered to have linear strains. Results in the following will be presented for this simpler case. Another case considered was applying uniform strain loading throughout the thickness of the panel and a nonlinear core assumption. The results from this more complicated case of load application are not much different than the simpler loading case. A perturbation approach was used resulting in an eigenvalue problem formulation [19].

Tables 1 and 2 give the critical loads (normalized with the Euler load) for symmetric sandwich beams with length ratio a/h_tot = 5 and varying face thickness ratios f/h_tot, where f = f_t = f_b is the face thickness and h_tot = 2(f + c) is the total beam thickness.

Table 1 Critical Loads for E_f/E_c = 500; normalized with the Euler load (no shear) A and S in the wave numbers stand for anti-symmetric and symmetric, respectively

Table 2 Critical Loads for E_f/E_c = 1000; normalized with the Euler load (no shear) A and S in the wave numbers stand for anti-symmetric and symmetric, respectively

The sandwich beam is made of isotropic face and core with E_f/E_c = 500 and 1000 and Poisson’s ratios ν_f = 0.35 and ν_c = 0. These tables compare the Elasticity results to the wrinkling predictions from EHSAPT, the HSAPT [5], and the Hoff-Mautner (semi-empirical constant = 0.5) [20]. The tables also show the mode and percent Error with respect to Elasticity.

It can be concluded that the EHSAPT is the most accurate theory and esp. by comparison to the HSAPT [5]. Indeed, the HSAPT is inaccurate in predicting wrinkling loads for sandwiches with very thin faces, under-predicting the critical load by as much as about 70% for the more moderately stiffer core configuration with E_f /E_c = 500 and f/h_tot = 0.01. In addition, the HSAPT predicts symmetric wrinkling modes, while the EHSAPT predicts anti-symmetric wrinkling modes, similar to Elasticity.

5 Accuracy Study III: Blast Loading of a Simply Supported Sandwich Panel

In this section, the dynamic response of a simply supported sandwich beam, initially at rest, then subjected to a temporal blast load that exponentially decays in time and has a half-sine spatial profile along the beam is studied. The applied load in kN/m (with time t in milli-sec) is:

$$ \kern0.24em {q}^t\left(x,t\right)={q}_0\sin \frac{\pi x}{a}\;{e}^{-\beta t}, $$

(25a)

where q₀ = 510 KN/m and β = 1.25 milli-sec⁻¹ which decays to less than 0.1% of its original magnitude after 5.5 milli-sec. The above blast load parameters, as well as the material and geometry data were taken from the experimental investigations of Gardner et al. [27]. The faces are E-glass vinyl-ester composite: Young’s modulus E₁^c = 13,600 MPa, density ρ^f = 1800 kg/m³, and the isotropic core is Corecell™ A300 styrene acrylonitrile (SAN) foam: Young’s modulus E^c = 32 MPa, ρ^c = 58.5 kg/m³, Poisson’s ratio ν^c = 0.3, and shear modulus G^c = E^c/[2(1 + ν^c)]. The geometry of the sandwich configuration is: face thickness f_t = f_b = 5 mm, core thickness 2c = 38 mm, width b = 102 mm, and span of beam a = 152.4 mm.

In this case, the displacement functions that satisfy the boundary conditions are [17]:

$$ \kern0.24em {u}_0^{t,b,c}={U}_0^{t,b,c}(t)\cos \frac{\pi x}{a};\kern1.2em {w}_0^{t,b,c}={W}_0^{t,b,c}(t)\sin \frac{\pi x}{a};\kern1.2em {\phi}_0^c={\Phi}_0^c(t)\cos \frac{\pi x}{a}. $$

(25b)

Substituting (25) into (7a–13c) (neglecting the nonlinear terms but including the dynamic terms), turns the partial differential equations of motion into linear ordinary differential equations in time:

$$ \kern0.24em \left[M\right]\left\{{\ddot{U}}_0(t)\right\}+\left[K\right]\left\{{U}_0(t)\right\}=\left\{F(t)\right\}, $$

(25c)

where the 7 × 7 matrix [M] and [K] are the mass matrix containing the inertial terms and the stiffness matrix, respectively. The vector of the unknown generalized coordinates are

$$ \kern0.24em \left\{{U}_0(t)\right\}={\left\{{U}_0^b(t),{U}_0^c(t),{\Phi}_0^c(t),{U}_0^t(t),{W}_0^b(t),{W}_0^c(t),{W}_0^t(t)\right\}}^T, $$

(25d)

and the load vector

$$ \kern0.24em \left\{F(t)\right\}={e}^{-\beta t}{\left\{0,0,0,0,0,0,{q}_0\right\}}^T. $$

(25e)

The ordinary differential equations can be solved using standard numerical integration methods.

The transverse displacements w₀^t, w₀^c and w₀^b, at the mid-span location x = a/2 versus time are shown in Fig. 6. In this figure we show the results from Elasticity, EHSAPT, and HSAPT. The two high-order sandwich panel theories are practically on top of each other and display the same trend in behavior of the top, core, and bottom displacements as Elasticity, i.e. that the top face travels down first, followed by the core, then the bottom face sheet. EHSAPT and HSAPT match the mid-core transverse displacement of Elasticity. The high order theories over estimate the maximum displacement of the top face by a modest amount, no more than 5%. The bottom face transverse displacements from EHSAPT and HSAPT do not exactly follow Elasticity, but give values within less than 6% error over the time range in Fig. 2.

Fig. 6

Transverse displacement at the top face, middle of core and bottom face at the mid-span location for Elasticity, EHSAPT and HSAPT during the initial phase of blast

It should also be noted that the First Order Shear Deformation Theory (FOSDT) can be very inaccurate in its prediction of transverse displacement, as shown in Sect. 3, and, of course, cannot capture the differences in the displacements of the face sheets and the core.

Figure 7 shows the axial displacements u₀^t, u₀^c and u₀^b, at the edge x = 0 versus time. EHSAPT and HSAPT capture the high cyclic behavior of u₀^c that Elasticity displays, with EHSAPT being closer in value to Elasticity than HSAPT. The first peak in the core axial displacement, u₀^c of EHSAPT, is 10% under Elasticity, while the first peak in u₀^c of HSAPT is 32% under Elasticity. Both high-order theories and Elasticity predict very similar behavior with time of the top and bottom face sheet axial displacements, u₀^t and u₀^b.

Fig. 7

Axial displacement at the top face, middle of core and bottom face at the support location (x = 0) for Elasticity, EHSAPT and HSAPT during the initial phase of blast

The shear stress at the top and bottom face/core interfaces at x = 0 is shown in Fig. 8. EHSAPT is the only theory that can show the differences in the shear stresses at the top and bottom face/core interfaces like Elasticity, while HSAPT predicts that the shear stress is constant throughout the thickness and seems to be about the average value of EHSAPT and Elasticity. EHSAPT gives a minimum shear stress (most negative shear stress) at the top and bottom face/core interface under the minimum Elasticity values by just 0.5%.

Fig. 8

The shear stress, τ_xz, at the top (T) and bottom (B) face/core interfaces during the initial phase of blast

6 Conclusion

The extended high order sandwich beam theory is capable of including the unique features of sandwich construction, i.e. large transverse shear and core compressibility. In this paper, the basic premises and the formulation of this theory, in both its static and dynamic versions, is described in detail. In this theory, which is derived for a general asymmetric construction, all displacement continuity conditions at the interface of the core with the top and bottom face sheets are enforced. A comparison to the elasticity solution shows that this extended high-order theory can be used with any combinations of core and face sheets and not only the very “soft” cores that the other high order sandwich theories demand.

Results have been presented for the case of static transverse loading of a simply supported sandwich beam by comparison to the Elasticity, the Classical sandwich beam theory, the First Order Shear theory and the HSAPT model [5]. The results show that the extended high order theory is very close to the Elasticity solution in terms of both the displacements and the transverse stress or strain, as well as axial stress through the core, and, in addition, the shear stress distributions in the core for core materials ranging from very soft to almost half the stiffness of the faces. In particular, it captures the very large range of core shear stress and the nearly parabolic profile in the cases of cores that are not “soft”.

A case study involving an exponentially decaying blast load with a spatial half-sine profile across the top of the beam is used to compare the dynamic EHSAPT to a Dynamic Elasticity benchmark. The case study showed that the EHSAPT captures very well the complex behavior of the transverse and axial displacements in the faces and the core, as well as the stresses, and in particular, the lag in the bottom versus top displacements versus time.

In addition, the wrinkling predictions of the EHSAPT are compared with predictions from Elasticity and in all cases the EHSAPT was very close to the Elasticity predictions. On the contrary, the HSAPT [5] was in significant error for the relatively thinner faces. The large discrepancy between HSAPT and EHSAPT for very low face over total thickness ratios (when the beam is most susceptible to wrinkling) indicates that including the axial rigidity of the core (as is done in the EHSAPT) is very important during wrinkling.