Interference and Diffraction

Abstract

In Chap. 2 we learned about several interesting properties of waves, including constructive and destructive interference. Figure 2.8 illustrates the constructive and destructive interference that occurs when two wave pulses travel in opposite directions on a one-dimensional medium such as a rope.

In Chap. 2 we learned about several interesting properties of waves, including constructive and destructive interference. Figure 2.8 illustrates the constructive and destructive interference that occurs when two wave pulses travel in opposite directions on a one-dimensional medium such as a rope. In the case of continuous waves, constructive and destructive interference can lead to standing waves, as shown in Fig. 2.9. We now discuss what happens when waves travel in a two-dimensional medium (such as water waves on the surface of a pond) or a three-dimensional medium (such as light waves in a room).

In Fig. 2.11 we showed how propagation of water waves in a ripple tank can be studied by projecting light through them so that they project shadows on a screen or on the table below the ripple tank. In this chapter we begin our study of interference with water waves in a ripple tank and then proceed to light waves (where we can see the end result but not the propagating wavefronts themselves).

5.1 Interference of Waves from Two Identical Sources

Two examples of interference between waves from two identical sources are shown in Fig. 5.1. In Fig. 5.1a, water waves in a ripple tank from two identical sources add up in certain directions (where they have the same phase) and cancel each other in certain directions (where their phases are opposite to each other). The lighter areas in the photo are regions of cancellation. The alternating light and dark bars correspond to regions where waves add together. In Fig. 5.1b, sound waves from two loudspeakers supplied with a single frequency by the same amplifier outdoors produce loud and soft sounds in different directions due to constructive and destructive interference. (In the case of two loudspeakers inside a room, however, the interference patterns are much more complicated due to many “images” of the loudspeakers formed by reflections from the walls and other surfaces.)

Fig. 5.1

Two examples of interference: a water waves in a ripple tank from two identical sources (Photograph by Mark Welter). b Sound waves from two loudspeakers driven by the same amplifier

In Fig. 5.1, the two identical sources are assumed to be in phase with each other, so constructive interference occurs wherever the distance to both sources is the same (such as along the center line). What happens if the two sources vibrate in opposite phase (if, for example, the wires to one loudspeaker are reversed)? Then the positions of constructive and destructive interference are interchanged. That is, destructive interference occurs along the center line where the distance to both sources is the same, and constructive interference occurs when the distance to one source is a half-wavelength greater. (Some people inadvertently connect their loudspeakers this way, which moves the stereo sound image but also distorts it because it moves by a different amount for each different frequency represented in the music.)

5.2 Light Passing Through Two Slits: Young’s Experiment

The interference of light from two identical sources was first demonstrated by Thomas Young in 1801; it provided one of the strongest pieces of evidence for the wave nature of light.

A convenient arrangement for demonstrating Young’s experiment is shown in Fig. 5.2. Light from a point source located at A illuminates two identical slits S₁ and S₂, which then act as two identical sources to produce an interference pattern on a screen, as shown. The spacing of the bright lines D depends upon the ratio of the wavelength λ to the slit spacing d and the distance L to the screen:

Fig. 5.2

Interference between light waves from two narrow slits illuminated by the same light source (Young’s experiment). The spacing of the bright lines depends on the ratio of wavelength to slit spacing

$$ D /L =\uplambda /d. $$

(5.1)

The interference pattern formed by red light is therefore wider than that produced by blue light as is shown in Fig. 5.3.

Fig. 5.3

(Courtesy of Kodansha, Ltd.)

Interference patterns produced by a red and b blue light

▲ Example

Two slits spaced 0.5 mm apart are located 40 cm from a screen. Describe the resulting pattern when the slits are illuminated with red light (λ = 633 nm) and with blue light (λ = 450 nm).

Solution

Substituting the given data for red light into Eq. (5.1),

$$ D = L\uplambda/d = (0.4\,{\text{m}})\left( {633 \times 10^{{{-}9}} {\kern 1pt} {\text{m}}} \right)/\left( {0.5 \times 10^{{{-}3}} {\kern 1pt} {\text{m}}} \right) = 5.06 \times 10^{{{-}4}} {\kern 1pt} {\text{m}} = 0.51\,{\text{mm}}. $$

A bright fringe will occur at the center, and at distances of 0.51, 1.1, 1.52 mm, and so on. There will be dark fringes at 0.25, 0.76 mm, and so on.

For blue light, D = Lλ/d = (0.4 m)(450 × 10^–9 m)/(0.5 × 10^–3 m) = 3.60 × 10^–4 m = 0.36 mm.

Bright fringes will occur at 0, 0.36, 0.72 mm, and so on, with dark fringes at 0.18, 0.54 mm, and so on.

What happens if the slits are illuminated with white light? The center bright fringe will be white (because the interference patterns for all the component colors have a maximum there), but the next maximum on each side will be a “rainbow” of colors, with violet having the smallest spacing and red the largest.

5.3 Interference in Thin Films

Thin transparent films, such as soap bubbles or oil on water, show patterns of color due to interference. In this case, the interference is between light reflected at the upper and lower surfaces of the thin film, as shown in Fig. 5.4. An observer will see different parts of an oil slick (A and B, for instance) as having different colors, because light of a different wavelength will interfere at A as compared to B. This phenomenon is known as iridescence. Iridescence occurs because the optical path length depends on the location of the observer or light source.

Fig. 5.4

Interference between light reflected at the upper and lower surfaces of a thin film of oil floating on water. Light reflected at A will have a different color than light reflected at B

Soap bubbles and films produce colors in the same way as oil films. The only difference is that the thin film has air on both sides. Just before a bubble breaks, it usually becomes dark because the film is so thin that only destructive interference takes place, as shown in Fig. 5.5. Museums often have interactive soap film exhibits in which wire frames are withdrawn from a tank of a special soap film solution so that interference effects may be admired and studied.

Fig. 5.5

(Courtesy of Kodansha, Ltd.)

Soap films show patterns of color due to interference. The top of the film shown on the right appears dark because the film is so thin that only destructive interference takes place

Phase of the Reflected Wave

To explain the dark area in a soap bubble, we have to consider the phase of the reflected wave, as we did in Sect. 2.3. Light reflected at the first surface of the soap bubble undergoes a phase reversal, much like the pulse on a rope does at a fixed end (see Fig. 2.5a). At the second or soap-to-air surface, the reflected light has the same phase as the incident light, much like the pulse on a rope at a free end (Fig. 2.5b). Thus, if the soap film is very thin, the two reflections will come back with opposite phase and will interfere destructively, thus the black appearance.

Where the film has a thickness of λ/4 (a quarter-wavelength), the wave that reflects at the second surface will have its phase retarded by half a cycle, since it has traveled a half-wavelength in the soap, and thus it will be in phase with the light reflected at the first surface. Constructive interference occurs, and we see a bright fringe of light. Where the film has a thickness λ/2, we have destructive interference again, and so forth. Both situations are shown in Fig. 5.6.

Fig. 5.6

Interference occurs when light is reflected from the top and bottom of a thin film

Figure 5.7 illustrates how interference patterns can be formed by light reflected at the top and bottom of an air wedge between two glass plates. In this case, the thickness t of the air wedge at the mth fringe is given by t = mλ/2, where λ represents the wavelength of light used to illuminate the wedge. Interference patterns of this type can be used to measure the thickness of very thin objects or to determine the flatness of a surface.

Fig. 5.7

Two glass plates separated by a wedge of air

Figure 5.8 shows two plane glass plates illuminated with light from a sodium source placed one on top of the other. The uniformly spaced light and dark fringes indicate that the two plates forming the air film are flat. If the plates had uneven surfaces, the fringes would appear curved.

Fig. 5.8

(Courtesy of Kodansha, Ltd.)

Two plane glass plates illuminated with light from a sodium source are placed one on top of the other. A very thin sheet of paper inserted at one end forms a wedge-like air film. The resulting interference pattern consists of uniformly spaced parallel lines

An interference pattern between a flat and a spherical glass surface is shown in Fig. 5.9. Each fringe is created by an air film of a certain thickness. The circular fringes are called Newton’s rings.

Fig. 5.9

(Courtesy of Kodansha, Ltd.)

Newton’s rings produced using sodium light (left) and white light (right)

5.4 Michelson Interferometer

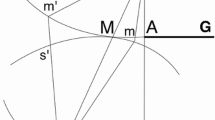
Another example of interference is created by the Michelson interferometer in Fig. 5.10. Light from source S is split into two beams by the half-silvered mirror A; one beam is reflected by the movable mirror M and one beam by the stationary mirror M′. When they recombine, they interfere to form bright or dark fringes, depending upon the relative path lengths they have traveled. Alternate bright and dark fringes can be counted as they pass a reference mark. If n fringes are counted as mirror M moves through a distance d, then the wavelength λ of the light is given by: λ = 2d/n. The Michelson interferometer can be used to determine the wavelength of light λ or the distance d with great accuracy.

Fig. 5.10

a Michelson interferometer. Light from the source is split into beams 1 and 2 by a half-silvered mirror. They recombine at the observer to create an interference pattern. b A Michelson interferometer for use in introductory physics laboratories (© Cenco Physics/Fundamental Photographs, NYC)

The Michelson-Morley experiment (1887) showed that the speed of light (and thus the wavelength) is the same when measured parallel and perpendicular to Earth’s motion through space. This experiment was of great significance in establishing Einstein’s special theory of relativity.

Later, with his formulation of the general theory of relativity, Einstein predicted the existence of gravitational waves, ripples in the fabric of space–time created by accelerating masses. Einstein was doubtful that an instrument with sufficient sensitivity to detect changes in space–time could ever be devised. However, a century after Einstein’s prediction of the existence of gravitational waves, work was completed on the Laser Interferometer Gravitational-Wave Observatory (LIGO), the first gravitational wave observatory.

At the heart of LIGO are two enormous laser interferometers, one in Louisiana, the other in Washington state (Fig. 5.11). With 4-km long arms, the two LIGO detectors are the world’s largest and most sensitive interferometers, capable of measuring a change in arm length over 1000 times smaller than a proton.

Fig. 5.11

(Courtesy of Caltech/MIT/LIGO Lab)

An aerial view of the laser interferometer gravitational-wave observatory (LIGO) detector near Hanford, WA

As with the Michelson interferometer, the central components of each L-shaped detector are a laser light source, beam splitter, and mirrors at the ends of the arms (Fig. 5.12). After being divided into two by the beam splitter, light travels down the two steel vacuum tubes that form the arms of the L. Reflected light from mirrors at the ends of the tubes combine to form an interference pattern. A change in the interference pattern formed by the recombined light beams signals the arrival of a gravitational wave.

Fig. 5.12

The key components of each of LIGO’s L-shaped detectors are a laser, beam splitter, and mirrors at the ends of the two arms

In 2015, LIGO detected gravitational waves produced by the merging of two black holes over 1.3 billion light-years away from the Earth. Heralded as a breakthrough of monumental scientific importance, these observations validated Einstein’s prediction of the existence of gravity waves and ushered in the era of gravitational wave astronomy, a powerful new way of probing the far reaches of the universe.

5.5 Applications of Interference

Antireflection Coatings

Lenses of sophisticated cameras and other optical instruments may combine many lens elements. As light passes through such a lens combination, a considerable amount of light would be lost by reflection at the many lens surfaces. This loss of light can be minimized by coating the lens with a thin layer of a transparent material having an index of refraction between air and glass. If the layer is a quarter-wavelength thick, light reflected at the upper surface of this layer will interfere with the light reflected at the lower surface in such a way as to cancel the reflection. This cancellation will be complete only for a single wavelength, of course, which is usually near the center of the visible spectrum (yellow light). If the coating has the right thickness to cancel out reflection of yellow light, blue light (short wavelength) and red light (long wavelength) will still be reflected, and this is why coated lenses appear to have a purple color. (Examine a high-quality camera to verify this.)

Glass with an antireflection coating is often used to protect paintings. Although it is strictly antireflecting for only one wavelength (color), it is fairly effective in eliminating reflections over the entire visible range.

Multilayer Mirrors

An ordinary mirror, consisting of glass with a coating of aluminum or silver, typically reflects about 90% of the light incident on it. This is certainly enough for most ordinary purposes, but for some applications (such as laser cavities) a higher reflectivity is needed. This is accomplished by using several layers of transparent material with alternating high and low indexes of refraction (n_H = 2.3 and n_L = 1.2, for example), as shown in Fig. 5.13. Partial reflection occurs at each interface. If the thicknesses are chosen so that all the reflected beams are in phase, it is possible to achieve nearly 100% reflection. For this reason, multilayer mirrors are used in a wide range of applications which require especially high reflectance at a given wavelength.

Fig. 5.13

A multilayer mirror with close to 100% reflection uses transparent layers with alternating high and low refractive indexes. The thicknesses of the films are chosen so that all the reflected beams will be in phase

Many examples of multilayer mirrors can be found in nature. For example, the silvery scales of some fish are made reflective by multiple layers. These mirrors reflect a range of colors by having a variety of layer thicknesses. Another interesting example from the animal world is the tortoise beetle, which has multiple layers in its wing cases, making them iridescent. The beetle can vary the moisture content of these thin films, which changes the thickness and hence the color of the reflected light from gold to reddish copper. Pearls and abalone shells also derive their luster from layers of semi-transparent nacre.

Artists have tried to incorporate interference colors in their work. The great glassmaker Louis Tiffany, for example, incorporated thin films within the glass to produce his iridescent favrile glass. Many contemporary sculptors incorporate multilayer mirrors into their work.

Multilayer Interference Filters

Closely related to multilayer mirrors are multilayer interference filters that pass a narrow range of wavelengths and reflect the rest. Generally, thin coatings of silver or other metal alternate with thin transparent layers. Because they absorb very little light (nearly all the light that is not transmitted is reflected), they are very efficient and are used in color TV cameras, for example, to separate the image into its three primary color components.

Iridescent Inks and Pigments

Iridescence inks, also known as optically variable inks, display two distinct colors depending on the viewing angle. These inks are often used to prevent counterfeiting. Many countries, including the United States, employ these inks to produce markings on currency, such as numerals or designs, which change color as the bill is viewed from different angles. Identifying counterfeit bills and other forged documents is possible because a color copier or scanner can only copy a document at one fixed angle and is unable to capture the color shifting properties of the iridescent inks.

Interference pigments are tiny, transparent mica flakes coated on all sides with a thin layer of either titanium dioxide (TiO₂) or iron oxide (FeO₂). Both oxides are highly reflective and refractive. Light is refracted and reflected at the boundaries between the metal oxide and mica. The metal oxide layer reflects light twice, from the outer surface and from the boundary with the mica flake. The delay between the first and second reflection phase shifts the light waves. The shift cancels out some wavelengths of light and reinforces others. The reinforced wavelengths appear as the dominant iridescent color.

There are numerous commercial and artistic applications of interference pigments. These include a variety of pearlescent or “metallic” paint formulations used in cosmetics and hard coatings on automobiles, as shown in Fig. 5.14. Artists find that these paints produce effects not possible with conventional pigments. The colors produced by iridescent pigments result in a color shift when the viewing angle changes.

Fig. 5.14

(Courtesy of C. J. Wilson)

Pearlescent paints produce stunning effects not possible with conventional pigments

5.6 Diffraction

When waves encounter an obstacle, they tend to bend around it. This is an example of a phenomenon known as diffraction. Waves passing through a slit tend to spread out due to diffraction at each boundary, as shown in the ripple tank in Fig. 5.15. The amount of diffraction depends upon the ratio of the wavelength to the slit width. In Fig. 5.15a, the wavelength is substantially smaller than the slit width and little diffraction occurs; in Fig. 5.15b, the wavelength is comparable to the slit width and considerable diffraction occurs.

Fig. 5.15

Diffraction of water waves in a ripple tank as they pass through a slit (Photographs by Mark Welter)

Like waves in a ripple tank, ocean waves may diffract when they encounter an obstacle, for example, an offshore rock formation, or pass through an opening such as the gap in the breakwater shown in Fig. 5.16. As with all types of waves, the amount of diffraction depends on the ratio of the wavelength to the size of the obstacle or the opening.

Fig. 5.16

Ocean waves diffract as they pass through an opening in a breakwater (Dmitris1 (https://commons.wikimedia.org/wiki/File:BreakWaterDiffraction_Ashkelon1.jpg), https://creativecommons.org/licenses/by-sa/4.0/legalcode)

If you stand beside an open doorway, you can hear sounds from inside the room but you cannot see into the room. Sound waves have wavelengths comparable to the width of the doorway, and thus they are highly diffracted as they pass through; light waves, however, have wavelengths that are much smaller than the doorway and thus the effects of diffraction are negligible.

In addition to spreading out, waves passing through a slit exhibit another interesting type of behavior, also due to diffraction: dark and bright fringes form on either side of the central bright area. If you look through a narrow slit between your fingers at a light source, especially a bulb with a straight-line filament or a fluorescent tube, you should see alternating bright and dark lines due to diffraction. The narrower you make the slit, the greater will be the spacing between these bright and dark lines.

Fringes from Single-Slit Diffraction

One way to try to understand these alternating bright and dark fringes is to envision the slit being divided into eight or ten smaller slits, as shown in Fig. 5.17.

Fig. 5.17

Diffraction of light as it passes through a single slit can be understood by imagining that the slit is divided into eight smaller slits. At a point where the distance from slit 1 is λ/2 greater than from slit 5, the contributions of these two slits cancel, as do other pairs

At the position of the first dark fringe, the path traveled by light from imaginary slit 1 is a half-wavelength greater than that traveled by light from slit 5; similarly, the path traveled by light from slit 2 is a half-wavelength greater than light from slit 6, and so on. Thus, light from the imaginary slits cancels in pairs and darkness results. At the first bright fringe, the path differences are a full wavelength, and so light from slit 1 reinforces light from slit 5 and so on. When light having a wavelength λ passes through a slit of width a to a screen a distance L away, the spacing D(0) of the first dark fringe can be calculated from the formula (provided L >> a):

$$ D(0) /L =\uplambda /a $$

(5.2)

Note the similarity of this formula to formula (5.1), which gave the position of the first bright fringe in an interference pattern, but remember that now we are describing the first dark fringe in a diffraction pattern. From formula (5.2), the total width of the beam (between the dark fringes on either side of the center) is given by 2D(0) = 2λL/a. Note that the beam gets wider as the slit width a gets narrower.

▲ Example

Green light falls on a slit 1.00 × 10⁻⁴ m wide and produces the first dark fringe 5.5 × 10⁻³ m from the center of the diffraction pattern on a screen 1.00 m away. Find the wavelength of the green light.

Solution

Solving Eq. (5.2) for λ and inserting the given data,

$$ \begin{aligned} & D(0) /L = \lambda /a\,{\text{or}}\,\lambda = aD(0) /L \\ & \lambda = aD(0) /L = (1 \times 10^{ - 4} {\kern 1pt} {\text{m}}){\kern 1pt} (5.5 \times 10^{ - 3} {\kern 1pt} {\text{m}}) /1\,{\text{m}} = 5.5\, \times \,10^{ - 7} {\kern 1pt} {\text{m}}. \\ \end{aligned} $$

The spacing D(1) of the first bright fringe right next to the dark fringe is given by the formula:

$$ D(1) /L = 3\uplambda / 2a. $$

(5.3)

To see a two-dimensional diffraction pattern, look at a light source through a piece of woven cloth or a fine mesh screen. The finer the mesh, the greater will be the spread in the diffraction pattern you observe.

Diffraction effects are not only noticed when waves pass through a slit, but when they encounter a barrier, as when an opaque object casts a shadow. Figure 5.18 shows how a bright spot appears at the center of the shadow of a penny due to diffraction of light at the edge. Diffracted light from every point on the edge travels the same distance to the center of the shadow, and thus the waves add up to produce the bright spot.

Fig. 5.18

Diffraction of light by a penny results in a bright spot at the center of the shadow

The photographs in Fig. 5.19 show the diffraction of light around a screw and a safety pin. Note the different effects around the edges of the objects and at the openings within the safety pin.

Fig. 5.19

Diffraction effects at the edges of the shadows of a a screw and b a safety pin (Photographs by Gordon Gore)

5.7 Combined Interference and Diffraction

When light passes through two or more narrow slits, both interference and diffraction effects can be observed. Figure 5.20 illustrates a typical pattern produced by the overlapping phenomena. Diffraction and interference are two different phenomena; try not to confuse them. When water waves pass through two slits, diffraction causes the waves to spread out so that they interfere over a large area. The same thing happens when light passes through a double slit.

Fig. 5.20

When light passes through a double slit, both interference and diffraction are observed

Diffraction determines the width of the central bright area. In particular, the width depends on the ratio λ/a, where λ is the wavelength and a is the slit width. When the slits are made narrower, the central bright area expands. The central bright area is pretty much the same whether there is one slit or two slits.

● Spacing of Fringes from a Double Slit

When there are two or more slits, interference fringes are observed within the central bright area. The spacing of these bright and dark fringes depends upon the ratio λ/d, where d is the spacing between the slits. When the two slits are made narrower, but remain the same distance apart, the spacing of the interference fringes remains unchanged, but more of them can be seen in the central bright area, of course (see Fig. 5.21).

Fig. 5.21

Diffraction determines the width of the central bright region; interference determines how many light and dark lines will appear in this region

Observe that:

• 1. Changing a changes the size of the central bright area.

• 2. Changing d changes the spacing of the interference fringes.

• 3. Changing λ changes both the size of the central bright area and the spacing of the interference fringe.

5.8 How Diffraction Limits Resolution

If a circular opening is illuminated by light from a point source, the diffraction pattern will be a set of circular fringes. When a lens is used to form an image, the image of each point is actually a small circular diffraction disk; the size of the disk depends upon the diameter of the lens and the wavelength of the light. A larger diameter decreases the size of the disk, while a longer wavelength increases it. In the image formed by a lens, two points will appear to be separate if their diffraction disks do not overlap by more than the radius of the disks, as shown in Fig. 5.22a. In Fig. 5.22b the central maximum of one pattern lies on the first minimum of the other. In Fig. 5.22c the patterns are at the limit of resolution.

Fig. 5.22

Diffraction patterns due to two pinholes with varying spacing. In b and c, the holes are so close together that the central peaks in their diffraction patterns overlap

You can test the resolution of your eye lens by viewing a piece of paper with two brightly lighted pinholes. As you back away from the paper, at some distance you will no longer see points of light but a single one. Generally, the light coming from two point sources can be resolved if the angle between the objects is greater than 1.22 times the ratio of the wavelength of the light to the diameter of the eye aperture. Using a pupil diameter of 5 mm and a wavelength of 500 nm gives an angular resolution of 1.22 × 10^–4 rad or 0.007°. The limit of resolution can be obtained by multiplying the angular resolution (in rad) times the viewing distance. At a distance of 10 km, this suggests that we can resolve two objects that are about 1.22 m apart, so we should just be able to distinguish the two headlights of an oncoming car. At a typical reading distance of 25 cm, the limit of resolution is about 0.03 mm or about the diameter of a human hair.

Georges Seurat and other Pointillist painters depend upon the limits of resolution of the viewers’ eyes to blend dots of different colors together into a single color (see Fig. 5.23). The viewer can easily see the individual dots up close, but these blend into a single color as he or she moves away. How close should the dots be in order to blend together at a viewing distance of one meter? Of two meters? (Do you think Seurat calculated this or did he learn it by experiment?).

Fig. 5.23

In A Sunday Afternoon on the Island of La Grande Jatte, Seurat applied small strokes or dots of color so that, due to limits of resolution, from a distance they blend together (Georges Seurat [Public domain], via Wikimedia Commons)

The face of a television tube is covered with small dots or rectangles of red, blue, and green phosphors. How close must these dots be spaced in order for the colors to blend at a viewing distance of one meter?

The Great Wall of China was the greatest engineering feat of the pre-industrial age. It remains the longest and most massive structure ever built. There are a number of legends about the wall. One is that it is the only man-made structure that can be seen from the Moon. It is easy to show, however, that from the Moon the human eye cannot resolve the ramparts of the wall, even at their widest separation. Since the distance from Earth to the Moon is about 3 × 10⁸ m, the minimum angle needed to resolve the 7-m wide wall is about 1.8 × 10^–8 rad. The resolving power of the human eye is about 3 × 10^–4 rad, or about 10,000 times too large. In fact, NASA scientists have confirmed that the astronauts on the Moon did not see the Great Wall. The only man-made feature on Earth that is visible from the Moon is air pollution.

5.9 Multiple Slits and Gratings

What happens to patterns such as that shown in Fig. 5.20 when more slits are added? Provided that a, d, and λ remain the same, the number and spacing of the bright lines stays the same; the only thing that happens is that they get narrower and considerably brighter as light from more slits constructively interferes. Diffraction gratings, having many equally spaced slits, are very useful devices. They can break up light into its spectrum of colors in much the same manner as a prism, only better.

The relationship connecting d, λ, and L for a diffraction grating is the same as for a double slit, namely D/L = λ/d. For a diffraction grating, d is equal to the reciprocal of the number of slits per centimeter, n: d = 1/n.

▲ Example

A diffraction grating has 1.0 × 10⁴ slits per centimeter. What is the distance between two slits?

Solution

Since d is equal to the reciprocal of the number of slits per centimeter,

$$ d = (1\,{\text{cm}}) /\left( {1/10^{4} } \right) = 1.0\, \times \,10^{ - 4} {\kern 1pt} {\text{cm}} = 1.0\, \times \,10^{ - 6} {\kern 1pt} {\text{m}}. $$

▲ Example

Determine the distance from the center of the interference pattern to the first bright line on a screen 2.5 m from the diffraction grating when red light (λ = 633 nm) is used to illuminate the grating. Use the distance between two slits found in the previous example.

Solution

Substituting the given data into Eq. (5.1) and solving for D,

$$ D = (2.5\,{\text{m}})\left( {6.33\, \times \,10^{ - 7} {\text{m}}} \right) /\left( {1.0\, \times \,10^{ - 6} {\text{m}}} \right) = 1.58\,{\text{m}}. $$

An observant student viewing a spectrum through a diffraction grating will notice that the colors are reversed from the way they appear in the spectrum produced by a prism. Blue light is refracted more than red light, so it is bent through a greater angle by the prism. On the other hand, the angle of deviation by a diffraction grating depends upon λ/d, so red light (which has the greater wavelength λ) is bent through a greater angle.

In addition to transmission gratings, there are also reflection gratings, which are essentially mirrors with tiny parallel lines or grooves. A very nice example of a reflection grating is a compact disc (CD), whose playing surface has concentric circles of pits spaced 1.6 μm (1.6 × 10^–6 m) apart (see Chap. 13). White light reflected from the surface of a CD shows a brilliant spectrum of colors, as shown in Fig. 5.24.

Fig. 5.24

Light from a candle flame is broken into a dazzling array of spectral colors by the circles of pits on a CD (Stephanie Fitzpatrick—American Association of Physics Teachers High School Photo Contest)

5.10 Using Diffraction Gratings to Produce 3D Effects

Chromostereoscopy is the name given to the process that produces a stereoscopic effect using high-tech holographic diffraction gratings. The gratings, which may be found in commercially available “ChromaDepth^® glasses,” purposely exaggerate dispersion. They give the illusion of colors taking up different positions in space, with red being in front and blue being behind. The gratings are specially designed so that 75% or more of the light is diffracted into the first order on one side only. Thus, the grating behaves like a prism with very high dispersion, except that red is dispersed far more than blue. The grating over the left eye diffracts to the right, and that over the right eye to the left, so that a red dot appears to be raised above the page because of the effects of stereoscopic vision. A blue dot is raised much less.

A rather detailed analysis of these gratings is given by Sicking et al. The grating is made up of small steps spaced 30 μm apart that are etched onto the grating. The result is a grating with about ten times the dispersion of a glass prism.

5.11 Photonic Crystals

Photonic crystals are sub-wavelength structures that can be periodic in one, two, or three dimensions. Constructed from semi-transparent materials, the index of refraction of photonic crystals varies periodically. Two types of photonic arrangements are shown in Fig. 5.25. A photonic crystal’s periodicity results in what are known as band gaps that prevent the propagation of light within a certain range of wavelengths. Light that is not allowed to pass through a photonic crystal is reflected. In many ways, photonic crystals are the optical counterpart to electrical semiconductors. With semiconductors, the flow of electric charge is controlled; in the case of photonic crystals, it’s the propagation of light that’s manipulated.

Fig. 5.25

Two examples of photonic crystal structure: a an array of sub-microscopic holes in a semi-transparent substrate. b “Woodpile” stacks of dielectric material (Public domain via Wikimedia Commons)

There are numerous examples of naturally occurring photonic crystals. Fashioned from organic materials, they are often responsible for the iridescence and opalescence observed in minerals, flora, and fauna. Prime examples include the photonic structures that produce the brilliance of some gemstones, a notable one being opal.

In opal, an ordered arrangement of silica (SiO₂) spheres results in a periodic variation in refractive index (Fig. 5.26). At each change in refractive index, light is partially reflected and partially transmitted. The light reflected at these discontinuities may result in either constructive or destructive interference depending on wavelength as well as the spacing between spheres. If the reflected light waves combine constructively, the light will be completely reflected and no light will be transmitted.

Fig. 5.26

An opal’s brilliance is due to light interacting with an ordered arrangement of silica spheres (TinaImages/Shutterstock.com)

In the animal kingdom perhaps no creature is more beautiful that the morpho butterfly. The morpho’s brilliant coloration, as seen in Fig. 1.5, is due to small photonic structures residing on the scales that cover the insect’s wings. On the surface of each scale is a Christmas tree-shaped structure whose “branches” are perpendicular to the scale. These sub-microscopic photonic structures are spaced at 220-nm intervals, a spacing conducive to reinforcing 440-nm blue light. When viewed from above, the color of the morpho’s wing lies in the blue–green region of the spectrum. As the viewing angle increases, the iridescence shifts toward the violet, ultimately reaching the ultraviolet at a grazing viewing angle. Since the eye is not sensitive to ultraviolet light, all that is seen is the drab brown of the pigment melanin.

Photonic crystals are also the source of the spectacular colors found in the “eye” of the feathers of the male peacock, as shown in Fig. 5.27. The coloration is due to repetitive, two-dimensional structures consisting of air holes in an array of melanin cylinders that cover the feathers.

Fig. 5.27

The bright colors exhibited by the “eye” of a peacock feather are produced by tiny, intricate two-dimensional crystal-like structures (iPhoto-Thailand/Shutterstock.com)

Potential applications of photonic crystals seem to be unlimited. Indications are that they may one day be key components in solar cells, sensing devices, high-speed communication systems, fiber lasers, optical computer chips, and flat displays.

5.12 Summary

Waves from two identical sources produce maxima and minima due to constructive and destructive interference. Light waves from two narrow slits illuminated by the same source produce alternating bright and dark bands on a screen whose spacing depends on the ratio of the wavelength to the spacing of the two slits. Thin transparent films, such as soap bubbles or oil on water, show patterns of color due to interference between light reflected at the upper and lower surfaces of the film. Newton’s rings are an interference pattern formed by a spherical and flat glass surface. Michelson’s interferometer splits a light beam with a half-silvered mirror; the two beams travel different paths and interfere when they recombine. Lenses in optical instruments are often coated with a λ/4 layer to cancel surface reflections by means of interference.

Diffraction, which leads to a spreading out of waves, occurs when light encounters an obstacle or passes through a slit. When light passes through two or more narrow slits, both interference and diffraction effects can often be observed. Diffraction limits the resolution of circular apertures (including our eyes), a phenomenon applied to art by the Pointillist painters.

Photonic crystals are sub-wavelength structures that have the ability to control light in much the same way that semiconductors control electricity. Many examples of photonic crystals can be found in nature. Potential applications of photonic crystals include use in sensing devices, solar cells, high-speed communication systems, fiber lasers, and optical computer chips.

◆ Review Questions

• 1. What is the difference between interference and diffraction?

• 2. What role does diffraction play in the formation of a two-slit interference pattern?

• 3. Describe what happens to a two-slit interference pattern as the slits are brought closer together.

• 4. Describe what happens to a two-slit interference pattern as the slits are made narrower.

• 5. Describe a two-slit interference pattern made with white light. What color is the central bright fringe? Explain.

• 6. Why don’t we see interference patterns in a room when we turn on two lights of the same color?

• 7. Radio waves and light waves are both electromagnetic. Why do radio and television signals bend around buildings but light does not?

• 8. A thin film strongly reflects blue light. Should it be made thicker or thinner to reflect red light?

• 9. What are Newton’s rings and how are they produced? Draw a diagram to explain.

• 10. Why does a pinhole image get fuzzier when the pinhole gets smaller?

• 11. Why is a telescope of large diameter said to have a greater resolving power?

• 12. Explain why a very thin soap film can appear black even when it is illuminated.

• 13. What causes the spectrum of colors seen in gasoline spilled on a wet street?

▼ Questions for Thought and Discussion

• 1. If increasing the size of a lens increases its resolving power, why do photographers “stop down” a camera lens to get a sharper picture?

• 2. How does the limit of resolution of the human eye depend on the brightness of lighting in a room?

• 3. How does the diffraction pattern from a diffraction grating having many evenly spaced slits differ from that of a double slit?

• 4. CDs are read with red laser light. By using blue light to read DVDs, the storage capacity is increased. Can you explain why?

• 5. How does the wavelength of light compare with the size of a human hair? Of an atom?

• 6. Light of a single wavelength light falls on a diffraction grating. What happens to the interference pattern if the same light falls on a grating that has more lines per centimeter? What happens to the interference pattern if a longer-wavelength light falls on the same grating? Explain how these two effects are consistent in terms of the relationship of wavelength to the distance between slits.

■ Exercises

• 1. What is the thinnest film that will strongly reflect light having a wavelength of 500 nm in the film?

• 2. Make a sketch of Newton’s rings resulting from white light showing the arrangement of the colors.

• 3. If the speed of sound is 343 m/s, what is the wavelength of a sound having a frequency of 262 Hz (middle C)? Will it be diffracted appreciably in passing through a doorway?

• 4. Draw a sketch of a Michelson interferometer. Discuss its operation.

• 5. White light illuminates two slits spaced 0.2 mm apart. How far from the center will the first red diffraction line occur on a screen 50 cm from the slit? How far from the center will the first blue line occur?

• 6. Blue light of wavelength 4.8 × 10⁻⁷ m passes through a single slit and falls on a screen 1.2 m away. What is the width of the slit if the center of the first dark band is 5.0 × 10⁻³ m away from the center of the bright central band?

• 7. A diffraction grating has 1000 lines/cm. How far from the center will the first red line appear on a screen that is 70 cm away?

● Experiments for Home, Laboratory, and Classroom Demonstration

Home and Classroom Demonstration

• 1. Thin film interference with soap bubbles. White light reflecting off the front and back surfaces of a soap film can produce beautiful bands of color by interference. A suitable soap solution can be made by mixing one part dishwashing detergent with 15 parts water. Mix in a pan large enough to accept a frame approximately eight inches wide, which can be made from a coat hanger. Bend the hanger into either a circular or square shape. After dipping the frame into the solution, view the soap film with white light shining on the film from behind. Do you see bands of color? What colors do you see in each band? Do the bands repeat? How does the thickness of each band of color compare as you observe them from the top to the bottom of the frame? After the soap solution has moved downward, note that the top of the soap film has become black. Why does this occur?

• 2. “Floaters” in the eye. The fluid inside the eye contains blood cells and cellular debris shed from the lining of the eye. These cells, often referred to as floaters, manifest themselves as little visible spheres and chains that seem to move around randomly inside the eye. What we see are actually diffraction patterns that are projected on the receptor-rich fovea. Floaters may be observed by looking at a bright light through squinting eyes. Looking at a light through a pinhole in a card also works well. Perhaps the best way to see floaters is just to relax and wait for them to appear. The number of floaters seems to increase with age.

• 3. Two-slit interference. Place two razor blades or blades from a utility knife side by side with their cutting edges aligned. Using the blades, cut parallel slits in an overexposed 35-mm slide or a soot-covered microscope slide. The slits should be 1–1.5 cm long. With one eye, look at a light source through the slits (a showcase bulb with a vertical filament works best). Do you see colored fringes? Slowly rotate the slits around an axis between the slits to change the effective distance between the slits and note the effect on the interference pattern. Place a colored filter over the bulb and observe the resulting interference pattern. How is this pattern different from the white light pattern?

• 4. Finger slit diffraction. View a vertical filament (showcase) light bulb through the opening between your index and middle fingers. As you bring your fingers together, you should note that the light spreads out and bright and dark fringes appear. Look closely as you squeeze your fingers together, reducing the width of the slit.

• 5. Gift wrap interference filters. Colorful transparent gift wrap often consists of a sheet of plastic coated with a thin transparent film. Examine a sample of this material. You should observe faint interference colors running along the length of the plastic. Hold the sheet in front of a white light source and note the color of the light transmitted through a certain region. Observe this same region by reflected light. How are the colors of the reflected light and transmitted light related? Why? Repeat this procedure for another region on the sheet.

• 6. Resolution of the eye. Make two small holes about 5 mm apart in a sheet of paper (10–20 mm apart for classroom demonstration) and place a light source behind the card. View the holes up close and gradually move away until the images of the two holes merge into one. This is the limit of resolution of your eye. The angle (in rad) is approximately equal to the distance between the holes divided by the viewing distance; to convert this to degrees, multiply by 57.3 (180/π). The angular resolution of the eye depends upon pupil size (hence, upon light level in the room), but it should be in the neighborhood of 0.01°.

• 7. Photography through diffraction gratings. Photograph different scenes through a diffraction grating. Mercury vapor lamps and gas-filled advertising signs are particularly interesting.

• 8. Diffraction from a compact disc. Place a CD on a flat surface with the shiny side facing up. Hold a penlight or white LED directly over the center hole of the CD (2–3 cm above it) so that the reflected image of the light is at the center hole. Note that a circular spectrum similar to the one in Fig. 5.24 is produced. Adjust the distance between the light source and the disc until the red ring is at the edge of the disc. What colors, in addition to red, do you see? Are these colors the same as the ones seen in Fig. 5.24? Explain your observations.

• 9. ChromaDepth® glasses. Draw and color a picture using colored markers. View your picture through the diffraction spectacles and note the 3D effect (see Sect. 5.10).

Laboratory (See Appendix J)

• 5.1 Diffraction and Interference of Water Waves (Ripple Tank)

• 5.2 Diffraction Grating

• 5.3 Diffraction from Tracks of a Compact Disc

• 5.4 Michelson Interferometer

Glossary of Terms

diffraction

The spreading of waves when they pass through an opening or around a barrier.

interference

The superposition of two identical waves to create maxima and minima.

Michelson interferometer

An instrument that splits a light beam with a half-silvered mirror and creates an interference pattern between the two beams when they recombine after traveling two different paths.

Newton’s rings

An interference pattern of concentric circles formed by multiple reflections between a flat glass surface and a convex surface.

photonic crystal

Three-dimensional, periodic , sub-wavelength structure fashioned from semi-transparent material.

Pointillism

A technique used by painters to create colors by partitive (additive) mixing of small dots of paint.

resolution, limit of

The ability to separate the images of two objects that are very close to each other. The images can no longer be resolved when their diffraction patterns overlap.