A Scalable Parallel Framework for Multicellular Communication in Bacterial Quorum Sensing

Abstract

Certain species of bacteria are capable of communicating through a mechanism called Quorum Sensing (QS) wherein they release and sense signaling molecules, called autoinducers, to and from the environment. Despite stochastic fluctuations, bacteria gradually achieve coordinated gene expression through QS, which in turn, help them better adapt to environmental adversities. Existing sequential approaches for modeling information exchange via QS for large cell populations are time and computational resource intensive, because the advancement in simulation time becomes significantly slower with the increase in molecular concentration. This paper presents a scalable parallel framework for modeling multicellular communication. Simulations show that our framework accurately models the molecular concentration dynamics of QS system, yielding better speed-up and CPU utilization than the existing sequential model that uses the exact Gillespie algorithm. We also discuss how our framework accommodates evolving population due to cell birth, death and heterogeneity due to noise. Furthermore, we analyze the performance of our framework vis-á-vis the effects of its data sampling interval and Gillespie computation time. Finally, we validate the scalability of the proposed framework by modeling population size up to 2000 bacterial cells.

S. Roy and M. A. Islam—Primary co-authors.

1 Introduction

Large population of bacteria communicate with one another by releasing signaling molecules, called autoinducers, into the environment. Bacteria are also capable of sensing the environmental autoinducer concentration and regulating the expression of certain specific genes in a coordinated manner. This mechanism of communication and mutual regulation is called Quorum Sensing (QS) [1]. Communication via QS has been observed in a wide range of bacteria species, such as marine bacteria (like Vibrio fischeri) and pathogenic bacteria [2, 3].

Since each cell responds uniquely to its environment, any cellular regulation and signaling is prone to stochastic fluctuation. There have been attempts to study how population of bacteria achieve coordinated gene expression, despite such noise [4]. Sequential stochastic modeling of QS considers all reactions within the system, one reaction at a time. This makes modeling of large population of cells significantly more expensive, with respect to time and computational resources [2]. Thus, several works on parallel implementation of stochastic simulation of biological system have been proposed (though all of them do not pertain to QS alone). For example, a parallel software framework, using discrete agent-based simulation, has been proposed in [5]. It models the behavior of large cell population and updates molecular concentration using coupled Partial Differential Equations (PDE). A coarse-grained parallel approach is implemented in [6], to perform independent stochastic simulation. In [7], a C++ based stochastic and multi-scale simulation toolkit is proposed for chemically reacting system. The performance of Gillespie Stochastic Simulation is accelerated in [8] using Graphics Processing Units (GPUs). A parallel algorithm for off-lattice individual-based models of multicellular populations is presented in [9]. Gillespie’s First Reaction is applied in [10] to present a stochastic simulation software framework for biochemical reaction networks. A graph-based model for parallel, distributed and portable applications is introduced in [11], and finally, a parallel algorithm is designed in [12], focusing on simulation of reaction-diffusion based system.

Let us consider an example of bacterial growth in rich media, where inter-cellular communication may be assumed to be negligible. Such a system can be implemented in parallel due to absence of significant dependency among the cells. However, in case of QS, cellular interaction via autoinducers plays a pivotal role in the coordinated behavior of the system. An ideal parallel QS framework must therefore incorporate, both, modeling accuracy of molecular (especially autoinducer) concentration, as well as efficiency in terms of time and resource utilization. Among the aforementioned literature, only [12] takes cellular interaction via environment into consideration. However, even that work neither discusses the inevitable trade-off between the parallelism and accuracy, nor the capability of accurately modeling population dynamics due to cell birth and death.

Contribution: In this paper we take the first step towards developing a scalable parallel framework for modeling biochemical network that meets both the requirements of accuracy and speed-up. We apply this framework to model QS in bacteria, where each cell is a process that exchanges messages with the master (or coordinator) process. It incorporates a simple approximation to maintain the uniformity of the environmental parameters. An initial version of this framework is discussed in [13]. Our simulation experiments show that this framework captures the dynamics of molecular concentration as accurately as the standard sequential QS model [2]. We analyze our system in light of how sampling interval affects the overall accuracy and variation of computation overhead due to varying concentration of molecules. We also discuss how this framework handles evolution due to cell birth and death. We show that our framework exhibits higher speed-up and more balanced CPU usage when compared to sequential model. Furthermore, we incorporate cellular heterogeneity and phenotypic variability by sampling the QS system parameters from Gaussian distribution. It is noteworthy that existing literature on QS [2, 14] has modeled up to a population of 240 cells, whereas our proposed framework has been used to simulate a population of 2000 cells. Scalability experiments are performed on 50 cores of Forge high performance computing clusters built on Rocks 6.1.1, while other experiments are performed in Ubuntu 14.04 system with 8 CPUs.

This paper is organized as follows. Section 2 presents an overview of the overall QS system. Section 3 discusses the details of the Gillespie algorithm, sequential model and the parallel QS framework. Section 4 compares the experimental results. Finally, Sect. 5 closes the paper with concluding remarks.

2 System Overview

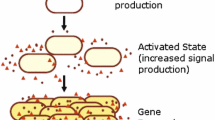
Our Quorum Sensing (QS) system consists of a population of cells and their shared environment, defined as the concentration of autoinducers outside the cells (external autoinducer). Figure 1 shows a population of cells and LuxI/LuxR regulatory network within bacterium Vibrio fischeri [3].

Fig. 1.

Population of cells and macro view of each cell with the LuxI/LuxR regulatory network

In a QS system, bacteria communicate with each other through autoinducers (AHL), produced due to the synthesis of protein LuxI. These molecules are small in size and can diffuse freely through cell membrane into the environment and from the environment back into cell. The diffusion process changes the concentration of environment, which in turn, affects the whole population. The overall system remains coupled through this diffusion process. Within a cell, the LuxR protein binds with AHL to form the monomer (LuxR.AHL). Then, through dimerization, this monomer forms $\text {(LuxR.AHL)}_{2}$, repressing transcription of luxI gene. Diffusion rate of intra-cellular autoinducer AHL depends on the concentration of AHL itself, and extra-cellular autoinducer $(\text {AHL}_\text {ext})$. The chemical reactions and corresponding rate constants are taken from [3].

Below, we have provided a list of the chemical reactions (in accordance with the reduced QS model discussed in [3]). The propensity of the LuxI expression reaction is shown in Eq. 1 and the rate constant parameters for the reactions are listed in Table 1.

Table 1. List of constant parameters [3] used in our framework

$$\begin{aligned} f(x_3,t) \overset{\mathrm {\Delta }}{=} tt_{LuxI}\Big (\frac{k_{dlux} + {{\alpha }_i}x_3}{k_{dlux} + {\alpha }_i}\Big ) \end{aligned}$$

(1)

3 Sequential and Parallel QS Frameworks

In this section we discuss the details of the sequential model for QS and the proposed parallel framework.

3.1 System Variables

Let us consider a system with $\chi$ reactions. We define the reactions set $\varGamma = \{ \gamma _i \ | i \in \mathbb {N}, i \le \chi \}$, set of reaction rate constants $K = \{ k_i | i \in \mathbb {N}, i \le \chi \}$, and the concentration of $j^{th}$ reactant in reaction $\gamma _i$ as $\omega _i^j$. We consider a molecular concentration matrix $M_{n \times m}$, where n and m are the number of cells and molecule species in the QS system, respectively. Thus, $M_i$ denotes molecular concentration vector of the $i^{th}$ cell. Thus, $M_{i,5}$ stores the $AHL_{ext}$ concentration for $i^{th}$ cell. Since $AHL_{ext}$ is a global system variable, $M_{i,5}$ remains same for all cells.

3.2 Gillespie Algorithm

The Gillespie Algorithm, also called Stochastic Simulation Algorithm (SSA), is a procedure for simulating changes in the molecular concentration of chemical species in a chemically reacting system. Hence the behavior of each cell and the advancement of simulation time within the QS system is determined by executing the Gillespie algorithm. The Gillespie algorithm (shown below) calculates propensity (likelihood) $a_i$ of reaction $\gamma _i$, and the total propensity A as follows:

$$\begin{aligned} a_i = k_i \times \prod _{j = 1}^{|\omega _i|} \omega _i^j \end{aligned}$$

(2)

$$\begin{aligned} A = \sum _{i \in \varGamma } a_i \end{aligned}$$

(3)

In each step, the Gillespie algorithm takes four input parameters: the set of reaction rules $(R_r)$, reaction rate constant $(R_c)$, initial simulation time t and molecular concentration matrix M. The Gillespie algorithm probabilistically chooses a single reaction $(\gamma _j)$, based on the individual reaction propensities. Finally, Gillespie updates the reactant concentration of $\gamma _j$ according to its stoichiometric coefficients.

3.3 Sequential Model

In the sequential QS model, each cell contains one copy of the regulatory network (as shown in Fig. 1). All the reactions in the entire population, including diffusion reaction between cell and environment, is considered as a single global system. As shown in Line 4 of sequential algorithm, the Gillespie algorithm is invoked in a loop, until the current time t exceeds the total simulation time T. Note that the sequential QS, when used in conjunction with the exact Gillespie algorithm, yields accurate result. Therefore, we implement the sequential model as a benchmark of accuracy for our proposed parallel QS framework.

Fig. 2.

Overview of steps in the parallel QS framework

3.4 Parallel Framework

The parallel QS framework is implemented using the Multiprocessing library of Python [15]. Here we discuss the different aspect of the parallel framework.

Steps in Parallel Framework: As shown in Fig. 2, the virtual master process takes 3 inputs: reaction rules ($R_r$), environment and constant ($R_c$). (1) The master spawns several parallel processes. Here, each cell is modeled as a memoryless process, termed cell process. In a large scale system several cell processes are assigned to a single core. (2) In each time intervals, master sends molecular concentration and environment information to each cell process and invokes Gillespie Algorithm. (3) Each cell process runs the Gillespie algorithm locally and (4) returns the updated molecular concentration to the master. Following this, the master node (5) updates environment variable, (6) population dynamics and (7) global time, before returning to first step. This cycle continues until simulation duration is reached.

Master Process: The master process reads and sends sampling interval $\varPsi$, $R_r$, $R_c$ and $M_i$ to all the cell processes, at each time instance t. Sampling interval ($\varPsi$) is defined as the time interval between which the master process collects concentration data from all the cell processes. After each $\varPsi$ interval, the master receives the updated $M_i$ from each $Z_i$. It is noteworthy that in the sequential approach, a single reaction takes place at a time. Consequently, any change to $AHL_{ext}$ is instantly reflected to $M_{i,5}$ (for all i). However, in the parallel approach, each cell process $Z_i$ autonomously invokes Gillespie and updates $M_{i,5}$. Thus, we ensure uniformity of $AHL_{ext}$ in the system using Eq. 4.

Cell Processes: Each cell process $Z_i$ invokes the Gillespie algorithm and returns updated $M_i$ to the master. Let us discuss two key aspects of the ParallelQS algorithm.

Time Synchronization: In each time instance, the master must wait till it has heard from all cell processes ($Z_i$s). Following this, it increments the overall system time t by sampling interval $\varPsi$.

Time Increment: Gillespie calculates the increment in simulation time t as $ln(1/r_1)/A$, where $r_1$ is random number between 0 and 1. Thus, there exists an inverse relationship between time variable t and overall propensity A (i.e., $t \propto \frac{1}{A}$). Note that the sequential model calculates A (Eqs. 2 and 3) based on all reactions in the system, whereas each $Z_i$ in the parallel framework calculates $A_i$ only based on the reactions specific to itself, implying that $A_i \ll A$. Hence, the time increment for the parallel framework is expected to be greater than that of the sequential approach.

Adjustment of Global $AHL_{ext}$ Concentration: We assume that $AHL_{ext}$ is homogeneously distributed within the system boundary, making it a global system variable. A cell is capable of interacting with any $AHL_{ext}$ molecule. Master estimates the adjusted system AHL concentration at time $t + 1$, $AHL_{ext} (t + 1)$, by incrementing $AHL_{ext}(t)$ by the net difference of $AHL_{ext}(t)$ concentration from local cellular AHL concentrations, over all cells, using the equation below:

$$\begin{aligned} AHL_{ext}(t + 1)=AHL_{ext}(t) + \sum _{j = 2}^{n + 1}{(AHL_{ext}^{j}(t + 1) - AHL_{ext}(t))} \end{aligned}$$

(4)

Here $AHL_{ext}^{j}(t + 1)$ is the local AHL concentration of the $j^{th}$ cell process at time $t + 1$.

Adjustment of Molecular Concentration Due to Population Dynamics. The proposed framework is capable of modeling dynamic population (i.e. cellular birth and death). Each cell $Z_i$ undergoes division once simulation time t exceeds its division time $\beta _i$. For each $Z_i$, we sample $\beta _i$ from exponential distribution with $\mu = 45$ min. Each cell division causes the mother cell to split into two daughter cells, each containing half the molecular concentration of mother cell. Given initial volume of all cells $V_{cell}$, each $Z_i$ has a time-dependent volume, given by –

(5)

Initial volume of a daughter cell is half the volume of its mother cell. The propensity of each reaction is also updated to account for time-dependent volume. In our QS system, cell density is kept constant by compensating each cell division by death of randomly picked cell (as discussed in [2]).

4 Results

We consider 6 molecule species in our reduced QS system – (A) LuxI, (B) LuxR, (C) $\text {(LuxR.AHL)}_{2}$, (D) AHL (E) LuxR.AHL and (F) $\text {AHL}_\text {ext}$. Parallel framework is implemented using Python 2.7 and Python Multiprocessing library [15]. Scalability experiments are performed on 50 cores of Forge high performance cluster; for other simulation experiments, we use Ubuntu system with Linux system with 8 CPUs of 1.6 GHz each.

4.1 Accuracy

We analyze how closely the dynamics of molecular concentration (matrix M) generated by parallel QS framework aligns with that of the sequential model. On both sequential and parallel approaches, we simulate 50 cells for 200 min and sampling interval $\psi = 0.05$.

Fig. 3.

Comparison of average molecule concentration dynamics of 6 molecular species – (A) LuxI, (B) LuxR, (C) $\text {(LuxR.AHL)}_{2}$, (D) AHL (E) (LuxR.AHL) and (F) $\text {(AHL}_\text {ext}\text {)}$ for population of 50 cells.

Fig. 4.

Increase in sampling interval ($\varPsi$) increases Mean Absolute Error (MAE), but decreases running time (RT), between sequential and parallel QS framework.

Similarity of Molecular Concentration. Fig. 3 shows that the average concentration dynamics of molecules (A)–(F) (over 10 trials) are nearly identical for sequential and parallel approaches.

Effect of Sampling Interval. The choice of $\varPsi$ in the parallel framework affects the number of the data points master receives from each Z[i]. If $\varPsi$ is high, we expect our framework to exhibit inaccuracy in concentration dynamics due to lack of sufficient data. Here we consider Mean Absolute Error (MAE) as our metric of accuracy i.e. higher the MAE between two sets of plot points, greater is the dissimilarity. Since the sequential model is our benchmark, we calculate the deviation of $AHL_{ext}$ of the parallel framework $(\phi _p)$ from the sequential model $(\phi _S)$ on d data points, as $MAE(\phi _s,\phi _p) = \frac{1}{d} \times \sum _d{|M_{i,5}^{s} (d) - M_{i,5}^{p} (d)|}$.

Simulation on 50 cells for duration of 200 min shows that the MAE of $\text {AHL}_\text {ext}$ plots between the two approaches increases with the increase in $\varPsi$ (Fig. 4). We observe that a higher $\varPsi$, though enhances running time (RT) by minimizing communication overhead, degrades accuracy.

4.2 Population Dynamics

We model cellular birth and death in QS for a population size 1000 cells and duration 100 min. In Fig. 5(A), a single color represents the LuxI concentration of a bacterial cell over time, while the discontinuity and drop in the curves show cell death and division, respectively.

Fig. 5.

Population dynamics: LuxI concentration during cellular birth and death under conditions of (A) no noise and (B) noise with standard deviation 0.005.

Our proposed parallel framework is capable of modeling noise arising from stochastic fluctuation in gene expression that can cause phenotypic variability in isogenic population [16]. In Fig. 5(B), we show cellular birth and death under condition of noise generated by sampling constant parameters $R_C$ from Gaussian distribution with standard deviation 0.005. It is noteworthy that molecular concentration in Fig. 5(B), by virtue of the noise, exhibits greater phenotypic variability than the one in Fig. 5(A).

4.3 Processor Utilization

We compare the CPU utilization of the sequential and parallel frameworks on a population size of 100 cells and duration of 60 min on an 8-CPU machine.

Fig. 6.

Comparison of CPU utilization for the sequential and parallel QS frameworks

We use the psutil python library [17] to record the instantaneous CPU utilization for both frameworks. Figure 6 shows that the parallel framework exhibits a more uniform CPU utilization than the sequential approach.

4.4 Speed up

Let the execution (or wall clock) time of sequential and parallel QS algorithms be $\rho _s$ and $\rho _p$ respectively, and the simulation time for both algorithms be T. We define speedup . For sequential and parallel algorithms, we simulate a population of 10 to 50 cells for $T = 200$ min each. Given that T is same for both algorithms, we compare their real (or execution) time to analyze the speedup rendered by parallel QS framework. We generate semi-log plots for execution time for population sizes 10, 20, 30, 40 and 50. Figure 7(A) shows that our framework incurs extremely little increase in real time with growth in cell population size as compared to the sequential approach.

Fig. 7.

(A) Speed-up: Semi-log plot for speed-up for population sizes varying between 10 and 50. Parallel QS framework exhibits little growth in running time with increase in simulation time (B) Scalability: Log-log plot for scalability analysis for population sizes 25, 50, 100, 500, 1000, 2000. (Color figure online)

4.5 Scalability

Finally, we compare the sequential and parallel approaches on the basis of execution time for population sizes 25, 50, 100, 500, 1000 and 2000 cells. Figure 7 and (B) is a log-log plot showing that the parallel framework incurs significantly lower execution time. It is noteworthy that the sequential approach does not scale beyond 100 cells, thus the expected real time values for sequential approach (shown in dotted red line) is obtained through extrapolation.

5 Conclusion and Future Work

In this paper we present a scalable parallel framework for QS in bacteria. Simulation for varying population size, sampling interval and duration show that our framework models concentration dynamics almost as accurately as its sequential counterpart, while showing significant improvement in speed-up and CPU utilization. We also study the degradation in accuracy and improvement in running time of this model, with increase in sampling interval. We show that the framework incorporates cellular heterogeneity, phenotypic variability and scalability by sampling the QS system parameters from Gaussian distribution and modeling up to 2000 bacterial cells. Our future works involve the extension of the framework to accommodate spatial positioning of cells and environmental molecules to incorporate cellular heterogeneity. In the spatial model, the master process will recalculate the coordinates of the cells and environmental molecules after each sampling interval.