Enhancement of Design Methodologies of Anchored Mesh Systems Using the Discrete Element Method

Abstract

The understanding of the mechanical behavior of anchored mesh systems for slope stabilization represents a challenging task for engineers. Standard laboratory tests are in general not representative of the in-situ conditions. Moreover, the complex interaction between the mesh and the retained material is not trivial to reproduce numerically. In this study a simplified in-situ condition is analyzed using the discrete element method (DEM). Starting from the tensile stress-strain relationships acting on each wire it is possible to determine the force sustained by the mesh system and to derive the displacement field of the mesh panel. Therefore, the progressive activation of the mesh retaining capacity, during the loading of these structures can be obtained providing the evolution of the mechanical response of the system. The information obtained with the discrete element simulation highlights the possible improvements of the classical design methodologies and shows the potential of the presented approach for the comprehension of the mechanical behavior of anchored mesh systems.

1 Introduction

Anchored mesh systems (or cortical mesh) are nowadays widely used in the stabilization of shallow layers along slope and for debris control and containment. They are constituted by steel wire mesh rolls fixed to the slope face by means of steel anchors having a patterned spacing. The mesh is connected to a support cable at the top and at the toe of the slope; eventually additional support cables can be used along the slope.

Despite their broad utilization, the comprehension of the mechanical behavior of these cortical systems is limited with possible negative consequences on the adequacy of the current design methodologies. The main unknowns are related to the lack of field performance data and to the difficulties in reproducing the real serviceability conditions with laboratory tests. Indeed, the mechanical behavior of such systems strongly depends on the interaction between the mesh and the retained material as well as the specific constraint conditions.

Numerical approaches represent a good alternative to complex experimental studies, however the expected large deformations, the possibility of element ruptures as well as the high number of contacts and the soil-mesh interaction make the numerical modelling a non-trivial task. Two numerical methods have shown their effectiveness in simulating wire meshes: the finite element method (FEM) and the discrete element method (DEM). The former is limited to simple interaction problems (Cazzani et al. 2002; Castro-Fresno et al. 2008; Gentilini et al. 2013). The DEM, instead, has been recently extended to complex multi-body interaction problems (Albaba et al. 2017; Gabrieli et al. 2018).

In this study a discrete element approach is used to analyze a simplified in-situ condition of a mesh retaining system, extending a previous work (Gabrieli et al. 2018).

This paper has two main aims: (i) to underline some of the important factors that must be accounted for the proper design of these structures (ii) to show some potentials of this method in enhancing the classical design techniques.

2 Classical Design Methodologies for Anchored Mesh Systems

The design methodologies for cortical system have evolved throughout the last 50 years. Initially, they were based on engineering judgement and experience without a specific geotechnical design phase. Then, dimensioning methods, based on shallow instability failure mechanism, have been developed and are currently used in the practice. However, the effect of the simplifications introduced in these models should be deeply evaluated in the light of the new knowledge, to find a proper way to enhance the design of these mesh systems.

Different design methodologies are available in the literature; they are all based on the limit equilibrium method and do not consider the dependence of the stabilizing force on the mesh deformation. Furthermore, the soil failure mechanism is arbitrarily assumed a priori and differs according to the selected methodology (see Fig. 1). In the following three design methods, specific for soil slope, will briefly presented. For more details, the interested reader can refer to Blanco-Fernandez et al. (2011).

Fig. 1.

Three different failure mechanisms assumed by the LE approaches: (a) infinite slope (Da Costa and Sagaseta 2010), (b) block and wedge included between two rows of bolts (Castro-Fresno 2000), (c) slope divided in an upper block and a lower wedge (IberoTalud and Universidad de Cantabria 2005).

A first method (Da Costa and Sagaseta 2010) derives from the assumption of infinite slope (Fig. 1(a)); the stabilizing action of the mesh can be inserted as a stabilizing uniform pressure along the slope profile with a normal (p) and a tangential (t) component. The latter can be related to normal pressure by an interface friction coefficient between the mesh and the soil (t = p tanβ). The stabilizing pressure is therefore computed solving the equilibrium equation along the direction normal and parallel to the slope profile.

A second method (Castro-Fresno 2000) assumes a failure mechanism composed by an upper block and a lower wedge included between two rows of bolts (Fig. 1(b)). In the model, the mesh reaction is computed as a concentrated force Q with the same inclination of the bolts (i.e. the mesh reaction is equal to the force transmitted by the bolts to the slope) acting on the upper block. The value of the stabilizing force Q is given by the four equilibrium equations (two for each block) and an additional equation obtained maximizing Q as a function of the angle α of the lower wedge. This value can be therefore used for the selection of the appropriate mesh system.

An intermediate case (IberoTalud and Universidad de Cantabria 2005) between the two above reported divides the slope in an upper block and a lower wedge (Fig. 1(c)). As for the previous method, the stabilizing pressure p is computed solving the four equilibrium equations (two for each block) and maximizing p as a function of the angle α.

3 Discrete Element Modelling of Wire Meshes

The modelling of wire meshes with the discrete element method is based on the work of Nicot et al. (2001) where the impact of a rock block on a metallic structure was investigated.

In the present work the mechanical behavior of a double-twisted hexagonal wire mesh (type 8 × 10, wire diameter 2.7 mm) is analyzed. The mesh is simulated as an assembly of interconnected rigid cylindrical elements (Albaba et al. 2017; Gabrieli et al. 2017) with the open-source code YADE (Šmilauer et al. 2015). The mechanical behavior of the numerical wires (cylindrical elements) is given by user-defined stress-strain relationships in tensile direction, while compression and bending of the wire are not considered. Two different constitutive laws are used for the single and the double-twisted wires respectively; these relationships are directly derived from experimental tensile test on wires (Thoeni et al. 2013). A detailed description of the mesh as well as the model validation on experimental results can be found in the literature (Thoeni et al. 2013; Gabrieli et al. 2017).

4 Numerical Model of a Simplified In-situ Anchored Mesh System

A simplified in-situ condition is investigated. A mesh system, composed by three vertically aligned mesh panels of 2.88 × 3.00 m² each, is loaded by a cohesionless granular column (2.88 × 2 × 11 m³) until its failure. This soil column is retained by a rigid wall during the deposition phase, then the retaining wall is removed and the soil is let free to push onto the mesh. The mesh panels are anchored at their corners imposing a zero-displacement condition at the nodes belonging to square anchor plates of dimension d_p = 0.32 m; along the edges of the mesh strip symmetrical boundary conditions are imposed to account for the effect of adjacent panels. Finally, the bottom side of the mesh system is fixed to contain the soil at the slope toe.

The numerical soil is composed by approximatively 45k spherical particles with a mean diameter d₅₀ = 0.12 m. Periodic triaxial test has been used to derive the macroscopic friction angle and the stiffness of the soil.

The stress and the strain on each wire are recorded. The force sustained by the mesh panel is computed integrating the local forces acting on the constrained boundaries, both anchors and edges, while the correspondent displacements are registered, providing, as output, the evolution of the mesh mechanical response.

4.1 Mechanical Behavior of the Mesh

The mechanical behavior of the mesh is investigated in terms of force-displacement curve ($F$-$\bar{\delta }$) of the central panel; the force $F$ is computed as the two-norm of the three spatial components, while the displacement $\bar{\delta }$ is defined as the mean displacement, in the mesh out-of-plane direction (z-direction), of the middle panel surface. This panel has been chosen because it is less affected by the boundary conditions and also because it is the one which firstly reaches the failure conditions.

In Fig. 2(a) the force-displacement curve of the central mesh panel is reported with reference to the double-twisted hexagonal wire mesh. The numerical values are normalized with the value at failure of the force $F_{f}$ and the correspondent mean displacement $\bar{\delta }_{f}$. The nonlinear progressive activation of the mesh panel reaction is evident observing its $F$-$\bar{\delta }$ curve. Initially, it experiences a significant deformation up to $\bar{\delta } = \bar{\delta }_{f} /2$ with a low stabilizing reaction ($F\sim 0.2 \cdot F_{f}$): in this phase the deformations are mainly related to geometrical effects and the mesh reaction is therefore characterized by a low stiffness linked to the rearrangement of mesh cells and wires. For increasing values of deformation, the tensile proprieties of the mesh are mobilized and it starts to contribute to the containment of the instable layer. It is therefore evident that the mesh cannot be considered as an active structure and its stabilizing effect has to be correlated to the deformation level.

Fig. 2.

Mechanical behavior of the mesh panel: (a) force-displacement curves of the mesh panel and of the anchors (■), (b) effect of the friction coefficient $\beta$ on the force $F_{y}$ (solid line represents the computed $F_{y}$, dashed line represents an analytical $F_{y}^{a} = F_{z} \cdot$ tan $\beta$).

In the same figure the fraction of the total force transmitted by the mesh to the anchors is reported while the force directly pushing on its back is not considered; the force transmitted by the edges of the central panel can be easily derived from the difference between the two curves in Fig. 2(a).

The possibility to fully simulate the soil-mesh interaction allows to separately analyze the different force components. In analogy with the classical design techniques, the mesh reaction parallel to the slope profile $F_{y}$ has been measured for two different friction angles at the soil-mesh contact ($\beta$ = 15° and $\beta$ = 35°). This force is then compared in Fig. 2(b) with a back-calculated pure frictional force $F_{y}^{a} = F_{z} \cdot { \tan }\beta$ (dashed line) aiming to verify if this approximation at the soil-mesh interface, generally used in the classical design methods, is correct.

Observing the numerical results, the pure frictional assumption seems to hold for the higher value of $\beta$, whereas it significantly underestimates the interaction force $F_{y}$ for the lower value of the interface friction angle. This difference could be associated to the interlocking between mesh cells and small volumes. Indeed, they are trapped into the local “bulges” of the mesh that are usually neglected in the simplified design approaches.

4.2 Soil Deformation Mechanism

The displacement field of the instable soil layer is strongly influenced by the interaction with the retaining system. A precise definition of this mechanism requires an approach in which the coupling between the soil deformation and the correspondent stabilizing action of the mesh (i.e. activation of the retaining capacity) is accurately considered. This condition is ensured by the proposed DE approach. Moreover, it accounts for microscale effects (e.g. grain-mesh cell interlocking) and macroscopic geometrical effects (e.g. arching effect between the anchors).

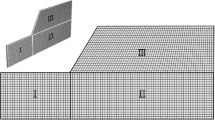
The studied configuration considers that the mesh response is activated by out-of-plane displacements. Then, a threshold value $u_{z}^{*}$ of the soil displacement is defined to characterize the failure mechanism. This value is assumed equal to $u_{z}^{*} = \bar{\delta }_{f} /2$ considering that such a displacement allows the stabilizing effect of the mesh to be activated.

In Fig. 3 the soil volumes undergoing a displacement greater than $u_{z}^{*}$ are highlighted with a different color. With reference to a section along a vertical alignment of the anchors (section A – A in Fig. 3(b)), as in classical design methodologies, a wedge-shaped volume pushing on each mesh panel is observed. This is due to the presence of the anchors which cause an arch effect partially stabilizing the instable soil behind. Instead, along a middle section between the anchors (section B – B in Fig. 3(b)) these volumes are no more separated and the mesh has to retain a single block. Therefore, the failure mechanism is more complex than a simple wedge-shaped block and the 3D effects are relevant.

Fig. 3.

Soil failure mechanism an instant prior to failure, light grey volumes identify the soil volumes having displacement $u_{z} > u_{z}^{*}$: (a) 3D view of the mesh system, (b) lateral view.

4.3 Effect of the Mesh Stiffness

An interesting aspect to be investigated with the discrete element approach is the change of the mesh stiffness and type. The insertion of superimposed external elements as, for instance, steel-wire ropes is here considered to modify the mesh panel stiffness. These elements are efficiently simulated with a DE approach, accounting for sliding and frictional effects at the rope-mesh interface as well as the possible local interlocking and the interaction with the retained material.

The same system as before is simulated introducing two diagonal ropes above each mesh panel; in analogy to the previous case the analysis has focused on the central panel. The diagonal ropes are fixed at their extremities in correspondence with the anchors. The mechanical response of the panel is reported in Fig. 4(a) where the deflection $\bar{\delta }_{f}$ represents the mean deflection experienced by the panel without ropes (as in Fig. 2). A 3D view of the mesh system an instant prior the failure is reported in Fig. 4(b).

Fig. 4.

(a) Mechanical response of the mesh panel with superimposed diagonal ropes: force sustained by the entire system (♦, DT^R+ R); extrapolated force contribution of the double-twisted mesh component only (■, DT^R). The solid black line is referred to the simple double-twisted mesh system (DT). (b) 3D view of the mesh system.

The addition of steel-wire ropes clearly improves the retaining capacity of the cortical system and reduce the mesh deflection: in the studied case the sustainable force is incremented by a factor of $\sim$2, the mean deflection at failure is reduced of $\sim 0.2$. The influence of the insertion of the diagonal ropes on the double-twisted mesh behavior can be observed isolating the contribute of the latter from the entire system mechanical response, DT^R and DT^R+ R respectively (Fig. 4(a)). It is interesting to note how the stiffness of the double-twisted mesh alone is increased inserting the steel-wire ropes with probable consequence on the soil failure mechanisms.

5 Conclusions

A discrete element study approach for flexible anchored system has been presented. Starting from a simplified in-situ condition with a common mesh type (DT hexagonal mesh) some aspects of the behavior of this system have been analyzed. Particularly, the numerical results highlight some relevant elements to be taken into consideration to improve the current design methodologies:

• the instantaneous retaining action of the mesh like in a LE approach provides a not realistic response of the mesh behavior. Indeed, the mesh shows a progressive activation of its mechanical response with the deformation (see Fig. 2(a)). The presented DE approach allows, instead, to account for the evolution of the mesh behavior permitting to associate at each sustained force (e.g. the force $F_{LEM}^{d}$ computed from a LE calculation) the correspondent deflection of the mesh panel ($\bar{\delta }_{DEM}^{d}$) as schematically reported in Fig. 2(a). This capability may be very useful to estimate the mesh deformations when particular limitations have to be met (e.g. interventions along railways).

• the failure mechanism cannot be a priori defined. Moreover, plain-strain conditions should be carefully assumed. Anyway, to the authors’ knowledge there are no evidences of a specific failure mechanism. The latter is in general more complex than what assumed in classical procedures (Fig. 1) and it is most likely influenced by the mesh mechanical behavior. Moreover, as reported in Fig. 3 plain-strain conditions are not fulfilled and significant 3D effects occur (e.g. stabilizing effect of anchor plates).

  On a first approximation, the wedge-shaped failure mechanisms considered in the classical design techniques can be conserved. In this case, due to the observed tridimensional effects, a safety coefficient is recommended to account for the amplification of the instable soil volume moving away from the anchors.

• the soil-mesh interface interaction (i.e. mesh reaction parallel to the slope) is relevant in this kind of models and must be carefully considered. The schematization with a constant friction coefficient (tanβ) seems to be not appropriate, at least, for low interface friction angles. Indeed, the numerical results show that the mesh reaction parallel to the slope ($F_{y}$) could be greater than the pure frictional force ($F_{z}\,\cdot\,tan\beta$, dashed lines in Fig. 2(b)); this difference may be related to other effects as the interlocking between the soil particles and/or the existence of bulged zones of the mesh above the anchors where small soil volumes may get stuck.

• The use of a different mesh type with a different stiffness (like with insertion of external ropes) changes the response of the systems in terms of force-displacement curve and may varies also the failure mechanism. For this reason, the normal pressure along the slope, currently used in the LEM to model the mesh type, should not be used as a mere “input” parameter but must be integrated in a more detailed calibration method.

Besides the analyzed aspects, the observation of real applications highlights that the exerted pressure localizes around the anchor plates and can be influenced by the soil deformation.

The numerical results obtained with the proposed approach have underlined some limitations of the classical design methodologies. In particular, the assumption of an initial “active” behavior seems to be the most inadequate. A realistic design approach should be displacement-based duly taking account for the incremental activation of the mesh stabilizing action. The proposed approach, in this perspective, represents a fundamental tool permitting, through an incremental procedure, to characterize the mechanical behavior of the mesh system evaluating the strong coupling between the mesh response and the evolution of the soil failure mechanisms.