Keywords

1 Introduction

1.1 Background

Terrestrial wireless networks have evolved into the Internet of Things (IoTs) paradigm, in which different terrestrial wireless networks will be integrated and millions of objects will be connected. In addition, satellite networks support more connections from the space, which cannot be solely supported by terrestrial wireless networks. Terrestrial wireless networks and satellite networks will be integrated into space information networks to provide ubiquitous coverage, massive connectivity, and enhanced capacity. Though satellite-terrestrial networks offer many advantages over terrestrial wireless networks, the topology and radio environment are much more complicated with high dynamics, making the efficient resource allocation extremely difficult. Furthermore, dynamic resource scheduling and efficient cooperative transmission are critical problems for space information networks, particularly, the sparse representation and fusion processing of massive data obtained by multiple platforms with heterogeneous sensors [1]. In the past decades, cognitive radio has been introduced as a new paradigm for enabling much higher spectrum utilization efficiency, providing more reliable and personal radio services, reducing harmful interference, and facilitating the interoperability or convergence of different wireless communication networks such as various satellite and terrestrial communication networks. Cognitive radios are goal-oriented, autonomously learn from experience and adapt to changing operating conditions [17, 18]. Cognitive radios have the potential to drive the next generation of radio devices and wireless communication system design and to enable a variety of niche applications in demanding environments such as dynamic spectrum access and sharing for unmanned aircraft systems [16] and integrated space and terrestrial networks.

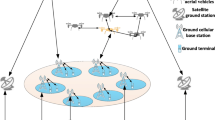
Along with the rapid increase of wireless communication applications, available radio spectrum becomes a limiting factor mainly due to fairly low utilization and out-of-date regulations. By sensing spectrum holes, secondary users (SUs) can make use of them to realize the communication without generating harmful interference to primary users (PUs). Cognitive radio technology has changed the traditional fixed allocation mode of spectrum resources, thus improving the spectrum utilization efficiency. Spectrum sensing, as the key step of cognitive radio, is the basis of dynamic spectrum access and sharing for the integrated space and terrestrial networks. In the context of evolution towards the fifth-generation mobile communications (5G) which cover spectrum from sub-6 GHz up to 100 GHz, wireless communication employs even broader channel bandwidth at even higher frequency band than ever before, which also results in higher requirements on both hardware and software. The wider frequency band SUs can sense at a time with less scanning time, the more chance to find and use the spectrum holes to realize the communication tasks. As showed in Fig. 1, to achieve the above aim, SUs need a wideband antenna, a wideband radio frequency (RF) front-end, and a high speed analog-to-digital converter (ADC), and a powerful signal processor as well.

Fig. 1.
figure 1

Traditional spectrum sensing

Full size image

The wideband antenna and the wideband filter were well developed [2]. By contrast, the most challenge module is the high-speed ADC. According to the Nyquist-Shannon sampling theorem, the sampling frequency must be at least twice the highest frequency of the signal. In the context of evolution towards high-speed and broadband, wireless communication works at a frequency from several hundred MHz to dozens of GHz, that means a high demand for the sampling rate of ADC, usually more than several GHz. So far the achievable sampling rate of the state-of-the-art ADC is only 6.4 GSPS [3]. And usually the higher sampling rate of ADC, the greater power it will consume. For spectrum sensing conducted by SUs, the most important thing which we care most is simply to find the available spectrum holes. For SUs, it is not necessary to take care of the detail of the spectrum resources which are utilized but the spectrum holes. Data we acquired through the Nyquist-Shannon sampling usually contains massive redundancies we do not need or do not care about. “Why go to so much effort to acquire all the data when most of what we get will be thrown away? Can not we just directly measure the part that will not end up being thrown away?” Donoho asked this question in his paper [4].

1.2 Related Work

Donoho, Candès and Tao proved that sparse signal may be reconstructed with even fewer samples than the Nyquist-Shannon sampling theorem requires which is the basis of compressed sensing (CS) [4, 5]. CS offers a joint compression- and sensing-processes, based on the existence of a sparse representation of the treated signal and a set of projected measurements [6]. Tian and Giannakis introduced CS into spectrum sensing field firstly [7]. And Polo and others proposed a hardware structure called analog-to-information converter (AIC) to replace the ADC in spectrum sensing [8]. Compressed spectrum sensing has become matured gradually. However, in the compressed measurement (low-speed sampling) process of the existing general compressed spectrum sensing algorithms, the compression ratio is set to a fixed value, which limits their adaptability to the radio environment with different sparseness.

Radio Environment Map (REM) has been introduced as a vehicle of network support to cognitive radios, which is basically an integrated database that provides multi-domain environmental information and prior knowledge for cognitive radios, such as the geographical features, available services and networks, spectral regulations, locations and activities of neighboring radios, policies of the users and/or service providers, and past experience [10, 13]. The REM can be exploited by the cognitive engine for most cognitive functionalities, such as situation awareness, reasoning, learning, planning, and decision support. In recent years, REM has been viewed as “enabler for practical cognitive radio networks” [19]. As an example, REM has been developed for the cognitive wireless regional area networks (IEEE 802.22), especially from the perspective of interference management and radio resource management [14]. REM has also been exploited to compensate the dynamically changing Doppler spread for high-speed railway broadband mobile communications [15]. Coordinated resource allocation based on REM was proposed to support satellite-terrestrial coexistence [12].

1.3 Contribution

In this paper, an adaptive compressed spectrum sensing algorithm based on REM for space information networks (REM-SIN) is proposed, which has better adaptability to the dynamically changing radio environment with different sparseness. Simulation results demonstrate that the proposed algorithm has a better adaptability to the channel environment with different sparseness than the existing general compressed spectrum sensing algorithms.

1.4 Organization

The remainder of this paper is organized as follows: In Sect. 2, we introduce compressed sensing and general compressed spectrum sensing algorithm at first. Then an adaptive compressed spectrum sensing algorithm is proposed based on REM-SIN. In Sect. 3, the adaptive algorithm is simulated with MATLAB. At last, the conclusion is drawn in Sect. 4.

2 System Model

2.1 Compressed Sensing

For a signal \( x \), if it can be expressed as \( x =\Psi s \) and many elements of N-dimensional vector \( s \) is zero or close to zero, we call \( x \) is sparse or compressible. And we call \( \Psi \) sparse projection matrix.

Using an \( M \times N \) matrix called measurement matrix \( \Phi \), we can measure the sparse signal \( x \) as shown by Eq. 1. And we can use the M-dimensional vector \( y \) to reconstruct the signal \( x \) via some reconstruction algorithm. That is the core of compressed sensing.

$$ y =\Phi x =\Phi \Psi s $$
(1)

Suppose that the maximum frequency of \( x \) is \( f_{M} \) and the time window for sensing is \( t \in \left[ {0,NT_{0} } \right] \), where \( T_{0} \) is the Nyquist-Shannon sampling interval, \( T_{0} = \frac{1}{{2f_{M} }} \). The process of converting an analog signal to a digital signal can be expressed in the discrete-time domain as shown by Eq. 2:

$$ x_{t} = Sr_{t} \, $$
(2)

where \( S \) is an \( K \times N \) projection matrix and \( r_{t} \) is a \( N \)-dimensional vector and acquired by Nyquist-Shannon sampling, \( r_{t} [n] = x(t)\left| {t = nT_{0} } \right.,n = 1, \ldots ,N \). Rows \( \left\{ {S_{k} } \right\}_{k = 1}^{K} \) of \( S \) can be viewed as a set of basis signals or matched filters [7], while the measurements \( \left\{ {x_{t} [k]} \right\}_{k = 1}^{K} \) are in essence the projection of \( x(t) \) onto the basis. If \( S \) is the identity matrix of size-N, Eq. 2 represents Nyquist-Shannon sampling. And if \( K < N \), Eq. 2 represents compressed sampling.

Compressed sensing supposes that \( x \) is sparse or compressible. So we can use the measurements \( x_{t} [k] \) and the projection matrix \( S \) to reconstruct the signal \( r_{t} \) and \( x(t) \) via solving the Eq. 3:

$$ \hat{r}_{t} = \arg \mathop {\hbox{min} }\limits_{{r_{t} \in \Re^{N} }} ||r_{t} ||_{0} ,\;{\text{subject}}\,{\text{to}}\,x_{t} = Sr_{t} $$
(3)

Equation 3 is a non-deterministic polynomial-time hard (NP-hard) problem. So we usually use an approximate Eq. 4 to replace Eq. 3 and convert the NP-hard problem to a convex optimization problem. In some sense, Eq. 4 is the ‘closest’ convex optimization problem to Eq. 3 [9]. More explicitly, when the projection matrix \( S \) satisfies the \( (2k,\delta_{2k} ) \)-Restricted Isometry Property (RIP) and \( 0 < \delta_{2k} < \sqrt 2 - 1 \), the solution to Eq. 4 is the same as the solution to Eq. 3 [20]. And the \( (k,\delta_{k} ) \)-RIP property is defined by (5) below.

$$ \hat{r}_{t} = \arg \mathop {\hbox{min} }\limits_{{r_{t} \in \Re^{N} }} ||r_{t} ||_{1} ,\;{\text{subject}}\,{\text{to}}\,x_{t} = Sr_{t} $$
(4)
$$ (1 - \delta_{k} )||x||_{2}^{2} \; \le \;||S_{T} x||_{2}^{2} \; \le \;(1 + \delta_{k} )||x||_{2}^{2} $$
(5)

Note that in (5), \( x \in \Re^{|T|} \), \( ||x||_{2}^{2} = \sum\limits_{i} {x_{i}^{2} } \), \( \delta_{k} \in (0,\;1) \), and \( k \) is a constant; \( T \subset \{ 1,2, \ldots ,N\} ,|T| \le k \); \( S_{T} \) is a submatrix of \( S \), and \( S_{T} \) is composed of columns of \( S \) as indicated by index \( T \); and \( \left| .\right| \) represents the number of elements in a set. Equation 4 is a convex optimization problem. There are many solutions, such as the basis pursuit (a kind of linear programming algorithms) [21] and orthogonal matching pursuit (a kind of greedy algorithms) [22].

2.2 General Compressed Spectrum Sensing

Since Tian and Giannakis introduced compressed sensing for wideband cognitive radios [7], scholars have made a lot of further investigations. The framework of general compressed spectrum sensing algorithms is shown in Fig. 2.

Fig. 2.
figure 2

General compressed spectrum sensing

Full size image

For spectrum sensing, SUs use antenna and radio frequency front-end to receive a wideband analog signal \( x(t) \) whose maximum frequency is \( f_{M} \) Hz. Under the guidance of the measurement matrix, we use AIC to compress the analog signal \( x(t) \) into the digital signal \( y[k] \). Even the AIC’s sampling rate is lower than \( 2f_{M} \) (Nyquist-Shannon sampling rate), we still can use \( y[k] \) to reconstruct \( x(t) \)’ digital form \( x[k] \) by related algorithms. Using the digital signal \( x[k] \), SUs can make detection decision and finish the spectrum sensing. That is the main process of general compressed spectrum sensing algorithms.

In compressed measurement (low-speed sampling) process of compressed spectrum sensing algorithms, AIC samples and transforms the analog signal \( x(t) \) into the digital signal \( y[k] \) with sampling rate which is lower than Nyquist-Shannon sampling rate and makes the signal can be reconstructed. Generally speaking, the more measurements, the more accuracy reconstructed signal has which makes the sensing result more accurate. However, more measurements needs higher sampling rate which means more data is produced.

We define the compression ratio as a parameter which controls the number of measurements. Specifically, the compression ratio is defined by

$$ \rho = k/2f_{M} $$
(6)

where k is the length of \( y[k] \) and equals to the number of rows of measurement matrix, and \( 2f_{M} \) is the Nyquist-Shannon sampling rate of \( x(t) \).

The sparser the signal is, the less measurements it needs when reconstructing the signal. For the existing compressed spectrum sensing algorithms, the compression ratio is usually set to a fixed value. Therefore, their adaptability to the channel environment with different sparseness is fairly limited.

2.3 Adaptive Compressed Spectrum Sensing

To solve the problem that the adaptability to the channel environment with different sparseness of general compressed spectrum sensing algorithms is not strong, we propose a new adaptive compressed spectrum sensing algorithm, which is based on radio environment map dedicated for space information networks (REM-SIN). Its framework is shown in Fig. 3.

Fig. 3.
figure 3

Adaptive compressed spectrum sensing based on REM-SIN

Full size image

Under the guidance of the measurement matrix and the check matrix, we use AIC to compressed measure (sample) the analog signal \( x(t) \) to get the digital signal \( y[k] \) and \( y_{1}^{{\prime }} [k] \). In the subsequent steps, \( y[k] \) is used to reconstruct the digital signal \( x[k] \). Corresponds to the progress of getting \( y_{1}^{{\prime }} [k] \), we use the check matrix to compressed measure (sample) \( x[k] \) to get the digital signal \( y_{2}^{{\prime }} [k] \). We call \( y_{1}^{{\prime }} [k] \) and \( y_{2}^{{\prime }} [k] \) the check sequence.

Because \( x(t) \) is unknown to us, we do not know how similar the reconstructed signal \( x[k] \) to \( x^{{\prime }} [k] \) is (\( x^{{\prime }} [k] \) is a digital signal sampled at Nyquist-Shannon sampling rate from \( x(t) \)). That is to say, we cannot evaluate or ensure the sensing result’s accuracy.

Inspired by cross validation, we can use the similarity between \( y_{1}^{{\prime }} [k] \) and \( y_{2}^{{\prime }} [k] \) to evaluate the similarity between \( x[k] \) and \( x^{{\prime }} [k] \), and evaluate the sensing result’s accuracy in the end. As we have known how accurate the sensing result is, we can adjust the compression ratio and repeat the sensing again when the sensing result’s error is unacceptable.

If we have known the prior knowledge of radio environment, we can set an initial compression ratio and other parameters to accelerate the adaptive process of compressed sensing.

The adaptive compressed spectrum sensing algorithm based on REM-SIN is detailed as follows:

  1. Step 1:

    PUs obtain the prior knowledge of radio environment from the REM-SIN and combine with the sensing demand, then set the initial compression ratio and other parameters, and then create the measurement matrix and the check matrix.

  2. Step 2:

    PUs receive \( x(t) \) and use AIC to compressed measure (sample) \( x(t) \) to get \( y[k] \) and \( y_{1}^{{\prime }} [k] \) under the guidance of the measurement matrix and the check matrix.

  3. Step 3:

    PUs use \( y[k] \) to reconstruct \( x[k] \) and use the check matrix to compressed measure (sample) \( x[k] \) to get \( y_{2}^{{\prime }} [k] \).

  4. Step 4:

    PUs measure the similarity between \( y_{1}^{{\prime }} [k] \) and \( y_{2}^{{\prime }} [k] \) to evaluate the reconstruction and sensing result’s accuracy. If the gap between \( y_{1}^{{\prime }} [k] \) and \( y_{2}^{{\prime }} [k] \) is unacceptable, increase the number of measurements by variable step size and return step 2. Else, use the reconstruction result \( x[k] \) to spectrum sensing.

  5. Step 5:

    PUs feed back the sensing result and other related information to the REM-SIN.

3 Simulation Results

In this section, we present the MATLAB simulation resulting using the proposed adaptive compressed spectrum sensing algorithm.

First of all, we use a 512-point discrete-frequency-domain signal to simulate the channel environment as shown in Fig. 4. We suppose that there are 4 wideband signals in the spectrum between 4900 MHz to 5102.4 MHz. Each wideband signal’s bandwidth is 6 MHz and its power is −83 dBm. The signal-to-noise ratio (SNR) is 20 dB.

Fig. 4.
figure 4

Simulated channel environment

Full size image

Then, SUs use the proposed adaptive algorithm to sense the spectrum. SUs can obtain the prior knowledge about the operational radio environment from the REM-SIN and then set the initial compression ratio to 0.3 and initialize the other parameters as well according to the sensing demand. For example, the number of rows of the measurement matrix and check matrix are initially set to 150 and 40, respectively; the step size for both long step and small step are set to 40 and 10, respectively; the threshold Euclidean distance between \( y_{1}^{{\prime }} [k] \) and \( y_{2}^{{\prime }} [k] \) is preset as \( 4 \times 10^{ - 12} \). The reconstruction algorithm employed in our simulation is the sparsity adaptive matching pursuit (SAMP) [11].

We can choose many statistics to measure the similarity between \( y_{1}^{{\prime }} [k] \) and \( y_{2}^{{\prime }} [k] \) like Euclidean distance, Minkowski distance, vector cosine angle, and so on. In this simulation, we choose Euclidean distance to measure the similarity between \( y_{1}^{{\prime }} [k] \) and \( y_{2}^{{\prime }} [k] \). The true value of error we defined is the Euclidean distance between \( x[k] \) and \( x^{{\prime }} [k] \). And we call the Euclidean distance between \( y_{1}^{{\prime }} [k] \) and \( y_{2}^{{\prime }} [k] \) the alternative value of error. Figure 5 show that two kind values of error have the same variation trend with the row number of measurement matrix with a high probability.

Fig. 5.
figure 5

Error’s variation with the row number of measurement matrix

Full size image

When the Euclidean distance between \( y_{1}^{{\prime }} [k] \) and \( y_{2}^{{\prime }} [k] \) is greater than \( 1 \times 10^{ - 11} \), we deem that there is a great disparity between \( x[k] \) and \( x^{{\prime }} [k] \), and increase the number of rows of measurement matrix with a large step, then repeat the compressed sensing. When the Euclidean distance between \( y_{1}^{{\prime }} [k] \) and \( y_{2}^{{\prime }} [k] \) is greater than \( 4 \times 10^{ - 12} \), it indicates there is a small disparity between \( x[k] \) and \( x^{{\prime }} [k] \), and increase the row number of measurement matrix with a small step, then repeat the compressed sensing. When the Euclidean distance between \( y_{1}^{{\prime }} [k] \) and \( y_{2}^{{\prime }} [k] \) is less than \( 4 \times 10^{ - 12} \), the disparity between \( x[k] \) and \( x^{{\prime }} [k] \) can be ignored, and then the reconstruction result \( x[k] \) is used for spectrum sensing.

The spectrum sensing results are shown in Figs. 6 and 7. Note that it is assumed that when the received signal power is lower than −90 dBm, the channel is idle.

Fig. 6.
figure 6

Spectrum sensing results

Full size image
Fig. 7.
figure 7

Spectrum sensing results after binary decision

Full size image

The simulation results show that by using the proposed adaptive algorithm, the compression ratio can be adjusted according to the channel environment so as to get accurate sensing results efficiently.

Figure 8 show the area under curve (AUC) value of the receiver operating characteristic (ROC) curve when employing different number of rows of the measurement matrix. As for the detection and false alarm performance, our proposed algorithm is basically the same as that of the SAMP algorithm. The advantage of our proposed algorithm is that it can evaluate the spectrum sensing results automatically and then make adjustment adaptively. In this way, there is no need to accurately estimate the spectrum sparsity of radio environment, which is essential yet challenging for the traditional compressed spectrum sensing algorithms.

Fig. 8.
figure 8

Area under curve (AUC) value of the receiver operating characteristic (ROC) curve vs. the number of rows of the measurement matrix

Full size image

4 Concluding Remarks

With the development of integrated satellite-terrestrial networks utilizing spectrum from sub-6 GHz up to 100 GHz to offer ubiquitous broadband applications, the topology and radio scenarios will become much more complicated with extremely wide radio spectrum to be shared. Accordingly, it is important to make compressed spectrum sensing more efficiently and adaptively to the dynamically changing radio environment. In this paper, an adaptive compressed spectrum sensing algorithm is proposed, which is based on REM dedicated for space information networks (REM-SIN) to improve the adaptability of compressed spectrum sensing algorithms to the channel environment with different sparseness. The simulation results show that by using the proposed algorithm, the compression ratio can be adjusted adaptively according to the channel environment and get accurate sensing results efficiently. For future work, it is worthwhile to analyze the impact of many practical factors (such as mobility of satellites and weather condition) on the spectrum sensing results and construct the REM-SIN for various applications.