1 Introduction

We consider the following system of fractional ordinary differential equations:

$$\begin{aligned} _0 D^{\alpha }_t x(t)=f(t,x(t)),~ t \in (0,T], ~\mathrm {satisfying}~ x(0)= x^0 , \end{aligned}$$
(1)

where \(x(t)=(x_1(t), x_2(t), \ldots , x_n(t))^\top \in \mathbb {R}^n\) for a positive integer n, \(T>0\) is a fixed constant, \(f : \mathbb {R}^{n+1} \mapsto \mathbb {R}^n\) a given mapping, \(x^0 \in \mathbb {R}^n\) a given initial condition, and \( {_0 D^{\alpha }_t x(t)}=({_0 D^{\alpha _1}_t x_1(t)}, {_0D^{\alpha _2}_t x_2(t)}, \ldots , {_0 D^{\alpha _n}_tx_n(t))} ^\top \) for \(\alpha _i \in (0,1)\) with \( {_0 D^{\alpha _i}_tx_i(t)}\) denoting the following Caputo’s \(\alpha _i\)-th derivative

$$ _{0} D^{\alpha _i }_t x_i(t)=\frac{1}{\varGamma (1-\alpha _i )} \int _{0}^{t} \ \frac{{x_i}'(\tau )}{(t-\tau )^{\alpha _i }} \, d\tau $$

for \(t > 0\) and \(i=1,2,...,n\), where \(\varGamma (\cdot )\) denotes the Gamma function.

In the open literature, there are a number of methods for solving (1). Adomian decomposition method [3, 5, 9], variational iteration method [11, 12], differential transform method [2] and homotopy analysis method [10, 14] have been used for the problem. Recently, we proposed a new one-step numerical integration scheme for (1) [8]. This method is easy to implement and computationally inexpensive. In this paper, we will show that the global error of the method is of order \(\mathcal {O}(h^{2})\), where h denotes the maximal mesh size to be defined.

The rest of the paper is organized as the follows. In Sect. 2, we first transform Eq. (1) into an equivalent Volterra integral equation, we then propose an approximation of Volterra integral equation based on a Taylor expansion. An error analysis of the approximation is also presented. In Sect. 3, we propose an algorithm for implementing the approximate equation and analyse its convergence. In Sect. 4, numerical examples are presented. Section 5 concludes the paper.

2 Approximation

We first rewrite (1) as the following Volterra integral equation:

$$\begin{aligned} x_i(t)=x^0_i +\frac{1}{\varGamma (\alpha _i)}\int _{0}^{t} \ {(t-\tau )^{\alpha _i-1}} f_i(\tau ,x(\tau ))\, d\tau , \end{aligned}$$
(2)

for \(t \in (0,T]\) and \(i = 1,2,...,n. \) It has been proven [1, 4, 6] that solving Eq. (1) is equivalent to solving (2). In this section, we will develop a numerical method based on a Taylor expansion to approximate (2) and estimate the approximation error.

Let N be a given positive integer. We divide (0, T) into N sub-intervals with mesh points \(t_i=i h\) for \(i=0,1,\ldots , N, \) where \(h=T/N\). Thus, we have

$$\begin{aligned} x_i(t_j)= & {} x^0_i +\frac{1}{\varGamma (\alpha _i)}\int _{0}^{jh} \ {(jh-\tau )^{\alpha _i-1}} f_i(\tau ,x(\tau ))\, d\tau \nonumber \\= & {} x^0_i +\frac{1}{\varGamma (\alpha _i)}\sum _{k=1}^{j}\int _{(k-1)h}^{kh} { (jh-\tau )^{\alpha _i-1}} f_i(\tau ,x(\tau )) d\tau . \end{aligned}$$
(3)

To approximate the integral on the RHS of (3), we assume that \(f_i(t,x(t))\) is twice continuously differentiable with respect to both t and x. For any k, we expend \(f_i(\tau ,x(\tau ))\) at any point in \(((k-1)h, kh)\), denoted as \(\tau ^i_{jk}\), into

$$\begin{aligned} f_i(\tau ,x(\tau ))&= f_i(\tau ^i_{jk},x(\tau ^i_{jk})) + K^i_{jk} (\tau -\tau ^i_{jk}) +c^i_{jk} (\tau -\tau ^i_{jk})^2, \end{aligned}$$
(4)

where \(c^i_{jk} \) is the coefficient of the reminder of the expansion and

$$ K^i_{jk} =\frac{\partial f_i}{\partial \tau } \Big |_{(\tau ^i_{jk}, x(\tau ^i_{jk}))} +\sum _{l=1}^{n}\frac{\partial f_i}{\partial x_l} \Big |_{(\tau ^i_{jk}, x(\tau ^i_{jk}))}\frac{\partial x_l}{\partial \tau }|_{(\tau ^i_{jk})} . $$

Therefore, replacing \(f_i(\tau ,x(\tau ))\) in (3) with the RHS of (4) and by direct integration we have

$$\begin{aligned} \frac{1}{\varGamma (\alpha _i)}\int _{(k-1)h}^{kh}&{ (jh-\tau )^{\alpha _i-1}} f_i(\tau ,x(\tau )) d\tau \nonumber \\ =&\,\, \frac{1}{\varGamma (\alpha _i)}\int _{(k-1)h}^{kh} { (jh-\tau )^{\alpha _i-1}}[ f_i(\tau ^i_{jk},x(\tau ^i_{jk}))+K^i_{jk} (\tau -\tau ^i_{jk})] d\tau +R^i_{jk} \nonumber \\ =&\,\, \frac{h^{\alpha _i}}{\varGamma (\alpha _i+1)}f_i(\tau ^i_{jk},x(\tau ^i_{jk}))[(j-k+1)^{\alpha _i}-(j-k)^{\alpha _i}] \nonumber \\&+\frac{K^i_{jk} }{\varGamma (\alpha _i)} \int _{(k-1)h}^{kh} { (jh-\tau )^{\alpha _i-1}} (\tau -\tau ^i_{jk}) d\tau +R^i_{jk} , \end{aligned}$$
(5)

where \(\displaystyle R^i_{jk}=\frac{1}{\varGamma (\alpha _i)}\int _{(k-1)h}^{kh} { (jh-\tau )^{\alpha _i-1}} c^i_{jk} (\tau -\tau ^i_{jk})^2 d\tau \).

From (5) it is clear that \(\tau ^i_{jk}\) should be chosen such that the integral term in (5) becomes zero so that the truncation error is \(R^i_{jk}\). The choice of \(\tau ^i_{jk}\) is given in the following theorem.

Theorem 1

For any feasible j and k, the unique solution to

$$ \int _{(k-1)h}^{kh} { (jh-\tau )^{\alpha _i-1}} (\tau -\tau ^i_{jk}) d\tau =0 $$

is

$$\begin{aligned} \tau ^i_{jk}=h \frac{[(j-k+1)^{\alpha _i+1}-(j-k)^{\alpha _i+1}]+(\alpha _i+1)[(j-k+1)^{\alpha _i}(k-1)-(j-k)^{\alpha _i} k]}{(\alpha _i+1)[(j-k+1)^{\alpha _i}-(j-k)^{\alpha _i}]}. \end{aligned}$$
(6)

Furthermore, \((k-1)h< \tau ^i_{jk} < kh\).

Proof

See the proof of Theorem 2.1 in [7].

Substituting the expression for \( \tau ^i_{jk}\) in (6) into (5) and combining the resulting expression with (3), we have the following representation for \(x_i(t_j)\).

$$\begin{aligned} x_i(t_j) = x^0_i +\frac{h^{\alpha _i}}{\varGamma (\alpha _i+1)}\sum _{k=1}^{j}f_i(\tau ^i_{jk},x(\tau ^i_{jk}))[(j-k+1)^{\alpha _i}-(j-k)^{\alpha _i}] +R^i_{j}, \end{aligned}$$
(7)

for \(j=1,2,\ldots ,N\), where \( \tau ^i_{jk}\) is given in (6) for \(k=1,2,\ldots ,j\) and \(R^i_j=\sum _{k=1}^{j} R^i_{jk} \). Omitting \(R^i_j\) in (7), we have an approximation to (3) with the truncation error \(R^i_j\). An upper bound for \(R^i_j\) is given in the following theorem.

Theorem 2

If f(t, x) is twice continuously differentiable in t and x, then we have \( |R^i_j| \le Ch^2, \) where C denotes a positive constant independent of h.

Proof

See the proof of Theorem 2.2 in [7].

From (7) it is clear that to compute \({x}_i (t_j)\), we need to calculate \(f_i(\tau ^i_{jk},x(\tau ^i_{jk}))\). However, \(x(\tau ^i_{jk})\) is not available directly from the scheme. Thus, approximations to \({x} (\tau ^i_{jk})\) need to be determined. In the next section, we propose a single step numerical scheme for implementing (7) when the remainder \(R_j^i\) is omitted.

3 Algorithm and Its Convergence

For any j and k satisfying \(1\le k \le j \le N\), since \(\tau ^i_{jk} \in (t_{k-1}, t_k)\) by Theorem 1, we use the following linear interpolation to approximate \(x_i(\tau ^i_{jk})\):

$$\begin{aligned}&x(\tau ^i_{jk}) = x(t_{k-1} )+\rho ^i_{jk} ( x(t_k) - x(t_{k-1}) ) +\mathcal {O}(h^2) E_n, \end{aligned}$$
(8)

where \( \rho ^i_{jk} : = \frac{\tau ^i_{jk} - t_{k-1} }{h} \in (0,1) \) and \(E_n = (1,1,...,1)^\top \in \mathbb {R}^n\). Using (8) , we approximate \(f_i(\tau ^i_{jk}, x(\tau ^i_{jk}))\) as follows.

$$\begin{aligned} f_i(\tau ^i_{jk}, x (\tau ^i_{jk} ) ) = f_i \left( \tau ^i_{jk}, x(t_{k-1} )+\rho ^i_{jk} (x(t_k) - x(t_{k-1})) \right) + \mathcal {O}(h^2). \end{aligned}$$
(9)

Replacing \(f_i(\tau ^i_{jk},x (\tau ^i_{jk} ) )\) in (7) with the RHS of (9), we have

$$\begin{aligned} x_i(t_j)= x^0_i +&h_{\alpha _i}\sum _{k=1}^{j} \Big [ f_i \left( \tau ^i_{jk}, x(t_{k-1}) + \rho ^i_{jk} (x(t_k)- x(t_{k-1})) \right) \nonumber \\&\cdot ((j-k+1)^{\alpha _i}-(j-k)^{\alpha _i}) \Big ]+\mathcal {O}(h^2) \end{aligned}$$
(10)

for \( j=1,2,\ldots ,N\), where \(h_{\alpha _i}=\frac{h^{\alpha _i}}{\varGamma (\alpha _i+1)}\) and \(\tau ^i_{jk}\) is defined in (6). Clearly, (10) defines a time-stepping scheme for (2) if we omit the term \(\mathcal {O}(h^2)\).

The above scheme is implicit as it is a nonlinear system in \(x(t_j)\). We now define an explicit single step scheme by further approximating the jth term in the sum in (10) by the following Taylor expansion:

$$\begin{aligned}&f_i(\tau ^i_{jj}, x(t_{j-1}) + \rho ^i_{jj} (x(t_j) - x(t_{j-1})) ) \nonumber \\&= f_i(\tau ^i_{jj},x (t_{j-1}) ) ) +\sum _{l=1}^{n}\frac{\partial f_i}{\partial x_l} \Big |_{(\tau ^i_{jj},x _(t_{j-1}))} (\rho ^i_{jj}(x_l(t_j)-x_l(t_{j-1}))) + \mathcal {O}(h^2). \end{aligned}$$
(11)

Thus, combining (11) and (10) yields

$$\begin{aligned} x_i(t_j) =&x^0_i + h_{\alpha _i}\sum _{k=1}^{j-1} \Big [ f_i \left( \tau ^i_{jk}, x(t_{k-1}) + \rho ^i_{jk} (x(t_k)- x(t_{k-1})) \right) \nonumber \\&((j-k+1)^{\alpha _i}-(j-k)^{\alpha _i}) \Big ] +h_{\alpha _i} f_i\left( \tau ^i_{jj},x (t_{j-1}) ) \right) \nonumber \\&+h_{\alpha _i}\sum _{l=1}^{n}\Big [\frac{\partial f_i}{\partial x_l}|_{(\tau ^i_{jj},x (t_{j-1}) ) )}(\rho ^i_{jj}(x_l(t_j)-x_l(t_{j-1})))\Big ] + \mathcal {O}(h^2). \end{aligned}$$
(12)

Let \(x^{j}: =(x_1^j, x_2^j, \ldots , x_n^j)^\top \) for \(j=0,1,...,N\) and omitting the truncation error terms of order \(\mathcal {O}(h^2)\) in (12), we define the following single step time-stepping scheme for approximating (2):

$$\begin{aligned} x_i^j =&x^0_i + h_{\alpha _i}\sum _{k=1}^{j-1} \Big [ f_i \left( \tau ^i_{jk}, x^{k-1}+ \rho ^i_{jk} (x^{k}-x^{k-1}) \right) ((j-k+1)^{\alpha _i}-(j-k)^{\alpha _i}) \Big ] \nonumber \\&+h_{\alpha _i} f_i\left( \tau ^i_{jj},x^ {j-1} \right) +h_{\alpha _i}\sum _{l=1}^{n}\Big [\frac{\partial f_i}{\partial x_l}|_{(\tau ^i_{jj},x^{ j-1}) }(\rho ^i_{jj}(x_l^j-x_l^{j-1}))\Big ] \end{aligned}$$
(13)

Re-organising (13), we have the following linear system for \(x^j\):

$$\begin{aligned} B^j x^j= C^j , \quad j=1,2,\ldots ,N. \end{aligned}$$
(14)

where \(B^j\) is the \( n\times n\) matrix given by

$$\begin{aligned} B^j = \begin{pmatrix} 1-b_{11}^j &{}-b_{12}^j &{}\ldots &{}-b_{1n}^j\\ -b_{21}^j &{}1-b_{22}^j &{}\ldots &{}-b_{2n}^j\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ -b_{n1}^j &{}-b_{n2}^j &{}\ldots &{}1-b_{nn}^j\\ \end{pmatrix} \end{aligned}$$
(15)

with

$$\begin{aligned} b_{il}^j =\rho ^i_{jj}h_{\alpha _i}\frac{\partial f_i}{\partial x_l} \Big |_{(\tau ^i_{jj},x^{j-1} )} \end{aligned}$$
(16)

for \(i=1,2,\ldots ,n\), \(l=1,2,\ldots ,n \) and \(C^j=(c_1^j, c_2^j, \ldots ,c_n^j )^\top \) with

$$\begin{aligned} c_i^j =&x^0_i + h_{\alpha _i}\sum _{k=1}^{j-1}\Big [ f_i\left( \tau ^i_{jk}, x^{k-1} + \rho ^i_{jk} (x^k- x^{k-1}) \right) ((j-k+1)^{\alpha _i}-(j-k)^{\alpha _i})\Big ] \nonumber \\&+h_{\alpha _i} f_i\left( \tau ^i_{jj},x^{j-1} \right) -\sum _{l=1}^{n}x_l^{j-1} b_{il}^j. \end{aligned}$$
(17)

It is clear that to calculate \(x^j,\) we need to solve the system of equations (14)–(17). It has been shown in [8] that (14)–(17) is uniquely solvable when h is sufficiently small.

For a given initial condition \(x^0\), using the above results, we propose the following algorithm for solving (3) numerically.

Algorithm A

  1. 1.

    For a given positive integer N, let \(t_j=jh\) for \(j=0,1,\ldots ,N\), where \(h=T/N\).

  2. 2.

    Calculate \(x^j \) for \(j=1,...,N\) using (14)–(17).

Using a linear interpolation and Taylor’s theorem, we are able to prove in the following theorem that, for any \(j=1,2,\ldots ,N\), \(x^j\) generated by the above algorithm converges to the solution of (2) at the rate \(\mathcal {O}(h^2)\) when \(h\rightarrow 0^+\).

Theorem 3

Let \(x(t_j)\) and \(x^j\) be respectively the solution to (3) and the sequence generated by Algorithm A. If f(t, x) is twice continuously differentiable in t and x, then there exists an \(\bar{h} >0\) such that when \( h <\bar{h}\)

$$\begin{aligned} ||x(t_j)-x^j||_{\infty } \le Ch^2, \quad j=1,2,\ldots ,N. \end{aligned}$$
(18)

Proof

In what follows, we let C denote a generic positive constant, independent of h. We now prove this theorem by mathematical induction.

When \(j=1\), from (12) we have

$$\begin{aligned} x_i (t_1)= x_i^0 +h_{\alpha _i} \left[ f_i (\tau _{11}^i,x^0 )+\sum _{l=1}^{n}\frac{\partial f_i}{\partial x_l} \Big |_{(\tau ^i_{11},x ^0 ) }(\rho ^i_{11}(x_l(t_1)-x_l^0)) \right] + \mathcal {O} (h^2) \end{aligned}$$
(19)

Re-organising (19) and using the definitions for \(B^j\) and \(C^j\), we have

$$\begin{aligned} B^{ 1} x(t_1)= C^{ 1} + \mathcal {O} (h^2) E_n. \end{aligned}$$
(20)

Solving (20) yields

$$\begin{aligned} x(t_1)=({B^1})^{-1} C^1 + \mathcal {O} (h^2) ({B^1})^{-1} E_n. \end{aligned}$$

From (14)–(17), we see that

$$\begin{aligned} x^1=({B^1})^{-1} C^1. \end{aligned}$$

Therefore,

$$\begin{aligned} ||x(t_1)-x^1||_{\infty }= \mathcal {O} (h^2) ||({B^1})^{-1} E_n ||_{\infty } \le Ch^2 ||({B^1})^{-1}||_{\infty }. \end{aligned}$$

It has been proven [8] that \(B^j, j=1,2, \ldots , N\) satisfies, when \(h<\bar{h}\),

$$\begin{aligned} \sigma ^j : = \min _{ 1\le i \le n} \left\{ |b_{ii}^j |-\sum _{j=1,j \ne i}^n|b_{ij}^j| \right\} \ge \beta >0 \end{aligned}$$
(21)

for a constant \(\beta \), independent of h, where \(\bar{h}=\min _{1 \le i \le n} {(\frac{\varGamma {(\alpha _i+1)}}{nM})}^{\frac{1}{\alpha _i}}\) and \(M=\max _{\begin{array}{c} 1 \le i \le n\\ 1 \le l \le n \end{array}} \left| \frac{\partial f_i}{\partial x_l} \right| \). Thus, using [13] and (21), we have

$$ ||({B^1})^{-1}||_{\infty } \le \frac{1}{\sigma ^1} \le \frac{1}{\beta }. $$

Therefore, we have

$$\begin{aligned} ||x(t_1)-x^1||_{\infty } \le Ch^2. \end{aligned}$$

When \(i \ge 2\) and \(h \le \bar{h}\), we assume that

$$\begin{aligned} ||x(t_j)-x^j||_{\infty } \le Ch^2, \quad 1 \le j \le i-1. \end{aligned}$$
(22)

We now show that \( ||x(t_j)-x^j||_{\infty } \le Ch^2\) for \(1 \le j \le i\).

Note that (12) can be re-written in the following form:

$$\begin{aligned} x_i(t_j)=x^0_i+A_i^{j}+D_i^{j}+\mathcal {O} (h^2), \end{aligned}$$
(23)

where

$$\begin{aligned} A_i^{j}=h_{\alpha _i}\sum _{k=1}^{j-1} \Big [ f_i \left( \tau ^i_{jk}, x(t_{k-1}) + \rho ^i_{jk} (x(t_k)- x(t_{k-1}) ) \right) ((j-k+1)^{\alpha _i}-(j-k)^{\alpha _i}) \Big ], \end{aligned}$$
(24)
$$\begin{aligned} D_i^{j}=h_{\alpha _i} f_i\left( \tau ^i_{jj},x (t_{j-1}) ) \right) +h_{\alpha _i}\sum _{l=1}^{n}\Big [\frac{\partial f_i}{\partial x_l}|_{(\tau ^i_{jj},x (t_{j-1}) )}(\rho ^i_{jj}(x_l(t_j)-x_l(t_{j-1})))\Big ]. \end{aligned}$$
(25)

Similarly, (13) can be re-written as follows.

$$\begin{aligned} x_i^j=x^0_i+\tilde{A}_i^{j}+\tilde{D}_i^{j}, \end{aligned}$$
(26)

where

$$\begin{aligned} \tilde{A}_i^{j}=h_{\alpha _i}\sum _{k=1}^{j-1} \Big [ f_i \left( \tau ^i_{jk}, x^{k-1} + \rho ^i_{jk} (x^k- x^{k-1}) \right) ((j-k+1)^{\alpha _i}-(j-k)^{\alpha _i}) \Big ], \end{aligned}$$
(27)
$$\begin{aligned} \tilde{D}_i^{j}=h_{\alpha _i} f_i\left( \tau ^i_{jj},x ^{j-1} \right) +h_{\alpha _i}\sum _{l=1}^{n}\Big [\frac{\partial f_i}{\partial x_l}|_{(\tau ^i_{jj},x^{j-1} ) }(\rho ^i_{jj}(x_l^j-x_l^{j-1}))\Big ]. \end{aligned}$$
(28)

Subtracting (26) from (23) gives

$$\begin{aligned} x_i(t_j)-x_i^j=(A_i^{j} -\tilde{A}_i^{j})+( D_i^j -\tilde{D}_i^j) +\mathcal {O}(h^2). \end{aligned}$$
(29)

Let us first estimate \(D_{i}^j -\tilde{D}_{i}^j\). From (25) and (28), we have

$$\begin{aligned} D_{i}^j -\tilde{D}_{i}^j =&\left[ h_{\alpha _i} f_i\left( \tau ^i_{jj},x (t_{j-1}) ) \right) +h_{\alpha _i}\sum _{l=1}^{n}\Big [\frac{\partial f_i}{\partial x_l}|_{(\tau ^i_{jj},x (t_{j-1}) )}(\rho ^i_{jj}(x_l(t_j)-x_l(t_{j-1})))\Big ] \right] . \nonumber \\&-\left[ h_{\alpha _i} f_i\left( \tau ^i_{jj},x ^{j-1} ) \right) +h_{\alpha _i}\sum _{l=1}^{n}\Big [\frac{\partial f_i}{\partial x_l}|_{(\tau ^i_{jj},x^{j-1} ) }(\rho ^i_{jj}(x_l^j-x_l^{j-1}))\Big ]\right] \nonumber \\ =&\,\, h_{\alpha _i} [ f_i(\tau _{jj}^i,x(t_{j-1}))- f_i(\tau _{jj}^i,x^{j-1}) ] \nonumber \\&+h_{\alpha _i}\rho _{jj}^i \left[ \sum _{l=1}^{n}\Big [\frac{\partial f_i}{\partial x_l}|_{(\tau ^i_{jj},x (t_{j-1})) }(x_l(t_j))- \frac{\partial f_i}{\partial x_l}|_{(\tau ^i_{jj},x^{j-1} )) }(x_l^j)\Big ]\right] \nonumber \\&- h_{\alpha _i}\rho _{jj}^i \left[ \sum _{l=1}^{n}\Big [\frac{\partial f_i}{\partial x_l}|_{(\tau ^i_{jj},x (t_{j-1})) }(x_l(t_{j-1}))- \frac{\partial f_i}{\partial x_l}|_{(\tau ^i_{jj},x^{j-1} ) }(x_l^{j-1})\Big ]\right] . \end{aligned}$$
(30)

Since \(f_i\) is twice continuously differentiable, using a Taylor expansion we get

$$\begin{aligned} \frac{\partial f_i}{\partial x_l}|_{(\tau ^i_{jj},x (t_{j-1}) ) }=\frac{\partial f_i}{\partial x_l}|_{(\tau ^i_{jj},x ^{j-1}) } +r _j^i, \end{aligned}$$
(31)

where

$$ r_j^i=\sum _{p=1}^{n}\frac{{\partial }^2 f_i}{{\partial } x_l \partial x_p}|_{(\tau ^i_{jj},\xi )} (x_p(t_{j-1})-x_p^{t-1}), $$

where \(\xi =x(t_{j-1})+\theta (x(t_{j-1})-x^{j-1})\) with \( \theta \in (0,1)\). From the assumption (22) we have \( r_j^i = \mathcal {O}(h^2).\) Similarly, since f is twice differentiable, using (22) it is easy to show \(f_i(\tau _{jj}^i,x_i(t_{i-1})) -f_i(\tau _{jj}^i,x_i^{j-1}) = \mathcal {O}(h^2). \)

Using (31) and the above estimates we have, from (30),

$$\begin{aligned} D_{i}^j -\tilde{D}_{i}^j&=h_{\alpha _i} \mathcal {O}(h^2) +h_{\alpha _i}\rho _{jj}^i \left[ \sum _{l=1}^{n}\Big [\frac{\partial f_i}{\partial x_l}|_{(\tau ^i_{jj},x ^{j-1}) }(x_l(t_j)-x_l^j+x_l(t_{j})r^i_j)\Big ]\right] \\&- h_{\alpha _i }\rho _{jj}^i \left[ \sum _{l=1}^{n}\Big [\frac{\partial f_i}{\partial x_l}|_{(\tau ^i_{jj},x ^{j-1}) }(x_l(t_{j-1})-x_l^{j-1}+x_l(t_{j-1})r^i_j)\Big ]\right] \\&=h_{\alpha _i}\rho _{jj}^i \left[ \sum _{l=1}^{n}\Big [\frac{\partial f_i}{\partial x_l}|_{(\tau ^i_{jj},x ^{j-1}) }(x_l(t_j)-x_l^j)\Big ]\right] \\&+ h_{\alpha _i }\rho _{jj}^i \left[ \sum _{l=1}^{n}\Big [\frac{\partial f_i}{\partial x_l}|_{(\tau ^i_{jj},x ^{j-1}) }(x_l^{j-1}-x_l(t_{j-1}))\Big ]\right] +\mathcal {O}(h^{2+\alpha _i}) \\&=h_{\alpha _i}\rho _{jj}^i \left[ \sum _{l=1}^{n}\Big [\frac{\partial f_i}{\partial x_l}|_{(\tau ^i_{jj},x ^{j-1}) }(x_l(t_j)-x_l^j)\Big ]\right] +\mathcal {O}(h^{2+\alpha _i}) , \end{aligned}$$

since \(h_{\alpha _i} = h^{\alpha _i}/\varGamma (1+\alpha _i)\) and (22). Thus, from the above expression and (29), we get

$$\begin{aligned} x_i(t_j)-x_i^j =&(A_{i}^j -\tilde{A}_{i}^j) + h_{\alpha _i}\rho _{jj}^i \left[ \sum _{l=1}^{n}\Big [\frac{\partial f_i}{\partial x_l}|_{(\tau ^i_{jj},x ^{j-1}) }(x_l(t_j)-x_l^j)\Big ]\right] + \mathcal {O}(h^2). \end{aligned}$$

Re-organising the above equation gives

$$\begin{aligned} B^j \big (x(t_j)-x^j\big )= A^j + \mathcal {O}(h^2) E_n , \quad j=1,2,\ldots ,N, \end{aligned}$$

where \(B^j\) is defined in (15)–(16) and \(A^j=(A_1^j -\tilde{A}_1^j, A_2^j -\tilde{A}_2^j, \ldots , A_n^j -\tilde{A}_n^j )^\top \). From this equation we have

$$\begin{aligned} x(t_j)-x^j={( B^j)}^{-1} \left( A^j + \mathcal {O}(h^2) E_n \right) , \quad j=1,2,\ldots ,N. \end{aligned}$$

Thus, we have

$$ \Vert x(t_j)-x^j\Vert _{\infty }=\Vert {( B^j)}^{-1} (A^j + \mathcal {O}(h^2) E_n)\Vert _{\infty } \le \Vert {( B^j)}^{-1}\Vert _{\infty } \left( \Vert A^j ||_{\infty }+ \mathcal {O}(h^2) \right) $$

for \(j=1,2,\ldots ,N.\) Using [13] and (21), we have

$$ ||({B^j})^{-1}||_{\infty } \le \frac{1}{\sigma ^j} \le \frac{1}{\beta }. $$

Therefore, we obtain

$$\begin{aligned} || x(t_j)-x^j||_{\infty } \le \frac{1}{ \beta }||A^j||_{\infty }+Ch^2. \end{aligned}$$
(32)

We now examine \( ||A^j||_{\infty }=|| A_i^j -\tilde{A}_i^j ||_{\infty }\). For notational simplicity, we let \(x^{jk} = x^{k-1}+\rho _{jk}^i(x^k-x^{k-1})\) and \(x(t_{jk}) = x(t_{k-1})+\rho _{jk}^i(x(t_k)-x(t_{k-1})\). From (24) and (27), we have

$$\begin{aligned} | A_i^j - \tilde{A}_i^j |&\le h_{\alpha _i}\sum _{k=1}^{j-1} \Big | [f_i(\tau _{jk}^i, x(t_{jk}))-f_i(\tau _{jk}^i,x^{ {jk}})][(j-k+1)^{\alpha _i}-(j-k)^{\alpha _i}] \Big | \nonumber \\ =&\,\, h_{\alpha _i}\sum _{k=1}^{j-1} \left| f_i(\tau _{jk}^i, x(t_{jk})) -f_i(\tau _{jk}^i, x^{ {jk}})\right| [(j-k+1)^{\alpha _i}-(j-k)^{\alpha _i}], \end{aligned}$$
(33)

since \(z^{\alpha _i}\) is an increasing function of z for \(\alpha _i \in (0,1)\). Because f is twice continuously differentiable, we have, using a Taylor expansion,

$$\begin{aligned} |f_i(\tau _{jk}^i,&x(t_{jk}))- f_i(\tau _{jk}^i,x^{ {jk}})| \le C \Vert x(t_{jk})-x^{{jk}}\Vert _{\infty }\\&= C \Vert [x(t_{k-1})+\rho _{jk}^i(x(t_k)-x(t_{k-1}))] -[x^{k-1}+\rho _{jk}^i(x^k-x^{k-1})] \Vert _{\infty }\\&= C \Vert [x(t_{k-1})-x^{k-1}]+\rho _{jk}^i[x(t_k)-x^k] +\rho _{jk}^i [ x^{k-1}-x(t_{k-1})] \Vert _{\infty }\\&\le C \left( \Vert x(t_{k-1})-x^{k-1}\Vert _{\infty } + \Vert x(t_k)-x_k)\Vert _{\infty }+ \Vert x(t_{k-1})-x^{k-1} \Vert _{\infty } \right) , \\ \end{aligned}$$

since \(\rho _{jk}^i \in (0,1)\). Thus, from Assumption (22), we have

$$ |f_i(\tau _{jk},x(t_{jk}))-f_i(\tau _{jk},x^{jk})| \le Ch^2. $$

Replacing \(|f_i(\tau _{ij},x(t_{jk}))-f_i(\tau _{ij},x^{{jk}})|\) in (33) with the above upper bound yields

$$\begin{aligned} | A_{i}^j -\tilde{A}_{i}^j |\le & {} h_{\alpha _i} Ch^2 \sum _{k=1}^{j-1}[(j-k+1)^{\alpha _i}-(j-k)^{\alpha _i}] = \frac{h^{\alpha _i}}{\varGamma ({\alpha _i}+1)}Ch^2(j^{\alpha _i}-1)\\&\le \frac{h^{\alpha _i}}{\varGamma ({\alpha _i}+1)}Ch^2N^{\alpha _i} =\frac{C}{\varGamma ({\alpha _i}+1)}h^2 (hN)^{\alpha _i}\\&=\frac{C}{\varGamma ({\alpha _i}+1)}h^2 T^{\alpha _i} \le Ch^2 \end{aligned}$$

for \(i = 1,2,..., n\). Thus, we have

$$ \Vert A^j-\tilde{A}^j\Vert _{\infty } \le Ch^2. $$

Combining the above error bound with (32), we have the estimate (18). Thus, the theorem is proved.

4 Numerical Results

In this section, we will use Algorithm A to solve two non-trivial examples. All the computations have been performed in double precision under Matlab environment on a PC with Intel Xeon 3.3 GHz CPU and 16 GB RAM.

Example 1

Consider the following system of fractional differential equations:

$$\begin{aligned}&\left\{ \begin{array}{ll} _0 D^{\alpha _1}_t x_1(t)=x_2(t), \\ _0 D^{\alpha _2}_t x_2(t)=x_3(t), \\ _0 D^{\alpha _3}_t x_3(t)=\frac{\varGamma (5)}{\varGamma (5-\alpha _1-\alpha _2-\alpha _3)}t^{4-(\alpha _1+\alpha _2+\alpha _3)}, &{} t \in (0,1], \end{array} \right. \\&x_1(0)=x_2(0)=x_3(0)=0, \end{aligned}$$

where \(\alpha _i \in (0,1)\), \(i=1,2,3\). The exact solution is

$$ x_1(t)=t^4, ~ x_2(t)=\frac{\varGamma (5)}{\varGamma (5-\alpha _1)}t^{4-\alpha _1}, ~ x_3(t)=\frac{\varGamma (5)}{\varGamma (5-\alpha _1-\alpha _2)}t^{4-(\alpha _1+\alpha _2)}. $$

We solve the problem using Algorithm A for various values of \(\alpha _i, i=1,2,3\) and \(h_k = 1/(2^k \times 10), k=1,...,6\). The computed errors \(E^i_{h_k} = \max _{1\le j\le 1/h_k} | x_i^j - x_i(t_j)|\) for the chosen values of \(\alpha _i\)’s are listed in Table 1. To estimate the rates of convergence, we calculate \(\log _2 (E_{h_k}/E_{h_{k+1}})\) for \(k=1,...,5\) and the computed rates of convergence, as well as CPU times, are also listed in Table 1. From the results in Table 1 we see that our method has a 2nd-order convergence rate for all the chosen values of \(\alpha \), as predicted by Theorem 3, indicating that our method is very robust in \(\alpha \). The CPU time in Table 1 shows that our method is very efficient.

Table 1. Computed errors, convergence order and CPU time for Example 1.
Full size table

Example 2

Consider the following fractional differential equation used in [14].

$$\begin{aligned}&\left\{ \begin{array}{ll} _0 D^{\alpha _1}_t x_1(t)=x_1(t), \\ _0 D^{\alpha _2}_t x_2(t)=2x^2_1(t), \\ _0 D^{\alpha _3}_t x_3(t)=3x_1(t)x_2(t), &{} t \in (0,1] \end{array} \right. \\&x_1(0)=1, x_2(0)=1, x_3(0)=0. \end{aligned}$$

The exact solution when \(\alpha _1=\alpha _2=\alpha _3=1\) is

$$ x_1(t)=e^t, \quad x_2(t)=e^{2t}, \quad x_3(t)=e^{3t}-1. $$

It is solved using Algorithm A for various values of h and \(\alpha _i, i=1,2,3\). The computed errors and rates of convergence when \(\alpha _1=\alpha _2=\alpha _3=1\) are listed in Table 2 from which we see that the computed rates of convergence is \(\mathcal {O}(h^2)\), confirming our theoretical result.

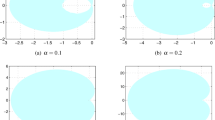
Table 2. Computed errors, convergence order and CPU time for Example 2.
Full size table

Since the exact solution to this Example 2 is unknown when \(\alpha _i <1\) for any i, we are unable to compute the rates of convergence. Instead, we solve the problem for \(\alpha _1=0.7, \alpha _2=0.5, \alpha _3=0.2\) using \(h=1/640\) and plot the computed solution, along with the solution for \(\alpha _i=1\) for \(i=1,2,3\), in Fig. 1. From Fig. 1 we see that \(x_1, x_2\) and \(x_3\) from the fractional system grow much faster than those from the integer system.

Fig. 1.
figure 1

Computed solutions of Example 2

Full size image

5 Conclusion

We have proposed and analysed a 1-step numerical integration method for a system of fractional differential equations, based a superconvergent quadrature point we have derived recently. The proposed method is unconditionally stable and easy to implement. We have shown the method has a 2nd-order accuracy. Non-trivial examples have been solved by our method and the numerical results show that our method is 2nd-order accurate for all the chosen values of the fractional orders, demonstrating our method is very robust.