Keywords

1 Introduction

The implementation of the projects connected with anthropogenic impact on water bodies should be preceded by the creation of a mathematical model followed by a series of numerical experiments that allow to assess all aspects of this impact both in the future and in various emergency situations [1, 2]. Modern methods of mathematical modeling, based on satellite information and a number of applied programs [3, 4], make it possible to analyze the situation data associated with pollutants which spread in the marine environment [5, 6]. However, the application of numerical methods requires the operative and sufficiently detailed parameters of mathematical models; that is not always possible to obtain even with the help of modern monitoring systems [6, 7]. So, during the fuel oil spill in the Kerch Strait on November 11, 2007, the first satellite images were available only five days later after the disaster. Regarding this, the possibility of obtaining information analytically from the hydrodynamic and turbulent diffusion equations formulas is studied that allow us to estimate (at first approximation) the size of the concentration areas of pollutants exceeding the ACL for a wide range of changes of hydro physical parameters.

2 Method of Calculation

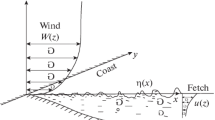
Let us first consider the transfer of pollutants by purely drift currents in open areas of the sea. We choose the origin of the rectangular coordinate system XYZ on the sea surface, the Z axis is directed vertically down, the X axis is in the direction of the wind force. In the case of shallow water (H ≪ h), the solution of the hydrodynamic equations is [8, 9]:

$$ u =\uptau{\rm H}\left( {1 - {\text{z}}/{\text{H}}} \right)/\left( {\uprho{\text{A}}} \right) $$
(1)

where: u - current velocity; H is the depth; h is the friction depth (h = \( \surd\)(f/(2A))); ρ is the density of water, τ is the wind stress tangent, f is the Coriolis parameter; A is the coefficient of vertical turbulent viscosity.

According to [8, 10], the following is true for the shallow sea

$$ {\text{A}} =\upgamma{\text{VH}}/\left( {4\uprho{\text{k}}} \right).\;\uptau =\upgamma \text{V}^{2} . $$
(2)

Here: V is the wind speed; γ = 0.00325 kg/m3, k = 0.015.

Substituting expression (2) into (1), we obtain:

$$ u = 4{\text{kV}}\left( {1 - {\text{z}}/{\text{H}}} \right),{\text{u}}_{\hbox{max} } = {\text{u}}\left( 0 \right) = {\text{u}}_{0} = 4{\text{kV}} $$
(3)

Let us estimate the maximum distance of transported pollutants in the direction of the wind force \( {\text{R}}_{\text{ACL}} \), at which the concentration of the pollutants S does not exceed the value of \( \text{S}_{\text{ACL}} \) (admissible concentration limit). We place the source of pollutants with the concentration \( {\text{S}}_{0} \) at the origin of the coordinate system; the X-axis is oriented in the direction of the maximum value of the wind speed V. The boundary-value task, describing the transportation of pollutants by wind currents, suppose as follows (3):

$$ {\partial }{\text{S}}/\partial {\text{t}} + {\text{u}}_{0} \partial {\text{S}}/\partial {\text{x}} = {\text{D}}\,\partial^{2} {\text{S}}/\partial {\text{x}}^{2}\rm{-}{\text{mS}} $$
(4)
$$ {\text{S}}\left( {0,0} \right) = {\text{S}}_{0} ;\,{\text{S}} \to 0\,{\text{if}}\,{\text{t}} \to \infty ;{\text{S}} \to 0\,{\text{if}}\,{\text{x}} \to \infty $$
(5)

where S0 = const; D и m – coefficients of turbulent diffusion and destruction (decay) accordingly,

$$ {\text{D}} > 0,{\text{m}} > 0,{\text{u}}_{0} > 0;0 \le {\text{x}} \le {\text{u}}_{0} {\text{t}} $$
(6)

Let us analyze the stationary solution S(x) of the problem (4) and (5). We write it as:

$$ {\text{S}}\left( {\text{x}} \right) = {\text{S}}_{0} \exp \left( { -\uplambda{\text{x}}} \right). $$
(7)
$$ {\text{here}}\,\uplambda = \left( {\sqrt {1 +\upvarepsilon} {-}1} \right){\text{u}}_{0} /\left( {2\,{\text{D}}} \right),\upvarepsilon = 4{\text{mD}}/{\text{u}}_{0}^{2} $$
(8)

It comes from (7) that the concentration decreases when the distance from the pollution source increases. Let us define the distance RACL, at which the concentration reaches its maximum permissible value SACL, that is: S(RACL) = SACL. Substituting x = RACL into the expression (7), we obtain SACL, = S0 exp(-λ RACL). From that we find: RACL = λ-1ln (S0/SACL), where S0 > SACL. Since at v > 1 m/s in real conditions of the shallow sea for small-scale and medium-scale turbulent processes ε ≪1 [8], from (8) exactly to ε2 values we have:

$$ \lambda = m/u_{0} ,\quad {\text{S}} = {\text{S}}_{0} e^{{ - \frac{m}{{u_{0} }}x}} {\text{R}}_{\text{ACL}} = \frac{{u_{0} }}{m}\ln \frac{{S_{0} }}{{S_{ACL} }} $$
(9)

Thus, it can be claimed that in the region \( {\text{x}} > {\text{R}}_{\text{ACL}} \), where \( {\text{R}}_{\text{ACL}} \) is determined by the formula (9), the concentration of pollutants will correspond to the sanitary norms.

Now we study the nonstationary solution of problem (4)–(6). Imagine it as:

$$ {\text{S}} = {\text{S}}_{0} { \exp }\left( { - {\text{mx}}/{\text{u}}_{0} } \right)(1 + {\text{m}}\theta )/{ \exp }\left( {m\theta } \right) $$
(10)

here \( \theta = t - x/u_{0} \). According to (6), \( \theta \ge 0 \).

Expression (10) is an exact solution of the boundary value problem (4)–(6). We rewrite it as follows:

$$ {\text{S}} = {\text{S}}_{0} {\text{F}}(\theta ){ \exp }\left( { - {\text{mx}}/{\text{u}}_{0} } \right),{\text{F}} = (1\theta )/{ \exp }({\text{m}}\theta ) $$
(11)

Since \( 0 \le {\text{F}}\left(\uptheta \right) \le 1 \), then the estimates (9) obtained in the previous case are valid. Taking into account (3), we write (9) it as follows:

$$ {\text{R}}_{\text{ACL}} = \left( {4{\text{k}}/{\text{m}}} \right)\ln \left( {{\text{S}}_{0} /{\text{S}}_{\text{ACL}} } \right) $$
(12)

It is seen from (12) that RACL is directly proportional to V (the wind speed) and inversely proportional to m (the destruction coefficient).

We consider now the case when \( {\text{S}}_{0} \) is a function of time t and satisfies the following conditions:

$$ {\text{S}}_{0} \left( 0 \right) = 0,\;{\text{S}}_{0} \left( {\text{t}} \right) \to 0\,{\text{if}}\,{\text{t}} \to \infty ;\quad { \hbox{max} }\,{\text{S}}_{0} \left( {\text{t}} \right) = {\text{C}} $$
(13)

We formulate the initial and boundary conditions for Eq. (4), when relations (6) are satisfied, in the following:

$$ {\text{S}}\left( {{\text{x}},0} \right) = 0,\;{\text{S}}\left( {0,{\text{t}}} \right) = {\text{S}}_{0} \left( {\text{t}} \right), \;{\text{S}} \to 0\,{\text{if}}\,{\text{x}} \to \infty ,{\text{S}} \to 0\,{\text{if}}\,{\text{t}} \to \infty $$
(14)

Then the exact solution of the boundary-value problem (4), (6), (14) for D = 0 can be represented as follows:

$$ {\text{S}} = {\text{S}}_{0} (\uptheta){ \exp }\left( { - {\text{mx}}/{\text{u}}_{0} } \right),\quad\uptheta = {\text{t}} - {\text{x}}/{\text{u}}_{0} $$
(15)

Since S0(θ) is bounded from above (see (13)), then, by analogy with the previous cases, for an arbitrary form of the function S0(t) satisfying conditions (13), the following equality holds:

$$ {\text{R}}_{\text{ACL}} = 4{\text{k }}\left( {{\text{V}}/{\text{m}}} \right){ \ln }\left( {{ \hbox{max} }\,{\text{S}}_{0} \left( {\text{t}} \right)/{\text{S}}_{\text{ACL}} } \right) $$
(16)

If D ≠ 0, we use the Laplace transform to solve the boundary value problem (4), (6), (14). Thus we have:

$$ \overline{S} ({\text{x}},\upnu) = \overline{S}_{0} (\upnu){ \exp }[\uplambda(\upnu){\text{x}}], $$
(17)
$$ {\text{where}}\,\uplambda = (1 - \sqrt {1 + 4\left( {\nu + m} \right)D/u_{0}^{2} } )\text{u}_{0} /\left( {2{\text{D}}} \right),\; \left( {{\text{Re}}\,\uplambda < 0} \right) $$
(18)
$$ \overline{S} ({\text{x}},\upnu) = \mathop \smallint \nolimits_{0}^{\infty } e^{ - \nu t} S\left( {x,t} \right)dt, \bar{S}_{0} (\nu ) = \mathop \smallint \nolimits_{0}^{\infty } e^{ - \nu t} S_{0} \left( t \right)dt. $$

Applying the inversion formula [11] to (17), we obtain:

$$ {\text{S}}\left( {{\text{x}},{\text{t}}} \right) = \frac{1}{2\pi i}\mathop \smallint \nolimits_{\nu - i\infty }^{\nu + i\infty } e^{\nu t} \bar{S}_{0} \left( \nu \right)e^{\lambda \left( \nu \right)x} dt $$
(19)

Further investigation of the integral (19) is carried out for a specific form of the function S0(t) satisfying the conditions (13) (see Fig. 1):

Fig. 1.
figure 1

S0(t), describing the entry of pollutants into the sea

Full size image
$$ S_{0} = C_{0} \alpha /\left( {1 - e^{ - \beta t} } \right)e^{ - \alpha t} ,\quad \alpha > 0,\beta > 0,\alpha + \beta < m $$
(20)
$$ \bar{S}_{0} = \alpha C_{0} /\left[ {\left( {\nu + \alpha } \right)\left( {\nu + \alpha + \beta } \right)} \right] $$
(21)

Taking into account (21) and using the theory of residues [11] to calculate the integral (19), we find:

$$ S = C_{0} \frac{\alpha }{\beta }\left[ {e^{ - \alpha t} e^{{\lambda \left( { - \alpha } \right)x}} - e^{{ - \left( {\alpha + \beta } \right)t}} e^{{\lambda \left( { - \alpha - \beta } \right)x}} } \right] $$
(22)

As it has been noted above, if v > 1 m/s, for real conditions of small-scale and medium-scale turbulent processes in the shallow sea, the inequality ε§1 is valid (see (8) and (20)). Then, according to (18), with exact quantities of order ε2, we have:

$$ \lambda \left( \alpha \right) = - \left( {m - \alpha } \right)/u_{0} ;\quad \lambda \left( {\alpha + \beta } \right) = - \left( {m - \alpha - \beta } \right)/u_{0} $$
(23)

Substituting (23) into (22) and taking into account (20), we obtain the Eq. (15), where the function S0(0) is given by formula (20). Then Eq. (16) will be valid, where, according to (20), we determine:

$$ max\,S_{0} \left( t \right) = C_{0} \left[ {\left( {\alpha /\left( {\alpha + \beta } \right)} \right)} \right]^{{\left( {\alpha + \beta } \right)/\beta }} $$
(24)

We can note that, in contrast to the previous case (D = 0), the solution found is not exact and will be valid only for specific functions of the form (20).

Thus, \( {\text{R}}_{\text{ACL}} \) obtained for open sea areas in stationary (12) and nonstationary (16) cases show that for small conditions if V > 1 m/s the small-scale and medium-scale turbulent processes of surface transport and decay of pollutants dominate over diffuse processes. \( {\text{R}}_{\text{ACL}} \), within the approximations adopted, does not depend on the depth of the sea and is completely determined by the hydrometeorological conditions (wind speed and direction), as well as the destructive features and conditions of the arrival of non-conservative pollutants into the sea.

3 Analysis of Numerical Experiments

Let us now study the transfer of pollutants in the coastal zone of the sea, taking into account surging phenomena. Let us consider the case of wind surges caused by a wind field moving along the shore. Let us set the OX axis along the shoreline in the direction of wind speed, the axis OY - perpendicular to the shore. In the framework of the linear theory of long waves averaged over the depth of the hydrodynamic equation, we represent it as follows [12, 13]:

$$ \partial u/\partial t - f\nu { = \tau /}\rho {H}\text{,}\,\partial\upnu/\partial t + fu = - g\partial \xi \text{/}\partial y $$
(25)
$$ \left( {\partial u/\partial x + \partial\upnu/\partial y} \right) + \partial \xi /\partial t = 0 $$
(26)

The solution of the system (25) and (26) corresponding to the stationary transfer v(y) directed perpendicular to the shore (v(0) = 0), being independent of x is the following [12]:

$$ v = - \tau \left[ {1 - exp\left( { - y/r} \right)} \right]/\left( {\rho Hf} \right) $$
(27)
$$ u =\uptau\,te\left( { - y/r} \right)/\left( {\rho \,H} \right),\xi =\uptau\,t\,exp\left( { - y/r} \right)/\left( {\rho \,c} \right) $$
(28)
$$ {\text{here}}\,c = \sqrt {gH} ,{\text{r}} = {\text{c}}/{\text{f}} - {\text{Rossby}}\,{\text{radius}} $$

Equations (27) and (28) show that the existence of a shore boundary leads to surges, and since the velocity is perpendicular to the shore and constant, water at the shore will continuously accumulate and the level ξ(y, t) will increase proportionally to time.

We estimate the transfer of pollutants in the coastal zone, using the formula (27). We place the source of contamination with the initial concentration S0 at a distance \( l \) from the shore at the origin, the X axis is oriented in the direction of the Ekman flow, perpendicular to the shoreline (parallel to the OY axis in the hydrodynamic equations (25) and (26)). Then, according to (2) and (27), the maximum value for the velocity of the Ekman flow \( v \) can be written as follows:

$$ u_{0} = max\left| v \right| = \gamma V^{2} \left[ {1 - exp\left( { - l/r} \right)} \right]/\left( {\rho Hf} \right). $$

In this case, taking into account (9), we obtain:

$$ R_{ACL} = \left[ {\gamma /\left( {m\rho Hf} \right)} \right]\left[ {1 - exp\left( { - l/r} \right)} \right]ln\left( {S_{0} /S_{ACL} } \right)V^{2} $$
(29)

Comparing the expressions (12) and (29), it should be noted that for the open sea regions there is a linear dependence of the \( {\text{R}}_{\text{ACL}} \) on the wind speed V, and in case if there is a shoreline and storm surges, it is quadratic. Equation (29) also shows that in the conditions of storm surges, \( {\text{R}}_{\text{ACL}} \) essentially depends on the geographic features of the given area of the coastal zone (depth H, remoteness of the pollution source from shore l, Coriolis parameter f).

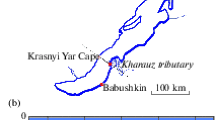
Figure 2 shows the results of \( {\text{R}}_{\text{ACL}} \) calculations performed for open areas of the Sea of Azov according to the meteorological stations Taganrog, Berdyansk, Kerch [14] if , n = 2, \( {\text{m}} = 25 \cdot 10^{ - 5} \cdot {\text{c}}^{ - 1} \), ZV BPK5.

Fig. 2.
figure 2

\( {\text{R}}_{\text{ACL}} \) calculated for the Sea of Azov with given distributions of the wind speed (1 line of the scale) in the areas of stations (a) Taganrog, (b) Berdyansk, (c) Kerch.

Full size image

Table 1 shows the values of \( {\text{R}}_{\text{ACL}} \) calculated for the case of surges, when the source of pollutants BPK5 is 700 m from the shore (n = 2, l = 700 m).

Table 1. The results of \( {\text{R}}_{\text{ACL}} \) calculations for characteristic ranges of maximum speed values of the north-east wind in the areas of the Berdyansk and Taganrog stations (l = 700 m)
Full size table

4 Conclusion

Thus, the results obtained allow us to forecast and assess the level of hazard and risks associated with the pollutants that spread in the marine environment. For example, as it can be seen from the table \( {\text{L}} = 1 - {\text{R}}_{\text{ACL}} \), which determines the size of the sanitary zone \( \left( {{\text{S}} < {\text{S}}_{\text{ACL}} } \right) \), can be negative even if V = 19 m/s.