Keywords

1 Introduction

In the exploration stage of a geothermal reservoir, the estimation of bottomhole temperatures is a fundamental activity to estimate the available energy potential and the feasibility of exploiting its resources for the generation of electric power [1]. For this, there are low cost geothermometric tools that allow obtaining an approximate bottomhole temperature based on the chemical composition of the sampled fluids of natural manifestations of geothermal reservoirs (thermal springs, geysers or volcanoes).

Today there are several geothermometric tools reported in the literature, several of which tend to overestimate temperatures, due in large part to the fact that the amount of data available for development is small or its origin is unreliable.

For the development of a geothermometric tool that improves the estimations of bottomhole temperatures, a geochemical data base of n = 708 is available, which contains measured temperatures and concentrations of eight main components of wells producing different parts of the world. Unfortunately, the geochemical database shows absence of data in some variables since they were not reported by the original authors.

The missing data in the geochemical database represents a limitation to attack the problem of estimation of bottomhole temperatures, since incomplete data sets can cause bias due to differences between observed and unobserved data. The most common approach to managing missing values is the analysis of complete cases [2]. However, Allison [3] observed that this approach reduces the sample size and study power. Alternatively, this problem can be solved by means of data imputation, which consists of the replacement of missing data by calculated values [4].

The imputation can be generally classified into statistical techniques and machine learning [5]. This work compares the performance of four statistical techniques for the imputation of missing data [6]: mean, median, stochastic linear regression, and Support Vector Machines (SVM). In the imputation of the geochemical database, using the techniques mentioned above, the data set (n = 150) that did not contain missing data were extracted, which were later split into two groups, a for training and another for testing. The results showed that the stochastic regression and SVM methods estimated more precise missing values than the substitution methods by the mean and median.

The rest of the document is organized as follows: Sect. 2 presents some studies related to the imputation of the mean, median, stochastic regression and SVM. Section 3 describes the mechanisms of missing data, as well as the proposed techniques for imputation of the geochemical database. Section 4 includes the information of the data, the experimental configuration and the results obtained from the evaluation of the performance of each method. Finally, the conclusions of the document and future work are exposed in Sect. 5.

2 Literature Review

Currently, no reported works have been found in the literature in which the imputation to geothermal fluids data is performed. However, there are reports studies in other areas, such as environmental pollution, air quality and medicine. Norazian, et al. [7] and Noor [8] applied the interpolation and imputation of the mean in a set of PM10 concentration data, simulated different percentages of missing data, and concluded that the mean is the best method only when the number of missing values is small. Razak, et al. [9] evaluated the methods of imputation of the mean, hot deck and maximization of expectations (EM) in PM10 concentrations, and concluded that the error of these methods is considerable when the percentage of missing data is very high (e.g., 50%). Junninen, et al. [10] compared the performance of various imputation methods in a set of air quality data, and concluded that multivariate statistical methods (e.g., regression-based imputation) are superior to univariate methods (e.g., linear, spline and nearest neighbor interpolation). Yahaya, et al. [11] compared univariate imputation techniques (e.g., mean, median, nearest neighbor, linear interpolation, spline interpolation and regression) in Weibull distributions, and obtained that no single imputation technique is the best for each sample size and for each percentage of missing values.

On the other hand, the imputation of values in the medical area has also been applied. Jerez, et al. [12] applied several methods of statistical imputation (e.g., mean, hot-deck and multiple imputation), and machine learning techniques (e.g., multi-layer perceptron, self-realization maps and k-nearest neighbor) in an extensive real breast cancer data set, where methods based on machine learning techniques were the most suited for the imputation of missing values. Engels, et al. [13] compared different methods of imputing missing data on depression, weight, cognitive functioning, and self-rated health in a longitudinal cohort of older adults, where the imputations that used no information specific to the person, such as using the sample mean, had the worst performance. In contrast, Shrive, et al. [14] compared different imputation techniques for dealing with missing data in the Zung Self-reported Depression scale, and showed that the individual mean and single regression method produced similar results, when the percent of missing information increased to 30%. Also, Newman [15], Olinsky, et al. [16], Aydilek, et al. [17] reported comparative studies of various imputation techniques such as stochastic regression, fuzzy c-means and SVR. Finally, Wang, et al. [18] demonstrated that the SVR impute method has a powerful estimation ability for DNA microarray gene expression data.

3 Methods to Treat Missing Data

The reasonable way to handle missing data depends on how the data points are missing. In 1976 Rubin [6] classified the data loss into three categories. In your theory, each data point has some probability of missing. The process that governs these probabilities is called the response mechanism or missing data mechanism. To explain these three categories Z is denoted as a variable with missing data, S as a set of complete variables, Rz as a binary variable that has a value of 1 if the data in Z is missing and 0 if observed. The categories of the Rubin classification can be expressed by the following statements:

Missing Completely At Random (MCAR)

$$ \Pr \left( {{\text{Rz}} = 1 | {\text{S}}, {\text{Z}}} \right) = { \Pr }\left( {{\text{Rz}} = 1} \right) $$
(1)

That is, the probability of missing a value in Z does not depend either on S or Z and therefore its estimates cannot depend on any variable.

Missing At Random (MAR).

$$ \Pr \left( {{\text{Rz}} = 1 | {\text{S}}, {\text{Z}}} \right) = \Pr ( {\text{Rz}} = 1 | {\text{S}}) $$
(2)

Where the loss of a value in Z depends on S but not on Z, therefore its estimation can depend on S.

Missing Not At Random (MNAR)

$$ \Pr \left( {{\text{Rz}} = 1 | {\text{S}},{\text{Z}}} \right) = \Pr \left( {{\text{Rz}} = 1 | {\text{Z}}} \right) $$
(3)

The absence of data in Z depends on Z itself, to generate estimates under this assumption, special methods are required.

Rubin’s distinction is important, since his theory establishes the conditions under which a method to deal with missing data can provide valid statistical inferences. On several occasions, the assumption that data loss is MAR is acceptable and that a treatment can be resorted to using imputation methods. Unfortunately, the assumptions that are necessary to justify a method of imputation are generally quite strong and often unverifiable [3].

3.1 Proposed Methods

The present work focuses on the imputation of the geochemical database based on the assumption that the loss is MAR. The available information may be used to estimate the missing values. The use of the complete analysis method Schafer [2] was discarded, which consists in ignoring the records that contain missing data, because applying this method is practical only when the number of incomplete records is less than 5% of the total data and the data loss is of the MCAR Buuren type [19]. The geochemical database is incomplete in more than 50% and its MAR type loss is assumed.

The single imputation methods are broadly classified into statistical and machine learning techniques [5]. The most commonly imputed forms of imputation are substitution by means, median and stochastic regression [15]. Within the current machine learning techniques, we can find of SVM. The imputation with statistical techniques provides estimates of lost values by replacing them with the observed data. When the variables are continuous, the simplest statistical parameters based on the mean and median are used.

3.2 Mean and Median Imputation

Substitution by the mean is an imputation technique where the missing data for any variable is completed with the average of the observed value of that variable [20]. The average is obtained by Eq. 4.

$$ \bar{x} = \frac{{\mathop \sum \nolimits_{i = 1}^{n} x_{i} }}{n} $$
(4)

On the other hand, impute the median is done from an ordered vector that contains the observed data of an incomplete variable, the missing values of said variable are imputed through Eq. 5.

$$ \begin{array}{*{20}l} {\tilde{x} = X_{{\left[ {\frac{n + 1}{2}} \right]}} , {\text{if}}\;n\;{\text{is }}\;{\text{even}}} \hfill \\ {\tilde{x} = \frac{{X_{{\left[ {\frac{n + 1}{2}} \right]}} + X_{{\left[ {\frac{n}{2}} \right]}} }}{2},{\text{if}}\;n\;{\text{is}}\;{\text{odd}}} \hfill \\ \end{array} $$
(5)

The use of these techniques entails the disadvantage that the variance of the imputed variable is systematically underestimated.

3.3 Imputation Stochastic Regression

A slightly more robust but popular method is stochastic regression, in which the variable with the missing data uses all other variables to produce a regression equation (depending on the complete cases).

$$ \hat{Y} = \beta_{0} + \beta_{1} X1 + \ldots + \beta_{p} XP + \epsilon $$
(6)

where \( \beta_{0} \) is the intersection, \( \beta_{1} , \ldots \beta_{p} \) are the rate of change of \( \hat{Y} \) for a unit change in \( X1, \ldots ,XP \) correspondent \( X1, \ldots ,XP \) are the predictors and \( \epsilon \) random noise added to \( \hat{Y} \). The random error term is a normal random variant with a mean of zero and a standard deviation equal to the standard error of the estimation of the regression equation [15]. The addition of the random error is a method used to avoid that the variance of the imputed variable is underestimated, and the correlations with the imputed variable are overestimated.

The most important thing when modeling the equation for an incomplete variable is the selection of predictors. The inclusion of as many predictors as possible tends to make the MAR assumption more plausible [3]. The missing values are replaced with predicted values of the regression equation.

One strategy for selecting predictive variables is to inspect their correlations and the response indicator, the latter measures the percentage of observed cases of one variable while there is absence in another. This means that a variable that has good correlation with the target variable must also have a high proportion of observed data to be a predictor.

3.4 SVM Imputation

In supervised learning techniques, imputation is considered a pattern classification task [5]. In them the missing values are the output obtained and the observed values are the inputs used for the training of the models. SVM is one of the machine learning techniques currently used for imputation.

Support Vector Regression (SVR) proposed by Drucker et al. [21], is the regression version of Support Vector Machines [22]. This method fits a hyperplane to a continuous dependent variable y in terms of one or more continuous independent variables, i.e. \( y = f\left( {\varvec{x},\varvec{\theta} } \right) \), where \( y \in {\mathbb{R}} \) is the dependent variable, \( \varvec{x} \in {\mathbb{R}}^{N} \) is a vector of N independent features, and \( \varvec{\theta}\in {\mathbb{R}} \) is a vector of model parameters. SVR estimates the hyperplane by minimizing the Structural Risk which guarantees a good generalization of the model by controlling its complexity [21]. This control is achieved by wrapping the hyperplane with a margin which (a) constrains the number of points that the function can represent, and (b) obtains a f in terms of a subset of the train sample which is called Support Vectors (SV). Additionally, SVR can handle data noise and nonlinearity: the former is achieved by including slack variables into the model’s formulation, whereas the latter is achieved by the Kernel Trick [23]. Although SVR has been neatly defined elsewhere [21], for the sake of completeness we now provide its formulation:

$$ \begin{array}{*{20}c} {{\text{Max}}. {\text{W}}\left( {\upalpha,\upalpha^{ *} } \right)} \\ { = - \frac{1}{2}\sum\nolimits_{{{\text{i}},{\text{j}} = 1}}^{\text{m}} {\left( {\upalpha_{\text{i}} -\upalpha_{\text{j}}^{ *} } \right)\left( {\upalpha_{\text{i}} -\upalpha_{\text{j}}^{ *} } \right)\left\langle {\upphi\left( {{\mathbf{x}}_{\text{i}} } \right),\upphi\left( {{\mathbf{x}}_{\text{j}} } \right)} \right\rangle } -\upvarepsilon\sum\nolimits_{{{\text{i}} = 1}}^{\text{m}} {\left( {\upalpha_{\text{i}}^{ *} +\upalpha_{\text{i}} } \right)} } \\ { + \mathop \sum \limits_{{{\text{i}} = 1}}^{\text{m}} \left( {\upalpha_{\text{i}}^{ *} -\upalpha_{\text{i}} } \right){\text{y}}_{\text{i}} } \\ {{\text{subject to}}\sum\nolimits_{{{\text{i}} = 1}}^{\text{m}} {\left( {\upalpha_{\text{i}} -\upalpha_{\text{i}}^{ *} } \right) = 0} } \\ {0 \le\upalpha_{\text{i}} ,\upalpha_{\text{i}}^{ *} \le {\text{C}}, \forall {\text{i}} = 1, \ldots ,{\text{m}},} \\ \end{array} $$
(7)

where \( {\text{C}} \) is the complexity penalization term, \( \varepsilon \) is the width of the margin, \( \phi \) is the kernel function, and \( \alpha ,\alpha^{*} \) corresponds to the weights of each element in the train set. Particularly, those \( \alpha ,\alpha^{*} \ge 0 \) correspond to the SV.

4 Experimentation

The main objective of this work is to evaluate the proposed unique imputation techniques, applied to a set of geochemical data to increase the sample that has and thus allow the development of a geothermometric tool that better estimates the bottomhole temperatures of a geothermal reservoir. To do this, we have a geochemical database with 708 rows, each one represents a well producing geothermal energy, by 9 columns that correspond to the measured temperature (℃) of the well and the chemical concentrations of Li, Na, K, Mg Ca, Cl, \( SO_{4} \) and \( HCO_{3} \) given in mg/L. Table 1 shows the descriptive statistics and the total of missing values.

Table 1. Statistical information for bottomhole temperatures and compositional database of geochemical fluids.
Full size table

As shown in Table 1, the temperature and the Na and K components have no missing data. However, the components Li, Mg, Ca, Cl, \( SO_{4} \) and \( HCO_{3} \) are incomplete. Figure 2 shows the percentages that represent the missing data of each variable (Fig. 1).

Fig. 1.
figure 1

Histogram of missing data. Shows the percentage of missing data in each variable of the geochemical database. The temperature, Na and K have no missing values, but the rest of the variables there is a percentage of missing data: Li 63%, HCO3 58%, SO4 26%, Cl 22%, Mg 16%, Ca 6%.

Full size image

Variables such as Li and \( HCO_{3} \) are incomplete by more than 50%. To avoid discarding possible useful data for the development of a geothermometric tool that improves the bottomhole temperature estimates of a geothermal energy producing well, unique imputation methods were implemented, using statistical techniques such as mean, median and stochastic regression and machine learning. such as SVM.

4.1 Experimental Configuration

The geochemical database was divided into two sets. A complete set with the 150 rows that have all their observed chemical elements and another with the 558 records with missing data. From the complete data set, 120 rows (80%) were taken for training of the models of each variable and 30 rows (20%) for testing. From the training set, the mean and median of each incomplete variable were obtained and the values obtained replaced the missing values of the incomplete set.

For the stochastic regression and SVM imputation, we first analyzed the relationship between the observed data of the variables, by means of the pairwise correlation and the response indicator (described in Sect. 3) to determine the predictor variables that would be included in the model of incomplete variables.

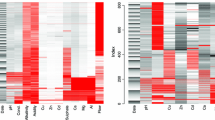
Figure 2a shows the correlation of the observed data for each pair of variables in the geochemical database. Figure 2b shows the percentage of observed data of one variable while the other variable has lost data. For example, to determine the predictive variables of Li, according to Fig. 2a, Li has a correlation above 0.5 with Na, K, Ca and Cl, as well as a correlation very close to 0 with Temperature, Mg, \( SO_{4} \) and \( HCO_{3} \). Moreover, according to Fig. 2b, when Li has missing data, the variables Temperature, Na, K and Ca have a proportion of data observed in more than 75%. Therefore, the predictive variables of Li can be Na, K and Ca.

Fig. 2.
figure 2

(a) Correlation matrix shows the correlation of the observed data for each pair of variables; the yellow boxes indicate a correlation of 1, while the blue boxes indicate a close negative correlation to 0. (b) Response indicator indicates the percentage of observed data of one variable while the other variable has lost data, the yellow color indicates 100% and the blue 0%. The Temperature, Na and K have columns in blue totally since these variables do not contain missing data. Both are read from left to right, from bottom to top. (Color figure online)

Full size image

The same analysis was carried out to select the predictive variables of the rest of the incomplete variables of the geochemical database. It is important to mention that in some variables very low correlations were found with the other variables and at the same time when the variable had missing data, they were also missing in the rest of the variables. Despite this, the variables that obtained the highest values in comparison with the others were selected as predictors. The predictors for each incomplete variable are shown in Fig. 3.

Fig. 3.
figure 3

Predictors matrix indicates in purple the predictors of each incomplete variable. It reads from left to right, from bottom to top.

Full size image

4.2 Method Validation

To quantify the accuracy of the imputation models in the prediction of missing data, the two precision measures detailed below were used:

Root Mean Squared Error (RMSE) which indicates the variance in the estimates, has the same units as the measured and calculated data. The smaller values indicate a better concordance between the true values and the estimated ones.

$$ RMSE = \sqrt {\left\langle {\left( {x_{c} - x_{m} } \right)^{2} } \right\rangle } $$
(8)

Mean Absolute Error (MAE) like the RMSE, smaller values of MAE indicate a better concordance between the true and calculated values. MAE outputs a number that can be directly interpreted since the loss is in the same units of the output variable.

$$ MAE = \left\langle {\left| {x_{c} - x_{m} } \right|} \right\rangle $$
(9)

4.3 Results and Discussion

The imputation techniques were implemented in the set of test data extracted from the complete set of the database, with this the RMSE and MAE errors could be measured between the predicted and the measured values. Tables 2 and 3 show the results of RMSE and MAE of the estimates of the mean, median, stochastic regression and SVM.

Table 2. Comparison of RMSE values obtained by the imputation methods of the mean, median, stochastic regression and SVM.
Full size table
Table 3. Comparison of MAE values obtained by the imputation methods of the mean, median, stochastic regression and SVM.
Full size table

The results presented in Tables 2 and 3 show that the imputations by the mean and median have the highest errors in most of the experiments compared to the stochastic regression and SVM methods. With the exception, for the variables Mg (16% of missing data) and \( HCO_{3} \) (58% of missing data), in which the imputation of the median was the best according to the MAE parameter. On the other hand, the stochastic regression was the best (according to RMSE and MAE) in the imputation of the variables of Ca and Cl, which presented 16% and 22% of missing data, respectively. While, the SVM method obtained the best results (according to RMSE) in the estimation of Li (63% missing data), Mg (16% of missing data), \( SO_{4} \) (26% missing data) and \( HCO_{3} \) (58% of Missing data). Finally, with these results it was found that the best methods to estimate the lost values of the variables of Ca and Cl is the stochastic regression; and for the variables Li, Mg, \( SO_{4} \) and \( HCO_{3} \) is SVM.

5 Conclusions

In this paper, the unique imputation methods were compared by means, median, stochastic regression and SVM, applying them in a geochemical data set of geothermal fluids. This study is aimed at obtaining a complete and larger geochemical database that allows the development of a geothermometric tool that best estimates the bottomhole temperatures of a geothermal reservoir. From the complete data set, the training (80%) and testing (20%) sets were obtained. From training set, the mean and median values were calculated to replace the missing values, as well as the regression and SVM imputation models were developed.

To evaluate the performance of these methods, two indicators were calculated, the mean absolute error (MAE) and mean square error (RMSE) between the test set and the values estimated by the methods. The results showed that the stochastic regression and SVM are superior to the mean and median. From these performance indicators, it is concluded that the best methods to estimate the lost values of the variables of Ca and Cl are stochastic regression; and for the variables Li, Mg, \( SO_{4} \) and \( HCO_{3} \) is SVM. Therefore, both techniques were used for the completion of the geochemical database.

As future work, our task will be to analyze the statistical distribution of the imputation errors for the possible choice of more sophisticated validation parameters not sensitive to the presence of discordant values. On the other hand, the future plans for the project are to carry out a detailed study of the new complete geochemical database to develop a new geothermometric model.