Keywords

1 Introduction

Morphing techniques can be used to represent the continuous transformation of a geometry, e.g. a polygon or a polyline, between two observations, i.e. a source and a target known geometries, and their main goal is to obtain a smooth and realistic transformation. However, the geometric characteristics of the observations can influence the quality of the interpolation. For example, a low-quality mesh is more likely to cause numerical problems and generate self-intersecting (invalid) geometries during interpolation. A high-quality mesh is more likely to generate natural transformations. This is a well-known problem, and several smoothing and remeshing methods and metrics have been proposed in the literature to measure and improve mesh quality [6, 11, 13]. However, to the best of our knowledge, there are no established methodologies to assess the quality of the interpolation with respect to the actual evolution of the object being represented.

In this paper we use the compatible triangulation method proposed in [6], and the rigid interpolation method proposed in [1, 3], with smoothing and remeshing methods, to represent the continuous evolution of deformable moving objects from a set of observations. Our main goal is to devise automatic processes to generate an approximation of the actual evolution of real-world phenomena with a known error, in the context of spatiotemporal data management and spatiotemporal databases. We implemented several smoothing and remeshing methods to improve the quality of the observations and studied its influence on the quality and validity of the intermediate geometries.

This paper is organized as follows. Section 2 introduces some background and related work. Section 3 presents the methods that were implemented and studied. The experimental results are presented and discussed in Sects. 4 and 5 presents the conclusions and future work.

2 Background

We use the sliced representation proposed in [5] to represent deformable moving objects, also known as moving regions. In the sliced representation, a moving object is an ordered collection of units, a unit represents the continuous evolution, i.e. the changes in position, shape and extent, of the moving object between two consecutive observations, and the evolution of the moving object within a unit is given by a function (Fig. 1) that should provide a good (realistic) approximation of the actual evolution of the object being represented, generate only valid intermediate geometries, and allow the processing of large datasets.

Fig. 1.
figure 1

Sliced representation.

Full size image

The first algorithm proposed in the spatiotemporal databases literature to create the so-called moving regions from observations was proposed in [12]. This method was extended in more recent works [7,8,9]. These methods use the concept of moving segments to represent the evolution of a moving region during a unit. The authors main focus is on the robustness and complexity of the algorithms, and they make tradeoffs that have a significant impact on the quality of the intermediate geometries. Indeed, these more recent algorithms are robust and have low complexity, but may cause deformation of the intermediate geometries, and the approximation error can be too big to be neglected in scientific work, e.g. if a rotation exists the intermediate geometries tend to inflate at the middle of the interpolation, and the methods used to handle concavities either do not perform well with noisy data [7, 10, 12] or make the intermediate geometries approximately convex during interpolation, causing deformation [8, 9].

On the other hand, several morphing techniques exist to represent the continuous evolution of a geometry between a source and a target geometry. These methods are successfully used in animation packages and computer graphics, and their main goal is to obtain a smooth and realistic interpolation. For example, when using compatible triangulation and rigid interpolation methods there are two main steps to compute the evolution of a deformable moving object between two observations. In step 1, we find a compatible triangulation between the two observations. The compatible triangulation method receives two polygons, P and Q, and generates two triangular meshes, P* and Q*. P and Q must have a one-to-one correspondence between their vertices, and P* and Q* must have a one-to-one correspondence between their triangles. In step 2, the rigid interpolation method is used to generate the evolution of the deformable moving object between P* and Q*.

3 Methods

The following methods were implemented: an angle-improving (Delaunay) edge-flips method, the weighted angle-based smoothing, the area equalization smoothing, the remeshing, and the edge-splits refinement methods proposed in [6], the classical Laplacian smoothing method, and the smoothing methods proposed in [2]. A new position is used if it improves the current geometry given some criteria, the new positions are updated sequentially, i.e. immediately, (Another option is to update them simultaneously, but we did not consider it.) and if not mentioned explicitly, the method is applied individually to each mesh.

3.1 Compatible Angle-Improving (Delaunay) Edge-Flips

To check if an edge is locally Delaunay we can perform two tests [4]. The edge p1p3 (Fig. 2, left) is locally Delaunay if the sum of the angles at the points p2 and p4 is less than or equal to 180°, or if the circumcircle (the dashed circle) of one of its adjacent triangles does not contain the opposite point in the other triangle. In this case, edge p1p3 is non-locally Delaunay and needs to be flipped to become edge p2p4, which is locally Delaunay. This method is applied to two compatible meshes simultaneously and preserves their compatibility. An edge is only flipped if it is non-locally Delaunay in both meshes.

Fig. 2.
figure 2

Delaunay edge-flips (left) and weighted angle-based smoothing (right).

Full size image

3.2 Weighted Angle-Based Smoothing

In [6] the authors propose using two rules to improve the angles of the triangles incident on a point c (Fig. 2, right). In the first one, the new position cnew is the average of all the ci computed for all the neighbors, pi, of c, namely:

$$ {\text{c}}_{new} = \frac{1}{k}\sum\nolimits_{i = 1}^{k} {c_{i} } $$
(1)

where k is the number of neighbors of c, and ci is obtained by rotating c around pi to coincide with the bisector of αi (the angle formed at pi). The second rule introduces weights to take small angles into account, and Eq. (1) becomes:

$$ {\text{c}}_{new} = \frac{1}{{\mathop \sum \nolimits_{i = 1}^{k} \frac{1}{{\alpha_{i}^{2} }}}}\sum\nolimits_{i = 1}^{k} {\frac{1}{{\alpha_{i}^{2} }}c_{i} } $$
(2)

where αi is the angle formed at pi. We implemented both rules. They are called W. Avg and W. Angle, respectively.

3.3 Area Equalization Smoothing

This method finds the new position of an interior point c which makes the areas of its k adjacent triangles as close as possible, by minimizing the following function:

$$ \left( {x^{\prime}, y^{\prime}} \right) = \arg min\sum\nolimits_{i = 1}^{k} {\left( {A_{i} - \frac{A}{k}} \right)^{2} } $$
(3)

where (x′, y′) is the new position of c, Ai is the area of the i-th adjacent triangle to c, and A is the area of the polygon containing the k triangles adjacent to c.

3.4 Compatible Edge-Splits Refinement

The edge-splits refinement method was implemented using the criterion proposed in [6], given by the following rule

$$ e = {\text{arg }}max_{e \in P \cup Q} \frac{\left| e \right|}{{\left( {\theta_{min} \left( e \right)} \right)^{2} }} $$
(4)

where e is an edge, |e| is the length of the edge, and \( \theta_{min} \left( e \right) \) is the minimum angle adjacent to e. This refinement is performed simultaneously on two compatible meshes and preserves their compatibility.

3.5 Laplacian Smoothing and Simple Smoothing

Laplacian smoothing defines the new position of an interior point c as the average of the positions of its k adjacent points

$$ c '= \frac{1}{k}\sum\nolimits_{i = 1}^{k} {p_{i} } $$
(5)

where c′ is the new position of c, k is the number of points adjacent to c, and pi is the position of the i-th adjacent point.

The ‘Simple’ smoothing method was proposed in [2], and it works by performing a circular search with a decreasing radius around an interior point, to find new valid positions for that point that maximize the minimum area or angle, depending on the parameterization, of the triangles connected to it. If a new valid position is not found, the search radius decreases by a fixed factor. This method is called S. Max Area and S. Max Angle, depending on the criterion used.

3.6 The Remeshing Algorithm

The remeshing algorithm is presented in Algorithm 1. We have not yet established metrics to define the quality of a mesh, and its optimum number of Steiner (interior) points. Therefore, we define a maximum number of iterations to control the execution of the algorithm.

figure a

4 Experimental Results

We performed tests to study the quality of the interpolation with respect of the actual evolution of real-world phenomena.

4.1 Dataset

We used a dataset obtained from a sequence of satellite images tracking the movement of two icebergs in the Antarctic. The data and the procedures used to obtain this dataset are described in [10]. The one-to-one point correspondences defined in the original dataset were refined manually.

4.2 Tests

We studied the evolution of the area and the perimeter, the validity, and the geometric similarity (with respect to a known geometry) of the intermediate geometries during interpolation, when using the various smoothing and remeshing methods presented, the compatible triangulation method proposed in [6], and the rigid interpolation method proposed in [1, 3]. We collected statistics on the meshes representing observations: the number of triangles and Steiner points, the minimum and maximum angles, the number of angles lower and bigger than a given angle, the maximum and minimum triangle areas and the ratio between them, and information about the area, the perimeter, and the position of the centroid.

To compute the geometric similarity between two geometries we used the Hausdorff distance. The geometries being compared may have a different number of vertices and are aligned using partial Procrustes superimposition before measuring their similarity. The alignment is performed using a set of ‘landmarks’, i.e. points that exist in the source, target, and intermediate geometries, and whose position does not change significantly between them.

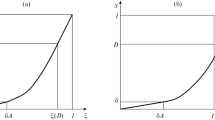
We are interested in a smooth and realistic evolution of the intermediate geometries. It makes sense that under these circumstances the evolution of the properties studied follows approximately monotonically increasing or decreasing functions. As such, we assume that during a unit the properties being studied evolve smoothly, and their expected minimum and maximum values are given by the source and target known geometries. Therefore, we consider a lower and upper bound, a deviation with respect to these bounds, and the inflection points of the functions that approximate the evolution of the properties studied during interpolation (Fig. 3, right). This allows us to compare the results obtained when using the different methods. For example, in (Fig. 3, left) we can observe that in some cases the area of the intermediate geometries is bigger or lower than the source and target areas. This may be an indication of an unnatural behavior. Inflection points can also be an indication of local or global deformation during interpolation. It makes sense to ‘penalize’ these situations.

Fig. 3.
figure 3

Evolution of the area of 1000 intermediate geometries (left), and upper and lower bounds, deviation and inflection points (right).

Full size image

Area Evolution During Interpolation.

For each method 1000 samples (intermediate geometries) were generated and their areas were recorded. Tests were performed to study the effect of using a different number (1, 5, 10, 20, and 40) of splits and iterations when using the Edge-Splits and the Remeshing methods, respectively.

The results suggest that the evolution of the area during interpolation follows approximately linear, quadratic and cubic functions. A method does not always follow the same function (although quadratic functions seem to be more common), and the evolution of the area can be represented differently by different methods (Fig. 3, left).

The results show that the Edge-Flips and the Edge-Splits (using 10 splits) are the least penalized methods (Fig. 4). The Remeshing method (using 5 iterations) is the most penalized. Increasing the number of iterations did not improve the results significantly, and, in general, as the number of iterations increases the enlargement of the geometry tends to become more and more evident. The biggest area deviations were 5% and 21% of the maximum expected area when using the Remeshing and the S. Max Area methods, respectively. In the case of the Edge-Splits method, the smallest area deviation was obtained when using 10 or less splits, and in some cases when using 40 splits. The results obtained using 10, 20, and 40 splits are similar, suggesting that there exists a ‘saturation’. The numbers on top of the bars in Fig. 4 indicate the number of times the area exceeded the expected upper and lower bounds during interpolation, e.g. the S. Max Area method was penalized in 4 of the 5 units representing the evolution of Iceberg 1 (Fig. 4, top), and the blocks stacked in the bars correspond to the percentage of the maximum area deviation for each method and unit. The results show that the S. Max Area method is the most unstable: it is the second most penalized method and reaches deviations larger than 20%. The other smoothing methods obtained similar results, and there is not a method that obtains the smallest area deviation in all cases.

Fig. 4.
figure 4

Maximum area deviation by method and unit (using Steiner points) for Iceberg 1 (top) and Iceberg 2 (bottom).

Full size image

Geometric Similarity During Interpolation.

We studied the geometric similarity of the intermediate geometries with respect to a known geometry (the source geometry of each unit). This can give information on how smoothly the geometry evolves during interpolation. For each unit, representing the continuous evolution of the iceberg between two observations, we generated 1000 intermediate geometries and collected data on the Hausdorff distance between each intermediate geometry and the source geometry. This metric is very sensitive to changes in the geometry. We consider inflexion points the most relevant indicator, e.g. the inflection point marked with a triangle (Fig. 5, top) may indicate an abrupt change in the geometry. (Figure 5, bottom-left and bottom-right) shows that the Remeshing and the D. E-Flips methods, and the Remeshing and the E-Splits methods, have less inflection points for iceberg 1 and 2, respectively.

Fig. 5.
figure 5

Example of inflection points (top), and number of inflection points by method for Iceberg 1 (bottom-left) and Iceberg 2 (bottom-right).

Full size image

The approximation functions (representing the evolution of the geometric similarity of the intermediate geometries) have a considerable number of inflection points, with more than 50% being within the established upper and lower bounds. And, not all of these points are an indication of a relevant (significant) change in the geometry. It would be interesting to study which of these points give more information about relevant changes in the geometry. Figure 6 presents the distance deviation.

Fig. 6.
figure 6

Distance deviations, Iceberg 1 (top), and Iceberg 2 (bottom).

Full size image

We also studied the evolution of the perimeter, but it is not presented here. The area and the perimeter can evolve in different ways, and a method can represent the evolution of one property better than the other, e.g. the Remeshing method tends to increase the area of the meshes during interpolation but gives the best results for the perimeter. We also observed that the one-to-one point correspondence between the source and target geometries has a significant influence on the results obtained and can produce invalid intermediate geometries. We obtained valid intermediate geometries for all the units used in the tests when using appropriate correspondences.

5 Conclusions and Future Work

We implemented and studied various smoothing and remeshing methods to improve the quality of triangular meshes, used with morphing techniques to represent the continuous evolution of deformable moving objects. While previous research on morphing techniques has focused on smooth and visually natural interpolations, our goal is to find which methods to use to obtain an interpolation, i.e. an approximation of the actual evolution of the object being represented, with a known error, that can be used in applied scientific work. These methods will be used to represent moving objects in spatiotemporal databases, and to implement operations to perform numerical analysis of real-world phenomena, e.g. the evolution of the shape and size of icebergs and cell morphology, or the propagation of forest fires.

We studied the evolution of the area, the perimeter and the geometric similarity, and the validity, of the intermediate geometries to study mesh quality metrics to evaluate the quality of the interpolation with respect to the actual evolution of the object being represented. The analysis of the statistics collected from the meshes shows that two meshes processed with different smoothing and remeshing methods can have exact or similar statistics but produce different results. This suggest that the statistics collected are not sufficient to characterize the quality of the meshes, and that there may be other factors that influence the evolution of the intermediate geometries. There is no method that is the best in all cases, and the same method can produce good results in some cases, and worse in others. This suggests that in some cases the method is not able to change certain geometric characteristics of the mesh, that can have a significant impact on the quality of the interpolation, e.g. long thin triangles at the mesh boundary can cause more or less significant local deformation during interpolation. The quality of the one-to-one point correspondence between two geometries can give rise to invalid geometries during interpolation and have a significant impact on the quality of the interpolation. Because of this, it was not possible to establish a clear relationship between the quality of the meshes and the quality of the interpolation, and we did not establish a metric to compute the approximation error of the interpolation with respect to the actual evolution of the object.

The Angle-Improving (Delaunay) Edge-Flips can be used by default since it is the method that, overall, obtains the best results, and its algorithmic complexity is reasonable (because of space constraints the algorithmic complexity of the methods is not presented here). This also applies when the evolution of the area or the algorithmic complexity are critical. In situations where the perimeter or the geometric similarity are a critical factor the Remeshing method can be used instead. The tests results suggest that the Remeshing method is more robust to abrupt local changes in the intermediate geometries.

In the future, we will collect and analyze other mesh statistics, study the relevance of the different inflection points, use more and diverse datasets, study which are the geometric features that are more relevant to the quality of the interpolation, and the use of well-known, well-established mesh quality improvement toolkits, e.g. the Mesh Quality Improvement Toolkit (MESQUITE) and the VERDICT library, to improve the quality of the meshes and collect mesh quality metrics.