Abstract
In this chapter, we will consider the problem of estimating a location vector which is constrained to lie in a convex subset of \(\mathbb {R}^P\). Estimators that are constrained to a set should be constrasted to the shrinkage estimators discussed in Sect.2.4.4 where one has “vague knowledge” that a location vector is in or near the specified set and consequently wishes to shrink toward the set but does not wish to restrict the estimator to lie in the set. Much of the chapter is devoted to one of two types of constraint sets, balls, and polyhedral cones. However, Sect.7.2 is devoted to general convex constraint sets and more particularly to a striking result of Hartigan (2004) which shows that in the normal case, the Bayes estimator of the mean with respect to the uniform prior over any convex set , \(\mathcal {C}\), dominates X for all \(\theta \in \mathcal {C}\) under the usual quadratic loss ∥δ − θ∥2.
Access provided by CONRICYT-eBooks. Download chapter PDF
7.1 Introduction
In this chapter, we will consider the problem of estimating a location vector which is constrained to lie in a convex subset of \(\mathbb {R}^P\). Estimators that are constrained to a set should be constrasted to the shrinkage estimators discussed in Sect.2.4.4 where one has “vague knowledge” that a location vector is in or near the specified set and consequently wishes to shrink toward the set but does not wish to restrict the estimator to lie in the set. Much of the chapter is devoted to one of two types of constraint sets, balls, and polyhedral cones. However, Sect.7.2 is devoted to general convex constraint sets and more particularly to a striking result of Hartigan (2004) which shows that in the normal case, the Bayes estimator of the mean with respect to the uniform prior over any convex set , \(\mathcal {C}\), dominates X for all \(\theta \in \mathcal {C}\) under the usual quadratic loss ∥δ − θ∥2.
Section 7.3 considers the situation where X is normal with a known scale but the constraint set is a ball, B, of known radius centered at a known point in \(\mathbb {R}^p\). Here again, a natural estimator to dominate is the projection onto the ball P B X. Hartigan’s result of course applies and shows that the Bayes estimate corresponding to the uniform prior dominates X, but a finer analysis lead to domination over P B X (provided the radius of the ball is not too large relative to the dimension) by the Bayes estimator corresponding to the uniform prior on the sphere of the same radius.
Section 7.4 will consider estimation of a normal mean vector restricted to a polyhedral cone, \(\mathcal {C}\), in the normal case under quadratic loss. Both the cases of known and unknown scale are treated. Special methods need to be developed to handle this restriction because the shrinkage functions considered are not necessarily weakly differentiable. Hence the methods of Chap.4 are not directly applicable. A version of Stein’s lemma is developed for positively homogeneous sets which allows the analysis to proceed.
In general, if the constraint set, \(\mathcal {C}\), is convex , a natural alternative to the UMVUE X, is P c X the projection of X onto \(\mathcal {C}\). Our methods lead to Stein type shrinkage estimators that shrink P c X which dominate P c X, and hence X itself, when \(\mathcal {C}\) is a polyhedral cone.
Section 7.5 is devoted to the case of a general spherically symmetric distribution with a residual vector when the mean vector is restricted to a polyhedral cone. As in Sect.7.4, the potential nondifferentiability of the shrinkage factors is a complication. We develop a general method that allows the results of Sect.7.4 for the normal case to be extended to the general spherically symmetric case as long as a residual vector is available. This method also allows for an alternative development of some of the results of Chap.6 that rely on an extension of Stein’s lemma to the general spherical case.
7.2 Normal Mean Vector Restricted to a Convex Set
In this section, we treat the case \(X \sim {\mathcal N}_{p}(\theta , \sigma ^{2} I_{p})\) where σ
2 is known and where the unknown mean θ is restricted to lie in a convex set
\(\mathcal {C} \subseteq \mathbb {R}^p\) (with nonempty interior and sufficiently regular boundary), and where the loss is L(θ, δ) = ∥δ − θ∥2. We show that the (generalized) Bayes estimator with respect to the uniform prior
distribution on \(\mathcal {C}\), say  , dominates the usual (unrestricted) estimator δ
0(X) = X. At this level of generality the result is due to Hartigan (2004) although versions of the result (in \(\mathbb {R}^1\)) date back to Katz (1961). We follow the discussion in Marchand and Strawderman (2004).
, dominates the usual (unrestricted) estimator δ
0(X) = X. At this level of generality the result is due to Hartigan (2004) although versions of the result (in \(\mathbb {R}^1\)) date back to Katz (1961). We follow the discussion in Marchand and Strawderman (2004).
Theorem 7.1 (Hartigan 2004)
Let \(X \sim {\mathcal N}_{p}(\theta , \sigma ^{2} I_{p})\) with σ
2 known and \( \theta \in \mathcal {C}\)
, a convex set with nonempty interior and sufficiently regular boundary \(\partial \mathcal {C}\) (
\(\partial \mathcal {C}\) is Lipshitz of order 1 suffices). Then the Bayes estimator, δ
U(X) with respect to the uniform prior on  , dominates δ
0(X) = X with respect to quadratic loss.
, dominates δ
0(X) = X with respect to quadratic loss.
Proof
Without loss of generality, assume σ 2 = 1. Recall from (1.20) that the form of the Bayes estimator is δ U(X) = X + ∇m(X)∕m(X) where, for any \(x \in \mathbb {R}^p\),
The difference in risk between δ U and δ 0 is R(θ, δ U) − R(θ, δ 0)
Hartigan’s clever development proceeds by applying Stein’s Lemma 2.3 to only half of the cross product term in order to cancel the squared norm term in the above. Indeed, since
(7.1) then becomes
with H(x, θ) = Δm(x) + (x − θ)T∇m(x). Hence it suffices to show H(x, θ) ≤ 0 for all \(\theta \in \mathcal {C} \) and \(x \in \mathbb {R}^p\). Using the facts that
and
it follows that
By Stokes’ theorem (see Sect.A.5 of the Appendix) this last expression can be expressed as
where η(ν) is the unit outward normal to \(\partial \mathcal {C}\) at ν and σ is the surface area Lebesgue measure on \( \partial \mathcal {C}\). Finally, since \(\mathcal {C}\) is convex and \(\theta \in \mathcal {C}\), the angle between η(ν) and θ − ν is obtuse for \(\nu \in \partial \mathcal {C}\) and so η T(ν)(θ − ν) ≤ 0, for all \(\theta \in \mathcal {C}\) and \(\nu \in \partial \mathcal {C}\), which implies the risk difference in (7.2) is nonpositive. □
Note that, if θ is in the interior of \(\mathcal {C}, \mathcal {C}^0\), then η ′(ν)(θ − ν) is strictly negative for all \(\nu \in \partial \mathcal {C}\), and hence, R(θ, δ U) − R(θδ 0) < 0 for all \(\theta \in \mathcal {C}^0\). However, if \(\mathcal {C}\) is a pointed cone at θ 0, then η T(ν)(θ 0 − ν) ≡ 0 for all \(\nu \in \partial \mathcal {C}\) and R(θ 0, δ U) = R(θ 0, δ 0).
Note also that, if \(\mathcal {C}\) is compact, the uniform prior on \(\mathcal {C}\) is proper, and hence, δ U(X) not only dominates δ 0(X) (on \(\mathcal {C}\)) but is also admissible for all p. On the other hand, if \(\mathcal {C}\) is not compact, it is often (typically for p ≥ 3) the case that δ U is not admissible and alternative shrinkage estimators may be desirable.
Furthermore, it may be argued in general, that a more natural basic estimator which one should seek to dominate is P c X, the projection of X onto \(\mathcal {C}\) which is the MLE. We consider this problem for the case where \(\mathcal {C}\) is a ball in Sect.7.3 and where \(\mathcal {C}\) is a polyhedral cone in Sect.7.4. □
7.3 Normal Mean Vector Restricted to a Ball
When the location parameter \( \theta \in \mathbb {R}^p\) is restricted, the most common constraint is a ball, that is, to a set for which ∥θ∥ is bounded above by some constant R. In this setting Bickel (1981) noted that, by an invariance argument and analyticity considerations, the minimax estimate is Bayes with respect to a unique spherically symmetric least favorable prior distribution concentrating on a finite number of spherical shells. This result extends what Casella and Strawderman (1981) obtained in the univariate case. Berry (1990) specified that when R is small enough, the corresponding prior is supported by a single spherical shell. In this section we address the issues of minimax estimation under a ball constraint.
Let \(X \sim {\mathcal N}_{p}(\theta , \sigma ^{2} I_{p})\), with unknown mean θ = (θ 1, …, θ p) and known σ 2, and with the additional information that \(\sum _{i=1}^p (\theta _i - \tau _i)^2 / \sigma ^2 \leq R^2\) where τ 1, …, τ p, σ 2, R are known. From a practical point of view, a constraint as the one above signifies that the squared standardized deviations |(θ i − τ i)∕σ|2 are on average bounded by R 2∕p. We are concerned here with estimating θ under quadratic loss L(θ, δ) = ∥δ − θ∥2. Without loss of generality, we proceed by setting σ 2 = 1 and τ i = 0, i = 1, …, p, so that the constraint is the ball \(B_R =\{ \theta \in \mathbb {R}^p \mid \|\theta \| \leq R\}\).
Since the usual minimax estimators take on values outside of B R with positive probability, they are neither admissible nor minimax when θ is restricted to B R. The argument given by Berry (1990) is the following. As for inadmissibility, it can be seen that these estimators are dominated by their truncated versions. Thus, the unbiased estimator X is dominated by the MLE δ MLE(X) = (R∕∥X∥∧ 1)X (which is the truncation of X on B R). Now, if an estimator which takes on values outside of B R with positive probability were minimax, its truncated version would be minimax as well, with a strictly smaller risk. This is a contradiction since the risk function is continuous and attains its maximum in B R. Further δ MLE(X) is not admissible since, due to its non differentiability, it is not a generalized Bayes estimator. See Sect.3.4. For further discussions on this issue related to inadmissibility of estimators taking values on the boundary of a convex parameter space, see the review paper of Marchand and Strawderman (2004) and the monograph of van Eeden (2006).
As alternative estimators to δ MLE(X), the Bayes estimators are attractive since they may have good frequentist performances in addition to their Bayesian property. Two natural estimators are the Bayes estimators with respect to the uniform distribution on the ball B R and the uniform distribution on its boundary, the sphere \(S_R =\{ \theta \in \mathbb {R}^p \mid \|\theta \| = R\}\). We will see that the latter is particularly interesting.
The model is dominated by the Lebesgue measure on \(\mathbb {R}^p\) and has likelihood L given by
Hence, if the prior distribution is the uniform distribution \({\mathcal U}_{R}\) on the sphere S R, the marginal distribution has density m with respect to the Lebesgue measure on \(\mathbb {R}^p\) given by
after expanding the likelihood in (7.3). Also, the posterior distribution given \(x \in \mathbb {R}^p\) has density π(θ|x) with respect to the prior distribution \({\mathcal U}_{R}\) given by
thanks to the second expression of m(x) in (7.4). As the loss is quadratic, the Bayes estimator δ R is the posterior mean, that is,
The Bayes estimator in (7.6) can be expressed through the modified Bessel function I ν, solutions of the differential equation z 2 φ ′′(z) + zφ ′(z) − (z 2 + ν 2)φ(z) = 0 with ν ≥ 0. More precisely, we will use the integral representation of the modified Bessel function
from which we may derive the formula
Using the parametrization in terms of polar coordinates, we can see from the proof of Lemma 1.4 that, for any function h integrable with respect to \({\mathcal U}_{R}\),
where σ(S) is the area measure of the unit sphere and, as in (1.9), where V = (0, π)p−2 × (0, 2π) and for (t 1, …, t n−1) ∈ V , φ R(t 1, …, t p−1) = (θ 1, …, θ p) with
Setting \(h(\theta ) = \exp (x^{\scriptscriptstyle \mathrm {T}} \theta )\) and choosing the angle between x and θ ∈ S R as the first angle t 1 gives
where
with V T = (0, π)p−3 × (0, 2π).
Therefore, according to (7.7), the marginal in (7.4) is proportional to
the proportionality constant being independent of R. Then the Bayes estimator δ R(X) can be obtained thanks to (1.20), that is, for any \(x \in \mathbb {R}^p\),
As only the quantities depending on x matter, we have using (7.9), for any \(x \in \mathbb {R}^p\),
where (7.8) has been used for the second to last equality.
Thus, according to (7.10), the Bayes estimator is expressed through a ratio of modified Bessel functions , that is, denoting by ρ ν(t) = I ν+1∕I ν with t > 0 and ν > −1∕2,
Before proceeding, we give two results from Marchand and Perron (2001).
-
(i)
For sufficiently small R, say R ≤ c 1(p), all Bayes estimators δ π with respect to an orthogonally invariant prior π (supported on B R) dominate δ MLE(X);
-
(ii)
The Bayes estimator δ R(X) with respect to the uniform prior on the sphere S R dominates δ MLE(X) whenever \(R \leq \sqrt {p}\).
Note that Marchand and Perron (2002) extend the result in (ii) showing that domination of δ R(X) over δ MLE(X) subsists for some m 0(p) such that \(m_0(p) \geq \sqrt {p}\) and for R ≤ m 0(p).
Various other dominance results, such as those pertaining to a fully uniform prior on B R and other absolutely continuous priors are also available from Marchand and Perron (2001), but we will focus here on results (i) and (ii) above, following Fourdrinier and Marchand (2010).
With respect to important properties of δ R(X), we point out that it is the optimal equivariant estimator for θ ∈ S R, and thus necessarily improves upon δ MLE(X) on S R. Furthermore, δ R(X) also represents the Bayes estimator which expands greatest, or shrinks the least towards the origin (i.e., ∥δ π∥≤∥δ R(X)∥ for all π supported on B R; Marchand and Perron 2001). Despite this, as expanded upon below, δ R(X) still shrinks more than δ MLE(X) whenever \(R \leq \sqrt {p}\), but not otherwise with the consequence of increased risk at θ = 0 and failure to dominate δ MLE(X) for large R. With the view of seeking dominance for a wider range of values of R, for potentially modulating these above effects by introducing more (but not too much) shrinkage, we consider the class of uniform priors supported on spheres S α of radius α; 0 ≤ α ≤ R; about the origin, and their corresponding Bayes estimators δ α. The choice is particularly interesting since the amount of shrinkage is calibrated by the choice of α (as formalized below), with the two extremes δ R(X) ≡ δ R(X), and δ 0 ≡ 0 (e.g., prior degenerate at 0). Moreover, knowledge about dominance conditions for the estimators δ α may well lead, through further analytical risk and unbiased estimates of risk comparisons (e.g., Marchand and Perron (2001), Lemma 5 and the Remarks that follow), to implications relative to other Bayes estimators such as the fully uniform on B R prior Bayes estimator.
Using Stein’s unbiased estimator of risk technique, Karlin’s sign change arguments, and a conditional risk analysis, Fourdrinier and Marchand (2010) obtain, for a fixed (R, p), necessary and sufficient conditions on α for δ α to dominate δ MLE(X).
Theorem 7.2
-
(a)
An unbiased estimator of the difference in risks
$$\displaystyle \begin{aligned} \varDelta_{\alpha}(\|\theta\|) = R(\theta, \delta_{\alpha})- R(\theta, \delta_{MLE}(X)) \end{aligned}$$is given by
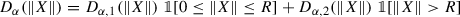 , with
$$\displaystyle \begin{aligned} \begin{array}{rcl} D_{\alpha, 1 }(r) &\displaystyle &\displaystyle = 2\alpha^2 +r^2 - 2p - 2\alpha r \rho_{p/2 -1} (\alpha r) - {\alpha}^2 \rho_{p/2 -1}^2 (\alpha r), and \\ {} D_{\alpha, 2 }(r) &\displaystyle &\displaystyle = 2\alpha^2 - m^2 - {\alpha}^2 \rho_{p/2 -1}^2 (\alpha r) + 2 Rr \{1-\frac{\alpha}{R} \rho_{p/2 -1} (\alpha r) \} -2(p-1)\frac{R}{r} . \end{array} \end{aligned} $$
, with
$$\displaystyle \begin{aligned} \begin{array}{rcl} D_{\alpha, 1 }(r) &\displaystyle &\displaystyle = 2\alpha^2 +r^2 - 2p - 2\alpha r \rho_{p/2 -1} (\alpha r) - {\alpha}^2 \rho_{p/2 -1}^2 (\alpha r), and \\ {} D_{\alpha, 2 }(r) &\displaystyle &\displaystyle = 2\alpha^2 - m^2 - {\alpha}^2 \rho_{p/2 -1}^2 (\alpha r) + 2 Rr \{1-\frac{\alpha}{R} \rho_{p/2 -1} (\alpha r) \} -2(p-1)\frac{R}{r} . \end{array} \end{aligned} $$ -
(b)
For p ≥ 3, and 0 ≤ α ≤ R, D α(r) changes signs as a function of r according to the order: (i) (−, +) whenever \(\alpha \leq \sqrt {p}\) , and (ii) (+, −, +) whenever \(\alpha >\sqrt {p}\).
-
(c)
For p ≥ 3 and 0 ≤ α ≤ R, the estimator δ α dominates δ MLE(X) if and only if
-
(i)
Δ α(R) ≤ 0 whenever \( \alpha \leq \sqrt {p}\) or
-
(ii)
Δ α(0) ≤ 0 and Δ α(R) ≤ 0, whenever \(\alpha > \sqrt {p}\).
-
(i)
Proof
-
(a)
Writing δ MLE(x) = x + g MLE(x) with
 (with r = ∥x∥) note that g
MLE is weakly differentiable. Then we have
(with r = ∥x∥) note that g
MLE is weakly differentiable. Then we have 
and, by virtue of Stein’s identity , R(θ, δ MLE) = E θ[η MLE(X)] with
 (7.12)
(7.12)Analogously, as derived by Berry (1990), the representations of δ α and \(\frac {d}{dt} \rho _{\nu }(t)\) given in (7.11) and Lemma A.8, along with (2.3), permit us to write R(θ, δ α) = E θ[λ α(X)] with
$$\displaystyle \begin{aligned} \lambda_{\alpha}(x)= 2\alpha^2 + r^2 - p - 2\alpha r \rho_{p/2 -1}(\alpha r) - {\alpha}^2 \rho_{p/2 -1}^2 (\alpha r). \end{aligned} $$(7.13)Finally, the given expression for the unbiased estimator D α(∥X∥) follows directly from (7.12) and (7.13).
-
(b)
We begin with three intermediate observations which are proven below.
-
(I)
The sign changes of D α,1(r) ;r ∈ [0, R]; are ordered according to one of the five following combinations: (+), (−), (−, +), (+, −), (+, −, +) ;
-
(II)
\(\lim _{r \rightarrow R^+} \{D_{\alpha } (r) \} = \lim _{r \rightarrow R^-} \{D_{\alpha } (r) \} + 2;\)
-
(III)
the function D α,2(r); r ∈ (R, ∞) is either positive, or changes signs once from − to + .
-
(I)
From properties (I), (II) and (III), we deduce that the sign changes of D α(r) r ∈ (0, ∞); an everywhere continuous function except for the jump discontinuity at R; are ordered according to one of the three following combinations: (+), (−, +), (+, −, +). Now, recall that δ α is a Bayes and admissible estimator of θ under squared error loss. Therefore, among the combinations above, (+) is not possible since this would imply that δ α is dominated by δ MLE in contradiction with its admissibility. Finally, the two remaining cases are distinguished by observing that, D α(0) = 2α 2 − 2p ≤ 0 if and only if \(\alpha \leq \sqrt {p}\).
Proof of (I): Begin by making use of Lemma A.8 to differentiate D α,1 and obtain:
Since, the quantities r −1 ρ p∕2−1(αr) and \(\rho _{p/2 -1}^{\prime } (\alpha r)\) are positive and decreasing in r by virtue of Lemma A.8, \( r^{-1} \;D_{\alpha ,1}^{\prime }(r)\) is necessarily increasing in r, r ∈ [0, R]. Hence, \(D_{\alpha ,1}^{\prime }(\cdot )\) has, on [0, R], sign changes ordered as either: (+), (−), or (−, +). Finally, observe as a consequence that D α,1(⋅) has at most two sign changes on [0, R], and furthermore that, among the six possible combinations, the combination (−, +, −) is not consistent with the sign changes of \(D_{\alpha ,1}^{\prime }\).
Proof of (II): Follows by a direct evaluation of D α,1(R) and D α,2(R) which are given in part (a) of this lemma.
Proof of (III): First, one verifies from (7.13), part (a) of Lemma A.8, and part (c) of Lemma A.9 that limr→∞ D α,2(r) is + ∞, for α < R; and equal to p − 1 if α = R. Moreover, part (a) also permits us to express D α,2(r); r > R; as \((1- \frac {\alpha }{R} \; \rho _{p/2 -1} (\alpha r)) \; \sum _{i=1}^{3} H_i(\alpha ,r)\) with
Hence, to establish property (III), it will suffice to show that each one of the functions H i(α, ⋅), i = 1, 2, 3, is increasing on (R, ∞) under the given conditions on (p, α, R). The properties of Lemma A.8 clearly demonstrate that H 3(α, ⋅) is increasing, and it is the same for H 2(α, ⋅) given also Lemmas A.8 and A.9 since
Finally, for the analysis of H 1(α, r), r > R, begin by differentiation and a rearrangement of terms to obtain
where, for r > R ≥ α,
But notice that T(α) = α 2(1 − ρ p∕2−1(αr))2 ≥ 0, and
by Lemma A.9, part (b), since r ≥ R ≥ α. The above establishes that T(R) ≥ T(α) ≥ 0 for all R ≥ α, that H 1(α, r) increases in r, and completes the proof of the Theorem.
-
(c)
The probability distribution of ∥X∥2 is \(\chi ^2_p(\lambda ^2)\), so that the potential sign changes of Δ α(λ) = E λ[D α(∥X∥)] are controlled by the variational properties of D α(⋅) in terms of sign changes (e.g., Brown et al. 1981). Therefore, in situation (i) with \(\alpha \leq \sqrt {p}\), it follows from part (b) of Lemma 7.2 that, as Δ α(⋅) varies on [0, ∞] (or [0, R]), the number of sign changes is at most one, and that such a change must be from − to + . Therefore, since δ α is admissible; and that the case Δ α(λ) ≥ 0 for all λ ∈ [0, R] is not possibleFootnote 1; we must have indeed that Δ α(⋅) ≤ 0 on [0, R] if and only if Δ α(R) ≤ 0 establishing (i). A similar line of reasoning implies the result in (ii) as well. □
We refer to Fourdrinier and Marchand (2010) for other results. In particular, large sample determinations of these conditions are provided. Both cases where all such δ α’s, or no such δ α’s dominate δ MLE are elicited. As a particular case, they establish that the boundary uniform Bayes estimator δ R dominates δ MLE if and only if R ≤ k(p) with \(\lim _{p \to \infty } k(p) / \sqrt {p} = \sqrt {2}\), improving on the previously known sufficient condition of Marchand and Perron (2001) for which \(k(p) \geq \sqrt {p}\). Finally, they improve upon a universal dominance condition due to Marchand and Perron, by establishing that all Bayes estimators δ π with π spherically symmetric and supported on the parameter space dominate δ MLE whenever R ≤ c 1(p) with \(\lim _{p \to \infty } c_1(p) / \sqrt {p} = \sqrt {1 / 3}\).
See Marchand and Perron (2005) for analogous results for other spherically symmetric distributions including multivariate t.
Other significant contributions to the study of minimax estimation of a normal mean restricted to an interval or a ball of radius R, were given by Bickel (1981) and Levit (1981). These contributions consisted of approximations to the minimax risk and least favourable prior for large R under squared error loss. In particular, Bickel showed that for p = 1, as R →∞, the least favourable distributions rescaled to [− 1, 1] converge weakly to a distribution with density \(\cos ^2 (\pi x/2)\), and that the minimax risks behave like 1 − π 2∕(8R 2) + o(R −2). There is also a substantial literature on efficiency comparisons of minimax procedures and affine linear minimax estimators for various models, and restricted parameter spaces; see Donoho et al. (1990) and Johnstone and MacGibbon (1992) and the references therein.
Finally, we observe that the loss function plays a critical role. In the case where p = 1 and loss is absolute error |d − θ|, δ MLE(X) is admissible. See Isawa and Moritani (1997) and Kucerovsky et al. (2009).
7.4 Normal Mean Vector Restricted to a Polyhedral Cone
In this section, we consider first the case when \(X \sim {\mathcal N}_{p}(\theta , \sigma ^{2} I_{p})\) where σ 2 is known and θ is restricted to a polyhedral cone \(\mathcal {C}\) and where the loss is ∥δ − θ∥2. Later in this Section, we will consider the case where σ 2 is unknown and, in Sect.7.5, the general spherically symmetric case with a residual vector. The reader is referred to Fourdrinier et al. (2006) for more details.
A natural estimator in this problem is \(\delta _{\mathcal {C}}(X)= P_{\mathcal {C}}X\), the projection of X onto the cone \(\mathcal {C}\). The estimator \(\delta _{\mathcal {C}}\) is the MLE and dominates X which is itself minimax provided \(\mathcal {C}\) has a nonempty interior. Our goal will be to dominate \(\delta _{\mathcal {C}}\) and therefore also δ 0(X) = X.
We refer the reader to Stoer and Witzgall (1970) and Robertson et al. (1988) for an extended discussion of polyhedral cones. Here is a brief summary. A polyhedral cone \(\mathcal {C}\) is defined as the intersection of a finite number of half spaces, that is,
for n fixed vectors a 1, …, a m in \(\mathbb {R}^p\).
It is positively homogeneous, closed and convex , and, for each \(x \in \mathbb {R}^p\), there exists a unique point \(P_{\mathcal {C}}x\) in \(\mathcal {C}\) such that \(\|P_{\mathcal {C}}x - x\| = \inf _{y \in \mathcal {C}} \|y-x\|\).
We assume throughout that \(\mathcal {C}\) has a nonempty interior, \(\mathcal {C}^o\) so that \(\mathcal {C}\) may be partitioned into \(\mathcal {C}_i\), i = 0, …, m, where \(\mathcal {C}_0 = \mathcal {C}^o\) and \(\mathcal {C}_i\), i = 1, …, m, are the relative interiors of the proper faces of \(\mathcal {C}\). For each set \(\mathcal {C}_i\) , let \(D_i=P_{\mathcal {C}}^{-1} \mathcal {C}_i\) (the pre-image of \(\mathcal {C}_i\) under the projection operator \(P_{\mathcal {C}}\) and \(s_i = \dim \mathcal {C}_i\)). Then D i, i = 0, …, m form a partition of \(\mathbb {R}^p\), where \(D_0 = \mathcal {C}_0\).
For each x ∈ C i, we have \(P_{\mathcal {C}}x = P_ix\) where P i is the orthogonal linear projection onto the s i −dimensional subspace L i spanned by \(\mathcal {C}_i\). Also for each such x, the orthogonal projection onto \(L_i^\bot \), is equal to \(P_{\mathcal {C}^{\ast }} x\) where \(\mathcal {C}^{\ast }=\{y \mid x^{\scriptscriptstyle \mathrm {T}} y \leq 0\}\) is the polar cone corresponding to \(\mathcal {C}\). Additionally, if x ∈ D i, then \(aP_ix + P_i^\bot x \in D_i\) for all a > 0, so D i is positively homogeneous in P i x for each fixed \(P_i^\bot x\) (see Robertson et al. 1988, Theorem 8.2.7). Hence we may express

The problem of dominating \(\delta _{\mathcal {C}}\) is relatively simple in the case where \(\mathcal {C}\) has the form \(\mathcal {C} = \mathbb {R}_+^k \oplus \mathbb {R}^{p-k}\) where \(\mathbb {R}_+^k = \{ (x_1, \ldots ,x_k) \mid x_i \geq 0, \; i=1, \ldots ,k\}\). In this case,
Furthermore, \(\delta _{\mathcal {C}} (X)\) is weakly differentiable and the techniques of Chap.3 (i.e. Stein’s lemma) are available.
As a simple example , suppose \(\mathcal {C} = \mathbb {R}^p_+,\) i.e. all coordinates of θ are nonnegative. Then \( \delta _{\mathcal {C}_{i}}(X) = X_i + \partial _i(X) \quad i=1, \ldots , p\) where
Also, we may rewrite (7.15) as  where \(O_1 = \mathbb {R}_+^p\), and O
j, for j > 1, represent the other 2p − 1 orthants and P
i is the projection of X onto the space generated by the face of O
1 adjacent to O
i.
where \(O_1 = \mathbb {R}_+^p\), and O
j, for j > 1, represent the other 2p − 1 orthants and P
i is the projection of X onto the space generated by the face of O
1 adjacent to O
i.
Then a James-Stein type shrinkage estimator that dominates X + is given by

where c i = (s i − 2)+ and s i is the number of positive coordinates in O i. Note that shrinkage occurs only in those orthants such that s i ≥ 3.
The proof of domination follows essentially by the usual argument of Chap.3, Sect.2.4, applied separately to each orthant since X + and X +∕∥X +∥2 are weakly differentiable in O i and

provided s i > 2. Note also that c i may be replaced by any value between 0 and 2(s i − 2)+.
Difficulties arise when the cone \(\mathcal {C}\) is not of the form \(\mathcal {C}=\mathbb {R}_+^k \oplus \mathbb {R}^{p-k}\) because the estimator \(P_{\mathcal {C}} X\) may not be weakly differentiable (see Appendix A.1). In this case, a result of Sengupta and Sen (1991) can be used to give an unbiased estimator of the risk. Here is a version of their result.
Lemma 7.1 (Sengupta and Sen 1991)
Let \(X \sim {\mathcal N}_{p}(\theta , \sigma ^{2} I_{p})\) and \(\mathcal {C}\) a positively homogeneous set. Then for every absolutely continuous function h(⋅) from \(\mathbb {R}_+\) to \(\mathbb {R}\) such that limy→0,∞ h(y)y k+p∕2 e −y∕2 = 0 for all k ≥ 0 and E θ[h 2(∥X∥2)∥X∥2] < ∞ we have

Note that for \(\mathcal {C} = \mathbb {R}^p\), Lemma 7.1 follows from Stein’s lemma
with g(X) = h(∥X∥2)X provided E[h(∥X∥2)∥X∥2] < ∞. The possible non-weak differentiability
of the function  prevents a direct use of Stein’s lemma for general \(\mathcal {C}\).
prevents a direct use of Stein’s lemma for general \(\mathcal {C}\).
Proof of Lemma 7.1
Note first that, if, for any θ, E θ[∥g(X)∥] < ∞, then
by the dominated convergence theorem . Without loss of generality, assume σ 2 = 1 and let

By the positive homogeneity of \(\mathcal {C}\), we have  and, by the independence of ∥X∥ and X∕∥X∥ for θ = 0, we have
and, by the independence of ∥X∥ and X∕∥X∥ for θ = 0, we have

When θ = 0, ∥X∥2 has a central Chi-square distribution with p degrees of freedom. Thus, with d = 1∕2p∕2 Γ(p∕2), we have
Integrating by parts, the first integral gives
and thus combining gives
Thus (7.17) becomes

where the final identity follows by the dominated convergence theorem . □
General dominating estimators will be obtained by shrinking each P i X in (7.15) on the set D i. Recall that each D i has the property that, if x ∈ D i, then \(a P_ix + P_i^\bot x \in D_i\) for all a > 0. The next result extends Lemma 7.1 to apply to projections P i onto sets which have this conditional homogeneity property.
Lemma 7.2
Let \(X\sim {\mathcal N}_{p}(\theta , \sigma ^{2} I_{p})\) and P be a linear orthogonal projection of rank s. Further, let D be a set such that, if x = Px + P ⊥ x ∈ D, then aPx + P ⊥ x ∈ D for all a > 0. Then, for any absolutely continuous function h(⋅) on \(\mathbb {R}_+\) into \(\mathbb {R}\) such that limy→0,∞ h(y)y (j+s)∕2 e −y∕2 = 0 for all j ≥ 0, we have

Proof
By assumption \((Y_1, Y_2) = (PX, P^\bot X) \sim (\mathcal {N}_p (\eta _1, \sigma ^2P), \mathcal {N}_p(\eta _2, \sigma ^2 P^\bot ))\) where (Pθ, P ⊥ θ) = (η 1, η 2). Also

where
On conditioning on Y 2 (which is independent of Y 1), and applying Lemma 7.1 to Y 1, we have

□
Now we use Lemma 7.2 to obtain the main domination result of this section.
Theorem 7.3
Let \(X\sim {\mathcal N}_{p}(\theta , \sigma ^{2} I_{p})\) where σ 2 is known and θ is restricted to lie in the polyhedral cone \(\mathcal {C}\) , (7.14) , with nonempty interior. Then, under loss L(θ, d) = ∥d − θ∥2∕σ 2 , the estimator

dominates the rule \(\delta _{\mathcal {C}}(X)\) given by (7.15) provided 0 < r i(t) < 2, r i(⋅) is absolutely continuous, and \(r_i^\prime (t) \geq 0\) , for each i = 0, 1, …, m.
Proof
The difference in risk between δ and \(\delta _{\mathcal {C}}\) can be expressed as

Now apply Lemma 7.2 (noting that (P i X)T(P i X − θ) = (P i X)T(X − θ)) to each summand in the second term to get

since each \(r_i^\prime (\cdot ) \geq 0\) and 0 < r i(⋅) < 2. □
As noted in Chap.3, the case of an unknown σ 2 is easily handled provided an independent statistic \(S\sim \sigma ^2 \chi _k^2\) is available. For completeness we give the result for this case in the following theorem.
Theorem 7.4
Suppose \(X\sim {\mathcal N}_{p}(\theta , \sigma ^{2} I_{p})\) and \(S \sim \sigma ^2 \chi _k^2\) with X independent of S. Let the loss be ∥d − θ∥2∕σ 2 . Suppose that θ is restricted to the polyhedral cone \(\mathcal {C}\) , (7.14) , with non-empty interior. Then the estimator

dominates \(\delta _{\mathcal {C}} (X)\) given in (7.15) provided 0 < r i(⋅) < 2 and r i(⋅) is absolutely continuous with \(r_i^\prime (\cdot ) \geq 0\) , for i = 0, …, m.
Many of the classical problems in ordered inference are examples of restrictions to polyhedral cones. Here are a few examples.
Example 7.1 (Orthant Restrictions)
Estimation problems where k of the coordinate means are restricted to be greater than (or less than) a given set constants, can be transformed easily into the case where these same components are restricted to be positive. This is essentially the case for \(\mathcal {C} = \mathbb {R}_+^k \oplus \mathbb {R}^{p-k}\) mentioned earlier.
Example 7.2 (Ordered Means)
The restrictions that θ 1 ≤ θ 2 ≤… ≤ θ p (or that a subset are so ordered) is a common example in the literature and corresponds to the finite set of half space restrictions θ 2 ≥ θ 1, θ 3 ≥ θ 2, …, θ p ≥ θ p−1 .
Example 7.3 (Umbrella Ordering)
The ordering θ 1 ≤ θ 2 ≤… ≤ θ k ≥ θ k+1 ≥ θ k+2, …, θ p−1 ≥ θ p corresponds to the polyhedral cone generated by the half space restrictions
In some examples, such as Example 7.1, it is relatively easy to specify P i and D i. In others, such as Example 7.2 and 7.3 it is more complicated. The reader is referred to Robertson et al. (1988) and references therein for further discussion of this issue.
7.5 Spherically Symmetric Distribution with a Mean Vector Restricted to a Polyhedral Cone
This Section is devoted to proving the extension of Theorem 7.4 to the case of a spherically symmetric distribution when a residual vector is present. Specifically we assume that (X, U) ∼ SS(θ, 0) where \(\dim X = \dim \theta = p, \dim U = \dim 0 = k \) and where θ is restricted to lie in a polyhedral cone, \(\mathcal {C}\), with non-empty interior. Recall that the shrinkage functions in the estimator (7.21) are not necessarily weakly differentiable because of the presence of the indicator functions \( I_{D_{i}} (X)\). Hence the methods of Chap.4 are not immediately applicable.
The following theorem develops the required tools for the desired extension of Theorem 7.4. It also allows for an alternative approach to the results in Sect.6.1 as well.
Theorem 7.5 (Fourdrinier et al. 2006)
Let \((X,U)\sim {\mathcal N}_{p+k}((\theta , 0), \sigma ^{2} I_{p+k})\) and assume \(f: \mathbb {R}^p \rightarrow \mathbb {R}\) and \(g: \mathbb {R}^p \rightarrow \mathbb {R}^p\) are such that
where both expected values exist for all σ 2 > 0. Then, if (X, U) ∼ SS p+k(θ, 0), we have
provided either expected value exists.
Proof
As (X, U) is normal, \(X\sim \mathcal {N}_p(\theta , \sigma ^2 I)\) and \(\|U\|{ }^2 \sim \sigma ^2 \chi _{k}^2\) are independent, using E[∥U∥2] = kσ 2 and E[∥U∥4] = σ 4 k(k + 2), we have, for each fixed σ 2,
For each θ (considered fixed), ∥X − θ∥2 + ∥U∥2 is a complete sufficient statistic for \((X, U) \sim \mathcal {N}_{p+k}((\theta , 0),\sigma ^2 I)\). Now noting
and
it follows from (7.22) and the completeness of ∥X − θ∥2 + ∥U∥2 that
almost everywhere. We show at the end of this section that the functions in (7.23) are both continuous in ∥X − θ∥2 + ∥U∥2, and hence, they are in fact equal everywhere.
Since the conditional distribution of (X, U) conditional on ∥X − θ∥2 + ∥U∥2 = R 2 is uniform on the sphere centered at (θ, 0) for all spherically symmetric distributions (including the normal), the result follows on integration of (7.23) with respect to the radial distribution of (X, U). □
The main result of this section results from an application of Theorem 7.3 to the development of the proof of Theorem 7.4.
Theorem 7.6
Let (X, U) ∼ SS p+k(θ, 0) and let θ be restricted to the polyhedral cone \({\mathcal C}\) , (7.14) , with nonempty interior. Then, under loss L(θ, d) = ∥d − θ∥2, the estimator

dominates \(P_{\mathcal {C}} X = \delta _{\mathcal {C}}(X)\) , given in (7.15) provided, 0 < r i(⋅) < 2, r i(⋅) is absolutely continuous and \(r_i^\prime (\cdot ) \geq 0\) for i = 0, …, m.
Proof
The key observation is that, in passing from (7.19) to (7.20) in the proof of Theorem 7.3, we used Lemma 7.2 and the fact that P i X T(PX i − θ) = P i X T(X − θ) to establish that

Hence, by Theorem 7.5,

It follows then, as in the proof of Theorem 7.3,

□
Theorem 7.5 is an example of a meta result which follows from Theorem 7.6, and states roughly that, if one can find an estimator X + σ 2 g(X) that dominates X for each σ 2 using a Stein-type differential equality in the normal case, then X + ∥U∥2∕(k + 2)g(X) will dominate X in the general spherically symmetric case, (X, U) ∼ SS 1+k(θ, U), under L(θ, δ) = ∥δ − θ∥2. The “proof” goes as follows.
Suppose one can show also that E[(X − θ)T g(X)] = σ 2 E[f(X)] in the normal case, and also that ∥g(x)∥2 + 2f(x) ≤ 0, for any \(x \in \mathbb {R}^p\). Then, in the normal case,
Using Theorem 7.5 (and assuming finiteness of expectations), it follows in the general case that
In this Section, application of the above meta-result had the additional complication of a separate application (to P i X instead of X) on each D i but the basic idea is the same. The results of Chap.6 which rely on extending a version of Stein’s lemma to the general spherically symmetric case can be proved in the same way.
We close this Section with a result that implies the claimed continuity of the conditional expectations in (7.23).
Lemma 7.3
Let (X, U) ∼ SS p+k(θ, 0) and let α ∈ N. Assume φ(⋅) is such that for any R > 0, the conditional expectation
exists. Then the function f is continuous on \(\mathbb {R}_+.\)
Proof
Assume without loss of generality that θ = 0 and φ(⋅) ≥ 0. Since the conditional distribution or (X, U) conditional on ∥X∥2 + ∥U∥2 = R 2 is the uniform distribution U R on the sphere S R = {y ∈ R p+k∕∥y∥ = R} centered at 0 with radius R, we have
Since ∥u∥2 = R 2 −∥x∥2 for any (x, u) ∈ S R and X has distribution concentrated on the ball \(B_r= \{ x\in \mathbb {R}^p | \|x\| \leq R\}\) in \(\mathbb {R}^p\) with density proportional to R 2−(p+k)((R 2 −∥x∥2)k∕2−1) we have that R p+k−2 f(R) is proportional to
where
and where σ r is the area measure on the sphere S r. Since H(⋅) and (k + α)∕2 − 1 are non-negative, the family of integrable functions r → K(R, r) = (R 2 − r 2)(k+α)∕2−1 H(r)I [0,R](r), indexed by R, is nondecreasing in R and bounded above for R < R 0 by the integrable function K(R 0, r). Then the continuity of g(R), and hence of f(R), is guaranteed by the dominated convergence theorem. □
Note that the continuity of (7.23) is not necessary for the application to (X, U) ∼ SS p+k(θ, 0) if (X, U) has a density, since then equality a.e. suffices.
Notes
- 1.
The risks of δ α and δ MLE cannot match either, since a linear combination of these two distinct estimators would improve on δ α.
References
Berry C (1990) Minimax estimation of a bounded normal mean vector. J Multivar Anal 35:130–139
Bickel PJ (1981) Minimax estimation of the mean of a normal distribution when the parameter space is restricted. Ann Stat 9(6):1301–1309
Brown LD, Johnstone I, MacGibbon KB (1981) Variation diminishing transformations: a direct approach to total positivity and its statistical applications. J Am Stat Assoc 76:824–832
Casella G, Strawderman WE (1981) Estimating a bounded normal mean. Ann Stat 9:870–878
Donoho DL, Liu RC, MacGibbon KB (1990) Minimax risk over hyperrectangles, and implications. Ann Stat 80(3):1416–1437
Fourdrinier D, Marchand E (2010) On Bayes estimators with uniform priors on spheres and their comparative performance with maximum likelihood estimators for estimating bounded multivariate normal means. J Multivar Anal 101:1390–1399
Fourdrinier D, Strawderman, Wells MT (2006) Estimation of a location parameter with restrictions or “vague information” for spherically symmetric distributions. Ann Inst Stat Math 58:73–92
Hartigan JA (2004) Uniform priors on convex sets improve risk. Stat Probab Lett 67:285–288
Isawa M, Moritani Y (1997) A note on the admissibility of the maximum likelihood estimator for a bounded normal mean. Stat Probab Lett 32:99–105
Johnstone IM, MacGibbon KB (1992) Minimax estimation of a constrained Poisson vector. Ann Stat 20:807–831
Katz MW (1961) Admissible and minimax estimates of parameters in truncated spaces. Ann Math Stat 32(1):136–142
Kucerovsky D, Marchand E, Payandeh AT, Strawderman WE (2009) On the bayesianity of maximum likelihood estimators of restricted location parameters under absolute value error loss. Stat Decis Int Math J Stoch Methods Model 27:145–168
Levit BY (1981) On asymptotic minimax estimates of the second order. Theory Probab Its Appl 25(3):552–568
Marchand É, Perron F (2001) Improving on the MLE of a bounded normal mean. Ann Stat 29(4):1078–1093
Marchand É, Perron F (2002) On the minimax estimator of a bounded normal mean. Stat Probab Lett 58:327–333
Marchand É, Perron F (2005) Improving on the MLE of a bounded location parameter for spherical distributions. J Multivar Anal 92(2):227–238
Marchand É, Strawderman WE (2004) Estimation in restricted parameter spaces: a review. In: DasGupta A (ed) A Festschrift for Herman Rubin. Lecture notes–monograph series, vol 45. Institute of Mathematical Statistics, Beachwood, pp 21–44
Robertson T, Wright FT, Dykstra RL (1988) Order restricted statistical inference. Wiley, New York
Sengupta D, Sen PK (1991) Shrinkage estimation in a restricted parameter space. Sankhyā 53:389–411
Stoer J, Witzgall C (1970) Convexity and optimization in finite dimensions I, Die Grundlehren der mathematischen Wissenschaften, vol 163. Springer, Berlin
van Eeden C (2006) Restricted parameter space estimation problems: admissibility and minimaxity properties. Lecture notes in statistics, Springer, New York
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Fourdrinier, D., Strawderman, W.E., Wells, M.T. (2018). Restricted Parameter Spaces. In: Shrinkage Estimation. Springer Series in Statistics. Springer, Cham. https://doi.org/10.1007/978-3-030-02185-6_7
Download citation
DOI: https://doi.org/10.1007/978-3-030-02185-6_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-02184-9
Online ISBN: 978-3-030-02185-6
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


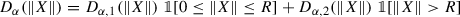 , with
, with
 (with r = ∥x∥) note that g
MLE is weakly differentiable. Then we have
(with r = ∥x∥) note that g
MLE is weakly differentiable. Then we have 
