Keywords

1 Introduction

In recent years, neuroscience has been a great source of inspiration in statistical methodology (e.g., [5, 19, 32]). The reason behind this interest, beside the obvious fascination with the quest for insights on how the brain works, is that neuroimaging modeling is at the crossroad between spatial statistics, time series, network analysis and high dimensional inference, thus allowing for an exciting interplay between different branches of statistics and other sciences. An area that is increasingly growing is the analysis of functional connectivity, which seeks to identify brain areas that behave similarly, potentially despite their spatial proximity or their membership to the same lobes and hemisphere.

The focus of this work is on estimating the relation between phenotypes and anatomical structure with functional brain behavior, employing functional magnetic resonance imaging (fMRI) as a measure of brain activity.

There is a rich literature related to the statistical study of functional connectivity patterns within the brain. Several approaches focus on representing the functional relationship among brain regions by means of a network, whose edges connect areas of the brain sharing similar behaviors in terms of functional properties. Nodes of the network are usually defined as regions of interest (ROIs), typically provided by experts in neuroscience (e.g., [7, 15]). Alternatively, ROIs can be identified with data-driven approaches [12] recovering lower dimensional structures in the high-dimensional fMRI data, such as Principal Component Analysis [3] or Independent Component Analysis.

A common approach to determine the functional edges interconnecting brain regions consists in thresholding the empirical correlations between fMRI series. The functional connectivity among subjects is then analyzed by assessing network properties (e.g. small-world, scale free connectivity) and comparisons are made using network summary statistics; see [10, 25] and references mentioned therein for a general review of these methods. A naive correlation-based approach, however, provides an incomplete representation of the brain’s functional connectivity, since it does not take into account covariates and has been shown to produce nonzero estimates for the correlation of independent brain regions [32]. Furthermore, when the number of brain regions is relatively big with respect to the lengths of the fMRI series, the empirical estimator of the correlation matrix may exhibit poor performance, especially if the covariance matrix is close to singularity.

Several alternative approaches have been investigated to obtain more reliable representations and robust descriptions of the functional networks, such as wavelet based correlation analysis [1] and graphical models [14], along with a broad discussion about properties of the resulting networks. Nevertheless, these approaches still fail to acknowledge the impact of covariates, and more in general, little work has been done in assessing the relation between such networks and brain structure or subject-specific covariates.

We address such issue by proposing a sequential hierarchical approach, which estimates the functional connectivity from denoised signals and then relates it to observed phenotypes. Although we build on hierarchical models in defining the probabilistic representation of the available quantities, we bypass the joint estimation procedure in order to provide a fast exploratory method, able to assess the relationship between phenotypes, brain constraints and neurophysiological dynamics. For the model fitting we adopt a modular strategy that leverages available methods in the literature. The modularization procedure consists of decomposing the hierarchical model in three sub-models: (i) a smoothing procedure to remove noise from the fMRI signal, (ii) a graphical model which encodes the functional brain connectivity and (iii) a regression model investigating the relation between phenotypes and functional connectivity patterns. Our approach retains ease of interpretation while accounting for functional relations across all the subjects; moreover, the robustness of inferential conclusions is assessed by means of a multiscale analysis.

The rest of the paper is organized as follows. In the following Sect. 2, we introduce the notation and define the general hierarchical specification of our modular approach. In Sect. 3 we detail the methods used in each module, along with the application to the data. Finally, Sect. 4 is dedicated to final remarks and our conclusions.

Fig. 1
figure 1

Hierarchical model representing the assumed probabilistic generative mechanism. Observed quantities are colored in light grey, unobservable in white

Full size image

2 Hierarchical Model

Our motivating application is drawn from the NKI1 pilot study, part of the “Enhanced Nathan Kline Institute-Rockland Sample project” conducted over 24 healthy subjects; the dataset used in this application was kindly provided by Greg Kiar and Eric Bridgeford (NeuroData—Johns Hopkins University). The resting state fMRI raw measurement have been preprocessed using the ndmg pipeline [24] and the C-PAC software; for additional details on this procedure, see https://fcp-indi.github.io/. Two subjects were removed from the analysis due to missing data in several features, and the final sample size for this application is equal to \(n=22\) subjects.

For each subject \(i = 1, \ldots , 22\), fMRI signals referred to \(v=1,\ldots ,70\) regions of interest (ROI) of the brain were collected at \(t=1,\ldots ,404\) equally spaced times, with a time span between measurements of 1400 ms. Let \(Y_{it} = (y_{it [1]}, \ldots , y_{it [70]})\) denote the vector of length 70 encoding the fMRI measurement for subject i at time t, for all the ROIs considered jointly, with generic element \(y_{it [v]}\) referred to the v-th ROI. Along with fMRI data, some additional features are available for every subject, such as age, mental status and handedness, which comprise the vector \(\mathbf {x}_i\) for each \(i = 1, \ldots , 22\). Some features related to the brain architecture, such as the lobe membership of each ROI, are also provided; these covariates are denoted as \(\mathbf {z}_v\), for \(v = 1, \ldots , 70\). Although each subject was scanned twice, we decided not to use data from the second scan, as it was not available for every subjects.

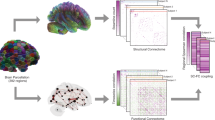
In order to study the presence and the type of relation between the measured brain signals and the available features, we consider a global generative mechanism for the observed quantities, summarized in Fig. 1. We assume that the fMRI data stems from a generative process in which subject-specific features and brain anatomy affect the functional brain behavior, and such characteristics are associated with a set of parameters \(\varvec{\theta } = \{\theta _{x}, \theta _{z}\}\) with elements referring respectively to the observed subject-specific features and ROI-specific properties. Furthermore, we suppose that the observed covariates affect the dependence structure among the functional time series, which we characterize by a graphical model or, equivalently, by its associated adjacency matrix \(\mathbf {K}_i\). In the neuroscientific literature, \(\mathbf {K}_i\) covers a central role, since it characterizes the functional network among brain regions (e.g., [10]). In our specific setting, each node of the functional network—or, equivalently, each row and column of the associated adjacency matrix—represents one of the 70 regions of interest. The edges summarize dependence among ROIs in a functional perspective; if two nodes are connected, the corresponding brain regions will mutually influence their functional activity, resulting in cross-correlated measurements of the clean signal, that we denote with \(Y_{it}^*\). If we suppose that the true signal can be accurately identified removing accidental noise from the observed data \(Y_{it}\), the crucial aim of this application is to estimate properly the set of parameters \(\varvec{\theta }\), since those quantities measure the effect of phenothypical variation on the neurophysiological dynamics.

A joint model specification for all the quantities involved in Fig. 1 might be fairly complicated, since it requires the specification of a joint likelihood for the observed series \(Y_{it}\) as a function of all the unknown quantities and observed covariates; the inclusion of subject-specific information within the estimation of the dependency structure of the functional network is particularly challenging. The same conclusion holds for a potential joint estimation of the cross-sectional dependencies among the signal. In this application, we will consider a modular approach for estimating the model in Fig. 1, in order to provide preliminary insights about the phenotypical effect on brain functional dynamics, and potentially guide further investigations.

The statistical model in Fig. 1 can be decomposed in stages or “modules”, with each component specifying a single model for one or more variables at time. For every module, several strategies of analysis are feasible, each of which has been extensively investigated and employed in the neuroscientific literature. We will consider then a separate approach in the estimation process, fitting each module and plugging-in the results from the previous step in the subsequent procedure. This plug-in approach, often called modularization [28] or two-step estimation [30], allows to build a complete model by combining different methods sequentially, with the output of a former stage used as input for the latter. Notable examples of application of modular approaches can be found in casual inference area with propensity score [31], pharmacology [6] and meta-analysis [27].

3 Modular Estimation Using Connectome Data

Modularization leads to two noticeable advantages in the estimation process. The first one is computational: since blocks are estimated disjointly, the parameter space to be explored in every module is small, and thus we can rely on relatively quickly estimation routines. This also allows for the possibility to conduct analysis under different settings in order to validate robustness of the results. The second benefit is that modularization reduces the effect of model misspecification, since fitting each step separately mitigates the propagation of error among consecutive steps and, potentially, reduces the impact of severe errors.

Our approach is particularly general and enables the inclusion of several techniques within each separate module; in the following we describe in details the modeling strategies adopted in every step along with their application to the data under investigation. For the ease of illustration, the hierarchical model in Fig. 1 was discussed from top to bottom, i.e. starting from what inference will focus on and describing how those quantities relate to the observed data; estimation, instead, will proceed in the opposite direction, using observed raw data as input to make inference on the parameters of interest.

3.1 Denoising

We firstly focus on obtaining the signal component from the observed time series data. Despite the elaborate preprocessing procedures, neuroimaging data are typically corrupted by noise that masks the true signal; especially with fMRI data, it is common to filter them before the analysis to increase the signal to noise ratio and hence the reliability of the results. Recall that \(Y_{it}, t = 1, \ldots , 404\), denotes the multivariate time series referred to the i-th subject for \(i = 1,\ldots , 22\), encoding the fMRI signal recorded over time. It is reasonable to assume that the path of the series over time domain is contaminated by some additive random noise that masks the original properties of the series itself; hence we assume that, at each time t, the observed fMRI signal for the i-th subject can be decomposed as

$$\begin{aligned} Y_{it} = Y^*_{it} + \varepsilon _{it} \qquad i = 1, \ldots , 22 \quad t = 1, \ldots 404 \end{aligned}$$
(1)

where \(Y^*_{it}\) is the clean signal and \(\varepsilon _{it}\) represents the noise component. Noise correction is a crucial step of mapping resting state signal fluctuations, however which method is the most appropriate to remove noise from such signal is still an open question, since it is not clear what the “ground truth” signal consists of when the subject is not focused on well identified activities [8]. Several methods can be employed to perform this denoising, for example smoothing splines or total variation (e.g., [16, Chapter 6]). We opt for a smoothing approach to denoising, and to estimate the clean signal \(Y_{it} ^*\), as denoted in Eq. (1), by means of smoothing splines (e.g., [4]). Let \(y_{it [v]}\) denote the univariate time series for ROI v in subject i, with \(v=1,\ldots ,70\) and \(i=1,\ldots ,22\), let \(y_{it [v]}^*\) denote its smoothed counterpart. The smoothed time series is the solution to the following minimization problem:

$$\begin{aligned} \underset{y_{i\cdot [v]}^*}{\text {argmin}}\left\{ \sum _{t=1} ^T \left( y_{it [v]} - y_{it [v]}^*\right) ^2 + \lambda \int { \left( \frac{\partial ^2}{\partial t^2} y_{it [v]}^*\right) ^2 \text {d}t}\right\} , \end{aligned}$$
(2)

where \(y^{*}_{i\cdot [v]} = (y^{*}_{i1[v]},\ldots y^{*}_{i404[v]})\). Smoothing the signal from each ROI separately, we neglect the spatial dimension of the fMRI data; however, since our aim is not focused on modelling the effect of spatial constraints, we did not include such information on purpose. This strategy also avoids the potential issues involved with spatial smoothing, for example changes in the correlation structure of the data and strengthening of spurious spatial dependency [2].

The parameter \(\lambda \) in Eq. 2 controls the trade-off between complexity and goodness-of-fit of the smoothed series, and its choice determines implicitly the amount of noise we wish to remove. Existing methods for selecting the tuning parameters take into account the temporal structure of the data, however they are built for noisier fMRI signals and tend to oversmooth in the case of resting state fMRI [13]. Although it is reasonable to tune this parameter with automated methods such as Generalized Cross Validation, we considered conducing a sensitivity analysis with respect to the choice of this parameter, and evaluate whether inferential conclusions are stable when the smoothed series capture different trends. In Fig. 2 we reported, for two subjects, original and smoothed fMRI data referred to a region in the inferiotemporal lobes of the left hemisphere. Smoothed series are reported with two different levels of smoothing, respectively \(\lambda = 2\) and \(\lambda = 10\). Figure 2 suggests that when the value of \(\lambda \) is increased, the estimated series become smoother and highlight the large scale variability, while when \(\lambda \) is fixed to a small value the estimated series tend to follow the accidental fluctuation.

Fig. 2
figure 2

An example of the original time series \(Y_{it}\) (solid line) and denoised estimates \(Y_{it}^*\) (dashed line), for subjects 3 and 14 with two different levels of the smoothing parameter \(\lambda \)

Full size image

3.2 Estimation of the Graphical Model

The dependence structure among the signal measured at different ROI is a key quantity in our model, since it connects the brain constraints and subject-specific features to the observed fMRI series, and describes the synchronization in brain activity for each pair of brain regions in each subject. Neuroscientific literature commonly refers to such structure as functional network, and several methods have been employed to provide a reasonable estimator for such quantity. A typical approach consists in representing functional connectivity by means of graphical models; in particular, Gaussian graphical models are becoming increasingly popular in neuroimaging (e.g., [14]), since they are able to capture conditional dependencies between brain regions with fast estimation routines and robust guarantees [17].

In order to estimate the functional network among brain regions, we first centered each smoothed time series with respect to its empirical mean. Assuming that for the i-th subject, at each time \(t = 1, \ldots , 404\), we observe a realization of a 70-variate Normal distribution with mean vector zero and precision matrix \(\varOmega _{i}\), conditional independence can be assessed estimating the precision matrix \(\varOmega _i\). Note that, even if the normality assumption is violated, \(\varOmega _i\) still provides a measure of the association between the functional series for the i-th subject. A popular and reasonable approach to estimate a graphical model induces sparsity in the estimation of the precision matrix \(\varOmega _i\) through an \(\ell _1\) penalty, favouring some elements of the estimated matrix to be shrunken toward zero and providing a well defined estimator when the covariance matrix is singular [17].

The problem solves, in its general form,

$$\begin{aligned} \hat{\varOmega }_i = \underset{\varOmega _i \in \mathcal {G}_{70}}{\text {argmax}} \Big \{ \log |\varOmega _i| - \text {Tr}(\varOmega _i^\intercal S_i) - \xi _i||\varOmega _i||_1\Big \}, \end{aligned}$$
(3)

where \(\mathcal {G}_{k}\) is the manifold of positive defined matrices of dimension k, \(S_i\) is the sample covariance matrix, \(\xi _i\) is a penalization parameter, \(|\cdot |\) indicates the matrix determinant while \(||\cdot ||_1\) the \(\ell _1\)-norm; see [11, 18] for detailed information on this particular optimization problem. Let \(\mathbf {K}_i\) denote the binary version of \(\varOmega _i\), with generic element \(\mathbf {k}_{i\,[u,v]} = \mathbb {I}(\varOmega _{i\,[u,v]}\ne 0)\). Every \(\mathbf {K}_i\) can be interpreted as the adjacency matrix of the functional network for subject i, and the generic element \(\mathbf {k}_{i\,[u,v]}\) indicates whether, for subject i, region u and region v are connected, for subjects \(i = 1,\ldots ,n\) and brain regions \(u = 2, \ldots , 70\) and \(v = 1, \ldots , u-1\).

The parameters \(\xi _i\) in Eq. 3 control the sparsity of the resulting matrix, and can be selected with several information criteria or stability principles [34]. Since we are assuming that the graphical models stem from the same generative process, we fix the value of \(\xi _i = \xi \) across subjects. Moreover, the choice of the smoothing level in the previous module has an important role in determining the characteristics of the resulting estimated graph, and since we aim to compare inferential conclusions at different level of the smoothed series, we opted for a fixed procedure in the choice of \(\xi \).

In choosing the global penalization value, however, standard criteria often selected over-sparse solutions. Although extra sparsity does not constitute a serious issue in high-dimensional graphical models, when interest is on describing the functional networks more conservative configuration are preferred [10]. We restricted the range of the penalization parameter \(\xi \) indirectly, by placing constraints on the resulting minimum value of the functional networks density, measured as proportion of non-zero entries of the network’s adjacency matrix. Different values for the minimum density were tried, ranging in the interval (0.05–0.20), with resulting estimates robust against different choices of the parameter.

In Fig. 3 we reported the estimated functional network for the same subjects reported in Fig. 2, using \(\lambda = 10\) and with a constraint on the functional networks density to values greater or equal to 0.10. We will use this setting for the remaining of the discussion, unless explicitly specified. Both functional networks report interesting patterns, for example a block structure that recalls hemisphere division. However, there are also substantial differences between the two networks, that justify the further step of our procedure.

Fig. 3
figure 3

Estimated functional networks for subjects 3 and 14. Black tiles correspond to edges, white to non-edges

Full size image

3.3 Regression with Covariates

The investigation of the relations between functional connectivity patterns and observed phenotypes is motivated by the subject-specific differences observed in the estimated graphs. The inclusion of covariates into the analysis of functional connectivity patterns aims to identify whether brain activity relates with personal features and behaviours and whether subject-specific information can provide insights on observed differences. Recent studies highlighted the relation among connectivity patterns and, among many others, diseases [33], violent behaviours [9, 29], or gender [20]. Functional networks, as opposed to structural information, contain important information regarding dynamical patterns of the brain architecture, and there is a promising extent of agreement between studies based either on functional or structural networks (e.g., [10]).

We investigate the relation among functional networks and covariates exploiting a simple model that encourages the interpretation of its coefficients and is able to provide interpretable insights on the effect of phenotypes over the structural network. Differently from standard models for network data—such as ERGM [23] or latent space models [21]—we want to focus on modeling multiple adjacency matrices \(\mathbf {K}_1, \ldots , \mathbf {K}_n\), instead of a single one.

We assume that the probability of a connection between each pair \(l = (u,v)\) of brain regions, with \(u = 2, \ldots , 70\) and \(v = 1, \ldots , u-1\) in the network \(\mathbf {K}_i\) can be modeled using an exponential family, with natural parameters as function of phenotypical information, such as age, mental status, handedness, and brain-region specific information, such as lobes membership.

More formally, let \(\text {Pr}(k_{il}=1) = \pi _{il}\) define the vectorised probability to observe a connection for subject i in the pair of brain regions l, with \(i = 1, \ldots , 22\) and \(l = 1, \ldots , 2415 = (70 \times 69)/2\). We model the logit of the connection probability as a function of phenotypical and brain-region information as follow:

$$\begin{aligned} \begin{aligned} \text {logit}(\pi _{il}) = \alpha + \theta _x^T\mathbf {x}_i +\theta _z^T\mathbf {z}_l \end{aligned} \end{aligned}$$

In particular we considered the following variables:

  • subject covariates \(\mathbf {x}_i\): age of the subject, mental health indicating the presence/absence/unknown status of a mental problem (absence used as reference class), handedness with three categories for left/right-handed and ambidextrous (ambidextrous as reference class).

  • edge covariates \(\mathbf {z}_l\): lobe membership, indicating whether the pair \(l = (u,v)\) of brain regions is in the same lobe (not belonging to the same lobe is taken as reference class).

The resulting estimates, for a value of the smoothing parameter \(\lambda = 10\), are reported in Table 1.

Table 1 Estimated coefficients for the GLM model, \(\lambda =10\)
Full size table

Our empirical findings suggest a strong tendency for brain regions located in the same lobe to create more connections in the functional network. Moreover, subjects with a positive mental diagnosis report, on average, a lower probability to observe connected brain regions, with respect to healthy subjects and given the effect of the remaining covariates. Individuals whose mental status is not known report, instead, a higher probability to observe a connection. Handedness of the subjects under investigation is not resulted to be a determinant of functional network. Lastly, the age of the subjects in this study seems to have an effect in the determination of the connections of the functional network, even though the magnitude of this effect is small enough to be negligible.

Table 2 Results of the multiscale sensitivity analysis conducted over different levels of \(\lambda \). Estimated coefficients are reported for some representative levels of \(\lambda \), with bold coefficients indicating an associated p-value less than 0.05
Full size table

3.4 Multiscale Analysis

In order to assess the robustness of our empirical findings, we performed a multiscale sensitivity analysis under different settings. The core idea of the multiscale approach is that whenever a signal can be measured at multiple resolutions, such as different level of smoothing in our case, information can and should be drawn exploiting all this information jointly. The principle that there is not one “correct” resolution at which the analysis should be performed is especially soothing in our context. As in resting state fMRI, it is not clear how noise may look [8], and it is important to consider more than just one resolution, or, equivalently, to explore different noise assumptions.

In the multiscale analysis, we track the evolution of the regression coefficients as the smoothness level increases. In Table 2, we re-estimated the entire model for different values of \(\lambda \) and evaluate changes in the regression coefficients. Smoother series (greater value of \(\lambda \)) correspond to sparser graphs; when the smoothness increases, in fact, the method is able to detect only large scale variations. Since low scale dependency are suppressed, the resulting graphical models tend to be more sparse. In general, results for the sensitivity analysis tend to validate findings presented in the previous section, and estimated coefficient in Table 2 seems coherent with what shown in Table 1.

In particular, the impact of lobes and diagnosis is quite stable across different smoothing levels, which can be interpreted as an indication of robustness with respect to different noise scenario. The handedness of the subject, on the other hand, seems to have a more erratic effect on the connectivity structure, but its contribution is not substantial in the cases analyzed. A noticeable change in such behavior can be observed for values of \(\lambda \ge 18\), which we interpreted as a symptomatic effect of over-smoothing in the denoising step.

4 Discussion

The analysis of neuroimaging data is a stimulating application field that embraces several disciplines; statistics covers a determinant role in this context, since it can provide deep insights on the underlying wiring mechanisms. However, statistical modeling of multiple brain networks is still in its infancy, and the inclusion of subject-specific information within repeated networks is incomplete from a literature viewpoint.

The approach suggested in this work has guided some preliminary insights on the relationship among functional networks, brain constraints and subject-specific phenotypes. One of the main advantages of our approach is its generality; within the modular structure, each block can be as complex as data allows for, leaving room for more appropriate model when needed. We have shown that even with rather simple modules, our empirical findings seem to give reasonable insights on the covariates effect on the functional dependence structure, and the sensitivity analysis performed at different levels of smoothing of the raw data did not seem to provide contradicting results.

The use of the modular approach is motivated by the computational burden and possible model misspecification that would otherwise affect a joint model. However, a two stages approach does not take full advantage of the hierarchical structure of the model, precluding the possibility to treat all uncertainties simultaneously.

An interesting future direction consists in the inclusion of models specific for network data, capable to take into account heterogeneity within the brains architecture. This aim could be achieved including random effects pairs for each ROI of the functional network [26], or using a more appropriate model for multiway data, for example adapting [22].