Network DEA Pitfalls: Divisional Efficiency and Frontier Projection

Abstract

Recently network DEA models have been developed to examine the efficiency of DMUs with internal structures. The internal network structures range from a simple two-stage process to a complex system where multiple divisions are linked together with intermediate measures. In general, there are two types of network DEA models. One is developed under the standard multiplier DEA models based upon the DEA ratio efficiency, and the other under the envelopment DEA models based upon production possibility sets. While the multiplier and envelopment DEA models are dual models and equivalent under the standard DEA, such is not necessarily true for the two types of network DEA models. Pitfalls in network DEA are discussed with respect to the determination of divisional efficiency, frontier type, and projections. We point out that the envelopment-based network DEA model should be used for determining the frontier projection for inefficient DMUs while the multiplier-based network DEA model should be used for determining the divisional efficiency. Finally, we demonstrate that under general network structures, the multiplier and envelopment network DEA models are two different approaches. The divisional efficiency obtained from the multiplier network DEA model can be infeasible in the envelopment network DEA model. This indicates that these two types of network DEA models use different concepts of efficiency. We further demonstrate that the envelopment model’s divisional efficiency may actually be the overall efficiency.

Part of this chapter is based upon Chen, Y., Cook, W.D., Kao, C. and Zhu, Joe, Network DEA pitfalls: Divisional efficiency and frontier projection under general network structures, European Journal of Operational Research, Vol. 226 (2013), 507–515, with permissions from Elsevier Science.

2.1 Introduction

Data envelopment analysis (DEA) is used to identify best practices or (efficient) frontier decision making units (DMUs), in the presence of multiple inputs and outputs (Charnes et al. 1978). DEA provides not only efficiency scores for inefficient DMUs, but also provides for frontier projections for such units onto an efficient frontier. In recent years, a number of DEA studies have focused on DMUs with internal network structures. For example, Cook et al. (2010) review DEA models for treating two-stage network structures. Others have developed DEA-based models for more complicated network structures (see Färe and Grosskopf (2000) and Tone and Tsutsui (2009)). While the focus of the current study is not to review all the existing network DEA approaches, we note that many of these approaches require significant modifications to the standard DEA structures. Therefore, a rational question to ask is whether the network DEA model retains the property of the standard DEA model, namely that it yields both (divisional) efficiency scores and a frontier projection in a single model.

Following a thorough review of the existing network DEA approaches, Chen et al. (2013) conclude that there are two types of structures based upon the standard DEA models used. One type is the multiplier-based network DEA models which calculate the overall network efficiency by integrating the ratio efficiency of each division in the network via geometric or arithmetic averages. Such a network model is then converted into a linear program that looks like the DEA multiplier model. The other type is developed by using the production possibility set for each division in the network. The resulting model takes on the appearance of the DEA envelopment model.

In the standard DEA context, the multiplier model is equivalent to the envelopment model which yields the DEA projection and the efficiency due to the linear programming duality. However, under the network structure, such duality may not lead to a particular pair of network multiplier and envelopment models, where frontier projections and divisional efficiency scores are generated in a single network DEA model.

The current chapter first uses a simple two-stage network structure to demonstrate that under the condition of constant returns to scale (CRS), the envelopment network DEA model does not necessarily provide information on divisional efficiency and only provides information on the frontier projection. This can be a pitfall when we use the envelopment network DEA approach. Such a pitfall is caused by the fact that the envelopment-based network DEA approach does not account for the intermediate measures (or links) in calculating the divisional efficiency. While the multiplier-based network DEA models provide both overall and divisional efficiency scores, their duals may not yield correct information on frontier projections without proper adjustments to those dual models.

Note in the standard DEA approach, variable returns to scale (VRS) is achieved by adding a convexity constraint into the CRS envelopment model or equivalently a free variable into the multiplier model. We demonstrate that under the network DEA model, the above equivalence no longer holds. We further show that envelopment and multiplier network DEA models are two very different approaches using different efficiency concepts. Further, divisional efficiency obtained from the multiplier network DEA model can be infeasible on the envelopment side. We also demonstrate that the envelopment model’s divisional efficiency may actually be the overall efficiency.

The rest of the chapter is organized as follows. Section 2.2 briefly introduces the multiplier and envelopment-based network DEA models under a simple two-stage network structure, where outputs from the first stage (division) are the only inputs to the second stage (division). Sections 2.3 and 2.4 then discuss the pitfalls for determining divisional efficiencies and frontier projections. In Sect. 2.5 we examine the VRS case. Section 2.6 is devoted to discussing network DEA models under general network structures. Conclusions follow in Sect. 2.7.

2.2 Two-Stage Network DEA

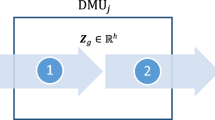
For simplicity, we consider a generic two-stage process as shown in Fig. 2.1, for each of a set of n DMUs. We assume each DMU _j (j = 1, 2, …, n) has m inputs x _ij , (i = 1, 2, …, m) to the first stage, and D outputs z _dj , (d =1, 2, …, D) from that stage. These D outputs then become the inputs to the second stage, hence behaving as intermediate measures. The outputs from the second stage are y _rj , (r =1, 2, …, s).

Fig. 2.1

Two-stage process

For DMU _j we denote the efficiency ratios for the first stage (division) as θ ¹ _j and the second as θ ² _j . Based upon the input-oriented DEA model of Charnes et al. (1978), we have the following standard DEA models for each stage (division):

$$ {\theta}_j^1= \max \frac{{\displaystyle \sum_{d=1}^D{w}_d{z}_{dj}}}{{\displaystyle \sum_{i=1}^m{v}_i{x}_{ij}}}\kern1em \mathrm{and}\kern1em {\theta}_j^2= \max \frac{{\displaystyle \sum_{r=1}^s{u}_r{y}_{rj}}}{{\displaystyle \sum_{d=1}^D{\tilde{w}}_d{z}_{dj}}} $$

(2.1)

$$ \begin{array}{ll}\kern2em \mathrm{Subject}\ \mathrm{to}\hfill & \kern5em \mathrm{Subject}\ \mathrm{to}\hfill \\ {}\kern1.8em \frac{{\displaystyle \sum_{d=1}^D{w}_d{z}_{dj}}}{{\displaystyle \sum_{i=1}^m{v}_i{x}_{ij}}}\le 1\hfill & \kern4.8em \frac{{\displaystyle \sum_{r=1}^s{u}_r{y}_{rj}}}{{\displaystyle \sum_{d=1}^D{\tilde{w}}_d{z}_{dj}}}\le 1\hfill \end{array} $$

where v _i , w _d , ${\tilde{w}}_d$, and u _r are unknown non-negative weights. In order to model the two-stage network based upon the two efficiency ratios defined in (2.1) the variables w _d are set equal to ${\tilde{w}}_d$ as in Kao and Hwang (2008) and in Liang et al. (2008). As a result, the two-stage overall efficiency ratio can be defined as θ ¹ _j  • θ ² _j which is equal to ${\theta}_j=\frac{{\displaystyle \sum_{r=1}^s{u}_r}{y}_{ro}}{{\displaystyle \sum_{i=1}^m{v}_i{x}_{io}}}$. To calculate the overall efficiency of θ _j , Kao and Hwang (2008) present the following model (this model is called centralized model in Liang et al. (2008))

$$ \begin{array}{l} Max\ {\theta}_j^1\bullet {\theta}_j^2=\frac{{\displaystyle \sum_{r=1}^s{u}_r}{y}_{ro}}{{\displaystyle \sum_{i=1}^m{v}_i{x}_{io}}}\hfill \\ {}s.t.{\theta}_j^1\le 1\kern1em \mathrm{and}\kern1em {\theta}_j^2\le 1\kern1em \mathrm{and}\kern1em {w}_d={\tilde{w}}_d\hfill \end{array} $$

(2.2)

Model (2.2) can be converted into the following linear program

$$ \begin{array}{l}\mathrm{Max}{\displaystyle \sum_{r=1}^s{u}_r{y}_{ro}}\hfill \\ {}\mathrm{s}.\mathrm{t}.\kern0.6em {\displaystyle \sum_{r=1}^s{u}_r{y}_{rj}}-{\displaystyle \sum_{d=1}^D{w}_d{z}_{dj}}\le 0\kern1em j=1,2,\dots, n\hfill \\ {}\kern1.8em {\displaystyle \sum_{d=1}^D{w}_d{z}_{dj}-{\displaystyle \sum_{i=1}^m{v}_i{x}_{ij}}}\le 0\kern1em j=1,2,\dots, n\hfill \\ {}\kern1.8em {\displaystyle \sum_{i=1}^m{v}_i}{x}_{io}=1\hfill \\ {}\kern1.8em {w}_d\ge 0,\kern0.5em d=1,2,\dots, D;\kern0.5em {v}_i\ge, \kern0.5em i=1,2,\dots, m;\kern0.5em {u}_r\ge, \kern0.5em r=1,2,\dots, s\hfill \end{array} $$

(2.3)

In a similar manner, we can develop output-oriented models. Model (2.3) yields the overall efficiency. After the overall efficiency is obtained, divisional efficiency can be obtained via efficiency decomposition (see Kao and Hwang (2008)). Specifically,

If we denote the optimal value to model (2.3) as θ ^* _o , then we have θ ^* _o  = θ ^1 * _o  • θ ^2 * _o . Note that optimal multipliers from model (2.3) may not be unique, meaning that θ ^1 * _o and θ ^2 * _o may not be unique. To test for uniqueness, we can first determine the maximum achievable value of θ ^1 * _o via

$$ \begin{array}{l}{\theta}_o^{1+}=\mathrm{Max}\ {\displaystyle \sum_{d=1}^D{w}_d{z}_{do}}\hfill \\ {}s.t.\kern1.5em {\displaystyle \sum_{r=1}^s{u}_r{y}_{ro}}={\theta}_o^{*}\hfill \\ {}\kern2.8em {\displaystyle \sum_{d=1}^D{w}_d{z}_{dj}-{\displaystyle \sum_{i=1}^m{v}_i{x}_{ij}}}\le 0\kern1em j=1,2,\dots, n\hfill \\ {}\kern2.8em {\displaystyle \sum_{r=1}^s{u}_r}{y}_{rj}-{\displaystyle \sum_{d=1}^D{w}_d{z}_{dj}}\le 0\kern1em j=1,2,\dots, n\hfill \\ {}\kern2.8em {\displaystyle \sum_{i=1}^m{v}_i}{x}_{io}=1\hfill \\ {}\kern2.8em {w}_d\ge 0,\kern0.5em d=1,2,\dots, D;\kern0.5em {v}_i\ge 0,\kern0.5em i=1,2,\dots, m;\kern0.5em {u}_r\ge 0,\kern0.5em r=1,2,\dots, s\hfill \end{array} $$

It then follows that the minimum of θ ^2 * _o is given by ${\theta}_o^{2-}=\frac{\theta_o^{*}}{\theta_o^{1+}}$. This also gives an efficiency decomposition of θ ^* _o  = θ ^1 + _o  • θ ^2 − _o .

Liang et al. (2008) provide a procedure for testing the uniqueness of efficiency decomposition. The maximum of θ ^2 * _o , which we denote by θ ^2 + _o , can be calculated in a manner similar to the above, and the minimum of θ ^1 * _o is then calculated as θ ^1 − _o  = θ ^* _o /θ ^2 + _o . Note that θ ^1 − _o  = θ ^1 + _o if and only of θ ^2 − _o  = θ ^2 + _o . Note also that if θ ^1 − _o  = θ ^1 + _o or θ ^2 − _o  = θ ^2 + _o , then θ ^1 * _o and θ ^2 * _o are uniquely determined via model (2.3).

Model (2.3) is based upon the ratio DEA efficiency and then is converted into a DEA multiplier-type linear program. Therefore, we can refer to this type of network DEA approach as multiplier-based. On the other hand, Tone and Tsutsui (2009) develop a slacks-based network DEA model by using the production possibility sets, where the intermediate measures z _dj (d = 1, …, D) are called links. Relative to Fig. 2.1, the constraints for the slacks-based model take the form:

$$ \begin{array}{ll}{\displaystyle \sum_{j=1}^n{\lambda}_j{x}_{ij}}+{s}_i^{-}={x}_{io}\hfill &\ i=1,\dots, \mathrm{m}\hfill \\ {}{\displaystyle \sum_{j=1}^n{\mu}_j{y}_{rj}}-{s}_r^{+}={y}_{ro}\hfill & r=1,\dots, \mathrm{s}\hfill \\ {}{\displaystyle \sum_{j=1}^n{\lambda}_j{z}_{dj}}={\displaystyle \sum_{j=1}^n{\mu}_j{z}_{dj}}\hfill & d=1,\dots, \mathrm{D}\hfill \end{array} $$

(2.4)

In Tone and Tsutsui (2009), models based upon (2.4) are referred to as the “fixed link” case.

Note that z _do are outputs from the first stage and are inputs to the second stage. Therefore, based upon the standard DEA model, the production possibility set can be defined as

$$ \begin{array}{ll}{\displaystyle \sum_{j=1}^n{\lambda}_j{x}_{ij}}+{s}_i^{-}={x}_{io}\hfill & i=1,\dots, \mathrm{m}\hfill \\ {}{\displaystyle \sum_{j=1}^n{\mu}_j{y}_{rj}}-{s}_r^{+}={y}_{ro}\hfill & r=1,\dots, \mathrm{s}\hfill \\ {}{\displaystyle \sum_{j=1}^n{\lambda}_j{z}_{dj}}\ge {\tilde{z}}_{do}\hfill & d=1,\dots, \mathrm{D}\hfill \\ {}{\displaystyle \sum_{j=1}^n{\mu}_j{z}_{dj}}\le {\tilde{z}}_{do}\hfill & d=1,\dots, \mathrm{D}\hfill \end{array} $$

(2.5)

where we use ${\tilde{z}}_{do}$ to denote unknown decision variables for the intermediate measures (or links as referred to in Tone and Tsutsui (2009)). As in Tone and Tsutsui (2009), these measures can be increased or decreased in the optimal solution of a network DEA model based upon (2.5). Tone and Tsutsui (2009) refer to (2.5) as the “free link” case.

The difference between (2.4) and (2.5) (or between “fixed link” and “free link”) is very minor. The slacks-based (envelopment) network DEA models based upon (2.4) and (2.5) will yield identical optimal slack values if the constraints related to ${\tilde{z}}_{do}$ become binding at optimality. Otherwise, if these constraints are not binding, then the two models based upon (2.4) and (2.5) will yield different optimal slack values. If one uses a radial measure, the difference between (2.4) and (2.5) is negligible with respect to the radial efficiency scores. Therefore, in the discussion to follow, we will not specifically distinguish “fixed link” and “free link” for the intermediate measures.

A version of the input-oriented envelopment network DEA model under “free link” intermediate measures can be written as

$$ \begin{array}{l}\mathrm{Max}{\displaystyle \sum_{i=1}^m\frac{s_i^{-}}{x_{io}}}\hfill \\ {}\mathrm{Subject}\ \mathrm{to}\ (5)\hfill \end{array} $$

(2.6)

Since the intermediate measures are the only outputs from stage-1, and the only inputs to stage-2, Tone and Tsutsui’s (2009) input-oriented slacks-based network DEA model will not have the divisional efficiency for stage 2. In other words, the divisional efficiency for stage 1 should be regarded as the overall efficiency, based upon Tone and Tsutsui’s (2009) definition under either “fixed link” or “free link”. In a similar manner, Tone and Tsutsui’s (2009) output-oriented slacks-based network DEA model will not have the divisional efficiency for stage 1, namely the divisional efficiency for stage 2 is the overall efficiency.

Moreover, as shown in Chen et al. (2009b), model (2.3) is equivalent to the following linear program, where the intermediate measures are treated as “free link” defined in Tone and Tsutsui (2009).

$$ \begin{array}{l} \min \tilde{\theta}\\ {}s.t.\kern1.25em {\displaystyle \sum_{j=1}^n{\lambda}_j{x}_{ij}}\le \tilde{\theta}{x}_{io}\kern2.75em i=1,\dots, \mathrm{m}\\ {}\kern2.25em {\displaystyle \sum_{j=1}^n{\mu}_j{y}_{rj}}\ge {y}_{ro}\kern2em r=1,\dots, \mathrm{s}\\ {}\kern2.25em {\displaystyle \sum_{j=1}^n{\lambda}_j{z}_{dj}}\ge {\tilde{z}}_{do}\kern3em d=1,\dots, \mathrm{D}\\ {}\kern2.25em {\displaystyle \sum_{j=1}^n{\mu}_j{z}_{dj}}\le {\tilde{z}}_{do}\kern2.5em d=1,\dots, \mathrm{D}\\ {}\kern2.4em {\tilde{z}}_{do}\ge 0,\kern2.5em d=1,\dots, \mathrm{D}\\ {}\kern2.3em {\lambda}_j\ge 0,\kern1em j=1,\dots, n\\ {}\kern2.3em {\mu}_j\ge 0,\kern1em j=1,\dots, n\\ {}\kern2.2em \tilde{\theta}\le 1\end{array} $$

(2.7)

Model (2.7) can be viewed as the radial version of the two-stage network DEA model of Tone and Tsutsui’s (2009) based upon (2.5). In this case, model (2.7), like the input-oriented slacks-based network DEA model (2.6), can only generate the overall efficiency. In this regard, θ* cannot be treated as the divisional efficiency of stage 1.

Models developed based upon (2.4) or (2.5) can be called envelopment DEA network models, as they are similar to the standard envelopment DEA model format. If we add ∑ λ _j  = ∑ μ _j  = 1 into (2.4) or (2.5), the existing DEA literature claims that the VRS envelopment network DEA model is obtained, since this is how VRS envelopment model is obtained under the standard DEA model. However, we believe that this issue needs to be further examined.

2.3 Two-Stage Network: Divisional Efficiency Pitfall

Consider the numerical example given in Table 2.1 where we have five DMUs and two intermediate measures. Table 2.2 reports the optimal slacks and intermediate measures when (2.4) and (2.5) are used. The last three columns report the overall efficiency based upon (2.2), and its efficiency decomposition for divisional efficiency scores based upon Kao and Hwang (2008) and Liang et al. (2008).

Table 2.1 Numerical example for two-stage network

Table 2.2 Optimal slacks and intermediate measures

It can be seen that the envelopment-based network DEA model can generate a score for overall efficiency and frontier projections, and the multiplier-based two-stage network DEA model (2.2) or (2.4) is able to generate the divisional efficiency scores for both stages. In other words, under the network DEA approach, both multiplier and envelopment-based models are needed to generate (i) overall efficiency, (ii) divisional efficiency, and (iii) frontier projections.

Under (2.5), model (2.2) or its equivalent model (2.7) yields the identical optimal intermediate measures as model (2.6). This also implies that the input-oriented slacks-based network DEA model does not yield information on divisional efficiency.

For the output-oriented situation, we can obtain the similar conclusion that while the multiplier network DEA model can decompose the overall efficiency into divisional efficiency scores, the slacks-based or envelopment network DEA model only yields information on the overall efficiency along with the frontier projection.

We finally consider the non-oriented case. For example, for (2.4) or (2.5), we can use sum of slacks or the ratio form from Tone and Tsutsui (2009). For example, we can have the following non-oriented envelopment network DEA model.

$$ \begin{array}{c}\mathrm{Max}\ {\displaystyle \sum_{i=1}^m\frac{s_i^{-}}{x_{io}}}+{\displaystyle \sum_{r=1}^s\frac{s_r^{+}}{y_{ro}}}\\ {}\mathrm{Subject}\ \mathrm{to}\ (4)\ \mathrm{or}\ (5)\hfill \end{array} $$

(2.8)

Or, it appears that we can build a radial version of (2.8), that is

$$ \begin{array}{l} \min \alpha -\beta \\ {}s.t.\kern1.25em {\displaystyle \sum_{j=1}^n{\lambda}_j{x}_{ij}}\le \alpha {x}_{io}\kern2.75em i=1,\dots, \mathrm{m}\\ {}\kern2.25em {\displaystyle \sum_{j=1}^n{\mu}_j{y}_{rj}}\ge \beta {y}_{ro}\kern2em r=1,\dots, \mathrm{s}\\ {}\kern2.25em {\displaystyle \sum_{j=1}^n{\lambda}_j{z}_{dj}}\ge {\tilde{z}}_{do}\kern3em d=1,\dots, \mathrm{D}\\ {}\kern2.25em {\displaystyle \sum_{j=1}^n{\mu}_j{z}_{dj}}\le {\tilde{z}}_{do}\kern2.5em d=1,\dots, \mathrm{D}\\ {}\kern2.2em {\tilde{z}}_{do}\ge 0,\kern2.5em d=1,\dots, \mathrm{D}\\ {}\kern2.2em {\lambda}_j\ge 0,\kern1em j=1,\dots, n\\ {}\kern2.2em {\mu}_j\ge 0,\kern1em j=1,\dots, n\\ {}\kern2.1em \alpha \le 1,\beta \ge 1\end{array} $$

(2.9)

where α and β represent the divisional efficiency scores for stages 1 and 2 respectively. Model (2.9) assumes “free link”. If “fixed link” is assumed, we use ${\displaystyle \sum_{j=1}^n{\lambda}_j{z}_{dj}}={\displaystyle \sum_{j=1}^n{\mu}_j{z}_{dj}}$ in model (2.9).

However, as shown in Chen et al. (2009b), α* = 1 and 1/β* is equal to the overall efficiency obtained from model (2.2) at optimality. This indicates that α and β actually do not represent the divisional efficiency scores. This implies that the slack based measures cannot be used to represent the divisional efficiency scores in model (2.8).

Table 2.3 reports the results from (2.8). Both (2.4) (“fixed link”) and (2.5) (“free link”) yield identical optimal slacks and intermediate measures, namely, the inequality constraints in (2.5) are binding at optimality. It can be seen from the input slacks that DMUs 1 and 5 are efficient and DMUs 2, 3, and 4 are weakly efficient. This corresponds to the situation α* = 1. Based upon the last two columns of Table 2.2, stage 1 in DMU5 is not efficient, for example.

Table 2.3 Slacks and intermediate measures based on non-oriented model

The above phenomenon can be regarded as a two-stage network DEA pitfall in calculating divisional efficiency. It is recommended that the envelopment-based network DEA model, for example, Tone and Tsutsui’s (2009), be used to calculate the frontier projection, and the multiplier-based approach is used to calculate the overall and divisional efficiencies.

This pitfall can be due to the fact that the envelopment-based network DEA model does not consider the optimal intermediate measures in its calculation of the divisional efficiency. In the current study, we argue that divisional efficiency should be based upon the DEA ratio efficiency as defined in (2.1) where (optimal) intermediate measures are considered. This is due to the fact that once the optimal intermediate measures are determined, they become inputs (or outputs) to a division.

2.4 Two-Stage Network: Frontier Projection Pitfall

While the envelopment-based network DEA model provides a frontier projection for inefficient DMUs, the dual to the multiplier-based network DEA model does not necessarily provide the frontier projection. For example, the dual to model (2.3) is

$$ \begin{array}{l} Min\;\theta \hfill \\ {}\begin{array}{cc}\hfill s.t.\kern.8em {\displaystyle \sum_{j=1}^n{\lambda}_j}{x}_{ij}\le \theta {x}_{io}\hfill & \hfill i=1,2,\dots, m\hfill \end{array}\hfill \\ {}\begin{array}{cc}\hfill \kern2em {\displaystyle \sum_{j=1}^n{\mu}_j{y}_{rj}}\ge {y}_{ro}\hfill & \hfill r=1,2,\dots, m\hfill \end{array}\hfill \\ {}\begin{array}{cc}\hfill \kern2em {\displaystyle \sum_{j=1}^n\Big({\lambda}_j}-{\mu}_j\Big){z}_{dj}\ge 0\hfill & \hfill d=1,2,\dots, D\hfill \end{array}\hfill \\ {}\begin{array}{cc}\hfill \kern2em {\lambda}_j,{\mu}_j\ge 0\hfill & \hfill \theta \le 1\hfill \end{array}\hfill \end{array} $$

(2.10)

As shown in Chen et al. (2010) or Chap. 4, (θ*x _io , z _do , y _ro ) is not on the frontier as the projection generated by model (2.10), and we have to determine an optimal z _do . Based upon the discussion in the previous section, we know that for an inefficient DMU to be projected onto the network DEA frontier, its intermediate measures will have to be adjusted (increased or decreased). In fact, Chen et al. (2010) show that model (2.10) is equivalent to model (2.7). Therefore, the dual to the multiplier-based network DEA model (namely model (2.10)) has to be adjusted as model (2.7) in order to calculate the optimal intermediate measures so that we obtain the correct frontier projection as (${\theta}^{*}{x}_{io},{\tilde{z}}_{do}^{*},{y}_{ro}$) or (θ*x _io , ∑ λ ^* _j z _ij , y _ro ).

Since Fig. 2.1 presents a simple network structure, we are able to modify the model (2.10) to model (2.7). In a complicated network structure, such task may not be possible.

Such frontier projections have an interesting aspect. We consider the two-stage network structure involving 24 Taiwanese non-life insurance companies studied in Kao and Hwang (2008). The two stages represent premium acquisition and profit generation respectively. The inputs to the first stage are operational expenses and insurance expenses, and the outputs from the second stage are underwriting profit and investment profit. There are two intermediate measures between the two stages, namely direct written premiums and reinsurance premiums.

Table 2.4 reports a set frontier projection points based upon model (2.7). Table 2.5 reports the overall efficiency and its decomposition based upon model (2.3). Note that none of the DMUs are efficient.

Table 2.4 Frontier projection

Table 2.5 Overall efficiency and its decomposition

Because of the existence of intermediate measures, we cannot apply the standard DEA to each stage separately. However, since we now have the frontier, we should be able to apply the standard DEA to each stage after we include the projected DMUs in Table 2.4. In other words, we now have a set of 48 DMUs, of which 24 are projections of the original DMUs.

The last two columns of Table 2.5 report the CRS efficiency scores. Interestingly, these scores are equal to the standard CRS scores when the original 24 DMUs are evaluated. That is,, the added projected DMUs do not change the CRS efficiency scores. Note that the projected DMUs are obtained from the network DEA model and represent the frontier for the two-stage process. Such a frontier cannot be obtained from the standard CRS model.

The above discussion may indicate that the network DEA model behaves very differently from the standard DEA model, although it is built upon the standard DEA model.

Finally, we point out that one may argue that the dual variables to the multiplier model (2.3) could be used to obtain the frontier projections. However, without the help of transforming the model (2.10) (which is the dual to model (2.3)) to model (2.7), we cannot obtain the frontier projections directly based upon the dual variables. The same is true that we cannot obtain the divisional efficiency directly based upon the dual variables to the envelopment model (2.7). In other words, both models (2.3) and (2.7) are needed to calculate the divisional efficiency and frontier projections. We will further demonstrate this point in the next section.

2.5 Two-Stage Network: Variable Returns to Scale

Discussions in Sects. 2.3 and 2.4 are based upon CRS. Under the standard DEA approach, by adding the convexity constraint (e.g. ∑ λ _j  = 1), we obtain the envelopment model under VRS. Note that under the standard DEA approach, the VRS multiplier model is obtained by introducing a free variable. The issue here is whether the multiplier network model is equivalent to the envelopment network model under the VRS condition. To address such an issue is computationally difficult because model (2.2) for VRS version cannot be converted into a linear program. An alternative approach is to use an additive form of weighed average of divisional efficiency scores (Chen et al. 2009a). However, Chen et al. (2009a) discover that CRS scores are greater than the related VRS scores for several DMUs in the case of 24 Taiwanese non-life insurance companies. This may indicate that the properties related to returns to scale in the standard DEA model do not apply in network DEA.

Kao and Hwang (2011) recently developed an alternative approach to study efficiency decomposition under both CRS and VRS conditions. Based upon model (2.3), we denote E ₀, E ¹₀ , and E ²₀ to be the system, stage 1, and stage 2 CRS efficiencies of the two-stage system, respectively. Now, let T ₀, T ¹₀ , and T ²₀ be the respective technical efficiencies (under VRS), and S ₀, S ¹₀ , and S ²₀ the respective scale efficiencies. Since the outputs of the first stage are the inputs of the second, if one wants to improve the efficiency of the first stage via increasing its outputs, then the efficiency of the second stage will be affected. Therefore, Kao and Hwang (2011) used the input-oriented VRS model to calculate T ¹₀ and the output-oriented VRS model to calculate T ²₀ , so that the intermediate products can remain intact. As in the conventional case, S ¹₀  = E ¹₀ /T ¹₀ and S ²₀  = E ²₀ /T ²₀ . Note that the former is an input-oriented scale efficiency and the latter output-oriented one. The technical and scale efficiencies of the overall system are the products of those of the first and second stages, respectively, i.e., T ₀ = T ¹₀  × T ²₀ and S ₀ = S ¹₀  × S ²₀ .

To calculate the input-oriented VRS technical efficiency of stage 1 and the output-oriented VRS technical efficiency of stage 2, the production possibility based envelopment models are:

$$ \begin{array}{l} \min.\theta \hfill \\ {}\mathrm{s}.\mathrm{t}.\kern1.5em {\displaystyle {\sum}_{j=1}^n{\lambda}_j{X}_{ij}}\le \theta {X}_{i0}\hfill \\ {}\kern2.7em {\displaystyle {\sum}_{j=1}^n{\lambda}_j{Z}_{dj}}\ge {Z}_{d0}\hfill \\ {}\kern2.7em {\displaystyle {\sum}_{j=1}^n{\lambda}_j}=1\hfill \\ {}\kern2.7em {\displaystyle {\sum}_{j=1}^n{\mu}_j{Z}_{dj}}\le {Z}_{d0}\hfill \\ {}\kern2.7em {\displaystyle {\sum}_{j=1}^n{\mu}_j{Y}_{rj}}\ge {Y}_{r0}\hfill \end{array} $$

(2.11)

$$ \begin{array}{l} \min.\eta \hfill \\ {}\mathrm{s}.\mathrm{t}.\kern1.5em {\displaystyle {\sum}_{j=1}^n{\lambda}_j{X}_{ij}}\le {X}_{i0}\hfill \\ {}\kern2.7em {\displaystyle {\sum}_{j=1}^n{\lambda}_j{Z}_{dj}}\ge {Z}_{d0}\hfill \\ {}\kern2.7em {\displaystyle {\sum}_{j=1}^n{\mu}_j{Z}_{dj}}\le {Z}_{d0}\hfill \\ {}\kern2.7em {\displaystyle {\sum}_{j=1}^n{\mu}_j{Y}_{rj}}\ge {Y}_{r0}/\eta \hfill \\ {}\kern2.7em {\displaystyle {\sum}_{j=1}^n{\mu}_j}=1\hfill \end{array} $$

(2.12)

Based on Kao and Hwang (2011), T ¹₀ and T ²₀ are calculated as follows:

$$ \begin{array}{ll}{T}_0^1= \max.\left({\displaystyle {\sum}_{d=1}^D{\tilde{w}}_d{Z}_{d0}}-{\tilde{w}}_0\right)/{\displaystyle {\sum}_{i=1}^m{v}_i{\tilde{X}}_{i0}}\hfill & {T}_0^1= \max.\kern0.5em {\displaystyle {\sum}_{r=1}^s{u}_r{\widehat{Y}}_{r0}}/\left({\displaystyle {\sum}_{d=1}^D{\widehat{w}}_d{Z}_{d0}}+{\widehat{w}}_0\right)\hfill \\ {}\mathrm{s}.\mathrm{t}.\kern1em {\displaystyle {\sum}_{r=1}^s{u}_r{Y}_{r0}}/{\displaystyle {\sum}_{i=1}^m{v}_i{X}_{i0}}={E}_0\hfill & \mathrm{s}.\mathrm{t}.\kern1em {\displaystyle {\sum}_{r=1}^s{u}_r{Y}_{r0}}/{\displaystyle {\sum}_{i=1}^m{v}_i{X}_{i0}}={E}_0\hfill \\ {}\kern2em {\displaystyle {\sum}_{d=1}^D{w}_d{Z}_{dj}}-{\displaystyle {\sum}_{i=1}^m{v}_i{X}_{ij}}\le 0\hfill & \kern2em {\displaystyle {\sum}_{d=1}^D{w}_d{Z}_{dj}}-{\displaystyle {\sum}_{i=1}^m{v}_i{X}_{ij}}\le 0\hfill \\ {}\kern2em {\displaystyle {\sum}_{r=1}^s{u}_r{Y}_{rj}}-{\displaystyle {\sum}_{d=1}^D{w}_d{Z}_{dj}}\le 0\hfill & \kern2em {\displaystyle {\sum}_{r=1}^s{u}_r{Y}_{\kern-0.23em rj}}-{\displaystyle {\sum}_{d=1}^D{w}_d{Z}_{dj}}\le 0\hfill \\ {}\kern2em \left({\displaystyle {\sum}_{d=1}^D{\tilde{w}}_d{Z}_{dj}}-{\tilde{w}}_0\right)-{\displaystyle {\sum}_{i=1}^m{v}_i{\tilde{X}}_{ij}}\le 0\hfill & \kern2em {\displaystyle {\sum}_{r=1}^s{u}_r{\widehat{Y}}_{\kern-0.4em rj}}-\left({\displaystyle {\sum}_{d=1}^D{\widehat{w}}_d{Z}_{dj}}+{\widehat{w}}_0\le 0\right)\hfill \end{array} $$

The linearized forms for calculating T ¹₀ and its dual are:

$$ \begin{array}{ll}{T}_0^1= \max.{\displaystyle {\sum}_{d=1}^D{\tilde{w}}_d{Z}_{d0}}-{\tilde{w}}_0\kern6.5em \mathrm{dual}\hfill & \kern1em \min.{\theta}_1\hfill \\ {}\kern2em \mathrm{s}.\mathrm{t}.\kern1em {\displaystyle {\sum}_{i=1}^m{v}_i{\tilde{X}}_{i0}}=1\kern9em {\theta}_1\hfill & \kern2em {\displaystyle {\sum}_{j=1}^n{\alpha}_j{X}_{ij}}\le {\theta}_1{X}_{i0}\hfill \\ {}\kern4em {E}_0{\displaystyle {\sum}_{i=1}^m{v}_i{X}_{i0}}-{\displaystyle {\sum}_{r=1}^s{u}_r{Y}_{r0}}=0\kern2em \eta \hfill & \kern2em {\displaystyle {\sum}_{j=1}^n{\alpha}_j}=1\hfill \\ {}\kern4em {\displaystyle {\sum}_{d=1}^D{w}_d{Z}_{dj}}-{\displaystyle {\sum}_{i=1}^m{v}_i{X}_{ij}}\le 0\kern3em {\lambda}_j\hfill & \kern2em {\displaystyle {\sum}_{j=1}^n{\alpha}_j{Z}_{dj}}\ge {Z}_{d0}\hfill \\ {}\kern4em {\displaystyle {\sum}_{r=1}^s{u}_r{Y}_{rj}}-{\displaystyle {\sum}_{d=1}^D{w}_d{Z}_{dj}}\le 0\kern3em {\mu}_j\hfill & \kern2em {\displaystyle {\sum}_{j=1}^n{\lambda}_j{X}_{ij}}\le \eta {E}_0{X}_{i0}\hfill \\ {}\kern4em {\displaystyle {\sum}_{d=1}^D{\tilde{w}}_d{Z}_{dj}}-{\tilde{w}}_0-{\displaystyle {\sum}_{i=1}^m{v}_i{\tilde{X}}_{ij}}\le 0\kern1em {\alpha}_j\hfill & \kern2em {\displaystyle {\sum}_{j=1}^n{\mu}_j{Y}_{rj}}\ge \eta {Y}_{r0}\hfill \\ {}\hfill & \kern2em {\displaystyle {\sum}_{j=1}^n\left({\lambda}_j-{\mu}_j\right){Z}_{dj}}\ge 0\hfill \end{array} $$

From the dual, which is an envelopment model, it is clear that ∑  ⁿ _j = 1 α _j Z _dj , ∑  ⁿ _j = 1 α _j X _ij , ∑  ⁿ _j = 1 λ _j X _ij , ∑  ⁿ _j = 1 μ _j Y _rj , and ∑  ⁿ _j = 1 λ _j Z _pj (or ∑  ⁿ _j = 1 μ _j Z _pj ) are the projections of VRS-Z _d0, VRS-X _i0, CRS-X _i0, CRS-Y _r0, and CRS-Z _d0, respectively. The CRS efficiency of stage two is η, which is equal to 1/E ²₀ . The CRS efficiency of stage one is E ¹₀ , or ηE ₀(=η × E ¹₀  × E ²₀ ).

Obviously, the dual model is very different from the envelopment-based model (2.11). Under careful inspection, one finds that the last three sets of constraints have nothing to do with calculating θ ₁, and can thus be deleted. In other words, VRS technical efficiency can be calculated independently of the CRS efficiencies.

Similarly, the linearized forms for T ²₀ and its dual are:

$$ \begin{array}{ll}{T}_0^2= \max.{\displaystyle {\sum}_{r=1}^s{\widehat{u}}_r{Y}_{r0}}\kern11.5em \mathrm{dual}\hfill & \kern1em \min.{\theta}_2\hfill \\ {}\kern2em \mathrm{s}.\mathrm{t}.\kern1.15em {\displaystyle {\sum}_{d=1}^D{\widehat{w}}_d{Z}_{d0}}+{\widehat{w}}_0=1\kern6.85em {\theta}_2\hfill & \kern1em \mathrm{s}.\mathrm{t}.\kern0.76em {\displaystyle {\sum}_{j=1}^n{\beta}_j{Z}_{dj}}\le {\theta}_2{Z}_{d0}\hfill \\ {}\kern4.45em {E}_0{\displaystyle {\sum}_{i=1}^m{v}_i{X}_{i0}}-{\displaystyle {\sum}_{r=1}^s{u}_r{Y}_{r0}}=0\kern2.9em \eta \hfill & \kern3em {\displaystyle {\sum}_{j=1}^n{\beta}_j}={\theta}_2\hfill \\ {}\kern4.35em {\displaystyle {\sum}_{d=1}^D{w}_d{Z}_{dj}}-{\displaystyle {\sum}_{i=1}^m{v}_i{X}_{ij}}\le 0\kern3.9em {\lambda}_j\hfill & \kern3em {\displaystyle {\sum}_{j=1}^n{\beta}_j{Y}_{rj}}\ge {Y}_{r0}\hfill \\ {}\kern4.35em {\displaystyle {\sum}_{r=1}^s{u}_r{Y}_{rj}}-{\displaystyle {\sum}_{d=1}^D{w}_d{Z}_{dj}}\le 0\kern3.7em {\mu}_j\hfill & \kern3em {\displaystyle {\sum}_{j=1}^n{\lambda}_j{X}_{ij}}\le \eta {E}_0{X}_{i0}\hfill \\ {}\kern4.4em {\displaystyle {\sum}_{r=1}^s{\widehat{u}}_r{Y}_{rj}}-{\displaystyle {\sum}_{d=1}^D{\widehat{w}}_d{Z}_{dj}}-{\widehat{w}}_0\le 0\kern0.85em {\beta}_j\hfill & \kern3em {\displaystyle {\sum}_{j=1}^n{\mu}_j{Y}_{rj}}\ge \eta {Y}_{r0}\hfill \\ {}\hfill & \kern3em {\displaystyle {\sum}_{j=1}^n\left({\lambda}_j-{\mu}_j\right){Z}_{dj}}\ge 0\hfill \end{array} $$

The projections for VRS-Z _d0 and VRS-Y _r0 are ${\displaystyle {\sum}_{j=1}^n}$(β _j /θ ₂)Z _dj and ${\displaystyle {\sum}_{j=1}^n}$(β _j /θ ₂)Y _rj , respectively. Other interpretations are similar to that of the first stage. Again, the VRS technical efficiency can be calculated independently of the CRS efficiencies.

The models for stages one and two can be combined as:

$$ \begin{array}{ll}\mathrm{Max}.\left({\displaystyle {\sum}_{d=1}^D{\tilde{w}}_d{Z}_{d0}}-{\tilde{w}}_0\right)+\left({\displaystyle {\sum}_{r=1}^s{\widehat{u}}_r{Y}_{r0}}\right)\kern.5em \mathrm{dual}\hfill & \min.{\theta}_1+{\theta}_2\hfill \\ {}\mathrm{s}.\mathrm{t}.\kern1.25em {\displaystyle {\sum}_{i=1}^m{v}_i{\tilde{X}}_{i0}}=1\kern10.1em {\theta}_1\hfill & \mathrm{s}.\mathrm{t}.\kern1em {\displaystyle {\sum}_{j=1}^n{\alpha}_j{X}_{ij}}\le {\theta}_1{X}_{i0},{\displaystyle {\sum}_{j=1}^n{\beta}_j{Z}_{dj}}\le {\theta}_2{Z}_{d0}\hfill \\ {}\kern2.5em {\displaystyle {\sum}_{d=1}^D{\widehat{w}}_d{Z}_{d0}}+{\widehat{w}}_0=1\kern6.8em {\theta}_2\hfill & {\displaystyle \kern2em {\sum}_{j=1}^n{\alpha}_j}=1,\kern1em {\displaystyle {\sum}_{j=1}^n{\beta}_j}={\theta}_2\hfill \\ {}\kern2.5em {E}_0{\displaystyle {\sum}_{i=1}^m{v}_i{X}_{i0}}-{\displaystyle {\sum}_{r=1}^s{u}_r{Y}_{r0}}=0\kern2.9em \eta \hfill & {\displaystyle \kern2em {\sum}_{j=1}^n{\alpha}_j{Z}_{dj}}\ge {Z}_{d0},\kern1em {\displaystyle {\sum}_{j=1}^n{\beta}_j{Y}_{rj}}\ge {Y}_{r0}\hfill \\ {}\kern2.5em {\displaystyle {\sum}_{d=1}^D{w}_d{Z}_{dj}}-{\displaystyle {\sum}_{i=1}^m{v}_i{X}_{ij}}\le 0\kern3.9em {\lambda}_j\hfill & {\displaystyle \kern2em {\sum}_{j=1}^n{\lambda}_j{X}_{ij}}\le \eta {E}_0{X}_{i0}\hfill \\ {}\kern2.5em {\displaystyle {\sum}_{r=1}^s{u}_r{Y}_{rj}}-{\displaystyle {\sum}_{d=1}^D{w}_d{Z}_{dj}}\le 0\kern3.6em {\mu}_j\hfill & \kern2.2em {\displaystyle {\sum}_{j=1}^n{\mu}_j{Y}_{rj}}\ge \eta {Y}_{r0}\hfill \\ {}\kern2.5em {\displaystyle {\sum}_{d=1}^D{\tilde{w}}_d{Z}_{dj}}-{\tilde{w}}_0-{\displaystyle {\sum}_{i=1}^m{v}_i{\tilde{X}}_{ij}}\le 0\kern1.4em {\alpha}_j\hfill & {\displaystyle \kern2em {\sum}_{j=1}^n\left({\lambda}_j-{\mu}_j\right){Z}_{dj}}\ge 0\hfill \\ {}\kern2.5em {\displaystyle {\sum}_{r=1}^s{\widehat{u}}_r{Y}_{rj}}-{\displaystyle {\sum}_{d=1}^D{\widehat{w}}_d{Z}_{dj}}-{\widehat{w}}_0\le 0\kern.9em {\beta}_j\hfill & \hfill \end{array} $$

The interpretations are straightforward. Note that θ ₁ and θ ₂ are independent, and can thus be calculated separately. If the model is developed under the envelopment form, then it will be something similar to model (2.9) with the convexity constraints of ∑ λ _j  = 1 and ∑ μ _j  = 1, which is obviously different from the dual of the VRS multiplier model derived here.

If there are multiple solutions, such that the decomposition of E ₀ = E ¹₀  × E ²₀ is not unique, then stage one (or stage 2) must be calculated first, then calculate the second stage by requiring the CRS efficiency of stage one is equal to E ¹₀ , i.e. ${\displaystyle {\sum}_{D=1}^D}$ w _d Z _d0 $\operatorname{}{\displaystyle {\sum}_{i=1}^m}$ v _i X _i0 = E ¹₀ .

The above discussion reveals the following interesting observation. While in the standard DEA model, the multiplier and envelopment models are equivalent, in the two-stage network DEA, such equivalence does not exist. This indicates that the multiplier-based and envelopment-based network DEA models are two different approaches. We will further illustrate this point in the next section. The next section will show that under general network structures, the multiplier and envelopment network models not only use different efficiency concepts, but also do not correspond with each other.

2.6 Multiplier Versus Envelopment Network DEA: Pitfall

We now assume that in addition to the intermediate measures (z _dj , (d =1, 2, …, D)), there are inputs to the second stage pictured in Fig. 2.1. We denote these inputs to the second stage shown as x ^{stage − 2} _hj (h =1, 2, …, H), using the same notations from Li et al. (2012). Figure 2.1 then becomes

Model (2.2) now becomes

$$ \begin{array}{l} \max {\theta}_1^o*{\theta}_2^o= \max \frac{{\displaystyle \sum_{d=1}^D{w}_d{z}_{do}}}{{\displaystyle \sum_{i=1}^m{v}_i{x}_{io}}}*\frac{{\displaystyle \sum_{r=1}^s{u}_r{y}_{ro}}}{{\displaystyle \sum_{d=1}^D{w}_d{z}_{do}}+{\displaystyle \sum_{h=1}^H{Q}_h{x}_{ho}^{stage-2}}}\hfill \\ {}\kern2em \begin{array}{cc}\hfill s.t.\kern2.4em \frac{{\displaystyle \sum_{d=1}^D{w}_d{z}_{dj}}}{{\displaystyle \sum_{i=1}^m{v}_i{x}_{ij}}}\le 1\hfill & \hfill \forall j\hfill \end{array}\hfill \\ {}\begin{array}{cc}\hfill \kern5.7em \frac{{\displaystyle \sum_{r=1}^s{u}_r{y}_{rj}}}{{\displaystyle \sum_{d=1}^D{w}_d{z}_{dj}}+{\displaystyle \sum_{h=1}^H{Q}_h{x}_{hj}^{stage-2}}}\le 1\hfill & \hfill \forall j\hfill \end{array}\hfill \\ {}\kern6em {v}_i,{w}_d,{Q}_h,{u}_r\ge 0,\forall i,d,h,r\hfill \end{array} $$

(2.13)

where θ ^o₁ and θ ^o₂ represent the ratio efficiencies for stages 1 and 2, respectively. Note that the “link” between the two stages is indicated by the same weights w _d for the intermediate measures. Due to the additional inputs to the second stage $\left({\displaystyle \sum_{h=1}^H{Q}_h{x}_{ho}^{stage-2}}\right)$, model (2.13) cannot be converted into a linear program. Li et al. (2012) introduce a heuristic method to solve this problem.

Model (2.13) is regarded as the multiplier model. To establish the envelopment DEA network model for Fig. 2.2, we follow Tone and Tsutsui (2009) and provide the following model based upon the concept of the production possibility set. Note that in this case, the intermediate measures are treated as “fixed link”.

Fig. 2.2

Two-stage process with additional inputs to the second stage

$$ \begin{array}{l} \min {\theta}^1+{\theta}^2\\ {}s.t.\kern1em {\displaystyle \sum_{j=1}^n{\lambda}_j{x}_{ij}}\le {\theta}^1{x}_{io}\kern1em i=1,\dots, \mathrm{m}\\ {}\kern2em {\displaystyle \sum_{j=1}^n{\lambda}_j{z}_{dj}}={\displaystyle \sum_{j=1}^n{\mu}_j{z}_{dj}}\kern1em d=1,\dots, \mathrm{D}\\ {}\kern2em {\displaystyle \sum_{j=1}^n{\mu}_j{x}_{hj}^{stage-2}}\le {\theta}^2{x}_{ho}^{stage-2}\kern1em h=1,\dots, \mathrm{H}\\ {}\kern2em {\displaystyle \sum_{j=1}^n{\mu}_j{y}_{rj}}\ge {y}_{ro}\kern1em r=1,\dots, \mathrm{s}\\ {}\kern2em {\theta}^1,{\theta}^2\le 1\\ {}\kern2em {\lambda}_j{\mu}_j\ge 0\end{array} $$

(2.14)

We use radial measures θ ¹, θ ² rather than slacks-based measures in model (2.14), because in the standard DEA approach, the radial measure in the envelopment model is equivalent to the ratio efficiency defined in the multiplier model.

The issue here is whether θ ^1* and θ ^2* obtained from model (2.14) represent the efficiency scores for stages 1 and 2. To address this issue, we need to compare models (2.13) and (2.14). Since as demonstrated in Li et al. (2012), model (2.13) can only be converted into a nonlinear program, we are not able to compare model (2.13) and the dual to model (2.14). Note however that the data set used in Li et al. (2012) yields a unique efficiency decomposition (divisional efficiency). Therefore, we can compare the divisional efficiency scores obtained from models (2.13) and (2.14).

Table 2.6 provides the data for the R&D system for the 30 Provincial Level Regions in China used in Li et al. (2012). The two stages are technology development process, and economic application process. The inputs to the first stage are: R&D expenditure (R&DE), R&D personnel (R&DP) and the proportion of regional science and technology funds in regional total financial expenditure (S&TF/TFE). The intermediate measures are the number of patents and the number of papers. The second stage also has an input of contract value (CV) in technology market. The outputs from the second stage are GDP, total exports (TE), urban per capita disposable annual income (UPCDAI), and gross output of high-tech industry (GOHI).

Table 2.6 Inputs and outputs of R& D for 30 provincial level regions in mainland China

Columns 2 and 3 of Table 2.7 report the unique divisional efficiency scores obtained from model (2.13) under Li et al.’s (2012) algorithm. Columns 4 and 5 report the divisional efficiency scores from model (2.14). We observe that except for 8 DMUs (6, 8, 9, 10, 16, 27, 29, 30), divisional efficiency scores from models (2.13) and (2.14) are very different. This indicates that models (2.13) and (2.14) produce different results under general network structures.

Table 2.7 Divisional efficiency scores

We next test whether the divisional efficiency scores for each DMU obtained from the multiplier model (2.13) are feasible solutions for θ ¹ and θ ² in the envelopment model (2.14). The last column in Table 2.7 indicates that DMUs 20 and 28’s model (2.13) divisional efficiency scores are infeasible under model (2.14). However, all DMUs’ divisional efficiency scores obtained from model (2.14) are feasible scores under model (2.13). In particular, model (2.14) yields projection points. If we apply model (2.13) to the projection points obtained from model (2.14), each DMU is efficient.

The above study indicates that (i) the multiplier and envelopment network DEA models are different with respect to defining divisional efficiency, and (ii) the projection points based upon the envelopment network DEA model are efficient under the multiplier network DEA model.

To further illustrate the above points, we modify the objective function of model (2.14) from (θ ¹ + θ ²) to (θ ¹ + θ ²)/2, which will not affect the solution. Then the dual of model (2.14) becomes:

$$ \begin{array}{ll}\mathrm{Min}.\left({\theta}^1+{\theta}^1\right)/2\kern8em \mathrm{dual}\hfill & \max.{\displaystyle {\sum}_{r=1}^s{u}_r{Y}_{r0}}\hfill \\ {}\mathrm{s}.\mathrm{t}\kern1em {\displaystyle {\sum}_{j=1}^n{\lambda}_j{X}_{ij}}\le {\theta}^1{X}_{i0}\kern4.9em {v}_i\hfill & \mathrm{s}.\mathrm{t}.\kern.8em {\displaystyle {\sum}_{i=1}^m{v}_i{X}_{i0}}=1/2\hfill \\ {}\kern2em {\displaystyle {\sum}_{j=1}^n{\mu}_j{X}_{hj}^{stage-2}}\le {\theta}^2{X}_{h0}^{stage-2}\kern1em {q}_h\hfill & \kern2em {\displaystyle {\sum}_{h=1}^H{q}_h{X}_{h0}^{stage-2}}=1/2\hfill \\ {}\kern2em {\displaystyle {\sum}_{j=1}^n{\mu}_j{Y}_{rj}}\ge {Y}_{r0}\kern5.5em {u}_r\hfill & \kern2em {\displaystyle {\sum}_{d=1}^D{w}_d{Z}_{dj}}-{\displaystyle {\sum}_{i=1}^m{v}_i{X}_{ij}}\le 0\hfill \\ {}\kern2em {\displaystyle {\sum}_{j=1}^n\left({\lambda}_j-{\mu}_j\right){Z}_{dj}}=0\kern3.4em {w}_d\hfill & \kern2em {\displaystyle {\sum}_{r=1}^s{u}_r{Y}_{rj}}-{\displaystyle {\sum}_{d=1}^D{w}_d{Z}_{dj}}\hfill \\ {}& \kern1.8em -{\displaystyle {\sum}_{h=1}^H{q}_h{X}_{hj}^{stage-2}}\le 0\hfill \\ {}\kern2em {\theta}^1,{\theta}^2\ \mathrm{free}\ \mathrm{in}\ \mathrm{s}\mathrm{ign}.\hfill & \kern2em {w}_d\ \mathrm{free}\ \mathrm{in}\ \mathrm{s}\mathrm{ign}.\hfill \end{array} $$

Since the system efficiency can be defined as ∑  ^s _r = 1 u _r Y _r0/$\Big($∑ ^m _i = 1 v _i X _i0 + ∑ ^H _h = 1 q _h X ^{stage − 2} _h0 $\Big)$, the constraint of the dual should be $\Big($∑ ^m _i = 1 v _i X _i0 + ∑  ^H _h = 1 q _h X ^{stage − 2} _h0 $\Big)$= 1, rather than ∑ ^m _i = 1 v _i X _i0 = 1/2 and ∑ ^H _h = 1 q _h X ^{stage − 2} _h0  = 1/2. This indicates that model (2.14) is too restrictive to provide correct solutions. (The objective function, (θ ¹ + θ ²)/2, intends to represent the system efficiency.) Moreover, the multiplier w _d should be positive. If we take these conditions into consideration, we would require that $\Big($∑ ^m _i = 1 v _i X _i0 + ∑ ^H _h = 1 q _h X ^{stage − 2} _h0 $\Big)$ = 1, or ∑  ^m _i = 1 v _i X _i0 = π and ∑ ^H _h = 1 q _h X ^{stage − 2} _h0  = 1 − π, and w _d to be positive. Then the dual becomes:

$$ \begin{array}{ll} \max {\displaystyle {\sum}_{r=1}^s{u}_r{Y}_{r0}}\kern9.5em \mathrm{dual}\hfill & \min {\theta}^2\hfill \\ {}\mathrm{s}.\mathrm{t}.\kern.6em {\displaystyle {\sum}_{i=1}^m{v}_i{X}_{i0}}=\uppi \kern8em {\theta}^1\hfill & \mathrm{s}.\mathrm{t}.\kern.8em {\displaystyle {\sum}_{j=1}^n{\lambda}_j{X}_{ij}}\le {\theta}^1{X}_{i0}\hfill \\ {}\kern1.8em {\displaystyle {\sum}_{h=1}^H{q}_h{X}_{h0}^{stage-2}}=1-\uppi \kern4em {\theta}^2\hfill & \kern2em {\displaystyle {\sum}_{j=1}^n{\mu}_j{X}_{hj}^2}\le {\theta}^2{X}_{h0}^{stage-2}\hfill \\ {}\kern1.8em {\displaystyle {\sum}_{d=1}^D{w}_d{Z}_{dj}}-{\displaystyle {\sum}_{i=1}^m{v}_i{X}_{ij}}\le 0\kern2em {\lambda}_j\hfill & \kern2em {\theta}^1={\theta}^2\hfill \\ {}\kern1.8em {\displaystyle {\sum}_{r=1}^s{u}_r{Y}_{rj}}-{\displaystyle {\sum}_{d=1}^D{w}_d{Z}_{dj}}\hfill & \\ {}\kern1.6em -{\displaystyle {\sum}_{h=1}^H{q}_h{X}_{hj}^{stage-2}}\le 0\kern1em {\mu}_j& \kern2em {\displaystyle {\sum}_{j=1}^n{\mu}_j{Y}_{rj}}\ge {Y}_{r0}\hfill \\ {}\kern2em \uppi\ \mathrm{free}\ \mathrm{in}\ \mathrm{s}\mathrm{ign}\hfill & \kern2em {\displaystyle {\sum}_{j=1}^n\left({\lambda}_j-{\mu}_j\right){Z}_{dj}}\ge 0\hfill \\ {}\hfill & \kern2em {\theta}^1,{\theta}^2\ \mathrm{free}\ \mathrm{in}\ \mathrm{s}\mathrm{ign}\hfill \end{array} $$

Although, theoretically, π is free in sign, the constraint of ∑ ^m _i = 1 v _i X _i0 = π ensures it to be positive (and so is 1 − π). The dual indicates that θ ¹ and θ ² are equal and do not represent divisional efficiencies, but rather they represent overall system efficiency.

The above discussion indicates that the so-called divisional efficiency scores in the envelopment model are not efficiency scores for divisions under the concept of ratio DEA efficiency, whether the network structure is a simple two-stage process or a general one.

2.7 Conclusions

The current chapter presents several pitfalls in network DEA modeling. We start the discussion with a simple two-stage network structure where only intermediate measures exist between the two stages and the first stage has inputs only and the second stage outputs only. This simple structure allows one to (i) establish an equivalence between the multiplier-based and envelopment-based network DEA models, and (ii) demonstrate the difference between the multiplier-based and envelopment-based network DEA models.

Under a general network structure, we demonstrate that the outcomes from the multiplier and envelopment models are not necessarily equivalent. The divisional efficiency scores obtained from the multiplier model can be infeasible under the envelopment model under the condition of CRS. We demonstrate that the divisional efficiency scores based upon the envelopment model do not necessarily represent divisional efficiencies, and may actually be the overall efficiency. This indicates that cautions needs to be taken when developing a network DEA model using production possibility sets.

It is our view that overall efficiency along with divisional efficiencies should be defined under the DEA multiplier (ratio) model, as in Kao and Hwang (2008) and Liang et al. (2008), for example. Such a definition is related to other definitions of efficiency used in engineering and science, as well as in business and economics. For example, the CCR efficiency was modeled on the definition from “combustion” engineering, where efficiency is defined as “the ratio of actual amount of heat liberated … to the maximum amount which could be liberated” (Charnes et al. (1978)). Many of the business efficiency measures appear in the form of ratios, such as earnings per share and profit per employee.

While in conventional DEA, the envelopment model or the distance function-based efficiency is equivalent to multiplier (ratio) efficiency, in the case of network DEA, the distance function-based envelopment models do not necessarily yield information on divisional efficiency. Although the envelopment network DEA models might give the appearance of providing optimal divisional efficiency, we show that in reality the envelopment efficiency is a measure of overall efficiency.

As a result of the current study, many existing production possibility set-based network DEA models including Tone and Tsutsui’s (2009) slacks-based approach need to be re-examined with respect to their rationale for the (divisional) efficiency definition. Our study indicates that current envelopment models are not able to calculate divisional efficiencies. However, this does not mean that it is impossible to calculate divisional efficiencies by using envelopment models; rather there would appear to be a need to develop new envelopment-based models for accomplishing this task.

Finally, due to the fact that we are not able to obtain multiplier divisional efficiency scores under the condition of VRS (because the resulting model cannot be solved as a linear program), we cannot perform such a comparison under the condition of VRS. Therefore, it is important to develop algorithms that will enable one to derive multiplier-based divisional efficiency under VRS.