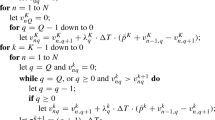Keywords

1 Introduction

Dynamic price optimization, as a branch of revenue management, investigates the price as a key decision variable in a dynamic business environment. In particular, it studies how to “operationalize” pricing decisions by considering additional dimensions like time and inventories. Perhaps the most canonical example is the ground-breaking work by Gallego and van Ryzin (1993) who study the optimal price trajectory based on the actual realization of sales and the length of remaining sales period. Since then, a wide variety of dynamic pricing models came into existence. In those models, demands may be deterministic or stochastic (Gallego and van Ryzin 1993), the set of prices predetermined or arbitrary (Feng and Xiao 2000), the number of price changes limited or unlimited (Feng and Gallego 1995), time continuous or discrete (Dudey 1992), customers strategic or myopic (Aviv and Pazgal 2003), the setting of the game completely known or revealing over time (Lazear 1986), and sellers monopolistic or competing (Belobaba 1987). See Talluri and van Ryzin (2004) or Bitran and Caldency (2003) for an extensive review of the literature.

Competition, although present in almost every real setting, has not received enough attention in the dynamic pricing literature, compared to other aspects. This paper attempts to fill the gap by presenting a stylized model of dynamic markdown competition. We consider two retailers who compete in a market with a fixed level of initial inventory. The initial inventory level is only known to the corresponding retailer, and not to the other. To maximize the profit, each retailer would permanently mark down once at a time of his individual choice. The model assumes deterministic demands, a single chance of price change, and a predetermined set of prices. We consider a two-parameter strategy set where a retailer chooses the timing of markdown as a function of the current time, his inventory level, and the other’s move so far. We characterize the equilibrium of the game and derive managerial insights.

Dynamic markdown competition—where a retailer marks down as a counter to the competitor’s move—is a familiar facet of business practice. Consider, for example, the cut-throat competition in the game device market:

Microsoft cut the price of its Xbox game console by about a third in the U.S. and Canada and announced a similar price cut for Japan Wednesday. The move had been expected by market watchers and comes on the heels of Sony Computer Entertainment America’s price reduction for the PlayStation 2 on Tuesday. Effective immediately, Xbox consoles will cost $199.99 in the U.S., down from $299.99, Microsoft says in a statement. Xbox, Sony’s PlayStation 2, and Nintendo’s GameCube now all cost about $200 in the U.S. In Japan, where Xbox sales have been sluggish since its launch late February, the Xbox will be cut to $193 from $270 effective May 22, Microsoft says. (Evers 2002).

Our model extracts two elements of the business practice captured in the article—the timing of markdown in response to the competitor’s move and based on its own inventory position.

This is not the first research work on dynamic price competition. For example, Dudey (1992) studies a model where two duopolistic firms face multiple customers, one at a time in sequence. For each customer, the two firms simultaneously submit their price quotes, and the customer would take the lower offer so far as the price is lower than her reservation price. Each firm starts with a fixed quantity of inventory, so that the price quote is a function of the time, her own inventory level and the other firm’s inventory level, as well as the customer’s reservation price. Assuming that both firms have complete information of the game (including the evolution of inventory positions), the paper characterizes the equilibrium strategy of each firm.

Varian (1980) and Lal (1990) interpret price promotions as a mixed equilibrium strategy among competing retailers. Lal (1990), for example, considers three retailers, two national brands and one local brand, in a market consisting of switchers and loyals. Loyals are loyal to their preferred national brand, while switchers always buy the cheapest available. The dilemma facing a national brand is that he cannot extract all the surplus from his loyals and win switchers’ market segment, too, due to the threat coming from the local brand. Thus, implicit collusion is supported as a non-cooperative equilibrium, where the two national brands take turns lowering the price in the form of promotion. Hence, the regular price extracts loyals’ surplus, and the promotional price attracts switchers. In a similar market setting, Rao (1991) also studies two retailers—a national brand and a local brand—competing in promotion. Each firm makes a three-stage sequential decision of regular price, promotion depth and promotion frequency. Two firms simultaneously take actions at each stage, and the outcome of the previous stages is jointly observed before moving on to the next stage. They characterize the equilibrium of the multi-stage, multi-decision game with complete information. In the above line of work the players in this game are allowed to change prices, but not as an ex-post counter to the other’s decisions.

Netessine and Shumsky (2004) study horizontal competition in which two airlines compete over “overflow passengers.” Each airline has a fixed capacity and offers two classes, high-fare and low-fare, of seats at two different prices. Each airline faces a random demand to each class, which is exogenously given. Each airline sets a “booking limit” to the number of low-fare seats, so the overflow customers denied tickets at one airline attempt to purchase tickets at the other airline. The paper investigates the strategy of each airline in choosing the booking limit in this non-cooperative game with complete information.

Our model differs from the above work in that it is set up as a non-cooperative game with incomplete information, and players’ strategy is the timing of markdown. The rest of the paper is organized as follows. In Sect. 2 we provide the details of the model. Section 3 analyzes the problem of a monopolistic retailer who would choose the time of markdown in the base model. Section 4 forms the core of the paper where we demonstrate the equilibrium strategies of two duopolistic retailers in choosing the markdown time. The last section concludes with a summary and managerial implications.

2 The Model

Consider a pair of retailers (denoted by i = 1, 2) competing in a seasonal or fashion product market. At time 0, each retailer, facing uncertain demand, orders a fixed quantity of the product, based on his individual forecast. The order arrives before the selling season starts. The two retailers are symmetric in terms of market power and cost structure, but may differ in their forecasts and order quantities. The forecast as well as the order quantity is privately known to the respective retailer. The order quantity by one retailer is viewed to the other as a random variable drawn from a common distribution F over [0, ∞). At time 1 the selling season starts, and the demand rate at each possible pair of retail prices is revealed to both retailers. Retailers have no chance to replenish the stock even if they realize the demand is larger than initially forecasted.

In standard microeconomics, the demand function defines the ‘total’ demand level at each price. It does not capture how the demand materializes across time. To fix this, we introduce a ‘demand trajectory’ that shows the distribution of demand over time. In the present paper we assume a specific demand trajectory in the form of \( {e}^{-\tau / \beta } \) over time τ ∈ [0, ∞), where β( > 0) is the ‘demand rate’ defining the demand intensity. Thus, the demand arriving in the time interval [0, t] is here given by \( {\int}_0^t{e}^{-\tau / \beta }d\tau \) or \( \beta \left[1-{e}^{-t/ \beta}\right] \), and the total demand over the entire season is β. This particular demand trajectory assumes that the demand of the product peaks upon its introduction and exponentially declines over time. Even if the selling season is infinitely long in this setup, the exponential decay (with the right choice of β) will ensure that the demand fades away fast in time, thereby approximating the demand pattern of a seasonal or fashion product. Further, note that the demand realization process has no uncertainties once the demand parameter is revealed. Obviously, it is a strong assumption, but it keeps the analysis tractable. In addition, the deterministic model will serve as an anchor case to stochastic models in developing a heuristic or an upper bound (see Gallego and van Ryzin 1993).

Note that the higher the demand rate β, the slower the demand decays over time and the larger the total demand. β is determined by the prices set by the retailers. Each retailer starts the season with the price set at p 0, but may choose to mark down to p 1(< p 0) at a time of his individual choice. p 0 and p 1 are prefixed prior to the season. This price change would change the demand rates for both retailers. To simplify the notation, let β ij (i, j ∈ {0, 1}) denote the demand rates β facing the retailer whose own price is p i and the other’s is p j . For example, if his price is p 0 and hers is p 1, he faces β 01 and she faces β 10 as the demand rate. We assume that β 10 > β 11 > β 00 > β 01. In case he marks down and she does not, for example, his demand rate β 10 will be the highest of the four cases (due to the combination of a larger market and bigger market share), and hers β 01 will be the lowest. If both mark down, the demand rate β 11 facing each retailer falls somewhere between the two extremes, but will be higher than β 00 the initial demand rate, due to a larger market.

We assume that sales are permanently lost from the market if the retailer visited stocks out. One scenario that supports this assumption is the following: If a potential customer visits a retailer who is out of stock, she will not learn about the existence of the product, so she will not search for it at the other retailer’s. More generally, we assume that stockouts at one retailer’s do not affect the sales at the other retailer’s. This adds another strong assumption that if one stocks out, the current demand intensity continues to hold at the other retailer.

Compared to the existing literature, the present model imposes a series of simplifying assumptions of deterministic demands, a single chance of price change, and a prefixed set of prices. Further, we do not discount cash flow for simplicity, and assume that any unsold items at the end of the season are thrown away at zero salvage value and zero cost. In return, the model highlights the timing of competitive markdowns under asymmetric information (about the initial stock level).

3 The Case of a Monopolistic Retailer

Before we study the case of competition, we first consider a monopolistic retailer who starts the season at price p 0 with the stock level S. Assume that the demand parameter at price p i is β i for i = 0, 1, where p 0 > p 1 and β 0 < β 1. Suppose now that the retailer would choose the time to mark down. The demand trajectory enables us to evaluate the impact of a price change on the season’s overall profit to each retailer and to formulate the markdown-timing problem as follows.

$$ {\displaystyle \underset{t\ge 0}{ \max }}{\int}_0^t{p}_0{e}^{-\tau /{\beta}_0}d\tau +{\int}_t^T{p}_1{e}^{-\tau /{\beta}_1}d\tau ={p}_0{\beta}_0\left(1-{e}^{-t/{\beta}_0}\right)+{p}_1{\beta}_1\left({e}^{-t/{\beta}_1}-{e}^{-T/{\beta}_1}\right), $$
(P1)

where

$$ {\beta}_0\left(1-{e}^{-t/ {\beta}_0}\right)+{\beta}_1\left({e}^{-t/ {\beta}_1}-{e}^{-T/ {\beta}_1}\right)\le S. $$
(15.1)

Inequality (15.1) is the capacity constraint that ensures that total sales do not exceed the initial inventory, where T denotes the time of running out of stock. We assume that T can take the value of infinity, which happens when S is large enough.

We form the Lagrangian function:

$$\begin{array}{lll}{\mathcal{L}\left(t,T,\lambda \right)={p}_0{\beta}_0\left(1-{e}^{-t/ {\beta}_0}\right)+{p}_1{\beta}_1\left({e}^{-t/ {\beta}_1}-{e}^{-T/ {\beta}_1}\right)} \\ \quad\quad\quad\quad\quad-\lambda \left[{\beta}_0\left(1-{e}^{-t/ {\beta}_0}\right)+{\beta}_1\left({e}^{-t/ {\beta}_1}-{e}^{-T/ {\beta}_1}\right)-S\right]\end{array}$$
(P2)

where λ is the Lagrangian multiplier associated with the capacity constraint. After straightforward manipulation, the Kuhn–Tucker theorem yields the following result.

Theorem 1

To the monopolistic retailer with a starting inventory S, the optimal time t ∗ (S) to mark down is given by

$$ {t}^{\ast }(S)=\left\{\begin{array}{cc}\infty, & \mathrm{if}\kern0.5em S<{\beta}_0;\\ {}\frac{\beta_0{\beta}_1}{\beta_1-{\beta}_0}\kern0.5em \ln \kern0.5em \frac{p_0-\lambda (S)}{p_1-\lambda (S)}& \mathrm{if}\kern0.5em {\beta}_0\le S\le {S}^{\ast };\\ {}\frac{\beta_0{\beta}_1}{\beta_1-{\beta}_0}\kern0.5em \ln \kern0.5em \frac{p_0}{p_1}& \mathrm{if}\kern0.5em S>{S}^{\ast },\\ {}\kern2.00em \end{array}\right. $$

where λ(S), the (non-negative) Lagrangian multiplier to the capacity constraint, satisfies

$$ S={\beta}_0\left[1-{\left(\frac{p_1-\lambda (S)}{p_0-\lambda (S)}\right)}^{\frac{\beta_1}{\beta_1-{\beta}_0}}\right]+{\beta}_1{\left(\frac{p_1-\lambda (S)}{p_0-\lambda (S)}\right)}^{\frac{\beta_0}{\beta_1-{\beta}_0}}, $$
(15.2)

and S ∗ is the smallest value of S with λ(S) = 0; that is,

$$ {S}^{\ast }={\beta}_0\left[1-{\left(\frac{p_1}{p_0}\right)}^{\frac{\beta_1}{\beta_1-{\beta}_0}}\right]+{\beta}_1{\left(\frac{p_1}{p_0}\right)}^{\frac{\beta_0}{\beta_1-{\beta}_0}}. $$
(15.3)

Also, β 0 < S ∗ < β 1 .

If the retailer has tight supply, he will never mark down, or equivalently, his optimal markdown time will be infinity. This is because in the absence of cash flow discounting, he has no incentive to mark down if he can sell everything he has even if it takes a long time. The cutoff inventory level is β 0, which is the quantity he can sell without a markdown. Here the choice of the value ∞ is somewhat arbitrary. To be exact, the solution to ( P2) in this range of S is t ∗(S) = T ∗, where T = T ∗ satisfies (15.1) in equality. This means that the retailer marks down at the time he runs out of stock. This is equivalent to the event of no markdown ever (especially as observed by the other retailer if she exists as in later sections), hence comes our choice of infinity. In the other extreme case (i.e., an ample inventory), he cannot sell all he has, so he will maximize his profit by lowering the price at time \( \frac{\beta_0{\beta}_1}{\beta_1-{\beta}_0} \ln \frac{p_0}{p_1} \), which remains constant to any retailer whose inventory level is larger than S ∗. In the middle range of the inventory, the timing of his markdown will depend on the inventory level. The higher the inventory level, the quicker comes the markdown. In this case, the retailer will time the markdown to sell all his inventory. Loosely speaking, t ∗(S) is decreasing in S ∈ [0, ∞).Footnote 1 The monopolist with a high inventory will be more anxious, so he will rush to cut the price to move the volume.

4 Markdown Competition

We now turn to the case of two retailers competing in the choice of markdown timing. The strategy for each retailer is the choice of its markdown time, taking the other retailer’s strategy as given. More specifically, retailer i( = 1, 2) (he) will choose the time \( {\sigma}_i\left({S}_i,{\mathcal{H}}_t\right) \) to mark down, where σ i is not only a function of his private inventory level S i , but also of the history \( {\mathcal{H}}_t \) of the game up until his decision time t. In our model that has assumed away demand uncertainties, the relevant information contained in \( {\mathcal{H}}_t \) is the actions taken by the other retailer j (she) and the current time. The strategy determines in advance what to do in each contingency, as the game evolves and uncertainties are resolved. The strategy will maximize the expected profit at each time point for the rest of the game based on the realized path.

Retailer i’s expected profit depends on his own inventory level S i , as well as retailer j’s strategy σ j that depends on her inventory level S j . To derive his optimal strategy, retailer i must take into account the uncertainties about S j to predict her strategy and develop his own strategy. Our equilibrium concept is similar to Bayesian subgame-perfect equilibrium (Kreps 1990). Further, we restrict our attention to ‘symmetric’ equilibrium in which the two retailers use the same strategy function and play with different arguments.

Now consider the set \(\mathcal{S} =\{\tilde{\sigma } (t_{a},t_{b},\mathcal{H}_{t})\vert 0 \leq t_{a} \leq t_{b}\}\) (or \(\{\tilde{\sigma }(t_{a},t_{b})\}\) for short) of two-parameter strategies for each retailer that operate as follows: “Wait and see if the other retailer marks down; if the latter does before t b , then mark down either immediately or at t a , whichever comes later. If the other does not mark down until t b , then don’t wait any longer and mark down before the other.” When both retailers play strategies in \( \mathcal{S} \), retailer i faces three alternative scenarios depending on retailer j’s markdown time τ. τ may fall in one of the three time intervals I a : = [0, t a ), I b : = [t a , t b ), and I c : = [t b , ∞]. If it falls in I a , retailer i is not “ready” yet, so he will wait and mark down later at t a . If in I b , he will immediately match retailer j’s markdown. In I c , retailer i will move first without further waiting for retailer j’s move.

While this strategy set appears to contain a wide set of plausible actions, it is not exhaustive by any means. For example, one can consider a three-parameter strategy like “Wait and see if the other retailer marks down; if the latter does before t a , then mark down at t′ a ( > t a ). If the latter does after t a but before t b , then mark down at t b . If the other does not mark down until t b , then don’t wait any longer and mark down before the other.” Clearly, this example, although not so convincing on its own, alludes to an infinite number of possible strategy sets, underscoring the fact that \( \mathcal{S} \) is just one of them.

Now retailer i’s decision is to find a pair (t a ∗(S 1), t b ∗(S 1)), or simply (t a ∗, t b ∗), that determine his optimal strategy in \( \mathcal{S} \). To derive t a ∗ first, suppose that the game started at time 0, and soon retailer j marked down at time t in I a . The current demand rate for retailer i is β 01, but his markdown decision would change it to β 11. We now solve

$$ {\displaystyle \underset{t_a\ge t}{ \max }}{\int}_t^{t_a}{p}_0{e}^{-\tau / {\beta}_{01}}d\tau +{\int}_{t_a}^T{p}_1{e}^{-\tau / {\beta}_{11}}d\tau ={p}_0{\beta}_{01}\left(1-{e}^{-{t}_a/ {\beta}_{01}}\right)+{p}_1{\beta}_{11}\left({e}^{-{t}_a/ {\beta}_{11}}-{e}^{-T/ {\beta}_{11}}\right) $$
(P3)

subject to

$$ {\beta}_{01}\left({e}^{-t/ {\beta}_{01}}-{e}^{-{t}_a/ {\beta}_{01}}\right)+{\beta}_{11}\left({e}^{-{t}_a/ {\beta}_{11}}-{e}^{-T/ {\beta}_{11}}\right)\le {S}_i-{\beta}_{00}\left(1-{e}^{-t/ {\beta}_{00}}\right). $$

After adding a constant \( \underset{0}{\overset{t}{\int }}{p}_0{e}^{-\tau / {\beta}_{01}}d\tau \) to the objective and slight modification of the constraint, we have:

$$ {\displaystyle \underset{t_a\ge t}{ \max }}{\int}_0^{t_a}{p}_0{e}^{-\tau / {\beta}_{01}}d\tau +{\int}_{t_a}^T{p}_1{e}^{-\tau / {\beta}_{11}}d\tau ={p}_0{\beta}_{01}\left(1-{e}^{-{t}_a/ {\beta}_{01}}\right)+{p}_1{\beta}_{11}\left({e}^{-{t}_a/ {\beta}_{11}}-{e}^{-T/ {\beta}_{11}}\right) $$
(P3')

subject to

$$ {\beta}_{01}\left(1-{e}^{-{t}_a/ {\beta}_{01}}\right)+{\beta}_{11}\left({e}^{-{t}_a/ {\beta}_{11}}-{e}^{-T/ {\beta}_{11}}\right)\le {S}_{it}, $$

where \( {S}_{it}:={S}_i-\left[{\beta}_{00}\left(1-{e}^{-t/ {\beta}_{00}}\right)-{\beta}_{01}\left(1-{e}^{-t/ {\beta}_{01}}\right)\right]:={S}_i-{\varDelta}_t. \) It is easy to verify that \( {\varDelta}_t \) is positive and monotone increasing in t.

This problem has the same structure as ( P1), with β 0, β 1 and S i replaced by β 01, β 11 and S it . Hence, we have the following solution from Theorem 1.

$$ {t}_a^{\ast }({S}_{it})=\left\{\begin{array}{cc}\infty, \kern2.00em & \mathrm{if}\ {S}_{it}\le {\beta}_{01};\\ {}\frac{\beta_{01}{\beta}_{11}}{\beta_{11}-{\beta}_{01}} \ln\ \frac{p_0-\lambda ({S}_{it})}{p_1-\lambda ({S}_{it})},& \mathrm{if}\ {\beta}_{01}<{S}_{it}<{S}^{\circ };\\ {}\frac{\beta_{01}{\beta}_{11}}{\beta_{11}-{\beta}_{01}} \ln\ \frac{p_0}{p_1},& \mathrm{if}\ {S}_{it}\ge {S}^{\circ },\end{array}\right. $$
(15.4)

where λ(S it ), the (non-negative) Lagrangian multiplier to the capacity constraint, satisfies

$$ {S}_{it}={\beta}_{01}\left[1-{\left(\frac{p_1-\lambda ({S}_{it})}{{\kern.18em p}_0-\lambda ({S}_{it})}\right)}^{\frac{\beta_{11}}{\beta_{11}-{\beta}_{01}}}\right]+{\beta}_{11}{\left(\frac{p_1-\lambda ({S}_{it})}{p_0-\lambda ({S}_{it})}\right)}^{\frac{\beta_{01}}{\beta_{11}-{\beta}_{01}}}, $$
(15.5)

and

$$ {S}^{\circ }={\beta}_{01}\left[1-{\left(\frac{p_1}{p_0}\right)}^{\frac{\beta_{11}}{\beta_{11}-{\beta}_{01}}}\right]+{\beta}_{11}{\left(\frac{p_1}{p_0}\right)}^{\frac{\beta_{01}}{\beta_{11}-{\beta}_{01}}}. $$
(15.6)

Also, note that β 01 < S ∘ < β 11.

Suppose now that the time point t a ∗ has passed without retailer j’s move. The new time interval I b starts, so retailer i will immediately adopt if the other marks down. But if she does not, retailer i cannot wait forever for her move, so he faces the problem of choosing “the preemptive markdown time” t b , i.e., the time to stop waiting and mark down first.

To find the optimal t b ∗, we first introduce some notation. For the moment, assume that t b ∗(⋅ ) is monotone decreasing. Let G(τ) denote the probability of the other retailer marking down by time τ, with \( \overline{G}\left(\tau \right):=1-G\left(\tau \right) \) and g(τ): = G′(τ). Also let \( {\overline{G}}^o\left(\tau \Big|t\right) \) denote the probability that retailer j will mark down later than time τ on the condition that she has not marked down until time t; i.e., \( {\overline{G}}^o(\tau |t):=1-{G}^o(\tau |t)=\overline{G}(\tau )/ \overline{G}(t) \), for τ ≥ t. Let g o and g respectively denote the probability density (or frequency) function of G o and G.

At time t( > t a ∗), retailer i will choose t b ∗ by solving the following ( P4):

$$ \begin{array}{l}{\displaystyle \underset{t_b\ge t}{ \max }{\int}_t^{t_b^{-}}}\left[{p}_0{\beta}_{00}\left({e}^{-t/ {\beta}_{00}}-{e}^{-\tau / {\beta}_{00}}\right)+{p}_1{\beta}_{11}\left({e}^{-\tau / {\beta}_{11}}-{e}^{-{T}_1(\tau )/ {\beta}_{11}}\right)\right]d{G}^{\circ}\left(\tau |t\right)\\ {}\kern1em +\left[{p}_0{\beta}_{00}\left({e}^{-t/ {\beta}_{00}}-{e}^{-{t}_b/ {\beta}_{00}}\right)+{p}_1{\beta}_{11}\left({e}^{-{t}_b/ {\beta}_{11}}-{e}^{-{T}_2/ {\beta}_{11}}\right)\right]{g}^{\circ }({t}_b|t)\\ {}\kern1em +{\int}_{t_b^{+}}^{\infty}\left[{p}_0{\beta}_{00}\left({e}^{-t/ {\beta}_{00}}-{e}^{-{t}_b/ {\beta}_{00}}\right)+{p}_1{\beta}_{10}\left({e}^{-{t}_b/ {\beta}_{10}}-{e}^{-\tau / {\beta}_{10}}\right)\right.\\ {}\kern1em +\kern0.15em \left.{p}_1{\beta}_{11}\left({e}^{-\tau / {\beta}_{11}}-{e}^{-{T}_3\left(\tau \right)/ {\beta}_{11}}\right)\right]d{G}^{\circ}\left(\tau |t\right)\\ {}\kern1em +\left[{p}_0{\beta}_{00}\left({e}^{-t/ {\beta}_{00}}-{e}^{-{t}_b/ {\beta}_{00}}\right)+{p}_1{\beta}_{10}\left({e}^{-{t}_b/ {\beta}_{10}}-{e}^{-{T}_4/ {\beta}_{10}}\right)\right]{g}^{\circ }(\infty |t),\end{array} $$
(P4)

subject to the following capacity constraints

$$ \begin{array}{c}\kern4.00em {\beta}_{00}(1-{e}^{-\tau / {\beta}_{00}})+{\beta}_{11}({e}^{-\tau / {\beta}_{11}}-{e}^{-{T}_1(\tau )/ {\beta}_{11}})\le {S}_i,\kern5.55pt \forall \tau \in [t,{t}_b)\\ {}\kern7.00em {\beta}_{00}(1-{e}^{-{t}_b/ {\beta}_{00}})+{\beta}_{11}({e}^{-{t}_b/ {\beta}_{11}}-{e}^{-{T}_2/ {\beta}_{11}})\le {S}_i\\ {}{\beta}_{00}(1-{e}^{-{t}_b/ {\beta}_{00}})+{\beta}_{10}({e}^{-{t}_b/ {\beta}_{10}}-{e}^{-\tau / {\beta}_{10}})+{\beta}_{11}({e}^{-\tau / {\beta}_{11}}-{e}^{-{T}_3(\tau )/ {\beta}_{11}})\le {S}_i,\forall \tau \in ({t}_b,\infty )\\ {}\kern7.00em {\beta}_{00}(1-{e}^{-{t}_b/ {\beta}_{00}})+{\beta}_{10}({e}^{-{t}_b/ {\beta}_{10}}-{e}^{-{T}_4/ {\beta}_{10}})\le {S}_i.\end{array} $$

In the above, T i (i = 1, 2, 3, 4) represents the time to run out of inventory under four different scenarios; T 1(τ) is the time to run out of stock when both retailers mark down at time τ ∈ [0, τ b ), T 2 when both mark down at t b , T 3(τ) when i first marks down at t b and j follows at τ ∈ (t b , ∞), and T 4 when i first marks down at t b and j does not follow. The objective function in ( P4) represents the expected profit to retailer i when he plays \(\tilde{\sigma }_{i}(t_{a}^{{\ast}},t_{b})\) while retailer j plays \(\tilde{\sigma }_{j}(t_{a}^{{\ast}},t_{b}^{{\ast}})\).

Note that G can be derived from the distribution of random variables S j via t a ∗(⋅ ) and t b ∗(⋅ ), and is a mixed (i.e., continuous and discrete) distribution. Regrettably, ( P4) is very difficult to solve. One way to tackle the problem is to form a Lagrangian and obtain its saddle point (Luenberger 1969). To derive the equilibrium strategy, we obtain the FOC of the Lagrangian for ( P4), and then invoke the symmetric equilibrium assumption, so retailer i’s choice of t b should be equal to retailer j’s optimal t b ∗, hence \( {t}_b^{\ast^{-1}}\left({t}_b\right)={t}_b^{\ast^{-1}}\left({t}_b^{\ast}\left({S}_i\right)\right)={S}_i \). Then, we have (see the details in the Appendix):

$$ \begin{array}{c}\left({p}_0{e}^{-{t}_b^{\ast}/ {\beta}_{00}}-{p}_1{e}^{-{t}_b^{\ast}/ {\beta}_{11}}\right)F\left({S}_i\right)+{p}_1\left({e}^{-{t}_b^{\ast}/ {\beta}_{11}}-{e}^{-{t}_b^{\ast}/ {\beta}_{10}}\right)F\left({t}_a^{\ast^{-1}}\left({t}_b^{\ast}\right)+{\varDelta}_{t_b}\right)\\ {}\kern1em -{\lambda}_1\left({t}_b^{\ast}\right)\left[{\beta}_{00}\left(1-{e}^{-{t}_b^{\ast}/ {\beta}_{10}}\right)-{\beta}_{11}\left({e}^{-{t}_b^{\ast}/ {\beta}_{11}}-{e}^{-{T}_1\left({t}_b^{\ast}\right)/ {\beta}_{11}}\right)-{S}_i\right]\\ {}\kern1em -{\lambda}_2^{\prime}\left({t}_b^{\ast}\right)\left[{\beta}_{10}\left(1-{e}^{-{t}_b^{\ast}/ {\beta}_{10}}\right)-{\beta}_{11}\left({e}^{-{t}_b^{\ast}/ {\beta}_{11}}-{e}^{-{T}_2/ {\beta}_{11}}\right)-{S}_i\right]\\ {}\kern1em -{\lambda}_2\left({t}_b^{\ast}\right)\left({e}^{-{t}_b^{\ast}/ {\beta}_{10}}-{e}^{-{T}_2/ {\beta}_{11}}\right)\\ {}\kern1em +{\lambda}_3\left({t}_b^{\ast}\right)\left[{\beta}_{00}\left(1-{e}^{-{t}_b^{\ast}/ {\beta}_{10}}\right)+{\beta}_{11}\left({e}^{-{t}_b^{\ast}/ {\beta}_{11}}-{e}^{-{T}_3\left({t}_b^{\ast}\right)/ {\beta}_{11}}\right)\right]\\ {}\kern1em -{\overline{\varLambda}}_3\left({t}_b^{\ast}\right)\left({e}^{-{t}_b^{\ast}/ {\beta}_{00}}-{e}^{-{t}_b^{\ast}/ {\beta}_{10}}\right)+\left({p}_0{e}^{-{t}_b^{\ast}/ {\beta}_{00}}-{p}_1{e}^{-{t}_b^{\ast}/ {\beta}_{10}}\right)F\left({\beta}_{01}\right)\\ {}\kern1em +{\lambda}_4\left({t}_b^{\ast}\right)\left[{\beta}_{00}\left(1-{e}^{-{t}_b^{\ast}/ {\beta}_{00}}\right)+{\beta}_{10}\left({e}^{-{t}_b^{\ast}/ {\beta}_{10}}-{e}^{-{T}_4/ {\beta}_{10}}\right)-{S}_i\right]=0.\end{array} $$
(15.7)

A corner solution to ( P4) occurs when retailer i has an initial inventory less than β 01. He would ultimately sell out even at the regular price, so he would never mark down, or his markdown time will be infinity.

Hence, the following theorem summarizes the equilibrium.

Theorem 2

Consider the set \(\mathcal{S} =\{\tilde{\sigma } (t_{a},t_{b},\mathcal{H}_{t})\vert 0 \leq t_{a} \leq t_{b}\}\) of two-parameter strategies for each retailer that operate as follows: “Wait and see if the other retailer marks down; if the latter does before t b , then mark down either immediately or at t a , whichever comes later. If the other does not mark down until t b , then don’t wait any longer and mark down before the other.” Let

$$ {t}_a^{\ast }({S}_{it})=\left\{\begin{array}{cc}\infty, \kern2.00em & \mathrm{if}\ {S}_{it}\le {\beta}_{01};\\ {}\frac{\beta_{01}{\beta}_{11}}{\beta_{11}-{\beta}_{01}} \ln\ \frac{p_0-\lambda ({S}_{it})}{p_1-\lambda ({S}_{it})},& \mathrm{if}\ {\beta}_{01}<{S}_{it}<{S}^{\circ };\\ {}\frac{\beta_{01}{\beta}_{11}}{\beta_{11}-{\beta}_{01}} \ln\ \frac{p_0}{p_1},\kern1em & \mathrm{if}\ {S}_{it}\ge {S}^{\circ },\end{array}\right. $$
(15.4)

where λ(S it ), the (non-negative) Lagrangian multiplier to the capacity constraint, satisfies

$$ {S}_{it}={\beta}_{01}\left[1-{\left(\frac{p_1-\lambda \left({S}_{it}\right)}{p_0-\lambda \left({S}_{it}\right)}\right)}^{\frac{\beta_{11}}{\beta_{11}-{\beta}_{01}}}\right]+{\beta}_{11}{\left(\frac{p_1-\lambda \left({S}_{it}\right)}{p_0-\lambda \left({S}_{it}\right)}\right)}^{\frac{\beta_{01}}{\beta_{11}-{\beta}_{01}}}, $$

and

$$ {S}^{\circ }={\beta}_{01}\left[1-{\left(\frac{p_1}{p_0}\right)}^{\frac{\beta_{11}}{\beta_{11}-{\beta}_{01}}}\right]+{\beta}_{11}{\left(\frac{p_1}{p_0}\right)}^{\frac{\beta_{01}}{\beta_{11}-{\beta}_{01}}}. $$

And, let

$$ {t}_b^{\ast }({S}_i)=\left\{\begin{array}{cc}\infty, \kern2.00em & if\ {S}_i\le {\beta}_{01};\\ {}{B}^{\ast }({S}_i),& \mathit{\mathrm{otherwise},}\end{array}\right. $$

where B = B ∗ (S i ) satisfies ( 15.7 ). If B ∗ (⋅) is monotone decreasing and \( {t}_b^{\ast }(S)\ge {t}_a^{\ast}\left(S-{\varDelta}_t\right) \) for each t, S ∈ [0,∞), then \(\tilde{\sigma }_{i}(t_{a}^{{\ast}},t_{b}^{{\ast}})\) forms the equilibrium in \( \mathcal{S} \) of the markdown game.

The equilibrium is depicted in Figs. 15.1 and 15.2. Each instance of initial inventory S determines the two parameters (t a ∗, t b ∗), which in turn define his markdown strategy. As an example, suppose two retailers 1 and 2 start with inventory positions S 1 and S 2, respectively, as shown in Fig. 15.1. At the beginning both retailers sell at the regular price p 0. As time passes (moving up in the Y axis on the figure), retailer 2 with a higher inventory S 2 reaches the time point t b ∗(S 2) and marks down to price p 1. Let t: = t b ∗(S 2). Since \( {t}_a^{\ast}\left({S}_1-{\varDelta}_t\right)>t \) in the figure, retailer 1 does not immediately match the markdown, but instead waits until \( {t}_a^{\ast}\left({S}_1-{\varDelta}_t\right) \) and marks down. Thus, the two markdowns will be separated by some time. Now consider another pair of retailers that start with inventory levels S 1 and S′2 as in Fig. 15.2. Again, retailer 2 moves first at time t b ∗(S′2): = t′. But this time \( {t}_a^{\ast}\left({S}_1-{\varDelta}_{t^{\prime }}\right)<{t}^{\prime } \), so retailer 1 will immediately follow the markdown. This is the case where markdowns are “clustered” around the same time. The first mover disturbs the status quo to the other, who is then forced to take a mitigating action.

Fig. 15.1
figure 1

Equilibrium for markdown competition—case 1

Full size image
Fig. 15.2
figure 2

Equilibrium for markdown competition—case 2

Full size image

5 Managerial Implications and Conclusion

The paper studies how two retailers compete in choosing markdown times. We have restricted our search to a set \( \mathcal{S} \) of two-parameter strategies that capture a lot of plausible behaviors. The equilibrium strategy is a function of three elements—the competitor’s move so far, the current time (relative to t a ∗ and t b ∗), and his own inventory level (captured through \( {t}_a^{\ast}\left({S}_i-{\varDelta}_t\right) \)). In our deterministic model, the latter two are overlapping. In equilibrium one retailer’s markdown may prompt the other to match instantaneously, especially if the latter has a large inventory and the selling season is almost over (e.g., S it is large and λ is zero). Unfortunately, we could not obtain a closed-form solution to one parameter t b ∗, but the structure of the solution provides several managerial insights.

First, the markdown policy has a direct impact on its preceding inventory decisions. One can view the inventory and markdown decisions together as a bigger sequential game—first considering the subgame ( P4) of markdown competition, and then rolling up the solution to the inventory decision. That is, one should solve the following inventory-markdown integrated problem:

$$\displaystyle{ \max _{S}\Pi (\tilde{\sigma }(t_{a}^{{\ast}}(S),t_{ b}^{{\ast}}(S)) - C(S), }$$
(P5)

where \(\Pi (\tilde{\sigma }(t_{a}^{{\ast}}(S),t_{b}^{{\ast}}(S))\) is the expected profit under the optimal strategy \(\tilde{\sigma }(t_{a}^{{\ast}}(S),t_{b}^{{\ast}}(S))\) [solving ( P4)], and C(S) is the cost of procuring S. This may lead to larger or smaller inventory levels than the traditional newsvendor solution, depending on model parameters. On the one hand, the unit margin or the underage cost is not as high as the newsvendor operation without a markup, so the optimal inventory level will be smaller than the newsvendor solution. On the other hand, however, the demand will be higher at a marked-down price. Hence, the retailer who is willing to mark down if necessary may possibly choose a larger-than-newsvendor inventory level if the markdown still grants the retailer a positive margin.

Second, we anticipate that markdowns will be frequently clustered around a certain time. Note in Fig. 15.2 that clustering happens when the two retailers start with similar levels of inventory. Since their demand signals are likely to be positively correlated or if they have a uni-modal density function like the normal distribution, they will order similar quantities, so clustering of markdowns will be more likely. See Gul and Lundholm (1995) and its references for other instances of clustering.

Third, the present work proposes an alternative model of price dispersion. Economists have long studied various models of price dispersion as a deviation from the traditional “law of one price” (see Varian 1980 and its references). For example, Varian (1980) (plus its Errata, Varian 1981) analyzes the competition among n retailers facing two types of customers—informed and uninformed. Informed customers know the price distribution of a certain item and purchase the item at the store with the lowest price. Uninformed customers randomly choose a store and buy the item there if the price is lower than her reservation price. Each store’s strategy is the assignment of probabilities to different prices to charge. Varian demonstrates, among others, that no symmetric equilibrium exists where all stores charge the same price, and even strongly, that there would be no point masses in the equilibrium pricing strategies. Thus, price-randomization is the only equilibrium, hence arises price dispersion. Our model presents another possibility of price dispersion. It differs from Varian in two major ways (besides other differences like permanent vs. temporary price changes, and information asymmetry vs. symmetry). First, the model allows a retailer to choose a dynamic strategy of taking, or not taking, an action upon observing the other’s move, while each retailer in Varian sets a price randomly drawn from a pre-determined density function. The difference boils down to whether retailers can monitor each other’s price. Obviously, it will vary across different markets and products, but given the Internet and the mass media, prices are getting easier to monitor these days.

The other key difference of our model it that it captures the inventory position as a driver of price dispersion. Note from the figures that the retailer’s markdown time is a decreasing function of his initial inventory position. Markdown happens either on its own initiative (due to a high inventory level and a disappointing demand rate) or motivated by the competitor’s markdown. In either case, competition redirects the market demand from one retailer with a low inventory to another with a high inventory. On the one hand, it is similar to the behavior of a monopolist who “shapes demands” across different products by dynamically adjusting the prices of two products to shift the demand away from a low-stock product to a high-stock product. But markdown competition would enhance economic efficiency by achieving inventory pooling. Note this happens in a decentralized manner and despite informational asymmetry—as envisioned by Hayek (1945) (who assumed there is “only one price for any commodity” in one market). Unfortunately, for lack of a consumer choice model, our model would be insufficient to formally investigate the efficiency issue.

Fourth and last, note from Fig. 15.1 or Theorem 2 that a markdown will happen only after a certain time A ∗ \( (:=\frac{\beta_{01}{\beta}_{11}}{\beta_{11}-{\beta}_{01}} \ln \frac{p_0}{p_1}) \). This comes from two observations: (1) the preemptive markdown time t b ∗(⋅ ) is a decreasing function of the initial inventory level, and (2) even if a retailer has a lot of inventory (larger than S ∘), his optimal markdown time remains at A ∗. This seems consistent with our perception that markdowns are what we expect towards the end of lifecycle.

The paper deliberately took a minimalist approach, loaded with a series of simplifying assumptions. Relaxation of these assumptions (e.g., deterministic demand) would be desirable. But given that we could not obtain any crisp results from the present simple model, I would rather hope to see a model that is even simpler and yet insightful, or empirical study that would supplement our modeling approach.